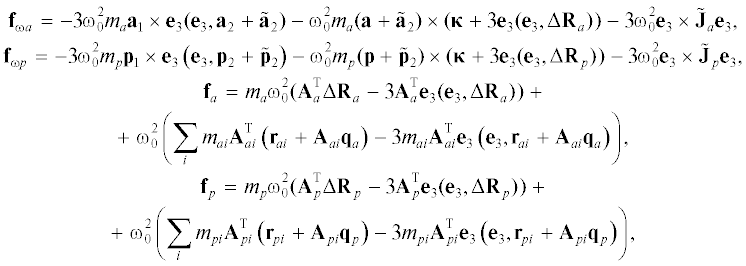Известия РАН. Теория и системы управления, 2019, № 3, стр. 147-163
Алгоритмы стабилизации космического аппарата с нежесткими элементами
М. Ю. Овчинников a, С. С. Ткачев a, А. И. Шестопёров a, *
a ИПМ им. М.В. Келдыша РАН
Москва, Россия
* E-mail: alex.shestoperov@yandex.ru
Поступила в редакцию 06.11.2018
После доработки 21.12.2018
Принята к публикации 28.01.2019
Аннотация
Изучаются методы стабилизации корпуса космического аппарата с двумя нежесткими элементами – антенной и панелью. Процессу стабилизации корпуса препятствуют вибрации, возникающие в нежестких элементах в ходе орбитального и углового маневрирования космического аппарата и ухудшающие точность его ориентации. Поэтому исследуемые методы также рассматриваются в контексте задачи гашения колебаний в нежестких элементах. Рассматриваются как классические методы управления – ляпуновское управление и линейно-квадратичное управление, так и набирающее популярность SDRE-управление (State Dependent Riccati Equation Control), использующее уравнение Риккати с параметрами, зависящими от вектора состояния. Также описываются алгоритмы управления, в основе которых лежит редуцированная модель космического аппарата с нежесткими элементами. При этом полагается, что управление космическим аппаратом с нежесткими элементами осуществляется только при помощи устройств, расположенных на его корпусе.
Введение. Одной из основных целей управления космическим аппаратом (КА) является задача стабилизации его корпуса в заданном угловом положении.
При разработке алгоритмов стабилизации часто предполагается, что КА – твердое тело, однако многие аппараты требуют иного подхода к моделированию их движения [1, 2]. К таковым, например, относятся телекоммуникационные аппараты с антеннами большого размера, аппараты исследования дальнего космоса с большими солнечными панелями, аппараты с роботизированными манипуляторами и выносными штангами. Отличительной особенностью указанных аппаратов является наличие в их конструкции нежестких элементов (НЭ) большой протяженности, которые зачастую изготавливаются из легких материалов. В ходе орбитального и углового маневрирования КА в НЭ возникают колебания, способные не только ухудшать точность ориентации всего аппарата, но даже приводить к неустойчивости требуемых режимов движения. Таким образом, в случае КА с НЭ задача стабилизации корпуса КА напрямую связана с задачей гашения колебаний в НЭ.
В [3–5] приводится обзор методов управления КА с НЭ. Стоит отметить, что в основе большинства методов лежат ставшие классическими ляпуновское управление и линейно-квадратичное управление (ЛКУ).
В данной работе на примере модели КА с НЭ исследуется возможность применения вышеуказанных классических методов управления для решения задач стабилизации корпуса КА в заданном угловом положении и гашения колебаний в НЭ. Также рассмотрен один из быстроразвивающихся методов управления нелинейными системами, SDRE-управление [6, 7]. Большая размерность вектора состояния системы вынуждает использовать алгоритмы, способные работать на основе редуцированной модели движения КА. Применяя метод редукции, предложенный в работах [8, 9], ЛКУ и SDRE-управление строятся на основе уравнений углового движения его корпуса.
Заметим, что для гашения колебаний в НЭ требуется, вообще говоря, установка демпфирующих устройств. Для этого могут быть использованы пьезоэлектрические устройства [10], крепящиеся на НЭ. Однако практический интерес представляет задача, когда управление КА осуществляется только при помощи актюаторов, расположенных на корпусе КА. Указанное требование является важнейшей особенностью модели КА, рассматриваемого в работе.
1. Постановка задачи и модели движения КА с НЭ. Изучается движение КА, состоящего из трех тел: корпуса – твердого тела и двух НЭ, вокруг его центра масс в центральном ньютоновом гравитационном поле Земли. Центр масс КА движется по геостационарной орбите. В качестве НЭ выступают панель и антенна. Панель, закрепленная с помощью одностепенного шарнира, вращается с постоянной угловой скоростью. Антенна закреплена консольно.
Требуется построить управление, стабилизирующее корпус аппарата в заданном угловом положении в инерциальном пространстве. Основным фактором, препятствующим стабилизации КА, являются колебания его нежестких элементов, поэтому в совокупности с основной задачей требуется минимизировать их влияние на точность ориентации КА.
Управление КА осуществляется только при помощи маховиков, расположенных на корпусе КА.
1.1. Системы координат. В работе используются следующие правые декартовы системы координат:
$OXYZ$ – инерциальная система координат, ее начало лежит в центре масс Земли $O$, ось $OZ$ перпендикулярна плоскости экватора, $OX$ направлена на точку весеннего равноденствия;
${{O}_{s}}xyz$ – связанная с корпусом КА система координат, ее начало лежит в центре масс корпуса спутника, оси – его главные центральные оси;
${{O}_{a}}{{x}_{a}}{{y}_{a}}{{z}_{a}}$ – связанная с антенной система координат, ее начало расположено в точке крепления антенны к корпусу спутника, оси – главные оси инерции для недеформированной антенны;
${{O}_{p}}{{x}_{p}}{{y}_{p}}{{z}_{p}}$ – связанная с панелью система координат, ее начало помещается в точке крепления к шарниру, оси – главные оси инерции для недеформированной панели;
${{O}_{p}}{{\xi }_{p}}{{\eta }_{p}}{{\zeta }_{p}}$ – связанная с шарниром система координат, ось ${{O}_{p}}{{\xi }_{p}}$ – ось поворота в шарнире, две другие перпендикулярны ей.
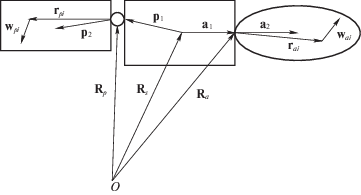
1.2. Модель движения КА с НЭ. Элементарные точечные i-е массы корпуса, антенны и панели задаются относительно центра масс Земли соответственно векторами ${{{\mathbf{R}}}_{{si}}}$, ${{{\mathbf{R}}}_{{ai}}}$, ${{{\mathbf{R}}}_{{pi}}}$ (индекс s соответствует корпусу спутника, a – антенне, p – панели, см. рис. 1):
Смещение точки P НЭ относительно ее недеформированного положения представляется в виде бесконечного ряда [1]
Так как величины ${{{\mathbf{p}}}_{1}}$ и ${{{\mathbf{a}}}_{1}}$ естественно задавать в системе координат ${{O}_{s}}xyz$; ${{{\mathbf{p}}}_{2}}$, ${{{\mathbf{r}}}_{{pi}}}$ и ${{w}_{{pi}}}$ – в системе ${{O}_{p}}{{x}_{p}}{{y}_{p}}{{z}_{p}}$; ${{{\mathbf{a}}}_{2}}$, ${{{\mathbf{r}}}_{{ai}}}$ и ${{w}_{{ai}}}$ – в системе ${{O}_{a}}{{x}_{a}}{{y}_{a}}{{z}_{a}}$, то при выводе уравнений движения все векторы должны быть записаны в одной системе координат, в качестве которой взята система ${{O}_{s}}xyz$. Соответствующие матрицы перехода опущены, чтобы не усложнять записи.
Будем использовать следующие обозначения и формулы: ${{m}_{s}}$ – масса тела корпуса КА; ${{m}_{{si}}}$ – масса i-й точки корпуса КА; mp – масса панели; ${{m}_{{pi}}}$ – масса i-й точки панели; ${{m}_{a}}$ – масса антенны; ${{m}_{{ai}}}$ – масса i-й точки тела антенны; $m = {{m}_{s}} + {{m}_{p}} + {{m}_{a}}$ – суммарная масса КА с НЭ; ${{({{\lambda }_{0}},{{{\mathbf{\lambda }}}^{Т }})}^{Т }}$ – кватернион ориентации; ${\mathbf{\omega }}$ – абсолютная угловая скорость корпуса КА; ${{{\mathbf{e}}}_{p}}$ – единичный вектор оси шарнира; ${{{\mathbf{\omega }}}_{p}} = {\mathbf{\omega }} + {{{\mathbf{e}}}_{p}}{{\psi }_{0}}$ – абсолютная угловая скорость панели, где ${{\psi }_{0}} = const$– угловая скорость поворота панели в шарнире; qa, qp – амплитуды собственных мод колебаний антенны и панели; ${{\tilde {p}}_{2}}$ – смещение центра масс панели за счет ее деформации, которое определяется выражением
Для вывода уравнений движения КА в работе используется процедура, описанная в [2]. Математическая модель движения рассматриваемого аппарата имеет вид
(1.1)
${\mathbf{S}}\left( {\begin{array}{*{20}{c}} {{\mathbf{\dot {\omega }}}} \\ {{{{{\mathbf{\ddot {q}}}}}_{a}}} \\ {{{{{\mathbf{\ddot {q}}}}}_{p}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - {\mathbf{\omega }} \times {{{\mathbf{J}}}_{s}}{\mathbf{\omega }} + {{{\mathbf{T}}}_{s}} - {{{\mathbf{N}}}_{{\omega a}}} - {{{\mathbf{f}}}_{{\omega a}}} - {{{\mathbf{N}}}_{{\omega p}}} - {{{\mathbf{f}}}_{{\omega p}}}} \\ { - {{{\mathbf{f}}}_{a}} - {{{\mathbf{N}}}_{a}}} \\ { - {{{\mathbf{f}}}_{p}} - {{{\mathbf{N}}}_{p}}} \end{array}} \right),$Предполагается, что на КА действуют только силы гравитации. Слагаемые в (1.1), описывающие воздействие гравитации на НЭ КА, представляются как
где введены обозначенияВлияние гравитации на угловое движение КА с НЭ определяется моментом
(1.3)
${\mathbf{T}} = 3\omega _{0}^{2}{{{\mathbf{e}}}_{3}} \times {{{\mathbf{J}}}_{s}}{{{\mathbf{e}}}_{3}} - {{{\mathbf{f}}}_{{\omega a}}} - {{{\mathbf{f}}}_{{\omega p}}} = 3\omega _{0}^{2}{{{\mathbf{e}}}_{3}} \times {\mathbf{J}}{{{\mathbf{e}}}_{3}}.$Ориентация корпуса аппарата задается параметрами Родрига–Гамильтона ${{\left( {{{\lambda }_{0}},{\mathbf{\lambda }}} \right)}^{{\text{T}}}}$, которые подчиняются следующим кинематическим соотношениям:
(1.4)
$\begin{gathered} {{{\dot {\lambda }}}_{0}} = - \frac{1}{2}\left( {{\mathbf{\omega }},\,{\mathbf{\lambda }}} \right), \\ {\mathbf{\dot {\lambda }}} = \frac{1}{2}\left( {{{\lambda }_{0}}{\mathbf{\omega }} + {\mathbf{\lambda }} \times {\mathbf{\omega }}} \right). \\ \end{gathered} $Уравнения движения (1.1) в совокупности с кинематическими соотношениями (1.4) используются при моделировании движения КА с НЭ.
1.3. Модели движения, использующиеся при построении управления. При построении законов управления полагается, что величина управляющего момента много больше величины гравитационного момента. Без учета влияния последнего нелинейная модель движения, использующаяся при построении управления, принимает следующий вид:
(1.5)
$\begin{gathered} {\mathbf{\dot {\omega }}} = - {{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}}{{({\mathbf{M}} - {\mathbf{S}}_{q}^{T}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}^{{ - 1}}}( - {{{\mathbf{N}}}_{q}} - {\mathbf{\Omega q}}) + {{{\mathbf{J}}}^{{ - 1}}}({{{\mathbf{E}}}_{{3 \times 3}}} + {{{\mathbf{S}}}_{q}}{{({\mathbf{M}} - {\mathbf{S}}_{q}^{T}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}^{{ - 1}}}{\mathbf{S}}_{q}^{T}{{{\mathbf{J}}}^{{ - 1}}})( - {{{\mathbf{N}}}_{\omega }} + {\mathbf{u}}), \\ {{{{\mathbf{\dot {V}}}}}_{q}} = {{({\mathbf{M}} - {\mathbf{S}}_{q}^{T}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}^{{ - 1}}}\left( { - {{{\mathbf{N}}}_{q}} - {\mathbf{\Omega q}}} \right) - {{({\mathbf{M}} - {\mathbf{S}}_{q}^{T}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}^{{ - 1}}}{\mathbf{S}}_{q}^{T}{{{\mathbf{J}}}^{{ - 1}}}\left( { - {{{\mathbf{N}}}_{\omega }} + {\mathbf{u}}} \right), \\ {{{\dot {\lambda }}}_{0}} = - \frac{1}{2}\left( {{\mathbf{\omega }},{\mathbf{\lambda }}} \right), \\ {\mathbf{\dot {\lambda }}} = \frac{1}{2}\left( {{{\lambda }_{0}}{\mathbf{\omega }} + {\mathbf{\lambda }} \times {\mathbf{\omega }}} \right), \\ {\mathbf{\dot {q}}} = {{{\mathbf{V}}}_{q}}. \\ \end{gathered} $Здесь $u = {{{\mathbf{T}}}_{s}}$ – вектор, содержащий только управляющие воздействия, ${\mathbf{q}} = {{({\mathbf{q}}_{a}^{T},{\mathbf{q}}_{p}^{T})}^{T}}$ – вектор амплитуд колебательных мод НЭ,
Требуемое угловое положение задается кватернионом ориентации, который полагается равным ${{(1,{{0}^{T}})}^{T}}$. Если КА находится в окрестности этого положения, для построения закона управления используют линеаризацию уравнений (1.5), что можно записать в виде системы
где ${\mathbf{x}} = {{(\begin{array}{*{20}{c}} {{{{\mathbf{\omega }}}^{T}}}&{{{{\mathbf{\lambda }}}^{T}}}&{{\mathbf{V}}_{q}^{T}}&{{{q}^{T}}} \end{array})}^{T}}$ – вектор состояния КА с НЭ, а постоянные матрицы A и B равны:Особенностью задачи построения управления КА с НЭ на основе (1.6) является большая размерность вектора состояния x. Действительно, вектор x имеет размерность $2\left( {3 + {{n}_{a}} + {{n}_{p}}} \right)$, где ${{n}_{a}}$ и ${{n}_{p}}$ – число колебательных мод антенны и панели, учтенных в модели КА с НЭ соответственно. Чем больше размерность вектора q(t), тем точнее задана модель движения. Однако рост размерности вектора q(t) приводит к увеличению вычислительной сложности алгоритмов управления, использующих матрицу системы A размерности $2(3 + {{n}_{a}} + {{n}_{p}}) \times 2(3 + {{n}_{a}} + {{n}_{p}})$. Решением данной проблемы служат алгоритмы, построенные на основе редуцированной модели движения.
2. Алгоритмы управления КА с НЭ. В данном разделе приводятся методики управления, главной целью которых является задача стабилизации корпуса КА в заданном угловом положении. Для решения задачи используются управляющие устройства, расположенные только на корпусе аппарата, а именно набор маховиков. При этом дополнительно необходимо учитывать ограничения на величину управления.
Как отмечалось ранее, наличие НЭ в конструкции КА накладывает требования на разрабатываемые алгоритмы управления. Во-первых, они должны гасить вибрации в НЭ (или как минимум предотвращать увеличение их амплитуд), которые негативно влияют на точность ориентации КА. Во-вторых, для построения законов, основанных на линейной модели движения (1.6), зачастую требуется ее редукция. Особый интерес вызывают законы управления, не требующие знания амплитуд q(t) колебательных мод.
В первую очередь исследуется возможность использования для решения задачи стабилизации классических методов управления: ляпуновского управления и ЛКУ.
2.1. Ляпуновское управление. Ляпуновское управление строится на основе нелинейной модели движения КА с НЭ (1.5). Закон управления и соответствующая функция Ляпунова выбираются таким образом, чтобы обеспечить асимптотическую устойчивость требуемого углового положения корпуса КА. Рассматривается функция Ляпунова вида
(2.1)
$V = \frac{1}{2}{{{\mathbf{\omega }}}^{2}} + {{k}_{\lambda }}\left( {1 - {{\lambda }_{0}}} \right),\quad {{k}_{\lambda }} > 0,$Ляпуновское управление строится таким образом, чтобы производная функции Ляпунова (2.1), найденная в силу уравнений движения системы (1.5), была равна $ - {{k}_{\omega }}{{{\mathbf{\omega }}}^{2}}$, т.е. принимала неположительные значения. Тогда по теореме Барбашина–Красовского требуемое положение равновесия асимптотически устойчиво. В итоге, искомый закон управления имеет вид
(2.2)
$\begin{gathered} {\mathbf{u}} = {{{\mathbf{N}}}_{\omega }} - {{({{{\mathbf{E}}}_{{3 \times 3}}} + {{{\mathbf{S}}}_{q}}{{({\mathbf{M}} - {\mathbf{S}}_{q}^{T}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}^{{ - 1}}}{\mathbf{S}}_{q}^{T}{{{\mathbf{J}}}^{{ - 1}}})}^{{ - 1}}} \times \\ \times \;\left( {{\mathbf{J}}\left( {\frac{1}{2}{{k}_{\lambda }}{\mathbf{\lambda }} + {{k}_{\omega }}{\mathbf{\omega }}} \right) + {{{\mathbf{S}}}_{q}}{{{({\mathbf{M}} - {\mathbf{S}}_{q}^{T}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}}^{{ - 1}}}({{{\mathbf{N}}}_{q}} + {\mathbf{\Omega q}})} \right),\quad {{k}_{\omega }} > 0. \\ \end{gathered} $Управление (2.2) позволяет стабилизировать систему при любых начальных условиях.
Главные моменты инерции рассматриваемого в работе аппарата имеют порядок 105 кг ⋅ м2. Следовательно, на геостационарной орбите величина гравитационного момента (1.3), действующего на КА, приблизительно равна 10–5 Н ⋅ м. Это значение на несколько порядков меньше максимального управляющего момента маховиков, который полагается равным 0.4 Н ⋅ м.
Численная иллюстрация работы алгоритма (2.2) получена при следующих начальных условиях:
1) угловая скорость ${\mathbf{\omega }} = {{\left( {\begin{array}{*{20}{c}} {0.02}&{0.01}&0 \end{array}.03} \right)}^{T}}$ град/с,
2) кватернион ориентации ${{({{\lambda }_{0}},\,{{{\mathbf{\lambda }}}^{T}})}^{T}}$ – векторная часть ${\mathbf{\lambda }} = {{\left( {\begin{array}{*{20}{c}} {0.5}&{0.5}&{0.5} \end{array}} \right)}^{T}}$ (соответствует повороту на большой угол) и ${\mathbf{\lambda }} = {{\left( {\begin{array}{*{20}{c}} {0.01}&{0.01}&{0.01} \end{array}} \right)}^{T}}$ (соответствует окрестности положения равновесия), скалярная часть
3) начальный угол поворота панели ${{\varphi }_{0}} = 10$ град,
4) ${{\psi }_{0}} = 7.2 \times {{10}^{{ - 5}}}$ рад/с – угловая скорость поворота панели в шарнире,
5) число колебательных мод ${{n}_{a}} = 5$, ${{n}_{p}} = 2$,
6) амплитуды колебательных мод
7) скорости изменения амплитуд колебательных мод
8) шаг управления ${{\tau }_{{{\text{у п р }}}}} = 0.25$ с,
9) при численном интегрировании используется метод Рунге–Кутты 4-го порядка с постоянным шагом, шаг интегрирования ${{\tau }_{{{\text{и н т }}}}} = 0.01$ с,
10) максимальный управляющий момент маховиков 0.4 Н ⋅ м.
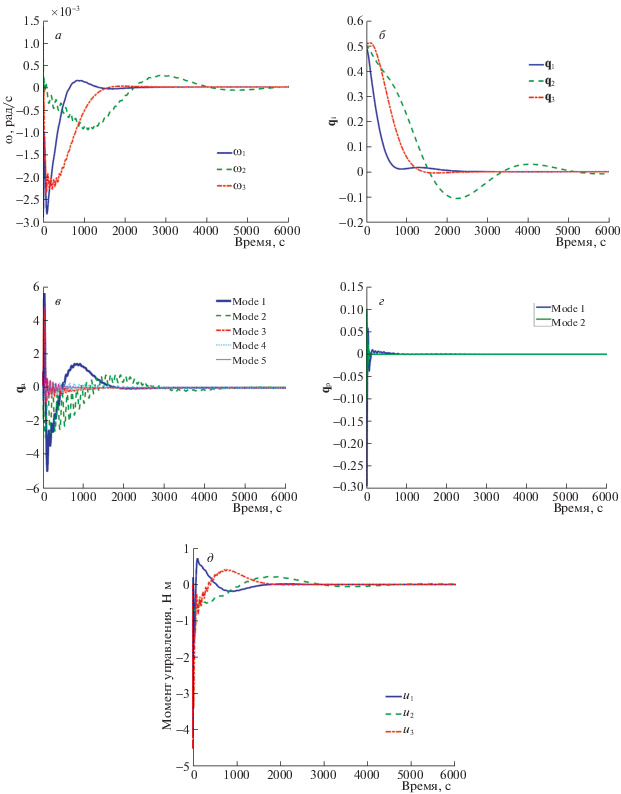
Расчеты производятся при двух значениях кватерниона ориентации: ${\mathbf{\lambda }} = {{\left( {\begin{array}{*{20}{c}} {0.01}&{0.01}&{0.01} \end{array}} \right)}^{T}}$ (рис. 2) и ${\mathbf{\lambda }} = {{\left( {\begin{array}{*{20}{c}} {0.5}&{0.5}&{0.5} \end{array}} \right)}^{T}}$ (рис. 3). Первый задает угловое положение, находящееся в окрестности требуемой ориентации корпуса КА, второй описывает вращение КА с НЭ на большие углы. Как и ожидалось, алгоритм в обоих случаях демпфирует вращение КА (рис. 2, а, 3, а) и обеспечивает заданную ориентацию корпуса (рис. 2, б, 3, б). Параметры ляпуновского управления полагались следующими: ${{k}_{\omega }} = 0.1$ Н ⋅ м ⋅ с, ${{k}_{\lambda }} = {{10}^{{ - 3}}}$ Н ⋅ м. Однако применительно к задаче управления КА с НЭ ляпуновское управление обладает тремя существенными недостатками.
Рис. 2.
Ляпуновское управление (малый угол): угловая скорость (а), векторная часть кватерниона ориентации (б), амплитуды колебательных мод антенны (в), амплитуды колебательных мод панели (г), управляющий момент (д)
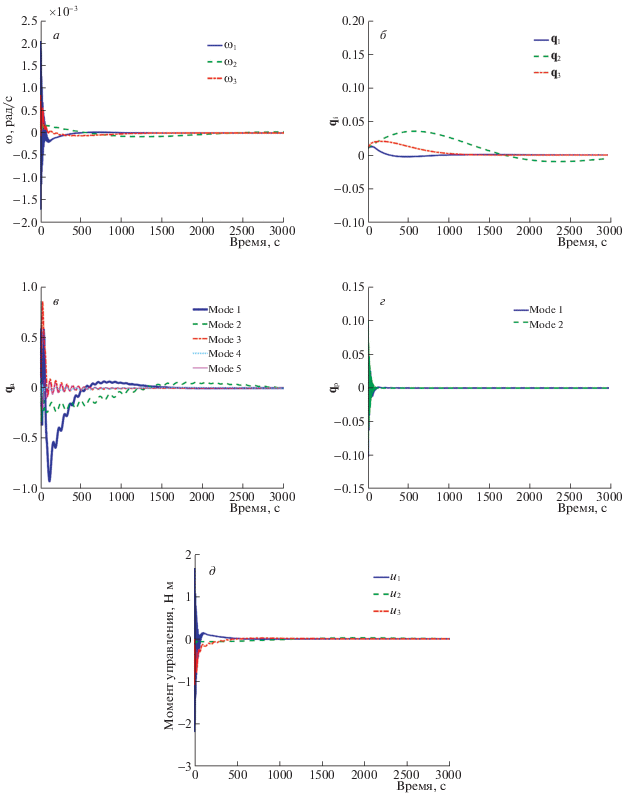
Рис. 3.
Ляпуновское управление (большой угол): угловая скорость (а), векторная часть кватерниона ориентации (б), амплитуды колебательных мод антенны (в), амплитуды колебательных мод панели (г), управляющий момент (д)
1. Величина управления никак не ограничивается, что приводит к невозможности реализовать требуемое управляющее воздействие (рис. 2, д, 3, д). Рисунок 3, д показывает, что при повороте КА на большой угол управляющий момент достигает 4 Н ⋅ м (в линейном случае – около 2 Н ⋅ м) при максимально возможном значении 0.4 Н ⋅ м.
2. Никак не ограничивается влияние на моды колебаний, что приводит к излишнему разбалтыванию НЭ (рис. 2, в, 2, г, 3, в, 3, г). В частности, наибольшее значение амплитуды одной из колебательных мод антенны в процессе перехода из положения ${\mathbf{\lambda }} = {{\left( {\begin{array}{*{20}{c}} {0.5}&{0.5}&{0.5} \end{array}} \right)}^{T}}$ в нулевое превысило начальное значение в 60 раз (рис. 3, в), что может превзойти допустимые отклонения.
3. Требует знания амплитуд колебательных мод, что налагает дополнительные требования на процедуру идентификации состояния системы [11].
Из указанных проблем невозможность реализации законов управления с помощью имеющихся на борту актюаторов требует первоочередного рассмотрения. По этой причине далее в работе представлены методы управления, допускающие ограничение на величину управляющих воздействий.
2.2. Линейно-квадратичное управление. ЛКУ является классическим типом управления, позволяющим ограничить величину управляющих воздействий ${\mathbf{u}}$ [12]. Применяющееся для линейной модели КА с НЭ (1.6) оно минимизирует функционал
(2.3)
$J = \int\limits_0^\infty {({{{\mathbf{x}}}^{T}}{\mathbf{Qx}} + {{{\mathbf{u}}}^{T}}{\mathbf{Ru}})dt} ,$Закон управления (2.4) (при условии ${\mathbf{Q}} > 0$) обеспечивает асимптотическую устойчивость положения равновесия ${\mathbf{x}} = 0$ [12]. Иначе говоря, с помощью закона управления (2.4) имеется возможность не только стабилизировать корпус КА в заданном угловом положении, но и погасить колебания в нежестких элементах конструкции.
Численный пример работы закона управления (2.4) приводится при тех же начальных условиях, что и в случае ляпуновского управления. Однако ввиду того, что в основе ЛКУ заложена линеаризованная моделью КА с НЭ, рассматривается только случай начальной ориентация корпуса КА из окрестности требуемого положения, т.е. ${\mathbf{\lambda }} = {{\left( {\begin{array}{*{20}{c}} {0.01}&{0.01}&{0.01} \end{array}} \right)}^{T}}$.
Параметры ЛКУ полагались равными
На рис. 4, а, б видно, что управление справляется с задачей стабилизации корпуса КА в заданном угловом положении. Хотя, по сравнению с ляпуновским управлением (2.2), время, требующееся на стабилизацию, увеличилось, величина управления стала меньше и достигла приемлемого уровня (рис. 4, д). Это происходит за счет слагаемого ${{{\mathbf{u}}}^{T}}{\mathbf{Ru}}$, штрафующего за большие значения управляющих воздействий.
Рис. 4.
ЛКУ: угловая скорость (а), векторная часть кватерниона ориентации (б), амплитуды колебательных мод антенны (в), амплитуды колебательных мод панели (г), управляющий момент (д)
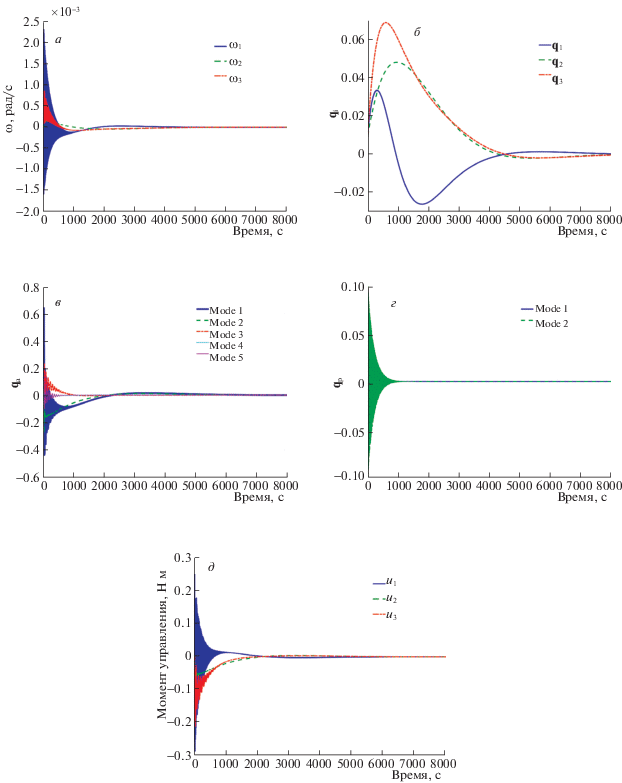
Стоит отметить, что не только угловая скорость и векторная часть кватерниона стремятся к нулю, но также уменьшаются и амплитуды упругих колебаний НЭ (рис. 4, а, б).
Благодаря минимизации слагаемого ${{{\mathbf{x}}}^{T}}{\mathbf{Qx}}$ в функционале (2.3) не наблюдается значительного увеличения амплитуд колебательных мод в НЭ относительно их начальных значений в ходе переходного процесса (рис. 4, в, г).
Заметим, что ЛКУ (2.4) требует знания амплитуд колебательных мод, так же как и ляпуновское управление. Решением данной проблемы служит ЛКУ, в основу которого положена редуцированная математическая модель, содержащая в себе лишь угловое движение КА с НЭ.
2.3. ЛКУ, основанное на редуцированной математической модели КА с НЭ. Для построения ЛКУ, основанного на редуцированной модели, линейная система (1.6) представляется в виде двух подсистем:
(2.5)
$\left( {\begin{array}{*{20}{c}} {{\mathbf{\dot {y}}}} \\ {\dot {z}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{A}}}_{\omega }}}&{{{A}_{{\omega q}}}} \\ 0&{{{A}_{{qq}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\mathbf{y}} \\ z \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{{B}_{\omega }}} \\ {{{B}_{q}}} \end{array}} \right)u.$Вектор ${\mathbf{y}} = {{(\begin{array}{*{20}{c}} {{{{\mathbf{\omega }}}^{T}}}&{{{{\mathbf{\lambda }}}^{T}}} \end{array})}^{T}}$ описывает угловое движение корпуса КА, а вектор $z = {{(\begin{array}{*{20}{c}} {V_{q}^{T}}&{{{q}^{T}}} \end{array})}^{T}}$ отвечает за поведение НЭ. Здесь
(2.6)
${{{\mathbf{A}}}_{\omega }} = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{0}}}_{{3 \times 3}}}}&{{{{\mathbf{0}}}_{{3 \times 3}}}} \\ {\frac{1}{2}{{{\mathbf{E}}}_{{3 \times 3}}}}&{{{{\mathbf{0}}}_{{3 \times 3}}}} \end{array}} \right),$Как отмечено в работе [13], простое отбрасывание второго уравнения в системе (2.5) и построение ЛКУ на базе редуцированной части системы (в нашем случае, описывающей угловое движение корпуса КА) приводит к нежелательным возмущениям нежестких элементов. Метод построения ЛКУ на основе редуцированной модели рассмотрен в [8, 9]. Для их подавления предлагается добавить в функционал качества слагаемое, минимизация которого приведет к подавлению указанных возмущений.
Для реализации рассматриваемой методики необходимо, чтобы при построении управления второе уравнение системы (2.5) допускало требуемое положение равновесия, т.е. выполнялось следующее равенство:
Из (2.7) вектор состояния $z$, описывающий колебания нежестких элементов, выражается через вектор управления
Первое уравнение системы (2.5), описывающее угловое движение корпуса КА, после подстановки в него (2.8) переписывается так:
(2.9)
${\mathbf{\dot {y}}} = {{{\mathbf{A}}}_{\omega }}{\mathbf{y}} + ({{{\mathbf{B}}}_{\omega }} - {{{\mathbf{A}}}_{{\omega q}}}{\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}}){\mathbf{u}}.$Используя (2.8), функционал системы (2.5)
(2.10)
$J = \int\limits_0^\infty {({{{\mathbf{y}}}^{T}}{{{\mathbf{Q}}}_{{\mathbf{y}}}}{\mathbf{y}} + {{{\mathbf{u}}}^{T}}({\mathbf{R}} + {{{({\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}})}}^{T}}{{{\mathbf{Q}}}_{z}}{\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}}){\mathbf{u}})dt} .$Функционал (2.10) содержит слагаемое ${{{\mathbf{u}}}^{T}}{{({\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}})}^{T}}{{{\mathbf{Q}}}_{z}}{\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}}{\mathbf{u}}$, которое минимизирует возмущающее влияние управления на НЭ. ЛКУ, основанное на редуцированной модели (2.9) и минимизирующее функционал (2.10), имеет вид
где ${{{\mathbf{R}}}_{x}} = {\mathbf{R}} + {{({\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}})}^{T}}{{{\mathbf{Q}}}_{z}}{\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}}$, ${{{\mathbf{B}}}_{x}} = {{{\mathbf{B}}}_{\omega }} - {{{\mathbf{A}}}_{{\omega q}}}{\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}}$ и $P$ – решение уравнения РиккатиКак и ЛКУ (2.4), управление (2.11) стабилизирует корпус КА в заданном угловом положении.
В численном примере работы алгоритма (2.11) используются те же начальные условия, что и в случае ЛКУ (2.4). Параметры управления полагались равными
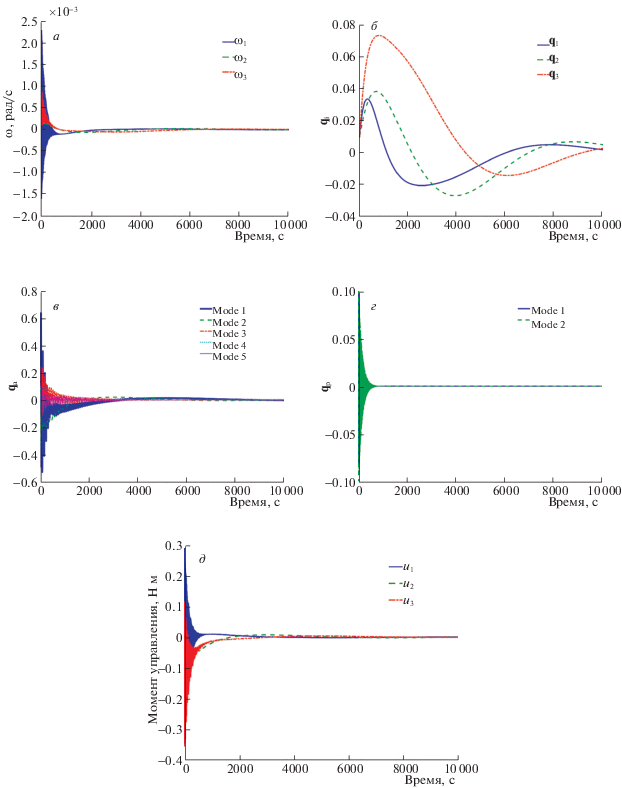
Численные результаты показывают (рис. 5), что выводы, полученные при моделировании ЛКУ, справедливы и здесь. Однако при этом оно формируется без необходимости определения амплитуд колебательных мод и минимизирует возмущения НЭ, возникающие в процессе стабилизации корпуса аппарата. При этом необходимо отметить, что информация о формах колебаний, которая содержится в матрицах системы (2.5), все же нужна для вычисления управляющих воздействий.
Рис. 5.
Редуцированное ЛКУ: угловая скорость (а), векторная часть кватерниона ориентации (б), амплитуды колебательных мод антенны (в), амплитуды колебательных мод панели (г), управляющий момент (д)
Основной недостаток линейно-квадратичных законов управления (2.4) и (2.11) заключается в том, что они обеспечивают асимптотическую устойчивость заданного углового положения объекта лишь в его линейной окрестности. Одним из быстроразвивающихся методов для проектирования регуляторов, в основе которых лежит нелинейная модель объекта, является SDRE-управление [6].
2.4. SDRE-управление, основанное на редуцированной математической модели КА с НЭ. В основе SDRE-управления лежит ЛКУ, использующее уравнение Риккати, параметры которого зависят от состояния системы [6].
SDRE-управление строится для автономной, нелинейной системы
(2.12)
$\dot {x}\left( t \right) = f\left( x \right) + B\left( x \right)u\left( t \right),\quad f\left( 0 \right) = 0,$(2.13)
$J = \int\limits_0^\infty {({{x}^{T}}\left( t \right)Q\left( x \right)x\left( t \right) + {{u}^{T}}\left( t \right)R\left( x \right)u\left( t \right))dt} ,$Выделение из функции $f\left( x \right)$ вектора состояния
приводит систему (2.12) к системе линейной структуры с матрицами $A\left( x \right)$ и $B\left( x \right)$:(2.15)
$\dot {x}\left( t \right) = A\left( x \right)x\left( t \right) + B\left( x \right)u\left( t \right).$Как следует из [6], управление для нелинейной системы (2.15) с функционалом качества (2.13) представляется в следующем виде:
(2.16)
$u\left( t \right) = - K\left( x \right)x\left( t \right) = - {{R}^{{ - 1}}}\left( x \right){{B}^{T}}\left( x \right)P\left( x \right)x\left( t \right).$Здесь $P\left( x \right)$ является решением алгебраического уравнения Риккати:
Таким образом, отличие закона управления (2.16) от стандартного ЛКУ состоит в том, что матрицы системы (2.15) A(x) и B(x), параметры управления Q(x), R(x) и, следовательно, решение алгебраического уравнения Риккати (2.17) зависят от состояния системы. Отметим, что алгебраическое уравнение Риккати должно решаться на каждом шаге управления.
В настоящей работе SDRE-управление строится на основании редуцированной модели системы, т.е. на основании уравнений, отвечающих за угловое движение КА. Предполагается, что начальные значения угловой скорости, а также амплитуд колебательных мод НЭ q и скоростей их изменения ${{{\mathbf{V}}}_{q}}$ достаточно малы, поэтому модель линеаризуется по этим переменным. Нелинейными являются лишь кинематические соотношения для поворота корпуса аппарата. В этом случае уравнения (1.5) нелинейны лишь по кватерниону ориентации. Разложение вида (2.14) снова приводит к системе (2.5) с той лишь разницей, что матрица ${{{\mathbf{A}}}_{\omega }}$ заменяется на матрицу
Закон управления описывается формулой, аналогичной (2.11), и имеет вид
(2.18)
${\mathbf{u}} = - {\mathbf{R}}_{х }^{{ - 1}}\left( y \right){\mathbf{B}}_{x}^{T}\left( y \right){\mathbf{P}}\left( y \right){\mathbf{y}},$(2.19)
${\mathbf{A}}_{{\omega SDRE}}^{T}\left( {\mathbf{y}} \right){\mathbf{P}}\left( {\mathbf{y}} \right) + {\mathbf{P}}\left( {\mathbf{y}} \right){{{\mathbf{A}}}_{{\omega SDRE}}}\left( {\mathbf{y}} \right) - {\mathbf{P}}\left( {\mathbf{y}} \right){{{\mathbf{B}}}_{x}}{\mathbf{R}}_{x}^{{ - 1}}{\mathbf{B}}_{x}^{T}{\mathbf{P}}\left( {\mathbf{y}} \right) + {{{\mathbf{Q}}}_{y}} = 0.$Уравнение (2.19) решается на каждом шаге управления с помощью функции, которая реализует алгоритм, предложенный в работе [14]. В его основе лежит алгоритм Клейнмана. В [15] отмечено, что решение уравнения Риккати с помощью данного алгоритма требует $60{{n}^{3}}$ операций с плавающей точкой.
В отличие от закона управления (2.11), наличие нелинейности по кватерниону позволяет приводить корпус КА в заданное положение из любого начального углового положения.
В численном примере работы алгоритма (2.18) используются те же начальные условия, что и в случае ляпуновского управления. Так как основным толчком к исследованию данного алгоритма послужила невозможность поворота корпуса КА с помощью линейно-квадратичных методов управления (2.4) и (2.11) на большие углы, то его начальная ориентация определяется кватернионом ${\mathbf{\lambda }} = {{\left( {\begin{array}{*{20}{c}} {0.5}&{0.5}&{0.5} \end{array}} \right)}^{T}}$. Параметры управления полагались равными
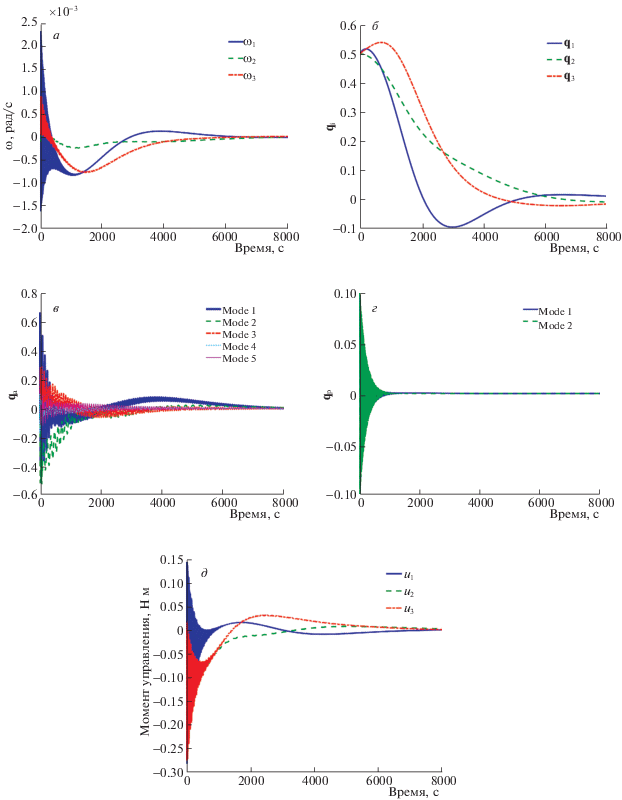
Из графиков видно, что SDRE-управление успешно стабилизирует корпус КА (рис. 6, а, б) и гасит амплитуды колебательных мод, не позволяя последним сильно отклоняться от их начальных значений (рис. 6, в, г). Как и в случае с вышерассмотренными линейно-квадратичными законами управления (2.4) и (2.11), управляющий момент не превышает допустимых 0.4 Н ⋅ м (рис. 6, д).
Рис. 6.
SDRE-управление: угловая скорость (а), векторная часть кватерниона ориентации (б), амплитуды колебательных мод антенны (в), амплитуды колебательных мод панели (г), управляющий момент (д)
К сожалению, область устойчивости данного алгоритма пока не исследована. Источником оптимизма служит то, что SDRE-управление содержит в себе все черты классического ЛКУ, а в линейном приближении и вовсе с ним совпадает. Данный вопрос требует дальнейших изысканий.
Заключение. Методики управления, целью которых является стабилизация корпуса КА и гашение колебаний в НЭ, были апробированы на полной модели движения КА с НЭ.
Ляпуновское управление решает указанные задачи, причем стабилизация корпуса аппарата возможна при его любой начальной ориентации и любых начальных значениях амплитуд колебательных мод и скоростей их изменения. Однако отсутствие механизмов ограничения управления и возбуждения мод колебаний приводит к трудностям в реализации такого типа управления на практике. Указанные затруднения преодолевает ЛКУ, которое благодаря виду функционала качества позволяет штрафовать за чрезмерное увеличение затрат ресурсов управления.
Большая размерность вектора состояния КА с НЭ и желание построить алгоритм управления, опираясь лишь на угловое движение корпуса КА, привело к построению ЛКУ, в основе которого была заложена редуцированная модель движения. Этот закон управления не только стабилизирует корпус КА в заданном угловом положении, но и за счет модификации функционала качества предотвращает возмущения в НЭ, возникающие в процессе стабилизации корпуса КА.
Основной недостаток линейно-квадратичных методов заключается в том, что они работают лишь в окрестности требуемого положения КА.
Наиболее подходящим в условиях рассматриваемой задачи, по-видимому, является SDRE-управление. Сохраняя в себе основные преимущества ЛКУ, оно используется для управления нелинейными системами. Поэтому в отличие от классического ЛКУ SDRE-управление, построенное на основе уравнений относительного движения корпуса КА и не требующее знаний колебательных мод НЭ, позволяет разворачивать аппарат на произвольные углы. Численное моделирование продемонстрировало, что с помощью SDRE-управления обеспечивается стабилизация корпуса КА с НЭ в требуемом положении и происходит гашение колебаний в НЭ. При этом алгоритм обеспечивает ограничение управляющего момента в заданных рамках. Главным минусом алгоритма является проблема обеспечения глобальной асимптотической устойчивости при его использовании. Этот вопрос требует дальнейших исследований.
Список литературы
Santini P. Stability of Flexible Spacecrafts // Acta Astronautica. 1976. V. 3. Issues 9, 10. P. 685–713.
Ovchinnikov M.Yu., Tkachev S.S., Roldugin D.S., Nuralieva A.B., Mashtakov Y.V. Angular Motion Equations for a Satellite with Hinged Flexible Solar Panel // Acta Astronautica. 2016. V. 128. P. 534–539.
Hyland D.C., Junkins J.L., Longman R.V. Active Control Technology for Large Space Structures // J. Guidance, Control, and Dynamics. 1993. V. 16. № 5. P. 801–821.
Junkins J.L., Kim Y. Introduction to Dynamics and Control of Flexible Structures. Washington DC: AIAA Education Series, 1993. P. 452.
Mazzini L. Flexible Spacecraft Dynamics, Control and Guidance: Technologies by Giovanni Campolo // Cham. Springer Aerospace Technology. Springer, 2016. P. 363.
Çimen T. Survey of State-Dependent Riccati Equation in Nonlinear Optimal Feedback Control Synthesis // J. Guidance, Control, and Dynamics. 2012. V. 35. № 4. P. 1025–1047.
Gasbarri P., Monti R., Sabatini M. Very Large Space Structures: Non-Linear Control and Robustness to Structural Uncertainties // Acta Astronautica. 2014. V. 93. P. 252–265.
Sesak J.R., Coradetti T. Decentralized Control of Large Space Structures via Forced Singular Perturbation // Proc. AIAA 17th Aerospace Sciences Meeting. New Orleans, LA, USA, 1979.
Sesak J.R. Control of Large Space Structures via Singular Perturbation Optimal Control // Proc. AIAA Conf. on Space Platforms: Future Needs and Capabilities. Los Angeles, CA, USA, 1978.
Angeletti F., Gasbarri P., Sabatini M. Optimal Design of a Net of Adaptive Structures for Micro-vibration Control in Large Space Mesh Reflectors // Proc. 69th Intern. Astronautical Congr. Bremen, Germany, 2018.
Ivanov D.S., Meus S.V., Ovchinnikov A.V., Ovchinnikov M.Yu., Shestakov S.A., Yakimov E.N. Methods for the Vibration Determination and Parameter Identification of the Spacecraft with Flexible Structures // J. Computer And Systems Sciences International. 2017. V. 56. № 2. P. 311–327.
Liberzon D. Calculus of Variations and Optimal Control Theory. Princeton: Princeton University Press, 2012. P. 256.
Balas M.J. Active Control of Flexible Systems // J. Optimization Theory and Applications. 1978. V. 25. № 3. P. 415–436.
Arnold W.F., Laub A.J. Generalized Eigenproblem Algorithms and Software for Algebraic Riccati Equations // Proc. IEEE. 1984. V. 72. P. 1746–1754.
Menon P.K., Lam T., Crawford L.S., Cheng V.H.L. Real-time Computational Methods for SDRE Nonlinear Control of Missiles // Proc. 2002 American Control Conf. Anchorage, AK, USA, 2002.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления