Известия РАН. Теория и системы управления, 2019, № 3, стр. 4-9

Введение. Рассмотрим объект управления, имеющий единственное неустойчивое нулевое состояние равновесия. Пусть требуется выбрать допустимый (например, кусочно-непрерывный) закон управления, обеспечивающий устойчивость движения объекта в окрестности его состояния равновесия. Такая задача имеет, по крайней мере, две особенности, не свойственные задачам управления устойчивыми объектами.

Во-первых, поскольку величина управления обычно ограничена, то невозможно обеспечить устойчивость в целом стабилизируемого состояния равновесия.

Во-вторых, как бы ни были малы действующие на объект возмущения, управление не может быть отключено, так как это приведет к возникновению таких отклонений от состояния равновесия, которые не удастся компенсировать ограниченным управлением.

Первая особенность приводит к введению в обиход критерия качества, представляющего собой область притяжения стабилизируемого состояния равновесия [1]. Законы управления, оптимальные по этому показателю, названы автором оптимальными по устойчивости. Структура таких законов и методы их построения (особенно для линейных стационарных объектов) достаточно подробно исследованы в монографиях [2, 3] для общего случая, в [4, 5] для магнитного подвеса, и в [6] (с примерами управления механическими системами типа перевернутого маятника).

Для второй особенности характерным является показатель качества, оценивающий затраченную на управление энергию. Для линейных стационарных объектов и скалярного управления такая задача была решена в [7] в предположении, что затраченная на управление энергия пропорциональна интегралу от квадрата управляющего воздействия.

Целью настоящей статьи является распространение полученных результатов на случай векторного управления и на некоторый класс нелинейных объектов.

1. Постановка задачи. Будем рассматривать случай, при котором движение объекта управления описывается обыкновенным дифференциальным уравнением вида

где x = x(t) – вектор состояния, являющийся точкой n-мерного векторного пространства $X = {{\mathbb{R}}^{n}}$, f(x) – дифференцируемая функция вектора состояния x, такая, что f (0) = 0, u = u(t) = u(x(t)) – вектор управления (закон управления), значения которого являются точками m-мерного векторного пространства $U = {{\mathbb{R}}^{m}}$, g(x) – матрица вида Введем следующие определения.

DF1. Неустойчивое по Ляпунову изолированное состояние $\hat {x}$ равновесия назовем неустойчивым в узком смысле, если найдется такая его окрестность, что все начинающиеся в этой окрестности движения сходятся к $\hat {x}$ при $t \to - \infty $.

Таким образом, для неустойчивого в узком смысле состояния равновесия $\hat {x}$ не существует траекторий, сходящихся к $\hat {x}$ при t → +∞.

DF2. Диффеоморфизм h: X → X пространства состояний в себя назовем расщепляющим уравнения движения на неустойчивую и устойчивую подсистемы, если выполняются следующие четыре условия.

1. Пространство состояний X разбивается диффеоморфизмом h на прямую сумму подпространств Y и Z так, что X = h(Y ⊕ Z), dimY + dimZ = dimX.

2. Уравнение движения заменой переменных x = h(y, z) расщепляется на две подсистемы с общим управлением вида

3. Подсистема (1.2) в отсутствии управления имеет единственное неустойчивое в узком смысле состояние равновесия, которое, не нарушая общности, будем считать совпадающим с нулевым вектором.

4. Подсистема (1.3) при нулевых значениях переменных y и u имеет единственное асимптотически устойчивое в целом нулевое состояние равновесия.

В дальнейшем, при выполнении условий определения DF2 подсистему (1.2) будем называть неустойчивой, а подсистему (1.3) – устойчивой.

Очевидно, что если нулевое состояние равновесия исходной системы асимптотически устойчиво в целом, то при минимизации расхода энергии на управление оптимум будет достигнут при отсутствии управления (нулевом управлении). При этом область притяжения нулевого состояния равновесия совпадает со всем пространством состояний, и поэтому нулевое управление в этом случае принадлежит к классу оптимальных по устойчивости.

В случае неустойчивого в отсутствии управления нулевого состояния равновесия и существования расщепляющего диффеоморфизма h оптимальное по устойчивости управление может быть достигнуто построением закона управления, зависящего только от вектора состояния неустойчивой подсистемы (1.2). При этом область притяжения нулевого состояния равновесия совпадает с прямым произведением W × Z, где W – максимальная область притяжения неустойчивой подсистемы [1–6].

Распространяя постановку задачи, сформулированной в [7] на случай векторного управления, будем считать, что расход энергии на управление определяется интегральным критерием

где u – вектор управления (вектор-столбец), а R – положительно-определенная симметрическая матрица. Таким образом, под знаком интеграла находится положительно-определенная квадратичная форма.

Если при выполнении условий определения DF2 некоторый закон управления ${{u}_{{yz}}}(y,z)$ обеспечивает устойчивость нулевого состояния равновесия всей системы, то закон управления u(y), задаваемый равенством $u(y) = {{u}_{{yz}}}(y,0)$, являющийся сужением закона управления ${{u}_{{yz}}}(y,z)$ на пространство состояний неустойчивой подсистемы, будет обеспечивать меньшие значения показателя качества (1.4) при ненулевых начальных значениях вектора состояния устойчивой подсистемы. Таким образом, при выполнении условий определения DF2 для расщепляющего диффеоморфизма, значения закона управления, являющегося оптимальным по интегральному критерию (1.4), будут зависеть только от вектора состояния неустойчивой подсистемы. Для поиска такого закона используем метод динамического программирования [8].

2. Решение задачи. Запишем уравнение Беллмана для неустойчивой подсистемы (1.2) и интегрального критерия качества (1.4) в виде

В этом уравнении $S(y)$ – оптимальное значение показателя качества (функция Беллмана), а $S{\text{'}}(y)$ – его градиент. Приравнивая нулю градиент подлежащего минимизации выражения (${\text{gra}}{{{\text{d}}}_{u}}({{u}^{{\text{T}}}}Ru + S{\text{'}}(y)[F(y) + G(y)u])$ = 0), получим для оптимального значения управления равенство $\hat {u} = - 0.5{{({{R}^{{ - 1}}})}^{{\text{T}}}}{{G}^{{\text{T}}}}(y){{(S{\text{'}}(y))}^{{\text{T}}}}$, а после подстановки в (2.1) оптимального значения $\hat {u}$ – уравнение $S{\text{'}}(y)[F(y) + 0.5G(y)\hat {u}(y)] = 0$. Это уравнение имеет два решения: $S{\text{'}}(y) = 0$, соответствующее отсутствию управления и не обеспечивающее устойчивость нулевого состояния равновесия, и нетривиальное решение

Учитывая уравнение (1.2), этот результат означает, что при оптимальном управлении уравнение движения подсистемы (1.2) примет вид $dy{\text{/}}dt = - F(y)$, т.е. может быть получено из уравнения неустойчивой подсистемы обращением времени. Этот результат сформулируем в виде следующего утверждения.

Теорема TH1. Пусть для объекта с неустойчивым нулевым состоянием равновесия правая часть уравнения движения (1.1) непрерывно дифференцируема и линейно зависит от управления. Пусть, кроме того, существует диффеоморфизм, расщепляющий уравнения движения на неустойчивую и устойчивую подсистемы (определение DF2). Если при этом существует непрерывный закон управления, заданный в некоторой окрестности нулевого состояния равновесия, который обеспечивает асимптотическую устойчивость нулевого состояния равновесия системы (1.1) и минимизирует интегральный показатель качества (1.4), то этот закон управления зависит только от вектора состояния неустойчивой подсистемы и для него выполняется соотношение (2.2).

Таким образом, если $\hat {u}(y)$ – оптимальный закон управления, то уравнения движения системы, записанные как (1.2) и (1.3), примут вид

При этом движение по оптимальным траекториям подсистемы (2.3) совпадают с движениями исходной неустойчивой подсистемы при обращении времени.

Очевидным следствием теоремы TH1 является следующее утверждение.

Теорема TH2. Оптимальный по критерию (1.4) закон управления, удовлетворяющий условиям теоремы TH1, обеспечивает область притяжения нулевого состояния равновесия, совпадающую с прямым произведением области притяжения нулевого состояния равновесия подсистемы (2.3) и пространства состояний устойчивой подсистемы. Область притяжения нулевого состояния равновесия подсистемы (2.3) является областью определения оптимального закона управления, совпадает с внутренностью замыкания ячейки неустойчивой подсистемы, для траекторий которой нулевой вектор является α-предельной точкой.

Рассмотрим частные случаи применения полученных результатов.

Пример 1. Условия теоремы TH1 выполняются для любого стационарного объекта, дифференциальное уравнение неустойчивой подсистемы которого может быть записано в виде

В этом случае оптимальный по критерию (1.4) закон управления задается равенством

Пример 2. Для линейного стационарного управляемого объекта, уравнение движения которого записаны в виде $dx{\text{/}}dt = Ax + Bu$, оптимальный по критерию (1.4) закон управления будет линейным законом, оставляющим на месте корни характеристического многочлена с отрицательной вещественной частью и изменяющий на противоположные знаки корней с положительной вещественной частью, что согласуется с результатами, полученными в работе [7]. Понятно, что для построения такого закона можно обойтись без поиска расщепляющего отображения.

Пример 3. Если для линейного управляемого стационарного объекта со скалярным управлением неустойчивая подсистема имеет первый порядок, а управление ограниченно по модулю, то в области линейности закон управления должен удовлетворять условиям теоремы TH1, а вне области линейности принимать максимальное или минимальное значения. Движение неустойчивой части первого порядка в этом случае описывается уравнением $dy{\text{/}}dt = \lambda y + \beta u$, $\left| u \right| \leqslant c$. Оптимальное управление в зоне линейности задается равенством $\hat {u} = - 2\lambda y{\text{/}}\beta $, а в зоне насыщения равно $\hat {u} = - c{\text{sign}}\left( {2\lambda y{\text{/}}\beta } \right)$. Такой закон будет к тому же и оптимальным по устойчивости [1–6].

Пример 4. Построим по алгоритму примера 3 закон управления для системы четвертого порядка с неустойчивой подсистемой второго порядка. Пусть уравнение движения записано в виде

При отсутствии ограничений на управление оптимальным по интегральному критерию (1.4) в соответствии с примером 2 будет линейный закон

При наличии ограничений вида $\left| u \right| \leqslant c$ на величину управляющего воздействия выделим в явном виде уравнение неустойчивой подсистемы. Для этого запишем уравнения движения в матричной форме

Невырожденным линейным преобразованием

приведем уравнения движения к виду

Ясно, что при этом движение неустойчивой подсистемы описывается уравнением второго порядка

Оптимальный закон управления в зоне линейности равен $\hat {u} = - 4{{y}_{2}}$, ${{y}_{2}} = dy{\text{/}}dt$.

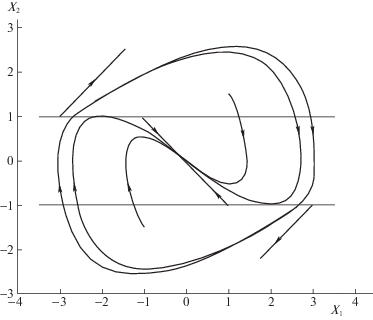
На рис. 1 представлены фазовые траектории исследуемой подсистемы в координатах ${{y}_{1}} = y$, ${{y}_{2}} = dy{\text{/}}dt$, $\left| u \right| \leqslant c$. Показаны прямолинейные отрезки траекторий, линии перехода в зону насыщения, отрезки траекторий, касающихся линий перехода (они определяют область, в которой величина управления не достигает ограничений) и отрезки без контакта на линиях перехода, пересекаемые предельным циклом. Точки касания на линиях перехода имеют координаты ${{y}_{1}} = \pm 2$, а предельный цикл пересекает линии перехода между точками ${{y}_{1}} = \pm 2$, ${{y}_{1}} = \pm 3$. Отметим, что область притяжения состояния равновесия в этом примере ограничена предельным циклом и меньше области управляемости, для которой точки ${{y}_{1}} = \pm 4$, ${{y}_{2}} = 0$ являются граничными.

Пример 5. Пусть движение неустойчивой подсистемы описывается уравнением второго порядка, ее неустойчивое нулевое состояние равновесия лежит внутри единственного устойчивого предельного цикла, а ограничения на величину управления отсутствуют. Очевидно, что внутри предельного цикла оптимальное управление должно удовлетворять условиям теоремы TH1, а вне цикла должно равняться нулю. Например, если движение неустойчивой подсистемы описывается уравнением

то при $u = 0$ будет существовать устойчивый предельный цикл L, траектория которого описывается уравнением

Оптимальный по критерию (1.4) закон управления будет равен

внутри предельного цикла.

При полученном законе управления предельный цикл сохраняется, а стабилизируемое состояние равновесия не является асимптотически устойчивым в целом. Покажем, что в рассматриваемом случае изменением закона управления в малой окрестности предельного цикла можно добиться асимптотической устойчивости в целом и получить закон управления, оптимальный по устойчивости. Если управление отсутствует, то производная функционала (dy/dt)²+ y² по времени, взятая в силу уравнений движения, равна нулю в точках предельного цикла. В достаточно малой окрестности ${{S}_{\varepsilon }}(L)$ цикла при $u \ne 0$ (с точностью до малых высшего порядка) эта производная равна $udy{\text{/}}dt$. Положим $\hat {u} = - kdy{\text{/}}dt,k > 0$, в точках внутри ${{S}_{\varepsilon }}(L)$, а в точках внутри предельного цикла, не лежащих в ${{S}_{\varepsilon }}(L)$,

и  $\hat {u} = 0$ в остальных точках. Такой закон управления будет обеспечивать асимптотическую устойчивость в целом нулевого состояния равновесия и будет оптимальным по критерию (1.4) для начальных условий, норма которых меньше $1 - \varepsilon $.

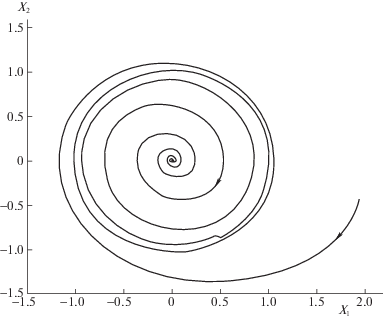
На рис. 2 показаны фазовые траектории такой системы при $k = 1$, $\varepsilon = 0.02$.

Пример 6. Для одномерного пространства состояний неустойчивой подсистемы, уравнение которой имеет вид $dy{\text{/}}dt = {{y}^{2}} + u$, решение уравнения Беллмана приведет к закону управления $u(y) = - ({\text{sign}}(y) + 1){{y}^{2}}$.

Заметим, что в последнем примере теорема TH1 не используется. Тем не менее, сформулированные в TH1 условия оптимальности и теорема TH2 существенно помогают понять структуру оптимального закона.

Заключение. Полученные результаты позволяют достаточно легко находить оптимальные по расходу энергии законы управления в случае существования диффеоморфизма, расщепляющего уравнения движения на устойчивую и управляемую неустойчивую подсистемы. Такой диффеоморфизм заведомо существует в виде линейного обратимого оператора для линейных управляемых объектов, поэтому для них при часто встречающихся видах допустимых законов управления (например, линейных с насыщением) задача поиска оптимальных законов решается с достаточной полнотой.