Известия РАН. Теория и системы управления, 2019, № 3, стр. 10-23
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ПОВОРОТОМ ТВеРДОГО ТЕЛА ПРИ ПОМОЩИ ВНУТРЕННЕЙ МАССЫ
Ф. Л. Черноусько a, А. М. Шматков a, *
a ИПМех РАН
Москва, Россия
* E-mail: shmatkov@ipmnet.ru
Поступила в редакцию 17.01.2019
После доработки 19.01.2019
Принята к публикации 28.01.2019
Аннотация
Исследована двумерная задача о наискорейшем повороте твердого тела путем перемещения внутренней массы. Предполагается, что твердое тело вместе с внутренней подвижной массой является замкнутой механической системой. В общем случае соотношения для траектории движения массы, оптимального управления и функции Беллмана выражены через эллиптические интегралы, в которые входят две неизвестных. Поиск этих величин требует численного решения двух нелинейных скалярных уравнений, составленных на основании краевых условий. Если положение массы в конечный момент времени не задано, задача сводится к решению единственного скалярного уравнения на известном отрезке, причем соответствующий корень единственен для любых граничных условий и всегда существует. В частном случае, когда внутренняя масса мала по сравнению с массой твердого тела, получены оптимальные траектории, имеющие форму дуг окружности. Исследована связь между приближенным и точным решениями, а также приведены численные примеры использования полученных соотношений.
Введение. Исследования, посвященные различным вопросам робототехники, в настоящее время весьма актуальны [1–3]. В большинстве применяемых механических устройств перемещение аппарата (робота, движущегося объекта) зависит от непосредственного взаимодействия движущихся частей с окружающей средой. Это вызывает ряд затруднений, например, в случае, если окружающая среда агрессивна. Поэтому механические системы, в которых движение происходит под действием перемещающихся внутренних масс, представляют интерес для робототехники [4–6]. Кроме того, подвижные внутренние массы можно использовать, в принципе, для управления ориентацией космических аппаратов. В ряде случаев можно пренебречь влиянием внешних факторов либо для движения в целом, либо для некоторых его этапов. В данной работе анализируются, сравниваются и обобщаются результаты, кратко изложенные в работах [7, 8].
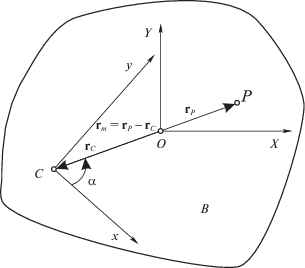
1. Постановка задачи. Рассмотрим твердое тело B массы M и материальную точку P массы m, показанные на рис. 1. Пусть оба объекта могут осуществлять только плоскопараллельные движения. Предположим, что в начальный момент времени система покоится, и пренебрежем всеми внешними силами и моментами сил. Тогда система замкнута и может двигаться исключительно под действием внутренних сил взаимодействия между телом и точкой. В этом случае общий центр масс обоих объектов покоится и может быть использован в качестве начала неподвижной декартовой системы координат $OXY$. Кроме того, рассмотрим движущуюся декартову систему координат $Cxy$, связанную с телом $B$, причем ее центр C находится в центре масс этого тела. Пусть положение материальной точки $P$ по отношению к началу координат C задано вектором ${{{\mathbf{r}}}_{m}}$, а векторы ${{{\mathbf{r}}}_{P}}$ и ${{{\mathbf{r}}}_{C}}$ задают положения точек $P$ и C по отношению к началу координат системы $OXY$. Имеем ${{{\mathbf{r}}}_{m}} = {{{\mathbf{r}}}_{P}} - {{{\mathbf{r}}}_{C}}$ (рис. 1).
Поскольку центр масс O покоится, в силу первого закона Ньютона справедливо следующее соотношение:
(1.1)
$M{{{\mathbf{r}}}_{C}} + m{{{\mathbf{r}}}_{P}} = M{{{\mathbf{r}}}_{C}} + m({{{\mathbf{r}}}_{C}} + {{{\mathbf{r}}}_{m}}) = 0.$Из (1.1) получаем
Пусть ${{{\mathbf{v}}}_{C}} = {{{\mathbf{\dot {r}}}}_{C}}$ – скорость точки $C$, а ω – угловая скорость тела B. Закон сохранения количества движения для механической системы, состоящей из тела B и материальной точки P, дает
(1.3)
$M{{{\mathbf{v}}}_{C}} + m({{{\mathbf{v}}}_{C}} + \omega \times {{{\mathbf{r}}}_{m}} + {{{\mathbf{\dot {r}}}}_{m}}) = 0,$(1.4)
${{{\mathbf{v}}}_{C}} = - \mu (\omega \times {{{\mathbf{r}}}_{m}} + {{{\mathbf{\dot {r}}}}_{m}}).$Обозначим через J момент инерции тела B относительно оси, проходящей через центр масс $C$ этого тела перпендикулярно плоскости $OXY$. Предположим, что эта ось – главная центральная ось инерции тела B. Закон сохранения углового момента для рассматриваемой механической системы можно записать в следующем виде:
(1.5)
$M{{{\mathbf{r}}}_{C}} \times {{{\mathbf{v}}}_{C}} + J\omega + m({{{\mathbf{r}}}_{C}} + {{{\mathbf{r}}}_{m}}) \times ({{{\mathbf{v}}}_{C}} + \omega \times {{{\mathbf{r}}}_{m}} + {{{\mathbf{\dot {r}}}}_{m}}) = 0.$Подставим ${{{\mathbf{r}}}_{C}}$ из (1.2) и ${{{\mathbf{v}}}_{C}}$ из (1.4) в соотношение (1.5). Получим
(1.6)
$(\mu {{\left| {{{{\mathbf{r}}}_{m}}} \right|}^{2}} + J{\text{/}}M)\omega + \mu {{{\mathbf{r}}}_{m}} \times {{{\mathbf{\dot {r}}}}_{m}} = 0.$Радиус инерции a тела $B$ определен соотношением
Обозначим через $x$ и $y$ декартовы координаты вектора ${{{\mathbf{r}}}_{m}}$ относительно системы координат $Cxy$. Пусть $u$ и $\text{v}$ — проекции вектора относительной скорости ${{{\mathbf{\dot {r}}}}_{m}}$ точки $P$ на оси абсцисс и ординат системы $Cxy$, а $\varphi $ – угол поворота тела B в системе координат $OXY$. Тогда с учетом (1.7) уравнение (1.6) можно переписать в форме
(1.8)
$\dot {x} = u,\quad \dot {y} = \text{v},\quad \dot {\varphi } = \frac{{\mu (yu - x\text{v})}}{{{{a}^{2}} + \mu ({{x}^{2}} + {{y}^{2}})}},\quad {{u}^{2}} + {{\text{v}}^{2}} \leqslant {{V}^{2}},$Пусть в начальный t = 0 и конечный $t = T$ моменты времени выполнены следующие граничные условия:
(1.9)
$x(0) = {{x}_{0}},\quad y(0) = {{y}_{0}},\quad \varphi (0) = {{\varphi }_{0}},\quad \varphi (T) = {{\varphi }_{T}}.$Поставим задачу о поиске управлений $u$ и $\text{v}$, переводящих систему (1.8) из начального состояния в конечное, согласно (1.9), за минимальное время T.
В дальнейшем, помимо указанного в (1.9) терминального условия, при котором конечное положение материальной точки P не задано, будут кратко рассмотрены и иные, накладывающие на это положение некоторые ограничения.
2. Точное решение задачи в общем случае. Выполним следующую замену переменных [8]:
(2.1)
$\tilde {x} = \frac{{\sqrt \mu }}{a}x,\quad \tilde {y} = \frac{{\sqrt \mu }}{a}y,\quad \tilde {u} = \frac{u}{V},\quad \tilde {v} = \frac{\text{v}}{V},\quad \tilde {t} = \frac{{V\sqrt \mu }}{a}t$(2.2)
$\dot {x} = u,\quad \dot {y} = \text{v},\quad \dot {\varphi } = \frac{{yu - x\text{v}}}{{1 + {{x}^{2}} + {{y}^{2}}}},\quad {{u}^{2}} + {{\text{v}}^{2}} \leqslant 1.$Перейдем к полярным переменным
Здесь $\alpha $ и $r$ – полярные координаты вектора ${{{\mathbf{r}}}_{m}}$, а ${{r}_{\xi }}$ и $\xi $ – полярные координаты вектора управления в системе $Cxy$. Тогда из (2.2) имеем
(2.3)
$\dot {x} = \dot {r}cos\alpha - r\dot {\alpha }sin\alpha = {{r}_{\xi }}cos\xi ,\quad \dot {y} = \dot {r}sin\alpha + r\dot {\alpha }cos\alpha = {{r}_{\xi }}sin\xi {\kern 1pt} {\kern 1pt} .$Сначала умножим первое из уравнений (2.3) на $cos\alpha $ и сложим со вторым, умноженным на $sin\alpha $, а затем вычтем из второго уравнения (2.3), умноженного на $cos\alpha $, первое, умноженное на $sin\alpha $. Получим
Тогда, поскольку
(2.4)
$\dot {r} = {{r}_{\xi }}cos(\xi - \alpha ),\quad \dot {\alpha } = \frac{{{{r}_{\xi }}}}{r}sin(\xi - \alpha ),\quad \dot {\varphi } = - \frac{{r{{r}_{\xi }}sin(\xi - \alpha )}}{{1 + {{r}^{2}}}}.$Введя новые управления
(2.5)
$\dot {r} = \hat {u},\quad \dot {\alpha } = \frac{{\hat {v}}}{r},\quad \dot {\varphi } = - \frac{{r\hat {v}}}{{1 + {{r}^{2}}}}.$Заметим, что из второго и третьего соотношений в (2.5) следует, что направления изменения углов $\alpha $ и $\varphi $ всегда противоположны.
Граничные условия (1.9) примут вид
(2.6)
$r(0) = {{r}_{0}},\quad \alpha (0) = {{\alpha }_{0}},\quad \varphi (0) = {{\varphi }_{0}},\quad \varphi (T) = {{\varphi }_{T}}.$В дальнейшем всюду положим ${{\alpha }_{0}} = 0$ и ${{\varphi }_{0}} = 0$, поскольку, как видно из системы (2.5), это можно сделать без ограничения общности.
Применим принцип максимума Л.С. Понтрягина [9] и запишем гамильтониан для системы (2.5):
(2.7)
$\mathop {\dot {p}}\nolimits_r = \left( {\frac{{{{p}_{\alpha }}}}{{{{r}^{2}}}} + {{p}_{\varphi }}\frac{{1 - {{r}^{2}}}}{{\mathop {(1 + {{r}^{2}})}\nolimits^2 }}} \right)\hat {v},\quad \mathop {\dot {p}}\nolimits_\alpha = 0,\quad \mathop {\dot {p}}\nolimits_\varphi = 0.$Получаем оптимальные управления
(2.8)
${{\hat {u}}_{*}} = \frac{{{{p}_{r}}}}{{\sqrt {\mathop {\left( {\frac{{{{p}_{\alpha }}}}{r} - \frac{{{{p}_{\varphi }}r}}{{1 + {{r}^{2}}}}} \right)}\nolimits^2 + p_{r}^{2}} }},\quad {{\hat {v}}_{*}} = \frac{{\frac{{{{p}_{\alpha }}}}{r} - \frac{{{{p}_{\varphi }}r}}{{1 + {{r}^{2}}}}}}{{\sqrt {\mathop {\left( {\frac{{{{p}_{\alpha }}}}{r} - \frac{{{{p}_{\varphi }}r}}{{1 + {{r}^{2}}}}} \right)}\nolimits^2 + p_{r}^{2}} }}.$Разделим первое уравнение в (2.5) на второе и тем самым перейдем к новой независимой переменной $\alpha $, после чего подставим $\mathop {\hat {u}}\nolimits_* $ и ${{\hat {v}}_{*}}$. Тогда
(2.9)
$\frac{{dr}}{{d\alpha }} = r\frac{{\hat {u}}}{{\hat {v}}} = \frac{{{{p}_{r}}{{r}^{2}}(1 + {{r}^{2}})}}{{{{p}_{\alpha }}(1 + {{r}^{2}}) - {{p}_{\varphi }}{{r}^{2}}}}.$Выразим pr из (2.9):
(2.10)
${{p}_{r}} = \frac{{{{p}_{\alpha }}(1 + {{r}^{2}}) - {{p}_{\varphi }}{{r}^{2}}}}{{{{r}^{2}}(1 + {{r}^{2}})}}\frac{{dr}}{{d\alpha }}.$Разделим первое уравнение в (2.7) на второе уравнение в (2.5) и получим
(2.11)
$\frac{{d{{p}_{r}}}}{{d\alpha }} = \frac{{{{p}_{\alpha }}}}{r} + \frac{{{{p}_{\varphi }}r(1 - {{r}^{2}})}}{{\mathop {(1 + {{r}^{2}})}\nolimits^2 }}.$В дальнейшем для сокращения записей будем обозначать штрихом производные по $\alpha $. Продифференцируем правую часть (2.10) по $\alpha $ и приравняем правой части (2.11). Тогда
Обозначим $r{\text{'}} = p(r)$. Тогда, согласно [10], можно положить $r{\text{''}} = pdp{\text{/}}dr$, и это соотношение можно рассматривать как линейное дифференциальное уравнение относительно $\psi (r) = {{p}^{2}}$.
Поскольку угол поворота тела B в конечный момент времени задан, согласно (1.9), то ограничимся случаем ${{p}_{\varphi }} \ne 0$, в котором траектория отлична от прямой линии [8]. Следовательно,
(2.12)
$\psi (r) = {{C}_{0}}\mathop {\left( {\frac{{{{r}^{2}}(1 + {{r}^{2}})}}{{{{C}_{\alpha }} + {{C}_{\alpha }}{{r}^{2}} - {{r}^{2}}}}} \right)}\nolimits^2 - {{r}^{2}},$(2.13)
$\frac{{dr}}{{d\alpha }} = r\,{\text{ctg}}(\xi - \alpha ),\quad \frac{{d\varphi }}{{d\alpha }} = \frac{{ - {{r}^{2}}}}{{1 + {{r}^{2}}}}.$Из соотношения $\psi = {{(r{\text{'}})}^{2}}$ и первого уравнения в (2.13) можно получить равенство ${\text{ctg}}(\xi - \alpha ) = {{ \pm \sqrt {\psi (r)} } \mathord{\left/ {\vphantom {{ \pm \sqrt {\psi (r)} } r}} \right. \kern-0em} r}$. Это позволяет найти оптимальные управления ${{u}_{ * }}$ и ${{\text{v}}_{ * }}$ как функции текущих значений полярных координат $r$ и $\alpha $, тем самым построив синтез оптимального управления.
На основании соотношения $\psi = {{(r{\text{'}})}^{2}}$ и второго уравнения в (2.13) можно заметить, что текущие значения углов $\alpha $ и $\varphi $ монотонно зависят от r. Следовательно, в общем случае решение представляет собой спираль. В конечный момент времени имеем
(2.14)
${{\alpha }_{T}} = \pm \int\limits_{{{r}_{0}}}^{{{r}_{T}}} \frac{{dr}}{{\sqrt {\psi (r)} }},\quad {{\varphi }_{T}} = \mp \int\limits_{{{r}_{0}}}^{{{r}_{T}}} \frac{{{{r}^{2}}dr}}{{(1 + {{r}^{2}})\sqrt {\psi (r)} }},$Заметим, что в системе (2.2) при ${{u}^{2}} + {{\text{v}}^{2}} = 1$ время – натуральный параметр [11], т.е. равно длине кривой s. В свою очередь уравнение для длины кривой в полярных координатах [11] с учетом (2.12) имеет вид
Отсюда и из соотношений
(2.15)
$T = \left| {\int\limits_{{{r}_{0}}}^{{{r}_{T}}} \frac{{{{r}^{2}}(1 + {{r}^{2}})\sqrt {{{C}_{0}}} dr}}{{({{C}_{\alpha }} + {{C}_{\alpha }}{{r}^{2}} - {{r}^{2}})\sqrt {\psi (r)} }}} \right|.$Формулы (2.14) можно преобразовать к виду
(2.16)
${{\alpha }_{T}} = \pm \int\limits_{{{r}_{0}}}^{{{r}_{T}}} \frac{{rdr}}{{{{r}^{2}}\sqrt {\psi (r){\text{/}}{{r}^{2}}} }},\quad {{\phi }_{T}} = \mp \int\limits_{{{r}_{0}}}^{{{r}_{T}}} \frac{{rdr}}{{(1 + {{r}^{2}})\sqrt {\psi (r){\text{/}}{{r}^{2}}} }}.$Если в соотношениях (2.14) использовать замену переменной интегрирования $\zeta = {{r}^{2}}$ и положить $\psi (r) = \psi (\sqrt \zeta ) = \Psi (\zeta )$, то получим
Аналогично можно записать выражение (2.15) в форме
Отсюда вытекает, что выражения (2.14) и (2.15) можно свести к эллиптическим интегралам [12] относительно переменной $\zeta $.
В случае двухточечной задачи, когда ${{r}_{T}}$, ${{\alpha }_{T}}$ и ${{\varphi }_{T}}$ фиксированы, уравнения (2.14) позволяют найти постоянные C0 и ${{C}_{\alpha }}$ из граничных условий. Если же конечное значение ${{\alpha }_{T}}$ свободно, то ${{p}_{\alpha }} \equiv 0$. Тогда ${{C}_{\alpha }} = 0$ и $\psi (r) = {{C}_{0}}\mathop {(1 + {{r}^{2}})}\nolimits^2 - {{r}^{2}}$, а выражения (2.14), (2.15) сводятся к эллиптическим интегралам относительно переменной r. Второе соотношение в (2.14) позволяет найти C0, зная ${{r}_{0}}$, ${{r}_{T}}$ и ${{\varphi }_{T}}$.
Если свободно только значение ${{r}_{T}}$, то в силу соответствующего условия трансверсальности получаем ${{p}_{r}}(T) = 0$. Тогда на основании (2.9) имеем $\psi ({{r}_{T}}) = 0$, что позволяет выразить значение C0 из (2.12) через ${{r}_{T}}$ и ${{C}_{\alpha }}$. Значения ${{r}_{T}}$ и ${{C}_{\alpha }}$ найдем из соотношений (2.14). В частном случае правая часть уравнения (2.11) равна нулю при
Получаем ${{p}_{r}} \equiv 0$ и тем самым ${{\hat {u}}_{*}}(t) \equiv 0$ и ${{\hat {v}}_{*}}(t) \equiv \pm 1$, что означает движение по окружности с радиусом r0. Значение ${{C}_{0}} = {{4r_{0}^{2}} \mathord{\left/ {\vphantom {{4r_{0}^{2}} {{{{(1 + r_{0}^{2})}}^{4}}}}} \right. \kern-0em} {{{{(1 + r_{0}^{2})}}^{4}}}}$ следует из (2.12) для $\psi (r) \equiv 0$.
В дальнейшем ограничимся случаем, когда свободно не только значение ${{\alpha }_{T}}$, но и ${{r}_{T}}$, т.е. конечное положение материальной точки полностью произвольно, что соответствует (2.6). Тогда из (2.12) с учетом ${{C}_{\alpha }} = 0$ и $\psi ({{r}_{T}}) = 0$ имеем ${{C}_{0}} = {{r_{T}^{2}} \mathord{\left/ {\vphantom {{r_{T}^{2}} {{{{(1 + r_{T}^{2})}}^{2}}}}} \right. \kern-0em} {{{{(1 + r_{T}^{2})}}^{2}}}}$. Второе соотношение в (2.14) позволяет найти ${{r}_{T}}$ на основании условий (2.6), после чего из первого соотношения в (2.14) можно найти угол ${{\alpha }_{T}}$, а из (2.15) – значение функции Беллмана, т.е. $T$ как функцию r0, ${{\alpha }_{0}}$. Интересно, что в случае (2.6) интегралы для ${{\alpha }_{T}}$ и ${{\varphi }_{T}}$ в (2.14) не меняют свой вид при замене переменной $r$ на $1{\text{/}}r$.
Однако полученное решение не всегда удобно для применения. В робототехнике особый интерес представляет ситуация, когда $\mu \ll 1$ и ${{r}_{T}} \ll 1$, т.е. когда масса материальной точки $P$ мала по сравнению с массой тела $B$ и точка $P$ находится недалеко от центра масс системы $O$. В этом случае при движениях тела $B$ величина угла ${{\alpha }_{T}}$ поворота точки $P$ может быть значительной. Тогда возникает вопрос о возможности удовлетворительной аппроксимации формы траектории движения точки $P$ какой-либо простой кривой, что важно как для практических целей, так и для целей дальнейших теоретических исследований. Получить ответ на этот вопрос, основываясь только на формуле для угла ${{\alpha }_{T}}$ в (2.14), затруднительно. Поэтому целесообразно решить задачу оптимального управления для $\mu \ll 1$ отдельно.
3. Решение задачи при $\mu \ll 1$. В этом случае вместо замены переменных (2.1) сделаем замену
(3.1)
$\tilde {t} = \frac{{Vt}}{a},\quad \tilde {x} = \frac{x}{a},\quad \tilde {y} = \frac{y}{a},\quad \tilde {u} = \frac{u}{V},\quad \tilde {v} = \frac{\text{v}}{V},\quad z = \frac{\varphi }{\mu }.$Тогда, сохранив прежние обозначения, получим из (1.8)
(3.2)
$\dot {x} = u,\quad \dot {y} = \text{v},\quad \dot {z} = \frac{{yu - x\text{v}}}{{1 + \mu ({{x}^{2}} + {{y}^{2}})}},\quad {{u}^{2}} + {{\text{v}}^{2}} \leqslant 1.$Используя то, что $\mu \ll 1$, уравнения (3.2) можно упростить и заменить системой
(3.3)
$\dot {x} = u,\quad \dot {y} = \text{v},\quad \dot {z} = yu - x\text{v},\quad {{u}^{2}} + {{\text{v}}^{2}} \leqslant 1.$К системе (3.3) применим принцип максимума Л.С. Понтрягина [9] и запишем гамильтониан
где ${{p}_{x}}$, ${{p}_{y}}$ и ${{p}_{z}}$ – сопряженные переменные, удовлетворяющие уравнениям(3.5)
$\mathop {\dot {p}}\nolimits_x = {{p}_{z}}\text{v},\quad \mathop {\dot {p}}\nolimits_y = - {{p}_{z}}u,\quad \mathop {\dot {p}}\nolimits_z = 0.$Максимум гамильтониана (3.4) как функции управлений $u$ и $\text{v}$ с учетом ограничения, указанного в (3.3), достигается, если
(3.6)
$\begin{gathered} u = ({{p}_{x}} + {{p}_{z}}y){\text{/}}D,\quad \text{v} = ({{p}_{y}} - {{p}_{z}}x){\text{/}}\Upsilon , \\ \Upsilon = \sqrt {{{{({{p}_{x}} + {{p}_{z}}y)}}^{2}} + {{{({{p}_{y}} - {{p}_{z}}x)}}^{2}}} . \\ \end{gathered} $При этом ограничение в (3.3) превращается в равенство ${{u}^{2}} + {{\text{v}}^{2}} = 1$, т.е. скорость точки $P$ максимальна, что обычно для управлений, оптимальных по быстродействию.
Из соотношений (3.3) и (3.5) следует, что
(3.7)
$\mathop {\dot {p}}\nolimits_x = {{p}_{z}}\dot {y},\quad \mathop {\dot {p}}\nolimits_y = - {{p}_{z}}\dot {x},\quad \mathop {\dot {p}}\nolimits_z = 0.$Проинтегрируем (3.7) и получим
где ${{c}_{x}}$, ${{c}_{y}}$ и c – постоянные интегрирования. Подставив равенства (3.8) в формулы (3.6), имеем(3.9)
$\begin{gathered} u = (2cy + {{c}_{x}}){\text{/}}\Upsilon ,\quad \text{v} = ( - 2cx + {{c}_{y}}){\text{/}}\Upsilon , \\ \Upsilon = \sqrt {{{{(2cy + {{c}_{x}})}}^{2}} + {{{( - 2cx + {{c}_{y}})}}^{2}}} . \\ \end{gathered} $Соотношения (3.9) определяют оптимальные управления. Если подставить их в выражение для гамильтониана (3.4), то можно получить, что $H = \Upsilon $. Поскольку система дифференциальных уравнений (3.3) автономна, гамильтониан (3.4) для рассматриваемой задачи при оптимальном управлении является, согласно [9], постоянным и положительным. Кроме того, вектор сопряженных переменных может быть нормирован на любую постоянную положительную величину. Поэтому без потери общности можно положить $H = \Upsilon = 1$. Теперь заметим, что, согласно формуле для $\Upsilon $ из (3.9), равенство ${{\Upsilon }^{2}} = 1$ можно записать в виде
(3.10)
$4{{c}^{2}}({{x}^{2}} + {{y}^{2}}) + 4c({{c}_{x}}y - {{c}_{y}}x) + c_{x}^{2} + c_{y}^{2} = 1.$Уравнение (3.10) при $c \ne 0$ задает окружность. Следовательно, в общем случае оптимальные траектории точки P по отношению к телу $B$ представляют собой дуги окружностей.
Подставим $\Upsilon = 1$ в формулы (3.9) для $u$ и $\text{v}$, а получившиеся в результате этой подстановки выражения – в уравнения (3.3) для $x$ и $y$. Получим
Сначала рассмотрим общий случай. Интегрирование системы дифференциальных линейных уравнений (3.11) дает
(3.12)
$\begin{gathered} x(t) = {{c}_{y}}{\text{/}}(2c) + Acos2ct + Dsin2ct, \\ y(t) = - {{c}_{x}}{\text{/}}(2c) - Asin2ct + Dcos2ct,\quad c \ne 0, \\ \end{gathered} $Подставив формулы (3.13) в уравнения (3.12), найдем
(3.14)
$\begin{gathered} x(t) = {{x}_{0}} - A + Acos2ct + Dsin2ct, \\ y(t) = {{y}_{0}} - D - Asin2ct + Dcos2ct,\quad c \ne 0. \\ \end{gathered} $Подставим соотношения (3.14) в уравнения (3.3) для получения оптимальных управлений. Имеем
(3.15)
$\begin{gathered} u(t) = 2с ( - Asin2ct + Dcos2ct), \\ \text{v}(t) = 2с ( - Acos2ct - Dsin2ct),\quad c \ne 0. \\ \end{gathered} $С учетом связи ${{u}^{2}} + {{\text{v}}^{2}} = 1$ между оптимальными управлениями формулы (3.15) дают
Теперь подставим выражения (3.14) и (3.15) в уравнение для $\dot {z}$ из (3.3) и получим
(3.17)
$\dot {z} = 2c(({{A}^{2}} + {{D}^{2}})(1 - cos2ct) + ({{x}_{0}}A + {{y}_{0}}D)cos2ct + ({{x}_{0}}D - {{y}_{0}}A)sin2ct),\quad c \ne 0.$Проинтегрируем дифференциальное уравнение (3.17) и найдем
(3.18)
$\begin{gathered} z(T) - z(0) = ({{A}^{2}} + {{D}^{2}})(2cT - sin2cT) + \\ + \;({{x}_{0}}A + {{y}_{0}}D)sin2ct + ({{x}_{0}}D - {{y}_{0}}A)(1 - cos2ct),\quad c \ne 0. \\ \end{gathered} $Перед тем, как решить поставленную задачу для краевых условий (1.9), рассмотрим случай, когда конечное положение системы фиксировано:
Подставив решение (3.14) в граничные условия (1.9) и (3.19), получим
(3.20)
$\begin{array}{*{20}{c}} {A = \frac{1}{2}({{x}_{0}} - {{x}_{1}} + ({{y}_{0}} - {{y}_{1}})\,{\text{ctg}}\,\phi ),\quad \phi = cT,} \\ {D = \frac{1}{2}({{y}_{0}} - {{y}_{1}} - ({{x}_{0}} - {{x}_{1}})\,{\text{ctg}}\,\phi ),\quad c \ne 0.} \end{array}$Подставим (3.20) в условие (3.16). Тогда
(3.21)
${{T}^{2}} = \rho _{1}^{2}\mathop {\left( {\frac{\phi }{{sin\phi }}} \right)}\nolimits^2 ,\quad {{\rho }_{1}} = \sqrt {{{{({{x}_{0}} - {{x}_{1}})}}^{2}} + {{{({{y}_{0}} - {{y}_{1}})}}^{2}}} .$Теперь подставим соотношения (3.20) в формулу (3.18) и получим
(3.22)
$\begin{array}{*{20}{c}} {4F = \rho _{1}^{2}f(\phi ),\quad f(\phi ) = \frac{{2\phi - sin2\phi }}{{si{{n}^{2}}\phi }},} \\ {F = {{z}_{1}} - {{z}_{0}} - {{y}_{0}}{{x}_{1}} + {{x}_{0}}{{y}_{1}},\quad {{z}_{0}} = z(0).} \end{array}$На интервале $\left| \phi \right| < \pi $ функция $f(\phi )$ – нечетная и монотонная, причем растет от $ - \infty $ до $\infty $.
Теперь опишем процедуру решения задачи оптимального быстродействия при терминальных условиях (3.19). Сначала рассмотрим общий случай $F \ne 0$ и ${{\rho }_{1}} > 0$. В этом случае уравнение (3.22) для поиска $\phi $ имеет единственное решение на интервале $\phi \in ( - \pi ,\pi )$, такое, что $\phi \ne 0$, sign $\phi $ = = ${\text{sign}}\,F$. После нахождения $\phi $ можно вычислить T, используя соотношение
следующее из (3.21), а также найти $c = \phi {\text{/}}T \ne 0$. Постоянные A и D заданы соотношениями (3.20), оптимальные управления – формулами (3.15), а оптимальная траектория – уравнениями (3.14).Теперь рассмотрим вырожденный случай $F = 0$, ${{\rho }_{1}} > 0$. В этом случае из определения $\phi $ в (3.20), соотношения для $F$ в (3.22), а также уравнения (3.23) следует, что $\phi = 0$, $c = 0$ и $T = {{\rho }_{1}}$. Тогда из формул (3.6) и (3.11) вытекает, что оптимальная траектория – отрезок прямой. С учетом граничных условий получим
В этом случае решение также единственно.
Остается рассмотреть особый случай, когда ${{\rho }_{1}} = 0$ и $F \ne 0$. В соответствии с (3.21) и (3.22)
Учитывая, согласно (3.22), асимптотическое поведение функции $f(\phi )$ при $\left| \phi \right| \to \pi $, а также (3.24), получаем
(3.25)
$\phi = \pi \,{\text{sign}}\,F,\quad T = \sqrt {2\pi \left| F \right|} ,\quad c = \phi {\text{/}}T.$В этом случае уравнения (3.20) для A и D содержат особенности. Обращаясь к соотношениям (3.14) в случае (3.24), можно заметить, что они удовлетворяют терминальным условиям (3.19) для любых A и D при условии, что выполнено соотношение (3.16). В итоге оптимальную траекторию и оптимальное управление можно записать в следующем виде:
(3.26)
$\begin{gathered} x(t) = {{x}_{0}} + {{R}_{1}}(cos(2ct - \theta ) - cos\theta ),\quad {{R}_{1}} = T{\text{/}}(2\pi ), \\ y(t) = {{y}_{0}} - {{R}_{1}}(sin(2ct - \theta ) + sin\theta ), \\ u(t) = - {\kern 1pt} {\kern 1pt} {\text{sign}}\,Fsin(2ct - \theta ),\quad \text{v}(t) = - {\kern 1pt} {\kern 1pt} {\text{sign}}\,Fcos(2ct - \theta ), \\ \end{gathered} $Теперь рассмотрим задачу с исходными граничными условиями (1.9). В этом случае для поиска значений x(T) и y(T) нужно использовать соответствующие условия трансверсальности. Тогда вместо (3.21) получим
(3.27)
$A = ({{x}_{0}} - {{y}_{0}}\,{\text{tg}}\,\phi ){\text{/}}2,\quad D = ({{x}_{0}}\,{\text{tg}}\,\phi + {{y}_{0}}){\text{/}}2.$Введем обозначения
Функция $g(\phi )$ – нечетная и монотонная при $\left| \phi \right| < \pi {\text{/}}2$. На этом интервале она растет от $ - \infty $ до $\infty $.
В общем случае при $z(T) \ne z(0)$ и ${{\rho }_{0}} \ne 0$ решение можно получить аналогично тому, как это было сделано для случая фиксированной конечной точки. Сначала необходимо найти величину $\phi $ из уравнения
Значение $\phi \ne 0$ единственно и $\left| \phi \right| < \pi {\text{/}}2$, а ${\text{sign}}\,\phi = {\text{sign}}({{z}_{1}} - {{z}_{0}})$. Тогда можно найти $T$ и $c$, используя соотношения
Постоянные A и D заданы формулами (3.27), а единственная оптимальная траектория и соответствующее ей оптимальное управление заданы соотношениями (3.14) и (3.15).
Вырожденный случай ${{z}_{1}} = {{z}_{0}}$ тривиален, поскольку начальное положение точки P совпадает с конечным и T = 0.
В особом случае, когда ${{\rho }_{0}} = 0$ и ${{z}_{1}} \ne {{z}_{0}}$, точка P в начальный момент времени t = 0 находится в центре масс $O$ рассматриваемой механической системы, который в данном случае совпадает с центром масс $C$ тела $B$. Тогда по аналогии с (3.25) получим
(3.29)
$\phi = \frac{\pi }{2}{\text{sign}}({{z}_{1}} - {{z}_{0}}),\quad T = \sqrt {\pi \left| {{{z}_{1}} - {{z}_{0}}} \right|} ,\quad c = \frac{\phi }{T}.$Соответствующие оптимальные управления и оптимальные траектории неединственны. Их можно найти с помощью соотношений, похожих на формулы (3.26):
Заметим, что можно распространить использованный при $\mu \ll 1$ подход и на общий случай, когда параметр $\mu < 1$, но не является малым. Полученные выше траектории (3.14) и соответствующие им законы управления (3.15) также могут быть использованы в этом случае, но с учетом следующего замечания. Для определенности рассмотрим ситуацию, когда конечное состояние системы фиксировано (3.19) и $c \ne 0$. Как и прежде, постоянные $A$ и $D$ заданы формулами (3.20). Для поиска значений двух постоянных $c$ и $T$ есть два соотношения: условие (3.16) и равенство
(3.30)
${{z}_{1}} - {{z}_{0}} = \int\limits_0^T \omega (t)dt,\quad \omega (t) = \frac{{yu - x\text{v}}}{{1 + \mu ({{x}^{2}} + {{y}^{2}})}},$4. Сравнение точного решения с приближенным. Хотя уравнения (3.3) и можно рассматривать как приближенные для исходной системы (1.8) при $\mu \ll 1$, однако траектории движения точки $P$, получающиеся в результате решения оптимизационной задачи для (3.3), нельзя без дополнительного доказательства считать непрерывно стремящимися при $\mu \to 0$ к траекториям, являющимся решением такой же задачи для (1.8). Это объясняется существенно нелинейным характером систем (1.8) и (3.3) и свойствами оптимального решения, которое может сложным образом зависеть от параметра $\mu $.
Точное решение, заданное формулами (2.14) и (2.15) в случае свободного правого конца траектории, т.е. при ${{C}_{\alpha }} = 0$, после замены переменных (3.1) имеет вид
(4.1)
$\begin{gathered} \alpha (r) = \pm \int\limits_{{{r}_{0}}}^r \frac{{d\varrho }}{{\sqrt {\psi (\varrho )} }},\quad \varphi (r) = \mp \int\limits_{{{r}_{0}}}^r \frac{{\mu {{\varrho }^{2}}d\varrho }}{{(1 + \mu {{\varrho }^{2}})\sqrt {\psi (\varrho )} }}, \\ t(r) = \left| {\int\limits_{{{r}_{0}}}^r \frac{{(1 + \mu {{\varrho }^{2}})\sqrt {{{C}_{0}}} d\varrho }}{{\sqrt {\psi (\varrho )} }}} \right|,\quad {{C}_{0}} = {{\mu r_{T}^{2}} \mathord{\left/ {\vphantom {{\mu r_{T}^{2}} {\mathop {(1 + \mu r_{T}^{2})}\nolimits^2 ,}}} \right. \kern-0em} {\mathop {(1 + \mu r_{T}^{2})}\nolimits^2 ,}} \\ \psi (\varrho ) = {{C}_{0}}(1{\text{/}}(\mu r_{T}^{2}) - \mu {{\varrho }^{2}})(r_{T}^{2} - {{\varrho }^{2}}),\quad {{r}_{T}} = \sqrt {x_{T}^{2} + y_{T}^{2}} . \\ \end{gathered} $Здесь $\alpha $ и $r$ – полярные координаты точки $P$ в системе $Cxy$. Заметим, что по-прежнему для упрощения записей будем полагать $\alpha (0) = 0$ и $\varphi (0) = 0$.
С точки зрения робототехники наибольший интерес представляет случай, когда ${{r}_{T}} < 1$, что с учетом условия $\mu \ll 1$ дает ${{r}_{T}}\sqrt \mu < 1$. Кроме того, без ограничения общности можно полагать $\alpha \geqslant 0$. Тогда $r \leqslant {{r}_{T}}$ и интегралы в (4.1) можно записать, используя обычную [12] подстановку $\varrho \, = \,{{r}_{T}}\,{\text{sin}}\,\eta $, в следующей форме:
(4.2)
$\begin{gathered} \alpha (r) = \int\limits_{{{\eta }_{0}}}^{{{\eta }_{r}}} \frac{{(1 + \mu r_{T}^{2})d\eta }}{{\sqrt {1 - {{\mu }^{2}}r_{T}^{4}si{{n}^{2}}\eta } }},\quad {{\eta }_{r}} = arcsin\frac{r}{{{{r}_{T}}}}, \\ \varphi (r) = - \alpha (r) + \int\limits_{{{\eta }_{0}}}^{{{\eta }_{r}}} \frac{{(1 + \mu r_{T}^{2})d\eta }}{{(1 + \mu r_{T}^{2}si{{n}^{2}}\eta )\sqrt {1 - {{\mu }^{2}}r_{T}^{4}si{{n}^{2}}\eta } }}, \\ t(r) = {{r}_{T}}\int\limits_{{{\eta }_{0}}}^{{{\eta }_{r}}} \frac{{(1 + \mu r_{T}^{2}si{{n}^{2}}\eta )d\eta }}{{\sqrt {1 - {{\mu }^{2}}r_{T}^{4}si{{n}^{2}}\eta } }},\quad {{\eta }_{0}} = arcsin\frac{{{{r}_{0}}}}{{{{r}_{T}}}}. \\ \end{gathered} $Как было указано выше, все интегралы в (4.2) – эллиптические и не могут быть взяты в элементарных функциях. Однако можно воспользоваться тем, что все они содержат выражение $1 - {{\mu }^{2}}r_{T}^{4}si{{n}^{2}}\eta $, которое, в силу допущений ${{r}_{T}} < 1$ и $\mu \ll 1$, можно положить тождественно равным единице. Тогда нетрудно найти все интегралы в (4.2) аналитически и записать
(4.3)
$\begin{gathered} \alpha (r) = {{\chi }^{2}}({{\eta }_{r}} - {{\eta }_{0}}) + O({{\mu }^{2}}),\quad \chi = \sqrt {\mu r_{T}^{2} + 1} , \\ \varphi (r) = - \alpha (r) + \chi ({\text{arctg}}(\chi {\text{tg}}\,{{\eta }_{r}}) - {\text{arctg}}(\chi {\text{tg}}\,{{\eta }_{0}})) + O({{\mu }^{2}}), \\ \varphi ({{r}_{T}}) = - \alpha ({{r}_{T}}) + \chi \pi {\text{/}}2 - \chi {\text{arctg}}(\chi {\text{tg}}\,{{\eta }_{0}}) + O({{\mu }^{2}}), \\ t(r) = {{r}_{T}}({{\eta }_{r}} - {{\eta }_{0}}) + r_{T}^{3}\left( { - \frac{1}{4}sin2{{\eta }_{r}} + \frac{1}{2}{{\eta }_{r}} + \frac{1}{4}sin2{{\eta }_{0}} - \frac{1}{2}{{\eta }_{0}}} \right)\mu + O({{\mu }^{2}}). \\ \end{gathered} $Из выражения для $\alpha (r)$ в (4.3) можно получить
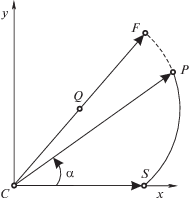
(4.4)
$r(\alpha ) = {{r}_{T}}sin\left( {\frac{\alpha }{{{{\chi }^{2}}}} + {{\eta }_{0}} + O({{\mu }^{2}})} \right) = {{r}_{T}}sin((1 - \mu r_{T}^{2})\alpha + {{\eta }_{0}}) + O({{\mu }^{2}}).$Уравнение (4.4) аппроксимирует окружность радиусом ${{r}_{T}}{\text{/}}2$, проходящую через начало системы координат $Cxy$. На рис. 2 центр этой окружности – точка $Q$. Траектория материальной точки $P$ – дуга этой окружности, начинающаяся в точке $S$ и кончающаяся в точке $F$. Как следует из формул (4.3), тело B при этом поворачивается на угол
(4.5)
$\varphi (r) = - \frac{1}{4}r_{T}^{2}\left( {2{{\eta }_{r}} - 2{{\eta }_{0}} - sin2{{\eta }_{r}} + sin2{{\eta }_{0}}} \right)\mu + O({{\mu }^{2}}).$В случае, когда ${{r}_{0}} = 0$, в конечный момент времени $T$ из формул (4.3) и (4.5) получаем
(4.6)
$\alpha ({{r}_{T}}) = \frac{\pi }{2} + r_{T}^{2}\mu + O({{\mu }^{2}}),\quad z(T) \equiv \frac{{\varphi ({{r}_{T}})}}{\mu } = - \frac{\pi }{4}r_{T}^{2} + O\left( \mu \right),\quad T = \frac{\pi }{2}{{r}_{T}} + \frac{\pi }{4}r_{T}^{3}\mu + O({{\mu }^{2}}).$Если исключить слагаемые, зависящие от $\mu $, из соотношений (4.4) и (4.6), то можно заметить, что при ${{r}_{0}} = 0$ оптимальная траектория является половиной окружности радиуса ${{r}_{T}}{\text{/}}2$ с центром на оси ординат, причем эта окружность проходит через начало системы координат Cxy.
Итак, приближенное решение, полученное для случая $\mu \ll 1$, близко к оптимальному в следующем смысле: оптимальная траектория является окружностью с точностью до слагаемых порядка $O({{\mu }^{2}})$; оптимальные значения полярных координат точки P и величина угла поворота тела $B$ отличаются от соответствующих приближенных значений на величины порядка $O(\mu )$; приближенная величина функционала равна оптимальному значению с точностью до слагаемых порядка $O(\mu )$.
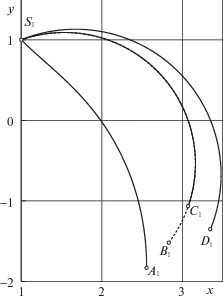
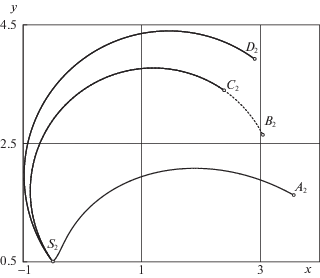
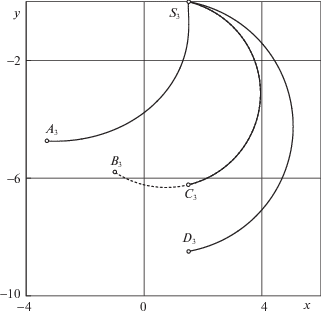
5. Результаты вычислений. На рис. 3–5 и связанной с ними таблице показаны три примера применения полученных результатов для различных значений параметров $\mu $ и ${{\varphi }_{T}}$, а также разных начальных положений точки $P$. В дальнейшем всюду будем понимать под $i$ номер примера, причем первый из них соответствует рис. 3. Точки ${{S}_{i}}$ на рисунках показывают начальные положения материальной точки P, а координаты этих точек, как и соответствующие значения величин ${{M}_{i}}$, ${{m}_{i}}$, ${{\mu }_{i}}$ и ${{a}_{i}}$, даны в таблице. Значения ${{\varphi }_{{Ti}}}$ – требуемые углы поворота твердого тела $B$ для каждого из примеров. Во всех случаях значение $V$ было принято равным единице. Точки ${{A}_{i}}$ – конечные положения материальной точки P, вычисленные, согласно первой из формул (2.16). Траектории, начинающиеся в ${{S}_{i}}$ и кончающиеся в ${{A}_{i}}$, оптимальны и дают значения времени оптимального быстродействия, равные ${{T}_{{Ai}}}$. Траектории, начинающиеся в точках ${{S}_{i}}$ и кончающиеся в точках ${{C}_{i}}$, соответствуют точному решению упрощенной задачи (3.3) и величинам времени оптимального быстродействия, равным ${{T}_{{Ci}}}$. Эти траектории являются дугами окружностей. Значения угла поворота твердого тела $B$ для них всегда меньше ${{\varphi }_{{Ti}}}$ и равны ${{\varphi }_{{Ci}}}$. Для удобства сравнения с остальными решениями на рисунках отмечены точки ${{B}_{i}}$, которые получены продолжением по окружности оптимальных фрагментов окружностей, т.е. соответствующим перемещением материальной точки $P$ и связанным с ним поворотом твердого тела $B$, вплоть до получения требуемых величин ${{\varphi }_{{Ti}}}$. Эти траектории также являются дугами окружностей. Значения времени движения для них равны ${{T}_{{Bi}}}$. Траектории, начинающиеся в ${{S}_{i}}$ и кончающиеся в ${{D}_{i}}$, соответствуют приближенному решению, полученному с использованием формулы (3.30). Значения времени движения для них равны ${{T}_{{Di}}}$.
Из таблицы видно, что решениям, оканчивающимся в точках ${{A}_{i}}$, действительно соответствуют меньшие значения времени движения по сравнению со значениями для точек ${{T}_{{Bi}}}$ и ${{T}_{{Di}}}$. С другой стороны, несмотря на то, что траектории для различных алгоритмов значительно отличаются друг от друга, величины времени движения близки друг к другу. Интересно, что значения ${{T}_{{Bi}}}$ во всех трех случаях оказались лучше значений ${{T}_{{Di}}}$ и отличаются от оптимальных всего лишь на несколько тысячных.
Заключение. Итак, для получения решения поставленной задачи о повороте твердого тела при помощи внутренней массы можно использовать три алгоритма. Первый представляет собой точное оптимальное решение (2.16) исходной задачи. Его недостаток – необходимость вычисления значения эллиптического интеграла. Второй алгоритм является точным оптимальным решением приближенной задачи (3.3). Его преимущество в том, что оптимальные траектории представляют собой дуги окружности, а недостаток состоит в том, что реальный угол поворота твердого тела оказывается меньше требуемого. Третий алгоритм основан на том же самом решении, что и второй, но в его рамках краевое условие на угол поворота тела выполняется точно. Однако это решение является приближенным. В рассмотренных численных примерах различие между этими алгоритмами с точки зрения времени движения мало, но траектории отличаются значительно.
Полученные результаты могут представлять интерес с точки зрения робототехники для так называемых капсульных роботов, не имеющих внешних движителей и способных перемещаться за счет движения внутренних масс. Такие роботы могут быть герметичными.
Эти результаты, в принципе, могут быть приложимы для управления ориентацией космических аппаратов.
Таблица 1.
Исходные данные и результаты вычислений
| $i$ | 1 | 2 | 3 |
|---|---|---|---|
| ${{M}_{i}}$ | 900 | 800 | 1200 |
| ${{m}_{i}}$ | 100 | 200 | 400 |
| ${{\mu }_{i}}$ | 0.10 | 0.20 | 0.25 |
| ${{a}_{i}}$ | 2 | 3 | 4 |
| ${{S}_{i}}$ | (1.0; 1.0) | (–0.5; 0.5) | (1.5; 0.0) |
| ${{A}_{i}}$ | (2.56; –1.83) | (3.57; 1.62) | (–3.30; –4.74) |
| ${{B}_{i}}$ | (2.82; –1.53) | (3.04; 2.65) | (–1.07; –5.74) |
| ${{C}_{i}}$ | (3.07; –1.07) | (2.39; 3.39) | (1.50; –6.22) |
| ${{D}_{i}}$ | (3.35; –1.35) | (2.91; 3.91) | (1.50; –8.48) |
| ${{\varphi }_{{Ti}}}$ | 0.2 | 0.3 | 0.5 |
| ${{\varphi }_{{Ci}}}$ | 0.166 | 0.234 | 0.342 |
| ${{T}_{{Ai}}}$ | 4.15 | 6.73 | 10.9 |
| ${{T}_{{Bi}}}$ | 4.17 | 6.81 | 11.2 |
| ${{T}_{{Ci}}}$ | 3.64 | 5.81 | 8.54 |
| ${{T}_{{Di}}}$ | 4.22 | 6.96 | 12.0 |
Список литературы
Filaretov V.F., Yukhimets D.A. Planning Smooth Paths for Mobile Robots in an Unknown Environment // Journal of Computer and Systems Sciences International. 2017. V. 56. № 4. P. 738–748.
Lapshin V.V. Robot Motion Control in Zero-Gravity Conditions // Journal of Computer and Systems Sciences International. 2017. V. 56. № 1. P. 157–163.
Vorochaeva L.Yu., Yatsun A.S., Yatsun S.F. Simulation of the Motion of a Five-Link Crawling Robot with Controlled Friction on a Surface Having Obstacles // Journal of Computer and Systems Sciences International. 2017. V. 56. № 3. P. 527–552.
Schmoeckel F., Worn H. Remotely Controllable Microrobots Acting as Nano Positioners and Intelligent Tweezers in Scanning Electron Microscopes (SEMs) // Proc. Intern. Conf. Robotics and Automation, IEEE. V. 4. N.Y., 2001. P. 3903–3913.
Vartholomeos P., Papadopoulos E. Dynamics, Design and Simulation of a Novel Microrobotic Platform Employing Vibration Microactuators // Transactions of ASME. J. Dynamical Systems, Measurement and Control. 2006. V. 128. P. 122–133.
Chernousko F.L. Two-dimensional Motions of a Body Containing Internal Moving Masses // Meccanica. 2016. V. 51. № 12. P. 3203–3209.
Черноусько Ф.Л. Оптимальное управление движением двухмассовой системы // ДАН. 2018. Т. 480. № 5. С. 528–532.
Шматков А.М. Поворот тела за кратчайшее время перемещением точечной массы // ДАН. 2018. Т. 481. С. 498–502.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1969. 384 с.
Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1976. 576 с.
Рашевский П.К. Курс дифференциальной геометрии. М.–Л.: ГИТТЛ, 1950. 428 с.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Физматгиз, 1962. 1100 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления