Известия РАН. Теория и системы управления, 2019, № 3, стр. 106-112

Введение. Система визуальных маркеров состоит из специальных изображений, размещаемых в окружающей среде, и распознавающего устройства, которое считывает и декодирует зашифрованную в маркерах информацию [1]. Самыми известными из существующих визуальных маркеров являются Bar- и QR-коды, представляющие собой последовательность черно-белых полос или квадратов [2]. Такие маркеры используются повсеместно для тэгирования товаров в магазинах, шифрования ссылок на интернет-ресурсы и размещения их в виде изображений в нужных местах, навигации автономных систем по маркерам-якорям [3] и т.д.

Одним из ключевых недостатков существующих решений является то, что как система генерации, так и система распознавания маркеров сделаны независимо друг от друга и придуманы человеком. Во-первых, такие визуальные коды способны закодировать неоптимальное количество бит, так как контрастные черно-белые пятна являются лишь малым подмножеством семейства всех возможных визуальных маркеров и спроектированы вручную, существуют более эффективные способы кодирования информации. Во-вторых, распознавание таких маркеров требует фронтального и близкого расположения объектива камеры к маркеру; дизайн QR-кодов не предусматривает возможность их считывания в плохих условиях может быть значимым негативных фактором их использования.

1. Предлагаемое решение. В данной статье объединяются процессы генерации и распознавания маркеров, позволяя алгоритму самому решить, как именно должны выглядеть маркеры, которые впоследствии будут считываться этой же моделью. Оба процесса объединены в одну общую обучаемую систему, которая будет обучать генерацию и распознавание одновременно, оптимизируя эти процессы друг под друга. После обучения модели генерации и распознавания можно использовать раздельно, по своей структуре они будут идентичны существующим решениям, что даст возможность безболезненно заменить устаревшие маркеры на новые без дополнительных технических сложностей.

Представленная система обучаемых маркеров генерирует разные типы визуальных кодов и соответствующих им систем распознавания в зависимости от поставленной задачи. В процессе обучения можно эмулировать условия освещения, углы наклона, количество передаваемой информации, размер маркеров и т.д. Это позволяет создавать маркеры, оптимизированные конкретно под заданную цель [4, 5].

2. Постановка задачи. Определим код как последовательность бит:

Назовем маркером M_k(b_n) изображение размера k × k × 3, соответствующему коду b_n. Пусть ${{\mathcal{S}}_{k}}$(b_n, ${{\theta }_{\mathcal{S}}}$) – функция кодирования, преобразующая код в маркер. Параметры кодировщика ${{\theta }_{\mathcal{S}}}$ изначально задаются случайно и определяются в процессе обучения модели. Тогда для заданного кода b_n маркер можно получить следующим образом:

Определим фоновый патч P_s как изображение s × s × 3, случайно выбранное из большой неразмеренной базы картинок окружающей среды.

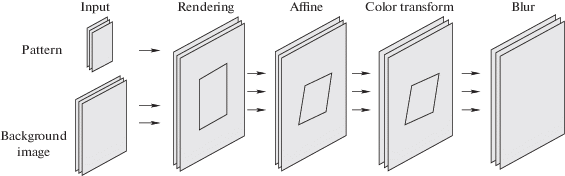
Определим функцию рендеринга $\mathcal{R}$(M_k, P_s, ${{\phi }_{\mathcal{R}}}$), которая для заданных маркера и фонового патча возвращает паттертн MP_s размера s × s × 3. Паттерн – это изображение, в котором маркер помещен в центр фонового патча, а ${{\phi }_{\mathcal{R}}}$ – необучаемые параметры трансформаций (аффинное преобразование, цветовая коррекция, размытие), которые детально будут описаны в следующем разделе.

Введем понятие функции локализации $\mathcal{L}$(MP_s, ${{\theta }_{\mathcal{L}}}$), которая возвращает координаты углов маркера, размещенного в паттерне, в виде восьми действительных чисел c(MP_s) = (x₁, y₁, …, x₄, y₄). На этапе обучения настоящие значения координат углов однозначно определяются параметрами функции рендеринга ${{\phi }_{\mathcal{R}}}$.

Наконец, функция декодирования ${{\mathcal{D}}_{n}}$(MP_s, c, ${{\theta }_{\mathcal{D}}}$) предсказывает зашифрованный в исходном маркере код как

Функция декодирования возвращает реальные числа, которые могут быть трансформирования в оригинальный код как

Финальная структура модели записывается в компактной форме

или, более детально, как где Θ = (${{\theta }_{\mathcal{S}}}$, ${{\theta }_{\mathcal{L}}}$, ${{\theta }_{\mathcal{D}}}$) – обучаемые параметры.

Для обучения модели и оценки качества решения введем функцию потерь, основанную на поэлементной функции сигмоиды:

L стремится к –1 в случае идеального распознавания и к 0 для худшего случая. После определения функции потерь обучение модели можно записать как где ${{\mathbb{E}}_{{x\sim p(x)}}}$F(x) – математическое ожидание функции F по случайной величине x из распределения p(x).

В процессе обучения коды для (2.7) генерируются случайно из равномерного распределения b_n ~ U(n) = {–1, 1}ⁿ. Как только код сгенерирован, он подается на вход общей модели (2.5), итоговое предсказание меряется в (2.6). Кроме глобальной функции потерь каждая из подсетей обучается локально на стандартных функциях потерь типа кроссэнтропии и метода наименьших квадратов, которые не представляют особого интереса.

3. Архитектура слоев сети. В данной секции описывается структура новых слоев нейронной сети, которые используются в итоговой модели.

3.1. Слой рендеринга размещает маркер в центре фонового патча. Он заменяет субтензор в оригинальном изображении на матрицу пикселей маркера. Процесс реализован так, что преобразование дифференцируемо, это позволяет обучать модель, содержащую слой рендеринга, с помощью метода обратного распространения ошибки.

3.2. Слой трансформации осуществляет аффинную трансформацию паттерна, которое уже содержит маркер. Несмотря на то, что преобразуется изображение целиком, нас интересуют только изменения в форме маркера, незначительные изменения фонового патча не влияют на обучающий процесс. Слой трансформации эмулирует пространственные сдвиги и повороты, как будто бы если камера снимает маркер со случайного расстояния и под случайным углом.

Аффинное преобразование определено матрицей и столбцом

переводящими координаты линейно. Такая трансформация полностью описывается шестью параметрами. Эти параметры случайно выбираются из нормального распределения с заранее заданным стандартным отклонением и средним, соответствующим тождественной трансформации. Так как преобразование применяется к изображению, изменение координат недостаточно, необходимо пересчитать значения цветов пикселей. Это осуществляется с помощью билинейной интерполяции [6], которая, как и аффинное преобразование, дифференцируема и обратное распространение ошибки легитимно.

3.3. Слой цветовой коррекции случайно изменяет цвет, яркость и контрастность изображения, делая модель устойчивой к цветовым искажениям, присутствующим при съемке в реальном мире. Цветовая коррекция состоит из умножения значения каждого пикселя I на константу, возведения в степень и сдвига:

Параметры A, B, C выбираются случайно из равномерных распределений из заданного промежутка. Для большей устойчивости модели область значений параметров выбрана шире, чем может встретиться в окружающей среде.

3.4. Слой размытия применяет к изображению двумерную свертку с гауссовским ядром. Размер ядра и дисперсия выбираются случайно. Данная трансформация эмулирует эффект размытия при съемке в окружающей среде, которая может появиться из-за плохой камеры или большого расстояния до объекта.

Представленные выше слои позволяют имитировать искажения реального мира, что при обучении даст возможность модели быть устойчивой к похожим трансформациям.

4. Архитектуры сетей. Итоговая модель представляет собой последовательность отдельных искусственных нейронных сетей, обучаемых по принципу end-to-end, т.е. выходной тензор каждой сети является входным тензором для следующей и т.д., при этом вход первой и выход последней сети должны быть одинаковыми [7]. В данной секции подробно рассматривается строение используемых сетей.

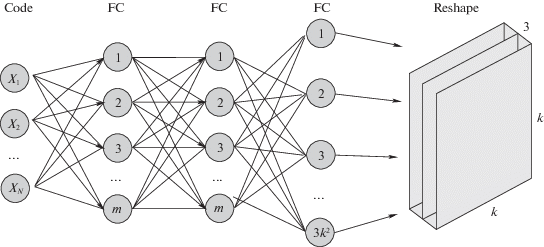
4.1. Сеть кодирования. Пусть X = {0, 1}^N – бинарный вектор информации, который требуется зашифровать в изображение, соответственно количество передаваемых бит составляет 2^N. Архитектура сети, переводящей вектор в изображение, показана на рис. 1. Сеть принимает на вход вектор {0. 1}^N, применяет несколько последовательных полносвязных слоев и меняет выход последнего для соответствия размеру маркера k × k × 3. После обучения модели семейство выходов сети кодирования и являются визуальными маркерами, описанными выше. Каждому уникальному вектору информации ставится во взаимно однозначное соответствие конкретное изображение–маркер.

4.2. Сеть рендеринга. Эта сеть (рис. 2) является центральной частью системы, соединяющей кодировщик и декодировщик. Она размещает визуальный маркер в центре фонового изображения и применяет трансформации, эмулирующие шум реального мира. Сеть принимает на вход b визуальных маркеров (b × k × k × 3) и фоновых изображений (b × s × s × 3). Далее, последовательно применяются слои рендеринга, трансформации, цветовой коррекции и размытия.

Данная сеть используется только на этапе обучения, делая генерацию и расшифровку маркеров устойчивыми к представленным возмущениям.

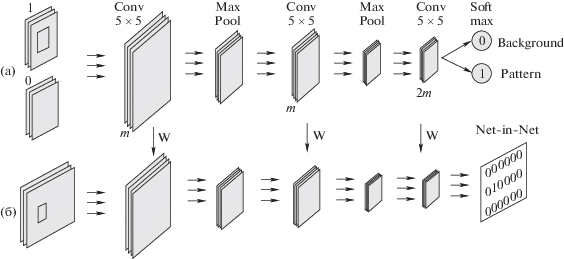
4.3. Сеть детектирования. Так как при реальной съемке визуальный код не будет расположен ровно по центру изображения, в модель добавлена сеть детектирования, цель которой найти маркер на изображении и предсказать его точные координаты для облегчения процесса дальнейшего декодирования. Сеть состоит из двух подсетей (рис. 3), первая из которых учится на изображениях фиксированного размера с паттерном и без, предсказывая наличие или отсутствие маркера.

С учетом того, что сеть является полносверточной, т.е. не содержит полносвязных слоев, ее можно применить к изображению любого размера. В таком случае на выходе будет не бинарное число, а матрица из 0 и 1, где 1 показывает примерное положение маркера, если он присутствует на изображении, так как входное изображение и выходная бинарная матрица пространственно связаны. Вторая подсеть в обучении не участвует, она используется только на этапе тестирования.

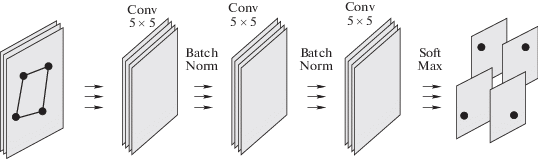
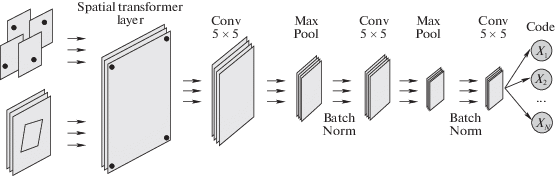
4.4. Сеть локализации. Данная сеть (рис. 4) принимает на вход фоновый патч с маркером и предсказывает четыре карты признаков, каждая из которых соответствует координатам угловой точки маркера. Сеть обучается на паре (паттерн, координаты точек), где координаты точек берутся из слоя трансформации сети рендеринга.

4.5. Сеть декодирования. Сеть (рис. 5) принимает изображение с маркером и результат сети локализации и предсказывает зашифрованный вектор информации. По четырем угловым точкам применяется дифференцируемое обратное пространственное преобразование [6, 8], разворачивающее маркер в его исходную форму. В идеальном случае это будет тот же маркер, который подавался на вход сети рендеринга, но ввиду небольших ошибок в сети определения угловых точек получившийся маркер чуть сдвинут или обрезан. Сверточные слои, которые следуют за пространственной трансформацией, учатся предсказывать исходный набор бит, зашифрованных в маркере.

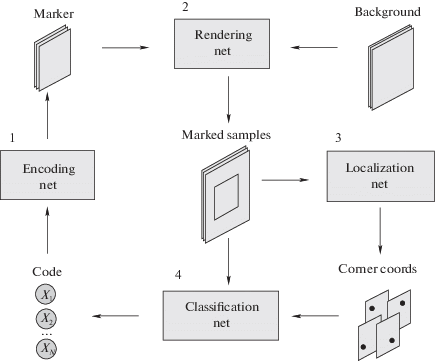
4.6. Финальная модель. Общая структура предлагаемой в данной работе модели кодирования и декодирования информации в визуальных маркерах показана на рис. 6. Модель состоит из нескольких блоков, каждый из которых принимает результат работы предыдущего. Сеть принимает на вход бинарный код, преобразует его в маркер, накладывает помехи, находит точное положение углов маркера и предсказывает бинарный код. Отличительная особенность представленной модели в том, что для ее обучения не нужны вообще никакие размеченные данные. Все, что нужно для обучения, это бинарные коды, которые генерируются случайно. После обучения модели сети кодирования и декодирования используются независимо.

5. Эксперименты. Так как описанная модель требует некоторого количества изображений фоновых патчей, в качестве данных была использована подвыборка датасета Places2 [9], содержащая реальные изображения интерьера разных зданий. Выбор конкретного подмножества также влияет на внешний вид маркера. Например, фоновые изображения помещения бассейна и музея отличаются друг от друга, что стимулирует модель генерировать разные семейства маркеров.

После множества экспериментов эмпирически были выбраны параметры по умолчанию, наиболее близко эмулирующие реальный мир: размер маркера k = 32 пикселя; сеть кодирования состоит из одного полносвязного слоя; дисперсия слоя аффинной трансформации σ = 0.1; параметры слоя цветовой коррекции случайно из U[–0.2, 0.2], гауссовское ядро слоя размытия с σ ∈ ∈ [0.4, 1.4]; сеть декодирования состоит из 96, 96, 96, 192 фильтров.

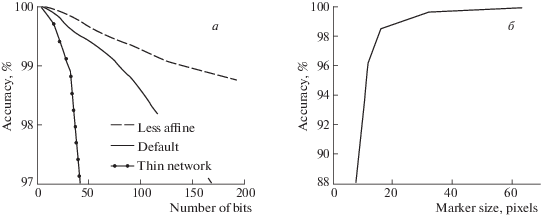
Для оценки емкости модели были проведены эксперименты с разными размерами маркера k, количеством шифруемых бит n, глубиной сети кодирования. На рис. 7 показана зависимость качества модели от этих параметров (т.е. процент правильно расшифрованных бит). Сеть с параметрами, определенными выше, способна распознавать 64 бита с точностью выше 99%, если же уменьшить параметр аффинной трансформации до 0.05, т.е. требовать более фронтальное положение камеры относительно маркера, количество распознаваемых бит повышается до 160.

Эксперименты показывают, что система способна распознавать маркеры под разными углами наклона с низкой долей ошибок. Модель выучивает стабильные образы с разными цветовыми пятнами, отчасти похожие на QR-коды. Но т.к. используются три цветовых канала, а не один, и формы пятен произвольные, емкость таких маркеров выше, чем у QR-кодов аналогичного размера.

Работа сетей распознавания и декодирования проверялась для изображений произвольного размера. Ввиду того, что детектор настроен находить маркеры определенного размера, на вход сети подается исходное изображение в различных масштабах. Далее предложенные алгоритмом на разных масштабах регионы объединяются в один по методу non-maximum-seppression – стандартной практике в задачах детектирования. Наконец, паттерны классифицируются сетью декодирования, которая возвращает зашифрованный код для каждого из присутствующих маркеров.

Заключение. В работе приведен новый общий подход к построению семейств визуальных маркеров, которые кодируют информацию в изображении. Алгоритм декодирования обучался совместно с алгоритмом генерации, что позволило оптимизировать обе составляющие части друг под друга. Представлена архитектура сети рендеринга с новыми слоями, имитирующими шум реального мира. Показано с помощью количественных и качественных экспериментов, что предложенная модель успешно справляется с поставленной задачей, в том числе и на тестах в реальном мире.