Известия РАН. Теория и системы управления, 2019, № 4, стр. 3-15
МЕТОД ПОСТРОЕНИЯ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ В УПРАВЛЯЕМОЙ ДИНАМИЧЕСКОЙ СИСТЕМЕ ВТОРОГО ПОРЯДКА
Л. А. Климина a, *, Ю. Д. Селюцкий a
a НИИ механики МГУ
Москва, Россия
* E-mail: klimina@imec.msu.ru
Поступила в редакцию 03.12.2018
После доработки 28.12.2018
Принята к публикации 28.01.2019
Аннотация
Рассматривается неконсервативная механическая система с одной степенью свободы. Требуется обеспечить существование установившихся колебаний с заданными свойствами. Поведение системы моделируется автономной динамической системой второго порядка с одним варьируемым параметром, описывающим коэффициент усиления управляющего воздействия. Предложен численно-аналитический итерационный метод отыскания коэффициента усиления. Получены условия орбитальной устойчивости установившихся колебаний. Приведен пример применения метода. Предложенный подход может быть использован как для решения задач управления, так и для отыскания периодических решений автономных динамических систем второго порядка.
Введение. Задача формирования колебаний с заданными свойствами актуальна для широкого спектра приложений и обсуждается во многих современных работах, в том числе для случая систем с одной степенью свободы, например, [1–9].
Эффективность стратегий управления, обеспечивающих существование установившихся колебаний с определенными свойствами, часто проверяют на примере задачи управления тяжелым маятником. В [5] задача стабилизации колебаний математического маятника решена с использованием метода пассификации [10], управление зависит от координаты и скорости. В [6] рассмотрены два подхода к управлению неавтономной маятниковой системой: активное управление с нелинейным насыщением [11] и пассивное демпфирование, предполагающее добавление в механическую систему дополнительного объекта, имеющего одну степень свободы. В указанных работах построенное управление имеет достаточно сложную структуру, присутствует обратная связь и по координате, и по скорости.
Отметим, что для построения управления, обеспечивающего существование периодических колебаний, можно использовать (с некоторой модификацией) подходы к отысканию периодических решений неконсервативных систем. Например, для управления осциллятором при наличии малых неконсервативных воздействий в [7–9] используются подходы, родственные методу, предложенному в [12]. В [13] для построения периодического движения вибрационной системы применяется следствие метода усреднения [14], устанавливающее соответствие между неподвижными точками усредненной системы и периодическими решениями полной. Среди алгоритмов отыскания периодических решений, применимых в отсутствие малого параметра, можно выделить методы, использующие численное интегрирование системы (метод стрельбы), и численно-аналитические процедуры. К последним относятся методы для неавтономных систем с периодической зависимостью от времени, например, предложенные в [15, 16] (для распространения таких подходов на автономные системы требуется предварительная замена переменных, как правило, весьма нетривиальная), а также проекционные методы, например, [17, 18]. Последние чувствительны к влиянию высоких гармоник.
В настоящей работе рассматривается автономная механическая система маятникового типа с одной степенью свободы. На систему действуют консервативные и неконсервативные силы. Помимо этого присутствует управляющее воздействие с обратной связью и одним варьируемым параметром. Например, управление может быть представлено моментом, линейным по угловой скорости либо пропорциональным знаку угловой скорости, где коэффициент пропорциональности требуется выбрать так, чтобы обеспечить желаемые свойства движения системы. Пусть сформулированы определенные требования к установившемуся режиму колебаний. Например, установившиеся колебания должны охватывать известное положение равновесия и обладать заданным значением средней механической энергии. Ставится задача подобрать коэффициент усиления управляющего воздействия, обеспечивающий наличие такого установившегося режима, предпочтительно притягивающего.
Подобные задачи управления возникают, например, при настройке рабочих режимов механизмов и технических систем. В частности, к такой задаче можно свести управление внешней нагрузкой в локальной цепи малогабаритной ветроэнергетической установки [2].
В настоящей работе предложен численно-аналитический метод построения управления, обеспечивающего существование установившегося режима колебаний с заданными свойствами для неконсервативной системы, не содержащей малого параметра. Метод представляет собой численно-аналитическую итерационную процедуру. Первая итерация совпадает с результатом применения критерия, построенного в [12]. Новый метод является обобщением метода, предложенного в [19], на случай систем, не обладающих свойством центральной симметрии. Метод может быть применен не только для построения управления, но и для поиска периодических решений автономных неконсервативных динамических систем второго порядка.
В работе рассматривается пример применения метода к задаче о колебаниях управляемого тяжелого маятника в потоке воздуха. Управляющее воздействие представлено моментом в шарнире маятника, пропорциональным знаку угловой скорости маятника. Коэффициент пропорциональности является варьируемым параметром. При помощи предложенного метода решена следующая задача: определить коэффициент усиления управляющего воздействия, обеспечивающий существование установившихся колебаний с заданным значением средней механической энергии (колебания охватывают нижнее из равновесий маятника). Для притягивающих периодических движений описаны области притяжения.
Обсуждаются отличительные особенности нового метода и его преимущества по сравнению с известными.
1. Постановка и формализация задачи. Рассмотрим механическую систему с одной степенью свободы, движение которой описывается безразмерными уравнениями следующего вида:
(1.1)
$\begin{gathered} \dot {x} = \frac{{\partial H(x,y)}}{{\partial y}}, \\ \dot {y} = - \frac{{\partial H(x,y)}}{{\partial x}} + a\left( {Q(x,y) - u(x,y)} \right), \\ u(x,y) = bf(x,y). \\ \end{gathered} $Здесь точкой обозначена производная по безразмерному времени; x – безразмерная обобщенная координата, y – безразмерный импульс; $H(x,y) = 0.5{{k}^{{ - 1}}}(x){{y}^{2}} + P(x)$ – функция Гамильтона, описывающая полную механическую энергию системы; $k(x) > 0$ – аналитическая функция, определяемая структурой кинетической энергии системы; $P(x) \geqslant 0$ – аналитическая функция, описывающая потенциальную энергию системы; a > 0 – безразмерный коэффициент; $Q(x,y)$ – безразмерная обобщенная сила, соответствующая внешним неконсервативным силам (аналитическая функция); $u(x,y)$ – управление. Предполагается, что управление есть произведение коэффициента b, который подлежит выбору, и некоторой заданной функции $f(x,y)$, характеризующей структуру обратной связи и обладающей следующим свойством: $yf(x,y) > 0$ при $y \ne 0$. Таким образом, управление выбирается в виде диссипативной или антидиссипативной функции (в зависимости от знака b). Например, управление может иметь вид $u = by$ или u = $b\operatorname{sgn} (y)$.
Задача состоит в том, чтобы, выбрав соответствующий коэффициент b усиления управляющего воздействия, реализовать (если это возможно) в системе (1.1) притягивающие периодические колебания с заданным средним по времени значением $h$ функции $H(x,y)$, что соответствует определенной средней механической энергии. Предполагается, что колебательные режимы должны “охватывать” некоторое заданное равновесие системы (1.1). Также требуется описать область притяжения “построенного” колебательного режима. Помимо этого требуется указать диапазон значений h, которые возможно реализовать при управлении выбранной структуры. Отметим, что предложенный далее метод легко обобщить на случай, когда требуется обеспечить определенное значение амплитуды колебаний, и на другие подобные задачи построения колебаний с желаемыми свойствами.
Задача данной работы может быть формализована следующим образом: для заданного $h$ установить достаточные условия существования значения $b = \tilde {b}(h)$, такого, что система (1.1) при $b = \tilde {b}(h)$ обладает периодическим решением, охватывающим изолированное равновесие $({{x}_{0}},0)$, таким, что среднее по времени значение функции $H(x,y)$ вдоль этого решения равно h. Если такое $b = \tilde {b}(h)$ существует, то найти его, определить, является ли соответствующее периодическое решение притягивающим; и если является, то указать область притяжения.
2. Отыскание коэффициента усиления, обеспечивающего существование цикла. Предположим, что неподвижные точки системы (1.1) найдены и среди них выбрана изолированная неподвижная точка $({{x}_{0}},0)$, которую должны охватывать периодические решения. Далее будем считать ${{x}_{0}} = 0$ (для сокращения изложения). Будем рассматривать систему (1.1) в полосе $ - {{A}_{0}} < x < C$. Здесь ${{A}_{0}}$ и C – некоторые положительные константы, которые требуется выбрать так, что цикл с заданным средним значением h функции $H(x,y)$, если существует, заведомо расположен внутри полосы $ - {{A}_{0}} < x < C$.
Начнем с решения вспомогательной задачи. Пусть задано некоторое значение A из интервала $0 < A < {{A}_{0}}$. Фазовой точке $( - A,0)$ отвечает некоторая величина ${{h}_{0}} = P( - A)$. Будем искать значение $\hat {b}(A)$ параметра b, обеспечивающее в системе (1.1) существование периодического решения, проходящего через фазовую точку $( - A,0)$. Определим последовательные приближения следующего вида:
(2.1)
$\begin{gathered} y_{0}^{ + }(x;A) = \operatorname{Re} \sqrt {2k(x)({{h}_{0}} - P(x))} ,\quad y_{0}^{ - }(x;A) = - \operatorname{Re} \sqrt {2k(x)({{h}_{0}} - P(x))} , \\ {{b}_{0}}(A) = {{\left( {\int\limits_{ - A}^A {(f(x,y_{0}^{ + }(x;A))} - f(x,y_{0}^{ - }(x;A)))dx} \right)}^{{ - 1}}}\int\limits_{ - A}^A {(Q(x,y_{0}^{ + }(x;A))} - Q(x,y_{0}^{ - }(x;A)))dx; \\ \end{gathered} $(2.2)
$\begin{gathered} y_{n}^{ - }(x;A) = - \operatorname{Re} \sqrt {2k(x)\left( {{{h}_{0}} - P(x) + a\int\limits_{ - A}^x {(Q(s,y_{{n - 1}}^{ - }(s;A)) - {{b}_{{n - 1}}}f(s,y_{{n - 1}}^{ - }(s;A)))} ds} \right)} \,; \\ x_{n}^{ - } = \overline {\mathop {\lim }\limits_{z \in ( - A,\;C)} } \{ \left. {z\;} \right|y_{n}^{ - }(x;A) < 0\quad {\text{п р и }}\quad x \in ( - A,z)\} ; \\ \end{gathered} $Здесь $y_{n}^{ + }(x;A)$ и $y_{n}^{ - }(x;A)$ – построенные на n-м шаге аппроксимации фазовых кривых, описывающих части искомого цикла, которые лежат в верхней и нижней полуплоскостях фазовой плоскости соответственно; $x_{n}^{ + }$ и $x_{n}^{ - }$ – найденные на n-м шаге аппроксимации значения переменной x в самой правой точке искомого фазового цикла; ${{b}_{n}}(A)$ – полученная на n-м шаге аппроксимация искомого значения коэффициента усиления.
Нулевая итерация (2.1) совпадает с результатом формального применения метода, предложенного в [12], к системе (1.1): “формального” в том смысле, что в [12] требуется, чтобы параметр a был малым, но в данной задаче такое условие, вообще говоря, не выполнено.
Отметим, что если система (1.1) обладает свойством центральной симметрии, то на каждом шаге получим $y_{n}^{ + }(x;A) = - y_{n}^{ - }( - x;A)$ и $x_{n}^{ + } = x_{n}^{ - } = A$, в этом случае численная реализация метода и доказательство утверждений о пределе последовательностей (2.2) значительно упрощаются [19]. В данной работе отсутствует предположение о центральной симметрии системы (1.1). В связи с этим верхняя и нижняя части искомого цикла строятся как пределы последовательностей, каждая из которых состоит из участков траекторий гамильтоновых систем, которые различны для верхней и нижней полуплоскостей. Каждая последующая “порождающая” гамильтонова система получается путем подстановки в правую часть системы (1.1) предыдущего приближения $y_{{n - 1}}^{ + }(x;A),y_{{n - 1}}^{ - }(x;A)$ для участка периодической траектории. Так, на n-м шаге гамильтонианы этих “порождающих” систем имеют вид
Следующие приближения $y_{n}^{ + }(x;A),y_{n}^{ - }(x;A)$ являются траекториями систем, определяемых гамильтонианами $H_{n}^{ + }(x,y)$, $H_{n}^{ - }(x,y)$, при уровне гамильтониана ${{h}_{0}}$ соответственно.
Если каждая из последовательностей $y_{n}^{ + }(x;A)$ и $y_{n}^{ - }(x;A)$ сходится при всех x, то и последовательности $x_{n}^{ + }$, $x_{n}^{ - }$ и ${{b}_{n}}(A)$ сходятся. Пусть при этом для достаточно больших n выполнено $y_{n}^{ + }(x_{n}^{ + };A) = y_{n}^{ - }(x_{n}^{ - };A) = 0$ и пусть пределы $\tilde {x}_{{}}^{ + }$, $\tilde {x}_{{}}^{ - }$ последовательностей $x_{n}^{ + }$, $x_{n}^{ - }$ совпадают друг с другом: $\tilde {x}_{{}}^{ + } = \tilde {x}_{{}}^{ - }$. Тогда предел последовательности ${{b}_{n}}(A)$ является искомым значением $\hat {b}(A)$. При этом лежащая в верхней полуплоскости часть цикла, существующего в системе (1.1) при $b = \hat {b}(A)$, описывается пределом $\tilde {y}_{{}}^{ + }(x;A)$ последовательности $y_{n}^{ + }(x;A)$; лежащая в нижней полуплоскости часть цикла, существующего в системе (1.1) при $b = \hat {b}(A)$, описывается пределом $\tilde {y}_{{}}^{ - }(x;A)$ последовательности $y_{n}^{ - }(x;A)$.
Если же последовательности (2.2) не сходятся, это, вообще говоря, не означает отсутствия искомого значения параметра $b = \hat {b}(A)$, а означает только, что если оно существует, оно не может быть найдено предложенным методом (можно привести соответствующие примеры). Таким образом, сходимость метода есть достаточное условие существования искомого коэффициента $b = \hat {b}(A)$, но не необходимое.
Отметим, что в силу свойств, аналогичных свойствам поворота векторного поля [20] имеет место следующее утверждение: если значение $\hat {b}(A)$ существует, то оно единственно (обсуждение подобного свойства для центрально-симметричной системы содержится в [19]).
Предположим, что для заданного A последовательности (2.2) сходятся. Тогда для решения основной задачи вычислим среднее значение $\tilde {h}(A)$ функции $H(x,y)$ вдоль найденной периодической траектории $(\tilde {X}(t;A),\tilde {Y}(t;A))$, существующей в системе (1.1) при $b = \hat {b}(A)$ (эта траектория описывается функциями $\tilde {y}_{{}}^{ + }(x;A)$ и $\tilde {y}_{{}}^{ - }(x;A)$):
(2.3)
$\begin{gathered} \tilde {h}(A) = \frac{1}{T}\int\limits_0^T {H(\tilde {X}(t;A),\tilde {Y}(t;A))} {\kern 1pt} {\kern 1pt} dt = \\ = {{\left( {\int\limits_{ - A}^{{{{\tilde {x}}}^{ + }}(A)} {\frac{1}{{\tilde {y}_{{}}^{ + }(x;A)}}} dx - \int\limits_{ - A}^{{{{\tilde {x}}}^{ + }}(A)} {\frac{1}{{\tilde {y}_{{}}^{ - }(x;A)}}} dx} \right)}^{{ - 1}}}\left( {\int\limits_{ - A}^{{{{\tilde {x}}}^{ + }}(A)} {\frac{{H(x,\tilde {y}_{{}}^{ + }(x;A))}}{{\tilde {y}_{{}}^{ + }(x;A)}}} dx - \int\limits_{ - A}^{{{{\tilde {x}}}^{ + }}(A)} {\frac{{H(x,\tilde {y}_{{}}^{ - }(x;A))}}{{\tilde {y}_{{}}^{ - }(x;A)}}} dx} \right). \\ \end{gathered} $Отметим, что значение $\tilde {h}(A)$ вычисляется с использованием найденного ранее значения $b = \hat {b}(A)$.
Применим алгоритм (2.1)–(2.3) для всех значений A из некоторого диапазона $0 < A < {{A}_{0}}$ (при численной реализации выбирается некоторый шаг по A). Предположим, что для всех таких A последовательности (2.2) сходятся. Получим зависимость между средним уровнем h механической энергии на установившихся колебаниях и величиной коэффициента b. Эта зависимость параметризована величиной A. Другими словами, $\tilde {b}\left( h \right) = \{ \left. {\hat {b}\left( A \right)} \right|\tilde {h}(A) = h\} $.
Зависимость $\tilde {h}(A)$, вообще говоря, может оказаться немонотонной, а зависимость $\tilde {b}\left( h \right)$ – соответственно неоднозначной. В последнем случае можно выбрать любое из значений $\tilde {b}\left( h \right)$ в качестве искомого коэффициента усиления управляющего сигнала, или же, например, то значение, при котором шире область притяжения соответствующего цикла.
3. Устойчивость и область притяжения. Имеет место следующее утверждение, позволяющее установить свойство притяжения цикла: если при некотором $A = {{A}_{1}}$ производная функции $\hat {b}(A)$ отрицательна, то при $b = \hat {b}({{A}_{1}})$ цикл системы (1.1), проходящий через точку $( - {{A}_{1}},0)$, является притягивающим; если же производная функции $\hat {b}(A)$ при $A = {{A}_{1}}$ положительна, то при $b = \hat {b}({{A}_{1}})$ цикл системы (1.1), проходящий через точку $( - {{A}_{1}},0)$, является отталкивающим. Это утверждение вытекает из свойств поворота векторного поля.
Для того чтобы описать области притяжения циклов, существующих при различных значениях параметра b, применим метод (2.1)–(2.3) для всех A из некоторого диапазона $0 < A < {{A}_{0}}$ (при численной реализации задается некоторый шаг по A). В результате получим зависимость $b = \hat {b}(A)$, описывающую циклы, существующие в системе (1.1) при различных b. В частности, если для двух или более значений A соответствующие значения $\hat {b}(A)$ совпадают между собой, то при таком значении $b = \hat {b}(A)$ существует несколько циклов и неустойчивые циклы ограничивают области притяжения орбитально устойчивых циклов. Для полноты полученного таким образом описания требуется сходимость процедуры (2.1), (2.2) при всех соответствующих значениях A. Другими словами, для того, чтобы получить исчерпывающую информацию об областях притяжения построенных орбитально устойчивых циклов, требуется сходимость метода в достаточно широком диапазоне значений A.
Рассмотрим пример применения метода (2.1)–(2.3), включающий анализ областей притяжения построенных периодических решений, к конкретной механической системе.
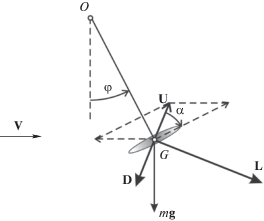
4. Пример применения метода. Рассмотрим тяжелый аэродинамический маятник, расположенный в стационарном горизонтальном потоке воздуха (рис. 1). Близкие задачи обсуждаются в последнее время в ряде работ [21–23], связанных с поиском автоколебательных и авторотационных режимов маятниковых систем в задачах преобразования энергии потока. Пример, приведенный в данной работе, отличается ориентацией лопасти относительно державки и характером расположения центра масс объекта. В [24] максимизируется амплитуда колебаний тяжелого маятника с вязким трением, в качестве управления выступает положение тяжелой точки на державке, причем построенное управление имеет релейный вид и переключения происходят при смене знака угловой координаты или угловой скорости маятника.
Аэродинамический маятник представляет собой твердое тело, которое может вращаться вокруг неподвижной горизонтальной оси $O$. Маятник состоит из державки OG и лопасти – пластины. Пластина перпендикулярна державке. Центр масс маятника совпадает с точкой $G$. Маятник расположен в поле силы тяжести в горизонтальном потоке воздуха. Вектор ${\mathbf{V}}$ скорости потока лежит в плоскости качаний маятника.
Далее используются следующие обозначения: $\varphi $ – угол поворота державки OG, отсчитывается от вертикали; r – длина державки OG; $m$ – масса маятника; J – момент инерции маятника относительно оси вращения.
Введем следующие кинематические характеристики движения: $\omega = r{{V}^{{ - 1}}}d\varphi {\text{/}}dt$ – безразмерная угловая скорость маятника; V – величина скорости потока; $U$ – воздушная скорость точки G; $\alpha = {\text{arctg}}({\text{sin}}\varphi {\text{/}}(\omega - {\text{cos}}\varphi ))$ – мгновенный угол атаки (угол между вектором U и пластиной).
Аэродинамическое воздействие на маятник описывается на основе квазистатического подхода [25, 26]:
Здесь $D$ – сила сопротивления; $L$ – подъемная сила; $\rho $ – плотность воздуха, $S$ – характерная площадь пластины; ${{C}_{D}}(\alpha )$, ${{C}_{L}}(\alpha )$ – безразмерные коэффициенты силы сопротивления и подъемной силы.
Аэродинамические коэффициенты аппроксимируются следующими функциями, отражающими их характерные свойства:
Предполагается, что в шарнире О приложен момент величины $T = - {{T}_{0}}{\text{sgn}}\omega $. Его можно интерпретировать как релейный управляющий момент. Если момент T является диссипативным (т.е. ${{T}_{0}} > 0$), то возможна альтернативная интерпретация: сухое трение в шарнире.
Уравнения движения системы в безразмерных переменных могут быть представлены в форме системы вида (1.1) (здесь угол $\varphi $ отвечает переменной x, $\omega $ – переменной y; точкой обозначена производная по безразмерному времени $\tau = Vt{\text{/}}r$):
(4.1)
$\begin{gathered} \dot {\varphi } = \omega , \\ \dot {\omega } = - p\sin \varphi + a\left( {Q(\varphi ,\omega ) - b\operatorname{sgn} \omega } \right), \\ Q(\varphi ,\omega ) = \sqrt {{{{(\omega - \cos \varphi )}}^{2}} + {{{\sin }}^{2}}\varphi } \left( {{{C}_{L}}(\alpha )\sin \varphi - {{C}_{D}}(\alpha )(\omega - \cos \varphi )} \right), \\ a = \frac{{\rho S{{r}^{3}}}}{{2J}},\quad b = \frac{{2{{T}_{0}}}}{{\rho Sr{{V}^{2}}}},\quad p = \frac{{mg{{r}^{3}}}}{{J{{V}^{2}}}}. \\ \end{gathered} $Далее будем считать p = 1. Поскольку система (4.1) имеет цилиндрическое фазовое пространство, достаточно рассматривать $\varphi $ на интервале $[ - \pi ,\pi )$.
При $a < {{a}_{1}} \approx 2.1$ маятник имеет два равновесия. Далее будем рассматривать a в этом диапазоне. Под действием аэродинамических сил (в случае b = 0) нижнее равновесие тяжелого маятника смещается “по потоку”, а верхнее – “против потока”. При этом неподвижная точка $({{\varphi }_{1}},0)$, отвечающая верхнему равновесию, остается седловой, а неподвижная точка $({{\varphi }_{0}},0)$, соответствующая нижнему равновесию, асимптотически устойчива. При ненулевом значении b правая часть системы (4.1) терпит разрыв вдоль прямой $\omega = 0$. В результате на прямой $\omega = 0$ в выколотой окрестности каждого равновесия $({{\varphi }_{i}},0)$ возникает особое множество ${{\wp }_{i}}$, такое, что для всех точек $(\varphi ,0)$ этого множества выполнено неравенство $\left| {Q(\varphi ,0)} \right| \leqslant \left| b \right|$.
Применим процедуру (2.1)–(2.3) для отыскания коэффициента b, обеспечивающего существование колебательного режима маятника с заданной средней по времени механической энергией. В случае положительных значений b такая задача может быть интерпретирована как описание зависимости средней энергии установившихся колебаний от коэффициента сухого трения в оси маятника. Отметим, что данная система не является центрально-симметричной, в отличие от аэродинамического маятника, периодические движения которого были описаны в [27].
Цикл системы (4.1), если он существует, охватывает равновесие $({{\varphi }_{0}},0)$. В соответствии с предложенным алгоритмом начнем с решения вспомогательной задачи. Будем искать цикл, проходящий через точку $( - A,0)$, где $ - \pi < A < {{\varphi }_{0}}$. При численной реализации метода используется критерий “практической” сходимости: если на некоторой итерации величина Δn = $\mathop {\max }\limits_x {\text{|}}y_{n}^{ \pm }(x;A) - y_{{n - 1}}^{ \pm }(x;A){\text{|}}$ становится меньше порогового значения (в нашем случае было выбрано значение 0.001), то считаем, что итерационный процесс сошелся.
Для всех значений A, при которых последовательности (2.2) сходятся, вычислим h вдоль построенных численно фазовых кривых $\tilde {y}_{{}}^{ + }(x;A)$ и $\tilde {y}_{{}}^{ - }(x;A)$, используя формулу (2.3).
На рис. 2 представлена зависимость $\tilde {b}\left( h \right)$, полученная при численной реализации метода (2.1)–(2.3) для двух различных значений параметра a: $a = 0.01$ и $a = 1$. На рис. 3 представлены графики $(n,{{\Delta }_{n}})$, характеризующие скорость сходимости метода для нескольких разных значений h и a.
Рис. 2.
Зависимость значения h от коэффициента b при a = 0.01 и a = 1. Сплошные кривые – семейства притягивающих циклов, пунктир – семейства неустойчивых циклов
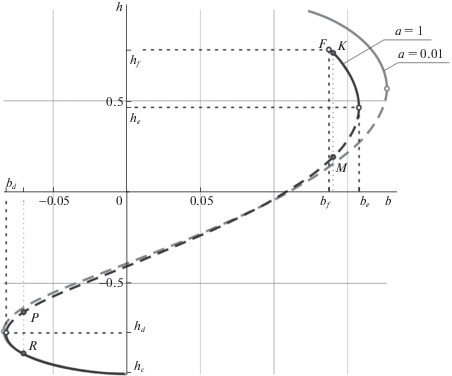
Рис. 3.
Зависимость невязки от номера итерации при a = 0.01 и a = 1, соответствующая различным значениям h

Сплошные ветви кривых на рис. 2 соответствуют семействам притягивающих установившихся колебаний, пунктирные ветви – семействам отталкивающих установившихся колебаний. На рис. 2 отмечены бифуркационные значения параметра b для случая a = 1 (для других значений a они могут быть введены аналогично). При прохождении параметра b справа налево через значение $b = {{b}_{c}} = 0$ происходит следующая бифуркация: притягивающее особое множество ${{\wp }_{0}}$, окружающее нижнее равновесие, “стягивается” в одну точку, из которой “рождается” орбитально устойчивый цикл. При сколь угодно малом отрицательном b вокруг изолированного равновесия $({{\varphi }_{0}},0)$ снова существует особое множество ${{\wp }_{0}}$, но оно отталкивающее. Вся область внутри “рожденного” цикла (включая множество ${{\wp }_{0}}$), кроме равновесия, относится к области притяжения цикла. Извне область притяжения “рожденного” цикла ограничена неустойчивым циклом. При $b = {{b}_{d}}$ (${{\left. {{{b}_{d}}} \right|}_{{a = 1}}} \approx - 0.082$) происходит слияние притягивающего и отталкивающего циклов. Притягивающие циклы со значениями $h$ из интервала ${{h}_{c}} < h < {{h}_{d}}$ реализуются при отрицательных значениях коэффициента b.
При существовании притягивающего цикла со значениями $h$ из интервала ${{h}_{e}} < h < {{h}_{f}}$ его область притяжения ограничена изнутри неустойчивым циклом. Извне она ограничена фазовой траекторией, приходящей в крайнюю точку особого множества ${{\wp }_{1}}$. Такие циклы реализуются при положительных значениях коэффициента b (управление, имитирующее сухое трение). При $b = {{b}_{e}}$ (${{\left. {{{b}_{e}}} \right|}_{{a = 1}}} \approx 0.158$) происходит слияние притягивающего и отталкивающего циклов. При $b = {{b}_{f}}$ (${{\left. {{{b}_{f}}} \right|}_{{a = 1}}} \approx 0.137$) притягивающий цикл разрушается, придя на границу особого множества ${{\wp }_{1}}$, окружающего неподвижную точку $({{\varphi }_{1}},0)$. Соответствующая точка на кривой $\tilde {b}\left( h \right)$ обозначена через F (рис. 2). Значения $h > {{h}_{f}}$ отвечают ротациям, а не колебаниям маятника.
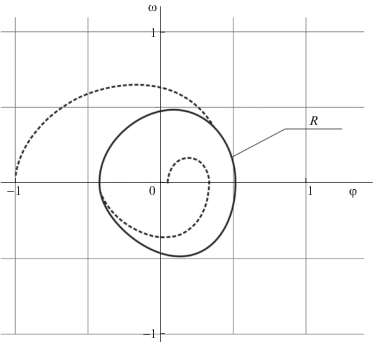
Рассмотрим подробнее поведение системы (4.1) при a = 1 и коэффициенте усиления $b = - 0.07$. На рис. 2 этому случаю отвечают точки P и R. На рис. 4 показаны соответствующие циклы (пары кривых $\tilde {y}_{n}^{ + }(x;A)$ и $\tilde {y}_{n}^{ - }(x;A)$), полученные методом (2.1)–(2.2) (притягивающий – жирной сплошной линией, отталкивающий – пунктирной линией), а также фазовые траектории системы (4.1), построенные методом Рунге–Кутты (тонкие сплошные линии) при $b = - 0.07$. Видно, что результаты численного применения нового метода полностью согласуются с результатами прямого численного интегрирования системы.
Рис. 4.
Элементы фазового портрета системы (4.1) при a = 1, $b = - 0.07$, построенные численно методом (2.1), (2.2) (притягивающий цикл – сплошная жирная линия, отталкивающий цикл – пунктир) и методом Рунге–Кутты (сплошные тонкие линии)
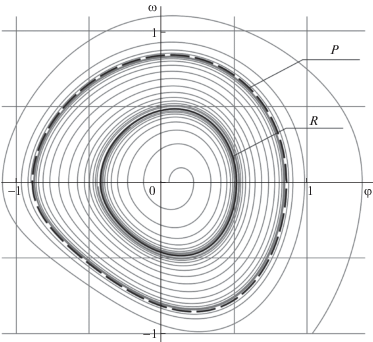
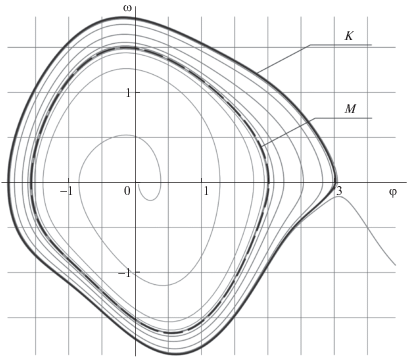
Рассмотрим подробнее поведение системы (4.1) при a = 1 и коэффициенте усиления b = 0.14. На рис. 2 этому случаю отвечают точки K и M. На рис. 5 показаны соответствующие циклы, полученные методом (2.1)–(2.2), а также фазовые траектории системы (4.1), построенные методом Рунге–Кутты. Результаты численного применения нового метода полностью согласуются с результатами прямого численного интегрирования системы.
Рис. 5.
Элементы фазового портрета системы (4.1) при a = 1, b = 0.14, построенные численно методом (2.1), (2.2) (притягивающий цикл – сплошная жирная линия, отталкивающий цикл – пунктир) и методом Рунге–Кутты (сплошные тонкие линии)
На рис. 6 представлен пример того, какой вид имеют итерационные приближения для цикла K, т.е. кривые $y_{n}^{ + }(x;A)$, $y_{n}^{ - }(x;A)$ при a = 1. Нулевое приближение определяется методом, предложенным в [12], и совпадает с циклом математического маятника.
Итак, для реализации искомого программного управления при различных значениях h требуется использовать значения коэффициента b усиления в диапазоне ${{b}_{d}} < b < {{b}_{e}}$. Таким образом, для обеспечения возможности реализации программного управления ограничение на величину управляющего момента должно быть не меньше, чем $\max (\left| {{{b}_{d}}} \right|,\left| {{{b}_{e}}} \right|)$. Предположим, что в каждый момент известна точная информация о текущем значении угла и угловой скорости маятника, и что ограничение на управление совпадает с $\max (\left| {{{b}_{d}}} \right|,\left| {{{b}_{e}}} \right|)$, т.е. в нашем примере – с ${{b}_{e}}$. Тогда, для максимально быстрого выхода в окрестность программной траектории, предпочтительно использовать следующую стратегию: предположим, что фазовая точка, отвечающая начальным условиям, расположена внутри (снаружи) программного цикла; вначале устанавливаем $b = - {{b}_{e}}$ ($b = {{b}_{e}}$); в момент, когда траектория $\left( {\varphi (t),\omega (t)} \right)$ пересечет одну из кривых $\tilde {y}_{{}}^{ + }(\varphi ;\tilde {A}(h))$ или $\tilde {y}_{{}}^{ - }(\varphi ;\tilde {A}(h))$, следует изменить значение коэффициента усиления на $b = \tilde {b}(h)$. Примеры соответствующих переходных процессов при a = 1 изображены на рис. 7 пунктирными линиями.
Итак, при a = 1 данных о программных значениях коэффициента управления и о программных траекториях, полученных при помощи алгоритма (2.1)–(2.3), достаточно для осуществления выхода на программный режим со значениями $h \in ({{h}_{c}},{{h}_{d}}) \cup ({{h}_{e}},{{h}_{f}})$ из широкого диапазона начальных условий.
5. Обсуждение результатов. Путем численной реализации метода (2.1)–(2.3) описана зависимость среднего значения механической энергии установившихся колебаний аэродинамического маятника от коэффициента b усиления релейного управляющего воздействия. Описаны свойства устойчивости найденных циклов. В частности, из рис. 2 видно, что при рассмотренном релейном управлении можно реализовать притягивающие колебательные режимы с относительно небольшими значениями средней энергии (${{h}_{c}} < h < {{h}_{d}}$), а также с относительно большими (${{h}_{e}} < h < {{h}_{f}}$). Колебания с “промежуточными” значениями энергии при управлении заданного вида неустойчивы. Они разделяют области притяжения орбитально устойчивых периодических режимов.
Рассмотренный пример показывает эффективность предложенного метода для построения периодических решений систем вида (1.1), в том числе в случае разрывной правой части. Существенное отличие предложенного метода от известных численно-аналитических итерационных процедур построения периодических решений (например, [15–18]) заключается в том, что порождающая система нулевого приближения нелинейна. При формировании колебаний автономной системы предложенный метод имеет следующие преимущества по сравнению с известными подходами: не требуется переход к неавтономным уравнениям (в отличие от работ [15, 16]); наличие высоких гармоник в программном периодическом решении не имеет априорного влияния на скорость сходимости (в отличие от проекционных методов); возможно решение задачи при специфических ограничениях на структуру управления, например, при условии, что управление зависит только от фазовой скорости (в отличие от работ [5, 6]).
Отметим, что величина параметра а влияет на скорость сходимости и на сам факт сходимости процедуры (2.1), (2.2). Примеры численной реализации метода показывают, что итерационный процесс (2.2) быстро сходится при достаточно малых a, а также вблизи точек слияния циклов (рис. 3), т.е. как раз тогда, когда методы отыскания периодических решений, основанные на прямом численном интегрировании, работают относительно медленно.
Однако, начиная с некоторого “достаточно большого” значения а метод, как правило, перестает сходиться. Наиболее медленная сходимость метода (2.1), (2.2) и даже отсутствие сходимости наблюдались вблизи бифуркационных точек, соответствующих $b = {{b}_{c}}$ и $b = {{b}_{f}}$, т.е. когда цикл проходил близко к особым множествам ${{\wp }_{0}}$ или ${{\wp }_{1}}$.
Заключение. Для динамической системы с одной степенью свободы предложен численно-аналитический метод построения управления, обеспечивающего существование установившегося режима колебаний с заданным значением средней механической энергии. В отличие от многих других подходов метод применим, в том числе, и для поиска управления, зависящего только от фазовой скорости.
Метод основан на отыскании коэффициента усиления управляющего воздействия (варьируемого параметра модели), при котором на фазовой плоскости системы существует периодическая траектория, проходящая через заданную точку. Получены условия орбитальной устойчивости стационарных колебаний. Описаны преимущества метода по сравнению с другими численно-аналитическими подходами, применимыми для аналогичных задач.
На примере задачи о тяжелом аэродинамическом маятнике продемонстрированы возможности метода, приведены результаты численного моделирования, иллюстрирующие скорость сходимости, описан диапазон параметров задачи, при которых метод имеет преимущества по сравнению с подходом, основанным на прямом численном интегрировании системы.
Список литературы
Morozov A.D., Kostromina O.S. On Periodic Perturbations of Asymmetric Duffing–Van-der-Pol Equation // Int. J. Bifurc. Chaos. 2014. V. 24. № 5. P. 1450061.
Klimina L. Dynamics of a Slider-crank Wave-type Wind Turbine // Proc. 14th IFToMM World Congress. Taipei, 2015. P. 582–588.
Dosaev M., Klimina L., Selyutskiy Y. Wind Turbine Based on Antiparallel Link Mechanism // New Trends in Mechanism and Machine Science. Springer, 2017. P. 543–550.
Rostami A.B., Fernandes A.C. Mathematical Model and Stability Analysis of Fluttering and Autorotation of an Articulated Plate into a Flow // Communications in Nonlinear Science and Numerical Simulation. 2018. V. 56. P. 544–560.
Seifullaev R.E., Fradkov A., Liberzon D. Energy Control of a Pendulum with Quantized Feedback // Automatica. 2016. V. 67. P. 171–177.
Tusset A.M., Janzen F.C., Piccirillo V., Rocha R.T., Balthazar J.M., Litak G. On Nonlinear Dynamics of a Parametrically Excited Pendulum Using Both Active Control and Passive Rotational (MR) Damper // J. Vibration and Control. 2018. V. 24. № 9. P. 1587–1599.
Chen C., Zanette D.H., Guest J.R., Czaplewski D.A., López D. Self-sustained Micromechanical Oscillator with Linear Feedback // Physical Review Letters. 2016. V. 117. № 1. P. 017203.
Тхай В.Н. Стабилизация колебаний автономной системы // АиТ. 2016. Т. 6. С. 38–46.
Васюкова О.Э., Климина Л.А. Моделирование автоколебаний управляемого физического маятника с учетом зависимости момента трения от нормальной реакции в шарнире // Нелинейная динамика. 2018. Т. 14. № 1. С. 33–44.
Fradkov A.L., Andrievsky B.R. Passification-based Robust Flight Control Design // Automatica. 2011. V. 47. P. 2743–2748.
Felix J.L.P., Balthazar J.M., Brasil R.M. On Saturation Control of a Non-ideal Vibrating Portal Frame Foundation Type Shear-building // J. Vibration and Control. 2005. V. 11. №1. P. 121–136.
Понтрягин Л.С. О динамических системах, близких к гамильтоновым // ЖЭТФ. 1934. Т. 4. № 9. С. 234–238.
Болотник Н.Н., Зейдис И.М., Циммерманн К., Яцун С.Ф. Динамика управляемых движений вибрационных систем // Изв. РАН. ТиСУ. 2006. № 5. С. 157–167.
Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. М.: Наука, 1958.
Самойленко А.М. Численно-аналитический метод исследования периодических систем обыкновенных дифференциальных уравнений. I // Укр. мат. журн. 1965. Т. 17. № 4. С. 82–93.
Ронто Н.И., Самойленко А.М., Трофимчук С.И. Теория численно-аналитического метода: достижения и новые направления развития. IV // Укр. мат. журн. 1998. Т. 50. № 12. С. 1656–1672.
Buonomo A., Schiavo A.L. A Constructive Method for Finding the Periodic Response of Nonlinear Circuits // IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications. 2003. V. 50. № 7. P. 885–893.
Брагин В.О., Вагайцев В.И., Кузнецов Н.В., Леонов Г.А. Алгоритмы поиска скрытых колебаний в нелинейных системах. Проблемы Айзермана, Калмана и цепи Чуа // Изв. РАН. ТиСУ. 2011. Т. 4. С. 3–36.
Климина Л.А. Метод поиска периодических траекторий центрально-симметричных динамических систем на плоскости // Дифференц. уравнения. 2019. Т. 55. № 2. С. 159–168.
Баутин Н.Н., Леонтович Е.А. Методы и приемы качественного исследования динамических систем на плоскости. М.: Наука, 1990.
Samsonov V.A., Dosaev M.Z., Selyutskiy Y.D. Methods of Qualitative Analysis in the Problem of Rigid Body Motion in Medium // Intern. J. Bifurcation and Chaos. 2011. V. 21. № 10. P. 2955–2961.
Fernandes A.C., Rostami A.B. Hydrokinetic Energy Harvesting by an Innovative Vertical Axis Current Turbine // Renewable Energy. 2015. V. 81. P. 694–706.
Berci M., Dimitriadis G. A combined Multiple Time Scales and Harmonic Balance Approach for the Transient and Steady-state Response of Nonlinear Aeroelastic Systems // J. Fluids and Structures. 2018. V. 80. P. 132–144.
Formalskii A.M. Stabilization and Motion Control of Unstable Objects. Berlin/Boston: Walter de Gruyter, 2015.
Досаев М.З., Самсонов В.А., Селюцкий Ю.Д. О динамике малой ветроэлектростанции // ДАН. 2007. Т. 416. № 1. С. 50–53.
Досаев М.З., Линь Ч.-Х., Лю В.-Л., Самсонов В.А., Селюцкий Ю.Д. Качественный анализ стационарных режимов малых ветровых электростанций // ПММ. 2009. Т. 7. № 3. С. 368–374.
Klimina L., Lokshin B. Construction of Bifurcation Diagrams of Periodic Motions of an Aerodynamic Pendulum via the Method of Iterative Averaging // 14th Intern. Conf. “Stability and Oscillations of Nonlinear Control Systems” (Pyatnitskiy’s Conference) (STAB2018). IEEE. M., 2018. P. 1–3.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления