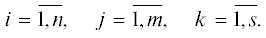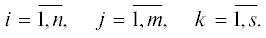Известия РАН. Теория и системы управления, 2019, № 4, стр. 16-28

Управление динамикой системы с дифференциальными связями

Р. Г. Мухарлямов^*

РУДН
Москва, Россия

Поступила в редакцию 18.06.2018
После доработки 21.12.2018
Принята к публикации 28.01.2019

DOI: 10.1134/S0002338819030132

Аннотация

Предлагается метод решения задачи управления системой с учетом динамики исполнительных устройств. Цель управления и кинематические свойства системы определяются голономными и неголономными связями, наложенными на фазовые координаты объекта управления. Управляющие воздействия формируются с учетом условий стабилизации связей при численном решении уравнений динамики замкнутой системы.

0. Введение. Процесс моделирования динамики управляемой системы состоит в построении дифференциальных уравнений замкнутой системы, решения которых удовлетворяют требуемым условиям. Известные динамические аналогии [1, 2] позволяют использовать принципы и методы классической механики для построения уравнений динамики звеньев технической системы, состоящей из элементов различной физической природы. Необходимые свойства движения механической системы обычно задаются некоторыми соотношениями между координатами и скоростями точек системы, которые определяются как уравнения связей или сервосвязи [3], соответствующие целям управления [4]. В [5] описываются методы построения дифференциальных уравнений системы с программными связями, когда накладываются дополнительные условия на движение системы вдоль интегрального многообразия, определяемого уравнениями связей, и в его окрестности. Голономные связи задают геометрические свойства траекторий движения изображающей точки в пространстве координат, уравнениями неголономных связей можно описывать распределение траекторий изображающей точки в соответствии с необходимыми кинематическими свойствами [6, 7]. Определение управляющих воздействий в соответствии с традиционным методом множителей Лагранжа, используемым в классической механике, приводит к тому, что связи, наложенные на систему, представляют первые интегралы уравнений динамики замкнутой системы, и аналитическое решение будет удовлетворять уравнениям связей только в том случае, если начальные условия также согласованы с уравнениями связей.

Так, для определения выражений множителей Лагранжа λ в уравнениях движения механической системы

(0.1)

$\frac{{dx}}{{dt}} = \text{v},\quad M(x)\frac{{d\text{v}}}{{dt}} = X(x,\text{v},t) + B(x,\text{v},t)\lambda ,$

(0.2)

$f(x,t) = 0,\quad \sigma (x,\text{v},t) = 0,$

(0.3)

$x({{t}_{0}}) = {{x}^{0}},\quad \text{v}({{t}_{0}}) = {{\text{v}}^{0}},$

$x = \left( {{{x}_{1}}, \ldots ,{{x}_{n}}} \right),\quad f = \left( {{{f}_{1}}, \ldots ,{{f}_{m}}} \right),\quad \sigma = \left( {{{\sigma }_{{m + 1}}}, \ldots ,{{\sigma }_{r}}} \right),\quad B = {{\Phi }^{{\text{T}}}},\quad \Phi = \left( {\begin{array}{*{20}{c}} {\frac{{\partial f}}{{\partial x}}} \\ {\frac{{\partial \sigma }}{{\partial \text{v}}}} \end{array}} \right),$

используются равенства

(0.4)

$\frac{{{{d}^{2}}f(x,t)}}{{d{{t}^{2}}}} = 0,\quad \frac{{d\sigma (x,\text{v},t)}}{{dt}} = 0.$

При этом аналитическое решение системы (0.1)–(0.3) будет удовлетворять уравнениям связей только при выполнении условий

(0.5)

$f({{x}^{0}},{{t}_{0}}) = 0,\quad \frac{{df({{x}^{0}},{{\text{v}}^{0}},{{t}_{0}})}}{{dt}} = 0,\quad \sigma ({{x}^{0}},{{\text{v}}^{0}},{{t}_{0}}) = 0.$

Из выражений (0.4) следует, что в случае нарушения условий (0.5):

(0.6)

$f({{x}^{0}},{{t}_{0}}) = {{f}^{0}},\quad \frac{{df({{x}^{0}},{{\text{v}}^{0}},{{t}_{0}})}}{{dt}} = {{\dot {f}}^{0}},\quad \sigma ({{x}^{0}},{{\text{v}}^{0}},{{t}_{0}}) = {{\sigma }^{0}},$

отклонения от уравнений связей вдоль аналитического решения будут возрастать:

$f = {{f}^{0}} + {{\dot {f}}^{0}}t,\quad \sigma = {{\sigma }^{0}}.$

В [8] подчеркивается, что при этом численное решение оказывается неустойчивым по отношению к уравнениям связей и стабилизация связей возможна, если инвариантное множество уравнений динамики, соответствующее связям, устойчиво асимптотически. Для решения проблемы стабилизации связей предлагается вместо уравнений (0.4) для определения выражения вектора λ использовать уравнения связей, накладываемых на ускорения d ²x/dt²:

(0.7)

$\frac{{{{d}^{2}}f(x,t)}}{{d{{t}^{2}}}} + 2\alpha \frac{{df(x,t)}}{{dt}} + {{\omega }^{2}}f(x,t) = 0,\quad \frac{{d\sigma (x,\text{v},t)}}{{dt}} + \gamma \sigma (x,\text{v},t) = 0,$

$\alpha ,\omega - {\text{const}},\quad \alpha > 0,\quad\quad\quad\gamma = \gamma (x,\text{v},t) > 0.$

Метод, предложенный в [8] для систем дифференциально-алгебраических уравнений индекса 3, оказался популярным и эффективно используется при решении задач небесной механики [9–11] и моделировании динамики систем твердых тел [12–14]. В случае, когда уравнения динамики линейны относительно вектора λ, индекс системы дифференциально-алгебраических уравнений равен числу дифференцирований уравнений связей, необходимому для определения выражения λ, плюс единица. Были предложены разнообразные модификации метода J. Baumgarte, которые сводились к использованию различных численных методов решения дифференциальных уравнений и подбору коэффициентов $\alpha ,\omega ,\gamma $ [15, 16].

Развитие метода J. Baumgarte для систем индекса m + 1 предложено в [17]. Для определения выражения множителя λ в правой части уравнения системы

(0.8)

$\frac{{{{d}^{m}}x}}{{d{{t}^{m}}}} = X\left( {x,\frac{{dx}}{{dt}}, \ldots ,\frac{{{{d}^{{m - 1}}}x}}{{d{{t}^{{m - 1}}}}},t} \right) + B(x,t)\lambda ,$

(0.9)

$f(x,t) = 0,$

используется линейная комбинация уравнения связей (0.9) с производными до порядка m, что приводит к дифференциальному уравнению возмущений связей:

(0.10)

${{\alpha }_{j}}{{y}^{{\left( j \right)}}} = 0,$

$y = f(x,t),\quad {{y}^{{\left( j \right)}}} = \frac{{{{d}^{j}}y}}{{d{{t}^{j}}}},\quad j = \overline {1,m} .$

В равенстве (0.10) и в дальнейшем предполагается суммирование по одинаковым индексам:

${{\alpha }_{j}}{{y}^{{\left( j \right)}}} = {{\alpha }_{1}}{{y}^{{\left( 1 \right)}}} + \ldots + {{\alpha }_{m}}{{y}^{{\left( m \right)}}}.$

Коэффициенты α_j дифференциального уравнения (0.10) должны быть выбраны так, чтобы корни характеристического уравнения α_jμ^j = 0 имели отрицательные действительные части, для чего предложено использовать многочлен вида α_jμ^j = ${{(\mu + \gamma )}^{m}},\quad\quad\gamma - {\text{const}}$.

В работе [18] излагается гибридная схема интегрирования управляемой системы, состоящей из нежесткой механической подсистемы и жесткой управляемой подсистемы:

$\frac{{dx}}{{dt}} = \text{v},\quad M(x)\frac{{d\text{v}}}{{dt}} = X(x,\text{v}) + {{F}^{{\text{T}}}}(x,t)\lambda + P(x,\text{v},w,u),$

$\frac{{dw}}{{dt}} = W(x,\text{v},w,u),$

$f(x,t) = 0,\quad F = \left( {\frac{{\partial f}}{{\partial x}}} \right).$

Для стабилизации связей, наложенных на механическую подсистему, используется метод J. Baumgarte. Определяются области изменения параметров α, ω, соответствующие решению дифференциальных уравнений методами Адамса–Башфорта.

В общей постановке задача стабилизации связей сводится к определению выражений множителей Лагранжа или управляющих воздействий, при которых связи описываются частными интегралами уравнений динамики управляемой системы, и соответствующее интегральное многообразие устойчиво асимптотически. Такое достраивание уравнений динамики замкнутой системы относится к обратным задачам динамики [19–23]. Правая часть системы дифференциальных уравнений dx/dt = X(x, t), допускающей частные интегралы f(x, t) = 0, в [24, 25] определяется из равенств:

$FX + {{f}_{t}} = \Phi (f,x,t),$

${{\text{v}}^{\nu }} = {{F}^{ + }}(\Phi (f,x,t) - {{f}_{t}})\quad {{F}^{ + }} = {{F}^{{\text{T}}}}{{(F{{F}^{T}})}^{{ - 1}}},\quad \Phi (0,x,t) = 0.$

Произвольная функция Φ(f, x, t) может быть использована для обеспечения асимптотической устойчивости интегрального многообразия [26] и ограничения отклонений решения дифференциального уравнения при численном интегрировании [27].

Стабилизация связей, заданных уравнениями (0.2), обеспечивается, если левая часть уравнения дифференциальных связей φ(x, $\text{v}$, t) = 0 , φ = ($\dot {f}$, σ) удовлетворяет условию

(0.11)

$\frac{{d\varphi (x,\text{v},t)}}{{dt}} = \Phi (f,\varphi ,x,\text{v},t),\quad \Phi (0,0,x,\text{v},t) = 0,$

$f = ({{f}_{1}}, \ldots ,{{f}_{m}}),\quad \dot {f} = \left( {\frac{{d{{f}_{1}}}}{{dt}}, \ldots ,\frac{{d{{f}_{m}}}}{{dt}}} \right),$

из которого определяется множитель λ в правой части уравнения динамики (0.1) [28]. В частности, равенство (0.11) можно представить линейным дифференциальным уравнением [29]

(0.12)

$\frac{d}{{dt}}\left( {\begin{array}{*{20}{c}} f \\ {\dot {f}} \\ \sigma \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0&{{{I}_{m}}}&0 \\ {{{K}_{{10}}}}&{{{K}_{{11}}}}&{{{K}_{{12}}}} \\ {{{K}_{{20}}}}&{{{K}_{{21}}}}&{{{K}_{{22}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} f \\ {\dot {f}} \\ \sigma \end{array}} \right),$

которое при ${{K}_{{10}}} = {{\omega }^{2}}{{I}_{m}}$, ${{K}_{{11}}} = 2\alpha {{I}_{m}}$, ${{K}_{{12}}} = {{K}_{{20}}} = {{K}_{{21}}} = 0$, ${{K}_{{22}}} = \gamma {{I}_{r}}$ соответствует методу J. Baumgarte. Уравнения возмущений связей (0.12) позволяют учитывать отклонения от уравнений связей с весовыми коэффициентами. Динамика механической системы может быть описана уравнениями динамики расширенной системы [30], динамические показатели которой составлены с учетом возможных отклонений от уравнений связей [31, 32].

Как показывают численные эксперименты, степень точности решения задачи стабилизации связей управляемых механических систем и их аналогов, описываемых дифференциально-алгебраическими уравнениями индекса 3, зависит от построения правых частей уравнений возмущений связей (0.11) и используемых численных методов [14–17, 27, 29, 33]. Разумный выбор функции $\Phi (f,\varphi ,x,\text{v},t)$ позволяет ограничиться простейшими методами численного интегрирования. С другой стороны, если уравнения возмущений связей не обеспечивают стабилизацию связей, соответствующую методу Эйлера решения дифференциальных уравнений, применением метода Рунге–Кутты [33] можно добиться устойчивости интегрального многообразия.

Известные модификации метода J. Baumgarte применительно к системам индекса m + 1, m > 2 либо ограничиваются частным видом комбинации уравнений связей с их производными [17], либо непосредственно используют метод J. Baumgarte для подсистемы, описываемой уравнениями механики [18]. Решение задачи управления системой с учетом динамики исполнительных устройств приводит к необходимости разработки общих методов стабилизации связей в системах более высокого порядка.

1. Постановка задачи. В случае, когда уравнения связей накладывают ограничения только на фазовые координаты объекта, для решения задачи управления с учетом динамики приводов приходится использовать производные от уравнений связей более высокого порядка, соответствующего структуре управляемой системы. Требуется оценить возможные отклонения от уравнений связей замкнутой системы и определить общий вид уравнений возмущений связей, имеющих асимптотически устойчивое тривиальное решение. Стабилизация связей при численном решении уравнений динамики накладывает дополнительные условия на уравнения возмущений связей.

2. Уравнения динамики замкнутой системы. Динамика управляемой системы с учетом приводов описывается системой дифференциальных уравнений

(2.1)

$\left\{ {\begin{array}{*{20}{c}} {\frac{{d{{q}^{i}}\quad}}{{dt}} = {{\text{v}}^{i}},\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad} \\ {\frac{{d{{\text{v}}^{i}}\quad}}{{dt}} = {{a}^{i}}\left( {q,\text{v},w,t} \right),\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad} \\ {\frac{{d{{w}^{j}}\quad}}{{dt}} = {{b}^{j}}\left( {q,\text{v},w,t} \right) + {{b}^{{jk}}}\left( {q,\text{v},w,t} \right){{u}_{k}},} \end{array}} \right.$

(2.2)

${{q}^{i}}({{t}_{0}}) = q_{0}^{i},\quad {{\text{v}}^{i}}({{t}_{0}}) = \text{v}_{0}^{i},\quad \quad{{w}^{j}}({{t}_{0}}) = w_{0}^{j},$

Здесь $q = ({{q}^{1}}, \ldots ,{{q}^{n}}),\text{v} = ({{\text{v}}^{1}}, \ldots ,{{\text{v}}^{n}})$ определяют соответственно обобщенные координаты и скорости объекта управления, $w = ({{w}^{1}}, \ldots ,{{w}^{m}})$ – вектор состояния исполнительного органа, (aⁱ), $({{b}^{j}}),\quad({{b}^{{jk}}})$ – известные матрицы соответствующих размерностей. Управляющие воздействия u₁, …, u_s призваны обеспечить выполнение уравнений связей, наложенных на обобщенные координаты и скорости объекта:

(2.3)

${{f}^{\mu }}(q,t) = 0,\quad \mu = \overline {1,m} ,\quad$

(2.4)

${{\varphi }^{\kappa }}(q,\text{v},t) = 0,\quad \kappa = \overline {m + 1,r} ,$

при изменении значений переменных ${{q}^{i}} = {{q}^{i}}(t),\;{\kern 1pt} {{\text{v}}^{i}} = {{\text{v}}^{i}}(t)$ в соответствии с решением системы (2.1) и начальных условиях (2.2), удовлетворяющих равенствам

(2.5)

${{f}^{\mu }}({{q}_{0}},{{t}_{0}}) = 0,\quad {{\varphi }^{\rho }}({{q}_{0}},{{\text{v}}_{0}},{{t}_{0}}) = 0,\quad {{\psi }^{\rho }}({{q}_{0}},{{\text{v}}_{0}},{{w}_{0}},{{t}_{0}}) = 0,\quad\quad$

${{\varphi }^{\mu }}(q,\text{v},t) = \frac{{\partial {{f}^{\mu }}}}{{\partial {{q}^{i}}}}{{\text{v}}^{i}} + \frac{{\partial {{f}^{\mu }}}}{{\partial t}},\quad {{\psi }^{\rho }}(q,\text{v},w,t) = \frac{{\partial {{\varphi }^{\rho }}}}{{\partial {{q}^{i}}}}{{\text{v}}^{i}} + \frac{{\partial {{\varphi }^{\rho }}}}{{\partial {{\text{v}}^{i}}}}{{a}^{i}}(q,\text{v},w,t) + \frac{{\partial {{\varphi }^{\rho }}}}{{\partial t}},$

$\quad\mu = \overline {1,m} ,\quad \rho = \overline {1,r} .$

Для обеспечения выполнения уравнений связей (2.3), (2.4) необходимо, чтобы функции ${{f}^{\mu }},{{\varphi }^{\kappa }},{{\psi }^{\rho }}$ и их производные, вычисленные в силу уравнений системы (2.1), оставались равными нулю:

(2.6)

${{f}^{\mu }}(q,t) = 0,\quad {{\varphi }^{\rho }}(q,\text{v},t) = 0,\quad {{\psi }^{\rho }}(q,\text{v},w,t) = 0,$

(2.7)

${{\dot {\psi }}^{\rho }}(q,\text{v},w,t) = 0,$

(2.8)

${{\dot {\psi }}^{\rho }}(q,\text{v},w,t) = \frac{{\tilde {d}{{\psi }^{\rho }}}}{{dt}} + \frac{{\partial {{\psi }^{\rho }}}}{{\partial {{w}^{j}}}}{{b}^{{jk}}}(q,\text{v},w,t){{u}_{k}}(q,\text{v},w,t),$

$\frac{{\tilde {d}{{\psi }^{\rho }}}}{{dt}} = \frac{{\partial {{\psi }^{\rho }}}}{{\partial {{q}^{i}}}}{{\text{v}}^{i}} + \frac{{\partial {{\psi }^{\rho }}}}{{\partial {{\text{v}}^{i}}}}{{a}^{i}}(q,\text{v},w,t) + \frac{{\partial {{\psi }^{\rho }}}}{{\partial {{w}^{j}}}}{{b}^{j}}(q,\text{v},w,t) + \frac{{\partial {{\psi }^{\rho }}}}{{\partial t}},$

$\mu = \overline {1,m} ,\quad \rho = \overline {1,r} ,\quad k = \overline {1,s} .$

Равенства (2.8) накладывают ограничения на выбор управляющих воздействий u_k = ${{u}_{k}}(q,\text{v},w,t)$. Будем предполагать, что матрица $(\varphi _{i}^{\rho })$, $\varphi _{i}^{\rho } = \partial {{\varphi }^{\rho }}{\text{/}}\partial {{\text{v}}^{i}}$, ρ = 1, …, r, имеет максимальный ранг и строки матрицы $(\psi _{j}^{\rho }{{b}^{{jk}}}),\quad$ $\psi _{j}^{\rho } = \partial {{\psi }^{\rho }}{\text{/}}\partial {{w}^{j}}$, линейно независимы при всех q, $\text{v}$, w, t из области допустимых значений.

Из равенств (2.7), (2.8) следует система линейных алгебраических уравнений для определения выражений управляющих воздействий u_k = u_k(q, $\text{v}$, w, t), k = 1, …, s :

(2.9)

${{g}^{{\rho k}}}{{u}_{k}} = - \frac{{\tilde {d}{{\psi }^{\rho }}}}{{dt}},\quad {{g}^{{\rho k}}} = \psi _{j}^{\rho }{{b}^{{jk}}}(q,\text{v},w,t).$

Если строки матрицы g^ρk линейно независимы, то при s > r общее решение системы уравнений (2.9) состоит из двух слагаемых:

(2.10)

${{u}_{k}} = {{u}^{0}}u_{k}^{\tau } + u_{k}^{\nu },\quad k = \overline {1,s} .$

Здесь u⁰ произвольный множитель, $u_{k}^{\tau }$ – определитель, первая строка которого состоит из нулей, кроме единицы, соответствующей столбцу с номером k, остальные строки заполнены элементами матрицы (g^ρk) и произвольными величинами g^σk, $\sigma = \overline {r + 1,s - 1} $. Второе слагаемое определяется выражением

(2.11)

$u_{k}^{\nu } = - {{\delta }_{{kl}}}{{g}^{{\sigma l}}}{{\omega }_{{\sigma \rho }}}\left( {\frac{{\tilde {d}{{\psi }^{\rho }}}}{{dt}}} \right),$

${{\omega }^{{\rho \sigma }}}{{\omega }_{{\sigma \gamma }}} = \delta _{\gamma }^{\rho },\quad \gamma = \overline {1,r} ,\quad {{\omega }^{{\rho \sigma }}} = {{g}^{{\rho k}}}{{\delta }_{{kl}}}{{g}^{{\sigma l}}}.$

В случае r = s система уравнений (2.9) имеет решение:

${{u}_{k}} = - {{g}_{{k\rho }}}\left( {\frac{{\tilde {d}{{\psi }^{\rho }}}}{{dt}}} \right),\quad ({{g}_{{k\rho }}}) = {{({{g}^{{\rho k}}})}^{{ - 1}}},\quad k,\rho = \overline {1,r} .$

С учетом выражений (2.10), (2.11) уравнения динамики (2.1) замкнутой системы принимают следующий вид:

(2.12)

$\left\{ \begin{gathered} \frac{{d{{q}^{i}}}}{{dt}} = {{\text{v}}^{i}}, \hfill \\ \frac{{d{{\text{v}}^{i}}}}{{dt}} = {{a}^{i}}(q,\text{v},w,t), \hfill \\ \frac{{d{{w}^{j}}}}{{dt}} = {{b}^{j}}(q,\text{v},w,t) + {{b}^{{jk}}}(q,\text{v},w,t)\left( {{{u}^{0}}u_{k}^{\tau } - {{\delta }_{{kl}}}{{g}^{{\sigma l}}}{{\omega }_{{\sigma \rho }}}\left( {\frac{{\tilde {d}{{\psi }^{\rho }}}}{{dt}}} \right)} \right), \hfill \\ \end{gathered} \right.$

${{q}^{i}}({{t}_{0}}) = q_{0}^{i},\quad {{\text{v}}^{i}}({{t}_{0}}) = \text{v}_{0}^{i},\quad \quad{{w}^{j}}({{t}_{0}}) = w_{0}^{j},$

Функции

${{f}^{\mu }}(q,t) = {{c}^{\mu }},\quad {{\varphi }^{\rho }}(q,\text{v},t) = {{c}^{\rho }},\quad {{\psi }^{\rho }}(q,\text{v},w,t) = {{c}^{{r + \rho }}},$

где c^μ, c^ρ, c^r ^{+ ρ} – произвольные постоянные, составляют первые интегралы системы дифференциальных уравнений (2.12).

3. Устойчивость. Если начальные условия (2.2) соответствуют равенствам (2.5), то вдоль решений уравнений системы (2.12) выполняются условия (2.6), (2.7). Однако погрешности в задании начальных условий и использование численных методов решения уравнений системы (2.12) приводят к нарушению этих условий. Для оценки отклонений от уравнений связей введем переменные

(3.1)

${{y}^{\mu }} = {{f}^{\mu }}(q,t),\quad {{y}^{{m + \rho }}} = {{\varphi }^{\rho }}(q,\text{v},t),\quad {{y}^{{m + r + \rho }}} = {{\psi }^{\rho }}(q,\text{v},w,t),$

$\mu = \overline {1,m} ,\quad \rho = \overline {1,r} ,$

которые в соответствии с условиями (2.7), (2.8) связаны соотношениями

(3.2)

$\frac{{d{{y}^{\mu }}\quad}}{{dt}} = {{y}^{{m + \mu }}},\quad \frac{{d{{y}^{{m + \rho }}}\quad}}{{dt}} = {{y}^{{m + r + \rho }}},\quad \frac{{d{{y}^{{m + r + \rho }}}\quad}}{{dt}} = 0.$

Если начальные значения (2.2) соответствуют равенствам

(3.3)

${{f}^{\mu }}({{q}_{0}},{{t}_{0}}) = y_{0}^{\mu },\quad {{\varphi }^{\rho }}({{q}_{0}},{{\text{v}}_{0}},{{t}_{0}}) = y_{0}^{{m + \rho }},\quad {{\psi }^{\rho }}({{q}_{0}},{{\text{v}}_{0}},{{w}_{0}},{{t}_{0}}) = y_{0}^{{m + r + \rho }},$

то из условий (3.2) следует, что отклонения от уравнений связей будут возрастать с течением времени:

${{y}^{{m + \rho }}} = y_{0}^{{m + \rho }} + y_{0}^{{m + r + \rho }}t,\quad {{y}^{\mu }}\quad = y_{0}^{\mu } + y_{0}^{{m + \mu }}t + \frac{1}{2}y_{0}^{{2m + \mu }}{{t}^{2}}.$

Возможные отклонения решений уравнений динамики замкнутой системы от уравнений связей должны быть компенсированы за счет управляющих воздействий. Поэтому выражения u_k = = u_k(q, $\text{v}$, w, t) должны быть определены так, чтобы функции (2.6) составляли частные интегралы системы дифференциальных уравнений (2.1) [7]. Для этого уравнения (2.7), (2.8), определяющие выражения управляющих воздействий, следует заменить равенствами

(3.4)

${{\dot {\psi }}^{\rho }}(q,\text{v},w,t) = {{\Phi }^{\rho }}(q,\text{v},w,y,t),$

$y = ({{y}^{1}}, \ldots ,{{y}^{{m + 2r}}}),\quad \rho = \overline {1,r} ,$

правые части которых составляют произвольные функции, удовлетворяющие условиям

${{\Phi }^{\rho }}(q,\text{v},w,0,t) = 0,\quad \rho = \overline {1,r} .$

Из уравнений (3.4) следуют выражения управляющих воздействий, учитывающих отклонения от уравнений связей:

${{u}_{k}} = {{u}^{0}}u_{k}^{\tau } + {{\delta }_{{kl}}}{{g}^{{\sigma l}}}{{\omega }_{{\sigma \rho }}}\left( {{{\Phi }^{\rho }}(q,\text{v},w,y,t) - \frac{{\tilde {d}{{\psi }^{\rho }}}}{{dt}}} \right),\quad k = \overline {1,s} .$

В итоге уравнения динамики замкнутой системы будут представлены в виде

(3.5)

$\left\{ \begin{gathered} \frac{{d{{q}^{i}}\quad}}{{dt}} = {{\text{v}}^{i}},\quad \hfill \\ \frac{{d{{\text{v}}^{i}}\quad}}{{dt}} = {{a}^{i}}(q,\text{v},w,t),\quad \hfill \\ \frac{{d{{w}^{j}}\quad}}{{dt}} = {{{\tilde {b}}}^{j}}(q,\text{v},w,t) + \tilde {b}_{\rho }^{j}(q,\text{v},w,t){{\Phi }^{\rho }}(q,\text{v},w,y,t), \hfill \\ \end{gathered} \right.$

${{\tilde {b}}^{j}}(q,\text{v},w,y,t) = {{b}^{j}}(q,\text{v},w,t) + {{b}^{{jk}}}(q,\text{v},w,t)\left( {{{u}^{0}}u_{k}^{\tau } - {{\delta }_{{kl}}}{{g}^{{\sigma l}}}{{\omega }_{{\sigma \rho }}}\frac{{\tilde {d}{{\psi }^{\rho }}}}{{dt}}} \right),$

$\tilde {b}_{\rho }^{j}(q,\text{v},w,t) = {{b}^{{jk}}}(q,\text{v},w,t){{\delta }_{{kl}}}{{g}^{{\sigma l}}}{{\omega }_{{\sigma \rho }}},$

$i = \overline {1,n} ,\quad j = \overline {1,m} .$

Из равенств (2.8), (3.1), (3.3), (3.5) следует система дифференциальных уравнений

(3.6)

$\left\{ \begin{gathered} \frac{{d{{y}^{\mu }}\quad}}{{dt}} = {{y}^{{m + \mu }}}, \hfill \\ \frac{{d{{y}^{{m + \rho }}}\quad}}{{dt}} = {{y}^{{m + r + \rho }}}, \hfill \\ \frac{{d{{y}^{{m + r + \rho }}}\quad}}{{dt}} = {{\Phi }^{\rho }}(q,\text{v},w,{{y}^{\mu }},{{y}^{{m + \rho }}},{{y}^{{m + r + \rho }}},t), \hfill \\ \end{gathered} \right.$

составляющих уравнения возмущений связей, заданных выражениями (2.6), и соответствующие им начальные условия:

(3.7)

${{y}^{\mu }}({{t}_{0}}) = y_{0}^{\mu },\quad {{y}^{{m + \mu }}}({{t}_{0}}) = y_{0}^{{m + \mu }},\quad {{y}^{{m + r + \rho }}}({{t}_{0}}) = y_{0}^{{m + r + \rho }}.$

Представим уравнения (3.5), (3.6) и совокупность начальных условий (2.2), (3.7) в компактном виде:

(3.8)

$\frac{{d{{x}^{\alpha }}}}{{dt}} = {{X}^{\alpha }}(x,t) + b_{\rho }^{\alpha }(x,t){{\Phi }^{\rho }}(x,y,t),$

(3.9)

$\frac{{d{{y}^{\beta }}\quad}}{{dt}} = {{Y}^{\beta }}(x,y,t),$

${{y}^{\beta }} = {{g}^{\beta }}(x,t),$

(3.10)

${{x}^{\alpha }}({{t}_{0}}) = x_{0}^{\alpha },\quad {{y}^{\beta }}\quad({{t}_{0}}) = y_{0}^{\beta },\quad \alpha = \overline {1,m + 2n} ,\quad \beta = \overline {1,m + 2r} ,$

${{x}^{i}} = {{q}^{i}},\quad {{x}^{{n + i}}} = {{\text{v}}^{i}},\quad {{x}^{{2n + j}}} = {{w}^{j}};$

${{X}^{i}} = {{\text{v}}^{i}},\quad {{X}^{{n + i}}} = {{a}^{i}}(x,t),\quad {{X}^{{2n + j}}} = {{\tilde {b}}^{j}}(x,t),$

$b_{\rho }^{i}(x,t) = 0,\quad b_{\rho }^{{n + i}}(x,t) = 0,\quad b_{\rho }^{{2n + j}}(x,t) = \tilde {b}_{\rho }^{j}(x,t),$

${{g}^{\mu }}(x,t) = {{\varphi }^{\mu }}(q,t),\quad {{g}^{{m + \rho }}}(x,t) = {{\varphi }^{\rho }}(q,\text{v},t),\quad {{g}^{{m + r + \rho }}}(x,t) = {{\psi }^{\rho }}(q,\text{v},t),$

${{Y}^{\mu }}(x,y,t) = {{y}^{{m + \mu }}},\quad {{Y}^{{m + \rho }}}(x,y,t) = {{y}^{{m + r + \rho }}},$

${{Y}^{{m + r + \rho }}}(x,y,t) = {{\Phi }^{\rho }}(x,y,t),\quad {{\Phi }^{\rho }}(x,0,t) = 0.$

Множество точек в пространстве переменных q, $\text{v}$, w, удовлетворяющих равенствам (3.1) при

(3.11)

${{y}^{\beta }} = 0,\quad \beta = \overline {1,m + 2r} ,$

составляет интегральное многообразие системы уравнений (3.8), и его устойчивость определяется поведением решений системы уравнений возмущений связей (3.9) в окрестности тривиального решения (3.11).

Определение 1. Интегральное многообразие системы уравнений (3.8) устойчиво, если для любого ε существует такое δ, что при всех начальных условиях (3.10), удовлетворяющих неравенствам ||y₀|| ≤ δ, решение y = y(t) уравнений системы (3.9) будет удовлетворять условию ||y(t)|| ≤ ε при всех t > t₀.

Определение 2. Интегральное многообразие системы уравнений (3.8) устойчиво асимптотически, если оно устойчиво и выполняется условие $\mathop {{\;lim}}\limits_{t \to \infty } {\text{||}}y(t){\text{||}} = 0$.

Определение 3. Интегральное многообразие системы уравнений (3.8) экспоненциально устойчиво, если оно устойчиво и выполняется условие $\left\| {y(t)} \right\| \leqslant \left\| {{{y}_{0}}} \right\|{{e}^{{ - \lambda (t - {{t}_{0}})}}}$, $\lambda > 0$.

Свойства устойчивости тривиального решения системы (3.9) определяются выбором произвольных функций ${{\Phi }^{\rho }}(x,y,t)$, ${{\Phi }^{\rho }}(x,0,t) = 0$. Условия устойчивости могут быть получены посредством функций Ляпунова. Если функции Φ^ρ представить линейной комбинацией возмущений связей: ${{\Phi }^{\rho }}(x,y,t) = h_{\beta }^{{m + r + \rho }}(x,t){{y}^{\beta }}$, то система (3.9) получается линейной:

(3.12)

$\frac{{d{{y}^{\beta }}\quad}}{{dt}} = h_{\sigma }^{\beta }(x,t){{y}^{\sigma }},\quad \beta ,\sigma = \overline {1,m + 2r} .$

Пусть квадратичная форма V = 0.5m_σβy^σy^β с постоянными коэффициентами является положительно определенной и удовлетворяет неравенствам ${{m}_{1}}{\text{||}}y{\text{|}}{{{\text{|}}}^{2}} \leqslant V \leqslant {{m}_{2}}{\text{||}}y{\text{|}}{{{\text{|}}}^{2}}$. Если производная функции V, вычисленная в силу уравнений системы (3.12):

$\frac{{dV\quad}}{{dt}} = {{p}_{{\sigma \beta }}}(x,t){{y}^{\sigma }}{{y}^{\beta }},\quad {{p}_{{\sigma \beta }}}(x,t) = {{m}_{{\sigma \gamma }}}h_{\beta }^{\gamma }(x,t),\quad \beta ,\gamma ,\sigma = \overline {1,m + 2r} ,$

ограничена условием

$\frac{{dV\quad}}{{dt}} \leqslant - s{{\left\| y \right\|}^{2}},$

то выполняется неравенство

${{\left\| y \right\|}^{2}} \leqslant \frac{{{{m}_{2}}}}{{{{m}_{1}}}}{\text{||}}{{y}_{0}}{\text{|}}{{{\text{|}}}^{2}}{{e}^{{ - \lambda \left( {t - {{t}_{0}}} \right)}}},\quad \lambda = \frac{{2s}}{{{{m}_{2}}}},$

и интегральное многообразие системы уравнений (3.8) устойчиво экспоненциально.

В случае, когда коэффициенты $h_{\sigma }^{\beta }$ уравнений системы (3.12) являются постоянными, тривиальное решение асимптотически устойчиво, если все корни характеристического уравнения имеют отрицательные действительные части.

4. Стабилизация связей. При численном решении системы уравнений (3.8), (3.9) с начальными условиями (3.10) асимптотическая устойчивость тривиального решения системы (3.9) не гарантирует ограниченности отклонений от уравнений связей (2.3), (2.4) и на правые части уравнений (3.9) необходимо наложить дополнительные условия.

Пусть при t = t₀ начальные условия (3.10) удовлетворяют условию ${\text{||}}{{y}_{0}}{\text{||}} \leqslant $ ε, и для решения системы уравнений

$\frac{{d{{x}^{\alpha }}}}{{dt}} = {{\tilde {X}}^{\alpha }}(x,t),$

${{\tilde {X}}^{\alpha }}(x,t) = {{X}^{\alpha }}(x,t) + b_{\rho }^{\alpha }(x,t){{\Phi }^{\rho }}(x,y(x,t),t),\quad {{x}^{\alpha }}({{t}_{0}}) = x_{0}^{\alpha },$

используется простейшая разностная схема

$x_{{k + 1}}^{\alpha } = x_{k}^{\alpha } + {{(\Delta {{x}^{\alpha }})}_{k}},\quad {{(\Delta {{x}^{\alpha }})}_{k}} = \tau {{\tilde {X}}^{\alpha }}({{x}_{k}},{{t}_{k}}),\quad k = \overline {1,N} .$

Представим функции $y_{{k + 1}}^{\beta } = {{g}^{\beta }}({{x}_{{k + 1}}},{{t}_{{k + 1}}})$ разложением в ряд по степеням $\tau = {{t}_{{k + 1}}} - {{t}_{k}}$:

(4.1)

${{g}^{\beta }}({{x}_{{k + 1}}},{{t}_{{k + 1}}}) = {{g}^{\beta }}({{x}_{k}},{{t}_{k}}) + {{\left( {\frac{{\partial {{g}^{\beta }}}}{{\partial {{x}^{\alpha }}}}} \right)}_{k}}{{(\Delta {{x}^{\alpha }})}_{k}} + \tau {{\left( {\frac{{\partial {{g}^{\beta }}}}{{\partial t}}} \right)}_{k}} + g_{{k + 1}}^{{\beta \left( 2 \right)}}.$

Если изменение возмущений связей описывается линейной системой дифференциальных уравнений (3.12), то равенство (4.1), где последнее слагаемое означает остаточный член, приводится к виду

$y_{{k + 1}}^{\beta } = \delta _{\sigma }^{\beta }y_{k}^{\sigma } + \tau h_{\sigma }^{\beta }({{x}_{k}},{{t}_{k}})y_{k}^{\sigma } + g_{{k + 1}}^{{\beta \left( 2 \right)}}.$

Следовательно, при выполнении ограничений

${\text{||}}{{y}_{k}}{\text{||}} \leqslant \varepsilon {\text{,}}\quad {\text{||}}(\delta _{\sigma }^{\beta } + \tau h_{\sigma }^{\beta }({{x}_{k}},{{t}_{k}})){\text{||}} \leqslant \vartheta < 1,\quad {\text{||}}g_{{k + 1}}^{{\beta (2)}}{\text{||}} \leqslant (1 - \vartheta )\varepsilon $

будет справедливо неравенство

${\text{||}}{{y}_{{k + 1}}}{\text{||}} \leqslant {\;}\varepsilon {\text{.}}$

Если для решения системы уравнений (3.8) используется метод Рунге-Кутты второго порядка

$x_{{k + 1}}^{\alpha } = x_{k}^{\alpha } + {{(\Delta {{x}^{\alpha }})}_{k}},$

${{(\Delta {{x}^{\alpha }})}_{k}} = \tau (1 - {{\vartheta }_{1}}){{\tilde {X}}^{\alpha }}({{x}_{k}},{{t}_{k}}) + \tau {{\vartheta }_{1}}{{\hat {X}}^{\alpha }}({{x}_{k}},{{t}_{k}}),$

${{\hat {X}}^{\alpha }}({{x}_{k}},{{t}_{k}}) = {{\tilde {X}}^{\alpha }}({{x}_{k}} + \tau {{\vartheta }_{2}}X({{x}_{k}},{{t}_{k}}),{{t}_{k}} + \tau {{\vartheta }_{2}}),$

то ограничение ${\text{||}}{{y}_{{k + 1}}}{\text{||}} \leqslant {\varepsilon \;}$ будет справедливо при выполнении условий

${\text{||}}{{y}_{k}}{\text{||}} \leqslant \varepsilon {\text{,}}\quad 2{{\vartheta }_{1}}{{\vartheta }_{2}} = 1,\quad {\text{||}}g_{{k + 1}}^{{\beta (3)}}{\text{||}} \leqslant (1 - \vartheta )\varepsilon {\text{,}}$

$\left\| {\left( {\delta _{\sigma }^{\beta } + \tau h_{\sigma }^{\beta }({{x}_{k}},{{t}_{k}}) + \frac{1}{2}{{\tau }^{2}}\left( {{{{(h_{\sigma }^{\beta }({{x}_{k}},{{t}_{k}}))}}^{2}} + \frac{{dh_{\sigma }^{\beta }({{x}_{k}},{{t}_{k}})}}{{dt}}} \right)} \right)} \right\| \leqslant \vartheta < 1.$

Условия стабилизации связей, соответствующие методам Рунге–Кутты более высокого порядка, определены в [33].

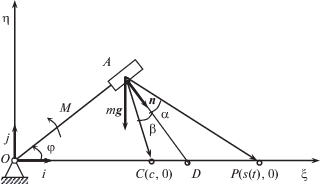
5. Управление элементом адаптивной оптической системы. Рассмотрим задачу управления элементом адаптивной оптической системы [34]. Элемент системы будем моделировать устройством, состоящим из невесомого кривошипа OA с неподвижной точкой O в плоскости Oξη, и закрепленного на нем зеркала A массы $m$ (рисунок). На зеркало действует сила тяжести mg, направленная в сторону, противоположную направлению оси Oη. Положение зеркала A на плоскости Oξη определяется углом $\varphi $ отклонения кривошипа от оси Oξ и расстоянием l до начала координат, которое будем считать постоянным. Вдоль оси Oξ по закону s = s(t) движется точка P, из которой исходит луч света, направленный на зеркало A. Кривошип приводится во вращение двигателем постоянного тока. Требуется определить выражение управляющего напряжения $u$, приложенного к якорной цепи двигателя, вращающего кривошип, при котором луч, отраженный от зеркала, попадает в фиксированную точку C(c, o), расположенную на оси Oξ. Обозначим через n единичный вектор нормали AD к поверхности зеркала, α – угол падения луча, β – угол отражения.

Цель управления состоит в поддержании равенства α = β. Уравнение связи, выражающее цель управления,

${{l}^{2}}({{с }^{2}} - {{s}^{2}}(t)){{\sin }^{2}}\varphi - 2lcs(t)\cos \varphi (s(t) - c){{\sin }^{2}}\varphi = 0$

следует из равенств

$\frac{{PD}}{{\sin \alpha }} = \frac{{PA}}{{\cos \varphi }},\quad \frac{{CD}}{{\sin \beta }} = \frac{{CA}}{{\cos \varphi }},\quad PD \cdot CA = PA \cdot CD,$

$CD = \frac{{l - c\cos \varphi }}{{\cos \varphi }},\quad PD = \frac{{s(t)\cos \varphi - l}}{{\cos \varphi }},$

$P{{A}^{2}} = {{l}^{2}} + s(t) - 2ls(t)\cos \varphi ,\quad C{{A}^{2}} = {{l}^{2}} + {{c}^{2}} - 2lc\cos \varphi .$

Исключив особые случаи ${{\sin }^{2}}\varphi = 0$ и $s(t) - c = 0$, представим уравнение связи выражением

(5.1)

$l(s(t) + c) - 2cs(t)\cos \varphi = 0.$

Пусть динамика рассматриваемой системы описывается уравнениями

(5.2)

$\left\{ \begin{gathered} \frac{{d\varphi }}{{dt}} = \omega ,\quad \frac{{d\omega }}{{dt}} = - \frac{g}{l}\cos \varphi + \frac{M}{{m{{l}^{2}}}},\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \hfill \\ \frac{{dM}}{{dt}} = \text{v},\quad \frac{{d\text{v}}}{{dt}} = - \frac{R}{L}\text{v} - \frac{{{{k}_{a}}{{k}_{b}}}}{{nL}}\omega + \frac{{{{k}_{a}}}}{L}u. \hfill \\ \end{gathered} \right.$

Здесь приняты следующие обозначения: φ – угол поворота кривошипа, g – ускорение свободно падающего тела, l – длина кривошипа $OA$, L – индуктивность цепи якоря двигателя, n – передаточное отношение редуктора, u – напряжение цепи якоря, i – ток в цепи якоря, e – электродвижущая сила, ω_∂ – угловая скорость вала двигателя, M – момент двигателя, R – сопротивление цепи якоря двигателя, k_a – коэффициент пропорциональности: $\text{v} = {{k}_{a}}i$, ${{k}_{b}}$ – коэффициент пропорциональности: $e = {{k}_{b}}{{\omega }_{\partial }}$.

Перепишем систему уравнений (5.2) в новых обозначениях:

(5.3)

$\frac{{d{{x}^{i}}}}{{dt}} = {{X}^{i}}(x) + {{b}^{i}}u,\quad i = \overline {1,4} ,$

$x = ({{x}^{1}},{{x}^{2}},{{x}^{3}},{{x}^{4}}),\quad {{x}^{1}} = \quad\varphi ,\quad {{x}^{2}} = \quad\omega ,\quad {{x}^{3}} = M,\quad {{x}^{4}} = \text{v},$

${{X}^{1}}(x) = \omega ,\quad {{X}^{2}}(x) = - {{k}_{\varphi }}\cos \varphi + {{k}_{M}}M,\quad {{X}^{3}}(x) = \text{v},\quad {{X}^{4}}(x) = - {{k}_{\text{v}}}\text{v} - {{k}_{\omega }}\omega ,$

${{b}^{1}} = {{b}^{2}} = {{b}^{3}} = 0,\quad {{b}^{4}} = \frac{{{{k}_{a}}}}{L}.\quad {{k}_{\varphi }} = \frac{g}{l},\quad {{k}_{M}} = \frac{1}{{m{{l}^{2}}}},\quad {{k}_{\text{v}}} = \frac{R}{L},\quad {{k}_{\omega }} = \frac{{{{k}_{a}}{{k}_{b}}}}{{nL}}.$

Будем определять отклонение от уравнения связи и его производные величинами

(5.4)

${{y}^{k}} = {{g}^{k}}(x,t),\quad k = \overline {1,4} ,$

${{g}^{1}}(x,t) = g_{0}^{1} + g_{1}^{1}(x){{s}^{1}}(t),$

$g_{0}^{1} = lc,\quad g_{1}^{1}(x) = (l - 2c\cos \varphi ),\quad {{s}^{{k + 1}}}(t) = \frac{{d{{s}^{k}}(t)}}{{dt}},\quad {{s}^{1}}(t) = s(t).$

(5.5)

$\frac{{d{{y}^{k}}}}{{dt}} = {{y}^{{k + 1}}},\quad {{y}^{5}} = {{g}^{5}}(x,u,t).$

Из равенств (5.4), (5.5) последовательно определяются величины

${{g}^{{k + 1}}}(x,t) = \frac{{d{{g}^{k}}(x,t)}}{{dt}} = g_{i}^{k}(x){{X}^{i}}(x) + \frac{{\partial {{g}^{k}}(x,t)}}{{\partial t}} = g_{i}^{k}(x){{s}^{i}}(t),$

$g_{i}^{k}(x) = \frac{{\partial {{g}^{k}}(x,t)}}{{\partial {{x}^{i}}}},\quad i = \overline {1,k} ,\quad k = 1,2,3,$

$g_{1}^{2}(x) = 2c\omega \sin \varphi ,$

$g_{1}^{3}(x) = c(2{{\omega }^{2}}\cos \varphi - {{k}_{\varphi }}\sin 2\varphi + 2{{k}_{M}}M\sin \varphi ),\quad g_{2}^{3}(x) = 4c\omega \sin \varphi ,$

$g_{1}^{4}(x) = 2c({{k}_{\varphi }}\omega - {{\omega }^{3}}\sin \varphi + {{k}_{M}}(\omega M\cos \varphi + \text{v}\sin \varphi )),$

$g_{2}^{4}(x) = 3c(2{{\omega }^{2}}\cos \varphi - {{k}_{\varphi }}\sin 2\varphi + 2{{k}_{M}}M\sin \varphi ),$

$g_{3}^{4}(x) = 6c\omega \sin \varphi .$

$g_{j}^{j}(x) = (l - 2c\cos \varphi ),\quad j = \overline {1,5} .$

Равенство

${{g}^{5}}(x,u,t) = \Phi (x,g(x,t),t),\quad g = ({{g}^{1}},{{g}^{2}},{{g}^{3}},{{g}^{4}}),$

представляет уравнение для определения выражения $u = u(\varphi ,\omega ,M,\text{v})$:

(5.6)

$g_{j}^{5}(x){{s}^{j}}(t) + g_{{41}}^{4}(x){{b}^{4}}{{s}^{4}}(t)u = \Phi (x,g(x,t),t),\quad j = \overline {1,5} ,$

$g_{1}^{5}(x) = g_{{1i}}^{4}(x){{X}^{i}}(x),$

$g_{2}^{5}(x) = g_{{2i}}^{4}(x){{X}^{i}}(x) + g_{1}^{4}(x),$

$g_{3}^{5}(x) = g_{{3i}}^{4}(x){{X}^{i}}(x) + g_{2}^{4}(x),$

$g_{4}^{5}(x) = g_{{4i}}^{4}(x){{X}^{i}}(x) + g_{3}^{4}(x),$

$g_{5}^{5}(x) = g_{4}^{4}(x),$

$g_{j}^{5}(x) = g_{{ji}}^{4}(x){{X}^{i}}(x) + g_{{j - 1}}^{4}(x),\quad g_{0}^{4}(x) \equiv 0.$

Из уравнения (5.6) следует выражение

(5.7)

$u = \frac{{L(\Phi (x,g(x,t),t) - g_{j}^{5}(x){{s}^{j}}(t))}}{{2c{{k}_{a}}s(t)\sin \varphi }},$

$g_{{11}}^{4}(x) = 2c(({{k}_{M}}\text{v} - {{\omega }^{3}})\cos \varphi - \omega {{k}_{M}}M\sin \varphi ),$

$g_{{12}}^{4}(x) = 2c({{k}_{M}}M\cos \varphi + {{k}_{\varphi }} - 3{{\omega }^{2}}\sin \varphi ),$

$g_{{13}}^{4}(x) = 2c{{k}_{M}}\cos \varphi ,$

$g_{{14}}^{4}(x) = 2c{{k}_{M}}\sin \varphi ,$

$g_{{21}}^{4}(x) = 6c({{\omega }^{2}}\sin \varphi - {{k}_{\varphi }}\cos 2\varphi + {{k}_{M}}M\cos \varphi ),$

$g_{{22}}^{4}(x) = 12c\omega \sin \varphi ,$

$g_{{23}}^{4}(x) = 6c{{k}_{M}}\cos \varphi ,$

$g_{{24}}^{4}(x) = 0,$

$g_{{31}}^{4}(x) = 6c\omega \cos \varphi ,$

$g_{{32}}^{4}(x) = 6c\sin \varphi ,$

$g_{{33}}^{4}(x) = g_{{34}}^{4}(x) = 0,$

$g_{{41}}^{4}(x) = 2c\sin \varphi ,$

$g_{{42}}^{4}(x) = g_{{43}}^{4}(x) = g_{{44}}^{4}(x) = 0.$

Полагая $\Phi (x,y,t) = h_{\beta }^{4}(x,t){{y}^{\beta }}$, уравнения возмущений связей можно представить системой линейных дифференциальных уравнений:

(5.8)

$\frac{{d{{y}^{1}}}}{{dt}} = {{y}^{2}},\quad \frac{{d{{y}^{2}}}}{{dt}} = {{y}^{3}},\quad \frac{{d{{y}^{3}}}}{{dt}} = {{y}^{4}},\quad \frac{{d{{y}^{4}}}}{{dt}} = h_{\beta }^{4}(x,t){{y}^{\beta }}.$

Подстановка выражения (5.7) в правую часть последнего уравнения системы (5.2) приводит к уравнениям замкнутой системы управления. Если коэффициенты системы уравнений (5.8) постоянны и корни характеристического уравнения имеют отрицательные действительные части, то закон изменения угла φ отклонения кривошипа, соответствующий уравнению связи (5.1), будет устойчив асимптотически.

Если начальные условия $\varphi ({{t}_{0}}) = \varphi {\text{||}}{{g}_{{(0)}}}{\text{||}} \leqslant {{\varepsilon }_{0}}$, $\omega ({{t}_{0}}) = {{\omega }_{0}}$, $M({{t}_{0}}) = {{M}_{0}}$, $\text{v}({{t}_{0}}) = {{\text{v}}_{0}}$ таковы, что выполняется ограничение ${\text{||}}{{g}_{{(0)}}}{\text{||}} \leqslant \varepsilon $, ${{g}_{{(j)}}} = (g_{{(j)}}^{1},g_{{(j)}}^{2},g_{{(j)}}^{3},g_{{(j)}}^{{4\quad}})$, $g_{{(j)}}^{k} = {{g}^{k}}({{x}_{{(j)}}},{{t}_{{(j)}}})$, $j = \overline {0,J} $, и для решения системы уравнений (5.3) используется разностная схема

$x_{{(j + 1)}}^{i} = x_{{(j)}}^{i} + \tau ({{X}^{i}}({{x}_{{(j)}}}) + {{b}^{i}}u({{x}_{{(j)}}},{{t}_{{(j)}}})),\quad {{x}_{{(j)}}} = x({{t}_{{(j)}}}),$ ${{t}_{{(j)}}} = j\tau ,\quad \tau = {{t}_{{(j + 1)}}} - {{t}_{{(j)}}},\quad j = \overline {0,J} $,

то для обеспечения условия ${\text{||}}{{g}_{{(j)}}}{\text{||}} \leqslant \varepsilon $ при всех j = $\overline {1,J} $ достаточно выполнения неравенств

${\text{||}}(\delta _{\beta }^{k} + \tau h_{\beta }^{k}({{x}_{{(j)}}},{{t}_{{(j)}}})){\text{||}} \leqslant \alpha < 1,\quad \frac{{{{\tau }^{2}}}}{2}{\text{||}}{{G}_{{(j)}}}{\text{||}} \leqslant (1 - \alpha )\varepsilon ,$

$h_{2}^{1} = h_{3}^{2} = h_{4}^{3} = 1,\quad h_{1}^{1} = h_{3}^{1} = h_{4}^{1} = h_{1}^{2} = h_{2}^{2} = h_{4}^{2} = h_{1}^{3} = h_{2}^{3} = h_{3}^{3} = 0,$

${{G}_{{(j)}}} = (G_{{(j)}}^{1},G_{{(j)}}^{2},G_{{(j)}}^{3},G_{{(j)}}^{{4\quad}}),\quad k,\beta = \overline {1,4} ,$

$({{\tau }^{2}}{\text{/}}2)G_{{(j)}}^{k} - $ остаточные члены разложения в ряд функций ${{g}^{k}}({{x}_{{(j)}}},{{t}_{{(j)}}})$.

Заключение. Применение традиционных подходов для определения управляющих воздействий, обеспечивающих выполнение заданных уравнений связей, приводит к неустойчивости соответствующего интегрального многообразия. Учет динамики исполнительных органов накладывает более жесткие условия на решение задачи стабилизации связей при численном решении уравнений динамики замкнутой системы, вызванные необходимостью использования производных от уравнений связей более высокого порядка. Модифицированные методы стабилизации связей, основанные на построении систем дифференциальных уравнений, имеющих асимптотически устойчивые частные интегралы, позволяют существенно расширить множество управляющих воздействий, обеспечивающих стабилизацию связей и их производных в системах высокого порядка.

Рисунок.

Элемент адаптивной оптической системы

Список литературы

Ольсон Г. Динамические аналогии. М.: Изд-во иностр. лит., 1947. 224 с.
Layton R.A. Principles of Analytical System Dynamics. N.Y.: Springer, 1998. 158 p.
Анри Беген. Теория гироскопических компасов Аншютца и Сперри и общая теория систем с сервосвязями. М.: Наука, 1967. 171 с.
Коренев Г.В. Цель и приспособляемость движения. М.: Наука, 1974. 524 с.
Галиуллин А.С., Мухаметзянов И.А., Мухарлямов Р.Г., Фурасов В.Д. Построение систем программного движения. М.: Наука, 1971. 352 с.
Мухарлямов Р.Г. К обратным задачам качественной теории дифференциальных уравнений // Дифференц. уравнения. 1967. Т. 3. № 10. С. 1673–1681.
Матухина О.В. О задаче моделирования кинематики и динамики управляемых систем с программными связями // Инженерный журнал: наука и инновации, 2018. Вып. 4. https://doi.org/10.18698/2308-6033-2018-4-1753
Baumgarte J. Stabilization of Constraints and Integrals of Motion in Dynamical Systems // Computer Methods in Applied Mechanics and Engineering. 1972. № 1. P. 1–16.
Baumgarte J. Stabilized Kepler Motion Connected with Analytic Step Adaptation // Celest. Mech. 1976. V. 13. Issue 1. P. 105–109.
Авдюшев В.А. Численное моделирование орбит. Томск: Изд-во HTЛ, 2010. 282 с.
Буров А.А., Косенко И.И. О дифференциально-алгебраических уравнениях Лагранжа // ПММ. 2014. Т. 78. № 6. С. 818–832.
Витенбург Й. Динамика систем твердых тел. М.: Мир, 1980. 294 с.
Amirouche F. Fundamentals of Multibody Dynamics: Theory and Applications. Boston: Birkh$\ddot {a}$user, 2006.
Shih-Tin Lin, Jiann-Nan Huang. Numerical Integration of Multibody Mechanical Systems using Baumgarte’s Constraint Stabilization Method // J. Chinese Institute of Engineers. 2002. V. 25. № 2. P. 243–252.
Ascher U.M., Hongsheng Chin, Petzold L.R., Reich S. Stabilization of Constrained Mechanical Systems with DAEs and Invariant Manifolds // J. Mechanics of Structures and Machines. 1995. V. 23. Issue 2. P. 135–158.
Ascher U.M. Stabilization of Invariant of Discretized Differential Systems // Numerical Algorithms. 1997. V. 14. Issue 1. P. 1–24.
Ascher U.M., Hongsheng Chin, Reich S. Stabilization of DAEs and Invariant Manifolds // Numer. Math. 1994. V. 67. Issue 2. P. 131–149.
Shih-Tin Lin, Ming-Chong Hong. Stabilization Method for the Numerical Integration of Controlled Multibody Mechanical System: A Hybrid Integration Approach // JSME International J. Ser. C. 2001. V. 44. Issue 1. P. 79–88.
Суслов Г.К. О силовой функции, допускающей заданные интегралы. Киев. Изд-во Киевск. ун-та, 1890. 114 с.
Жуковский Н.Е. Определение силовой функции по данному семейству траекторий // Полное собр. соч. Т. I. М.–Л.: ОНТИ НКТП СССР, 1937. С. 293–308.
Леви-Чивита, Амальди У. Курс теоретической механики. Т. 2. Ч. 2. М.: Изд-во иностр. лит., 1952. 544 с.
Галиуллин А.С. Методы решения обратных задач динамики. М.: Наука, 1986. 224 с.
Bozis G., Ichtiaroglou S. Existence and Construction of Dynamical Systems having a Prescribed Integral of Motion-an Inverse Problem // Inverse Problems. 1987. V. 3. Issue 2. P. 213–227.
Еругин Н.П. Построение всего множества систем дифференциальных уравнений, имеющих заданную интегральную кривую // ПММ. 1952. Т. 21. № 6. С. 659–670.
Мухарлямов Р.Г. О построении дифференциальных уравнений оптимального движения по заданному многообразию // Дифференц. уравнения. 1971. Т. 7. № 10. С. 1825–1834.
Мухарлямов Р.Г. О построении множества систем дифференциальных уравнений устойчивого движения по интегральному многообразию // Дифференц. уравнения. 1969. Т. 5. № 4. С. 688–699.
Мухарлямов Р.Г. О решении систем нелинейных уравнений // ЖВМ и МФ. 1971. Т. 11. № 4. С. 829–836.
Мухарлямов Р.Г. Об уравнениях движения механических систем // Дифференц. уравнения. 1983. Т. 19. № 12. С. 2048–2056.
Mukharlyamov R.G., Deressa Chernet Tuge. Stabilization of Redundantly Constrained Dynamic System // Вестн. РУДН. Сер. Математика, информатика, физика. 2015. № 1. С. 60–72.
Мухарлямов Р.Г. Управление динамикой систем с позиционными связями // Аналитическая механика, устойчивость и управление: Тр. XI Междунар. Четаевской конф. Т. 3. Секц. 3. Управление. Ч. II. Казань: КНИТУ-КАИ, 2017. С. 140–146.
Козлов В.В. Динамика систем с сервосвязями. I // Нелинейная динамика. Т. 11. № 2. С. 353–376.
Козлов В.В. Динамика систем с сервосвязями. II // Нелинейная динамика. Т. 11. № 3. С. 579–611.
Beshaw A.W. Dynamic Equation of Constrained Mechanical System // Вестн. РУДН. Сер. Математика, информатика, физика. 2014. № 3. С. 115–124.
Адаптивная оптика: Сб. статей / Пер. с англ. Под ред. Э.А. Витриченко. М.: Мир, 1980. 456 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал