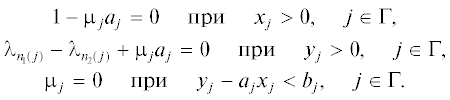Известия РАН. Теория и системы управления, 2019, № 4, стр. 132-143

Введение. Классический метод потенциалов для стандартной транспортной задачи (СТЗ) хорошо известен. По своей сути он является модификацией симплекс-метода для специального класса задач линейного программирования. Метод позволяет осуществить движение за конечное число итераций от некоторого допустимого базисного решения к оптимальному базисному решению [1]. Известен модифицированный метод потенциалов для задачи с ограничениями на пропускные способности коммуникаций [2]. Известны также обобщения метода потенциалов для решения многоиндексной транспортной задачи [3, 4]. В научных работах представлен вариант метода потенциалов для задачи о перевозках, т.е. задачи с произвольной сетевой структурой [5]. Однако все вышеперечисленные модификации алгоритма относятся к задачам анализа заданной коммуникационной сети. В данной статье приведен модифицированный метод потенциалов для детерминированной задачи линейного синтеза коммуникационной сети для задачи о спросе и предложении. А именно описана задача, когда одновременно с формированием оптимального плана перевозки решается задача нахождения оптимального распределения однородного сепарабельного ресурса, которое определяет значения функций производственных мощностей пунктов производства и функций пропускных способностей коммуникаций, тем самым решая задачу оптимального синтеза сети.

Рассматривается задача синтеза сети для модели Гейла о спросе и предложении [6]. Пусть задан ориентированный граф с индексами вершин из множества P = {i = 1, …, η} и дугами  j из множества Γ. Введем следующие обозначения: D(i) – множество индексов дуг, входящих в вершину i коммуникационной сети, а C(i) – соответственно исходящих. Имеем также некоторую совокупность из n вершин с индексами вершин из множества A = {i = 1, …, n} (подмножество множества Р), которые будем называть источниками (или пунктами производства). Будем считать выполненным свойство i ∈ A ⇒ D(i) = ∅, т.е. из вершин-источников дуги только выходят. Рассмотрим также некоторое множество из m вершин с индексами вершин из множества C = {i = η – m + + 1, …, η}, которые назовем стоками (или пунктами потребления) и для которых предполагаем свойство i ∈ C ⇒ C(i) = ∅, т.е. в вершины-стоки дуги только входят. Пусть оставшиеся вершины в количестве (η – n – m) образуют множество вершин с индексами вершин из множества B = {i = = n + 1, …, η – m}, которые мы будем называть промежуточными вершинами. Пусть каждой вершине i ∈ A поставлена в соответствие некоторая неотрицательная функция производственной мощности ϕ_i(x) ≥ 0, x ∈ X, где X – множество допустимых распределений ресурсов. Кроме того, известны неотрицательные функции φ_j(x) ≥ 0, задающие пропускные способности дуг сети в зависимости от выбранного распределения ресурсов [7]. Таким образом, ресурсы распределяются как между вершинами-источниками, так и между дугами сети, определяя тем самым мощности источников и пропускные способности коммуникаций. Для вершин-стоков известны величины потребностей в продукте – d_j.

Как известно, модель с несколькими пунктами производства и ограниченными запасами продукта сводится к задаче с одним пунктом производства с неограниченным запасом продукта [8]. А именно добавляется один фиктивный пункт производства с неограниченным запасом продукта, который соединяется дугами со всеми пунктами производства. Функции производственных мощностей пунктов производства из множества А становятся функциями пропускных способностей соответствующих добавленных дуг. Вершины из множества А становятся промежуточными (транзитными) вершинами. Легко показать эквивалентность обоих моделей.

Задача состоит в рассмотрении допустимых распределений ресурсов и связанных с ними допустимых потоков однородного продукта, которые за счет предложения продукта в источниках удовлетворяют потребности в продукте в стоках сети.

1. Математическая постановка задачи. Рассмотрим в качестве функций пропускных способностей дуг φ_j(x) = b_j + a_jx_j линейные функции. Заметим, что рассматривается сепарабельный ресурс, поэтому функции пропускных способностей дуг зависят только от вложения ресурса в данную дугу, т.е. от одной переменной x_j, таким образом имеем φ_j(x_j). Задача в этом случае имеет следующий вид:

Предполагаем, что a_j > 0, b_j ≥ 0, j ∈ Γ. Отметим, что первоначально рассматривается случай, когда a_j > 0. Общий случай, когда a_j ≥ 0, представлен далее, где вектор y есть план перевозки продукта, а d_j, как и выше, – величины потребностей в продукте в вершинах-стоках. Дадим краткий комментарий ограничениям задачи (1.1). Вершины из множества B являются транзитными, вершины из множества A также являются транзитными после добавления фиктивного источника. Для транзитных вершин коммуникационной сети справедливо требование о равенстве входящего и исходящего потоков, откуда справедлива первая группа ограничений:

Вершины из множества C потребляют продукт, поэтому для них разность входящего и исходящего потоков равна величине потребления, откуда справедлива вторая группа ограничений:

Величина потока по любой из дуг не превосходит пропускной способности дуги, откуда справедлива третья группа ограничений: y_j – a_jx_j ≤ b_j,  j ∈ Γ.

Задача (1.1) является задачей линейного программирования. Запишем двойственную к ней задачу (1.2):

где λ и μ – двойственные переменные, n₁(j) – индекс вершины-начала для дуги j, а n₂(j) – индекс вершины-окончания соответственно. Как и в известных модификациях метода потенциалов для задач транспортного типа, под “потенциалами” понимаем значения двойственных переменных λ_i. Применительно к задачам (1.1) и (1.2) справедлива следующая теорема, основанная на применении известной теоремы теории двойственности линейного программирования [2].

Теорема 1. Для оптимальности вектора (x, y) задачи (1.1) необходимо и достаточно существование вектора (λ, μ), удовлетворяющего ограничениям задачи (1.2) и связанного с вектором (x, y) следующими соотношениями (условия дополняющей нежесткости):

Суть приведенного ниже алгоритма состоит в последовательном просмотре опорных планов задачи (1.1), значения целевой функции для которых монотонно не возрастают. За конечное число шагов находится опорный план задачи (1.1), для которого существует вектор (λ, μ), удовлетворяющий ограничениям задачи (1.2) и соотношениям (1.3). Откуда в силу вышеприведенной теоремы 1 и следует оптимальность найденного решения.

2. Описание алгоритма (a_j > 0). Перейдем к изложению алгоритма.

Определение 1. Будем называть дугу j θ-дугой, если y_j = b_j > 0, x_j = 0.

Определение 2. Будем называть дугу j 0-дугой, если y_j = 0.

Ограничения задачи (1.1) можно свести к эквивалентной системе равенств, записав ограничения на пропускные способности дуг в виде y_j – a_jx_j + z_j = b_j и добавив ограничение z_j ≥ 0, j ∈ Γ. Тогда справедливо следующее утверждение.

Утверждение 1. Вектор (x, y, z) является опорным планом задачи (1.1) тогда и только тогда, когда после удаления всех θ-дуг в графе не остается циклов из дуг с ненулевыми потоками.

Доказательство. Известно, что вектор (x, y, z) – опорный план задачи тогда и только тогда, когда столбцы, соответствующие его ненулевым компонентам, образуют линейно независимую систему векторов. Структура матрицы ограничений задачи (1.1) показана на рис. 1. Обозначим матрицу инцидентности графа как I_N.

Дуга j является θ-дугой тогда и только тогда, когда z_j = 0, x_j = 0. Следовательно, столбцы, соответствующие этим переменным, не входят в рассматриваемую систему. Тогда нетрудно заметить, что в любую нулевую комбинацию векторов (представление нулевого вектора) столбец, соответствующий переменной y_j, входит с нулевым коэффициентом.

Из структуры матрицы ограничений нетрудно видеть, что столбцы системы являются линейно независимыми тогда и только тогда, когда столбцы матрицы инцидентности дуг системы, не являющиеся θ-дугами, линейно независимы. Согласно теории графов, это равносильно тому, что эти дуги образуют лес. Это в свою очередь равносильно тому, что эти дуги не образуют циклов. Доказательство завершено.

Определение 3. Дуга j, принадлежащая некоторому связующему поддереву, называется правильно ориентированной, если начало дуги n₁(j) принадлежит пути, соединяющему конец дуги n₂(j) с корнем дерева.

Пусть имеется некоторое связующее поддерево с множеством дуг Γ_Т, которое в дальнейшем будем называть текущим поддеревом. Пусть также имеется некоторое допустимое решение (x, y) задачи (1.1), такое, что:

1) дуги, не принадлежащие множеству Γ_Т, являются либо 0-дугами, либо θ-дугами;

2) все 0-дуги, принадлежащие множеству Γ_Т, правильно ориентированы.

Тогда из утверждения 1 следует, что (x, y) – опорный план задачи (1.1). Будем придерживаться следующих правил вычисления переменных μ для произвольного связующего поддерева. Положим μ_j = 0, если j ∈ Γ_T и j является встречной θ-дугой. Для остальных j положим μ_j = 0, если y_j < b_j и μ_j = 1/a_j, если y_j ≥ b_j.

Для любых двух вершин I₁ и I₂ в текущем поддереве Γ_Т существует и единственный путь из I₁ в I₂, который будем обозначать (I₁, I₂). Алгебраическую сумму переменных μ_j вдоль пути, соединяющего вершины I₁ и I₂, т.е. со знаком плюс, если дуга имеет направление, совпадающее с направлением пути, и со знаком минус в противном случае, будем условно обозначать ($\mathop {{{I}_{1}},{{I}_{2}}}\limits^ \to $).

Будем придерживаться следующих правил вычисления потенциалов λ для произвольного связующего поддерева. Положим λ₀ = 0, λ_i = ($\mathop {0,i}\limits^ \to $), i ∈ A ∪ B ∪ C. Будем далее проверять выполнение следующих неравенств:

Нетрудно проверить, что условия (2.1) и (2.2) выполнены для всех  j из множества Γ_Т.

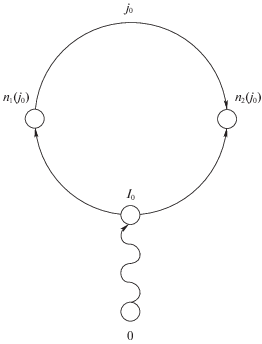
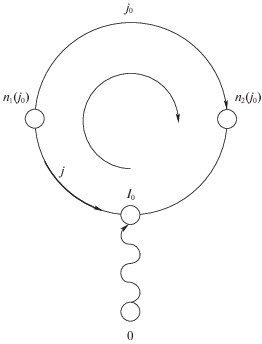
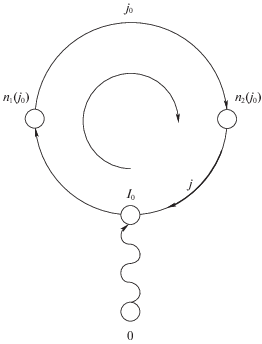
Рассмотрим сначала случай, когда нарушается некоторое неравенство j₀ из условий (2.1). Множество общих вершин путей (0, n₁(j₀)) и (0, n₂(j₀)) не пусто. Последнюю их общую вершину, если двигаться от корня дерева, обозначим I₀. Тогда пути (I₀, n₁(j₀)) и (n₂(j₀), I₀) вместе с дугой j₀ образуют цикл. Это и есть тот единственный цикл, который образуется при присоединении дуги j₀ к текущему поддереву Γ_Т (рис. 2).

Определим некоторые величины Е и Y для цикла с множеством дуг Н. Как будет обосновано далее, величина E показывает выгодность изменения потока вдоль цикла, а Y – предельно возможную величину этого изменения. За положительное направление обхода цикла примем направление дуги  j₀.

Введем дополнительные переменные Δμ_j и Δy_j  для дуг цикла H, а именно если направление дуги  j совпадает с направлением обхода, то положим

Если же направление дуги  j противоположно направлению обхода, то

Если  j есть встречная 0-дуга, то, положив Е = 0 и Y = 0, будем считать их вычисленными. Иначе присвоим им значения:

Утверждение 2. Если E ≥ 0, то ∃j: j ∈ (n₂(j₀), I₀), такой, что дуга j является θ-дугой или 0-дугой.

Доказательство. Допустим противное. Поскольку на участке цикла (I₀, n₁(j₀)) нет встречных 0-дуг, то из сделанного допущения следует, что Е есть алгебраическая сумма переменных μ_j вдоль всего цикла. Тогда

Из полученного противоречия следует неверность сделанного предположения, что и завершает доказательство утверждения.

Рассмотрим случай, когда E ≥ 0. В этом случае множество θ-дуг и 0-дуг пути (n₂(j₀), I₀) не пусто. Выберем первую из них.

Удалив ее из поддерева Γ_Т и добавив дугу j₀, получим новое связующее поддерево $\Gamma _{T}^{*}$, которое для имеющегося опорного плана (x, y) удовлетворяет условиям 1) и 2). Дерево $\Gamma _{T}^{*}$ будем считать новым текущим поддеревом. Если для него вычислить вектор ($\tilde {\lambda }$, $\tilde {\mu }$) по вышеизложенным правилам, то можно доказать следующее утверждение.

Утверждение 3. Пусть переменные (λ, μ) вычислены по вышеизложенным правилам для связующего поддерева Γ_Т, а ($\tilde {\lambda }$, $\tilde {\mu }$) – для связующего поддерева $\Gamma _{T}^{*}$ соответственно. Тогда

1) ${{\tilde {\lambda }}_{i}}$ = λ_i, i: n₂(j₀) ∉(0, i);

2) ${{\tilde {\lambda }}_{i}}$ = λ_i – Δ, i: n₂(j₀) ∈ (0, i), где Δ = ${{\lambda }_{{{{n}_{2}}(j)}}}$ – ${{\lambda }_{{{{n}_{1}}(j)}}}$ – ${{\mu }_{{{{j}_{0}}}}}$ > 0.

Доказательство. Пункт 1) утверждения очевиден, поскольку эти вершины i в новом поддереве $\Gamma _{T}^{*}$ имеют тот же путь (0, i), что и в поддереве Γ_Т.

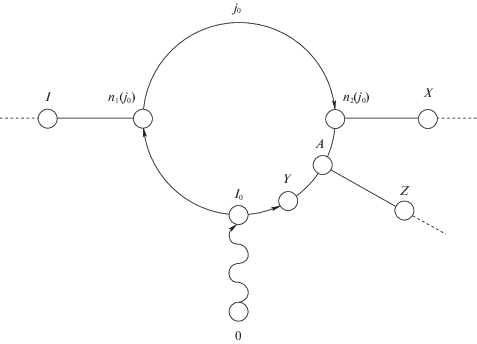
Для обоснования п. 2) рассмотрим вершины трех типов – x, y, z (рис. 3).

Первоначально рассмотрим вершины типа x:

Далее обоснуем п. 2) для вершин типа y. Заметим, что путь (n₂(j₀), y) не содержит 0-дуг и θ-дуг:

Проведем теперь обоснование для вершин типа z. Заметим, что путь (n₂(j₀), A) не содержит 0-дуг и θ-дуг:

Доказательство завершено.

Рассмотрим теперь случай, когда E < 0. Нетрудно видеть, что тогда Y > 0. Покажем, как в этом случае перейти к новому опорному плану задачи (1.1) с меньшим значением целевой функции. Для этого осуществим циклическое изменение потока в направлении дуги  j₀ на величину Y, т.е. положим ${{\tilde {y}}_{j}}$ = y_j + Y,  j ∈ H, если направление дуги  j совпадает с направлением обхода, ${{\tilde {y}}_{j}}$ = y_j – Y, j ∈ H, если направление дуги j не совпадает с направлением обхода и ${{\tilde {y}}_{j}}$ = y_j, j ∈ Γ\H. Положим также ${{\tilde {x}}_{j}}$ = x_j – Δμ_jY, j ∈ H и ${{\tilde {x}}_{j}}$ = x_j, j ∈ Γ\H. Величины Δμ_j были определены выше.

Утверждение 4. Вектор ($\tilde {x}$, $\tilde {y}$) есть допустимое решение задачи (1.1).

Доказательство. Очевидно, что циклическое изменение потока не нарушает балансовых ограничений на поток. Поэтому будем проверять выполнимость только следующих трех ограничений: ${{\tilde {y}}_{j}}$ ≥ 0, ${{\tilde {x}}_{j}}$ ≥ 0, ${{\tilde {y}}_{j}}$ – a_j${{\tilde {x}}_{j}}$ ≤ b_j. Сделаем это, учитывая правила вычисления величин Δμ_j, согласно формулам (2.3) и (2.4), а также формулам, приведенным выше для вычисления вектора ($\tilde {x}$, $\tilde {y}$). Рассмотрим четыре различных случая.

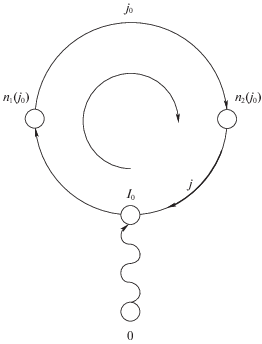
1. Направление дуги j совпадает с направлением обхода и j ∈ (I₀, n₁(j₀)) (рис. 4).

1а. При y_j ≥ b_j верны следующие соотношения: ${{\tilde {y}}_{j}}$ = y_j + Y ≥ 0, (первое ограничение).

Так как μ_j = 1/a_j, Δμ_j = μ_j = 1/a_j ≥ 0, то отсюда следует справедливость следующего: ${{\tilde {x}}_{j}}$ = x_j + + Δμ_jY ≥ x_j ≥ 0 (второе ограничение) и ${{\tilde {y}}_{j}}$ – a_j${{\tilde {x}}_{j}}$ = y_j + Y – a_j(x_j + Δμ_jY) = y_j – a_jx_j + Y(1 – a_jΔμ_j) = y_j – – a_jx_j ≤ b_j (третье ограничение).

1б. При y_j < b_j доказательство этого случая полностью совпадает с доказательством случая 2б, приведенным ниже.

2. Направление дуги j совпадает с направлением обхода и j ∈ (I₀, n₂(j₀)) (рис. 5).

2а. При y_j > b_j доказательство этого случая полностью совпадает с доказательством случая 1а, приведенным выше.

2б. При y_j ≤ b_j верны следующие соотношения:

${{\tilde {y}}_{j}}$ = y_j + Y ≥ 0 (первое ограничение).

Так как μ_j = 0, Δμ_j = μ_j = 0, Δy_j = b_j – y_j ≥ 0), то отсюда вытекает справедливость следующего: ${{\tilde {x}}_{j}}$ = x_j + Δμ_jY = x_j ≥ 0 (второе ограничение) и ${{\tilde {y}}_{j}}$ – a_j${{\tilde {x}}_{j}}$ = y_j + Y – a_j(x_j + Δμ_jY) ≤ y_j – a_jx_j + b_j – y_j = = b_j – a_jx_j ≤ b_j (третье ограничение).

3. Направление дуги j противоположно направлению обхода и  j ∈ (I₀, n₁(j₀)) (рис. 6).

3а. Верны следующие соотношения:

Δy_j = y_j – b_j > 0, ${{\tilde {y}}_{j}}$ = y_j – Y ≥ y_j – Δy_j = b_j ≥ 0 (первое ограничение).

Так как μ_j = 1/a_j, Δμ_j = –μ_j = –1/a_j ≥ 0, то ${{\tilde {x}}_{j}}$ = x_j + Δμ_jY = x_j – (1/a_j)Y ≥ (1/a_j)(a_jx_j – Δy_j) = (1/a_j)(a_jx_j – – y_j + b_j) ≥ 0 (второе ограничение) и ${{\tilde {y}}_{j}}$ – a_j${{\tilde {x}}_{j}}$ = y_j – Y – a_j(x_j + Δμ_jY) = y_j – a_jx_j – Y(1 + a_jΔμ_j) = y_j – – a_jx_j ≤ b_j (третье ограничение).

3б. При y_j ≤ b_j справедливы следующие соотношения:

Δy_j = y_j ≥ 0, ${{\tilde {y}}_{j}}$ = y_j – Y ≥ y_j – Δy_j = 0 (первое ограничение).

Так как μ_j = 0, Δμ_j = –μ_j = 0, то отсюда ${{\tilde {x}}_{j}}$ = x_j + Δμ_jY = x_j ≥ 0 (второе ограничение) и ${{\tilde {y}}_{j}}$ – a_j${{\tilde {x}}_{j}}$ = = y_j – a_jx_j – Y ≤ b_j – a_jx_j ≤ b_j (третье ограничение).

4. Направление дуги  j противоположно направлению обхода и  j ∈ (I₀, n₂(j₀)) (рис. 7).

4а. При y_j > b_j доказательство полностью совпадает с доказательством случая 3а, приведенным выше.

4б. При y_j ≤ b_j доказательство этого случая полностью совпадает с доказательством случая 3б, приведенным выше.

Доказательство завершено.

Далее убедимся, что новому допустимому решению ($\tilde {x}$, $\tilde {y}$) соответствует меньшее значение целевой функции, а именно докажем следующее утверждение.

Утверждение 5. Для нового допустимого решения ($\tilde {x}$, $\tilde {y}$) справедливо следующее неравенство:

Доказательство:

Утверждение доказано.

Утверждение 6. Существует дуга  j, j ∈ H, такая, что она является либо θ-дугой, либо 0-дугой.

Доказательство. Выберем произвольный индекс  j, такой, что

Допустим, что  j – правильно ориентированная дуга, тогда имеем следующее: ${{\tilde {y}}_{j}}$ = y_j + Y = y_j + + Δy_j = y_j + (b_j – q_j) = b_j, т.е. данная дуга является θ-дугой.

Пусть теперь  j имеет обратную ориентацию. Тогда если y_j > b_j, то ${{\tilde {y}}_{j}}$ = y_j – Y = y_j – Δy_j = y_j – – (–b_j + y_j) = b_j, т.е. данная дуга является θ-дугой. Если же 0 < y_j ≤ b_j, то ${{\tilde {y}}_{j}}$ = y_j – Y = y_j – Δy_j = = y_j – y_j = 0, т.е. данная дуга является 0-дугой. Утверждение доказано.

Покажем теперь, как выбрать дугу j₁, подлежащую удалению из множества Γ_Т. Путь (n₁(j₀), I₀) может содержать лишь сонаправленные с ним 0-дуги. Если их множество не пусто, то выберем в качестве j₁ последнюю из них. Иначе в качестве j₁ выберем любую из θ-дуг, множество которых в силу утверждения 5 в этом случае не пусто. Удалив дугу j₁ из множества Γ_Т и добавив дугу j₀, получим новое связующее поддерево $\Gamma _{T}^{*}$, которое для плана ($\tilde {x}$, $\tilde {y}$) удовлетворяет условиям 1 и 2. Заметим, что в силу условия 1 и утверждения 1 план ($\tilde {x}$, $\tilde {y}$) является опорным планом задачи (1.1).

Разберем теперь случай, когда нарушается неравенство  j₀ из условий (2.2). Рассмотрим тот же самый цикл, что и выше, в направлении, обратном дуге  j₀. Вычислим значения величин E и Y по формулам (2.3)–(2.5). Справедливо следующее утверждение.

Утверждение 7. Если E ≥ 0, то существует такая дуга  j, что  j ∈ (n₁(j₀), I₀) и  j является θ-дугой или 0-дугой.

Доказательство данного утверждения не приводим, поскольку оно доказывается аналогично утверждению 2.

В случае если E ≥ 0, удалим из дерева Γ_Т первую θ-дугу или 0-дугу пути (n₁(j₀), I₀) и добавим дугу j₀. Получим новое связующее поддерево $\Gamma _{T}^{*}$, удовлетворяющее условиям 1 и 2. Для соответствующего ему вектора ($\tilde {\lambda }$, $\tilde {\mu }$) справедливо следующее утверждение.

Утверждение 8:

1) ${{\tilde {\lambda }}_{i}}$ = λ_i, i: n₁(j₀) ∉ (0, i);

2) ${{\tilde {\lambda }}_{i}}$ = λ_I – Δ, i: n₁(j₀) ∈ (0, i), где Δ = ${{\lambda }_{{{{n}_{2}}(j)}}}$ – ${{\lambda }_{{{{n}_{1}}(j)}}}$ > 0.

Доказательство данного утверждения также не приводим, поскольку оно доказывается аналогично утверждению 3.

В случае, когда Е < 0, осуществим циклическое изменение потока в направлении, обратном дуге j₀, на величину Y. Получим новое допустимое решение ($\tilde {x}$, $\tilde {y}$) задачи (1.1) по тем же формулам, что и выше. Для решения ($\tilde {x}$, $\tilde {y}$) будут справедливы утверждения 4 и 5.

Покажем теперь, как выбрать дугу j₁, подлежащую удалению из Γ_Т. Путь (n₂(j₀), I₀) может содержать лишь сонаправленные с ним 0-дуги. Если их множество не пусто, то выберем последнюю из них. Иначе рассмотрим дугу j₀. Если она является 0-дугой, то оставим текущее поддерево без изменений. Иначе выберем путь (I₀, n₁(j₀)), который может содержать лишь сонаправленные с ним 0-дуги.

Если их множество не пусто, то выберем в качестве j₁ последнюю из них. Иначе в качестве j₁ выберем любую из θ-дуг цикла, множество которых в этом случае в силу утверждения 7 не пусто. Удалив дугу j₁ из множества Γ_Т и добавив дугу j₀, получим новое связующее поддерево $\Gamma _{T}^{*}$, которое для плана ($\tilde {x}$, $\tilde {y}$) удовлетворяет условиям 1 и 2. Откуда следует, что ($\tilde {x}$, $\tilde {y}$) является опорным планом задачи (1.1).

Таким образом, на каждом шаге происходит переход либо к новому опорному плану с меньшим значением целевой функции, либо к новому связующему поддереву, значения компонент вектора λ которого не больше, а хотя бы на одной вершине строго меньше, чем компоненты вектора λ предыдущего связующего поддерева. Это исключает возможность зацикливания приведенного алгоритма.

Поскольку различных связующих поддеревьев и опорных планов задачи (1.1) существует конечное число, то за конечное число шагов получим опорный план (x, y) и связующее поддерево Γ_Т, удовлетворяющие условиям 1 и 2, такие, что связанный с ними вектор (λ, μ) удовлетворяет неравенствам (2.1) и (2.2).

Рассмотрим следующий вектор (λ, $\tilde {\mu }$), такой, что ${{\tilde {\mu }}_{j}}$ = ${{\lambda }_{{{{n}_{2}}(j)}}}$ – ${{\lambda }_{{{{n}_{1}}(j)}}}$, если j ∈ Γ\Γ_Т,  j – θ, дуга и ${{\tilde {\mu }}_{j}}$ = μ_j для остальных  j. Заметим, что в силу соотношений (2.1) и (2.2) 0 ≤ μ_j ≤ $\frac{1}{{{{a}_{j}}}}$, j ∈ Γ.

Несложно проверить, что вектор (λ, $\tilde {\mu }$) является допустимым решением задачи (1.2) и связан условиями (1.3) с опорным планом (x, y). В силу теоремы 1 отсюда следует, что (x, y) есть оптимальный опорный план задачи (1.1).

Остается показать существование некоторого начального допустимого решения (x, y) и связующего поддерева Γ_Т, для которого выполнены условия 1 и 2. Это несложно сделать, опираясь на следующее утверждение.

Утверждение 9. Существует связующее поддерево исходного графа с правильной ориентацией всех его дуг.

Доказательство. Для каждой вершины исходного графа существует ориентированный путь из источника в данную вершину, так как иначе эту вершину можно было бы изначально исключить из рассмотрения вместе с инцидентными дугами.

Корень дерева примем за начальное поддерево. Соединим корень с произвольной вершиной, не принадлежащей поддереву, ориентированным путем. Рассмотрим участок этого пути от данной вершины до первой вершины, принадлежащей поддереву.

Новое поддерево содержит, по крайней мере, на одну вершину больше предыдущего, и все его дуги правильно ориентированы. Продолжая вышеописанную процедуру, за конечное число шагов построим связующее поддерево с правильной ориентацией всех его дуг. Доказательство завершено.

3. Описание алгоритма для общего случая a_j ≥ 0. Задача (1.1) рассматривалась нами в предположении, что a_j > 0,  j ∈ Γ. Исследуем теперь задачу в общем случае, когда a_j ≥ 0,  j ∈ Γ. Заметим также, что случай a_j < 0 не имеет содержательного смысла с точки зрения рассмотрения переменных x как ресурсных переменных. В общем случае задача имеет следующий вид:

где Γ₁ = {j ∈ Γ: a_j > 0} и Γ₂ = {j ∈ Γ: a_j = 0}.

Задача (3.1), вообще говоря, может не иметь допустимых решений. Рассмотрим теперь вспомогательную задачу, введя дополнительные переменные x_j ≥ 0   j ∈ Γ₂ и функции пропускных способностей δx_j + b_j ≥ 0   j ∈ Γ₂, где

Математическая постановка вспомогательной задачи имеет следующий вид:

Задача (3.2) относится к типу задач, алгоритм решения которых был подробно рассмотрен выше. Поэтому ее можно решать вышеизложенным методом обобщенных потенциалов.

Справедлива следующая теорема.

Теорема 2. Пусть (x*, y*) есть оптимальное решение задачи (3.2). Если существует i ∈ Γ₂, такое, что $x_{i}^{*}$ > 0, то множество допустимых решений задачи (3.1) пусто. Иначе (x*, y*) – оптимальное решение задачи (3.1).

Доказательство. Пусть (x*, y*) есть оптимальное решение задачи (3.2). Допустим, что множество B = {i ∈ Γ₂: $x_{i}^{*}$ > 0} не пусто. Если решение (x*, y*) не является крайней точкой допустимого множества, то оно, как известно, есть выпуклая комбинация некоторых оптимальных крайних точек. Тогда можно утверждать, что если  j₀ ∈ B, то существует оптимальная крайняя точка, для которой $x_{{{{j}_{0}}}}^{*}$ > 0, т.е. множество B для которого не пусто. Таким образом, можно считать без ограничения общности, что (x*, y*) – оптимальная крайняя точка.

Предположим теперь, что множество допустимых решений не пусто и вектор (x, y) есть некоторое допустимое решение задачи (3.1). Если

то легко показать, что задача (3.1) равносильна задаче на компакте:

Следовательно, задача имеет решение в силу теоремы Вейерштрасса. Так как задача (3.1) есть задача линейного программирования, то она имеет оптимальную крайнюю точку, которую обозначим ($\bar {x}$, $\bar {y}$). Если теперь дополнить вектор ($\bar {x}$, $\bar {y}$) компонентами x_j = 0   j ∈ Γ₂, то полученный вектор ($\tilde {x}$, $\tilde {y}$) будет крайней точкой задачи (3.2). Это следует из допустимости вектора ($\tilde {x}$, $\tilde {y}$) и того факта, что система столбцов, соответствующих положительным компонентам, не изменяется, т.е. остается линейно независимой.

Из теории линейного программирования известно, что существует последовательность крайних точек, начинающаяся с произвольной начальной точки ($\tilde {x}$, $\tilde {y}$) и заканчивающаяся оптимальной точкой (x*, y*). Соседние члены этой последовательности являются соседними крайними точками (т.е. их базисы отличаются одним вектором), и значение целевой функции на этих точках монотонно не возрастает.

Непосредственно из обоснования алгоритма обобщенных потенциалов следует, что переход из крайней точки в соседнюю крайнюю точку с небольшим значением целевой функции осуществляется изменением векторов y и x вдоль некоторого цикла, для которого E ≤ 0 и Y > 0.

Поскольку для вектора ($\tilde {x}$, $\tilde {y}$) соответствующее ему множество В пусто, а для вектора (x*, y*) не пусто, то в последовательности существует пара соседних точек (x₁, y₁) и (x₂, y₂), для которых множество B пусто и не пусто соответственно.

Такой переход можно осуществить лишь для цикла, содержащего правильно ориентированную дугу  j₀ множества Γ₂. Но тогда

Если в цикле содержатся дуги j множества Γ₂ обратной ориентации, то Δμ_j = 0. Пусть в цикле r дуг множества Γ₂ правильной ориентации. Тогда справедливо следующее:

Следовательно, такой переход невозможен и сделанное предположение о не пустоте множества допустимых решений задачи (3.1) неверно. Тем самым первая часть теоремы доказана.

Справедливость второй части теоремы следует непосредственно из того, что вектор (x*, y*) является допустимым решением задачи (3.1), а сама задача (3.1) есть сужение задачи (3.2) на некоторое подмножество множества допустимых решений. Теорема доказана.

Заключение. В статье представлен алгоритм решения оптимизационной задачи линейного синтеза коммуникационной сети, обеспечивающей минимум суммарных издержек на производство и перевозку однородного продукта потребителям. Рассматривается однородный сепарабельный ресурс, определяющий величины производственных функций источников и функций пропускных способностей коммуникаций сети. Поскольку предложенный метод является модификацией классического метода потенциалов для стандартной транспортной задачи, он был назван автором “методом обобщенных потенциалов”. Вычислительная схема метода основана на использовании эффективных алгоритмов дискретной оптимизации, таких, как построение связующего поддерева, путей и циклов в ориентированном графе [9]. Обоснована конечность предлагаемого алгоритма, исключающая ситуации зацикливания.