Известия РАН. Теория и системы управления, 2019, № 4, стр. 144-155

Введение. Внедрение систем усовершенствованного управления технологическими процессами (СУУ ТП) позволяет промышленным компаниям нефтепереработки и нефтехимии существенно улучшить технико-экономические показатели функционирования производства [1]. В большинстве случаев управление и контроль качества выходных продуктов технологического процесса осуществляется на основе лабораторных анализов. Данный способ является дорогостоящим и отнимает много времени, что приводит к длительным временным задержкам измерений и неэффективному управлению технологическим процессом.

В настоящее время широкое распространение в составе СУУ ТП получили модели для прогнозирования показателей качества выходных продуктов в режиме реального времени. Такие прогнозирующие модели также называются виртуальными анализаторами [2]. Они описывают технологический процесс посредством связи измеряемых технологических параметров (температура, давление, расход) с результатами лабораторных анализов выходной переменной и могут быть интегрированы в СУУ ТП с использованием специализированного программного обеспечения. На основании заданных критериев в СУУ ТП с помощью прогнозирующей модели формируется оптимальное управляющее воздействие [3].

При построении прогнозирующих моделей приходится сталкиваться с различными проблемами, в том числе с зашумленностью и отсутствием данных измеряемых технологических параметров, а также с их выбросами и мультиколлинеарностью (т.е. с наличием сильной корреляции между регрессорами) [4]. Большинство прогнозирующих моделей основано на методах математической статистики, таких, как многомерная регрессия, регрессия на главных компонентах, проекции на латентные (скрытые) структуры (ПЛС). Для разработки прогнозирующих моделей также могут быть использованы методы машинного обучения, такие, как искусственные нейронные сети, метод опорных векторов и др. [5].

Широкое распространение при построении прогнозирующих моделей получил метод ПЛС. Преимуществами данного метода является способность обрабатывать большое количество коррелированных переменных [6].

Нейронные сети часто используют, когда в данных присутствует нелинейность исследуемого процесса [6]. Выходной сигнал определяется нелинейной функцией взвешенной суммы входных сигналов, которые представляют собой выходные сигналы нейронов предыдущего слоя. Основной недостаток данного подхода заключается в частом переобучении (излишне точным соответствием нейронной сети конкретному набору обучающих примеров, при котором сеть теряет точность прогнозирования на тестовой выборке данных).

Многие работы по построению прогнозирующих моделей посвящены технологическим процессам, относящимся к первичной переработке нефти. Такие процессы, как правило, представляют собой несколько последовательно соединенных ректификационных колонн. Процессы реакционно-ректификационного типа практически не рассмотрены, в то время как они широко используются для получения различных продуктов органического и нефтехимического синтеза. Особенность совмещенных реакционно-ректификационных процессов заключается в совместном протекании обратимой химической реакции с частичным или практически полным разделением образующейся смеси посредством ее ректификации. Для данного типа процессов наибольшее распространение получили прогнозирующие модели на основе нейронных сетей. В [7] рассмотрена разработка прогнозирующей модели с использованием искусственной нейронной сети на основе алгоритма Левенберга–Марквардта. В [8] для построения прогнозирующей модели применяли рекуррентную нейронную сеть для идеальной реакционно-ректификационной колонны. Такая модель позволяет учитывать не только текущие значения входных переменных, но и их предшествующие значения.

В [9] был рассмотрен алгоритм обучения нейронной сети методом обратного распространения выходной ошибки на веса промежуточных нейронов. Коррекция весов проводилась методом наискорейшего спуска, пока не будет достаточно уменьшена среднеквадратическая ошибка. Полученная модель была протестирована на реакционно-ректификационном процессе синтеза пропилпротионата. Недостаток метода заключается в сложности интерпретации физико-химического смысла рассчитанных значений весов нейронной сети.

В отличие от традиционных подходов, в данной работе используется контур обратной связи по ошибке прогноза выходной переменной в прогнозирующей модели реакционно-ректификационного блока технологического объекта. Показано, что, несмотря на отсутствие обратных связей в реальном управляемом объекте, предлагаемый подход существенно повышает точность прогнозирования показателей качества выходного продукта реакционно-ректификационного процесса.

1. Описание технологического объекта и прогнозирующей модели. Реакционно‑ректификационный процесс (рис. 1) представляет собой две ректификационные колонны (К-1 и К-2) и расположенный между ними реактор синтеза (РС) с тремя слоями свежего катализатора. В качестве сырья в РС подается реакционная смесь, полученная на отработанном катализаторе реактора форконтактной очистки сырья (РФ). Реакционная смесь подается в РС под нижний слой катализатора, откуда отходящие пары поступают в ректификационную колонну К-1, сверху которой отводится дистиллят (Д), а реакционная смесь РС поступает в нижнюю ректификационную колонну К-2. Для построения модели, предсказывающей содержание примесей в выходном (кубовом) продукте (КП), использовались измеряемые технологические переменные: u⁽¹⁾ – расход орошения К-1 (F₁); u⁽²⁾ – расход реакционной массы, поступающей в К-2 (F₂); u⁽³⁾ – давление низа РФ (P₁); u⁽⁴⁾ – давление низа РС (P₂); u⁽⁵⁾ –температура низа колонны К-2 (T₁); u⁽⁶⁾ – температура паров с К-2 (T₂); u⁽⁷⁾ – температура на 5-й ступени К-2 (T₃).

Качество прогнозирующей модели зависит от данных, которые используются для ее построения. Обычно они хранятся в базе данных завода и не обладают достаточным объемом информации, так как могут содержать выбросы, а в данных, полученных лабораторным путем, неизвестно точное время отбора проб [10]. Также в реальных условиях довольно редко удается наблюдать статический режим технологического объекта, и обучающая выборка может содержать данные динамического режима. Для учета динамических свойств исследуемого технологического объекта его выходная переменная ${{y}_{t}}$ может быть представлена как свертка входного сигнала и импульсной характеристики [11]. Ошибка модели ${{e}_{t}}$ является разностью между наблюдаемым значением выходной переменной ${{y}_{t}}$ и значением, предсказанным по модели ${{\hat {y}}_{t}}$, поэтому измеренное значение можно представить в виде:

где $u_{{t - k}}^{{(i)}}$ – входные переменные модели; ${{y}_{t}}$ – наблюдаемое значение выходной переменной; N – количество входных переменных модели; t – моменты времени измерения выхода; ${{\hat {b}}_{0}}$ – свободный член; $\hat {b}_{k}^{{(i)}}$ – коэффициенты конечной импульсной характеристики (КИХ) по i-му входу на глубину модели $h$; е_t – ошибка модели. Совокупность коэффициентов КИХ можно записать в виде вектора $\hat {B} = {{[\hat {b}_{1}^{{(1)}}, \ldots ,\hat {b}_{h}^{{(1)}},\hat {b}_{1}^{{(2)}}, \ldots ,\hat {b}_{h}^{{(2)}}, \ldots ,\hat {b}_{1}^{{(N)}}, \ldots ,\hat {b}_{h}^{{(N)}}]}^{{\text{т }}}}$, где ^т – операция транспонирования, значения которых были получены методом ПЛС.

Уравнение модели имеет следующий вид:

где моменты времени измерения выхода $t = \overline {1,M} $ ($N = 7$, $h = 30$). Количество наблюдений $M$ выходной переменной в обучающей выборке (ОВ) и проверочной (тестовой) выборке (ПВ) равно ${{M}_{{{\text{О В }}}}} = 813$ и ${{M}_{{{\text{П В }}}}} = 203$ соответственно. При построении уравнения множественной регрессии (1.2) может возникнуть проблема мультиколлинеарности входов. Наличие высокой степени корреляции между входными переменными приводит к неустойчивости оценок $\hat {B}$.

Набор входных переменных модели (1.2) может быть представлен в виде вектора ${\mathbf{\tilde {u}}}$ = = ${{({{\tilde {u}}_{1}} \ldots {{\tilde {u}}_{c}} \ldots {{\tilde {u}}_{{Nh}}})}^{{\text{т }}}}$, элементы которого формируются следующим образом:

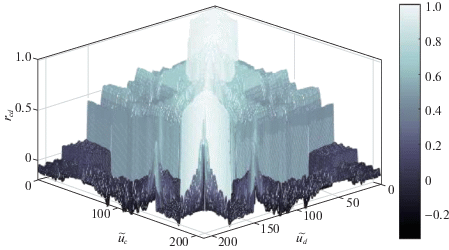
Теснота связи между переменными (регрессорами) вектора ${\mathbf{\tilde {u}}}$ определялась с помощью парных коэффициентов корреляции Пирсона. Коэффициент корреляции r_cd для каждой пары входных переменных оценивался по формуле [12]

где ${{\tilde {u}}_{{j,c}}}$ и ${{\tilde {u}}_{{j,d}}}$ – значения входных переменных ${{\tilde {u}}_{c}}$ и ${{\tilde {u}}_{d}}$ для j-го наблюдения $j = 1,\; \ldots ,\;M$; $\overline {{{U}_{c}}} $ и $\overline {{{U}_{d}}} $ – средние значения переменных ${{\tilde {u}}_{c}}$ и ${{\tilde {u}}_{d}}$; ${{S}_{c}}$ и ${{S}_{d}}$ – их стандартные отклонения; M – количество наблюдений ($M = {{M}_{{{\text{О В }}}}}$). Общее количество регрессоров в данном случае равно N × h = 7 × 30 = 210, т.е. с = 1, …, 210 и d = 1, …, 210. На рис. 2 изображены коэффициенты парной корреляции Пирсона между регрессорами модели (1.2).

Из рис. 2 очевидно, что между регрессорами присутствует линейная зависимость (мультиколлинеарность), так как довольно много значений ${{r}_{{cd}}}$ находятся в интервале (0.4, 0.7), а также присутствуют области корреляционной матрицы, где наблюдается сильная (${{r}_{{cd}}} > 0.7$) теснота связи. Для построения моделей технологических объектов в условиях мультиколлинеарности широкое распространение получил метод ПЛС [13, 14]. В этом методе проводится одновременная декомпозиция матрицы значений входных переменных:

и векторной выходной переменной $Y = {{[{{y}_{{{{t}_{1}}}}},{{y}_{{{{t}_{2}}}}},\; \ldots ,\;{{y}_{{{{t}_{M}}}}}]}^{{\text{т }}}}$, где матрица U и вектор Y имеют размеры $M \times Nh$ и $M \times 1$ соответственно; $M = {{M}_{{{\text{О В }}}}}$; t_M – момент времени, соответствующий окончанию активного эксперимента и поступлению последнего набора данных для обучающей выборки. Значение t_M выбирается, исходя из допустимой длительности проведения экспериментов (не допуская нарушений технологического регламента), и фиксируется оператором-технологом. Декомпозиция матрицы U и вектора Y происходит следующим образом: $U = С {{P}^{{\text{T}}}} + E$, Y = $С {{Q}^{{\text{T}}}} + F$, где C – матрица счетов, Р и Q – матрицы нагрузок, Е и F – матрицы остатков.

Для построения матриц счетов и нагрузок используется описанный ниже алгоритм. Перед началом алгоритма нормированные входные переменные U и Y центрируются следующим образом:

где ${{1}_{{M \times 1}}}$ – вектор-столбец размера $M \times 1$, все элементы которого равны единице; средние значения столбцов матрицы U ($i = \overline {1,N} $, $k = \overline {1,h} $) и среднее значение вектора Y рассчитывались как

На данном этапе также выбирается максимальное количество главных компонент A таким образом, чтобы оно не превышало количество входных переменных в модели ($A \leqslant Nh$). Для каждой главной компоненты с номером $a = 1,\; \ldots ,\;A$ выполняются шаги 1–6.

Изначально принимаем ${{E}_{{a - 1}}} = {{U}_{0}}$, ${{F}_{{a - 1}}} = {{Y}_{0}}$ и a = 1. Далее выполняется ниже описанный алгоритм.

Шаг 1. Вычисляем вектор взвешенных нагрузок ${{w}_{a}}$:

Шаг 2. Нормировка вектора взвешенных нагрузок ${{w}_{a}}$ осуществляется следующим образом:

Шаг 3. Счета матрицы U – ${{с }_{a}}$ определяются как

Шаг 4. На данном шаге рассчитываются U-нагрузки – ${{p}_{a}}$:

Шаг 5. Расчет Y-нагрузок – ${{q}_{a}}$ производим следующим образом:

Шаг 6. Вычисляем остатки ${{E}_{a}} = {{U}_{{a - 1}}} - {{с }_{a}}p_{a}^{{\text{T}}}$ и ${{F}_{a}} = {{Y}_{{a - 1}}} - {{с }_{a}}{{q}_{a}}$. Увеличиваем номер главной компоненты на единицу $a: = a + 1$ и повторяем описанные выше шаги.

Шаг 7. После достижения равенства a = A вычисляются коэффициенты регрессии $\hat {B} = W{{({{P}^{{\text{T}}}}W)}^{{ - 1}}}{{Q}^{{\text{T}}}}$, где $W$ – матрица со столбцами, состоящими из ${{\tilde {w}}_{a}}$-векторов:

где $\bar {\hat {y}}$ – среднее значение вектора $\hat {y} = u_{k}^{{\left( i \right)}}\widehat B$.

Для оценки качества полученной модели на конечном интервале времени были использованы коэффициент детерминации (R²), среднеквадратическая ошибка (СКО), а также информационный критерий Байеса–Шварца (BSC). Описанные выше критерии рассчитывались по следующим формулам.

1. Коэффициент детерминации:

2. СКО:

3. Информационный критерий Байеса–Шварца:

В (1.3)–(1.5) ${{y}_{i}}$ – наблюдаемое значение выходной переменной, ${{\hat {y}}_{i}}$ – ее значение, полученное по модели объекта, SS(RES′)_N – сумма квадратов остатков, $p = N + 1$ (N – число независимых переменных). Чем меньше значения BSC и СКО и чем ближе к единице значение R², тем лучше построенная модель соответствует исследуемому объекту.

2. Идентификация прогнозирующего фильтра в контуре обратной связи. Для повышения точности прогнозов (снижения дисперсии погрешности е) в модель был включен контур обратной связи (рис. 3). На этой схеме B(u) – символическое обозначение оператора реального объекта; $\hat {B}$ – оператор модели (1.2); $\hat {y}_{t}^{*}$ – скорректированный выход модели; q^–1 – оператор сдвига на один шаг назад; $F({{q}^{{ - 1}}})$ – передаточная функция фильтра; ${{\hat {e}}_{t}}$ – прогноз ошибки e_t.

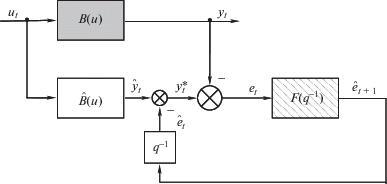
Включение обратной связи на первый взгляд представляется необоснованным, поскольку зависимость между входными и выходными переменными технологического объекта носит причинно-следственный характер и моделируемая установка не содержит обратных связей. Тем не менее, использование контура обратной связи в модель зачастую позволяет повысить точность прогнозирования (уменьшить СКО прогноза). Исключение составляет лишь случай отсутствия сериальной корреляции в последовательности ошибок прогноза, получаемого при помощи модели (1.2). Иными словами, обратная связь не оказывает влияния на точность прогноза, если без нее модель генерирует ошибки e₁, e₂ …, последовательность которых является белым шумом. В противном случае можно идентифицировать передаточную функцию фильтра F(q^–1), выход которого в каждый момент времени t является прогнозом будущей ошибки ${{\hat {e}}_{{t + 1}}}$, причем ${\text{M}}[{{\left( {{{e}_{{t + 1}}} - {{{\hat {e}}}_{{t + 1}}}} \right)}^{2}}] < {\text{M}}[e_{{t + 1}}^{2}]$ [15]. При этом желательно предварительно преобразовать прогнозируемую случайную величину к гауссовской, поскольку большинство статистических процедур обеспечивают оптимальные результаты именно для нормально распределенных величин.

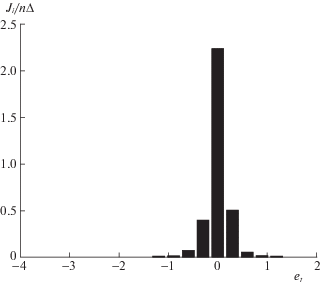
На рис. 4 представлена гистограмма ошибок модели (1.2). Символом J_i обозначено количество остатков, величина которых попала в i-й интервал; n – общее количество остатков; $\Delta = 0.3$ – ширина интервалов.

Гистограмма наводит на мысль о том, что плотность распределения случайной величины $\text{v}$ = 1.5 – e_t можно аппроксимировать плотностью гамма-распределения, параметры которого были оценены в среде Matlab:

где Г – гамма-функция Эйлера. Следует отметить, что максимальное значение функции (2.1) наблюдается в точке 1.3, а не в 1.5, как этого можно было бы ожидать на основании гистограммы на рис. 4. Одной из причин такого отклонения является асимметрия плотности гамма-распределения. В нашем случае отклонение составляет 1.5 – 1.3 = 0.2, что вполне допустимо, так как при смещении аргументов на 1.5 вправо гарантируются их положительные значения (формула (2.1) определяет плотность гамма-распределения только при положительных значениях аргумента).

Интегральную функцию распределения величины $\text{v}$ обозначим через ${{F}_{\text{v}}}(\text{v})$. Если теперь записать интегральную функцию распределения стандартизованной нормальной величины как F_N(·) (соответственно $F_{N}^{{ - 1}}$ – функция, обратная к F_N), то величину z_t = g(e_t) = $F_{N}^{{ - 1}}$(${{F}_{\text{v}}}$(1.5 – e_t)) можно приближенно считать распределенной по нормальному закону с нулевым средним и единичной дисперсией.

Для временного ряда z_t была построена модель авторегрессии-скользящего среднего (АРСС) порядка (N_η, N_θ), т.е. модель вида

где η_k, θ_k – константы; ε_t – гауссовский белый шум с нулевым средним и дисперсией $\sigma _{\varepsilon }^{2}$.

Порядок модели был выбран путем оценки точности прогнозов на обучающей выборке при каждом из сочетаний (N_η, N_θ). С этой целью использовалась функция “pem” (prediction error model) в вычислительной среде Matlab. Эта функция оценивает параметры прогнозирующей модели по критерию СКО прогнозов (заметим, что если выборка исходных данных подчинена нормальному закону распределения вероятностей, то оценки параметров, найденные методом наименьших квадратов, являются оценками максимального правдоподобия). В результате наилучшей оказалась модель АРСС порядка (2, 1) при η₁ = –0.9766 ± 0.4736; η₂ = 0.1664 ± 0.225; θ₁ = = –0.6164 ± 0.383; $\sigma _{\varepsilon }^{2} = {\text{0}}{\text{.8394}}$ ± 0.0833 (для оценок параметров указаны границы 95%-ных доверительных интервалов).

Таким образом, для прогнозирования использовалась модель

Воспользовавшись оператором сдвига на один шаг назад q^–1, полученную модель можно представить в виде

откуда найдем передаточную функцию фильтра для прогнозирования z_t+1 [15]:

Условное распределение величины z_{t + 1} при известных z_t, z_{t – 1}, z_{t – 2} … является нормальным распределением с математическим ожиданием ${{\hat {z}}_{{t + 1}}}$ и дисперсией ${\sigma }_{{\varepsilon }}^{2}$ [15]. Поэтому, принимая за прогноз невязки e_{t + 1} условное математическое ожидание этой величины, найдем

Эффективность модели прогнозирующего фильтра, полученной в результате анализа данных обучающей выборки, оценивалась на данных тестовой выборки. Результаты прогнозов иллюстрируются на рис. 5: сплошной линией изображены ошибки e_t, пунктирной – их прогнозные значения.

Каждому моменту времени t (ось абсцисс) соответствует ошибка модели без обратной связи e_t и ее прогноз ${{\hat {e}}_{t}}$, вычисленный в момент (t – 1).

Результаты расчета критериев идентификации модели с отсутствием обратной связи и ее включением в модель на обучающей и проверочной выборках приведены в таблице.

Оценка СКО модели с обратной связью, вычисленная по тестовой выборке данных, оказалась на (0.2346 – 0.2023)/0.2346 = 0.1377 ≈ 14% меньше, чем СКО модели без обратной связи.

3. Анализ остаточных ошибок. Как показано в предыдущем разделе, использование сериальной корреляции в последовательности ошибок модели (1.2) e₁, e₂, …, e_n позволяет прогнозировать ошибку e_{t + 1}, если известны ошибки e_t, e_{t – 1}, e_{t – 2}, …, e₁. Вычисленное прогнозное значение ${{\hat {e}}_{{t + 1}}}$ можно использовать в качестве поправки, повышающей точность предсказания выходной переменной ${{y}_{t}}$. В связи с этим возникает вопрос: возможно ли дальнейшее повышение точности путем предсказания ошибок прогнозирующего фильтра (2.3)? Для ответа на этот вопрос необходим анализ ошибок рассматриваемого фильтра. Если такое исследование не выявляет статистически значимой зависимости между этими величинами, то знание предыдущих ошибок не дает информации о будущих ошибках и, следовательно, уточнение прогноза невозможно.

Из соотношений (2.2) и (2.3) следует [15]

т.е. случайная величина ε_t является ошибкой прогноза значения z_t, вычисленного в момент времени t – 1. Таким образом, задача сводится к проверке гипотезы, согласно которой случайные величины ε₁, ε₂, …, ε_n взаимно независимы, т.е. спектральная плотность случайной последовательности ε₁, ε₂ … постоянна [15, 16].

Интересующую нас спектральную плотность можно исследовать при помощи периодограммы второго порядка выборки ε₁, ε₂, …, ε_n [16]:

где ${\bar {\varepsilon }}\; = \;\frac{1}{n}\sum\limits_{i = 1}^n {{{{\varepsilon }}_{i}}} ;$ j – мнимая единица.

Определим целое число m как (n – 1)/2 при нечетном n, при n четном полагаем m = (n – 2)/2. Если ε_t, $t = \overline {1,n} $, – взаимно независимые случайные величины с дисперсией ${\sigma }_{{\varepsilon }}^{2}$, то величины $4{\pi }{{I}_{k}}{/\sigma }_{{\varepsilon }}^{2}$, $k = \overline {1,m} $, также независимы и подчинены распределению $\chi $-квадрат с двумя степенями свободы [16].

Теперь рассмотрим меру отклонения эмпирической функции распределения F_m от теоретической F_χ:

где $I_{i}^{{\text{*}}}$ – i-й член вариационного ряда, т.е. последовательности, полученной упорядочением значений I_k по возрастанию: $I_{1}^{{\text{*}}} \leqslant I_{2}^{{\text{*}}} \leqslant \cdots \leqslant I_{m}^{{\text{*}}}$;

Функция распределения случайной величины $\sqrt m {{D}_{m}}$ при больших m (при m > 20) близка к функции распределения Колмогорова K(x) [17]:

Для вычисления этой функции при любых значениях аргумента разработаны эффективные алгоритмы [18]. В частности, K(1.02) = 0.75; K(1.36) = 0.95. В рассматриваемом случае m = 400, поэтому вероятность того, что случайная величина D_m примет значение, превышающее 1.02/20, равна 1 – 0.75 = 0.25. Соответственно вероятность того, что D_m окажется больше, чем 1.36/20, равна 1 – 0.95 = 0.05.

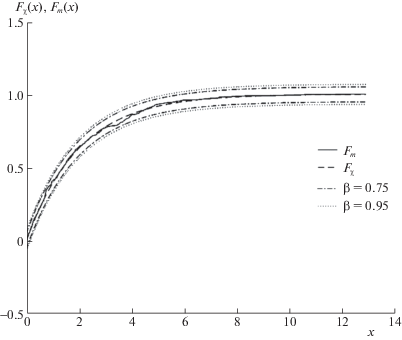
Рисунок 6 иллюстрирует применение критерия Колмогорова для проверки гипотезы о постоянстве спектральной плотности ошибок ε_t. Сплошной линией изображена эмпирическая функция F_m, пунктирной – гипотетическая функция F_χ, штрихпунктирной – границы 75%-ного доверительного интервала (β = 0.75), пунктиром из точек – границы 95%-ного доверительного интервала (β = 0.95).

Эмпирическая функция распределения не пересекает границу интервала, соответствующего доверительной вероятности β = 0.75. Следовательно, гипотезу о постоянстве спектральной плотности ошибок ε_t можно считать согласованной с экспериментальными данными.

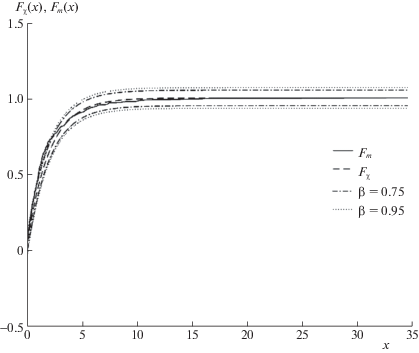
Для сравнения на рис. 7 представлен результат проверки гипотезы о постоянстве спектральной плотности ошибок модели без обратной связи.

Эмпирическая функция распределения пересекает границу доверительного интервала, соответствующего уровню доверия β = 0.95. Таким образом, проверяемую гипотезу следует отклонить, поскольку вероятность выхода за эту границу при условии постоянного спектра достаточно мала: 1 – 0.95 = 0.05.

Заключение. Использование контура обратной связи в модели технологического процесса позволило уменьшить СКО прогноза, несмотря на то, что реальная моделируемая установка не содержит обратных связей. Сравнение предсказанных значений с фактическими (рис. 5) показывает, что построенная модель прогнозирующего фильтра (2.3) дает неплохие прогнозы на “спокойных” (с небольшим и приблизительно постоянным разбросом) временных интервалах. Что же касается интервалов с “аномальными” значениями (Outliers), прогнозирующий фильтр, хоть и успешно предсказывает направление выбросов, допускает большую ошибку в предсказании их величины. По-видимому, свойства процесса e_t лучше описывались бы моделью с дополнительной составляющей в виде какого-либо (например, пуассоновского) потока событий (выбросов), но для оценки интенсивности потока выборка данных должна содержать хотя бы несколько десятков выбросов. Иными словами, судя по рис. 5, для рассматриваемого технологического объекта объем доступной для анализа выборки данных должен достигать не менее 1.5 тыс. измерений.