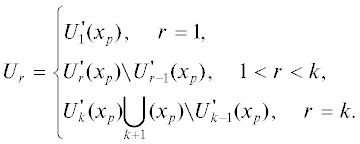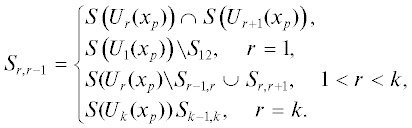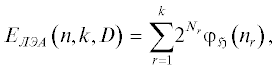Известия РАН. Теория и системы управления, 2019, № 4, стр. 74-82

Введение. Разреженные матрицы появляются при постановке задач из многих научных и инженерных областей. Эффективные методы хранения и обработки таких матриц в современных вычислительных системах вызывают интерес у широкого круга исследователей. Одним из актуальных приложений разреженных матриц является решение соответствующих задач дискретной оптимизации (ДО). Это касается таких известных постановок: размещение объектов, планирование ресурсов, маршрутизация, логистика, искусственный интеллект, анализ данных, робототехника и т.п. Выделение специальных структур в разреженных матрицах позволяют существенно сократить время решения. Большинство интересных задач являются NP-трудными. Многие задачи ДО, возникающие на практике, содержат огромное число неизвестных и ограничений, поэтому они трудно решаемы. С другой стороны, модели ДО для больших практических задач часто представляют собой системы, подсистемы которых слабо связанны между собой, и таких подсистем достаточно много. Поэтому естественным подходом для решения таких задач представляется разбиение на подзадачи. В связи с этим особую актуальность приобретают декомпозиционные подходы – способы разбиения больших задач на подзадачи [1–3]. Развитие информационных технологий, появление многопроцессорных комплексов, суперкомпьютеров создали условия для разработки алгоритмов ДО с распараллеливанием вычислений.

Эффективными алгоритмами для решения разреженных задач ДО являются локальные элиминационные алгоритмы (ЛЭА). ЛЭА объединяют локальные алгоритмы декомпозиции, алгоритмы несериального динамического программирования, а также алгоритмы сегментной элиминации. Распараллеливание вычислительного процесса ЛЭА может существенно ускорить решение задач ДО большой размерности. С развитием вычислительной техники более актуальным становится вопрос сокращения вычислений. Для решения разреженных задач ДО естественным образом выбирается алгоритм, использующий локальные области соответствующей матрицы. Приводятся результаты вычислительного эксперимента, где с помощью ЛЭА решались различные задачи ДО. Представлены результаты исследования эффективности локального алгоритма для решения квазиблочных задач. Также продемонстрировано, что асимптотическая средняя оценка эффективности локального алгоритма слабо зависит от алгоритма ДО, решающего подзадачи. Такая зависимость объясняется следующим образом: средняя оценка эффективности была исследована на множестве квазиблочных структур, но локальные алгоритмы будут эффективными для задач с ограниченной связностью блоков.

Важно выявление закономерностей в больших данных, в качестве которых выступают разреженные матрицы. При этом повышается эффективность алгоритма для решения задач, соответствующих матрицам; выделение класса задач, для которых применим метод, его ускорение, а также возможности решения задач большой размерности путем распараллеливания. Ниже сформулирована теорема, устанавливающая связь между параметрами матрицы и соответствующей квазиблочной структурой. Также исследованы и реализованы методы выделения квазиблочной структуры для разреженных матриц. Представлен алгоритм перестановки строк и столбцов в матрице для поиска квазиблочных структур в разреженных матрицах. Введены понятия и доказаны свойства графовых структур, соответствующих порядку элиминации. Данные теоремы дают основу доказательства важных свойств в проблеме нахождения оптимального исключения переменных. Протестировано влияние порядка элиминации на скорость ЛЭА. Предложен и реализован ряд модификаций ЛЭА для разреженных задач ДО с квазиблочной структурой. Реализовано распараллеливание задач с квазиблочной структурой на GRID. Представленный обзорный материал является презентацией недавно вышедшей в свет монографии [4]. Другая (оригинальная) часть представляет собой алгоритмы выделения квазиблочных структур для многомерных матриц. В качестве основного рассматривается алгоритм Ю.Ю. Финкельштейна [5], основанный на перестановке строк и столбцов для формирования блочно-лестничной (БЛ) структуры. Установлены недостатки подхода: они связаны с большим числом связывающих переменных между блоками, а также пустыми блоками, из-за чего применение таких структур затруднено. Реализованы модификации основного алгоритма, при помощи которых можно получить оптимальную структуру, пригодную для использования в решении практических задач. Приводится сравнение основного и модифицированного алгоритмов относительно параметров полученных структур, таких, как количество блоков и связывающих переменных между блоками. Установлена эффективность модификации. Описывается модификация основного алгоритма, применяемая для выделения блочно-древовидных (БД) структур.

1. Квазиблочная структура в разреженных матрицах. Матрица является разреженной, если содержит преимущественно нулевые элементы. Интерес к разреженности заключается в экономии на вычислениях. Зная структуру матрицы, можно разделять соответствующую задачу на подзадачи. Другими словами, информация о том, как упорядочены ненулевые элементы в матрице, позволяет произвести декомпозицию матрицы на блоки преимущественно с ненулевыми элементами и осуществлять решение задач в блоках независимо друг от друга.

Здесь естественным образом возникает проблема хранения разреженных матриц. Для хранения используются разные, например, ленточные представления. Выделяют полные и неполные схемы в зависимости от того, представлена вся матрица или только ее часть. Также выделяют упорядоченные и неупорядоченные схемы в зависимости от того, произволен порядок хранения элементов или упорядочен.

Для базовых операций с разреженными матрицами (а именно умножение матрицы на вектор, транспонирование матрицы, умножение матрицы на матрицу) существуют специальные алгоритмы. Также для многих алгоритмов необходимо определять матрицы перестановки. Ряд алгоритмов направлен на упорядочивание элементов в разреженных матрицах. Локальные стратегии обработки разреженных матриц (например, алгоритм минимальной степени) заключаются в упорядочивании разреженной матрицы. Также используется упорядочивание матриц для получения специальных форм (например, метод рекурсивного разбиения). Основой для всех алгоритмов, которые предназначены для решения систем уравнений с квадратной матрицей, является метод последовательного исключения неизвестных. Обзор литературы по разреженным матрицам представлен в [6].

Классифицируем разреженные матрицы. Очень широкими будем называть матрицы, в которых число столбцов превышает число строк в 2 раза и более. Широкие матрицы определим как матрицы, в которых число столбцов превышает число строк менее чем в 2 раза. В квадратных матрицах число столбцов равно числу строк, а в узких – число строк превышает число столбцов. Заметим, что матрицы многих классов задач можно отнести к одной из вышеназванных групп матриц. Существенно реже встречаются задачи, матрицы которых можно отнести к двум и более группам. Поэтому важно изучить структуру матриц таких задач в зависимости от каждой группы матриц. Многие задачи имеют особенности в матричной структуре. Эти особенности позволяют рассматривать большие матрицы как последовательность матриц меньшего ранга, связанных некоторым образом между собой. Другими словами, многие подзадачи, соответствующие таким матрицам, могут быть решены независимо друг от друга, что существенно экономит вычислительное время. В частности, такой структурой является БД-структура.

Определение 1. Матрица A, в которой n столбцов, m строк и z ненулевых элементов, таких что выполняется 0.5mn > z, называется разреженной.

Сформулируем необходимые понятия для определения БД-структуры в матрице. Для начала введем определения связывающего столбца в матрице и взаимосвязи столбцов.

Определение 2. Столбец  j матрицы А, в котором существует хотя бы пара ненулевых элементов a_ij и ${{b}_{{i',j}}}$ в строках i и $i{\text{'}} \ne i$, будем называть связывающим. Взаимосвязью двух столбцов  j₁ и  j₂ в матрице А называется единовременное вхождение ненулевых элементов этих столбцов в строку i.

Перейдем к определению графа взаимосвязей.

Определение 3. Графом взаимосвязей G(X, E) матрицы A называется граф, вершины которого соответствуют номерам ненулевых элементов матрицы, а для элементов матрицы, которые находятся в одной строке, между соответствующими вершинами есть ребро.

Подразумевается, что индексы вершин графа взаимосвязей и номера столбцов матрицы A эквивалентны. Введем понятие окрестности для столбца матрицы A в графовом представлении.

Определение 4. Множество вершин, т.е. связанных ребром с вершиной x в графе взаимосвязей G(X, E), обозначается $\Omega $ и называется окрестностью вершины x.

Для практических задач понятие окрестности достаточно тонкий вопрос, поскольку по факту вершины с близкими окрестностями объединяют в большие окрестности относительно групп вершин. Под близкими окрестностями подразумевается, что пересечение соответствующих множеств значительно больше их разности. Укрупнение происходит в зависимости от размерности матрицы A, числа ненулевых элементов в ней, а также возможностей вычислительной системы.

Перейдем к определению квазиблочных структур матрицы. Определим граф пересечения окрестностей [4]. Представим граф G(X, E) в виде системы окрестностей Ω₁ = (S₁, U₁), Ω₂ = = (S₂, U₂), …, Ω_k = (S_k, U_k) вершин ${{x}_{{{{j}_{1}}}}},\; \ldots ,\;{{x}_{{{{j}_{k}}}}}$, где S_r и U_r – множества номеров столбцов и строк соответствующей матрицы относительно r-й окрестности, r = 1, …, k.

Определение 5. Графом пересечений окрестностей ${{G}_{{\Omega }}}$ называется граф, вершины которого ${{\nu }_{{{{r}_{i}}}}}$ – окрестности ${{{\Omega }}_{{{{r}_{i}}}}} = ({{S}_{{{{r}_{i}}}}},{{U}_{{{{r}_{i}}}}})$, при этом вершины графа ${{\nu }_{{{{r}_{1}}}}}$ и ${{\nu }_{{{{r}_{2}}}}}$ соединяются ребром (r₁, r₂), если ${{S}_{{{{r}_{1}}}}} \cap {{S}_{{{{r}_{2}}}}} \ne \emptyset $.

Пусть для системы окрестностей графа G(X, E) выполняются следующие свойства.

Свойство 1. Объединение множеств номеров строк для каждой окрестности соответствует множеству номеров строк всей матрицы:

Свойство 2. Объединение множеств номеров столбцов для каждой окрестности соответствует множеству номеров столбцов всей матрицы

Свойство 3. Множества номеров столбцов, соответствующие любым двум окрестностям из заданной системы окрестностей, не пересекаются:

Свойство 4. Множества номеров строк, соответствующие любым трем окрестностям из заданной системы окрестностей, не пересекаются одновременно:

Перейдем к определению БД-структуры матрицы A.

Определение 6. Граф ${{G}_{{\Omega }}}$, для которого выполняются свойства 1–4 и при этом он является деревом, называется БД-структурой. Матрицу, соответствующую БД-структуре будем называть блочно-древовидной, выделенную вершину ${{\nu }_{r}}$ – корнем.

БД-структура определяется соотношением “предок–потомок”. При этом если (${{\nu }_{r}}$, ${{\nu }_{1}}$), …, (${{\nu }_{{p - 1}}}$, ${{\nu }_{p}}$) – путь от корня ${{\nu }_{r}}$ в вершину ${{\nu }_{p}}$, то ${{\nu }_{{p - 1}}}$ называют предком вершины ${{\nu }_{p}}$, а ${{\nu }_{p}}$ – потомком вершины ${{\nu }_{{p - 1}}}.$

Определение 7. Граф ${{G}_{{\Omega }}}$, для которого выполняются свойства 1–4, и при этом он является цепью, называется БЛ-структурой. Матрицу, соответствующую БЛ-структуре, будем называть блочно-лестничной.

Определим компоненты БД-структуры. Введем определение блока, степени БД-структуры и сепаратора.

Определение 8. Вершины ${{\nu }_{{{{r}_{i}}}}}$, соответствующие каждой r-й окрестности, будем называть блоками БД-структуры, количество блоков обозначим k.

Определение 9. Степенью БД-структуры будем называть ρ = max{ρ₁, …, ρ_k}, где ρ₁, …, ρ_k – степени каждого блока в БД-структуре.

Определение 10. Для данного связного графа G(X, E) и множества индексов вершин S $ \subseteq $ X, таких что подграф G[X\S] графа G(X, E) несвязан, S называется сепаратором.

В [4] доказана взаимосвязь между компонентами БД-структуры и параметрами разреженной матрицы с помощью следующей теоремы.

Теорема 1. Степень БД-структуры подчиняется соотношению 2$\quad \leqslant $ ρ $ \leqslant $ k – 1, если число блоков удовлетворяет неравенству 0.5(m + n + 2 – $\sqrt {{{{(n - m)}}^{2}} + 4(z - n + 1)} \leqslant k$ < min(m, 0.5(n + 1)). Степень БД-структуры подчиняется соотношению 2 $ \leqslant $ ρ $ \leqslant $ (–2k² + (n + 2m + 3)k + z – 2m – 2n – – mn)/(m – k), если число блоков удовлетворяет 0.25(n + 2m + 5 – $\sqrt {{{{(n - 2m + 3)}}^{2}} + 4(2z - 3n + 4)} \leqslant $ ≤ k < 0.5(m + n + 2 – $\sqrt {{{{(n - m)}}^{2}} + 4(z - n + 1)} $).

При этом параметры n, m, z связаны следующим образом:

для очень широких матриц m $ \leqslant $ 4, n $ \leqslant $ 2m, 2n – m + 1 $ \leqslant $ z < 0.5mn;

для широких матриц:

a) 4 $\quad \leqslant $ m $ \leqslant $ 6, m + 1 $ \leqslant $ n $ \leqslant $ 7, n + m – 1 $ \leqslant $ z < 0.5mn,

б) 5 $\quad \leqslant $ m $ \leqslant $ 7, 8 $ \leqslant $ n $ \leqslant $ 2m – 1, n + m – 1 $ \leqslant $ z < 0.5mn,

в) m $ \geqslant $ 8, m + 1 $ \leqslant $ n $ \leqslant $ 2m – 1, n + m – 1 $ \leqslant $ z < 0.5mn;

для квадратных матриц m = n, n $ \geqslant $ 4, 2n – 1 $ \leqslant $ z < 0.5n²;

для узких матриц:

а) 6 $ \leqslant $ m $ \leqslant $ 7, 5 $ \leqslant $ n $ \leqslant $ m – 1, m + n – 1 $ \leqslant $ z < 0.5mn,

б) m $ \geqslant $ 8, 5 $ \leqslant $ n $ \leqslant $ 7, m + n – 1 $ \leqslant $ z < 0.5mn,

в) m $ \geqslant $ 9, 8 $ \leqslant $ n $ \leqslant $ m – 1, m + n – 1$ \leqslant $ z < 0.5mn.

2. Алгоритмы выделения квазиблочных структур. Основные конструкции выглядят так. Пусть A_mхn – разреженная матрица, p – индекс вершины x_p, $p \in $ {1, 2, …, n}. Далее необходимо выделить окрестности вершины x_p последовательно возрастающих порядков. Выделение окрестностей заканчивается, когда при r = k выполняется условие $S_{{k + 1}}^{'}$(x_p) = $S_{k}^{'}$(x_p). После этого строится разбиение множества индексов строк, входящих в блоки, по следующему принципу:

Затем находятся следующие множества индексов столбцов:

Описанный алгоритм находит БЛ-структуру для разреженной матрицы. Заметим, что БЛ-структуры могут отличаться друг от друга, если первым будет выбран другой столбец в матрице. Данный алгоритм содержит следующий недостаток. Сепараторы могут оказаться очень большими, т.е. состоять из большого числа переменных. Это крайне усложняет работу с матрицей (например, используя ЛЭА). Поэтому есть смысл добавлять ограничение на размер сепаратора и, если он превышает допустимый, выполнять процедуру слияния блоков. Другими словами, если сепаратор между блоками S_{a, b} такой, что его мощность |S_{a, b}| < s_max, где s_max – допустимая величина сепаратора, то новый блок U_new будет соответствовать U_a ∪ U_b. Сепараторами этого блока будут множества S_{a – 1,a} и S_{b,b+ 1}, а свободными переменными – S_new = S_a ∪ ∪ S_b.

Реализован эксперимент сравнения основного алгоритма и его модификации. Тестовые задачи генерировались на основе уже существующих графов из библиотеки CSP, которая содержит различные классы графов для задач анализа данных, например из NASA и ISCAS. Были выбраны две группы: “дубликатор” и “крендель” согласно различиям в графовых структурах. Для построения ограничения бралось ребро графа, задавалось соответствующее множество переменных. Затем случайным образом определялись коэффициенты при переменных. Целевая функция строилась по всем вершинам графа, коэффициенты при переменных также определялись случайным образом. Для каждого графа применялись описанные выше алгоритмы упорядочивания переменных. Затем задачи с заданными порядками решались с помощью ЛЭА. Алгоритм для решения подзадач реализован на онлайн-платформе алгебраического языка моделирования AMPL (www.ampl.com), в качестве решателя выбран SCIP (solving constraint integer programs) – решатель задач целочисленного программирования. Он использует технологию ветвления задачи на более мелкие подзадачи и различные релаксации, в частности методы отсечения, а также дает возможность использовать произвольные ограничения. Кроме того, в [7] описан механизм, позволяющий ему решать выпуклые и невыпуклые задачи смешанного целочисленного программирования.

Рассмотрим некоторые результаты для тестовых задач. Класс “дубликатор” описывает сгенерированные случайным образом задачи не удовлетворяющие ограничениям. Здесь можно отметить, что существенным образом сократилось количество блоков и максимальный сепаратор значительно уменьшился. Класс “крендель” описывает граф, раскрашенный в два цвета, который построен таким образом, чтобы не удовлетворять ограничениям. Для задач этого класса существенно уменьшилось количество подзадач, которые потребуется решить.

3. Локальный алгоритм и порядок исключения переменных. Под задачей дискретной оптимизации подразумевается задача следующего вида:

G – конечное или счетное множество допустимых решений, а extr – экстремум функции, т.е. ее минимум или максимум. При этом x будем называть вектором решений, а f(x) – целевой функцией задачи. Задачей целочисленного линейного программирования (ЦЛП) будет называться такая задача, где f(x) линейна, а вектор решений принимает целочисленные значения. Обзор литературы по декомпозиционным методам решения блочных оптимизационных задач показан в [8].

Задачи дискретной оптимизации большой размерности, встречающиеся на практике, часто имеют разреженную структуру. Для решения таких задач эффективно использовать локальные методы Журавлева – класс комбинаторных методов, которые исследуют окрестности переменных, решают соответствующие окрестностям подзадачи и на основе полученных решений восстанавливают глобальное решение задачи. Выделение БД-структуры для разреженных матриц позволяют декомпозировать задачу и решать подзадачи для отдельных блоков независимо друг от друга. Для этого процесса необходимо понимать, каким образом связан ход алгоритма с декомпозицией, чтобы знать, может ли он использоваться для непосредственного выделения БД-структуры в матрице за счет внутренней организации процессов. Такие алгоритмы будем называть локальными алгоритмами, а встроенные в них алгоритмы для решения задач в блоках – внутренними. В теории локальных алгоритмов Журавлева выделены две основные теоремы – единственности и мажорантности [9]. В теореме единственности утверждается, что результат вычисления основных предикатов локального алгоритма с монотонными функциями (которые не возрастают/ не убывают на заданном множестве) не зависит от порядка рассмотрения элементов множества. Другими словами, в каком бы порядке мы не элиминировали переменные или подмножества переменных в задаче, оптимальное решение будет получено. В теореме мажорантности доказывается существование для всякого класса локально равных алгоритмов с одинаковой памятью наилучшего (мажорантного) локального алгоритма, т.е. алгоритма, который по заданной фиксированной системе окрестностей вычисляет заданные основные предикаты при фиксированных вспомогательных предикатах всегда, когда это делает любой другой алгоритм из рассматриваемого класса. Значит, от того, в каком порядке мы элиминируем переменные или подмножества переменных, зависит скорость нахождения оптимального решения. Доказательство этой теоремы имеет неконструктивный характер, т.е. не позволяет осуществить прямое построение эффективного наилучшего алгоритма. В [10] сформулирован критерий существования оптимального порядка элиминации, который заключается в следующем.

Теорема 2. Для графа взаимосвязей существует оптимальный порядок элиминации тогда и только тогда, когда можно построить дерево декомпозиции, каждая вершина которого является кликой в соответствующем графе ограничений.

Порядок элиминации ${\alpha }$ – это выбор порядка решения подзадач. Теорема 2 определяет, в каком случае существует такой порядок решения подзадач, при котором работа ЛЭА будет оптимальной. Задача поиска оптимального упорядочения является NP-полной [11], поэтому на практике для нахождения элиминационной последовательности переменных используются всевозможные эвристики. Для задач оптимизации со специальной структурой эвристики выступают как алгоритмы упорядочивания суперпеременных для последующей элиминации.

Далее будем рассматривать класс локальных методов – ЛЭА решения задач ДО, использующие окрестности переменных [10]. Важной особенностью ЛЭА является вычисление именно локальной информации (т.е. информации об элементах окрестностей элементов) при решении разреженных дискретных задач, поэтому ЛЭА позволяют осуществлять вычисление глобальной информации о решении всей задачи с помощью локальных вычислений (обычно решений подзадач). Основная идея ЛЭА состоит в последовательном исключении переменных с сохранением информации об этих переменных. Процедура ЛЭА разбивается на две части. Первая часть состоит в элиминации элементов, вычислении и запоминании информации в виде локальных решений и получении в конце значения критерия. Вторая часть – это поиск глобального решения всей задачи по найденным в прямой части таблицам с локальными решениями, обеспечивающими в прямой части достижение критерия. Первая часть ЛЭА состоит из нескольких этапов: определение порядка исключения переменных, согласно некоторой эвристике, запись локальной информации об этих переменных в виде новых зависимостей, добавляемых к задаче, а также исключение просмотренных элементов и использованных зависимостей, согласно порядку исключения переменных.

4. Сложность и эффективность ЛЭА. При использовании локальных алгоритмов для решения задач с БД-структурой возникают следующие вопросы. Во-первых, всегда ли возможно избежать полный перебор при решении таких задач? Если это возможно не всегда, представляет интерес получение соответствующих достаточных условий, позволяющих исключить полный перебор. Во-вторых, всегда ли использование локального алгоритма в сочетании с некоторым алгоритмом для решения задач в блоках эффективнее применения упомянутого алгоритма самого по себе? В-третьих, есть ли смысл рассматривать БД-структуры или их следует свести к другим, более простым? В связи с этим представляет интерес сравнение оценок эффективности алгоритмов в сочетании с некоторым алгоритмом, с помощью которого решаются задачи внутри блоков для решения некоторой задачи с БД-структурой и оценка эффективности алгоритма, использованного для решения всей задачи, так что в первом случае учитывается БД-структура задачи, а во втором – нет. Оценки эффективности ЛЭА при решении задач с БД-структурой характеризуются деревом пересечения окрестностей D с весами вершин n_r и весами ребер n_rr', с n булевыми переменными и k блоками:

где ${{\varphi }_{\mathfrak{H}}}$ – оценка эффективности алгоритма, решающего задачи в блоках B_r, а N_r определяется следующим образом:

Напомним, что под вычислительной сложностью алгоритма понимают количество условных шагов или операций, необходимых для решения задачи. При введении оценок сложности алгоритмов решения комбинаторных задач обычно различаются индивидуальная и массовая задачи (множество индивидуальных задач). При этом для оценки трудоемкости алгоритмов используются следующие характеристики: временная вычислительная сложность алгоритма – время, затрачиваемое алгоритмом для решения задачи, емкостная сложность алгоритма – объем памяти, необходимый для реализации алгоритма. Для сглаживания резких различий в поведении алгоритма при переходе от одной индивидуальной задачи к другой можно рассматривать все индивидуальные задачи одной размерности n вместе и определить сложность алгоритма для этой размерности задачи как число шагов (или условных операций) алгоритма в худшем случае, т. е. находится верхняя оценка сложности алгоритма, говорящая о том, что данный алгоритм решает задачу не более чем за T(n) условных единиц времени. Если для некоторого алгоритма верхняя оценка сложности меньше, чем для других алгоритмов, то говорят, что этот алгоритм имеет характеристику в худшем случае лучше, чем другие алгоритмы.

Ориентация на худший случай иногда приводит к пессимистическим прогнозам поведения алгоритмов, так, хорошо известный симплекс-алгоритм на практике работает как полиномиальный алгоритм (это же показывает и теоретический анализ его поведения в среднем), хотя оценка сложности в худшем случае для него является экспоненциальной.

В связи с этим с практической точки зрения часто больший интерес представляет средняя оценка вычислительной сложности, позволяющая судить о поведении алгоритма в среднем на некотором классе задач, однако средняя оценка вычислительной сложности тоже не дает полной характеристики эффективности алгоритма, так как возможны задачи, при решении которых сложность алгоритма превысит эту оценку.

Важной характеристикой алгоритма является асимптотическая оценка сложности – порядок скорости роста сложности алгоритма при увеличении размерности задачи. Асимптотические оценки вычислительной сложности алгоритмов позволяют судить об их поведении при решении задач большой размерности и определить границы применимости алгоритма. Асимптотическая средняя оценка эффективности $E\left( {\varphi ,n,k,\tilde {n}} \right)$ ЛЭА в сочетании с алгоритмом ДО, имеющим оценку эффективности φ(n), при решении БД-задач ДО с ограниченной связностью при n → ∞ имеет вид [12]:

Таким образом, ЛЭA достаточно эффективен даже для решения БД-задач ДО с небольшой связностью, причем его оценка эффективности существенно зависит от алгоритма, с помощью которого решаются подзадачи на каждом шагу алгоритма.

В [13] приведены эксперименты по исследованию эффективности ЛЭА. Для решения задач применялся решатель SYMPHONY и ЛЭА в сочетании с данным решателем. B результате было установлено что использование алгоритма в сочетании с ЛЭА гораздо эффективнее. Также было замечено, что при малых размерностях эффективность ЛЭА отсутствует.

5. Приближенные и параллельные алгоритмы. Приближенные методы широко применяются при решении задач ЦЛП, так как нахождение точного решения может потребовать значительных вычислительных ресурсов. Современные приближенные методы обычно являются комбинированными, т.е. содержат в себе элементы различных методов. Решение задачи приближенными методами обычно происходит в два этапа: построение и улучшение начального решения. При этом на первом этапе широко используются эвристические алгоритмы – алгоритмы, которые не основаны на строго обоснованных предположениях относительно свойств оптимального решения задачи. Примером эвристического алгоритма может быть алгоритм решения задачи коммивояжера, в котором на каждом шагу реализуется переход в ближайшую из оставшихся точку. Алгоритмы такого типа носят название “greedy” (“жадные” алгоритмы). Эти алгоритмы решают “локальную” задачу оптимизации; полученное решение может быть далеким от оптимума. Алгоритмы локальной оптимизации, связанные с введенным понятием окрестности, используются на втором этапе; при этом можно применять несколько алгоритмов этого типа, изменяя правила выбора окрестности.

ЛЭА допускает понижение перебора с помощью организации приближенного решения. Мощное направление в развитии приближенных подходов естественным образом возникло внутри точных методов (в основном методов ветвей и границ). При этом неоднократно отмечалось, что для значительного большинства прикладных задач совершенно достаточно вместо точного получить хорошее приближенное решение.

Трудности с решением достаточно больших подзадач ЛЭА обусловливают необходимость использования релаксаций. Они позволяют находить и отсеивать решения, которые наверняка не станут оптимальными. Любая задача ЦЛП с ограничениями может быть релаксирована с помощью ослабления ее ограничений. Основным недостатком ЛЭА является полный перебор по множествам сепараторов, что дает возможность большого объема перебора при больших размерах сепаратора. Преодолеть этот недостаток и способствовать успешному решению практически важных задач ЦЛП специальной структуры с большими размерами сепараторов может введение процедуры, позволяющей “предсказать” искомые оптимальные (или близкие к оптимальным) значения перемычек. Зная значения перемычек, задачи ЦЛП, соответствующие блокам, можно решать отдельно, независимо друг от друга. Очевидно, что возможность узнать каким-то образом оптимальные значения представляется сомнительной. Тем не менее можно найти значения перемычек, близкие к оптимальным, с помощью замены соответствующих блоков задач ЦЛП на их релаксации, а затем решить построенные задачи ЦЛП с помощью ЛЭА. Таким образом все возможные наборы перемычек перебираются полностью, однако трудоемкость выполнения каждого шага существенно снижена за счет решения не исходных, а релаксированных и поэтому более легко решаемых подзадач. Если все же и с релаксированными подзадачами рассматриваемая задача ЦЛП не поддается точному решению, можно применять случайный выбор значений перемычек. Кроме того, можно использовать неполный перебор перемычек.

Разработка параллельного программного обеспечения для научных целей – отдельная проблема. Выбор целевой вычислительной платформы для реализации ЛЭА может существенно влиять на используемый способ распараллеливания. Таким образом, развитие параллельного программного обеспечения часто требует большей привязанности к времени и энергии, чем разработки итеративных аналогов. В последнее десятилетие наблюдается повышенный интерес к GRID-вычислениям. Как указывалось выше, GRID-вычисления используют совокупность слабосвязанных разнородных вычислительных ресурсов как единый вычислительный ресурс. Существенное преимущество этой среды заключается в том, что она предоставляет огромное количество вычислительных ресурсов для большого числа пользователей. Создание вычислительных сетей позволяет пользователям задействовать простое объединение сотен тысяч подключенных компьютеров и обеспечить необходимую вычислительную мощность. GRID-вычисления представляют собой совокупность распределенных гетерогенных ресурсов, которые могут применяться в качестве группы выполняемых крупномасштабных приложений. GRID-вычисления используют совокупность слабосвязанных разнородных вычислительных ресурсов как единый объект. Реализовано распараллеливание задач с квазиблочной структурой. При этом осуществляется независимое решение промежуточных блочных задач на отдельных процессорах. Приводятся конкретные задачи булевого программирования с матрицами БЛ-/БД-структуры, которые успешно решаются на GRID-системе, хотя простое решение таких задач на одном процессоре было невозможно, а получить решение на GRID без ЛЭА достаточно затратно по времени [14]. Задача булевого программирования с БД-структурой имеет 15 блоков, в каждом из которых порядка 50 000 переменных и 100 ограничений. Количество сепараторов равно 4. Алгоритм распараллеливания работает 17 мин. Тест в БЛ-структуре содержит 5 блоков с количеством переменных и ограничений – 100 000 и 100. Количество сепараторов равно 4. Время решения составляет 6 ч.

Заключение. Эффективность локального алгоритма теоретически и экспериментально исследована недостаточно полно, поэтому остается актуальным поиск удачных модификаций ЛЭА и его сочетаний с различными точными и приближенными решателями ДО. В ранее приведенных конструкциях фигурировали линейные задачи. Однако представляет интерес обобщение на нелинейные и другие постановки, например, по аналогии, как это делается в [15, 16].