Известия РАН. Теория и системы управления, 2019, № 4, стр. 83-98
ПОЛУПАРНАЯ МНОГОАСПЕКТНАЯ КЛАСТЕРИЗАЦИЯ, ОСНОВАННАЯ НА НЕОТРИЦАТЕЛЬНОМ МАТРИЧНОМ РАЗЛОЖЕНИИ
И. А. Матвеев a, *, Ш. Чен b, **, Х. Шуэ c, Л. Ю d, Ш. Яо b
a ФИЦ ИУ РАН
Москва, РФ
b Нанкинский ун-т аэронавтики и космонавтики
Нанкин, КНР
c Юго-восточный ун-т
Нанкин, КНР
d Военно-инженерный ун-т НОАК
Нанкин, КНР
* E-mail: matveev@ccas.ru
** E-mail: lyandcxh@nuaa.edu.cn
Поступила в редакцию 21.01.2019
После доработки 18.03.2019
Принята к публикации 26.03.2019
Аннотация
С ростом доступности данных с несколькими представлениями кластеризация таких данных, основанная на неотрицательном матричном разложении, привлекает все больше внимания. В большинстве работ рассматривается постановка, при которой все объекты имеют образы во всех представлениях. На практике это часто бывает не так. Для решения этой проблемы предлагается новый алгоритм полупарной многоаспектной кластеризации. Для неполных данных выдвигается предположение о том, что их представления имеют равный индикаторный вектор и вводится матрица парности. Также объекты, близкие в каждом представлении, должны иметь одинаковые индикаторы, что дает возможность регуляризации и восстановления геометрической структуры многообразия. Предложенный алгоритм может работать как с неполными, так и с полными данными нескольких представлений. Экспериментальные результаты на четырех наборах данных показывают его эффективность по сравнению с известными современными алгоритмами.
Введение. Данные в практических задачах могут состоять из различных представлений или аспектов. Например, одна и та же фотография может быть дана в высоком или низком разрешении, веб-страницы могут быть классифицированы на основе содержимого и текста гиперссылок и т.п. Можно предположить, что использование информации из нескольких представлений обеспечивает лучшую производительность кластеризации, чем из одного [1]. Многоаспектная кластеризация, МАК (multi-view clustering, MVC) [2] стала актуальной темой исследований в прошлом десятилетии, было предложено большое число алгоритмов. Неотрицательное матричное разложение (НМР) [3, 4] является распространенным приемом МАК. Алгоритм НМР был впервые предложен для обучения классификаторов частей объектов, таких, как человеческие лица и текстовые документы [5–7]. Суть НМР состоит в том, чтобы найти две неотрицательные матрицы, произведение которых обеспечивает хорошее приближение к исходной матрице.
В последнее время НМР стал популярным методом кластеризации данных с несколькими представлениями, и, согласно литературе, он обеспечивает качество, сравнимое с большинством современных самообучаемых алгоритмов [8]. Один из способов (назовем его здесь объединенным НМР, или ОНМР) заключается в конкатенации (объединении) признаков из всех представлений и последующем запуске НМР непосредственно для этого объединенного набора. Простая конкатенация данных из разных представлений может привести к потере специфики некоторых представлений, что влияет на качество работы алгоритма. В методе мульти-НМР (МНМР) [9, 10] предложено разложение объединенной матрицы с ограничением, которое подталкивает решение задачи кластеризации каждого представления к общему консенсусу. Алгоритмы, основанные на МНМР, широко используются в различных приложениях, таких, как медицинская диагностика [11, 12], аннотация изображений [13–15], распознавание объектов [16], динамическая кластеризация по многим представлениям (online multi-view clustering) [17, 18].
Однако эти алгоритмы учитывают только ограничения, накладываемые парами представлений. Если же некоторые объекты отображены не во всех представлениях, кластеризация не гарантируется. При сопоставлении только пар представлений теряется информация о структуре исходного многообразия, породившего эти представления. Для того, чтобы восстановить эту структуру, предложены такие алгоритмы извлечения многообразий (manifold learning) и нелинейного снижения размерности, как локально-линейное встраивание (local linear embedding, LLE) [19], локальное изометрическое отображение (ISOMAP) [20], вычисление собственных векторов лапласиана матрицы связности (laplacian eigenmaps) [21]. Множественные нелинейные ограничения могут также хорошо приближать данные [22]. Все эти алгоритмы используют так называемую инвариантную идею [23], состоящую в том, что соседние точки многообразия с большой вероятностью имеют похожие вложения. Было показано, что эффективность обучения может быть значительно улучшена, если использовать геометрическую структуру и учитывать локальную инвариантность во время процедуры НМР [24, 25].
Следует отметить, что большинство существующих алгоритмов кластеризации основаны на идеальном предположении, что для каждого объекта известен его образец в каждом представлении, иначе говоря, для каждого образца в одном представлении можно найти его пару в другом представлении [9, 26–28]. Более общий случай состоит в том, что в некоторых представлениях отсутствуют образцы некоторых объектов, что приводит к получению неполных многоаспектных данных (semi-paired multi-view data). Отбрасывание не полностью представленных объектов приводит к переобучению на оставшихся данных и плохому обобщению для отброшенных. Разработаны методы, такие, как кластеризация с несколькими неполными представлениями (multiple incomplete views clustering, MIC) [29], которые пополняют недостающие образцы в каждом представлении, но в этом случае все зависит от качества пополнения. В [30] предложен метод частичной многоаспектной кластеризации, ЧМК (partial multi-view clustering, PVC) для неполных данных с двумя представлениями. Он работает путем создания скрытого подпространства, в котором образцы, соответствующие одному и тому же объекту в разных представлениях, находятся близко друг к другу. Регуляризованная графом частичная многоаспектная кластеризация, ГЧМК (graph-regularized partial multi-view clustering, GPMVC) [31] расширяет ЧМК для нескольких сценариев и использует регуляризацию лапласиана при помощи графа, настраиваемого для конкретного представления, что повышает качество работы. ЧМК работает только с парами представлений, при этом нельзя ввести ограничения на скрытую информацию для отдельного представления. ГЧМК ограничивает структуру скрытого представления глобально путем введения условий, ограничивающих многообразие, но эти глобальные ограничения могут быть недостаточно хорошими для выявления локальной геометрической структуры в каждом отдельном представлении. Метод неполного мультимодального группирования визуальных данных, НМГ (incomplete multi-modal visual data grouping, IMG) [32] также сочетает ЧМК с ограничением многообразия, но поскольку он работает только с двумя представлениями, его применение во многих практических задачах затруднено. Дважды выровненная неполная кластеризация с несколькими представлениями, ДВНК (doubly aligned incomplete multi-view clustering, DAIMC) [33] решает проблему неполных представлений путем введения соответствующей задачи на веса и обеспечения соответствия базовых матриц отдельных представлений. Разнесенное неотрицательное матричное разложение, РНМР (diverse nonnegative matrix factorization, DiNMF) [34] уменьшает избыточность, вводя штраф за корреляцию векторов базиса, что обеспечивает процесс обучения за линейное время.
В статье предложен новый алгоритм полупарной многоаспектной кластеризации, ПМАК (semi-paired multi-view clustering, SMC) путем объединения НМР с регуляризацией многообразия в каждом представлении, которое явно учитывает парную информацию между различными представлениями и геометрическую информацию в каждом конкретном представлении. Кроме того, благодаря введению матрицы отсутствующих образцов алгоритм может работать как с полностью, так и с частично представленными данными.
Здесь стоит выделить несколько преимуществ предложенного подхода.
1. Приведенный алгоритм ПМАК не удаляет непарные и не заполняет отсутствующие образцы. Таким образом, этот метод может в полной мере использовать информацию и избегает неопределенности при пополнении данных.
2. В то время как МНМР и ЧМК учитывают только парную информацию, предложенный алгоритм использует внутреннюю геометрию данных и включает ее в качестве дополнительного слагаемого регуляризации. Следовательно, аналогично регуляризованной графом неотрицательной матричной факторизации ГНМР, (graph regularized non-negative matrix factorization) [24], алгоритм в особенности хорош в пространствах вложения большой размерности. По сравнению с ГЧМК алгоритм имеет более строгие ограничения матрицы индикаторов и более сжатую формулировку.
3. ПМАК может быть эффективно решен с помощью итеративной оптимизации, сходимость которой в этом случае доказана. Другие градиентные методы имеют тот недостаток, что они очень чувствительны к выбору размера шага, что может быть очень неудобно для больших приложений.
Остальная часть статьи организована следующим образом: в разд. 1 дается краткий обзор известных работ по многоаспектной кластеризации на основе НМР. В разд. 2 представлен алгоритм и доказательство сходимости оптимизационного процесса. Экспериментальные результаты по кластеризации данных с несколькими представлениями приведены в разд. 3.
1. Обзор известных методов. Рассмотрим развитие методов кластеризации, основанных на НМР, и способы использования при этом данных нескольких представлений.
1.1. Неотрицательное матричное разложение. Пусть $X = [{{\vec {x}}_{1}},{{\vec {x}}_{2}},\; \cdots \;,{{\vec {x}}_{N}}] \in {{\mathbb{R}}^{{d \times N}}}$ – матрица, столбцы которой ${{\vec {x}}_{i}}$ являются векторами исходных данных. В терминах рассматриваемых далее методов кластеризации d – размерность пространства представления (пока единственного), N – число известных для него образцов. Это неотрицательная матрица, т.е. в ней содержатся лишь неотрицательные элементы: ${{x}_{{ij}}} \geqslant 0$, $X \geqslant 0$. НМР [3] стремится найти две неотрицательные матрицы U и V, такие, что
где $U = [{{u}_{{ik}}}] \in {{\mathbb{R}}^{{d \times K}}}$ – базисная матрица, а $V = [{{v}_{{jk}}}] \in {{\mathbb{R}}^{{N \times K}}}$ – индикаторная матрица, K – размерность скрытого пространства. Поиск НМР можно сформулировать как следующую оптимизационную задачу [4]:(1.2)
$\begin{gathered} \mathop {min}\limits_{U,V} {\text{||}}X - U{{V}^{{\text{T}}}}{\text{||}}_{F}^{2}, \\ \begin{array}{*{20}{c}} {U \geqslant 0,\;}&{V \geqslant 0.} \end{array} \\ \end{gathered} $Здесь и далее нижний индекс матричной нормы обозначает ее тип. В работе используются три типа норм (1-норма, 2-норма и F-норма (норма Фробениуса)), определяемые для матрицы $A \in {{\mathbb{R}}^{{m \times n}}}$ соответственно как
1.2. Регуляризованная графом неотрицательная матричная факторизация. В методе регуляризованной графом НМР (ГНМР) вводится весовая матрица W для отражения внутренней геометрической структуры данных в каждом представлении [24], матрица $W$ может быть определена следующим образом:
1) 0–1 взвешивание
(1.3)
${{W}_{{ij}}} = \left\{ \begin{gathered} 1,\quad {\text{е с л и }}\;{\text{о б р а з ц ы }}\;i\;{\text{и }}\;j\;{\text{б л и з к и }}, \hfill \\ 0\quad {\text{и н а ч е }}; \hfill \\ \end{gathered} \right.$2) взвешивание тепловым ядром
(1.4)
${{W}_{{ij}}} = exp\left\{ { - \frac{{\mathop {\left\| {\mathop {\vec {x}}\nolimits_i - \mathop {\vec {x}}\nolimits_j } \right\|}\nolimits^2 }}{\sigma }} \right\}.$ГНМР сводится к следующей оптимизационной задаче [24]:
(1.5)
$\begin{gathered} \mathop {min}\limits_{U,V} {\text{||}}X - U{{V}^{{\text{T}}}}{\text{||}}_{F}^{2} + \lambda {\text{Tr}}({{V}^{{\text{T}}}}LV), \\ \begin{array}{*{20}{c}} {U \geqslant 0,\quad V \geqslant 0,}&{} \end{array} \\ \end{gathered} $1.3. Мульти-НМР. Этот метод требует, чтобы матрицы коэффициентов, извлеченные из разных представлений, были регуляризованы для достижения общего консенсуса [9]. Обозначим через $\{ {{X}^{{(1)}}},{{X}^{{(2)}}}, \cdots ,{{X}^{{(m)}}}\} $ данные всех представлений, где для каждого представления ${{X}^{{(v)}}} \approx {{U}^{{(v)}}}{{({{V}^{{(v)}}})}^{T}}$. Для МНМР получается следующая задача оптимизации:
(1.6)
$\begin{gathered} \mathop {min}\limits_{{{U}^{{(v)}}},{{V}^{{(v)}}},{{V}^{ * }}} \sum\limits_{v = 1}^m {\text{||}}{{X}^{{(v)}}} - {{U}^{{(v)}}}{{({{V}^{{(v)}}})}^{{\text{T}}}}{\text{||}}_{F}^{2} + \sum\limits_{v = 1}^m {{\lambda }_{v}}{\text{||}}{{V}^{{(v)}}} - V{\text{*||}}_{F}^{2}, \\ \begin{array}{*{20}{c}} {}&{\mathop {{\text{||}}U_{k}^{{(v)}}{\text{||}}}\nolimits_1 }&{ = \;1,}&{v = 1,2,\;...{\kern 1pt} {\kern 1pt} ,\;m,} \\ {}&{{{U}^{{\left( v \right)}}}}&{ \geqslant \;0,}&{v = 1,2,\;...{\kern 1pt} {\kern 1pt} ,\;m,} \\ {}&{{{V}^{{(v)}}}}&{ \geqslant \;0,}&{v = 1,2,\;...{\kern 1pt} {\kern 1pt} ,\;m,} \\ {}&{V{\text{*}}}&{ \geqslant \;0.}&{} \end{array} \\ \end{gathered} $1.4. Частичная многоаспектная кластеризация. Метод ЧМК может работать с кластеризацией двух представлений, где в каждом представлении могут отсутствовать образцы [30]. Для объектов, имеющих образцы в обоих представлениях, ЧМК требует, чтобы представления этих образцов в низкоразмерном пространстве совпадали. Формально ЧМК приводит к следующей задаче минимизации:
(1.7)
$\begin{gathered} \mathop {min}\limits_{{{V}_{c}},{{V}^{{(1)}}},{{V}^{{(2)}}},{{U}^{{(1)}}},{{U}^{{(2)}}}} \mathop {\left\| {\left[ {\begin{array}{*{20}{c}} {X_{c}^{{(1)}}} \\ {{{{\bar {X}}}^{{(1)}}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{{V}_{c}}} \\ {{{{\bar {V}}}^{{(1)}}}} \end{array}} \right]{{U}^{{(1)}}}} \right\|}\nolimits_F^2 + \mathop {\left\| {\left[ {\begin{array}{*{20}{c}} {X_{c}^{{(2)}}} \\ {{{{\bar {X}}}^{{(2)}}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{{V}_{c}}} \\ {{{{\bar {V}}}^{{(2)}}}} \end{array}} \right]{{U}^{{(2)}}}} \right\|}\nolimits_F^2 + \lambda \mathop {\left\| {\left[ {\begin{array}{*{20}{c}} {{{V}_{c}}} \\ {{{{\bar {V}}}^{{(1)}}}} \end{array}} \right]} \right\|}\nolimits_1 + \lambda \mathop {\left\| {\left[ {\begin{array}{*{20}{c}} {{{V}_{c}}} \\ {{{{\bar {V}}}^{{(2)}}}} \end{array}} \right]} \right\|}\nolimits_1 , \\ {{U}^{{(1)}}} \geqslant 0,\quad {{U}^{{(2)}}} \geqslant 0,\quad {{V}_{c}} \geqslant 0,\quad {{{\bar {V}}}^{{(1)}}} \geqslant 0,\quad {{{\bar {V}}}^{{(2)}}} \geqslant 0, \\ \end{gathered} $2. Полупарная многоаспектная кластеризация. Пусть набор данных содержит $N$ объектов, каждый из которых может быть представлен несколькими образцами в не более чем $m$ представлениях. Обозначим через $\{ {{X}^{{(1)}}},{{X}^{{(2)}}}, \cdots ,{{X}^{{(m)}}}\} $ данные всех представлений, где ${{X}^{{(v)}}}$ = = $[\vec {x}_{1}^{{(v)}},\vec {x}_{2}^{{(v)}}, \cdots ,\vec {x}_{{{{n}^{{(v)}}}}}^{{(v)}}] \in {{\mathbb{R}}^{{{{d}^{{(v)}}} \times {{n}^{{(v)}}}}}}$, $v = 1,2,\; \cdots ,\;m$, и ${{n}^{{(v)}}}$ – число образцов в представлении с номером $v$. Соответственно ${{n}^{{(v)}}} \leqslant N$, поскольку некоторых образцов в представлениях недостает. Цель алгоритма ПМАК, как и обычного алгоритма кластеризации, состоит в том, чтобы объединить объекты в группы (кластеры).
Во-первых, для полностью спаренного набора данных с несколькими представлениями важно установить взаимосвязь каждого представления. Следуя идее МНМР, можно ограничить вектор индикатора парных экземпляров, используя парную информацию. В частности, естественно предположить, что образцы одного и того же объекта в разных представлениях близки. Как упоминалось ранее, МНМР ищет матрицу индикатора для каждого представления и общую матрицу консенсуса. Необходимо вычислить m + 1 матриц, которые близки друг к другу в F-норме. Согласно МНМР, $m$ матриц индикаторов объединяются в одну, таким образом парные образцы имеют один и тот же вектор индикатора после неотрицательного разложения матрицы. Таким образом, можно получить общую матрицу индикаторов неотрицательного консенсуса $V* \in {{\mathbb{R}}^{{N \times K}}}$ для каждого представления, где K – число базисных векторов. Эту идею можно сформулировать как минимизацию целевой функции:
(2.1)
$E = \sum\limits_{v = 1}^m \left\| {{{X}^{{(v)}}} - {{U}^{{(v)}}}\mathop {V{\text{*}}}\nolimits^{\text{T}} } \right\|_{F}^{2}$(2.2)
$C_{{ji}}^{{(\text{v})}} = \left\{ \begin{gathered} 1,\quad \vec {x}_{j}^{{(\text{v})}}\; - \;{\text{о б р а з е ц }}\;{\text{о б ъ е к т а }}\;i\;{\text{в }}\;{\text{п р е д с т а в л е н и и }}\;\text{v}, \hfill \\ 0\quad {\text{и н а ч е }}. \hfill \\ \end{gathered} \right.$Объединяя матрицы пар с (2.1), можно получить следующую целевую функцию:
(2.3)
${{E}_{1}} = \sum\limits_{v = 1}^m {\text{||}}{{X}^{{(v)}}} - {{U}^{{(v)}}}V{{{\text{*}}}^{{\text{T}}}}{{C}^{{(v){\text{T}}}}}{\text{||}}_{F}^{2}.$Однако в такой формулировке невозможно улучшить результат, если доля парных образцов низка, поскольку игнорируются прочие виды априорной информации, такие, как предположение о кластеризации и предположение о существовании многообразия. Таким образом, ключевым моментом является то, как использовать значимую априорную информацию, скрытую в дополнительных непарных данных. Согласно предположению о локальной инвариантности, если две точки данных близки друг к другу во внутренней геометрии распределения данных, то представления этих двух точек относительно нового базиса также близки друг к другу [24]. Введем слагаемое регуляризации многообразия, чтобы охватить геометрическую структуру в каждом представлении.
(2.4)
${{E}_{2}} = \frac{1}{2}\sum\limits_{i,j = 1}^{{{n}^{{(v)}}}} {\text{||}}({{C}^{{(v)}}}V{\text{*}})_{i}^{{\text{T}}} - ({{C}^{{(v)}}}V*)_{j}^{{\text{T}}}{\text{|}}{{{\text{|}}}^{2}}W_{{ij}}^{{(v)}},$(2.5)
$\begin{gathered} \mathop {min}\limits_{{{U}^{{(v)}}},{{V}^{ * }}} ({{E}_{1}} + \lambda {{E}_{2}}){\kern 1pt} , \\ {{U}^{{\left( v \right)}}} \geqslant 0,\quad V* \geqslant 0,\quad v = \overline {1,m} {\kern 1pt} , \\ \end{gathered} $2.1. Решение. Подобно оригинальному НМР с одним представлением, используется итеративная процедура решения задачи (2.5).
2.2. Фиксируем $V{\text{*}}$, обновляем ${{U}^{{(v)}}}$. Если $V{\text{*}}$ фиксировано для каждого представления, вычисление ${{U}^{{(v)}}}$ не зависит от ${{U}^{{(v')}}}$, $v' \ne v$. Для данных каждого представления можно найти ${{U}^{{(v)}}}$ независимо и целевая функция сводится к $E = mi{{n}_{{{{U}^{{(v)}}}}}}{\text{||}}{{X}^{{(v)}}} - {{U}^{{(v)}}}{{V}^{{ * {\text{T}}}}}{{C}^{{(v){\text{T}}}}}{\text{||}}_{F}^{2}$, что совпадает с оригинальной постановкой НМР. Таким образом, запишем правило обновления:
(2.6)
$u_{{ik}}^{{(v)}}: = u_{{ik}}^{{(v)}}\frac{{{{{({{X}^{{(v)}}}{{C}^{{(v)}}}V*)}}_{{ik}}}}}{{{{{({{U}^{{(v)}}}{{V}^{{ * {\text{T}}}}}{{C}^{{{{{(v)}}^{{\text{T}}}}}}}{{C}^{{(v)}}}V*)}}_{{ik}}}}}.$Нетрудно убедиться, что $u_{{ik}}^{{(v)}}$ остается неотрицательным после каждого шага.
2.3. Фиксируем ${{U}^{{(v)}}}$, обновляем $V{\text{*}}$. Пусть теперь ${{U}^{{(v)}}}$ зафиксировано. Обозначим через $\Psi $ матрицу лагранжевых множителей для ограничения $V* \geqslant 0$. Функция Лагранжа записывается как
Дифференцируем целевую функцию $L$ по $V{\text{*}}$:
Используя условия Каруша–Куна–Такера ${{\psi }_{{jk}}}v_{{jk}}^{ * } = 0$, получим
Таким образом, правило обновления записывается как
(2.7)
$v_{{jk}}^{ * }: = v_{{jk}}^{ * }\frac{{\mathop {\left( {\sum\limits_{v = 1}^m {{C}^{{(v){\text{T}}}}}{{X}^{{(v){\text{T}}}}}{{U}^{{(v)}}}} \right)}\nolimits_{jk} }}{{\mathop {\left( {\sum\limits_{v = 1}^m {{C}^{{(v){\text{T}}}}}{{C}^{{(v)}}}V{\text{*}}{{U}^{{(v){\text{T}}}}}^{{(v)}} + \lambda \sum\limits_{\text{v} = 1}^m {{C}^{{(v){\text{T}}}}}{{L}^{{(v)}}}{{C}^{{(v)}}}V{\text{*}}} \right)}\nolimits_{jk} }}.$В матричной форме (2.6) и (2.7) представляются как следующие мультипликативные правила:
(2.8)
${{U}^{{(v)}}}: = {{U}^{{(v)}}} \odot \frac{{{{X}^{{(v)}}}{{C}^{{(v)}}}V{\text{*}}}}{{{{U}^{{(v)}}}{{V}^{{ * {\text{T}}}}}{{C}^{{(v){\text{T}}}}}{{C}^{{(v)}}}V{\text{*}}}},$(2.9)
$V*: = V{\text{*}} \odot \frac{{\sum\limits_{v = 1}^m {{C}^{{(v){\text{T}}}}}{{X}^{{(v){\text{T}}}}}{{U}^{{(v)}}}}}{{\sum\limits_{v = 1}^m {{C}^{{(v){\text{T}}}}}{{C}^{{(v)}}}V{\text{*}}{{U}^{{(v){\text{T}}}}}{{U}^{{(v)}}} + \lambda \sum\limits_{\text{v} = 1}^m {{C}^{{(v){\text{T}}}}}{{L}^{{(v)}}}{{C}^{{(v)}}}V{\text{*}}}},$Алгоритм.
Дано: Набор данных $\{ {{X}^{{(1)}}},{{X}^{{(2)}}},\; \cdots ,\;{{X}^{{(m)}}}\} $; матрицы пар $\{ {{C}^{{(1)}}},{{C}^{{(2)}}},\; \cdots ,\;{{C}^{{(m)}}}\} $; параметр $\lambda $.
Найти: Базисные матрицы $\{ {{U}^{{(1)}}},{{U}^{{(2)}}},\; \cdots ,\;{{U}^{{(m)}}}\} $; индикаторную матрицу V*.
Шаг 1. Инициализация ${{U}^{{(v)}}},{{V}^{{(v)}}}$ для всех представлений $v = \overline {1,m} $.
Шаг 2. Фиксируем V*. Для всех $v = \overline {1,m} $ обновляем ${{U}^{{(v)}}}$, согласно (2.8).
Шаг 3. Фиксируем все ${{U}^{{(v)}}}$. Обновляем V*, согласно (2.9).
Шаг 4. Если минимум (2.5) достигнут, то конец, иначе переходим к шагу 2.
Использование следующих традиционных методов градиентного спуска также решает эту задачу:
(2.10)
$u_{{ik}}^{{(v)}}: = u_{{ik}}^{{(v)}} - \eta _{{ik}}^{{(v)}}\frac{{\partial E}}{{\partial u_{{ik}}^{{(v)}}}},\quad v_{{jk}}^{ * }: = v_{{jk}}^{ * } - \delta _{{jk}}^{{}}\frac{{\partial E}}{{\partial v_{{jk}}^{ * }}},$2.4. Доказательство сходимости. Следующая теорема обеспечивает сходимость целевой функции.
Теорема. Целевая функция задачи (2.5) не увеличивается в соответствии с правилами обновления (2.8) и (2.9).
Очевидно, что целевая функция задачи (2.5) неотрицательна. Подобно процессу доказательства в [4], можно дать следующее определение и лемму.
Определение. Назовем $G(h,h')$ вспомогательной функцией для F(h), если для всех $h$, $h'$ из области определения F(h) удовлетворяются условия $G(h,h') \geqslant F(h)$, $G(h,h) = F(h)$ [4].
Лемма. Если G является вспомогательной функцией для F, то F не увеличивается при следующем обновлении [4]:
Если V* фиксировано, можно определить
2.5. Анализ сложности. В алгоритме ПМАК сложность обновления ${{U}^{{(v)}}}$ в (2.8) равна $O({{d}^{{(v)}}}{{n}^{{(v)}}}K)$, что совпадает с оригинальным НМР. Сложность обновления V* в (2.9) равна
Если предположить, что целевая функция в (2.5) сходится после t шагов обновления, то общая сложность алгоритма ПМАК будет $O\left( {t{{O}_{1}}} \right)$. Кроме того, алгоритм ПМАК требует дополнительно
операций для построения матрицы ближайших соседей ${{W}^{v}}$. В общем случае для каждого представления $K \ll {{n}^{{(v)}}}$ и $K \ll {{d}^{{(v)}}}$. Обозначив наибольшую размерность представлений ${{d}_{{max}}}$, получим, что сложность ПМАК составляет не более $O(tmd_{{max}}^{3})$.3. Численные эксперименты. Проведена серия экспериментов над следующими четырьмя наборами данных с несколькими представлениями, статистика которых приведена в табл. 1.
Таблица 1.
Статистика наборов данных
| Набор данных | Размер | Число представлений | Число классов |
|---|---|---|---|
| Yale | 165 | 3 | 11 |
| ORL | 400 | 2 | 40 |
| MFD | 2000 | 3 | 10 |
| Википедия | 693 | 2 | 10 |
Набор данных Йельского университета (Yale dataset) содержит 11 различных изображений каждого из 15 различных объектов. Здесь использованы изображения, обрезанные до размера 64 × 64 пикселя в качестве представления высокого разрешения, обрезанные до 50 × 50 пикселей как представления со средним разрешением и 32 × 32 пикселя в качестве представления с низким разрешением.
Набор данных ORL (ORL dataset) содержит 10 различных изображений каждого из 40 различных лиц. Изображения сделаны в разное время, с различным освещением и мимикой. Здесь изображения обрезаны до 64 × 64 пикселя для представления с высоким разрешением и до 56 × 46 пикселя как представление с низким разрешением.
MFD dataset. Этот набор данных состоит из различных признаков (в терминологии статьи – представлений), вычисленных для отсканированных изображений рукописных цифр (‘0’ ~ ‘9’). Набор данных содержит 2000 экземпляров, каждый экземпляр дан в шести представлениях. Здесь использованы следующие три представления: коэффициенты Фурье формы символов, корреляции профилей и средние значения пикселей в окнах 2 × 3.
Набор данных Википедия содержит 693 мультимедийных документа, которые классифицированы по 10 категориям на основе семантической информации. Каждый документ в этом наборе данных представлен как изображение и текст.
3.1. Сравнение с аналогами. Чтобы оценить предлагаемый алгоритм ПМАК, для нескольких наборов данных было проведено его сравнение со следующими аналогами.
1. ОНМР. Этот метод работает путем объединения признаков для всех представлений и последующего запуска НМР на таком объединенном представлении.
2. МНМР [9]. Метод формулирует совместный процесс факторизации матрицы с ограничением, которое подталкивает решение кластеризации каждого представления к общему консенсусу.
3. ЧМК [30]. Метод работает путем создания скрытого подпространства, в котором парные образцы имеют общее представление, а непарные – индивидуальное.
4. НМГ [32].
Следует отметить, что ОНМР и МНМР не могут обрабатывать случаи неполных данных, отсутствующие экземпляры в каждом представлении заполняются средними значениями признаков. Такой подход используется в [33]. Для ЧМК и НМГ, которые работают только с данными двух представлений, модели обучались всем возможным комбинациям двух представлений, приведены наилучшие достигнутые результаты. Чтобы построить сценарий с неполными данными, удаляются некоторые случайно выбранные образцы в каждом представлении, так, что доля полученных непарных образцов варьируется от 0 до 50%. Для кластеризации применен алгоритм k-средних на базовой матрице и, так же как в [9], для измерения качества кластеризации использованы точность (AC) и нормализованная взаимная информация (NMI).
3.2. Результаты кластеризации. Каждый метод запускался 20 раз, чтобы уменьшить случайность. На рис. 1 показана усредненная величина NMI для четырех наборов данных, на рис. 2 – усредненная величина AC. По горизонтальной оси всех графиков отложена доля непарных данных. Можно видеть, что ПМАК почти всегда превосходит другие методы по показателям NMI и AC. На наборах данных Yale и ORL алгоритм ПМАК превосходит все остальные базовые алгоритмы с большим отрывом. И даже когда непарный уровень относительно велик, ПМАК все равно может получить стабильную производительность. Это связано с тем, что метод ПМАК объединяет не только информацию о парных экземплярах, но также и скрытую структуру многообразия в каждом представлении. Отметим, что МНМР и ОНМР на некоторых данных работают неудовлетворительно. Это свидетельствует о том, что использование лишь парных экземпляров не может приводить к хорошей кластеризации.
Рис. 1.
Качество кластеризации (нормализованная взаимная информация, NMI) по четырем наборам данных: а – Yale, б – ORL, в – Википедия, г – MFD

Рис. 2.
Качество кластеризации (точность, AC) по четырем наборам данных: а – Yale, б – ORL, в – Википедия, г – MFD
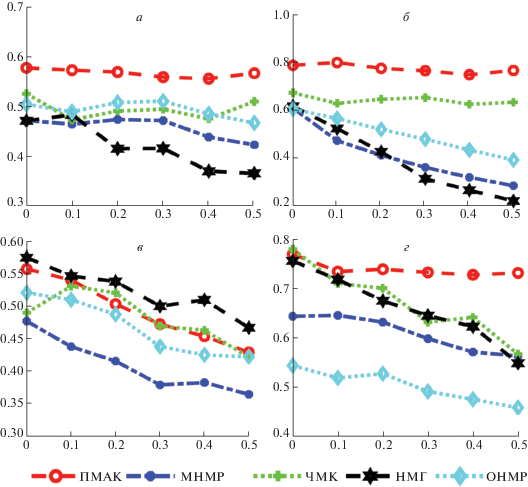
На рис. 1, в, 2, в представлены результаты расчетов по набору данных Википедии. Можно видеть, что все качество работы всех методов падает при увеличении доли непарных образцов. Это связано с тем, что в наборе данных Википедии есть два представления: изображения и текста. Размерность представления изображения составляет 128, а представления текста – 10, благодаря чему представление текста имеет относительно низкое измерение, которое даже меньше, чем число базисных векторов, использованное в экспериментах. Таким образом, некоторые алгоритмы кластеризации с несколькими представлениями не могут построить матрицы индикаторов, в то время как некоторые методы кластеризации с одним представлением, которые рассматривают парные данные как данные с одним представлением, могут достигать лучшей производительности. В наборе данных Википедии методы ПМАК, ЧМК и НМГ имеют близкое качество кластеризации. Однако ЧМК и НМГ могут работать только с наборами данных с двумя представлениями, что в значительной степени ограничивает область их применения.
На рис. 1, г, 2, г показаны результаты экспериментов на базе данных MFD. В отличие от наборов данных Yale и ORL, все представления которых являются растровыми изображениями (т.е. признаки во всех представлениях – это пиксели), в MFD представления более разнообразны. Видно, что ПМАК получает небольшое превосходство по сравнению с ЧМК и НМГ, когда нет пропущенных образцов, при появлении пропусков и увеличении их доли в данных преимущество продолжает расти, что выявляет большую устойчивость предложенного метода по сравнению с аналогами. Предложенный метод опережает ОНМР и МНМР на базе MFD для данных с пропусками, поскольку качество пополнения не гарантировано, а также эти методы игнорируют скрытую структуру в каждом представлении.
3.3. Исследование параметров. Проведены эксперименты с различными значениями $K$, чтобы показать влияние размерности скрытого пространства. В табл. 2–5 дано качество кластеризации по наборам данных Yale, ORL, Википедия и MFD соответственно. Каждый метод исполнялся 20 раз чтобы уменьшить случайность, в таблицах показаны среднее и стандартное отклонения (в единицах $( \times {{10}^{{ - 4}}})$) каждого метода. Эти результаты демонстрируют, что ПМАК превосходит другие алгоритмы, основанные на НМР, когда скрытый коэффициент $K$ постоянно изменяется, что важно, потому что меньший K также означает меньшую сложность вычислений.
Таблица 2.
Качество кластеризации на Yale (70% парных)
| K | NMI, % | AC, % | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ПМАК | НМГ | ЧМК | МНМР | ОНМР | ПМАК | НМГ | ЧМК | МНМР | ОНМР | |
| 4 | 50.5(5.1) | 40.5(4.0) | 45.9(2.1) | 45.3(2.9) | 45.3(5.2) | 42.4(9.6) | 35.9(9.7) | 38.4(9.1) | 38.3(6.5) | 39.1(7.2) |
| 6 | 53.6(13.5) | 41.4(2.9) | 48.4(3.2) | 50.6(2.5) | 48.9(6.3) | 45.2(25.4) | 36.4(3.6) | 41.6(6.6) | 43.6(12.2) | 43.6(7.1) |
| 8 | 56.0(7.6) | 44.8(1.4) | 51.0(8.1) | 50.9(4.1) | 50.7(3.3) | 48.7(16.6) | 39.3(7.0) | 45.6(17.4) | 44.6(8.0) | 46.2(6.2) |
| 10 | 58.7(7.7) | 45.0(6.5) | 52.4(5.4) | 51.54(7.6) | 51.8(4.4) | 52.2(19.6) | 41.0(11.0) | 47.9(19.2) | 45.9(11.8) | 48.0(9.5) |
| 12 | 60.2(5.5) | 46.6(5.7) | 51.7(5.3) | 50.8(4.8) | 54.3(6.1) | 52.0(10.4) | 41.0(13.5) | 45.5(15.9) | 45.1(9.1) | 49.7(6.8) |
| 14 | 60.7(15.7) | 45.5(6.8) | 53.60(5.7) | 51.8(8.40) | 53.1(7.5) | 52.2(35.5) | 11.1(7.6) | 48.0(13.0) | 46.0(11.7) | 49.0(11.9) |
| 16 | 63.2(13.4) | 45.6(6.3) | 54.42(7.5) | 52.8(13.0) | 53.5(9.4) | 53.6(25.5) | 40.4(11.2) | 47.1(19.7) | 46.7(15.7) | 49.8(10.0) |
| 18 | 63.7(8.6) | 45.1(6.4) | 54.8(5.2) | 53.1(3.2) | 53.8(6.3) | 55.9(22.1) | 39.4(13.2) | 49.7(15.5) | 46.8(10.7) | 49.2(7.6) |
| 20 | 64.3(10.4) | 45.7(8.9) | 53.13(13.7) | 50.9(7.3) | 55.2(5.6) | 54.9(22.1) | 41.2(15.0) | 46.6(21.1) | 43.8(16.9) | 51.0(8.1) |
Таблица 3.
Качество кластеризации на ORL (60% парных)
| K | NMI, % | AC, % | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ПМАК | НМГ | ЧМК | МНМР | ОНМР | ПМАК | НМГ | ЧМК | МНМР | ОНМР | |
| 5 | 70.3(1.8) | 51.5(0.4) | 64.7(1.6) | 54.1(5.8) | 57.1(1.7) | 46.6(7.8) | 28.7(1.3) | 40.3(4.0) | 27.7(8.5) | 33.7(5.0) |
| 10 | 81.3(1.5) | 54.1(1.0) | 71.8(1.5) | 55.5(1.6) | 60.2(1.5) | 61.50(3.5) | 31.8(2.6) | 50.2(5.1) | 28.8(2.7) | 36.8(3.7) |
| 15 | 86.0(4.1) | 54.4(1.8) | 74.8(1.8) | 56.2(2.8) | 61.9(1.6) | 67.6(19.2) | 31.3(3.2) | 54.5(5.1) | 30.1(2.6) | 39.1(3.7) |
| 20 | 88.8(2.1) | 53.3(1.6) | 76.8(2.3) | 55.3(2.5) | 62.2(1.2) | 70.8(11.6) | 31.0(3.5) | 58.0(9.2) | 30.3(3.7) | 40.6(3.6) |
| 25 | 90.9(1.9) | 51.8(2.1) | 77.2(2.3) | 56.0(1.8) | 63.5(1.1) | 73.4(20.1) | 29.1(4.2) | 59.1(14.0) | 31.1(1.9) | 41.4(3.8) |
| 30 | 91.8(2.5) | 51.4(4.6) | 79.6(2.3) | 56.0(2.1) | 63.8(1.1) | 74.9(21.0) | 29.2(7.6) | 62.9(12.7) | 31.2(4.1) | 42.2(3.6) |
| 35 | 92.5(2.6) | 50.5(5.0) | 78.6(1.7) | 56.9(1.2) | 64.0(2.3) | 75.7(21.7) | 27.8(10.5) | 59.7(7.5) | 31.9(4.1) | 43.5(5.7) |
| 40 | 92.7(1.5) | 49.8(4.3) | 77.6(6.5) | 57.0(1.3) | 64.3(1.2) | 75.5(18.3) | 26.8(4.0) | 59.7(11.0) | 32.1(2.1) | 43.5(2.8) |
Таблица 4.
Качество кластеризации на Википедии (90% парных)
| K | NMI, % | AC, % | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ПМАК | НМГ | ЧМК | МНМР | ОНМР | ПМАК | НМГ | ЧМК | МНМР | ОНМР | |
| 2 | 29.5(4.2) | 33.4(0.4) | 5.15(0.2) | 22.3(4.1) | 31.9(2.1) | 32.9(7.8) | 39.9(7.9) | 17.4(0.05) | 25.9(6.0) | 34.1(1.7) |
| 4 | 46.3(7.7) | 42.6(3.2) | 33.4(0.2) | 37.5(7.4) | 48.0(2.3) | 47.1(9.9) | 45.1(5.6) | 34.2(10.7) | 38.3(2.5) | 47.0(8.2) |
| 6 | 50.1(2.1) | 40.5(19.2) | 37.4(1.8) | 44.9(2.7) | 52.1(7.7) | 51.3(9.7) | 42.1(32.8) | 44.1(3.2) | 51.4(19.1) | 55.1(5.7) |
| 8 | 48.6(6.0) | 46.7(7.5) | 44.4(0.4) | 45.1(5.1) | 49.0(2.9) | 54.6(5.0) | 52.6(1.4) | 51.1(3.7) | 51.3(10.3) | 55.9(3.7) |
| 10 | 48.4(1.5) | 49.1(1.5) | 45.7(12.7) | 40.4(12.2) | 49.4(1.4) | 54.1(4.6) | 54.8(4.2) | 53.1(2.8) | 46.8(11.7) | 51.1(6.4) |
Таблица 5.
Качество кластеризации на MFD (80% парных)
| K | NMI, % | AC, % | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ПМАК | НМГ | ЧМК | МНМР | ОНМР | ПМАК | НМГ | ЧМК | МНМР | ОНМР | |
| 2 | 39.7(0.2) | 31.6(0.6) | 31.0(0.03) | 36.0(3.6) | 36.1(21.0) | 41.3(2.5) | 33.5(5.2) | 36.5(0.3) | 39.5(1.3) | 30.5(5.0) |
| 4 | 56.9(3.0) | 45.0(0.8) | 45.1(0.92) | 44.8(9.3) | 44.9(38.6) | 56.7(9.1) | 43.1(7.1) | 51.1(8.2) | 45.1(8.5) | 39.1(12.3) |
| 6 | 63.1(1.6) | 49.6(9.1) | 50.2(1.4) | 52.3(3.4) | 50.0(11.1) | 63.4(23.8) | 44.9(37.3) | 56.8(8.1) | 52.3(10.2) | 45.8(15.3) |
| 8 | 66.3(4.5) | 51.0(6.0) | 53.4(3.0) | 56.4(6.2) | 50.2(21.5) | 69.3(8.5) | 46.4(22.4) | 61.4(15.9) | 52.9(30.6) | 46.0(6.8) |
| 10 | 71.7(13.8) | 61.2(7.6) | 54.5(3.6) | 59.4(5.6) | 52.9(20) | 74.0(57.6) | 67.6(62.8) | 58.8(18.1) | 63.3(20.8) | 48.5(8.4) |
Целевая функция в (2.5) имеет два гиперпараметра: параметр регуляризации $\lambda $ и число соседей в слагаемом, ограничивающем многообразие. Параметр $lambda$ меняется в диапазоне ${{10}^{{ - 3}}} \sim {{10}^{3}}$, а число соседей – в диапазоне 2 ~ 20. Рисунок 3 показывает, что при доле парных 60% в наборе данных ORL предложенный алгоритм ПМАК получает относительно лучшую производительность при $\lambda = \{ 1{{e}^{{ - 1}}},1{{e}^{0}}\} $ и количестве соседей, равном 10. Число базисных векторов V* установлено равным 35.
3.4. Исследование числа представлений. Чтобы продемонстрировать, что метод ПМАК может использовать дополнительную информацию на множественных представлениях, проведены эксперименты с различным количеством представлений на наборах данных MFD и Yale. Рисунок 4 показывает качество кластеризации в зависимости от числа представлений. Процент пропуска в каждом представлении составляет 0.1, а результаты для одного представления получены методом ГНМР. Очевидно, что с увеличением количества представлений можно повысить качество кластеризации, что свидетельствует о том, что большее количество представлений может помочь нам найти больше дополнительной информации.
Рис. 4.
Исследование числа представлений: а – набор данных MFD, б – Yale. Сплошная линия – AC, пунктир – NMI

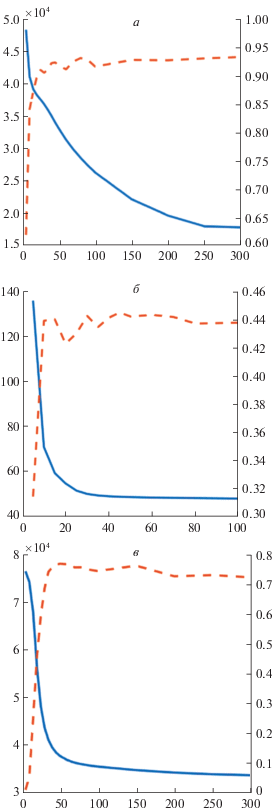
3.5. Исследование сходимости. Теорема из разд. 2 гарантирует сходимость алгоритма ПМАК. Поэтому в этом разделе исследуется только скорость сходимости. На рис. 5 показаны результаты для ORL с 60% парных экземпляров, Википедии – с 80% парных экземпляров и MFD – с 80% парных экземпляров. Горизонтальная ось графиков соответствует числу итераций. Видно, что ПМАК сходится примерно за 50 итераций.
Рис. 5.
Исследование сходимости: а – набор данных ORL, б – Википедия, в – MFD. Сплошная линия, левая шкала – целевая функция; пунктир, правая шкала – NMI
Заключение. Предложен новый алгоритм кластеризации данных с несколькими представлениями на основе НМР. Используя информацию, заданную парными экземплярами в представлениях, ПМАК обучает общую матрицу индикаторов консенсуса, чтобы получить низкоразмерное представление исходных данных. Благодаря введению слагаемого регуляризации многообразия метод может фиксировать скрытую геометрическую структуру в низкоразмерном пространстве для повышения качества кластеризации. Экспериментальные результаты показывают, что предложенный алгоритм превосходит многие современные алгоритмы и дает более надежный результат при большой доле непарных образцов.
Список литературы
Wang L., Chen S. Joint Representation Classification for Collective Face Recognition // Pattern Recognition. 2017. V. 63. P. 182–192.
Scheffer T., Bickel S. Multi-view Clustering // Proc. IEEE Int. Conf. Data Mining. Washington, DC, USA: IEEE Computer Society, 2004. P. 19–26.
Lee D.D., Seung H.S. Learning the Parts of Objects by Non-negative Matrix Factorization // Nature. 1999. V. 401. P. 788–791.
Lee D.D., Seung H.S. Algorithms for Non-negative Matrix Factorization // Proc. 13th Int. Conf. Neural Information Processing Systems. Cambridge, MA, USA: MIT Press, 2000. P. 535–541.
Xu W., Liu X., Gong Y. Document Clustering Based on Non-negative Matrix Factorization // Proc 26th Annual Int. ACM SIGIR Conf. Research and Development in Information Retrieval. Toronto, Canada, 2003. P. 267–273.
Qiang J., Li Y., Yuan Y., Liu W. Snapshot Ensembles of Non-negative Matrix Factorization for Stability of Topic Modelling // Applied Intelligence. 2018. V. 48. № 11. P. 3963–3975.
Vorontsov K., Potapenko A. Additive Regularization of Topic Models // Machine Learning. 2015. V. 101. № 1–3. P. 303–323.
Sang C.Y., Sun D.H. Co-clustering over Multiple Dynamic Data Streams Based on Non-negative Matrix Factorization // Applied intelligence. 2014. V. 41. № 2. P. 487–502.
Liu J., Wang C., Gao J., Han J. Multi-view Clustering via Joint Nonnegative Matrix Factorization // Proc. SIAM Int. Conf. Data Mining. Austin, TX, USA, 2013. P. 252–260.
Wang L., Chen S., Wang Y. A Unified Algorithm for Mixed ${{l}_{{2,p}}}$-minimizations and its Application in Feature Selection // Computational Optimization and Applications. 2014. V. 58. № 2. P. 409–421.
Liu K., Wang H., Risacher S., Saykin A., Shen L. Multiple Incomplete Views Clustering via Non-negative Matrix Factorization with its Application in Alzheimer’s Disease Analysis // Proc. IEEE 15th Int. Symp. Biomedical Imaging. Washington, DC, 2018. P. 1402–1405.
Ling Y., Pan X., Li G., Hu X. Clinical Documents Clustering Based on Medication/symptom Names Using Multi-view Nonnegative Matrix Factorization // IEEE Trans. Nanobioscience. 2015. V. 14. № 5. P. 500–504.
Kalayeh M.M., Idrees H., Shah M. NMF-kNN: Image Annotation Using Weighted Multi-view Non-negative Matrix Factorization // Proc. IEEE Conf. Computer Vision and Pattern Recognition. Columbus, OH, USA, 2014. P. 184–191.
Rad R., Jamzad M. Image Annotation Using Multi-view Non-negative Matrix Factorization with Different Number of Basis Vectors // J. Visual Communication and Image Representation. 2017. V. 46. P. 1–12.
Zhong F., Ma L. Image Annotation Using Multi-view Non-negative Matrix Factorization and Semantic Co-occurrence // Proc. IEEE Region 10 Conf. (TENCON). Singapore, 2016. P. 2453–2456.
Zhang X., Gao H., Li G., Zhao J., Huo J., Yin J., Liu Y., Zheng L. Multi-view Clustering Based on Graph-regularized Nonnegative Matrix Factorization for Object Recognition // Information Sciences. 2018. V. 432. P. 463–478.
Shao W., He L., Lu C., Yu P.S. Online Multi-view Clustering with Incomplete Views // Proc. IEEE Int. Conf. Big Data. Washington, DC, 2016. P. 1012–1017.
Shao W., He L., Lu C., Wei X., Yu P.S. Online Unsupervised Multi-view Feature Selection // IEEE 16th Int. Conf. Data Mining. Barcelona, Spain, 2016. P. 1203–1208.
Roweis S.T., Saul L.K. Nonlinear Dimensionality Reduction by Locally Linear Embedding // Science. 2000. V. 290. № 5500. P. 2323–2326.
Tenenbaum J.B., De Silva V., Langford J.C. A Global Geometric Framework for Nonlinear Dimensionality Reduction // Science. 2000. V. 290. № 5500. P. 2319–2323.
Belkin M., Niyogi P. Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering // Proc. 14th Int. Conf. Neural Information Processing Systems: Natural and Synthetic. Vancouver, Canada, 2001. P. 585–591.
Tao L., Ip H.H., Wang Y., Shu X. Low Rank Approximation with Sparse Integration of Multiple Manifolds for Data Representation // Applied Intelligence. 2015. V. 42. № 3. P. 430–446.
Hadsell R., Chopra S., LeCun Y. Dimensionality Reduction by Learning an Invariant Mapping // Proc. IEEE Computer Society Conf. Computer Vision and Pattern Recognition. N.Y., USA, 2006. P. 1735–1742.
Cai D., He X., Han J., Huang T.S. Graph Regularized Nonnegative Matrix Factorization for Data Representation // IEEE TPAMI. 2011. V. 33. № 8. P. 1548–1560.
Zong L., Zhang X., Zhao L., Yu H., Zhao Q. Multi-view Clustering via Multi-manifold Regularized Non-negative Matrix Factorization // Neural Networks. 2017. V. 88. P. 74–89.
Yang W., Gao Y., Cao L., Yang M., Shi Y. mPadal: a Joint Local-and-global Multi-view Feature Selection Method for Activity Recognition // Applied Intelligence. 2014. V. 41. № 3. P. 776–790.
Zhao H., Ding Z., Fu Y. Multi-view Clustering via Deep Matrix Factorization // Proc. 31st AAAI Conf. Artificial Intelligence. San Francisco, CA, USA, 2017. P. 2921–2927.
Xie X., Sun S. Multi-view Laplacian Twin Support Vector Machines // Applied Intelligence. 2014. V. 41. № 4. P. 1059–1068.
Shao W., He L., Philip S.Y. Multiple Incomplete Views Clustering via Weighted Nonnegative Matrix Factorization with L2,1 Regularization // Lecture Notes in Computer Science. V. 9284 / Eds A. Appice, P. Rodrigues, V. Santos Costa, C. Soares, J. Gama, A. Jorge. Cham: Springer, 2015.
Zhi S.Y., Zhou H. Partial Multi-view Clustering // Proc. 28th AAAI Conf. Artificial Intelligence. Quebec, Canada, 2014. P. 1968–1974.
Rai N., Negi S., Chaudhury S., Deshmukh O. Partial Multi-view Clustering Using Graph Regularized NMF // Proc. 23rd IEEE Int. Conf. Pattern Recognition. Cancun, Mexico, 2016. P. 2192–2197.
Zhao H., Liu H., Fu Y. Incomplete Multi-modal Visual Data Grouping // Proc. 25th Int. Joint Conf. Artificial Intelligence. N.Y., USA, 2016. P. 2392–2398.
Hu M., Chen S. Doubly Aligned Incomplete Multi-view Clustering // Proc. 27th Int. Joint Conf. Artificial Intelligence. Macao, China, 2018. P. 2262–2268.
Wang J., Tian F., Yu H., Liu C.H., Zhan K., Wang X. Diverse Non-negative Matrix Factorization for Multiview Data Representation // IEEE Trans. Cybernetics. 2018. V. 48. № 9. P. 2620–2632.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления



