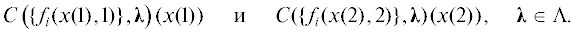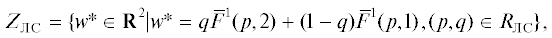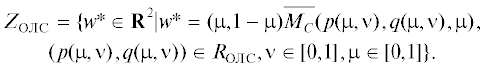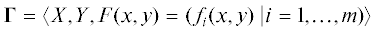Известия РАН. Теория и системы управления, 2019, № 4, стр. 106-120

0. Введение. Рассмотрим задачу многокритериальной (МК), или же векторной, оптимизации: найти

где F(x) = (f₁(х), …, f_m(х)), X – компакт в евклидовом пространстве, все частные критерии f_i(·) > 0 и непрерывны. Значением максимума в МК-задаче (0.1), который в отличие от скалярного максимума записывается с заглавной буквы, будем считать множество Слейтера в критериальном пространстве [1–3]. Реализацией этого значения (решением МК-задачи) является множество

Предположим сначала, что Х – конечное множество и что при выборе х $ \in $ Х ответственный за выбор (лицо, принимающее решения, далее – ЛПР) планирует применять смешанную стратегию, т.е. задавать для себя вероятность р(х), с которой он будет придерживаться решения х $ \in $ Х. Какую оценку вектора выигрышей ему правильно использовать? Стандартным ответом [4–6] на такой вопрос служит замена векторного критерия F(x) на его математическое ожидание ЕF, понимаемое как вектор (Еf₁, …, Еf_m) математических ожиданий компонент (по мере р(·)). Тем не менее, в общем случае с позиций исследования операций [1] данный ответ не очевиден.

Например, если Х – выпуклый компакт, то по теореме о среднем Еf_i = f_i(х(i)), где средние точки х(i) $ \in $ Х, вообще говоря, различны между собой при разных индексах i из {1, …, m}. Однако ЛПР, пусть и случайно, но выбирает только один вариант х $ \in $ Х на все критерии, так что вектор, составленный из  f_i(х(i)), может оказаться недостижимым в критериальном пространстве. В свою очередь для конечного множества $Х = \{ x{{{\text{ }}}^{j}}\} _{{j = 0}}^{T}$ обозначим кусочно-линейное продолжение f_i на выпуклую оболочку conv(X) этого множества через ${{\tilde {f}}_{i}}$, i = 1, …, m. Тогда если все ${{\tilde {f}}_{i}}$ вдруг будут линейными, то получим для р(x ^j) – вероятности выбора x ^j, что

и средняя точка не зависит от i. Лишь в такой ситуации стандартная замена корректна.

Вернемся теперь к исходной задаче (0.1) МК-оптимизации. Для параметризации и построения Х_S используется метод сверток [1–3], согласно которому МК-задача (0.1) на Мах F(x) заменяется параметрическим семейством скалярных задач на mах C({f_i}, λ)(x), где С – функция свертки частных критериев $\left\{ {{{f}_{i}}} \right\}_{{i = 1}}^{m}$ МК-задачи в единый скалярный критерий (монотонна по f), λ = = (λ₁, …, λ_m ) – вектор параметров свертки. Например, для линейной свертки (ЛС)

В случае вогнутости  f_i на X справедливо представление

и значение (0.1) с помощью ЛС параметризуется множеством

Ю.Б. Гермейер [1] ввел не требующую условия вогнутости логическую свертку, заменив операцию суммы на минимум, причем оказалось удобнее частные критерии при скаляризации не умножать, а делить [7] на весовые коэффициенты – параметры свертки. Такую свертку обозначим

и будем называть гермейеровской, или обратной логической, сверткой (ОЛС). В общих предположениях (с учетом неотрицательности  f_i ), согласно [1, 7], выполнено

Значение (0.1) при использовании ОЛС задается (возможно, с прибавлением некоторой части точек Слейтера из оболочки Эджворта–Парето [7]) множеством

Таким образом, ЛПР может по-разному представлять исходную МК-задачу (0.1) в зависимости от способа ее скаляризации – на получающееся решение вид применяемой свертки не влияет. Ситуация будет иной при использовании им смешанных стратегий. Если до перехода к свертке (т.е. до скаляризации) вектора критериев заменить частные критерии на их математические ожидания, то все так же не важно, какую свертку ему потом выбрать. Но если ЛПР считает правильным осреднять уже скаляризованную целевую функцию МК-задачи (при каждом значении параметра) после выбора свертки для ее представления, то разные свертки могут привести к различным результатам. Для пояснения заметим, что ${\text{E}}L(\{ {{f}_{i}}\} ,{\mathbf{\lambda }}) = L(\{ {\text{E}}{{f}_{i}}\} ,{\mathbf{\lambda }})$, но ${\text{E}}G(\{ {{f}_{i}}\} ,{\mathbf{\mu }}) \leqslant G(\{ {\text{E}}{{f}_{i}}\} ,{\mathbf{\mu }})$ и максимум по x правой части последнего неравенства может превысить максимум левой. В итоге мало шансов, что совпадут между собой и объединения по µ таких максимумов (умноженных на µ), и объединения максимизаторов. По аналогичным соображениям имеют право различаться множества, представляющие значение или реализации МК-максимума в смешанных стратегиях, в зависимости от используемых сверток. Цель данной статьи состоит в том, чтобы оценить отмеченные различия на простейшем примере, получаемом при дискретизации множества стратегий Студента (С) в модельной МК-игре ЛПР С и Преподавателя (П), рассмотренной в [8, 9].

В [9] предложено исследовать возможность обобщения на ОЛС результата из [4] об аксиоматическом описании решения в смешанных стратегиях для МК-игр с нулевой суммой, согласно [5], на базе применения ЛС. Такая возможность не подтвердилась для случая бесконечного Х = = [0, 1], изучаемого в [9]. Рассмотрение вопроса замены ЛС на ОЛС для конечных игр на примере Х = {0, 1} начато в [10], продолжим его в разд. 4. В целом, авторы полагают, что использование смешанных стратегий в МК-задачах не препятствует применению ОЛС со стороны ЛПР, и даже в ряде постановок ОЛС позволяет получить более адекватные оценки, чем ЛС.

Кроме того, если говорить о задаче МК-оптимизации с неопределенностью и для ее решения применять численные методы стохастического программирования, то вряд ли удастся обойтись без той или иной функции свертки. Однако от вида свертки будет зависеть ответ задачи. Указанные вопросы обсудим в разд. 2. Динамические МК-задачи тоже допускают различное толкование в зависимости от того, как постановщик задает скаляризацию и как входит в свертку переменная времени. Вкратце затронем эту тему в разд. 3 на примере модельной МК-задачи ЛПР С на бесконечном Х = [0, 1].

1. Модельная МК-задача ЛПР С. В модели [8] С выбирает долю х рабочего времени, которую он тратит на подготовку диплома. Допустим, что эффективность подготовки пропорциональна $\sqrt x $. Оставшееся рабочее время (1 – х) ЛПР С тратит на подработку, и значения его второго критерия пропорциональны $\sqrt {1 - x} $. Считается, что производительность любых занятий С падает с увеличением отводимого на них времени, обусловливая вогнутость по х частных критериев. Начнем с крайнего случая и в отличие от [8, 9] допустим, что ЛПР С не может распределять свое время между двумя видами деятельности, т.е. выбирает одну из двух стратегий $x \in X$ = {0, 1}, максимизируя векторный критерий F(x) = (f₁(х), f₂(х)) = ($\sqrt x $,$\sqrt {1 - x} $). Тогда обе его стратегии образуют Х_S и значение F(Х_S) МК-максимума состоит из двух точек (0, 1) и (1, 0) на координатных осях в пространстве критериев. Две эти точки получаем и при использовании ЛС со стороны С. Формула (0.2) приводит, кроме указанных, еще к оценке (0, 0), возникающей при двух ненулевых компонентах вектора параметров μ.

Предположим теперь, что С решил применять смешанные стратегии, и обозначим через p вероятность выбора им х = 1. Если С ориентируется на ЛС, то максимизация по p параметрического семейства ${\text{E}}L(\{ {{f}_{i}}\} ,{\mathbf{\lambda }})$ даст в качестве решения (множества P_S) весь отрезок [0, 1], т.е. любые p эффективны по Слейтеру (при каких-то λ). Причем все p из интервала (0, 1) соответствуют единственной величине λ = (1/2, 1/2). Значением среднего МК-максимума при расчете С на ЛС будет отрезок, соединяющий в критериальном пространстве точки (0, 1) и (1, 0). Если же С использует ОЛС, то вместо (0.2) получим

– МК-среднее значение МК-максимума при гермейеровской скаляризации. Множество (1.1) совпадает с (0.2) для данного примера и не содержит указанного выше отрезка, так как $\forall {\mathbf{\mu }} \ne (0,1),(1,0):\,\,\,G(\{ {{f}_{i}}\} ,{\mathbf{\mu }}) = 0\,\,\forall x$. Поэтому переход к смешанным стратегиям ЛПР С не меняет его результата с ОЛС. Таким образом, множества МК-средних значений (0.1), построенные с помощью разных сверток, различаются (хотя множество решений – оптимальных смешанных стратегий P_S не зависит от вида свертки).

По содержанию если представить себе повторяющуюся МК-задачу для С, где С перед выбором х = 0 или 1 бросает монетку, то можно сказать, что половину времени он отдает на первый критерий, а половину – на второй. Тогда правильнее ввести в множество Х дополнительную альтернативу х = 1/2 и говорить о точке (1/$\sqrt 2 $, 1/$\sqrt 2 $) в критериальном пространстве. Однако математическое ожидание даст более оптимистическую оценку (1/2, 1/2), которую конечно можно проинтерпретировать как половинный максимум по каждому критерию, но трудно объяснить для исходного вида критерия F. Использование осредненной ОЛС иллюстрирует пословицу “за двумя зайцами погонишься – ни одного не поймаешь” и дает пессимистическую оценку (0, 0) результата С, когда он делит свое время между обоими критериями сразу.

2. МК-задачи стохастической оптимизации. В примере разд. 1 все критерии ЛПР С были упрощенными и их математическое ожидание вычислялось явно. Общая скалярная задача стохастической оптимизации для непрерывной на выпуклом компакте Х функции  f, зависящей еще и от случайной величины (с.в.) ξ, ставится как задача поиска

где функция распределения с.в. ξ может быть не известной ЛПР в явном виде (задаваться эмпирически) при выборе им х $ \in $ Х, либо вычисление ее математического ожидания может являться отдельной непростой задачей [11, 12]. Вместе с тем если комбинировать итеративные методы локальной оптимизации с методом Монте-Карло для математического ожидания, то получаем алгоритмы, сходящиеся к локально оптимальному х с вероятностью 1 [11, 13].

В итеративных алгоритмах поиска МК-оптимума [7, 14] шаги метода локальной оптимизации функции свертки совмещают с перебором по сетке параметров свертки, точнее, по специальной ε-цепи из близких значений на сетке параметров. В отсутствие случайных факторов использование ЛС и ОЛС позволяет строить последовательность, предельные точки которой для выпуклых задач составляют множество Х_S. При наличии зависимости критериев от с.в., применяя шаги методов стохастической оптимизации к функции свертки, получим сходимость к математическому ожиданию функции свертки (при соответствующем значении параметра). Для ОЛС ее математическое ожидание и свертка математических ожиданий оказываются различными, так что и максимумы их различны. Отсюда ясно, что значение (1.1), объединяющее максимумы математических ожиданий ОЛС для разных параметров свертки, в общем, не совпадает с объединением максимумов математических ожиданий ЛС (равных ЛС от математических ожиданий) частных критериев, поскольку для выпуклых задач (т.е. допускающих применение ЛС) неважно, с помощью какой из сверток задать параметризацию максимума вектора математических ожиданий частных критериев.

Формально, обозначая через А_ЛС и А_ОЛС множества в критериальном пространстве, представляющие МК-максимум МК-среднего вектора частных критериев, получаемый с помощью параметрической максимизации математического ожидания функции свертки (для ЛС и ОЛС соответственно), можем записать, что

и

Таким образом, применение методов стохастического программирования в МК-задачах стохастической оптимизации дает решения, зависящие от выбранной в методе функции свертки. Подчеркнем, что нет однозначного ответа на вопрос, какое из этих решений является более правильным, ни с теоретической, ни с содержательной точек зрения.

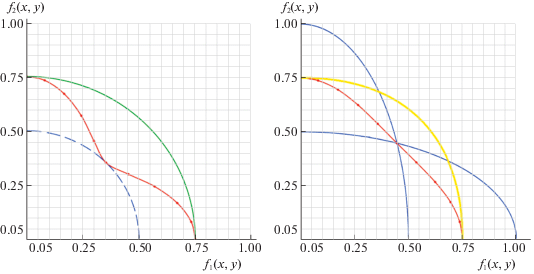
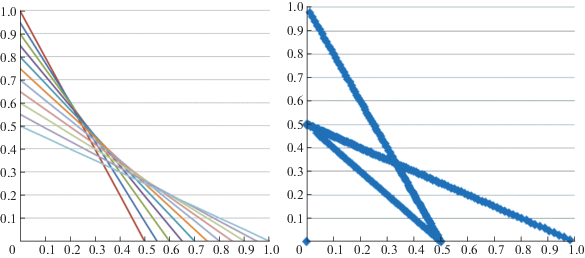
Для иллюстрации различий модифицируем МК-задачу ЛПР С из разд. 1, следуя [9]. Пусть векторный критерий у ЛПР С зависит от с.в. ξ, принимающей значения 1 и 2 с вероятностью 1/2, F(x, ξ) = (f₁(х, ξ), f₂(х, ξ)) = (ξ$\sqrt x $/2, $\sqrt {1 - x} $/ξ). И пусть также С может как угодно делить ресурс между своими занятиями, т.е. выбирать отводимую на учебу долю х рабочего времени из всего отрезка [0, 1] (использовать смешанные стратегии ему уже не нужно). Тогда слева на рис. 1 видно отличие А_ОЛС от А_ЛС в данном примере: линия для ЛС сплошная, а для ОЛС помечена точками. На левом графике штриховой линией еще показан МК-максимин, определяемый [1, 2] как

где EPH(W) $\mathop = \limits^{{\text{def}}} $ {w* $ \in $ R^m|w* < w, w $ \in $ W} – оболочка Эджворта–Парето [3] для W $ \subseteq $ R^m. Нетрудно доказать (см. утверждение 1 в [8]), что для любых выпуклых задач А_ОЛС $ \subseteq $ EPH(А_ЛС). При этом МК-максимин содержится в EPH(А_ОЛС), так что его можно считать нижней оценкой для А_ОЛС и А_ЛС при неизвестной функции распределения с.в. ξ (в полном соответствии со скалярными задачами [1]).

Для исследуемой постановки рассмотрим также стохастическое обобщение МК-минимакса, когда ЛПР выбирает х(ξ), уже зная конкретную реализацию с.в. ξ. Задача состоит в том, чтобы построить МК-оценку вектора его выигрышей, т.е. (формально) найти:

Таким образом, надо при каждом значении ξ определить МК-максимум и взять его математическое ожидание по ξ (при известной функции распределения). Для поиска МК-максимума можно применить метод сверток. Если распределение с.в. ξ задано сложно вычисляемой функцией или явно не задано, но доступны ее значения, то по методу Монте-Карло можно использовать случайные реализации с.в. ξ и осреднять соответствующие слейтеровские множества F(Х_S(ξ), ξ). Однако операция осреднения (и суммирования) множеств не является стандартной. Поэтому в [8] предложено осреднять/суммировать параметрические максимумы свертки (после скаляризации) и брать объединение по ее параметрам. Для модельного примера стохастической МК-задачи ЛПР С получим (в зависимости от используемой свертки) множества:

изображенные на рис. 1 справа. Тонкими линиями на правом графике рис. 1 показаны множества F(Х_S(1), 1) и F(Х_S(2), 2), среднее между которыми есть В_ОЛС (линия с точками), а В_ЛС выделено светлой жирной линией. Здесь результат применения ОЛС представляется более интуитивным, чем дающий явно завышенную оценку результат применения ЛС.

В [8] доказано, что в общем выпуклом случае А_ЛС $ \subseteq $ EPH(В_ЛС), А_ОЛС $ \subseteq $ EPH(В_ОЛС), В_ОЛС $ \subseteq $ $ \subseteq $ EPH(В_ЛС) и МК-минимакс содержится в EPH(В_ОЛС), где (согласно определению из [1, 2, 14]) МК-минимакс задается формулой

Для рассматриваемой модельной задачи ЛПР С значение МК-минимакса образуют на рис. 1 справа участки кривых F(Х_S(1), 1) и F(Х_S(2), 2) ниже точки их пересечения. Как и в скалярных задачах, МК-максимин меньше МК-минимакса (включен в EPH), т.е. между гарантированными оценками стохастического МК-максимума выполнено то же соотношение, что и между соответствующими значениями для известной функции распределения с.в. ξ.

3. Динамические постановки МК-задачи. Операция суммирования или осреднения МК-оптимумов может возникать также в динамических МК-задачах. Допустим, что F(х(1), 1) – значение вектора критериев в первый период времени, а F(х(2), 2) – во второй и ЛПР выбирает вектор (х(1), х(2)) из [0, 1] × [0, 1] с целью МК-максимизации среднего за два периода МК-результата, т.е. достижения

Однако возможно, что ЛПР не специфицирует свой векторный критерий как

а оставит его в скаляризованной форме двух параметрических семейств:

Причем, в силу несвязанности между собой ограничений на х(1) и на x(2), максимум полусуммы значений функции свертки равен полусумме максимумов функции C(·) и определяется как В_ОЛС или как В_ЛС, т.е. зависит от вида свертки С(·) (см. на рис. 1 справа). Похоже, что при любом усложнении постановки МК-задачи выбор функции свертки уже начинает влиять на получаемое решение (см. также ниже в разд. 4).

Для исследуемого модельного примера можно представить себе, что в первый момент времени условия принятия решений благоприятствуют второму критерию ЛПР С, а во второй – его первому критерию. Но с позиций МК-оптимизации это не значит, что в первый момент С должен максимизировать второй критерий, а во второй момент – первый. При разных значениях λ у него будут разные оптимальные стратегии, зависящие, в том числе, от выбранной им свертки. В частности, для ЛС с λ = (1/2, 1/2) максимизирующие свертку х^L(1, λ) = 0.2 и х^L(2, λ) = 0.8, а для ОЛС с µ = (1/2, 1/2) – наоборот, т.е. х^G(1, µ) = 0.8 и х^G(2, µ) = 0.2. Тем самым при одинаковой важности для него обоих критериев ЛПР, использующий ЛС, больше ресурса отдает на улучшение критерия, для которого ситуация благоприятная, а использующий ОЛС – улучшает вперед тот частный критерий, что находится в данный момент в худших условиях. В итоге ЛС приводит к более оптимистичной оценке оптимума, чем ОЛС, в задаче динамической векторной оптимизации. И при этом стратегия ЛПР С, уравнивающая итоговые значения критериев, имеет максимальную оценку в случае ЛС и минимальную в случае ОЛС (если считать по расстоянию в критериальном пространстве от точки (0, 0) – “ничего по обоим критериям”). Действительно (см. на рис. 1 справа), точка пересечения В_ЛС с биссектрисой первого ортанта лежит вне круга радиуса 0.75 с центром в начале координат, а для В_ОЛС аналогичная точка совпадает с такой же на графике МК-минимакса (когда вместо полусуммы по двум моментам времени берется минимальное из значений в каждый момент).

Отметим, что если ограничить выбор ЛПР С стратегиями, не меняющимися по времени, т.е. равенством х(1) = х(2), допустим, взять х(·) = 1/2, то в исходной постановке не получим точки оптимума, поскольку графики для А_ЛС и В_ЛС пересекаются лишь на осях координат и аналогично А_ОЛС и В_ОЛС, а также МК-максимин и МК-минимакс (ср. левую и правую части рис. 1). Данным рисунком еще раз подтверждается тот факт, что для МК-задач не характерно наличие седловой точки как в обычном смысле равновесия (хотя по каждому частному критерию в изучаемом примере имеется седловая точка), так и в общем смысле отсутствия выигрыша от использования информации (в данном случае о периоде времени или о реализациях с.в. ξ).

В [15] показано, что совпадение МК-максимина и МК-минимакса соответствует ситуации, когда многокритериальность несущественна, т.е. удается достичь максимума по всем критериям сразу. Поэтому нельзя принять условие такого равенства в качестве определения решения МК-игры. Ниже обсудим обобщения понятия равновесия Нэша на МК-случай.

4. Игровая МК-задача. Игровая постановка МК-задачи из разд. 2 была подробно проанализирована в [9], где вместо с.в. ξ фигурирует стратегия у $ \in $ Y второго ЛПР – игрока П, моделирующего преподавателя. Предполагается, что ЛПР П стремится путем выбора у $ \in $ {1, 2} минимизировать векторный критерий F(х, у), который максимизирует первый ЛПР – игрок С, выбирая х ∈ Х = = [0, 1]. Вектор-функция F(x, y) = (f₁(х, y), f₂(х, y)) = (y$\sqrt x $/2, $\sqrt {1 - x} $/y). Допускается применение П смешанных стратегий.

Для решения МК-игр двух лиц с противоположными интересами $\left\langle {F(x,y),\,X,Y} \right\rangle $, где F(x, y) = = (f₁ (x, y), …, f_m (x, y)), известен подход [16], обобщающий на МК-постановки понятие равновесия по Нэшу (седловой точки – для двух игроков с противоположными интересами). Следуя [16], решением данной МК-игры, или МК-равновесием, можно считать множество R таких точек (х*, у*), что х*$ \in $ Х_S (у*) и у*$ \in $ Y_S (х*), здесь индекс S указывает на множество оптимальных по Слейтеру реализаций МК-максимума вектор-функций F(х, у*) и –F(х*, у) соответственно. В случае конечных Х и Y Шепли [5] свел описание указанного множества R к семейству задач поиска решений скалярных игр с функциями выигрышей – ЛС частных критериев при произвольном наборе весовых коэффициентов, своих у каждого игрока. В рассматриваемом примере решение игры по Шепли оказалось неизбирательным: состояло [9] из всех пар (х, q), где q – вероятность выбора у = 2 игроком П. При замене ЛС на ОЛС получили более узкое множество.

Основное отличие в постановке МК-игры из [9] от условий [5] – отсутствие конечности множества Х стратегий С. При этом игроку С не требуются смешанные стратегии. Если аппроксимировать Х конечным множеством и допустить смешанные стратегии, то получим все исходные стратегии игрока С, но компоненты его вектор-функции выигрышей станут кусочно-линейными. Вопрос о существенности указанного отличия рассмотрим ниже. В общем случае конечного числа стратегий игрока С имеем Х = {0, 1/Т, 2/Т, …, (Т – 1)/Т, 1}, где Т – целое. Разрешим С применять смешанную стратегию p(·) > 0 с суммой компонент, равной 1, т.е. из симплекса P в (Т + 1)-мерном пространстве. Пусть, применяя p(·), игрок С рассчитывает, согласно [10], на средний выигрыш по обоим критериям:

для у $ \in $ Y = {1, 2} (верхний индекс Т у функции соответствует параметру дискретизации). Предложенное осреднение в МК-задаче отличается от формулы (1.1), поскольку здесь речь идет не о неконтролируемом факторе (с.в. ξ), а об изменении критерия игроком С при изменении им своего множества стратегий (с Х на P).

Для наглядности остановимся на предельном случае Т = 1 из разд. 2 и так же, как и там, обозначим через p вероятность выбора х = 1. Тогда векторный критерий С равен

и ${{\overline F }^{1}}(p,1) = \left( {p{\text{/}}2,1 - p} \right)$, а ${{\overline F }^{1}}(p,2) = \left( {p,(1 - p){\text{/}}2} \right)$. Подчеркнем, что если бы игрок С, используя смешанную стратегию, применял осреднение к свертке Гермейера, то его результат в данном примере не поднялся бы от 0 (см. в разд. 1). А так, в критериальном пространстве имеем для p $ \in $ [0, 1] два пересекающихся отрезка прямых из точки (0, 1/2) в (1, 0) и из точки (0, 1) в (1/2, 0), что является линейной аппроксимацией множеств F(Х_S(1), 1) и F(Х_S(2), 2) из разд. 2 (показанных на рис. 1 справа). В полученной задаче для ЛПР С при каждом у все достижимые точки оптимальны по Слейтеру, поэтому указанные отрезки определяют значения МК-максимума по p $ \in $ [0, 1] среднего по его смешанной стратегии вектора критериев игрока С при у = 1 и 2 соответственно.

Построим для рассматриваемого примера множества: R = R_ЛС – решение и Z_ЛС – значение МК-игры, согласно [5, 16], и их аналоги R_ОЛС и Z_ОЛС при использовании ОЛС вместо ЛС обоими игроками. Предположим, как в [9], что относительно смешанных стратегий противника игроки используют осреднение не каждого из своих критериев, а их свертки.

Обозначим через λ:= λ₁ вес первого критерия игрока С в ЛС. При фиксированном выборе у игроком П скаляризация ЛС с параметром λ у игрока С задается функцией

Ее среднее значение по у равно

где q – вероятность у = 2 в смешанной стратегии игрока П. Максимум по p реализуется следующей стратегией игрока С:

Аналогично минимум средней ЛС $\bar {L}(\alpha ,p,\,\,q)$ с параметром α для игрока П реализуется стратегией

Ситуация (1 – α, 2 – 3λ) является равновесной для скалярной игры, в которой С выбрал ЛС с параметром λ при λ ∈ [1/3, 2/3] (поскольку q⁰ $ \in $ [0, 1]), а П выбрал ЛС с параметром α. Так что при выборе всех возможных пар весовых коэффициентов получим все возможные пары (p, q), т.е. весь набор смешанных стратегий в качестве решения МК-игры, согласно [5] (в ЛС). Та же картина наблюдалась и до дискретизации множества Х (см. [9, рис. 7 а]).

Вычислим теперь равновесия в ОЛС при условии, что по смешанным стратегиям противника игрок осредняет уже не каждую компоненту вектора критериев, а их ОЛС. (Иначе по определению [16] и свойствам ОЛС пришли бы к тому же множеству (p, q), что и для ЛС.) Отметим, что после осреднения по своей стратегии каждым из игроков их частные критерии перестают быть противоположными. Поэтому даже при равенстве коэффициентов свертки у игроков средние значения их ОЛС могут не привести к игре с нулевой суммой (в отличие от ЛС, где осреднение свертки равносильно осреднению компонент).

Для игрока С, применяющего смешанные стратегии и ОЛС с параметром μ := μ₁, среднее значение ОЛС при выборе q игроком П равно

Для игрока П, использующего у = 2 с вероятностью q и ОЛС с параметром ν, значение ОЛС и ее среднее дают формулы

и (в случае μ, ν равно 0 или 1 соответствующие слагаемые опускаем). При заданном значении p и ν минимум по q последнего выражения реализуется на

Оптимальная стратегия игрока С при q = 1 равна

Для q = 0 оптимум достигается на что меньше предыдущего при μ > 1/2. При этом всегда p¹ ≤ p² (равенство будет только для μ = 0 или 1).

С учетом (4.2) получаем, что при μ > 1/2 и p¹ < ν (т.е. 2ν/(1 + ν) > μ и потому ν > 1/3) пары (p¹, 1) являются равновесными для игры С и П в ОЛС. Симметричные равновесия образуются парами (p², 0), когда μ < 1/2 и p² > ν (т.е. μ > ν/(2 – ν) и необходимо ν < 2/3). Для соответствующих μ и ν компонента p¹ в своей паре пробегает все значения из отрезка [1/3, 1], а p² – из [0, 2/3]. Сложнее случаи: при μ > 1/2, если 2ν/(1 + ν) < μ (т.е. p¹ > ν), а при μ < 1/2, если ν/(2 – ν) > μ (т.е. p² < ν). С такими μ и ν игроку С уже может оказаться выгодней вполне смешанная стратегия игрока П, которая способна быть равновесной лишь для последнего варианта в (4.2).

На базе соотношений между минимумами в (4.1) приведем явный вид для значений функции выигрыша игрока С:

Эта функция непрерывна по p, найдем ее максимум:

и реализацию максимума

В итоге, на основании (4.2) для фиксированной пары параметров $(\mu ,\nu )$ равновесными будут все следующие пары стратегий:

Перебрав все значения параметров $(\mu ,\nu )$, получим в пространстве стратегий квадрат [0,1] × [0,1] из равновесий. Отсюда выводим, что множество равновесных смешанных стратегий R_ОЛС совпадает с R_ЛС и тоже оказывается неизбирательным. Заметим, что при μ = 1/2, ν = 1/2 вполне смешанная стратегия q = 1/2 игрока П не выгодна для С, так как выбором p ≠ ν игрок С обеспечит q = 0 или 1 и выигрыш 2/3, в отличие от значения 1/2 для (4.1), которое дает ему выбор p = 1/2. Однако точка (1/2, 1/2) входит в R_ОЛС, а значит, ни одному игроку по отдельности не выгодно от нее отклониться.

В результате показали, что при переборе всех пар весовых коэффициентов ОЛС у первого и второго ЛПР получаются всевозможные пары (p, q) в качестве решения МК-игры в ОЛС, в отличие от того, что было до дискретизации Х (см. [9, рис. 7 б]). Таким образом, для простейшего варианта конечной игры С и П свертки ЛС и ОЛС повели себя одинаково при определении решения игры. Рассмотренный пример демонстрирует существенное отличие конечных и бесконечных МК-игр.

На основе указанных равновесий найдем множества в критериальном пространстве, соответствующие Z_ЛС и Z_ОЛС для данного примера. Распространим на него определения из [1, 7, 9], которые для ЛС и ОЛС (см. F(Х_S) и (0.2)) различаются:

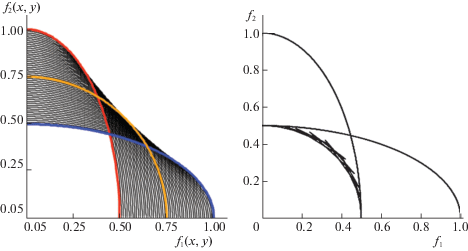
На рис. 2 построены оба варианта значения МК-игры. Так что, несмотря на совпадение равновесий, получаем несовпадение оценок выигрыша в МК-игре при использовании ЛС и ОЛС и приходим к разным значениям игры – множествам на рис. 2 слева и справа (на рис. 2 слева приведена аппроксимация Z_ЛС – точки искомого множества заполняют фигуру целиком; на рис. 2 справа аппроксимация Z_ОЛС для наглядности показана более жирными точками – ромбиками, определившими толщину линии). При этом ни Z_ЛС не содержит Z_ОЛС, ни наоборот. Вместе с тем нетрудно заметить, что Z_ОЛС $ \subseteq $ EPH(Z_ЛС), как и для множеств А и В (стохастических вариантов МК-максимума) из разд. 2.

Ситуация несовпадения значений при использовании разных сверток имеется и для случая МК-игры в чистых стратегиях да и просто для оценки МК-выигрыша игрока С при y = 1 (см. в разд. 1). Интересно сравнить рисунки для множеств, представляющих значение (Z_ЛС или Z_ОЛС) конечной игры на рис. 2 и значение (S_ЛС или S_ОЛС) игры с Х = [0, 1] (см. на рис. 3) по построению из [9]. Хотя рис. 2 и 3 расходятся, причем в части ОЛС сильней, но главное различие, похоже, определяется дискретизацией Х. Действительно, для Х = [0, 1] видна возможность приближения к рис. 2 путем спрямления образующих множества S_ЛС и S_ОЛС кривых с рис. 3 (рис. 5 и 6 из [9]), которое соответствует уже упоминавшимся в начале данного раздела отрезкам линейной аппроксимации множеств F(Х_S(1), 1) и F(Х_S(2), 2), показанных на правом графике рис. 1 тонкими линиями. Для T > 1 получается промежуточная картина, но далее на ней останавливаться не будем.

Таким образом, можно заменить основанную на ЛС аксиому WEIGHT из [4] на аналогичную при использовании ОЛС вместо ЛС и применить концепцию решения на базе ОЛС, тогда получим для данного примера то же множество равновесий, что и по [5, 16]. Однако МК-оценки выигрышей игроков на базе разных сверток отличаются. Это различие связано не столько со спецификой формулы (0.2) (появлением лишних точек Слейтера), сколько с иной, чем в [4, 5], трактовкой МК-осреднения при учете смешанных стратегий партнера, которая для ЛС не дает отличий от стандартной, а при использовании ОЛС уже проявляется (см. в разд. 1). Но подчеркнем, что предложенная в настоящей статье трактовка соответствует подходу стохастической оптимизации в приложении к МК-задачам и применение методов стохастического программирования для численного решения стохастических МК-задач будет приводить именно к таким значениям. Для стандартной трактовки, когда осредняются все частные критерии, а не их свертка, для рассматриваемого примера результаты с ЛС и с ОЛС будут совпадать. В частности, в качестве значения конечной МК-игры будет построено множество с рис. 2 слева, а при Х = [0, 1] – множество, изображенное слева на рис. 3. Тем не менее, ниже останемся в рамках трактовки осреднения, изначально принятой в работе.

На рис. 3 также видно, что S_ОЛС $ \subseteq $ EPH(S_ЛС). Исследуем выполнение включения в общей МК-игре по аналогии с доказательством утверждения из [8] на базе неравенства ${\text{E}}G(\{ {{f}_{i}}\} ,{\mathbf{\mu }}) \leqslant G(\{ {\text{E}}{{f}_{i}}\} ,{\mathbf{\mu }})$ из разд. 0. Обозначим

МК-игру двух лиц с нулевой суммой. Пусть, когда X, Y конечны, первый и второй игроки применяют смешанные стратегии p и q соответственно (для упрощения обозначений жирным шрифтом здесь и далее выделены векторы p(·) и q(·) с компонентами – вероятностями чистых стратегий). Предполагаем, что оба игрока ориентируются в таком случае на осредненные частные критерии Еf_i по своим смешанным стратегиям, а по смешанным стратегиям партнера каждый игрок осредняет используемую им свертку своих частных критериев. При бесконечности X и (или) Y далее будем считать их выпуклыми компактами и все частные критерии вогнутыми по x и выпуклыми по y.

Обозначим для игры Г через R_ЛС и R_ОЛС множества из всех равновесий по Нэшу в скалярных играх двух лиц с функциями выигрышей – свертками ЛС и ОЛС (или их средними по компонентам смешанной стратегии партнера) частных критериев (или их средних по своим стратегиям) с различными весами. Обозначим через Z_ЛС множество значений z с z_i = Ef_i для седловых пар (p, q) из R_ЛС, а через Z_ОЛС – множество векторов ${\mathbf{\mu }}{\text{E}}G(\{ {{f}_{i}}\} ,{\mathbf{\mu }})$ для пар (p(μ), q(μ)) из R_ОЛС, где μ – вектор коэффициентов свертки (из симплекса в m-мерном пространстве), а (p(μ), q(μ)) – равновесия в тех скалярных играх с ОЛС, в которых у первого игрока свертка с весовыми коэффициентами μ (при любых параметрах свертки у второго). В сделанных предположениях (с учетом перехода на смешанные стратегии p и q в конечной игре Г) равновесия для всех построенных указанным образом из Г скалярных игр существуют в силу вогнутости по x (и p) и выпуклости по y (и q) функции-свертки (ее математического ожидания).

У т в е р ж д е н и е 1. Для введенной МК-игры Г из условия R_ОЛС $ \subseteq $ R_ЛС следует Z_ОЛС $ \subseteq $ $ \subseteq $ EPH(Z_ЛС).

Д о к а з а т е л ь с т в о. Пусть R_ОЛС $ \subseteq $ R_ЛС, выберем (p, q) из R_ОЛС. В случае если X и (или) Y бесконечные, под соответствующими p и (или) q будем подразумевать чистые стратегии. Рассмотрим для (p, q) вектор w из Z_ОЛС, его компоненты

где Y = {y ^j}. Для таких k, что ${{\mu }_{k}} > 0$, выполнено

Поскольку по условию пара (p, q) еще и принадлежит R_ЛС, а математическое ожидание ЛС совпадает с ЛС математических ожиданий частных критериев, то вектор, состоящий из ${\text{E}}{{f}_{k}}(p,q)$, включен в Z_ЛС. И так как все компоненты w_k не превосходят ${\text{E}}{{f}_{k}}(p,q)$, k = 1, …, m, то w ∈ EPH(Z_ЛС). В силу произвольности (p, q) получили, что Z_ОЛС $ \subseteq $ EPH(Z_ЛС) в условиях утверждения 1 (в частности, для примеров из [8–10]).

У т в е р ж д е н и е 2. Для введенной МК-игры Г на бесконечных X и Y имеем R_ОЛС = R_ЛС и Z_ОЛС $ \subseteq $ EPH(Z_ЛС).

Д о к а з а т е л ь с т в о. В случае когда X и Y бесконечные, в силу рассмотрения для R_ЛС оптимума по Слейтеру (см. в разд. 0) представление решения МК-игры по [16] с помощью R_ЛС справедливо, согласно [5]. Это значит, что для всех пар (x, y) из R_ЛС выполнено $x \in {{X}_{S}}$ для F(x, y) при фиксированном y и наоборот. Указанное условие можно из [1, 7] записать и с помощью ОЛС. В обратную сторону: для (x, y) из R_ОЛС выполнено по свойствам ОЛС, что $x \in {{X}_{S}}$ для F(x, y) при данном y, и в силу выпуклости задачи из [2] вытекает, что x максимизирует при этом y еще и ЛС, а выбор y тоже минимизирует ЛС с данным x, т.е. (x, y) окажется из R_ЛС. Таким образом R_ОЛС = R_ЛС для игр без осреднения (на бесконечных X и Y). Далее применяем утверждение 1.

Из утверждения 2, перейдя к конечной МК-игре в смешанных стратегиях, когда частные критерии заменены их средними по (p, q), получим то же равенство R_ЛС = R_ОЛС и то же свойство Z_ОЛС $ \subseteq $ EPH(Z_ЛС). Отметим, что для этой постановки аксиомы, предложенные в [4] для понятия решения МК-игры, кроме WEIGHT, выполняются и для R_ОЛС. А так как, согласно [4], R_ЛС – максимальное (по включению) множество, являющееся решением (в смысле аксиоматики [4]) конечной МК-игры в смешанных стратегиях, то для подобной МК-игры из результатов [4] получаем R_ОЛС$ \subseteq $ R_ЛС. Утверждение 2 усиливает этот результат для стандартной постановки – с осреднением частных критериев, а не их свертки.

Для исследуемой постановки (с осреднением свертки, а не каждого критерия) пока не удается доказать аналогичное включение для значений игры Г без предположения о включении R_ОЛС$ \subseteq $ R_ЛС. Обоснуем более слабый общий результат. Рассмотрим сначала случай конечного Y и перехода к смешанным стратегиям второго игрока, т.е. к парам (x, q).

У т в е р ж д е н и е 3. Во введенной МК-игре Г с бесконечным X для любой точки w из Z_ОЛС найдется точка из Z_ЛС, которую w не доминирует (по Слейтеру).

Д о к а з а т е л ь с т в о. Выберем (x, q) из R_ОЛС. Тогда q реализует при выбранном x минимум ОЛС из Ef_i с некоторым вектором весовых коэффициентов ν и (из [1, 2]) минимум ЛС из Ef_i (с другими весами, пусть λ). В свою очередь x максимизирует для данного q математическое ожидание ОЛС (при векторе весовых коэффициентов μ) на X. Рассмотрим для (x, q) вектор w из Z_ОЛС, его компоненты

где Y = {y^j}. Для таких k, что ${{\mu }_{k}} > 0$, запишем, как и выше при доказательстве утверждения 1,

При этом для $(x*,q*)$ – седловой точки игры в ЛС с вектором весов λ у обоих игроков имеем, что поскольку стратегия q реализовала минимум ЛС в точке x, то

Следовательно, вектор с компонентами ${\text{E}}{{f}_{k}}(x,q)$ не может доминировать вектор z из Z_ЛС с компонентами ${\text{E}}{{f}_{k}}(x*,q{\text{*}})$. А так как все компоненты ${{w}_{k}}$ не превосходят ${\text{E}}{{f}_{k}}(x,q)$, то и w не может доминировать вектор z из Z_ЛС. В силу произвольности (x, q) получили утверждение 3 для рассматриваемого случая (которому соответствует пример из [9]).

Попытаемся аналогично проанализировать случай конечного X и бесконечного Y. Возьмем произвольную пару (p, y) из R_ОЛС (при некоторых весовых коэффициентах μ у первого ЛПР) и соответствующий вектор w из Z_ОЛС :

где X = {x ^j}, k = 1, …, m. Для таких k, что μ_k > 0, выполнено

С другой стороны, поскольку p реализует максимум ОЛС средних, т.е. ${\text{E}}{{f}_{i}}(p,y)$, для данного y (с весами μ), то для некоторого вектора весовых коэффициентов λ, согласно [7], стратегия p максимизирует и ЛС при том же y. Так что для $(p{\text{*}},\,y*)$ – седловой точки игры в ЛС с вектором весов λ у обоих игроков справедливо

Поэтому сравнить w с полученным $z = ({\text{E}}{{f}_{1}}(p*,y*),\;...,\;{\text{E}}{{f}_{m}}(p*,y*))$ не удается. Вопрос об обобщении утверждения 3 на случай конечного X остался открытым.

Основным недостатком рассмотренного подхода с осреднением свертки частных критериев в МК-играх является для ОЛС потеря симметрии результатов игроков, интересы которых исходно были противоположными. Действительно, если вернуться к модельному примеру игры двух лиц с рис. 2 [10], то при использовании игроками ЛС получим для ЛПР П, что значение $Z_{{{\text{Л С }}}}^{'}$ МК-игры для него совпадает с Z_ЛС (значением игры для ЛПР С). В случае ОЛС значение МК-игры для П определяется как

Заметим, что когда $\nu $ стремится к 0 или 1, среднее значение ОЛС игрока П стремится к бесконечности (в отличие от значения игры для ЛПР С). Причем если для первого варианта равновесия в (4.3) значение $\overline {{{M}_{{\text{П }}}}} (p,q,\nu )$ от ν не зависит и остается конечным (=3/2), то для второго варианта оно растет с приближением ν к 0, а для третьего – к 1. В итоге, в качестве аппроксимации для $Z_{{{\text{О Л С }}}}^{'}$ (с использованием ε-сети на $\nu \in [0,1]$) будем иметь вместо Z_ОЛС, изображенного справа на рис. 2, множество, изображенное справа на рис. 4 (фрагмент которого показан на рис. 4 слева). Чем мельче сеть, тем дальше уходят полосы на осях на рис. 4, их толщина для ${{w}_{k}} \geqslant 1$ одинакова (= 1/2), и они будут полностью закрашены. Линия на рис. 4 слева при ${{w}_{k}} < 0.5$, напротив, не имеет толщины, а просто на рисунке показана жирными точками-ромбиками.

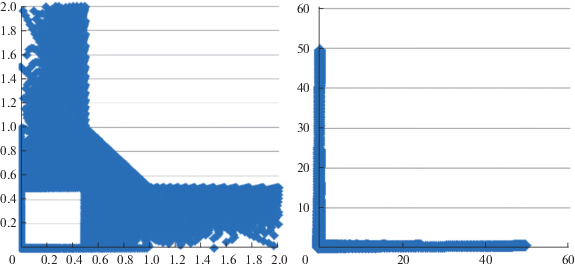
Сравнивая левые графики на рис. 2 и 4, видим, что для $Z_{{{\text{Л С }}}}^{'}$ и $Z_{{{\text{О Л С }}}}^{'}$ не верны соотношения утверждения 1, несмотря на совпадение R_ЛС и R_ОЛС. Для минимизирующего вектор-функцию выигрышей ЛПР П аналогичное утверждение требует небольшого уточнения. Обозначим через EPH_> оболочку Эджворта–Парето в задаче на минимум:

У т в е р ж д е н и е 4. Для введенной выше МК-игры Г из условия R_ОЛС $ \subseteq $ R_ЛС следует, что для минимизирующего векторный критерий игрока все точки w с ${{w}_{k}} \ne 0\,{\text{и з }}\,Z_{{{\text{О Л С }}}}^{'}\,{\text{п р и н а д л е ж а т }}\,{\text{EP}}{{{\text{H}}}_{ \geqslant }}(Z_{{{\text{Л С }}}}^{'}).$

Д о к а з а т е л ь с т в о. Пусть R_ОЛС $ \subseteq $ R_ЛС, выберем (p, q) из R_ОЛС. В случае если X и (или) Y бесконечные, под соответствующими p и (или) q будем подразумевать чистые стратегии. Рассмотрим для (p, q) вектор w из $Z_{{{\text{О Л С }}}}^{'}$, его компоненты

где X = {x ^j}. Для таких k, что ${{\nu }_{k}} > 0$, выполнено

По условию (p, q) принадлежит и R_ЛС, а так как математическое ожидание ЛС совпадает с ЛС математических ожиданий частных критериев, то вектор, состоящий из ${\text{E}}{{f}_{k}}(p,q)$, включен в $Z_{{{\text{Л С }}}}^{'}$ = Z_ЛС. И поскольку, как показано выше, все ненулевые компоненты w_k не меньше, чем ${\text{E}}{{f}_{k}}(p,q)$, k = 1, …, m, получаем, что при w > 0 выполнено $w \in $ EPH_>(Z_ЛС). В силу произвольности (p, q) доказали утверждение 4.

Теперь, с учетом поправки на участки на осях координат можно говорить о том, что утверждение 1 обобщается и для минимизирующего игрока: $Z_{{{\text{О Л С }}}}^{'}$ ∩ $\{ w > 0\} \subseteq {\text{EP}}{{{\text{H}}}_{ \geqslant }}({{Z}_{{{\text{Л С }}}}})$ при R_ОЛС $ \subseteq $ R_ЛС. Такое включение уже справедливо для левых графиков на рис. 2 и 4.

Заключение. Использование смешанных стратегий в МК-оптимизации не дает однозначности при совмещении со скаляризацией, поскольку не всегда математическое ожидание свертки частных критериев совпадает со сверткой их средних значений, например в случае логической свертки или свертки Гермейера. При этом переход к средним критериям не обусловлен содержательно и не факт, что конструктивен (например, для стохастических постановок – см. разд. 2). При рассмотрении МК-игр двух лиц с нулевой суммой (разд. 4) возникает практически интересная ситуация, когда по своей смешанной стратегии игрок осредняет значения частных критериев, а по смешанным стратегиям противника применяет осреднение свертки критериев. Тогда для ОЛС не получается доказать аксиому согласованности (CONS) из [4], продолжающую принцип оптимальности, принимаемый для себя каждым игроком по отдельности, на большее их число в игре, и тем самым обосновать включение R_ОЛС $ \subseteq $ R_ЛС. И как только речь идет об осреднении свертки, надо иметь в виду, что разные свертки могут дать различные результаты в качестве решения.

В настоящее время понятие об осреднении свертки встречается в литературе лишь в работах авторов статьи. В последних зарубежных публикациях (см., например, в [17], как и в классических [4–6]) по смешанным стратегиям сразу берется математическое ожидание частных критериев (отчего теряется специфика МК-задачи со случайным фактором), а также по большей части вслед за [5] применяется линейная скаляризация. Исследование предлагаемой статьи призвано привлечь внимание к односторонности подобного подхода. Для дальнейшего представляет интерес рассмотрение не только умозрительного примера игры из разд. 1, 4, но и ряда экономических моделей, в частности, из [18–20], для которых имеет смысл проанализировать, чем отличается решение и значение игры, если игроки-ЛПР ориентируются на скаляризацию функции выигрышей с помощью свертки Гермейера.