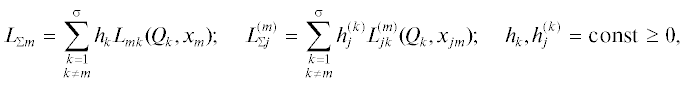Известия РАН. Теория и системы управления, 2019, № 4, стр. 47-61

Введение. Разработка конструктивных методов решения задач оптимального управления (ЗОУ) по переводу бесконечномерных объектов в заданное целевое множество с минимальным значением выбранного функционала качества до настоящего времени остается одной из основных проблем в теории оптимального управления системами с распределенными параметрами (СРП) [1–4].

В классической двухточечной формулировке ЗОУ типичные требования к конечному пространственно-распределенному состоянию СРП, как правило, либо невыполнимы вследствие неуправляемости объекта относительно этих состояний из-за несогласованности с граничными условиями модели СРП, либо обеспечиваются в классе технически нереализуемых управляющих воздействий [1, 2, 4, 5].

В подобной ситуации конструктивный подход к ЗОУ СРП состоит в переходе к заведомо разрешимой с реализуемыми результатами задаче управления при заданном в бесконечномерном фазовом пространстве СРП целевом множестве, которое отвечает достижимым значениям практически всегда существующих в прикладных задачах допусков на отклонение от требуемого конечного состояния объекта, оцениваемых применительно к представляющим наибольший интерес ситуациям в равномерной метрике на множестве пространственных переменных управляемой величины [4].

В работах [4, 6–10] предложен конструктивный алгоритмически точный (“альтернансный”) метод решения подобных бесконечномерных краевых задач, свободный от недостатков приближенных методов, ориентированных на дискретные аппроксимации моделей СРП.

Метод базируется на специальной процедуре последовательной конечномерной параметризации управляющих воздействий, существенном использовании дополнительной информации о базовых закономерностях предметной области и точной (в рамках рассматриваемых моделей) редукции исходной задачи к задаче полубесконечной оптимизации (ЗПО), которая решается на основе альтернансных свойств искомых экстремалей, распространяющих на ЗПО известные результаты теории нелинейных чебышёвских приближений [11].

В указанных публикациях альтернансный метод разработан и апробирован применительно к ЗОУ СРП с одной пространственно распределенной управляемой величиной и воздействием на объект только по одному из возможных каналов управления, т.е. с одним внутренним или граничным управляющим воздействием. В то же время целый ряд представляющих теоретический интерес и актуальных для приложений ЗОУ СРП формулируется в условиях одновременного воздействия на объект по различным каналам управления с целью существенного повышения эффективности оптимизируемых процессов по базовым технико-экономическим показателям (задачи многоканального управления). Сказанное относится, в частности, к ситуациям с использованием векторных управляющих воздействий, например, в виде совокупности различных сосредоточенных внутренних или граничных управлений с фиксированным характером их пространственного распределения [5, 12, 13].

Самостоятельный класс ЗОУ подобного типа возникает для взаимосвязанных СРП с различными управляющими воздействиями для каждого из объектов [14–18].

В настоящей работе альтернансный метод параметрической оптимизации распространяется на указанные задачи многоканального управления СРП. Предлагаются конструктивные алгоритмы реализации существенно усложняемых в таких задачах вычислительных процедур альтернансного метода применительно к возникающей проблеме поиска оптимальных значений параметров искомых управляющих воздействий с учетом специфического ограничения на одинаковую длительность процесса управления для каждого из них. Приводится представляющий самостоятельный интерес пример решения ЗОУ нестационарным процессом теплопроводности с двухканальным граничным управлением.

1. Постановка задачи. Пусть управляемые величины ${{Q}_{m}}({{x}_{m}},t),\,\,m = \overline {1,\sigma } $, системы $\sigma > 1$ взаимосвязанных объектов с распределенными параметрами описываются в зависимости от времени $t \in [0,t*]$ и пространственных координат ${{x}_{m}} \in [{{x}_{{0m}}},{{x}_{{1m}}}]$ системой σ линейных неоднородных пространственно одномерных уравнений в частных производных параболического типа с постоянными во времени (стационарными) коэффициентами [18, 19]:

с начальными и граничными условиями: векторными внутренними ${{\upsilon }_{m}}(t) = ({{\upsilon }_{{mi}}}(t)),\,\,i = \overline {1,{{s}_{m}}} $, или граничными ${{g}_{m}}(t) = ({{g}_{{0m}}}(t),{{g}_{{1m}}}(t))$ сосредоточенными управляющими воздействиями при $m = \overline {1,\sigma } $ и заданном характере пространственного распределения ${{F}_{{mi}}}({{x}_{m}})$ внутренних управлений, где для простоты исключается случай совместного использования ${{\upsilon }_{m}}$ и ${{g}_{m}}$.

Здесь ${{\alpha }_{{jm}}} = {\text{const}} \geqslant {\text{0;}}\,\,{{\beta }_{{jm}}} = {\text{const}} > {\text{0}}$; дифференциальные операторы в правых частях (1.1) самосопряженные; ${{F}_{{mi}}}({{x}_{m}}),\,{{f}_{m}}({{x}_{m}})$, ${{a}_{m}}({{x}_{m}}),\,{{b}_{m}}({{x}_{m}}),\,\,{{c}_{m}}({{x}_{m}})$ являются известными достаточно гладкими функциями своих аргументов, причем ${{a}_{m}}({{x}_{m}}) > 0,\,\,m = \overline {1,\sigma } $, и

где операторы ${{L}_{{mk}}},L_{{jk}}^{{(m)}}$ учитывают зависимости Q_m от остальных управляемых величин в форме реакций “сопрягающих” (переходных [14]) распределенных блоков на входные воздействия по ${{Q}_{1}},{{Q}_{2}},\;...,\;{{Q}_{\sigma }},$ взвешенные суммы которых с коэффициентами $h_{k}^{{}},h_{j}^{{(k)}}$ выступают в роли аддитивных дополнений к внутренним или граничным управлениям соответственно в (1.1) и (1.3) [14–16] (рис. 1):

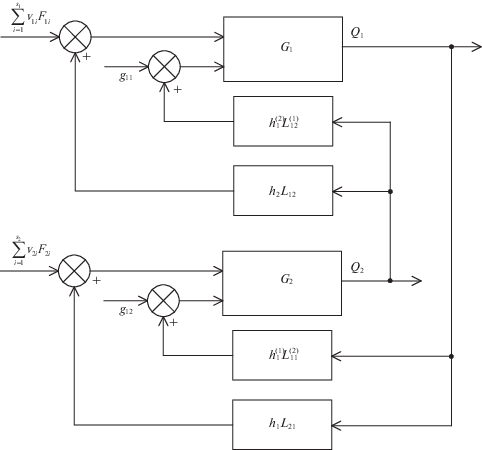
Здесь ${{G}_{{mk}}},G_{{jk}}^{{(m)}}$ – функции Грина каждого из таких блоков с входным воздействием Q_k.

В задачах управления одним объектом при $\sigma = 1$ в (1.1) будем иметь ${{L}_{{\Sigma m}}} = L_{{\Sigma j}}^{{(m)}} = 0$ в (1.4).

Допустимые значения управляющих воздействий в (1.1), (1.3) должны удовлетворять ограничениям

с заданными предельно допустимыми величинами их возможных значений.

За нефиксируемое заранее время t* требуется обеспечить приближение ${{Q}_{m}}({{x}_{m}},t*)$ к заданным пространственным распределениям $Q_{m}^{0}(x)$ для всех $m = \overline {1,\sigma } $ с оцениваемой в равномерной метрике допустимой точностью ${{\varepsilon }_{m}}$, согласно соотношениям

Пусть качество процесса управления объектом (1.1)–(1.7) характеризуется интегральным функционалом

где ${{P}_{{0m}}},{{P}_{{1m}}},{{P}_{{2m}}}$ – заданные достаточно гладкие функции своих аргументов и ${{x}_{{mc}}} \in [{{x}_{{0m}}},{{x}_{{1m}}}]$ – заданные фиксированные значения пространственных координат.

Рассмотрим следующую задачу оптимального управления. Необходимо определить стесненные ограничениями (1.7) векторные программные управляющие воздействия $W{\text{*}}(t)$:

где в частных случаях $W{\text{*}}(t) = (\upsilon _{m}^{*}(t))$ или $W{\text{*}}(t) = (g_{m}^{*}(t)),m = \overline {1,\sigma } ,$ которые переводят объект управления (1.1)–(1.7) из заданного начального состояния (1.2) в требуемое конечное согласно (1.8) при минимальном значении критерия оптимальности (1.9).

Переход к модальному описанию объекта управления. Применение к каждому из уравнений (1.1) для всех $m = \overline {1,\sigma } $ конечного интегрального преобразования по пространственному аргументу x_m с ядром, равным его собственным функциям ${{\Phi }_{{mn}}}({{M}_{{mn}}},{{x}_{m}}),\,\,n = 1,2,...,$ где $M_{{mn}}^{2}$ – собственные числа, приводит к описанию рассматриваемой СРП бесконечной системой обыкновенных дифференциальных уравнений первого порядка для временных мод ${{\bar {Q}}_{{mn}}}(t)$ разложения ${{Q}_{m}}({{x}_{m}},t)$ в бесконечный сходящийся в среднем ряд по ортонормированной с весом системе ${{\Phi }_{{mn}}}({{M}_{{mn}}},{{x}_{m}})$ [2, 18, 20]:

Здесь граничные условия (1.3) учитываются в правых частях уравнений (1.12) по известным правилам метода конечных интегральных преобразований уравнений (1.1)–(1.3) [20]; $Q_{\Sigma }^{{(m)}} = ({{Q}_{1}},...,{{Q}_{{m - 1}}},{{Q}_{{m + 1}}}$, ..., Q_σ); r_m(x_jm) – весовые функции конечных интегральных преобразований; $\bar {F}_{{mi}}^{{}}({{M}_{{mn}}}),{{\bar {f}}_{{mn}}}({{M}_{{mn}}}),$ ${{\bar {L}}_{{\Sigma mn}}}({{M}_{{mn}}},Q_{\Sigma }^{{(m)}},t)$ – моды разложения в ряды по ${{\Phi }_{{mn}}}({{M}_{{mn}}},{{x}_{m}})$ вида (1.11) функций ${{F}_{{mi}}}({{x}_{m}})$ в (1.1), ${{f}_{m}}({{x}_{m}})$ в (1.2) и операторов ${{L}_{{\Sigma m}}}$ в (1.1).

При моделировании СРП бесконечной системой уравнений (1.12) требования (1.8) к конечному состоянию объекта записываются в силу разложения (1.11) в следующей форме:

После подстановки (1.11) в (1.9) критерий оптимальности (1.9) представляется в виде

с соответствующей подынтегральной функцией f₀ переменных $\bar {Q} = ({{\bar {Q}}_{{mn}}});\;{\kern 1pt} m = \overline {1,\sigma } $; n = 1, 2, ... $W = ({{\upsilon }_{m}}(t),{{g}_{m}}(t)\;{\text{:}}\,{\kern 1pt} m = \overline {1,\sigma } )$.

Применительно к представлению СРП счетномерной системой уравнений (1.12) исходная задача сводится к отысканию оптимального управления $W{\text{*}}(t)$ и значения t*, обеспечивающих выполнение требований (1.13) при минимальном значении функционала качества (1.14) в условиях ограничений (1.7).

2. Параметризация управляющих воздействий и редукция к задаче полубесконечной оптимизации. На бесконечномерную задачу оптимального управления (1.7), (1.11)–(1.14) распространяется принцип максимума Понтрягина [21].

Базовые условия достижения максимума функции Понтрягина на оптимальном управлении $W{\text{*}}(t)$ в совокупности с дополнительной информацией о свойствах и закономерностях оптимизируемых процессов в конкретной предметной области в целом ряде модельных ситуаций вполне определяют характер программных оптимальных управляющих воздействий на участках их непрерывного изменения в форме явных зависимостей от управляемой величины и сопряженных переменных.

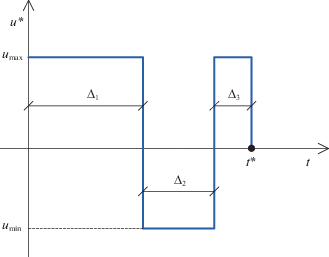
Возможные варианты компоновки оптимальных программ из этих участков реализуются с конечным числом разрывов в точках их “сшивания”, выступающих в роли параметрического описания $W{\text{*}}(t)$. Типичным примером является классическая задача оптимального быстродействия, в которой принцип максимума определяет кусочно-постоянную форму искомого сосредоточенного управления $u{\text{*}}(t)$, попеременно принимающего только свои заведомо фиксируемые предельно допустимые значения ${{u}_{{\max }}}$ и ${{u}_{{\min }}}$ с точностью до числа N и длительностей ${{\Delta }_{i}},\,i = \overline {1,N} $, интервалов его постоянства [1, 2, 4, 8] (рис. 2).

При этом, в общем случае, заранее неизвестно, какое конкретно значение ${{u}_{{\max }}}$ или ${{u}_{{\min }}}$ принимает $u{\text{*}}(t)$ на первом интервале. В такой ситуации необходимо либо найти независимо друг от друга решения двух задач оптимального управления с соответствующей параметризацией $W{\text{*}}(t)$ для обоих возможных вариантов с последующим выбором того из них, на котором достигается меньшая величина критерия оптимальности (в данном случае длительности процесса управления), в качестве искомого решения, либо заранее произвести отбор единственного варианта, если это оказывается возможным исходя из закономерностей предметной области конкретной рассматриваемой задачи. Пример, приведенный на рис. 2, соответствует случаю, в котором описанным способом устанавливается, что $u{\text{*}}(t) = {{u}_{{\max }}}\forall t \in (0,{{\Delta }_{1}})$.

Подобным путем, аналогично задачам с одним управляющим воздействием [4, 6–10, 22–25], может быть получено параметрическое представление l-й компоненты каждого из искомых управлений в (1.10), где $l = \overline {1,{{l}_{m}}} $ и ${{l}_{m}}$ – заданное число составляющих $\upsilon _{m}^{*}(t)\,$ или $g_{m}^{*}(t),$ с точностью до вектора $\Delta _{l}^{{(m)}} = (\Delta _{{lq}}^{{(m)}})$ определенным образом упорядоченной последовательности конечного числа $N_{{lm}}^{{}}$ параметров $\Delta _{{lq}}^{{(m)}},\,\,q = \overline {1,{{N}_{{lm}}}} $, однозначным образом характеризующих управляющие воздействия оптимальной структуры.

Всюду далее будем считать для простоты без потери общности основных результатов, что используется только одно из возможных векторных управляющих воздействий, полагая в (1.10) при σ = 1

или

и для $\sigma > 1$где в (2.2) выбирается только одно из двух значений $j = 0$ или $j = 1$ для каждого $m = \overline {1,\sigma } $.

Интегрирование уравнений (1.1)–(1.3) с параметризованным управлением $W{\text{*}}(\Delta _{l}^{{(m)}}$ : l = = $\overline {1,{{l}_{m}}} ;m = \overline {1,\sigma } $; t) позволяет определить конечное состояние объекта ${{Q}_{m}}({{x}_{m}},t*)$ в (1.8) и значение критерия оптимальности в (1.9) в форме явных непрерывно дифференцируемых зависимостей соответственно ${{Q}_{m}}({{x}_{m}},\Delta _{{}}^{\Sigma })$ и $I{\text{(}}\Delta _{{}}^{\Sigma }),$ $\Delta _{{}}^{\Sigma } = (\Delta _{l}^{{(m)}}),$ $m = \overline {1,\sigma } ;\;{\kern 1pt} l = \overline {1,{{l}_{m}}} $, от своих аргументов [4, 8].

В результате осуществляется точная редукция исходной задачи оптимального управления (1.1)–(1.9) к задаче полубесконечной оптимизации [4, 6–10]

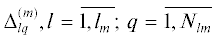на экстремум функции (2.3) конечного числа переменных , с бесконечным числом ограничений для каждого $m \in \{ \overline {1,\sigma } \} $ в (2.4), диктуемых требованиями (1.8) для всех ${{x}_{m}} \in [{{x}_{{0m}}},{{x}_{{1m}}}]$.

3. Алгоритмы оптимального по быстродействию двухканального управлеиия. Ограничимся далее для большей определенности и наглядности рассмотрением центральной задачи оптимального быстродействия [1, 4, 8, 22–25] для характерного случая двухканального управления одним или двумя объектами вида (1.1)–(1.3) при $\sigma = 1,\,\,{{l}_{m}} = 2$, в (2.1) или при $\sigma = 2,\,\,{{l}_{m}} = 1$, в (2.2), которая применительно к их модальному описанию сводится к виду (1.7), (1.12)–(1.14) с критерием оптимальности

Стандартная процедура принципа максимума для линейных уравнений объекта (1.12), как правило, приводит подобно [1, 4, 8, 22–25] к кусочно-постоянной (релейной) структуре всех компонент искомых управляющих воздействий, попеременно принимающих только свои предельно допустимые значения, согласно (1.7), в возможных условиях неопределенности выбора одного из них на первом интервале постоянства. Сказанное приводит, в общем случае, к необходимости решить четыре отдельные задачи двухканального управления с различными комбинациями этих величин.

В целом ряде прикладных задач удается заведомо отобрать единственный вариант, руководствуюясь физическими закономерностями конкретных оптимизируемых процессов. Весь дальнейший анализ относится к любой из указанных комбинаций с однозначно фиксируемой структурой оптимального управления.

Каждая из искомых составляющих оптимального управления однозначно характеризуется фигурирующими в роли параметров $\Delta _{{lq}}^{{(m)}}$ и подлежащими определению значениями $t_{{lq}}^{{(m)}}$; $l,m \in \{ 1,2\} ;q = \overline {1,{{N}_{{lm}}} - 1} ;t_{{l(q + 1)}}^{{(m)}} > t_{{lq}}^{{(m)}},$ моментов ее переключения с одного предельно допустимого уровня на другой и одинаковыми априори неизвестными конечными моментами $t_{{l{{N}_{{lm}}}}}^{{(m)}}$:

совпадающими с минимизируемой, согласно (3.1), длительностью t* процесса управления.

Таким образом, рассматриваемая двухканальная задача быстродействия сводится к ЗПО вида (2.3), (2.4), где

или

Здесь ${{N}_{{11}}},{{N}_{{21}}}$ в (3.4) и ${{N}_{{11}}},{{N}_{{12}}}$ в (3.5) – числа параметров, с точностью до которых определяются обе составляющие векторного управления.

В силу ограничения (3.2), сводимого к равенству $t_{{1{{N}_{{11}}}}}^{{(1)}} = t_{{2{{N}_{{21}}}}}^{{(1)}} = t{\text{*}}$ при σ = 1 или $t_{{1{{N}_{{11}}}}}^{{(1)}} = t_{{1{{N}_{{12}}}}}^{{(2)}} = t{\text{*}}$ при σ = 2, число неизвестных компонент $\Delta _{{}}^{\Sigma }$ равно ${{N}_{{11}}} + {{N}_{{21}}} - 1$ в (3.4) или ${{N}_{{11}}} + {{N}_{{12}}} - 1$ в (3.5). При этом одно из управляющих воздействий может рассматриваться в условиях свободного варьирования всех характеризующих его параметров, включая t*, а для другого значение t* должно быть исключено из числа искомых величин, уменьшая его на единицу. Оставляя, применительно к этим вариантам, в составе $\Delta _{{}}^{\Sigma }$ только свободно варьируемые переменные, получим вместо (3.4), (3.5) при $\sigma = 1$

или при σ = 2 или

Здесь в число $\tilde {N}_{1}^{{}}$ и $\tilde {N}_{2}^{{}}$ компонент $\Delta _{1}^{{\Sigma 1}}$, $\Delta _{1}^{{\Sigma 2}}$ и $\Delta _{2}^{{\Sigma 1}}$, $\Delta _{2}^{{\Sigma 2}}$ включены все рассматриваемые в качестве не стесняемых ограничением (3.2) параметры соответственно первого и второго управляющих воздействий (для случая σ = 2 – управляющие воздействия на первый (m = 1) и второй ($m = 2$) объект).

Введем далее, в целях общности анализа вариантов (3.6)–(3.9), обозначения $\Delta _{p}^{{\Sigma \eta }} = \Delta _{{\eta p}}^{{(\tilde {N}_{1}^{{}},\tilde {N}_{2}^{{}})}}$; $\eta ,p \in $ {1, 2}. При этом, подобно задачам с одноканальным управляющим воздействием при $m = \sigma = {{s}_{m}} = j = 1$ в (1.1)–(1.3) [8, 9], минимально достижимые в классе параметризованных управлений $W(\Delta _{p}^{{\Sigma \eta }},t) = W(\Delta _{{\eta p}}^{{(\tilde {N}_{1}^{{}},\tilde {N}_{2}^{{}})}},t)$ со свободно варьируемыми параметрами значения $\varepsilon _{{\eta pm\,\,\min }}^{{({{{\tilde {N}}}_{1}},{{{\tilde {N}}}_{2}})}}$ ошибок $\varepsilon _{m}^{{}}$ равномерного приближения ${{Q}_{m}}({{x}_{m}},\Delta _{{\eta p}}^{{({{{\tilde {N}}}_{1}},{{{\tilde {N}}}_{2}})}})$ к $Q_{m}^{0}({{x}_{m}})$ в (2.4)

не возрастают (как правило, монотонно убывают) с ростом размерности $\tilde {N}_{1}^{{}} + {{\tilde {N}}_{2}} - 1$ вектора $\Delta _{{\eta p}}^{{({{{\tilde {N}}}_{1}},{{{\tilde {N}}}_{2}})}}$:

Здесь точная нижняя грань ${{\varepsilon }_{{\eta pm\,\,\,\inf }}}$ в (3.11) оказывается равной минимаксу $\varepsilon _{{\eta pm\,\,\min }}^{{({{\rho }_{{\eta pm}}},{{\rho }_{{\eta pm}}})}}$, где ${{\rho }_{{\eta pm}}} = \infty \,\,{\text{п р и }}\,\,{{\varepsilon }_{{\eta pm\,\,\,{\text{inf}}}}} = 0$ и ${{\rho }_{{\eta pm}}} < \infty \,\,{\text{п р и }}\,\,{{\varepsilon }_{{\eta pm\,\,\,{\text{inf}}}}} > 0$ соответственно для управляемых и неуправляемых относительно $Q_{m}^{0}({{x}_{m}})$ объектов [8, 9].

Аналогично задаче с одноканальным управлением [8–10] можно показать, что при этом числа $\tilde {N}_{1}^{*}$ и $\tilde {N}_{2}^{*}$, соответствующие решению $\bar {\Delta }_{{\eta p}}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}}$ ЗПО (2.3), (2.4), (3.6)–(3.9), определяются по месту в цепочке неравенств (3.11) заданных в (2.4) величин для каждого из вариантов в (3.6)–(3.9), фиксируемых конкретным выбором значений $\eta ,p \in \{ 1,2\} $:

Однозначный выбор $\tilde {N}_{1}^{*}$ и $\tilde {N}_{2}^{*}$ по правилам (3.12)–(3.14) возможен при двухканальном управлении двумя объектами $(\sigma = \eta = 2)$ только для одного из значений $\varepsilon _{m}^{{}}$ в (2.4) с m = 1 или m = 2.

В частности определение $\Delta _{{}}^{\Sigma }$ для вариантов (3.8) или (3.9) соответственно для $\varepsilon _{1}^{{}}$ или $\varepsilon _{2}^{{}}$ ($\eta = 2,p = 1,m = 1$ или $\eta = 2,p = 2,m = 2$) гарантирует возможность выполнения только первого (в условиях (3.8)) либо второго (в условиях(3.9)) ограничения в (2.4) за счет выбора в качестве свободно варьируемых всех параметров первого (p = 1) или второго (p = 2) управляющего воздействия. При этом возможности выбора параметров другого управления стеснены ограничениями (3.2) и достигаемая точность $\varepsilon _{2}^{*}$ или $\varepsilon _{1}^{*}$ равномерного приближения соответственно $Q_{2}^{{}}(x_{2}^{{}},\bar {\Delta }_{{21}}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}})$ к $Q_{2}^{0}({{x}_{2}})$ или $Q_{1}^{{}}(x_{1}^{{}},\bar {\Delta }_{{22}}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}})$ к $Q_{1}^{0}({{x}_{1}})$ вместо заданных в (2.4) величин $\varepsilon _{2}^{{}}$ или $\varepsilon _{1}^{{}}$ остается неизвестной.

Решения $\bar {\Delta }_{{\eta p}}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}}$ задач (3.3)–(3.9) могут быть найдены в этих условиях конструктивным альтернансным методом, являющимся развитием теории нелинейных чебышевских приближений применительно к задачам полубесконечной оптимизации [4, 6–10].

Метод базируется на специальных альтернансных свойствах искомых оптимальных решений ЗПО, установленных при некоторых малостеснительных в прикладных задачах допущениях и существенно использующих базовые физические закономерности оптимизируемых процессов в конкретной предметной области. Согласно этим свойствам, заданные достижимые значения ошибки равномерного приближения к требуемому конечному состоянию СРП ${{\varepsilon }_{1}}$ при $\sigma = 1,2$ или ${{\varepsilon }_{2}}$ при σ = 2 (т.е. строгие равенства в (2.4)) достигаются в конце оптимального процесса в некоторых точках пространственной области определения управляемых величин. Суммарное число таких точек оказывается равным числу всех искомых параметров оптимального процесса, включая $\bar {\Delta }_{{\eta p}}^{{({{{\tilde {N}}}_{1}},{{{\tilde {N}}}_{2}})}},$ $\varepsilon _{2}^{*}$ или $\varepsilon _{1}^{*}$ при σ = 2 и априори нефиксируемые величины минимаксов в (3.11), если с ними должны совпадать по исходным требованиям значения ${{\varepsilon }_{1}}$ или ${{\varepsilon }_{2}}$ в (2.4).

Указанные равенства порождают замкнутую относительно всех неизвестных систему соотношений для результирующих значений функции состояния СРП. При наличии диктуемой закономерностями предметной области дополнительной информации о характере конечного пространственного распределения управляемых величин при оптимальном управлении обеспечивается редукция данной системы равенств к системе трансцендентных уравнений, решение которой стандартными численными методами исчерпывает решение исходной задачи оптимизации [4, 6–10, 22–25].

Применение описанной процедуры альтернансного метода в рассматриваемой задаче быстродействия (2.4), (3.3)–(3.9) приводит к следующим результатам.

С учетом отмеченных особенностей двухканального управления при σ = 2 альтернансные свойства $\bar {\Delta }_{{2p}}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}},\,\eta = 2$, порождают замкнутую систему равенств для заданных значений $\varepsilon _{1}^{{}}$ и $\varepsilon _{2}^{{}}$ в (2.4):

или применительно к вариантам (3.8) или (3.9) выбора Δ^Σ, которые выполняются в некоторых точках $x_{{m\psi }}^{0} \in [{{x}_{{0m}}},{{x}_{{1m}}}],\,\,m = 1,2$.

Суммарное число этих точек

оказывается равным числу $\psi {\text{*}}$ всех искомых неизвестных, к которым относятся $\tilde {N}_{1}^{*} + \tilde {N}_{2}^{*} - 1$ искомых параметров в (3.8), (3.9), а также $\varepsilon _{2}^{*}$ и минимакс $\varepsilon _{{211\min }}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}}$ в (3.10), если $\varepsilon _{1}^{{}} = \varepsilon _{{211\min }}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}}$ в (2.4) для варианта (3.15) или $\varepsilon _{1}^{*}$ и минимакс $\varepsilon _{{222\,\min }}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}}$, если $\varepsilon _{2}^{{}} = \varepsilon _{{222\,\min }}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}}$ в случае (3.16), т.е.:

В задаче двухканального управления одним объектом ($m = \sigma = \eta = 1$) базовая система $\psi _{1}^{{}}$ альтернансных соотношений для вариантов (3.6) при p = 1 или (3.7) при p = 2 и $\varepsilon _{m}^{{}} = \varepsilon _{1}^{{}}$ в (2.4) соответственно

или замкнута относительно неизвестных $\tilde {N}_{1}^{*} + \tilde {N}_{2}^{*} - 1$ параметров, выбираемых, согласно (3.6) или (3.7), и величины $\varepsilon _{{111\,\,\min }}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}}$, либо $\varepsilon _{{121\,\,\min }}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}}$, если $\varepsilon _{1}^{{}} = \varepsilon _{{111\,\,\min }}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}}$ в (3.19) или $\varepsilon _{1}^{{}} = \varepsilon _{{121\,\,\min }}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}}$в (3.20). В итоге будем иметь вместо (3.18)

Таким образом, во всех случаях требуется рассмотреть два возможных варианта, принимая за искомый параметр $t_{{1{{N}_{{11}}}}}^{{(1)}}$ или $t_{{2{{N}_{{21}}}}}^{{(1)}}$ в (3.6), (3.7) при σ = 1 и $t_{{1{{N}_{{11}}}}}^{{(1)}}$ или $t_{{1{{N}_{{12}}}}}^{{(2)}}$ в (3.8), (3.9) при σ = 2 с последующей оценкой получаемых результатов по достигаемой величине минимизируемого критерия оптимальности или предельно достижимых значений ${{\varepsilon }_{m}}$.

При наличии диктуемой закономерностями предметной области дополнительной информации о характере зависимостей ${{Q}_{m}}({{x}_{m}},\bar {\Delta }_{{\eta p}}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}}) - Q_{m}^{0}({{x}_{m}})$ от пространственных переменных ${{x}_{m}}$, которая позволяет идентифицировать значения $x_{{m\psi }}^{0}$ и знаки предельно допустимых отклонений ${{Q}_{m}}(x_{{m\psi }}^{0},\bar {\Delta }_{{\eta p}}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}}) - Q_{m}^{0}(x_{{m\psi }}^{0})$ в этих точках, обеспечивается редукция равенств (3.15), (3.16), (3.19), (3.20), составляемых для абсолютных величин указанных отклонений, к замкнутым системам уравнений следующего вида относительно самих разностей:

где каждой точке $x_{{m\psi }}^{0}$ однозначным образом соответствует свой знак $\varepsilon $.

Равенства (3.22) характеризуют максимальные по абсолютной величине отклонения ${{Q}_{m}}({{x}_{m}},\bar {\Delta }_{{\eta p}}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}}) - Q_{m}^{0}({{x}_{m}})$ на всем отрезке $[{{x}_{{0m}}},{{x}_{{1m}}}]$ определения Q_m и $Q_{m}^{0}$, и, следовательно, внутренние точки $\tilde {x}_{{m\psi }}^{0} \in (x_{{0m}}^{{}},x_{{1m}}^{{}})$, $\tilde {x}_{{m\psi }}^{0} \in \{ x_{{m\psi }}^{0}\} $ этих отрезков являются точками максимума или минимума (в зависимости от знака правой части в (3.22)) рассматриваемой разности, в которых выполняются необходимые условия экстремума:

Совместным решением системы трансцендентных уравнений (3.22), (3.23) стандартными численными методами относительно всех искомых неизвестных, включая значения $\tilde {x}_{{m\psi }}^{0}$, завершается предлагаемая процедура определения параметрических характеристик оптимальных программных управлений $W{\text{*}}(t)$.

Поиск параметрических характеристик векторных управляющих воздействий в условиях альтернативы выбора $\bar {\Delta }_{{\eta p}}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}}$, порождаемой ограничением (3.2), в совокупности с многовариантным набором правил (3.12)–(3.14), необходимостью идентификации точек $x_{{{{\psi }_{m}}}}^{0}$ и формы кривых ${{Q}_{m}}({{x}_{m}},\bar {\Delta }_{{\eta p}}^{{(\tilde {N}_{1}^{*},\tilde {N}_{2}^{*})}})$, зависящих от обоих управлений, приводят к существенным отличиям технологии применения альтернансного метода на основе соотношений (3.15), (3.16) или (3.19), (3.20) по сравнению с задачей одноканального управления при $m = \sigma = l_{m}^{{}} = 1$ в (2.1), (2.2), рассмотренной в [4, 6–10, 22–25].

4. Пример. В качестве представляющего самостоятельный интерес примера рассмотрим задачу оптимального быстродействия при двухканальном управлении по граничным условиям температурным полям неограниченной пластины [2, 12].

Пусть температурное поле ${{Q}_{1}}({{x}_{1}},t)$ неограниченной пластины описывается линейным однородным уравнением теплопроводности вида (1.1)–(1.3) при $m = \sigma = 1;\,L_{{\Sigma m}}^{{}} = L_{\Sigma }^{{(m)}} = 0$ в (1.4):

с заданными начальными и граничными условиями где $g_{{01}}^{{}}(t)$, $g_{{11}}^{{}}(t)$ – граничные управляющие воздействия, стесненные ограничениями с известными предельно допустимыми величинами ${{g}_{{01\min }}},\,\,{{g}_{{11\min }}} < 0;\,\,{{g}_{{01\max }}},{{g}_{{11\max }}} > 0$, и ${{\alpha }_{1}},{{\lambda }_{1}}$ – известные теплофизические постоянные.

Необходимо найти программные управляющие воздействия $g_{{01}}^{*}(t),\,g_{{11}}^{*}(t)$, обеспечивающие в условиях (4.4) заданную точность ${{\varepsilon }_{1}}$ равномерного приближения конечного состояния объекта ${{Q}_{1}}({{x}_{1}},t*)$ к требуемому $Q_{1}^{0}({{x}_{1}})$, согласно (1.8), при минимальном значении критерия оптимальности (3.1).

Каждое из искомых оптимальных по быстродействию управлений имеет вид кусочно-постоянной функции времени:

где для определенности в соответствии с физическими закономерностями процессов нестационарной теплопроводности принимается, что в типичных условиях нагрева пластины до температуры $Q_{1}^{0}({{x}_{1}}) > Q_{1}^{{}}({{x}_{1}},0) = 0\forall {{x}_{1}} \in [0,R]$ минимальная величина $t{\text{*}}$ достигается при максимальных значениях управляющих воздействий на первом интервале их постоянства:

Управляющие воздействия (4.5), (4.6) характеризуются своим параметрическим представлением вида (3.4) при ${{l}_{m}} = 2,\,\,m = \sigma = 1$ с точностью до ${{N}_{{11}}} + {{N}_{{21}}} - 1$ значений моментов переключения $t_{{1q}}^{{(1)}},\,\,q = \overline {1,{{N}_{{11}}}} $, для $g_{{01}}^{*}(t)$ и $t_{{2q}}^{{(1)}},\,\,q = \overline {1,{{N}_{{21}}}} $, для $g_{{11}}^{*}(t)$, включая одинаковые конечные моменты времени $t_{{1{{N}_{{11}}}}}^{{(1)}} = t_{{2{{N}_{{21}}}}}^{{(1)}} = t{\text{*}}$, согласно (3.2).

В итоге исходная задача быстродействия сводится к ЗПО (2.4), (3.2)–(3.4):

где вектор Δ^Σ определяется, согласно (3.4), и числа ${{N}_{{11}}},{{N}_{{21}}}$ должны быть найдены по заданной величине ${{\varepsilon }_{1}}$ в соответствии с правилами (3.6), (3.7), (3.12)–(3.14).

Ограничимся далее характерным случаем, при котором в (4.7) задана минимально достижимая величина ${{\varepsilon }_{1}}$ в классе двухинтервальных управлений $g_{{01}}^{*}(t)$ и $g_{{11}}^{*}(t)$, полагая в соответствии с (3.10) ${{\varepsilon }_{1}} = \varepsilon _{{111\min }}^{{(2,2)}}$ или ${{\varepsilon }_{1}} = \varepsilon _{{121\min }}^{{(2,2)}}$.

Тогда, согласно (3.12), $\tilde {N}_{1}^{*} = \tilde {N}_{2}^{*} = 2;$ системы ${{\psi }_{1}}$ равенств (3.19), (3.20) принимают следующий вид:

или где, согласно (3.6), (3.7) (рис. 3),

Эти системы оказываются замкнутыми в соответствии с (3.21) при ${{\psi }_{1}} = \tilde {N}_{1}^{*} + \tilde {N}_{2}^{*} = 4$ относительно четырех неизвестных параметров:

в соответствии с выбираемым способом поиска величины t* в условиях (3.2).

Зависимости результирующего температурного поля от своих аргументов в (4.8), (4.9), получаемые интегрированием уравнений объекта (4.1)–(4.3) при кусочно-постоянных управляющих воздействиях (4.5), (4.6), могут быть представлены в форме взвешенной суммы реакций $\Lambda _{{01}}^{{}}({{x}_{1}},t)$ и $\Lambda _{{11}}^{{}}({{x}_{1}},t)$ соответственно на ступенчатые управляющие воздействия ${{g}_{{01}}} \equiv 1$ при ${{g}_{{11}}} \equiv 0$ и ${{g}_{{11}}} \equiv 1$ при ${{g}_{{01}}} \equiv 0$:

Решения ${{\Lambda }_{{01}}}({{x}_{1}},t),\,{{\Lambda }_{{11}}}({{x}_{1}},t)$ краевой задачи (4.1)–(4.3) известны [20, 26, 27] и могут быть представлены в следующем виде:

Дальнейшая проблема состоит в идентификации точек $x_{{1\psi }}^{0}$ в (4.8), (4.9) и конфигурации кривых ${{Q}_{1}}({{x}_{1}},\bar {\Delta }_{{11}}^{{(2,2)}}) - Q_{1}^{0}({{x}_{1}})$) и ${{Q}_{1}}({{x}_{1}},\bar {\Delta }_{{12}}^{{(2,2)}}) - Q_{1}^{0}({{x}_{1}})$ на искомых решениях $\bar {\Delta }_{{11}}^{{(2,2)}}$ и $\bar {\Delta }_{{12}}^{{(2,2)}}$ рассматриваемой задачи с использованием известных закономерностей поведения результирующих температурных полей при управляющих воздействиях релейной формы [8, 22–25]. В результате обеспечивается редукция равенств (4.8), (4.9) к разрешаемой стандартными численными методами системе уравнений относительно всех искомых параметров оптимального процесса.

В силу соотношений (4.12), (4.13) конечное состояние оптимального процесса можно рассматривать как суперпозицию эффектов воздействия отдельно по каждому из граничных условий с известной в типичном случае $Q_{1}^{0}({{x}_{1}}) = Q_{{1c}}^{{}} = {\text{const}}$ конфигурацией температурных распределений для обеих составляющих при одноканальном кусочно-постоянном двухинтервальном управлении [8, 22].

Можно показать на этом основании аналогично [8, 22], что точки $x_{{1\psi }}^{0}$ и искомая форма кривых ${{Q}_{1}}(x_{1}^{{}},\bar {\Delta }_{{1p}}^{{(2,2)}}) - Q_{{1c}}^{{}},\,p = 1,2$, результирующих температурных состояний однозначно определяются как раз суммированием таких априори фиксируемых по своей структуре распределений температур. При этом для первого из набора переменных в (4.10) в число точек $x_{{1\psi }}^{0}$ входит граница ${{x}_{1}} = 0$ (рис. 4, а), а для второго – другая граница ${{x}_{1}} = R$ (рис. 4, б).

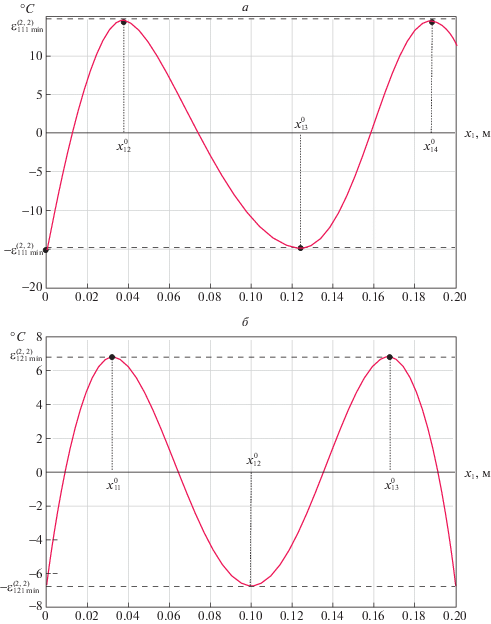
В итоге, подобно [8, 22–25] производится редукция замкнутой системы соотношений (4.8) или (4.9), дополняемой условиями достижения экстремума температурных распределений во внутренних точках $x_{{1\psi }}^{0} \in (0,R)$, к расчетным системам уравнений:

для варианта $t_{1}^{{}} = (\bar {t}_{{11}}^{{(1)}},\bar {t}_{{12}}^{{(1)}},\bar {t}_{{21}}^{{(1)}})$

или $t_{2}^{{}} = (\bar {t}_{{11}}^{{(1)}},\bar {t}_{{21}}^{{(1)}},\bar {t}_{{22}}^{{(1)}})$

в (4.11) (рис. 4).

Решение каждой из этих систем семи уравнений с тем же числом неизвестных t₁, $\varepsilon _{{111\,\,\min }}^{{(2,2)}},x_{{12}}^{0},x_{{13}}^{0},x_{{14}}^{0}$ в (4.16) или t₂, $\varepsilon _{{121\,\,\min }}^{{(2,2)}}x_{{11}}^{0},x_{{12}}^{0},x_{{13}}^{0}$ в (4.17) (с последующим выбором окончательного варианта по минимальной длительности процесса управления) исчерпывает решение исходной задачи.

На рис. 4 приведены некоторые расчетные результаты²², полученные при нагреве пластины из титанового сплава толщиной $R = 0.2$ м до температуры $Q_{{1c}}^{{}} = 960^\circ $:

Применительно к этим исходным данным найдены решения $\bar {t}_{{11}}^{{(1)}} = 1246\;{\text{c,}}\;\bar {t}_{{12}}^{{(1)}} = 1618\;{\text{c}},\;\bar {t}_{{21}}^{{(1)}}$ = = 1554 c, $\varepsilon _{{111\,\,\min }}^{{(2,2)}}$ = 14.8° $\bar {t}_{{11}}^{{(1)}} = 1981\,{\text{c}},\;\bar {t}_{{21}}^{{(1)}}$ = 1980 c, и $\bar {t}_{{22}}^{{(1)}} = 2203\,{\text{c}},\;\varepsilon _{{121\min }}^{{(2,2)}}$ = 6.8° систем уравнений (4.16) и (4.17) соответственно. При $\bar {t}_{{12}}^{{(1)}} < \bar {t}_{{22}}^{{(1)}}$ оптимальным по критерию быстродействия следует считать решение системы уравнений (4.16).

Заключение. Разработана конструктивная технология решения краевых задач многоканального оптимального управления линейными объектами с распределенными параметрами параболического типа в условиях оценки в равномерной метрике ограничений на конечные состояния управляемых величин. Предлагаемый подход базируется на процедуре редукции к специальной форме задачи полубесконечной оптимизации, на которую распространяется альтернансный метод отыскания ее решения с учетом существенных особенностей, связанных с векторным характером оптимизируемых управляющих воздействий, специфическими ограничениями на одинаковую длительность процесса управления для каждой из их компонент и возникновением соответствующих многовариантных наборов искомых решений. Получаемые результаты могут быть использованы применительно к достаточно широкому кругу задач оптимизации, включая задачи векторного управления как всей системой взаимосвязанных объектов с распределенными параметрами, так и каждым из этих объектов в отдельности без учета влияния на них остальных компонентов системы.