Известия РАН. Теория и системы управления, 2019, № 4, стр. 29-46

Введение. Переключаемые системы (ПС) служат математическими моделями многорежимных систем автоматического управления технологическими процессами и движущимися объектами [1–4]. Функционирование таких систем представляется непрерывно-дискретными процессами, которые имеют разнородное представление [4–6]. В рассматриваемых в статье системах непрерывное изменение, задающее движение объекта управления, описывается дифференциальными уравнениями, а дискретное изменение, моделирующее работу устройства управления, – рекуррентными уравнениями. Качество управления оценивается функционалом, в котором учитываются затраты на непрерывное управление и на каждое переключение. Выбор количества переключений, моментов переключений, а также собственно переключений – скачков состояния, вместе с выбором управления непрерывной частью определяют траекторию ПС и подлежат оптимизации. При этом не исключаются многократные переключения в фиксированный момент времени [2–4]. Исследуемая модель ПС обобщает дискретные системы автоматного типа, непрерывно-дискретные, логико-динамические и переключающие системы [2]. В свою очередь ПС являются частным случаем систем со сменой моделей движения [4].

Достаточные условия оптимальности управления динамическими системами, как правило, связаны с нахождением функции цены (функции Гамильтона–Якоби–Беллмана (ГЯБ)). Для синтеза оптимальных ПС предлагается, как и в [4], искать вспомогательные функции – так называемые образующие функции цены, из которых потом можно построить “настоящую” функцию цены. Дифференциальные и рекуррентные уравнения для этих вспомогательных функций выводятся на основе метода динамического программирования [7], при этом “настоящая” функция цены оказывается, вообще говоря, не нужна.

Вместе с задачей оптимального управления рассматривается задача минимизации количества переключений непрерывно-дискретного процесса. Эта задача состоит в нахождении наименьшего количества переключений, при котором значение функционала качества не превышает заданного значения. Проблема минимизации количества переключений нередко встречается в прикладных задачах, в которых число переключений, как правило, ограничено. Например, для вывода спутника на геостационарную орбиту используется разгонный блок “Бриз-М” [8], количество включений маршевого двигателя которого ограничено (не более 10 запусков). Это ограничение, разумеется, учитывается при разработке схемы полета. Потребность минимизации количества переключений возникает естественным образом, если затраты на каждое переключение существенные. В этом случае также желательно достичь цели управления с наименьшим количеством переключений.

Необходимые условия оптимальности гибридных систем при фиксированном количестве переключений получены в [9–11]. В этих работах, однако, исключаются процессы с мгновенными многократными переключениями. Задача минимизации переключений аналогична задаче быстродействия дискретных систем [12].

В статье доказаны достаточные условия оптимальности управления ПС, получены уравнения для нахождения оптимального позиционного управления, разработан алгоритм решения задачи минимизации переключений. Достаточные условия применены для решения линейно-квадратичной задачи управления ПС. Получены уравнения для синтеза условных оптимальных регуляторов. Приведен академический пример, демонстрирующий применение условий оптимальности.

1. Постановки задач. Пусть на заданном промежутке времени $T = [{{t}_{0}},{{t}_{F}}]$ динамическая система совершает $N$ переключений (скачков) в моменты времени ${{t}_{i}}$, $i = 1,\; \ldots ,\;N$, образующие неубывающую последовательность $\mathcal{T} = \{ {{t}_{1}}, \ldots ,{{t}_{N}}\} $:

Между неравными последовательными моментами переключений состояние системы изменяется непрерывно, согласно дифференциальному уравнению

а в моменты переключений – дискретно в соответствии с рекуррентным уравнением

В соотношениях (1.2) обозначены: $\mathcal{N} \triangleq \{ i = 0,1,\; \ldots ,\;N|{{t}_{i}} < {{t}_{{i + 1}}}\} $ – множество номеров ненулевых (по длине) частичных промежутков ${{T}_{i}} \triangleq [{{t}_{i}},{{t}_{{i + 1}}})$ непрерывного движения системы; x(t) – состояние системы в момент времени $t \in {{T}_{i}}$, $i \in \mathcal{N}$, $x(t) \in X \subset {{\mathbb{R}}^{n}}$; $u(t)$ – управление непрерывным движением системы в момент времени $t \in T$, $u(t) \in U \subset {{\mathbb{R}}^{p}}$; U – заданное множество допустимых значений управления. При ${{t}_{i}} = {{t}_{{i + 1}}}$ дифференциальное уравнение (1.2) опускается ($i \notin \mathcal{N}$), а значение $u({{t}_{i}})$ управления в этой точке t_i несущественно. В уравнении (1.3) ${{x}_{i}} \triangleq x({{t}_{i}})$ – состояние системы сразу после i-го переключения, ${{x}_{{i - }}}$ – состояние системы непосредственно перед i-м переключением:

${{\text{v}}_{i}}$ – управление переключением системы в момент ${{t}_{i}} \in \mathcal{T}$, ${{\text{v}}_{i}} \in V \subset {{\mathbb{R}}^{q}}$; V – заданное множество допустимых управлений переключениями. Функция $f:T \times X \times U \to {{\mathbb{R}}^{n}}$ непрерывна на всей области определения вместе с производной $\partial f{\text{/}}\partial x$; функция $g:T \times X \times V \to X$ ограничена. Предполагаем, что в уравнении (1.3) исключаются так называемые фиктивные переключения, при которых состояние системы не изменяется (${{x}_{i}} = {{x}_{{i - }}}$) и фактического переключения нет. Возможное равенство последовательных моментов в (1.1) означает, что система совершает мгновенные многократные переключения [2, 3].

Начальное состояние системы задано

Условие (1.5) не исключает одного или нескольких переключений в начальный момент времени t₀, поскольку первые несколько моментов переключений (1.1) могут совпадать. Момент t_F окончания процесса управления задан, а конечное состояние свободно – терминальных ограничений нет.

Множество допустимых процессов $\mathcal{D}({{t}_{0}},{{x}_{0}})$ составляют наборы $d = (\mathcal{T},x( \cdot ),u( \cdot ),\{ \text{v}\} )$, включающие: неубывающую последовательность $\mathcal{T} = \{ {{t}_{1}},\; \ldots ,\;{{t}_{N}}\} $ моментов переключений; траекторию $x( \cdot )$, составленную из функций $x:{{T}_{i}} \to X$, абсолютно непрерывных на каждом ненулевом (по длине) промежутке ${{T}_{i}}$, $i \in \mathcal{N}$; управление непрерывным движением – ограниченную измеримую на T функцию $u:T \to U$ и управление переключениями – последовательность $\{ \text{v}\} \triangleq \{ {{\text{v}}_{i}}\} _{{i = 1}}^{N}$ векторов ${{\text{v}}_{i}} \in V$; причем пары $(x( \cdot ),u( \cdot ))$ удовлетворяют уравнению (1.2) почти всюду на каждом промежутке ${{T}_{i}}$, $i \in \mathcal{N}$, тройки $({{x}_{{i - }}},{{x}_{i}},{{\text{v}}_{i}})$, $i = 1,\; \ldots ,\;N$, на $\mathcal{T}$ удовлетворяют рекуррентному уравнению (1.3); в начальный момент времени выполняется условие (1.5). Подчеркнем, что количество $N = \left| \mathcal{T} \right|$ переключений и моменты $\mathcal{T} = \{ {{t}_{1}},\; \ldots ,\;{{t}_{N}}\} $ переключений не фиксированы и у разных допустимых процессов могут не совпадать.

На множестве $\mathcal{D}({{t}_{0}},{{x}_{0}})$ допустимых процессов задан функционал качества

где функции ${{f}^{0}}:T \times X \times U \to \mathbb{R}$ и $F:X \to \mathbb{R}$ непрерывны и ограничены снизу, а функция g⁺ : $T \times X \times V \to {{\mathbb{R}}_{ + }}$ неотрицательная, ${{g}^{ + }}( \cdot ) \geqslant 0$. Последнее условие позволяет рассматривать каждое слагаемое ${{g}^{ + }}({{t}_{i}},{{x}_{{i - }}},{{\text{v}}_{i}})$ в (1.6) как затраты (или “штраф”) при переключении ${{x}_{{i - }}} \to {{x}_{i}}$. В силу непрерывности функции ${{f}^{0}}(t,x,u)$ по всем аргументам функция ${{f}^{0}}[t] = {{f}^{0}}(t,x(t),u(t))$ будет измеримой и ограниченной, т.е. суммируемой, для любого допустимого процесса d = $(\mathcal{T},x( \cdot ),u( \cdot ),\{ \text{v}\} )$. Поэтому функционал (1.6) определен на $\mathcal{D}({{t}_{0}},{{x}_{0}})$. Отметим, что в функционале (1.6) количество переключений N и моменты переключений не заданы, а находятся в результате оптимизации.

1.1. Задача оптимального управления. Требуется найти минимальное значение функционала (1.6) и оптимальный процесс $d* = (\mathcal{T}*,x*( \cdot ),u*( \cdot ),\{ \text{v}*\} ) \in \mathcal{D}({{t}_{0}},{{x}_{0}})$, на котором это значение достигается:

Если наименьшее значение (1.7) не существует, то может быть поставлена задача нахождения минимизирующей последовательности допустимых процессов [13]. Количество переключений у процессов минимизирующей последовательности может оставаться конечным или неограниченно возрастать. Бесконечное количество переключений у оптимального процесса становится невозможным, если усилить условие неотрицательности функции g⁺ в (1.6):

Применение таких “штрафов” в функционале качества исключает последовательности процессов с неограниченным ростом числа переключений как неминимизирующие.

1.2. Задача управления с фиксированным числом переключений. В прикладных задачах нередко возникают ограничения на количество переключений. Задача минимизации функционала (1.6) на множестве допустимых траекторий с заданным числом переключений формулируется следующим образом. Пусть ${{\mathcal{D}}_{N}}({{t}_{0}},{{x}_{0}})$ – множество допустимых процессов из $\mathcal{D}({{t}_{0}},{{x}_{0}})$ с N переключениями, быть может фиктивными. Подчеркнем, что количество переключений N у всех процессов из ${{\mathcal{D}}_{N}}({{t}_{0}},{{x}_{0}})$ одинаковое (равное N), но моменты переключений (1.1) у разных процессов могут не совпадать. Обозначим через ${{I}_{N}}({{t}_{0}},{{x}_{0}},d)$ функционал (1.6) при фиксированном количестве переключений N. Он определен на подмножестве ${{\mathcal{D}}_{N}}({{t}_{0}},{{x}_{0}})$ множества $\mathcal{D}({{t}_{0}},{{x}_{0}})$. Требуется найти минимальное значение функционала (1.6) на множестве ${{\mathcal{D}}_{N}}({{t}_{0}},{{x}_{0}})$ и процесс d^N $ \in {{\mathcal{D}}_{N}}({{t}_{0}},{{x}_{0}})$, на котором это значение достигается:

Такой процесс d^N будем называть условно оптимальным, имея в виду его оптимальность при дополнительном условии – заданном количестве переключений N.

Поставленные задачи (1.7), (1.8) представляют собой так называемые задачи со свободным конечным состоянием и фиксированным временем. В более общей постановке [13] на правый конец траектории могут быть наложены терминальные ограничения. Отметим, что поставленные задачи являются частным случаем задачи оптимального управления со сменой модели движения [4].

1.3. Задача минимизации количества переключений. В отличие от классических задач оптимального управления [13, 14] для ПС можно сформулировать новые задачи, связанные именно с количеством переключений. Например, в технических приложениях актуальна задача минимизации количества переключений управляемого процесса при обязательном достижении цели управления. Математическая формулировка такой технической задачи может быть следующей. Для ПС (1.1)–(1.5) требуется найти наименьшее количество переключений N^ε, при котором наименьшее значение функционала ${{I}_{{{{N}^{\varepsilon }}}}}({{t}_{0}},{{x}_{0}},d)$ не превосходит заданной величины ε:

В задаче (1.7) вместе с оптимальным управлением нужно найти и оптимальное количество переключений, в задаче (1.8) количество переключений N фиксировано, поэтому нужно получить только условное (с N переключениями) оптимальное управление. В задаче (1.9) нужно искать минимальное количество переключений N^ε, при котором условное (с N^ε переключениями) оптимальное управление обеспечивает достижение заданного уровня $\varepsilon $ функционала качества. Заметим, что вопрос минимизации переключений возникает при численном (приближенном) решении разных задач, например при аппроксимации функций. В этом случае величина $\varepsilon > 0$ задает точность приближенного решения.

1.4. Линейно-квадратичная задача управления. Пусть уравнения (1.2), (1.3) движения системы линейные:

а функционал (1.6) – квадратичный:

Ограничений на состояние системы и на значения управления нет, т.е. $X = {{\mathbb{R}}^{n}}$ и $U = {{\mathbb{R}}^{r}}$. Матрицы $A(t)$, $B(t)$, $C(t)$, $D(t)$ размеров $n \times n$, $n \times r$, $n \times n$, $r \times r$ ограничены и измеримы на T, матрицы ${{A}_{t}}$, ${{B}_{t}}$, ${{C}_{t}}$, ${{D}_{t}}$ соответствующих размеров ограничены на T. Матрицы $C(t)$, $D(t)$, ${{C}_{t}}$, ${{D}_{t}}$ и $F$ – симметрические, причем $C(t)$, ${{C}_{t}}$, $F$ – неотрицательно определенные, а $D(t)$, ${{D}_{t}}$ – положительно определенные. Величина ${{\lambda }_{t}}$ неотрицательная при всех $t \in T$. Линейно-квадратичная задача (ЛКЗ) может быть поставлена как задача оптимального управления (см. разд. 1.1 или 1.2) либо как задача минимизации переключений (см. разд. 1.3).

2. Моментные функции цены и образующие. Применение динамического программирования [7] для получения достаточных условий оптимальности позиционного управления связано с понятием функции цены (функции ГЯБ). Для ПС функция цены строится при помощи вспомогательных функций, так называемых образующих функции цены [3, 4]. Определим вспомогательные функции для задачи (1.7).

Обозначим через $\mathcal{D}(t,x)$ множество допустимых процессов, удовлетворяющих начальному условию $x(t) = x$, каждый из которых имеет конечное число переключений на $[t,{{t}_{F}}]$. Оставшиеся переключения происходят в моменты ${{t}_{1}}, \ldots ,\;{{t}_{k}}$, образующие неубывающую последовательность на промежутке $[t,{{t}_{F}}]$:

Заметим, что количество k оставшихся переключений и сами моменты ${{t}_{1}}, \ldots ,\;{{t}_{k}}$ переключений не фиксированы и у разных допустимых процессов могут не совпадать.

На множестве $\mathcal{D}(t,x)$ допустимых процессов определим функционал оставшихся потерь, аналогичный (1.6):

Функция цены $\varphi (t,x)$ по определению равна значению функционала оставшихся потерь (2.2), вычисленному на оптимальном процессе с начальным условием $x(t) = x$. Иначе говоря, функция цены равна минимальному значению функционала оставшихся потерь (2.2) на множестве допустимых процессов $\mathcal{D}(t,x)$:

Для задачи (1.7) определим образующую функции цены, значение ${{\varphi }^{k}}(t,x)$ которой равно значению функционала оставшихся потерь (2.2), вычисленному на процессе, который оптимален среди всех допустимых процессов, исходящих из начальной позиции (t, x) и имеющих ровно k переключений, быть может фиктивных. Если обозначить через ${{\mathcal{D}}_{k}}(t,x)$ множество допустимых процессов из $\mathcal{D}(t,x)$, имеющих ровно k переключений, быть может фиктивных, а через ${{I}_{k}}(t,x,d)$ – функционал (2.2) при фиксированном количестве k оставшихся переключений, то

Функцию $\varphi (t,x|{{t}_{1}},\; \ldots ,\;{{t}_{k}})$, равную значению функционала оставшихся потерь (2.2), вычисленному на траектории, которая оптимальна среди всех допустимых траекторий, исходящих из начальной позиции $(t,x)$ и имеющих k переключений, быть может фиктивных, которые происходят в моменты времени ${{t}_{1}}, \ldots ,\;{{t}_{k}}$, образующие неубывающую последовательность (2.1), назовем k-моментной функцией цены. Если обозначить через $\mathcal{D}(t,x|{{t}_{1}},\; \ldots ,\;{{t}_{k}})$ множество допустимых процессов из ${{\mathcal{D}}_{k}}(t,x)$ с k переключениями в моменты времени (2.1), то

По определению полагаем, что 0-моментная функция цены совпадает с нулевой образующей, т.е. $\phi (t,x) = {{\varphi }^{0}}(t,x)$.

Можно сказать, что моментная функция цены представляет собой функцию цены при дополнительном условии – фиксированных моментах переключений. Заметим, что образующая функции цены определяется аналогичным способом, а именно множество допустимых процессов сужается при помощи одного дополнительного условия – задания количества переключений. Поэтому образующая функции цены и моментная функция цены являются условными функциями цены [3]. Однако чтобы не было путаницы, лучше использовать разные термины и обозначения.

Согласно определениям, функция цены является нижней огибающей своих образующих

а образующая связана с моментной функцией цены равенством

Подставляя (2.6) в (2.5), можно представить функцию цены через ее моментные функции

Наименьшее значение функционала (2.2) вычисляется по функции цены

Вспомогательные функции (2.3), (2.4) аналогичны функциям, введенным в [3]. Отличие заключается в том, что условные функции цены в [3] зависели только от момента первого переключения из k оставшихся, а моментная функция (2.4) зависит от всех моментов переключений (2.1).

3. Уравнения для моментных функций цены. Выведем уравнения, которым удовлетворяют моментные функции цены и образующие. Метод динамического программирования отвечает принципу оптимальности Беллмана, согласно которому “последний участок оптимальной траектории является оптимальной траекторией”. Для оптимальных траекторий с фиксированным числом переключений из принципа оптимальности Беллмана вытекает следствие: “участок оптимальной траектории с k переключениями после первого переключения является оптимальной траекторией с k – 1 переключениями”. Используем эту формулировку при выводе уравнений.

Предполагаем, что все моментные функции имеют частные производные по t и x. Нулевую образующую или 0-моментную функцию цены ($\phi (t,x) = {{\phi }^{0}}(t,x)$) находим как значение функционала (2.2) на оптимальном процессе $(x( \cdot ),u( \cdot ))$ без переключений. Эта функция удовлетворяет уравнению ГЯБ

с терминальным условием

Одномоментная функция цены $\phi (t,x|{{t}_{1}})$ вычисляется на оптимальных траекториях с одним переключением в момент времени ${{t}_{1}} \geqslant t$. До переключения процесс $(x( \cdot ),u( \cdot ))$ управления оптимальный. Поэтому до переключения одномоментная функция цены удовлетворяет уравнению ГЯБ

при всех $t \leqslant {{t}_{1}}$. В момент переключения ${{t}_{1}} \in [t,{{t}_{F}}]$ оптимальная траектория совершает скачок, после которого она уже непрерывна, а значение функционала оставшихся потерь определяется $0$-моментной функцией цены. Поэтому в момент переключения ${{t}_{1}}$ одномоментная функция цены выражается через 0-моментную функцию, согласно равенству

Итак, получены уравнения для одномоментной функции цены. Остальные моментные функции находятся аналогично. Пусть известна (k – 1)-моментная функция цены $\phi (t,x|{{t}_{1}},\; \ldots ,\;{{t}_{{k - 1}}})$. Получим следующую k-моментную функцию $\phi (t,x|{{t}_{1}},\; \ldots ,\;{{t}_{k}})$. Для этого нужно решить уравнение ГЯБ

с терминальным условием для всех $(t,x) \in T \times X$, $t \leqslant {{t}_{1}} \leqslant \ldots \leqslant {{t}_{k}} \leqslant {{t}_{F}}$.

Таким образом, последовательность моментных функций строится в результате рекуррентной процедуры, которая начинается с решения уравнения ГЯБ (3.1) с терминальным условием (3.2) и продолжается решением уравнения (3.3) с условием (3.4) при $k = 1,2,\; \ldots $ По каждой моментной функции можно найти соответствующую образующую функции цены по формуле (2.6), а по всем образующим – функцию цены, согласно (2.5).

Моментные функции цены по сравнению с условными функциями цены [3] имеют переменное количество аргументов, которое увеличивается, согласно описанной процедуре. Отметим, что операцию поиска оптимальных моментов переключения при построении моментных функций цены не обязательно выполнять после каждого шага, eе можно отложить на несколько шагов и выполнить после нескольких итераций. Такая возможность оказывается полезной, например, при решении линейно-квадратичных задач оптимального управления.

Для построения моментных функций цены можно использовать решение вспомогательной задачи Больца

В этой задаче начальная позиция и момент окончания процесса управления заданы, а конечное состояние – свободно. Обозначим ее решение через $\phi ({{t}_{0}},{{x}_{0}}|{{t}_{1}},F( \cdot ))$, подчеркивая зависимость от терминального члена функционала (3.5). Функция $(t,x) \to \phi (t,x|{{t}_{1}},F( \cdot ))$ удовлетворяет уравнению ГЯБ

с терминальным условием

Фактически функция $\phi ({{t}_{0}},{{x}_{0}}|{{t}_{1}},F( \cdot ))$ является функционалом, зависящим от функции F(⋅). Будем ее называть функционалом цены в задаче Больца (3.5). Нахождение этого функционала представляется довольно сложной задачей из-за произвольности функции F(⋅). Поэтому для решения целесообразно ограничить класс функций F(⋅). Например, представить каждую функцию в виде ряда с конечным числом членов, т.е. задать конечным числом параметров (коэффициентами ряда). В линейно-квадратичных задачах терминальное слагаемое является квадратичной формой и определяется ее матрицей. В этом случае решение задачи Больца (3.5) известно.

Выразим моментные функции цены через этот функционал. Для 0-моментной функции цены $\phi (t,x)$ (или нулевой образующей ${{\varphi }^{0}}(t,x)$) по определению имеем

Одномоментная функция в момент переключения t₁ находится по 0-моментной функции, согласно уравнению

До момента переключения она представляется через функционал цены в задаче Больца

Для k-моментной функции цены $\phi (t,x|{{t}_{1}},\; \ldots ,\;{{t}_{k}})$ аналогично получаем следующие уравнения. В момент $t = {{t}_{1}}$ первого из k оставшихся переключений она удовлетворяет рекуррентному соотношению

До момента первого переключения (при ${{t}_{0}} \leqslant t < {{t}_{1}}$) она выражается через функционал цены

Таким образом, моментные функции цены находятся в результате рекуррентной процедуры (3.7), (3.8), которая начинается с 0-моментной функции цены (3.6), т.е. с функции ГЯБ для процессов без переключений.

4. Оптимальное позиционное управление. При решении уравнений (2.5), (2.6), (3.1), (3.3), (3.4) выполняются пять операций минимизации. В результате минимизации левой части (3.1) определяется оптимальное позиционное управление

непрерывным движением при отсутствии переключений. Минимизируя левую часть (3.3), получаем условное позиционное управление

При минимизации правой части (3.4) определяются оптимальное позиционное управление первым переключением системы из k оставшихся:

Минимизация (2.6) позволяет определить оптимальные моменты оставшихся k переключений:

Точки минимума (4.1)–(4.4) находятся при дополнительном условии – заданном количестве k оставшихся переключений, а оптимальное количество переключений определяется в результате минимизации (2.5) или (2.7):

Позиционные конструкции (4.1)–(4.5) позволяют найти оптимальный процесс. Действительно, пусть система находится в позиции $({{t}_{0}},{{x}_{0}})$, т.е. удовлетворяет начальному условию (1.5). Для этой позиции определяем оптимальное количество оставшихся переключений $N = {\mathbf{k}}({{t}_{0}},{{x}_{0}})$, а также оптимальные моменты $\{ {{{\mathbf{t}}}_{1}},\; \ldots ,\;{{{\mathbf{t}}}_{N}}\} $ переключений. Если ${{{\mathbf{t}}}_{1}} = {{t}_{0}}$, то первое переключение происходит в начальный момент времени. Система сразу совершает скачок ${{x}_{0}} \to {{x}_{1}} = g({{{\mathbf{t}}}_{1}},{{x}_{0}},{{\text{v}}_{1}})$ под действием управления ${{\text{v}}_{1}} = {\mathbf{v}}({{{\mathbf{t}}}_{1}},{{x}_{0}}|{{{\mathbf{t}}}_{2}},\; \ldots ,\;{{{\mathbf{t}}}_{N}})$. Если ${{{\mathbf{t}}}_{1}} > {{t}_{0}}$, то сначала на промежутке $[{{t}_{0}},{{{\mathbf{t}}}_{1}}]$ происходит непрерывное движение, согласно уравнению (1.2), с программным управлением $u(t) = {\mathbf{u}}(t,x(t)|{{{\mathbf{t}}}_{1}},\; \ldots ,\;{{{\mathbf{t}}}_{N}})$, а в конце этого промежутка из состояния ${{x}_{{1 - }}} = x({{{\mathbf{t}}}_{1}} - 0)$ происходит скачок ${{x}_{{1 - }}} \to {{x}_{1}} = g({{{\mathbf{t}}}_{1}},{{x}_{{1 - }}},{{\text{v}}_{1}})$ под действием управления ${{\text{v}}_{1}} = {\mathbf{v}}({{{\mathbf{t}}}_{1}},{{x}_{{1 - }}}|{{{\mathbf{t}}}_{2}},\; \ldots ,\;{{{\mathbf{t}}}_{k}})$. И в том и в другом случае система приходит в позицию $({{{\mathbf{t}}}_{1}},{{x}_{1}})$, в которой выполняются те же действия, за исключением поиска оптимального количества переключений (оно равно N – 1) и оптимальных моментов переключений, так как они уже найдены $\{ {{{\mathbf{t}}}_{2}},\; \ldots ,\;{{{\mathbf{t}}}_{N}}\} $. Если в начальной позиции $({{t}_{0}},{{x}_{0}})$ оптимальное количество переключений равно нулю: ${\mathbf{k}}({{t}_{0}},{{x}_{0}}) = 0$, то переключений нет и непрерывное движение системы совершается, согласно уравнению (1.2), под действием программного управления $u(t) = {\mathbf{u}}(t,x(t))$.

Таким образом, оптимальное позиционное управление для рассматриваемых систем представляет собой целый “управляющий комплекс”, состоящий из функций: ${\mathbf{u}}(t,x)$ и ${\mathbf{u}}(t,x|{{t}_{1}},\; \ldots ,\;{{t}_{k}})$ – условные оптимальные управления (4.1), (4.2) непрерывным движением системы, ${\mathbf{v}}({{t}_{1}},x|{{t}_{2}}$, ..., t_k) – условное оптимальное управление (4.3) переключениями, $(t,x) \to \{ {{{\mathbf{t}}}_{1}},\; \ldots ,\;{{{\mathbf{t}}}_{k}}\} $ – оптимальные моменты (4.4) оставшихся k переключений, ${\mathbf{k}}(t,x)$ – оптимальное количество (4.5) переключений процесса, исходящего из позиции $(t,x)$.

5. Достаточные условия оптимальности. В формулировке и доказательстве достаточных условий оптимальности используются понятия моментных функций цены, образующих функции цены, а также “управляющий комплекс” позиционных конструкций (4.1)–(4.5).

Теорема. Если для задачи (1.1)–(1.7) существуют последовательность функций $\phi (t,x|{{t}_{1}}$, ..., t_k), $k \in {{\mathbb{Z}}_{ + }}$, удовлетворяющих на области определения уравнениям (3.1)–(3.4), то для оптимальности допустимого процесса $d = (\mathcal{T},x( \cdot ),u( \cdot ),\{ \text{v}\} ) \in \mathcal{D}({{t}_{0}},{{x}_{0}})$ с моментами переключений $\mathcal{T} = \{ {{{\mathbf{t}}}_{1}},\; \ldots ,\;{{{\mathbf{t}}}_{N}}\} $, образующими неубывающую последовательность (1.1), достаточно, чтобы выполнялись следующие условия:

где ${{T}_{i}}\, = \,\,[{{{\mathbf{t}}}_{i}},{{{\mathbf{t}}}_{{i + 1}}})$, $\mathcal{N} = \{ i = 0,1,\; \ldots ,\;N|{{{\mathbf{t}}}_{i}} < {{{\mathbf{t}}}_{{i + 1}}}\} $. При N = 0 равенства (5.2), (5.4) опускаются, а условие (5.3) принимает вид

Доказательство. При N > 0 для процесса $(\mathcal{T},x( \cdot ),u( \cdot ),\{ \text{v}\} )$, удовлетворяющего уравнениям (1.2), (1.3) с управлениями (5.3), (5.4), уравнение (3.3) на промежутке ${{T}_{i}} = [{{{\mathbf{t}}}_{i}},{{{\mathbf{t}}}_{{i + 1}}})$, $i \in \mathcal{N}$, можно записать как

используя полную производную функции $\phi (t,x(t)|{{{\mathbf{t}}}_{{i + 1}}},\; \ldots ,\;{{{\mathbf{t}}}_{N}})$ по времени t в силу системы (1.2). Поэтому, интегрируя равенство (5.6) на промежутке ${{T}_{i}} = [{{{\mathbf{t}}}_{i}},{{{\mathbf{t}}}_{{i + 1}}})$, получаем

Для сокращения записей в (5.7) и далее обозначим ${{f}^{0}}[t] \triangleq {{f}^{0}}(t,x(t),u(t))$. Из (3.4) и (5.4) в момент времени ${{{\mathbf{t}}}_{{i + 1}}}$ следует, что

Здесь, согласно (1.4), ${{x}_{{i + 1 - }}} = x({{{\mathbf{t}}}_{{i + 1}}} - 0)$, так как ${{{\mathbf{t}}}_{i}} < {{{\mathbf{t}}}_{{i + 1}}}$. Подставляя (5.8) в (5.7), получаем

Если ${{{\mathbf{t}}}_{i}} = {{{\mathbf{t}}}_{{i + 1}}}$, то равенство (5.7) опускается, а уравнение (5.9) представляется в виде

так как ${{x}_{{i + 1 - }}} = {{x}_{i}}$, согласно (1.4). Таким образом, равенство (5.9) справедливо при всех i = = $0,1, \ldots ,N - 1$ с моментами переключений ${{{\mathbf{t}}}_{1}},\; \ldots ,\;{{{\mathbf{t}}}_{N}}$, образующими неубывающую последовательность (1.1).

Для последнего промежутка $[{{{\mathbf{t}}}_{N}},{{t}_{F}}]$ если ${{{\mathbf{t}}}_{N}} < {{t}_{F}}$, то уравнение (3.1), учитывая (5.5), принимает вид

Интегрируя это равенство с учетом терминального условия (3.2), получаем

Если же ${{{\mathbf{t}}}_{N}} = {{t}_{F}}$, то из (3.2) следует, что $F(x({{t}_{F}})) - \phi ({{t}_{N}},{{x}_{N}}) = 0$, так как ${{x}_{N}} = x({{t}_{F}})$. Таким образом, при ${{{\mathbf{t}}}_{N}} \leqslant {{t}_{F}}$ справедливо (5.10).

Выполняем суммирование равенств (5.9) при $i = 0,1,\; \ldots ,\;N - 1$ и добавляем к сумме равенство (5.10). Получаем

Отсюда следует, что $I({{t}_{0}},{{x}_{0}},d) = \phi ({{t}_{0}},{{x}_{0}}|{{{\mathbf{t}}}_{1}},\; \ldots ,\;{{{\mathbf{t}}}_{N}})$. Учитывая (5.2) и (2.7), имеем для функции цены равенство $\varphi ({{t}_{0}},{{x}_{0}}) = \phi ({{t}_{0}},{{x}_{0}}|{{{\mathbf{t}}}_{1}},\; \ldots ,\;{{{\mathbf{t}}}_{N}})$. Значит, $I({{t}_{0}},{{x}_{0}},d) = \varphi ({{t}_{0}},{{x}_{0}})$, т.е. значение функционала равно значению функции цены. Следовательно, процесс d оптимальный.

Доказательство теоремы при отсутствии переключений (когда по формуле (5.1) имеем N = 0) сводится к получению равенства $I({{t}_{0}},{{x}_{0}},d) = \phi ({{t}_{0}},{{x}_{0}})$ из уравнения (3.1) и условий (3.2), (5.5), так как при отсутствии переключений 0-моментная функция цены совпадает с функцией цены $\phi ({{t}_{0}},{{x}_{0}})$ = φ(t₀, x₀).

6. Алгоритм синтеза оптимального позиционного управления. Опишем алгоритм синтеза “управляющего комплекса” позиционных конструкций (см. разд. 4), выполняющего роль оптимального позиционного управления.

Шаг 0. Решая уравнение ГЯБ

с терминальным условием найти 0-моментную функцию цены $\phi (t,x)$ (функцию цены в задаче без переключений) и оптимальное позиционное управление непрерывным изменением состояния системы

Положить k = 1 и перейти к шагу k.

Шаг k. Решая рекуррентное уравнение

выразить позиционное управление первым из оставшихся k переключений

Решая уравнение ГЯБ

с терминальным условием (6.1), найти k-моментную функцию цены $\phi (t,x|{{t}_{1}},\; \ldots ,\;{{t}_{k}})$ и оптимальное позиционное управление непрерывным изменением состояния системы до первого из оставшихся k переключений:

Проверить условие окончания. Таких условий может быть несколько. Общим условием окончания синтеза служит неравенство

если оно выполняется для всех позиций $(t,x) \in T \times X$. Неравенство (6.2) означает, что оптимальный процесс с k переключениями, начинающийся в любой стартовой позиции $(t,x) \in T \times X$, не лучше процесса с k – 1 переключением. Тогда процесс с большим, чем k, количеством переключений также будет хуже (точнее, не лучше), чем процесс с k – 1 переключением, поскольку затраты на каждое переключение неотрицательные. Проверять, однако, это общее условие окончания синтеза затруднительно. Как правило, при вычислениях задают максимальное допустимое количество $N$ переключений. Тогда нужно проверять условие k > N.

При решении задачи минимизации количества переключений условием окончания служит неравенство (1.9), которое можно записать при помощи k-моментной функции цены

Если неравенство выполняется, то большего, чем $k$, количества переключений не требуется.

Таким образом, если условие окончания выполняется, то процедура синтеза заканчивается, в противном случае полагаем $k:\, = k + 1$ и переходим к шагу k.

В результате N шагов рекуррентной процедуры находятся моментные функции цены $\varphi (t,x)$, $\phi (t,x|{{t}_{1}})$, …, $\phi (t,x|{{t}_{1}},\; \ldots ,\;{{t}_{N}})$, условные оптимальные позиционные управления непрерывным движением системы ${\mathbf{u}}(t,x)$, ${\mathbf{u}}(t,x|{{t}_{1}})$, …, ${\mathbf{u}}(t,x|{{t}_{1}},\; \ldots ,\;{{t}_{N}})$ и переключениями ${\mathbf{v}}({{t}_{1}},x)$, ${\mathbf{v}}({{t}_{1}},x|{{t}_{2}})$, …, ${\mathbf{v}}({{t}_{1}},x|{{t}_{2}},\; \ldots ,\;{{t}_{N}})$. Минимальное значение функционала качества (1.6) с не более чем N переключениями вычисляется по формуле

С помощью оптимального позиционного управления можно найти условный оптимальный процесс $(\mathcal{T},x( \cdot ),u( \cdot ),\{ \text{v}\} )$ для любого начального состояния ${{x}_{0}} \in X$ системы (см. разд. 4). Это оптимальный процесс с не более чем N переключениями. Если же процедура синтеза была закончена при выполнении общего условия (6.3) с k = N, то условный оптимальный процесс будет оптимальным.

7. Решение линейно-квадратичной задачи оптимального управления. Рассмотрим ЛКЗ (1.10)–(1.12) синтеза ПС. Для построения моментных функций цены используем решение вспомогательной задачи Больца

где λ – скалярный параметр. Как известно, функция цены в ЛКЗ (7.1) квадратичная: причем симметрическая неотрицательно определенная матрица $\Phi (t)$ порядка n удовлетворяет дифференциальному уравнению Риккати с терминальным условием $\Phi ({{t}_{1}}) = F$. Оптимальное позиционное управление линейное: с матрицей коэффициентов $L(t) = {{D}^{{ - 1}}}(t){{B}^{{\text{Т }}}}(t)\Phi (t)$. Обозначим решение уравнения (7.3) через $\Phi (t|{{t}_{1}},F)$, подчеркивая зависимость этого решения от матрицы F терминального члена $\tfrac{1}{2}{{x}^{{\text{Т }}}}Fx$ + λ. От параметра λ решение уравнения (7.3) и управление (7.4) не зависят. Тогда функционал цены (см. разд. 3) в задаче (7.1) имеет вид

Будем искать моментные функции цены в ЛКЗ (1.10)–(1.12) квадратичного вида

где $\Phi $ – симметрическая неотрицательно определенная матрица порядка n. Согласно рекуррентной процедуре, описанной в разд. 3, в момент первого из оставшихся k переключений справедливо рекуррентное уравнение (3.7). Записываем его для ЛКЗ:

Подставляем функцию (7.6) в уравнение (7.7). Уничтожая свободные члены ${{\lambda }_{{{{t}_{1}}}}}$, …, ${{\lambda }_{{{{t}_{k}}}}}$, получаем алгебраическое уравнение Риккати

для матрицы квадратичной формы, а также выражение для оптимального позиционного управления первым из оставшихся $k$ переключений: где ${{L}_{{{{t}_{1}}}}}({{t}_{2}},\; \ldots ,\;{{t}_{k}}) = {{({{D}_{{{{t}_{1}}}}} + B_{{{{t}_{1}}}}^{{\text{Т }}}\Phi ({{t}_{1}}|{{t}_{2}},\; \ldots ,\;{{t}_{k}}){{B}_{{{{t}_{1}}}}})}^{{ - 1}}}B_{{{{t}_{1}}}}^{{\text{Т }}}\Phi ({{t}_{1}}|{{t}_{2}}, \ldots ,\;{{t}_{k}}){{A}_{{{{t}_{1}}}}}$.

До первого переключения моментная функция цены представляется через функционал цены (7.5) в задаче Больца. Записываем выражение (3.8) для ЛКЗ с учетом (7.5):

Подставляем функцию (7.6) в уравнение (7.10). Уничтожая свободные члены, получаем выражение для матрицы квадратичной формы

Таким образом, можно предложить следующий алгоритм синтеза оптимального позиционного управления линейной ПС с квадратичным критерием качества.

Шаг 0. Решая дифференциальное уравнение Риккати (7.3) с терминальным условием $\Phi ({{t}_{F}})$ = F, найти матрицу $\Phi (t)$ функции цены $\phi (t,x) = \tfrac{1}{2}{{x}^{{\text{Т }}}}\Phi (t)x$ в задаче без переключений, т.е. матрицу 0-моментной функции цены. Составить матрицу $L(t) = {{D}^{{ - 1}}}(t){{B}^{{\text{Т }}}}(t)\Phi (t)$ коэффициентов линейного управления (7.4) непрерывным движением системы. Положить k = 1 и перейти к шагу k.

Шаг k. Решая алгебраическое уравнение Риккати (7.8), найти матрицу $\Phi ({{t}_{1}}|{{t}_{1}},\; \ldots ,\;{{t}_{k}})$ k-моментной функции цены (7.6) в момент $t = {{t}_{1}}$ первого из оставшихся k переключений, а также матрицу ${{L}_{{{{t}_{1}}}}}({{t}_{2}},\; \ldots ,\;{{t}_{k}})$ коэффициентов линейного управления (7.9) переключением состояния системы. Решая дифференциальное уравнение Риккати (7.3) с терминальным условием Φ(t₁) = = $\Phi ({{t}_{1}}|{{t}_{1}}, \ldots ,{{t}_{k}})$, найти матрицу $\Phi (t) = \Phi (t|{{t}_{1}},\; \ldots ,\;{{t}_{k}})$ k-моментной функции цены $\varphi (t,x|{{t}_{1}},\; \ldots ,\;{{t}_{k}})$ до первого переключения, т.е. при $t < {{t}_{1}}$. Составить матрицу $L(t|{{t}_{1}},\; \ldots ,\;{{t}_{k}}) = {{D}^{{ - 1}}}(t){{B}^{{\text{Т }}}}(t)\Phi (t|{{t}_{1}},\; \ldots ,\;{{t}_{k}})$ коэффициентов линейного управления

непрерывным движением системы до первого переключения.

Проверить условие окончания. Таких условий может быть несколько (см. разд. 6). Общим условием окончания синтеза служит сложное для проверки неравенство (6.2). Как правило, при вычислениях задают максимально допустимое количество N переключений. Тогда нужно проверять условие k > N.

Если известно решение (7.5) вспомогательной задачи Больца (7.1), то описанный выше алгоритм можно модифицировать следующим образом.

Шаг 0. Найти матрицу $\Phi (t) = \Phi (t|{{t}_{F}},F)$ функции цены $\phi (t,x) = \tfrac{1}{2}{{x}^{{\text{Т }}}}\Phi (t)x$ в задаче без переключений, т.е. матрицу 0-моментной функции цены. Составить матрицу $L(t) = {{D}^{{ - 1}}}(t){{B}^{{\text{Т }}}}(t)\Phi (t)$ коэффициентов линейного управления (7.4) непрерывным движением системы. Положить k = 1 и перейти к шагу k.

Шаг k. Решая алгебраическое уравнение Риккати (7.8), найти матрицу $\Phi ({{t}_{1}}|{{t}_{1}}, \ldots ,{{t}_{k}})$ k-моментной функции цены (7.6) в момент $t = {{t}_{1}}$ первого из оставшихся k переключений, а также матрицу ${{L}_{{{{t}_{1}}}}}({{t}_{2}}, \ldots ,{{t}_{k}})$ коэффициентов линейного управления (7.9) переключением состояния системы. Найти матрицу $\Phi (t|{{t}_{1}}, \ldots ,{{t}_{k}}) = \Phi (t|{{t}_{1}},\Phi ({{t}_{1}}|{{t}_{1}}, \ldots ,{{t}_{k}}))$ $k$-моментной функции цены $\phi (t,x|{{t}_{1}}$, ..., t_k) до первого переключения, т.е. при $t < {{t}_{1}}$. Составить матрицу L(t | t₁, ..., t_k) = = ${{D}^{{ - 1}}}(t){{B}^{{\text{Т }}}}(t)\Phi (t|{{t}_{1}}$, ..., t_k) коэффициентов линейного управления (7.11) непрерывным движением системы до первого переключения. Условия окончания остаются прежними.

При решении задачи минимизации количества переключений условием окончания служит неравенство (6.3), которое для ЛКЗ имеет вид

Если неравенство выполняется, то большего, чем k, количества переключений не требуется.

Таким образом, если условие окончания выполняется, то процедура синтеза заканчивается, в противном случае полагаем $k: = k + 1$ и переходим к шагу k.

В результате N шагов рекуррентной процедуры находятся матрицы $\Phi (t)$, $\Phi (t|{{t}_{1}})$, …, $\Phi (t|{{t}_{1}}$, ..., t_N) моментных функций цены (7.6), матрицы L(t), $L(t|{{t}_{1}})$, …, $L(t|{{t}_{1}},\; \ldots ,\;{{t}_{N}})$ условных оптимальных позиционных управлений непрерывным движением системы (7.11), а также матрицы ${{L}_{{{{t}_{1}}}}}$, ${{L}_{{{{t}_{1}}}}}({{t}_{2}})$, …, ${{L}_{{{{t}_{1}}}}}({{t}_{2}},\; \ldots ,\;{{t}_{N}})$ условных оптимальных управлений (7.9) переключениями. Минимальное значение функционала качества (1.12) с не более чем $N$ переключениями вычисляется по формуле

С помощью оптимального позиционного управления можно найти условный оптимальный процесс $d = (\mathcal{T},x( \cdot ),u( \cdot ),\{ \text{v}\} )$ для любого начального состояния ${{x}_{0}} \in X$ системы (см. разд. 4). Это оптимальный процесс с не более чем N переключениями. Если же процедура синтеза была закончена при выполнении общего условия (6.3) с k = N, то условный оптимальный процесс будет оптимальным.

8. Пример. Пусть на заданном промежутке времени $T = [0,5]$ динамическая система совершает N переключений (скачков) в моменты времени ${{t}_{i}}$, $i = 1,\; \ldots ,\;N$, которые образуют неубывающую последовательность:

Между неравными последовательными моментами переключений состояние системы изменяется непрерывно, согласно дифференциальным уравнениям:

а в моменты переключений – дискретно в соответствии с рекуррентными уравнениями:

Здесь, как и ранее, $\mathcal{N} = \{ i = 0,1,\; \ldots ,\;N|{{t}_{i}} < {{t}_{{i + 1}}}\} $ – множество номеров ненулевых (по длине) частичных промежутков ${{T}_{i}} \triangleq [{{t}_{i}},{{t}_{{i + 1}}})$ непрерывного движения системы; x(t) – состояние системы в момент времени $t \in T$, $x = {{({{x}_{1}},{{x}_{2}})}^{{\text{Т }}}} \in {{\mathbb{R}}^{2}}$; $u(t)$ – значение управления непрерывным движением системы в момент времени $t \in T$, $u \in \mathbb{R}$. В уравнении (8.3) ${{x}_{i}} \triangleq x({{t}_{i}})$ – состояние системы сразу после i-го переключения, ${{x}_{{i - }}}$ – состояние системы непосредственно перед i-м переключением (1.4); ${{\text{v}}_{i}}$ – управление переключением системы в момент ${{t}_{i}} \in \mathcal{T}$, $\text{v} \in \mathbb{R}$.

Качество процесса управления оценивается квадратичным функционалом

где ${{x}_{0}}$ – начальное состояние системы, $d = (\mathcal{T},x( \cdot ),u( \cdot ),\{ \text{v}\} )$ – допустимый процесс управления. Неотрицательные коэффициенты $\lambda $ и $\eta $ определяют затраты на каждое переключение. Количество N и моменты переключений ${{t}_{1}}$, …, ${{t}_{N}}$ заранее не заданы и подлежат оптимизации. Требуется найти:

1) оптимальный процесс для начального состояния ${{x}_{0}} = {{(8,3)}^{{\text{Т }}}}$ при $\lambda = 0.005$, $\eta = {{10}^{5}}$;

2) наименьшее количество переключений, при котором значение функционала для начального состояния ${{x}_{0}} = {{(8,3)}^{{\text{Т }}}}$ при $\lambda = 0$, $\eta = {{10}^{5}}$ не превосходит величины $\varepsilon = 78.01$.

Рассматривается ЛКЗ. По сравнению с общей постановкой (1.1), (1.10)–(1.12) имеем:

В системе (8.2), (8.3) имеется один канал управления: первая координата управляема при непрерывном движении, а вторая – нет (она экспоненциально отклоняется от нуля). В момент переключения фактически происходит взаимная замена координат состояния – неуправляемая координата становится управляемой и наоборот, причем значение первой управляемой координаты корректируется при помощи управления. Таким образом, совершая переключения (т.е. меняя канал управления), можно попеременно управлять координатами системы.

Составим вспомогательную задачу Больца (7.1)

Здесь F – симметрическая неотрицательно определенная матрица второго порядка, $\lambda $ – скалярный параметр. Решение задачи ищем в виде квадратичной функции (7.2)

Записываем дифференциальное уравнение Риккати (7.3) с терминальным условием $\Phi ({{t}_{1}}|{{t}_{1}}$, F) = F для элементов матрицы Φ(t):

Решая эту задачу Коши, получаем

где $\tau = {{t}_{1}} - t$, $\Delta = ch\tau + {{F}_{{11}}}sh\tau $.

Теперь для задачи (8.1)–(8.4) применяем модифицированный алгоритм, описанный в разд. 7. Моментные функции цены имеют вид (7.6)

где $\Phi (t|{{t}_{1}},\; \ldots ,\;{{t}_{k}})$ – симметрическая неотрицательно определенная матрица второго порядка, а ${{t}_{1}}$, …, ${{t}_{k}}$ – моменты переключений: $0 \leqslant t \leqslant {{t}_{1}} \leqslant \ldots \leqslant {{t}_{k}} \leqslant 5$.

Шаг 0. По формулам (8.5) для нулевой матрицы F = O находим элементы матрицы Φ(t) = = $\Phi (t|5,O)$:

функции цены $\phi (t,x) = \tfrac{1}{2}{{x}^{{\text{Т }}}}\Phi (t)x$ в задаче без переключений, т.е. матрицу 0-моментной функции цены. Составляем матрицу $L(t) = ({{\Phi }_{{11}}}(t),{{\Phi }_{{12}}}(t))$ коэффициентов линейного управления u(t, x) = = $ - L(t)x$. Полагаем k = 1 и переходим к шагу k.

Шаг k. Записываем алгебраическое уравнение Риккати (7.8)

В правой части равенства (8.7) указываются элементы матрицы $\Phi ({{t}_{1}}|{{t}_{2}},\; \ldots ,\;{{t}_{k}})$ предыдущей (k – 1)-моментной функции цены в момент $t = {{t}_{1}}$ первого из оставшихся k переключений. В частности, при k = 1 это будут элементы (8.6) матрицы $\Phi ({{t}_{1}})$. Составляем матрицу ${{L}_{{{{t}_{1}}}}}({{t}_{2}}, \ldots ,{{t}_{k}})$ = = $({{\Phi }_{{11}}}({{t}_{1}}|{{t}_{2}}, \ldots ,{{t}_{k}}),{{\Phi }_{{12}}}({{t}_{1}}|{{t}_{2}}, \ldots ,{{t}_{k}}))$ коэффициентов линейного управления (7.9) переключениями системы. По формулам (8.5) для $F = \Phi ({{t}_{1}}|{{t}_{1}},\; \ldots ,\;{{t}_{k}})$ находим элементы матрицы $\Phi (t|{{t}_{1}},\; \ldots ,\;{{t}_{k}})$ k-моментной функции цены $\phi (t,x|{{t}_{1}},\; \ldots ,\;{{t}_{k}})$ до первого переключения, т.е. при $t < {{t}_{1}}$. Составляем матрицу $L(t|{{t}_{1}},\; \ldots ,\;{{t}_{k}}) = {{D}^{{ - 1}}}(t){{B}^{{\text{Т }}}}(t)\Phi (t|{{t}_{1}},\; \ldots ,\;{{t}_{k}})$ коэффициентов линейного управления (7.11) непрерывным движением системы до первого переключения.

Проверяем условие окончания. Для задач 1) и 2) они разные и обсуждаются ниже. Если условия не выполняются, то полагаем $k: = k + 1$ и переходим к шагу k.

На каждом шаге определяем наименьшее значение функционала (8.4) при фиксированном числе переключений

В задаче 1) условием окончания рекуррентной процедуры служит неравенство ${{I}_{k}} < {{I}_{{k + 1}}}$. Это условие является частным случаем общего условия окончания (6.2). Его можно использовать на практике при решении ЛКЗ. В задаче 2) процедура решения заканчивается, как только ${{I}_{k}} < \varepsilon $.

При численном решении задач 1), 2) моментные функции цены находились по точным формулам (8.5), (8.7), а минимизация моментов переключений выполнялась приближенно перебором на сетке с шагом 0.02 для N = 1, 2, 3, с шагом 0.1 для N = 4, 5, с шагом 0.2 для $N = 6,7,8$. В результате приближенного решения задачи 1) были получены следующие минимальные значения функционала качества:

Наименьшее значение достигается при четырех переключениях. На рис. 1, а изображена оптимальная траектория с четырьмя переключениями. Сплошными линиями представлены непрерывные участки траектории, пунктирными стрелками – переключения. Штрихпунктирная линия ${{x}_{1}} = {{x}_{2}}$ служит для лучшего восприятия скачков траектории.

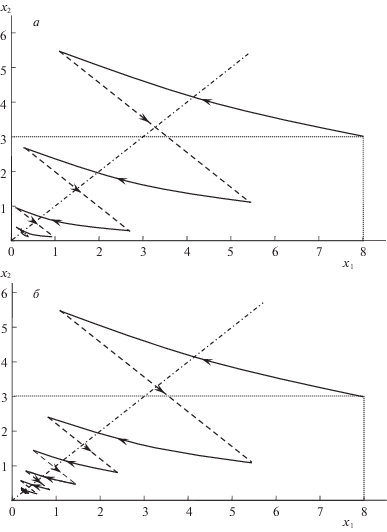
Для задачи 2) были получены следующие минимальные значения функционала качества:

При отсутствии фиксированных затрат на переключение (при $\lambda = 0$) последовательность I_k, $k = 0,1,\; \ldots $, будет невозрастающей. Как видим, при восьми переключениях выполняется требуемое неравенство ${{I}_{8}} < 78.01$. Поэтому рекуррентная процедура построения моментных функций цены заканчивается при k = 8. На рис. 1, б изображена оптимальная траектория с восемью переключениями.

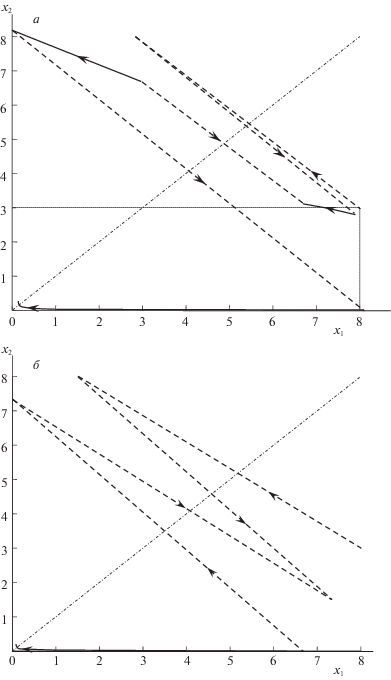
Отметим, что в рассматриваемой ЛКЗ возможны оптимальные процессы с мгновенными многократными переключениями. Они возникают при уменьшении коэффициента $\eta $. В этом случае затраты на скачки траектории уменьшаются по сравнению с затратами на непрерывное изменение состояния. На рис. 2 показаны оптимальные траектории с четырьмя переключениями. На рис. 2, а траектория, полученная при $\eta = 100$, имеет в начальный момент времени мгновенное двукратное переключение. Траектория на рис. 2, б получена при $\eta = 10$. Она имеет в начальный момент времени мгновенное четырехкратное переключение. При малых затратах на скачки траектории именно переключения играют основную роль в процессе управления.

Заключение. Задачи оптимального управления переключаемыми (гибридными) системами отличаются от задач управления непрерывно-дискретными системами свободными моментами переключений, которые могут выбираться при оптимизации процесса управления. Предлагаемые в статье достаточные условия оптимальности сводят задачу синтеза ПС к последовательности задач синтеза непрерывно-дискретных систем с фиксированными моментами переключений с последующей их оптимизацией. Иначе говоря, оптимизация моментов переключений откладывается и становится последней операцией синтеза. Такой подход с вычислительной точки зрения кажется громоздким, так как требует нахождения вспомогательных функций, так называемых моментных функций цены, из которых затем строится “настоящая” функция цены. Однако именно такой способ позволяет решить ЛКЗ синтеза ПС. Этот результат имеет важное теоретическое и практическое значение, поскольку решена классическая проблема Летова–Калмана аналитического конструирования оптимальных регуляторов, перенесенная на новый класс динамических систем – переключаемых (гибридных) систем управления. Заметим, что функция цены для рассматриваемой ЛКЗ не является квадратичной. Поэтому простой перенос известных классических результатов на ПС невозможен. Предлагаемый подход можно применить и для других моделей гибридных систем [12], в том числе систем со сменой математической модели движения [4].

Задача минимизации количества переключений может быть использована для приближенного решения задач оптимального управления путем сужения класса допустимых управлений и аппроксимации оптимальных траекторий [2]. Разработка этого направления представляется актуальной.