Известия РАН. Теория и системы управления, 2019, № 6, стр. 73-89
МЕТОДЫ ДИАГНОСТИРОВАНИЯ ЛИНЕЙНЫХ СИСТЕМ НА ОСНОВЕ СКОЛЬЗЯЩИХ НАБЛЮДАТЕЛЕЙ
А. Н. Жирабок a, b, *, А. В. Зуев b, c, А. Е. Шумский a
a Дальневосточный федеральный ун-т
Владивосток, Россия
b Институт проблем морских технологий ДВО РАН
Владивосток, Россия
c Институт автоматики и процессов управления ДВО РАН
Владивосток, Россия
* E-mail: zhirabok@mail.ru
Поступила в редакцию 10.06.2018
После доработки 19.02.2019
Принята к публикации 25.03.2019
Аннотация
Рассматривается задача функционального диагностирования технических систем, описываемых линейными дифференциальными уравнениями состояния с постоянными коэффициентами, в присутствии возмущений. Для решения задач обнаружения, поиска и идентификации дефектов используются скользящие наблюдатели. Предлагаемый подход базируется на идее построения редуцированной (имеющей меньшую размерность) модели исходной системы, обладающей избирательной чувствительностью по отношению к дефектам и возмущению, на основе которой строится скользящий наблюдатель. В зависимости от конкретных свойств построенной модели рассматриваются три варианта (в каждом из которых решается та или иная задача диагностирования): точной идентификации дефекта, обнаружения дефекта, приближенной идентификации дефекта. Кроме уменьшения сложности средств диагностирования предлагаемый подход позволяет ослабить ограничения, накладываемые на исходную систему, для возможности построения скользящих наблюдателей.
Введение. Одним из мощных средств повышения эффективности эксплуатации сложных технических систем является функциональное диагностирование (ФД), которое позволяет производить проверку правильности функционирования системы в процессе ее работы и оперативно давать информацию о возникших сбоях и дефектах. Задача ФД интенсивно исследуется уже более 30 лет (см., например, работы [1–5]). За это время было разработано несколько методов диагностирования – диагностические наблюдатели, фильтры Калмана, соотношения паритета, идентификация. Методом, дающим наибольшую информацию о возникших дефектах, является идентификация. Последние годы для ее реализации активно применяется подход, основанный на наблюдателях, работающих в скользящем режиме и использующих особенности этого режима [6].
Под скользящим режимом понимается особый вид движения наблюдателя (изменения его внутренних координат), описываемого дифференциальным уравнением с разрывной правой частью. Этот режим характеризуется тем, что движение происходит по некоторой поверхности в пространстве координат наблюдателя (так называемой поверхности скольжения), которая определяется заданной разрывной функцией, в результате чего становится возможным обеспечить желаемые параметры процесса оценивания. Далее наблюдателя со скользящим режимом работы будем называть скользящим наблюдателем.
Скользящие наблюдатели применяются для решения задачи идентификации дефектов в линейных [7, 8], нелинейных [9–12] и сингулярных системах [13], для обеспечения отказоустойчивого управления [14], в ряде практических приложений [15, 16]. Во всех этих работах на исходную систему накладывается ряд ограничений, в частности, одно из типичных требований состоит в том, что система должна быть минимально фазовой.
В настоящей статье метод на основе скользящих наблюдателей используется для решения задач обнаружения, поиска и идентификации дефектов в линейных системах при действии на них возмущений. В основе предлагаемого подхода лежит идея использования редуцированной (имеющей меньшую размерность) модели исходной системы, что дает возможность уменьшить сложность скользящих наблюдателей по сравнению с известными работами [7–12], где строятся наблюдатели полного порядка. Кроме того, удается ослабить ограничения на класс рассматриваемых систем по сравнению с известными методами [7, 8, 10, 14], в частности, снять требование минимальной фазовости, а также обобщить результаты, полученные в [17].
Ранее, в работах авторов настоящей статьи, строились диагностические наблюдатели, задача идентификации дефектов в них не решалась, однако методы, предложенные ранее авторами для построения диагностических наблюдателей минимальной размерности, существенно используются и для решения задачи построения скользящих наблюдателей.
1. Скользящие наблюдатели, основные соотношения. Рассмотрим класс технических систем, описываемых линейной моделью
Здесь $x(t) \in {{R}^{n}}$, $u(t) \in {{R}^{m}}$, $y(t) \in {{R}^{l}}$ – векторы состояния, управления и выхода; $F \in {{R}^{{n \times n}}}$, $G \in {{R}^{{n \times m}}}$, $D \in {{R}^{{n \times q}}}$, $L \in {{R}^{{n \times p}}}$ и $H \in {{R}^{{l \times n}}}$ – известные постоянные матрицы; $d(t) \in {{R}^{q}}$ – вектор-функция, описывающая дефекты: при их отсутствии $d(t) = 0$, при появлении дефекта d(t) становится неизвестной функцией времени; $\rho (t) \in {{R}^{p}}$ – неизвестная функция времени, описывающая действующие на систему возмущения. Предполагается, что известны и ограничены нормы $\left\| {d(t)} \right\|$ и $\left\| {\rho (t)} \right\|$ векторов d(t) и $\rho (t)$.
Коротко напомним основные результаты из [7, 17], используемые в настоящей работе, полагая, что $\rho (t) = 0$.
Предполагается, что система (1.1) удовлетворяет следующим условиям [7]: 1) $q \leqslant l < n$, H и D – матрицы полного ранга, 2) ${\text{rank}}(HD) = q$, 3) тройка $(F,D,H)$ – минимально-фазовая, т.е. инвариантные нули матрицы Розенброка для системы (1.1) устойчивы или отсутствуют [1, с. 171]. Известно [7], что при этих предположениях существует невырожденное преобразование координат $Mx = {{(z_{1}^{{\text{T}}}{\text{ }}z_{2}^{{\text{T}}})}^{{\text{T}}}}$, такое, что в новых координатах ${{z}_{1}} \in {{R}^{{n - l}}}$, ${{z}_{2}} \in {{R}^{l}}$ система (1.1) представляется моделью:
(1.2)
$\begin{gathered} {{{\dot {z}}}_{1}}(t) = {{F}_{{11}}}{{z}_{1}}(t) + {{F}_{{12}}}{{z}_{2}}(t) + {{G}_{1}}u(t),{\text{ }} \\ {{{\dot {z}}}_{2}}(t) = {{F}_{{21}}}{{z}_{1}}(t) + {{F}_{{22}}}{{z}_{2}}(t) + {{G}_{2}}u(t) + {{D}_{2}}d(t), \\ y(t) = {{z}_{2}}(t), \\ \end{gathered} $(1.3)
$\begin{gathered} {{{\dot {\hat {z}}}}_{1}}(t) = {{F}_{{11}}}{{{\hat {z}}}_{1}}(t) + {{F}_{{12}}}{{{\hat {z}}}_{2}}(t) + {{G}_{1}}u(t) - {{F}_{{12}}}{{e}_{y}}(t),{\text{ }} \\ {{{\dot {\hat {z}}}}_{2}}(t) = {{F}_{{21}}}{{{\hat {z}}}_{1}}(t) + {{F}_{{22}}}{{{\hat {z}}}_{2}}(t) + {{G}_{2}}u(t) - ({{F}_{{22}}} - F_{{22}}^{*}){{e}_{y}}(t) + {v}(t), \\ \hat {y}(t) = {{{\hat {z}}}_{2}}(t), \\ \end{gathered} $Положим ${{e}_{1}}(t) = {{\hat {z}}_{1}}(t) - {{z}_{1}}(t)$, тогда из (1.2) и (1.3) следует
Известно [7, 17], что скользящий режим позволяет обеспечить равенства ${{e}_{y}}(t) = 0$ и ${{\dot {e}}_{y}}(t) = 0$ за конечное время $\tau $, поэтому из предыдущих уравнений следует
где ${{v}_{{eq}}}(t)$ – сигнал, который может быть аппроксимирован переменной(1.5)
$d(t) = - g\left\| {{{D}_{2}}} \right\|{{(D_{2}^{{\text{T}}}{{D}_{2}})}^{{ - 1}}}D_{2}^{{\text{T}}}\frac{{P{{e}_{y}}(t)}}{{\left\| {P{{e}_{y}}(t)} \right\| + \delta }}$.Следует отметить, что правая часть этого выражения вычисляется в реальном времени и зависит только от ошибки ey(t) [17].
Таким образом, в [7] для решения задачи идентификации дефекта в минимально фазовой системе, строится скользящий наблюдатель полного порядка. В настоящей статье ставится задача разработки нового метода построения скользящего наблюдателя пониженной размерности при отсутствии ограничения на минимальную фазовость исходной системы. Кроме того, решаются задачи приближенной идентификации дефекта при минимизации влияния возмущения на результат идентификации и поиска дефекта (указания места его появления).
2. Построение редуцированной модели. Решение поставленных задач опирается на редуцированную модель системы (1.1), аналогичную модели, традиционно используемой при решении задача диагностики [2], которая в общем случае описывается уравнением
(2.1)
$\begin{gathered} {{{\dot {x}}}_{*}}(t) = {{F}_{*}}{{x}_{*}}(t) + {{G}_{*}}u(t) + {{J}_{*}}y(t) + {{D}_{*}}d(t) + {{L}_{*}}\rho (t), \\ {{y}_{*}}(t) = {{H}_{*}}{{x}_{*}}(t), \\ \end{gathered} $(2.2)
$\Phi F = {{F}_{*}}\Phi + {{J}_{*}}H,\quad {{R}_{*}}{{H}_{*}} = H\Phi ,\quad {{G}_{*}} = \Phi G,\quad {{D}_{*}} = \Phi D,\quad {{L}_{*}} = \Phi L.$В зависимости от особенностей системы (1.1), характера влияния на нее дефекта и возмущений возможны три случая и соответственно три варианта действий.
1. Существует матрица Φ, удовлетворяющая условиям $\Phi F = {{F}_{*}}\Phi + {{J}_{*}}H$ и ${{R}_{*}}{{H}_{*}} = H\Phi $, такая, что $\Phi L = 0$ и $\Phi D \ne 0$; последнее означает существование модели, не чувствительной к возмущениям и чувствительной к дефекту. Если в этом случае ставится задача обнаружения дефекта, она решается методами, изложенными, например, в [18]. Задача точной идентификации дефекта может быть решена методами, рассматриваемыми в разд. 3.
2. Существует матрица Φ, удовлетворяющая условиям $\Phi F = {{F}_{*}}\Phi + {{J}_{*}}H$ и ${{R}_{*}}{{H}_{*}} = H\Phi $, такая, что $\Phi D = 0$ и $\Phi L \ne 0$; последнее означает существование модели, не чувствительной к дефекту. Задача обнаружения дефекта решается методами, рассматриваемыми в разд. 4.
3. Для любой матрицы Φ, удовлетворяющей условиям $\Phi F = {{F}_{*}}\Phi + {{J}_{*}}H$ и ${{R}_{*}}{{H}_{*}} = H\Phi $, выполняются неравенства $\Phi D \ne 0$ и $\Phi L \ne 0$. Задача приближенной идентификации дефекта решается методами, рассматриваемыми в разд. 5.
В соответствии с описанными случаями ниже рассматриваются три задачи. Для их решения приведем метод построения модели (2.1) минимальной размерности, не чувствительной к возмущениям, на основе которой может быть построен скользящий наблюдатель. Для этого матрицы ${{F}_{*}}$ и ${{H}_{*}}$ размеров $k \times k$ и $1 \times k$ соответственно ищутся в канонической форме следующего вида:
(2.3)
${{F}_{*}} = \left( {\begin{array}{*{20}{c}} 0&1&0& \cdots &0 \\ 0&{{{\alpha }_{1}}}&1& \cdots &0 \\ 0&{{{\alpha }_{2}}}&0&1&0 \\ \cdots & \cdots & \cdots & \ddots & \cdots \\ 0&{{{\alpha }_{{k - 1}}}}&0& \cdots &0 \end{array}} \right),$Используя (2.3), получим из (2.2) уравнения для строк матриц Φ и J:
(2.4)
$\begin{gathered} {{\Phi }_{1}} = {{R}_{*}}H,\quad {{\Phi }_{1}}F = {{\Phi }_{2}} + {{J}_{{*1}}}H,\quad {{\Phi }_{i}}F = {{\Phi }_{{i + 1}}} + {{\alpha }_{{i - 1}}}{{\Phi }_{2}} + {{J}_{{*i}}}H, \\ i = \overline {2,k - 1} ,\quad {{\Phi }_{k}}F = {{\alpha }_{{k - 1}}}{{\Phi }_{2}} + {{J}_{{*k}}}H. \\ \end{gathered} $Для простоты рассмотрим $k = 3$, приводя, где это возможно, формулы для произвольного k. По аналогии с [2] уравнения (2.4) могут быть приведены к одному уравнению
Запишем его в виде
(2.5)
$(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - \,J_{{*1}}^{'}}&{ - \,J_{{*2}}^{'}}&{ - \,J_{{*3}}^{'}} \end{array}){{V}^{{(3)}}} = 0,$(2.6)
$J_{{*1}}^{'} = {{J}_{{*1}}} + {{\alpha }_{1}}{{R}_{*}},\quad J_{{*2}}^{'} = {{J}_{{*2}}} - {{\alpha }_{1}}{{J}_{{*1}}} + {{\alpha }_{2}}{{R}_{*}},\quad J_{{*3}}^{'} = {{J}_{{*3}}} - {{\alpha }_{2}}{{J}_{{*1}}}.$Для учета условия $\Phi L = 0$ перепишем третье уравнение из (2.4) при i = 2, 3 в следующем виде:
(2.7)
$\begin{gathered} {{\Phi }_{2}} = {{\Phi }_{1}}F - {{J}_{{*1}}}H = {{R}_{*}}HF - {{J}_{{*1}}}H, \\ {{\Phi }_{3}} = {{\Phi }_{2}}F - {{\alpha }_{1}}{{\Phi }_{2}} - {{J}_{{*2}}}H = ({{R}_{*}}HF - {{J}_{{*1}}}H)F - {{\alpha }_{1}}({{R}_{*}}HF - {{J}_{{*1}}}H) - {{J}_{{*2}}}H. \\ \end{gathered} $По аналогии с [18, 19] можно показать, что условие $\Phi L = 0$ может быть представлено как
(2.8)
$(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - \,J_{{*1}}^{'}}&{ - \,J_{{*2}}^{'}}&{ - \,J_{{*3}}^{'}} \end{array}){{B}^{{(3)}}} = 0,$(2.9)
${{B}^{{(k)}}} = \left( {\begin{array}{*{20}{c}} {HL}&{HFL}&{H{{F}^{2}}L}& \ldots &{H{{F}^{{k - 1}}}L} \\ 0&{HL}&{HFL}& \ldots &{H{{F}^{{k - 2}}}L} \\ 0&0&{HL}& \ldots &{H{{F}^{{k - 3}}}L} \\ \cdots & \cdots & \cdots & \ldots & \ldots \\ 0&0&0& \ldots &0 \end{array}} \right)$Поскольку строка $\begin{array}{*{20}{c}} {({{R}_{*}}}&{ - \,J_{{*1}}^{'}}&{...}&{ - \,J_{{*k}}^{'})} \end{array}$ удовлетворяет условию (2.5), из (2.5) и (2.8) следует уравнение
(2.10)
$(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - \,J_{{*1}}^{'}}&{...}&{ - \,J_{{*k}}^{'}} \end{array})({{V}^{{(k)}}}{\text{ }}{{B}^{{(k)}}}) = 0.$Оно имеет нетривиальное решение, если
Для построения модели минимальной размерности определяется минимальное k, при котором уравнение (2.10) имеет решение, и находится решение вида $(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - \,J_{{*1}}^{'}}&{...}&{ - \,J_{{*k}}^{'}} \end{array})$. Для этого решения задаются коэффициенты обратной связи ${{\alpha }_{1}}$, …, ${{\alpha }_{{k - 1}}}$, на основе соотношений (2.6) и (2.7) определяются строки ${{J}_{{*1}}}$, …, ${{J}_{{*k}}}$ и ${{\Phi }_{1}}$, …, ${{\Phi }_{k}}$ соответственно и принимается ${{G}_{*}} = \Phi G$ и ${{D}_{*}} = \Phi D$.
3. Решение первой задачи. Рассмотрим вначале случай, когда d(t) – скалярная функция. Найдем решение уравнения (2.10) при минимальном k с матрицами ${{R}_{*}},J_{{*1}}^{'},...,J_{{*k}}^{'}$ и получим соответствующие матрицы $\Phi $, ${{J}_{*}}$ и ${{G}_{*}}$. Таким образом, в модели (2.1) ${{L}_{*}} = \Phi L = 0$; предполагается, что при этом
Отметим, что условие ${{\Phi }_{i}}D = 0$, $i \ne 1$, аналогично требованию независимости первой подсистемы в (1.2) от функции d(t), сформулированному в [7].
Поскольку ${{y}_{*}} = {{R}_{*}}y$, то модель (2.1) с учетом (2.3) принимает вид
(3.2)
$\begin{gathered} {{{\dot {x}}}_{{*1}}}(t) = {{x}_{{*2}}}(t) + {{G}_{{*1}}}u(t) + {{J}_{{*1}}}y(t) + ad(t), \\ {{{\dot {x}}}_{{*2}}}(t) = {{x}_{{*3}}}(t) + {{G}_{{*2}}}u(t) + {{J}_{{*2}}}y(t) + {{\alpha }_{1}}{{x}_{{*2}}}(t), \\ {{{\dot {x}}}_{{*3}}}(t) = {{G}_{{*3}}}u(t) + {{J}_{{*3}}}y(t) + {{\alpha }_{2}}{{x}_{{*2}}}(t), \\ {{y}_{*}}(t) = {{R}_{*}}y(t) = {{x}_{{*1}}}(t); \\ \end{gathered} $Для оценки функции d(t) будем трактовать модель (3.2) как систему, для которой строится скользящий наблюдатель. Отметим, что ограничения, приведенные в разд. 1, которым, согласно [7], должна удовлетворять система (1.1), необходимы, в частности, для построения модели (1.2) с устойчивой матрицей F11. При построении скользящего наблюдателя на основе модели (3.2) устойчивость матрицы F11 обеспечивается путем выбора коэффициентов ${{\alpha }_{1}}$, …, ${{\alpha }_{{k - 1}}}$.
Известно несколько способов построения скользящего наблюдателя [7, 12], применим тот, который рассмотрен в [7] и изложен в разд. 1. Сравнивая (1.2) и (3.2), приходим к выводу, что
(3.3)
$\begin{gathered} {{{\dot {\hat {x}}}}_{{*1}}}(t) = {{{\hat {x}}}_{{*1}}}(t) + {{G}_{{*1}}}u(t) + {{J}_{{*1}}}y(t) + b{{e}_{y}}(t) + v(t), \\ {{{\dot {\hat {x}}}}_{{*2}}}(t) = {{{\hat {x}}}_{{*3}}}(t) + {{G}_{{*2}}}u(t) + {{J}_{{*2}}}y(t) + {{\alpha }_{1}}{{{\hat {x}}}_{{*2}}}(t), \\ {{{\dot {\hat {x}}}}_{{*3}}}(t) = {{G}_{{*3}}}u(t) + {{J}_{{*3}}}y(t) + {{\alpha }_{2}}{{{\hat {x}}}_{{*2}}}(t), \\ {{{\hat {y}}}_{*}}(t) = {{{\hat {x}}}_{{*1}}}(t), \\ \end{gathered} $Поскольку $F_{{22}}^{*}$ – скаляр, то матрица P также скаляр, примем P = 1; константа gd выбирается из условия ${{g}_{d}} > \left\| d \right\|$.
Из (3.2) и (3.3) с учетом того, что ${{y}_{*}} = {{x}_{{*1}}}$ и ${{\hat {y}}_{*}}(t) = {{\hat {x}}_{{*1}}}(t)$, нетрудно получить уравнение для ошибки ${{e}_{y}}(t)$:
Поскольку в скользящем режиме ${{\dot {e}}_{y}}(t) = 0$ и ${{e}_{y}}(t) = 0$, а коэффициенты ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$ выбраны из соображений устойчивости, из предыдущего уравнения получаем $0 = v(t) - ad(t)$, откуда по аналогии с (1.5) функция d(t) оценивается следующим образом:
(3.4)
$d(t) = - {{g}_{d}}\frac{{{\text{|}}a{\text{|}}}}{a}\frac{{{{e}_{y}}(t)}}{{{\text{|}}{{e}_{y}}(t){\text{|}} + \delta }}.$Таким образом, если существует модель (2.1), не чувствительная к возмущениям и чувствительная к дефекту, то может быть решена задача точной идентификации дефекта. Отметим, что в [10] решение подобной задачи потребовало выполнения дополнительного условия, которому должны удовлетворять матрицы $D$ и $L$: $\operatorname{Im} (D) \cap \operatorname{Im} (L) = \{ 0\} $.
Если $d(t) \in {{R}^{q}}$, то при некотором k находится $N \geqslant q$ линейно независимых решений уравнения (2.10) вида 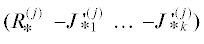 , $j = \overline {1,N} $, строится q моделей вида (3.2) и q наблюдателей вида (3.3), каждый из которых соответствует одному из решений. При этом
предполагается, что для каждой модели выполняются условия вида (3.1), а также
, $j = \overline {1,N} $, строится q моделей вида (3.2) и q наблюдателей вида (3.3), каждый из которых соответствует одному из решений. При этом
предполагается, что для каждой модели выполняются условия вида (3.1), а также
В случае $q > N$ возможна оценка только N компонент функции d(t). Для получения максимально возможного N следует искать решение уравнения (2.10), начиная со значения k, при котором $l(k + 1) \geqslant n$.
4. Решение второй задачи. При решении второй задачи на основе модели (2.1) строится скользящий наблюдатель, не чувствительный к дефекту и чувствительный к возмущениям. Он осуществляет оценку этих возмущений, которая далее используется в диагностическом наблюдателе, обеспечивающем обнаружение дефекта.
4.1. Построение скользящего наблюдателя. Модель (2.1), не чувствительная к дефекту, строится теми же методами, что и модель, не чувствительная к возмущениям, отличие состоит только в том, что в (2.9) матрица L заменяется на D. Каждый из скользящих наблюдателей имеет вид, аналогичный (3.3); в предположении, что $p \leqslant N$, ${\text{rank}}({{L}_{\Sigma }}) = p$, возмущение $\rho (t)$ может быть оценено следующим образом:
(4.1)
$\rho (t) = - {{g}_{\rho }}\left\| {{{L}_{\Sigma }}} \right\|{{(L_{\Sigma }^{{\text{T}}}{{L}_{\Sigma }})}^{{ - 1}}}L_{\Sigma }^{{\text{T}}}\frac{{{{e}_{y}}(t)}}{{\left\| {{{e}_{y}}(t)} \right\| + \delta }},\quad {{L}_{\Sigma }} = \left( {\begin{array}{*{20}{c}} {\Phi _{1}^{{(1)}}L} \\ \cdots \\ {\Phi _{1}^{{(p)}}L} \end{array}} \right),$4.2. Построение диагностического наблюдателя. Для решения задачи диагностирования строится диагностический наблюдатель, чувствительный к дефекту. Предполагается, что такой наблюдатель будет чувствителен и к возмущению, оценка величины которого в виде (4.1) используется при реализации процесса диагностирования.
Описание диагностического наблюдателя имеет вид, аналогичный (2.1):
(4.2)
$\begin{gathered} {{{\dot {x}}}_{0}}(t) = {{F}_{0}}{{x}_{0}}(t) + {{G}_{0}}u(t) + {{J}_{0}}y(t) + {{L}_{0}}\rho (t) + Kr(t), \\ {{y}_{0}}(t) = {{H}_{0}}{{x}_{0}}(t), \\ \end{gathered} $(4.3)
${{R}_{0}}H = {{H}_{0}}\Phi ',\quad \Phi 'F = {{F}_{0}}\Phi ' + {{J}_{0}}H,\quad {{G}_{0}} = \Phi 'G,\quad {{L}_{0}} = \Phi 'L,\quad \Phi 'D \ne 0$Как и в разд. 2, матрицы F0 и H0 ищутся в каноническом виде (2.3) с ${{\alpha }_{1}} = 0$, …, ${{\alpha }_{{k - 1}}} = 0$. Известно [2], что в этом случае матрицы R0 и J0 удовлетворяют уравнению
(4.4)
${{R}_{0}}H{{F}^{{{{k}_{0}}}}} = {{J}_{{01}}}H{{F}^{{{{k}_{0}} - 1}}} + {{J}_{{02}}}H{{F}^{{{{k}_{0}} - 2}}} + ... + {{J}_{{0{{k}_{0}}}}}H.$Запишем его в виде
(4.5)
$(\begin{array}{*{20}{c}} {{{R}_{0}}}&{ - {{J}_{{01}}}}&{ - {{J}_{{02}}}}&{...}&{ - {{J}_{{0{{k}_{0}}}}}} \end{array}){{V}^{{({{k}_{0}})}}} = 0,$Зная матрицу R0, из (4.4) можно найти минимальную размерность k0 и матрицу J0, затем на основе (4.3) – остальные матрицы, описывающие наблюдатель. Поскольку оценка (4.1) является приближенной, полную развязку от возмущения получить не удается, но степень робастности процесса диагностирования существенно повышается.
4.3. Обеспечение чувствительности к дефекту. Для получения чувствительности к дефекту должно выполняться условие $\Phi 'D \ne 0$. Обеспечить выполнение этого условия можно несколькими способами, рассмотрим их.
1. Для найденной описанным выше способом матрицы $\Phi {\text{'}}$ проверить условие $\Phi 'D \ne 0$ и, если оно не выполняется, найти другое решение уравнения (4.4) при прежней или увеличенной размерности наблюдателя.
2. Найти матрицу максимального ранга $D{\text{*}}$, такую, что $D{\text{*}}D = 0$. По аналогии с матрицей D предполагается, что матрица ${{D}^{{{\text{*T}}}}}$ описывает некоторый обобщенный дефект. Для построения модели, не чувствительной к этому дефекту, по аналогии с матрицей ${{B}^{{(k)}}}$ в (2.8) построить матрицу
(4.6)
$B_{0}^{{({{k}_{0}})}} = \left( {\begin{array}{*{20}{c}} {H{{D}^{{{\text{*T}}}}}}&{HF{{D}^{{{\text{*T}}}}}}&{H{{F}^{2}}{{D}^{{{\text{*T}}}}}}& \ldots &{H{{F}^{{{{k}_{0}} - 1}}}{{D}^{{{\text{*T}}}}}} \\ 0&{H{{D}^{{{\text{*T}}}}}}&{HF{{D}^{{{\text{*T}}}}}}& \ldots &{H{{F}^{{{{k}_{0}} - 2}}}{{D}^{{{\text{*T}}}}}} \\ 0&0&{H{{D}^{{{\text{*T}}}}}}& \ldots &{H{{F}^{{{{k}_{0}} - 3}}}{{D}^{{{\text{*T}}}}}} \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ 0&0&0& \ldots &0 \end{array}} \right).$Из условия
найти минимальную размерность ${{k}_{0}}$ и строку $(\begin{array}{*{20}{c}} {{{R}_{0}}}&{ - {{J}_{{01}}}}&{ - {{J}_{{02}}}}&{...}&{ - {{J}_{{0{{k}_{0}}}}}} \end{array})$, которая удовлетворяет уравнениюПостроение завершается определением матриц $\Phi '$, ${{G}_{0}} = \Phi 'G$ и ${{L}_{0}} = \Phi 'L$.
Поскольку матрица $\Phi '$ по построению удовлетворяет условию $\Phi '{{D}^{{{\text{*T}}}}} = 0$, то ${{D}^{*}}\Phi {{'}^{{\text{T}}}} = 0$. Отсюда по определению матрицы $D{\text{*}}$ следует $\Phi {{'}^{{\text{T}}}} = DQ$, или $\Phi ' = {{Q}^{{\text{T}}}}{{D}^{{\text{T}}}}$ для некоторой матрицы Q. Тогда $\Phi 'D = {{Q}^{{\text{T}}}}{{D}^{{\text{T}}}}D$; поскольку ${{D}^{{\text{T}}}}D \ne 0$, то и $\Phi 'D \ne 0$.
3. Использовать эвристический метод, в частности, положить ${{R}_{0}} = (1{\text{ 1 }}...{\text{1}})$ и найти минимальную размерность k0 и матрицу J0 из уравнения (4.4), а затем на основе (4.3) – остальные матрицы, описывающие наблюдатель.
Отметим, что идея использования оцененных возмущений в диагностическом наблюдателе рассматривалась в [9, 11] для нелинейных систем, где скользящий и диагностический наблюдатели строились на основе модели полного порядка. Задача в [9, 11] решалась на основе математического аппарата дифференциальной геометрии, что затрудняет применение ее к линейным системам. Кроме того, подход на основе редуцированной модели, предлагаемый в настоящей работе, позволяет уменьшить сложность средств диагностирования.
5. Решение третьей задачи. Если для любой матрицы $\Phi $, удовлетворяющей условиям (2.2), выполняются неравенства $\Phi D \ne 0$ и $\Phi L \ne 0$, то возможна только приближенная оценка дефекта путем построения скользящего наблюдателя, минимально чувствительного к возмущениям. Рассмотрим вначале случай, когда d(t) – скалярная функция.
Вклад возмущения в модель (2.1) традиционно оценивается нормой Фробениуса ${\text{||}}\Phi L{\text{|}}{{{\text{|}}}_{F}}$ матрицы $\Phi L$, которая с учетом результатов разд. 2 может быть представлена в виде ΦL = = $(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - J_{{*1}}^{'}}&{...}&{ - J_{{*k}}^{'}} \end{array}){{B}^{{(k)}}}$. Из полученных выше результатов следует, что задача минимизации вклада возмущения в невязку сводится к минимизации нормы ${\text{||}}(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - J_{{*1}}^{'}}&{...}&{ - J_{{*k}}^{'}} \end{array}){{B}^{{(k)}}}{\text{|}}{{{\text{|}}}_{F}}$ при выполнении условия (2.5).
Для решения этой задачи предлагается найти все линейно независимые решения уравнения (2.5) вида $(\begin{array}{*{20}{c}} {R_{*}^{{(j)}}}&{ - J_{{*1}}^{{'(j)}}}& \ldots &{ - J_{{*k}}^{{'(j)}}} \end{array})$ для некоторой размерности k, такие, что выполняются условия $\Phi _{1}^{{(j)}}D \ne 0$ и $\Phi _{i}^{{(j)}}D = 0$, $j = \overline {1,N} $, $i \ne 1$. Все эти решения сводятся в матрицу W:
Для решения этой задачи найдем сингулярное разложение матричного произведения WB(k), т.е. представим матрицу WB(k) как
где UB и VB – ортогональные матрицы, ${{\Sigma }_{B}}$ в зависимости от соотношения чисел строк и столбцов матрицы $W{{B}^{{(k)}}}$ имеет видТ е о р е м а. Указанный выбор вектора $w$ обеспечивает оптимальное решение в смысле минимума нормы ${\text{||}}(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - J_{{*1}}^{'}}&{...}&{ - J_{{*k}}^{'}} \end{array})B_{{}}^{{(k)}}{\text{|}}{{{\text{|}}}_{F}}$, равной минимальному сингулярному числу.
Д о к а з а т е л ь с т в о. Прямо следует из свойств сингулярного разложения.
Отметим, что если ${{\sigma }_{1}} = {\text{ }}0$, то $w{{B}^{{(k)}}} = 0$. Последнее означает, что линейная комбинация решений, представленных строками матрицы W, с вектором весовых коэффициентов $w = ({{w}_{1}}, \ldots ,{{w}_{N}})$ дает решение, не чувствительное к возмущениям. В случае ${{\sigma }_{1}} \ne {\text{ }}0$ указанная линейная комбинация дает решение с минимальным значением нормы ${\text{||}}(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - J_{{*1}}^{'}}&{...}&{ - J_{{*k}}^{'}} \end{array})B_{{}}^{{(k)}}{\text{|}}{{{\text{|}}}_{F}}$.
Из сказанного следует, что линейная комбинация решений, представленных строками матрицы W, с весами ${{w}_{1}}, \ldots ,{{w}_{N}}$ дает оптимальное решение с матрицами ${{R}_{*}}$, $J_{*}^{'}$ и $\Phi $, строки последней определяются соотношением ${{\Phi }_{i}} = {{w}_{1}}\Phi _{i}^{{(1)}} + ... + {{w}_{N}}\Phi _{i}^{{(N)}}$, $i = \overline {1,k} $. Далее находится матрица ${{G}_{*}} = \Phi G$, чем завершается синтез модели (3.2), минимально чувствительной к возмущениям. Отметим, что это решение будет оптимальным для найденной размерности модели; увеличение размерности сверх минимального значения может дать лучший вариант решения задачи по критерию минимума нормы ${\text{||}}(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - J_{{*1}}^{'}}&{...}&{ - J_{{*k}}^{'}} \end{array})B_{{}}^{{(k)}}{\text{|}}{{{\text{|}}}_{F}}$
После построения модели (3.2) методами, описанными в разд. 3, строится скользящий наблюдатель для оценки величины скалярного дефекта.
Для приближенной оценки дефекта $d(t) \in {{R}^{q}}$ следует выбрать q первых транспонированных столбцов матрицы UB в качестве векторов весовых коэффициентов ${{w}^{{(1)}}} = (w_{1}^{{(1)}}, \ldots ,w_{N}^{{(1)}})$, …, w(q) = = $(w_{1}^{{(q)}}, \ldots ,w_{N}^{{(q)}})$, которые используются для построения семейства скользящих наблюдателей вида (3.3).
6. Задача локализации дефектов. Для анализа задачи локализации дефектов будем рассматривать модель системы в виде
(6.1)
$\begin{gathered} \dot {x}(t) = Fx(t) + Gu(t) + \sum\limits_{i = 1}^w {{{D}_{i}}{{d}_{i}}(t)} + L\rho (t), \\ y(t) = Hx(t). \\ \end{gathered} $Напомним, что традиционно для решения задачи локализации дефектов строится банк диагностических наблюдателей, каждый из которых инвариантен (нечувствителен) к одной группе дефектов и чувствителен к другой. Решение о возникшем дефекте принимается на основе матрицы синдромов S, которая определяется следующим образом. Для дефекта, определяемого функцией ${{d}_{i}}(t)$ (далее будем говорить просто о дефекте di), строится вектор-синдром ${{S}^{i}}$ по следующему правилу: если $v$-й наблюдатель чувствителен к этому дефекту, полагаем $S_{v}^{i} = 1$, в противном случае $S_{v}^{i} = 0$, $i = \overline {1,w} $.
Совпадение синдромов ${{S}^{i}}$ и ${{S}^{j}}$ для некоторых ${{d}_{i}}$ и ${{d}_{j}}$ означает, что i-й и j-й дефекты в рамках рассматриваемого подхода неразличимы. В этом случае дефекты ${{d}_{i}}$ и ${{d}_{j}}$ помещаются в один класс ${{\Gamma }_{c}}$ для некоторого c. Дефекты, имеющие индивидуальные синдромы, образуют классы, включающие в себя только один дефект. В результате множество дефектов $({{d}_{1}},{\text{ }}{{d}_{2}},{\text{ }}...,{\text{ }}{{d}_{w}})$ раскладываются в семейство непересекающихся множеств (классов неразличимых в рамках используемого метода диагностирования дефектов) $\Gamma = \{ {{\Gamma }_{1}},{{\Gamma }_{2}},...,{{\Gamma }_{d}}\} $, $d \leqslant w$. Матрица синдромов $S$ состоит из множества векторов-синдромов, соответствующих различимым дефектам, как из столбцов.
Таким образом, строки матрицы синдромов соответствуют наблюдателям (невязкам), столбцы – классам неразличимых дефектов. Такая матрица может быть построена следующим образом. Для каждого дефекта ${{d}_{i}}$ из множества $({{d}_{1}},{{d}_{2}},...,{{d}_{w}})$ строится наблюдатель, не чувствительный к этому дефекту и чувствительный к некоторым другим. Если оказывается, что все построенные наблюдатели одинаково чувствительны и не чувствительны к некоторым дефектам ${{d}_{i}}$ и ${{d}_{j}}$, эти дефекты признаются неразличимыми и, как описано выше, помещаются в один класс ${{\Gamma }_{c}}$ для некоторого c.
При использовании подхода на основе скользящих наблюдателей возможны два варианта действий. Первый из них соответствует случаю, когда удается построить модель вида (3.1), не чувствительную ко всем дефектам и чувствительную к возмущению, которое при этом входит только в первое уравнение этой модели. Такая модель может быть построена методами, описанными в разд. 2, после замены в матрице (2.8) элемента L на $D' = ({{D}_{1}}{\text{ }}{{D}_{2}}{\text{ }}...{\text{ }}{{D}_{w}})$; на основе этой модели строится скользящий наблюдатель, оценивающий величину возмущения. Далее описанными в разд. 4 методами строится банк диагностических наблюдателей, каждый из которых соответствует определенной строке матрицы синдромов. Оцененное возмущение используется в них как исходное данное.
Рассмотренный вариант редко реализуем на практике, поскольку построить модель, инвариантную ко всем дефектам, удается только в отдельных частных случаях.
Во втором варианте строится банк моделей, каждая из которых не чувствительна к одной группе дефектов и чувствительна к другой, делается это следующим образом. Для i-й строки матрицы синдромов строится модель вида (3.2) методами, описанными в разд. 2, после замены в матрице (2.8) элемента L на $D_{i}^{*} = (\begin{array}{*{20}{c}} {{{D}_{{{{i}_{1}}}}}}& \cdots &{{{D}_{{{{i}_{c}}}}}} \end{array})$, где матрицы ${{D}_{{{{i}_{1}}}}}$,…, ${{D}_{{{{i}_{c}}}}}$ соответствуют нулевым элементам i-й строки матрицы синдромов. Рассмотрим первую из таких моделей более детально, предполагая, что ей соответствуют матрицы ${{R}^{{(1)}}}$ и ${{\Phi }^{{(1)}}}$ и она чувствительна к дефектам ${{d}_{{11}}},...,{{d}_{{1g}}}$ и, возможно, к возмущениям, при этом $\Phi _{j}^{{(1)}}L = \Phi _{j}^{{(1)}}{{D}_{{11}}} = ... = \Phi _{j}^{{(1)}}{{D}_{{1g}}} = 1$, $j = \overline {2,k} $. Обозначим
(6.2)
${{\dot {x}}_{{*1}}}(t) = {{x}_{{*2}}}(t) + {{G}_{{*1}}}u(t) + {{J}_{{*1}}}y(t) + {{e}_{{*1}}}(t).$Для этой модели методами, описанными в разд. 3, строится скользящий наблюдатель, для которого уравнение (1.4) принимает вид
Согласно изложенным выше правилам, функция ${{e}_{{*1}}}(t)$ может быть оценена скользящим наблюдателем в виде
(6.3)
${{\hat {e}}_{{*1}}}(t) = - {{g}_{{{{e}_{1}}}}}\frac{{{{e}_{{y1}}}(t)}}{{{\text{|}}{{e}_{{y1}}}(t){\text{|}} + \delta }},$Поскольку
После получения оценки полагаем
Аналогичным образом анализируются остальные строки матрицы синдромов, для которых выполняются условия вида $\Phi _{j}^{{(c)}}L = \Phi _{j}^{{(c)}}{{D}_{{c1}}} = ... = \Phi _{j}^{{(c)}}{{D}_{{cg}}} = 1$, $j = \overline {2,k} $, где с – номер рассматриваемой строки; в результате получается следующая система уравнений (для простоты предполагается, что эти условия выполняются для всех строк):
(6.4)
$\left( {\begin{array}{*{20}{c}} {\Phi _{1}^{{(1)}}L}&{\Phi _{1}^{{(1)}}{{D}_{{11}}}}& \ldots &{\Phi _{1}^{{(1)}}{{D}_{{1d}}}} \\ \cdots & \cdots & \ddots & \cdots \\ {\Phi _{1}^{{(v)}}L}&{\Phi _{1}^{{(v)}}{{D}_{{v1}}}}& \ldots &{\Phi _{1}^{{(v)}}{{D}_{{vd}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\rho (t)} \\ {{{d}_{1}}(t)} \\ \cdots \\ {{{d}_{d}}(t)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{{\hat {e}}}_{{*1}}}(t)} \\ \cdots \\ {{{{\hat {e}}}_{{*v}}}(t)} \end{array}} \right),$Полагая, что ${\text{rank}}({{\Phi }_{\Sigma }}) = d + 1$, решение системы (6.4) может быть представлено в виде
7. Пример. Для проверки работоспособности и эффективности предлагаемого в статье метода было проведено моделирование работы синтезированных наблюдателей для идентификации типовых дефектов в следящем электроприводе. Линеаризованная модель разомкнутого электропривода имеет вид
(7.1)
$\begin{gathered} {{{\dot {x}}}_{1}}(t) = {{k}_{1}}{{x}_{2}}(t) + {{d}_{1}}(t), \\ {{{\dot {x}}}_{2}}(t) = {{k}_{2}}{{x}_{3}}(t) + \rho (t) + {{d}_{2}}(t), \\ {{{\dot {x}}}_{3}}(t) = {{k}_{3}}{{x}_{2}}(t) + {{k}_{4}}{{x}_{3}}(t) + {{k}_{5}}u(t) + {{d}_{3}}(t), \\ \end{gathered} $Полагаем, что измеряемыми являются переменные ${{x}_{1}}(t)$ и ${{x}_{3}}(t)$, а дефекты моделируются следующим образом: ${{d}_{1}}(t) = {{\dot {\tilde {\alpha }}}_{{\text{р}}}}(t)$, что соответствует возникновению ошибки ${{\tilde {\alpha }}_{{\text{р}}}}(t)$ в показаниях датчика положения выходного вала редуктора; ${{d}_{2}}(t) = ({{k}_{{\text{м}}}}{\text{/}}({{J}_{{\text{н}}}} + \tilde {J}(t)) - {{k}_{{\text{м}}}}{\text{/}}{{J}_{{\text{н}}}}){{x}_{3}}(t)$, что соответствует изменению номинального момента инерции нагрузки на величину $\tilde {J}(t)$; ${{d}_{3}}(t) = - {{\tilde {R}}_{{\text{я}}}}(t){{x}_{3}}(t){\text{/}}{{L}_{{\text{я}}}}$, что соответствует изменению активного сопротивления цепи якоря электродвигателя на величину ${{\tilde {R}}_{{\text{я}}}}(t)$ (например, при его значительном нагреве). Возмущение $\rho (t) = - \tilde {M}(t){\text{/}}{{J}_{{\text{н}}}}$ обусловлено наличием внешнего нагрузочного момента $\tilde {M}(t)$, приведенного к валу двигателя.
Отметим, что поскольку ${{x}_{1}}(t)$ не входит в уравнения для других переменных, то дефект ${{d}_{1}}(t)$, соответствующий ошибке в показаниях датчика положения, может быть отображен так, как это указано в модели (7.1) – с помощью слагаемого ${{d}_{1}}(t)$.
В результате рассматриваемый электропривод (7.1) будет описываться моделью (1.1) со следующими матрицами:
Рассмотрим вначале случай, когда возмущением можно пренебречь и построим модель, не чувствительную к третьему дефекту как наиболее сложную. Непосредственные вычисления при k = 2 дают следующее:
Можно проверить, что уравнение (2.10) имеет решение с
Примем для простоты ${{\alpha }_{1}} = 0$, тогда из (2.4) и (2.6) получаем
(7.2)
$\begin{gathered} {{{\dot {x}}}_{{*1}}}(t) = {{x}_{{ * 2}}}(t) + {{d}_{1}}(t), \\ {{{\dot {x}}}_{{*2}}}(t) = {{k}_{1}}{{k}_{2}}{{y}_{2}}(t) + {{k}_{1}}{{d}_{2}}(t), \\ {{y}_{*}}(t) = {{x}_{{*1}}}(t), \\ \end{gathered} $Сравнивая (7.2) с (3.2), можно сделать вывод о том, что для оценки функции d1(t) скользящий наблюдатель (3.3) принимает вид
(7.3)
$\begin{gathered} {{{\dot {\hat {x}}}}_{{*1}}}(t) = {{{\hat {x}}}_{{ * 2}}}(t) + b{{e}_{{y1}}}(t) + v(t), \\ {{{\dot {\hat {x}}}}_{{*2}}}(t) = {{k}_{1}}{{k}_{2}}{{y}_{2}}(t), \\ {{{\hat {y}}}_{{*1}}}(t) = {{{\hat {x}}}_{{*1}}}(t), \\ \end{gathered} $Рассмотрим задачу построения модели, не чувствительной ко второму дефекту. Непосредственные вычисления дают следующее:
Нетрудно видеть, что уравнение (2.10) имеет решение при k = 1 с ${{R}_{*}} = (\begin{array}{*{20}{c}} {{{k}_{3}}}&{ - {{k}_{1}}} \end{array})$, $J_{*}^{'} = {{J}_{*}}$ = (0 –k1k4); матрица ${\Phi }$ имеет вид ${\Phi } = (\begin{array}{*{20}{c}} {{{k}_{3}}}&0&{ - {{k}_{1}}} \end{array})$, что дает ${{G}_{*}} = - {{k}_{1}}{{k}_{5}}$, ${{D}_{{*1}}} = {{k}_{3}}$, ${{D}_{{*3}}} = - {{k}_{1}}$ и редуцированную модель
(7.4)
$\begin{gathered} {{{\dot {x}}}_{*}}(t) = - {{k}_{1}}{{k}_{4}}{{y}_{2}}(t) - {{k}_{1}}{{k}_{5}}u(t) + {{k}_{3}}{{d}_{1}}(t) - {{k}_{1}}{{d}_{3}}(t), \\ {{y}_{{*2}}}(t) = {{x}_{*}}(t), \\ \end{gathered} $Из (3.3) следует, что скользящий наблюдатель принимает вид
(7.5)
$\begin{gathered} {{{\dot {\hat {x}}}}_{*}}(t) = - {{k}_{1}}{{k}_{4}}{{y}_{2}}(t) - {{k}_{1}}{{k}_{5}}u(t) + b{{e}_{{y2}}}(t) + v(t), \\ {{{\hat {y}}}_{{*2}}}(t) = {{{\hat {x}}}_{*}}(t), \\ \end{gathered} $Из вида моделей (7.2) и (7.4) следует, что первая содержит функции d1(t) и d2(t), вторая – d1(t) и d3(t). Как правило, при решении задачи ФД принимается предположение об однократных дефектах, поэтому перечисленные дефекты можно отличить друг от друга с помощью матрицы синдромов, описанной в разд. 6 и имеющей вид
Здесь строки соответствуют оценкам ${{\hat {d}}_{1}}(t)$ и ${{\hat {d}}_{3}}(t)$, столбцы – дефектам. Решение на основе этой матрицы принимается следующим образом: если от нуля отличны оценки ${{\hat {d}}_{1}}(t)$ и ${{\hat {d}}_{3}}(t)$, то возник первый дефект и его величина может быть оценена; если от нуля отлична только оценка ${{\hat {d}}_{3}}(t)$, возник третий дефект и его величина также может быть оценена; если от нуля отлична только оценка ${{\hat {d}}_{1}}(t)$, то возник второй дефект, его величина не может быть оценена; если ${{\hat {d}}_{1}}(t) = 0$ и ${{\hat {d}}_{3}}(t) = 0$, то дефектов нет.
Отметим, что модель, не чувствительную к первому дефекту, строить нет необходимости, так как она не даст дополнительной информации о дефектах.
Остановимся на случае, когда возмущением пренебречь нельзя. Поскольку возмущение и второй дефект входят в описание системы одинаково, то модель, не чувствительная к возмущению, имеет вид (7.4), соответствующий наблюдатель описывается уравнениями (7.5). Из (7.4) следует, что различить первый и третий дефекты теперь не удается, но идентификация какого-либо из них возможна; ясно также, что второй дефект невозможно обнаружить, так как эффект его влияния смешан с эффектом влияния возмущения.
Проведем моделирование системы (7.1) с наблюдателями (7.3) и (7.5). При моделировании задавались следующие значения параметров рассматриваемого следящего электропривода: ${{J}_{{\text{н}}}} = 0.0001$ кг ⋅ м2, ${{k}_{\omega }} = {\text{0}}{\text{.02}}$ B ⋅ c, ${{k}_{{\text{у}}}} = {\text{100}}$, ${{R}_{{\text{я}}}} = 0.4$ Oм, ${{L}_{{\text{я}}}} = 0.004\;{\text{Г}}$, ${{k}_{{\text{м}}}} = 0.02$ H ⋅ м/А, ${{i}_{{\text{р}}}} = 100$. Для обеспечения заданных показателей качества управления в прямой цепи электропривода использовалось типовое последовательное корректирующее устройство с передаточной функцией
При этом в качестве входного воздействия на электропривод подавалось следующее желаемое значение угла поворота выходного вала редуктора: $\alpha _{{\text{р}}}^{{\text{ж}}}(t) = {\text{sin}}\,(t)$.
При моделировании возмущение имитировалось функцией $\tilde {M}(t) = 0.07\sin (0.8{\text{ }}t){\text{ Hм}}$ на интервале 0–10 c; первый дефект – функцией ${{\tilde {\alpha }}_{{\text{р}}}}(t) = 0.005\sin (1.57{\text{ }}t - 3.14)$ рад на интервале 2–6 c, а третий дефект – функцией $\tilde {R}(t) = 0.1(1 - {{e}^{{ - (t - 4)}}})$ Ом на интервале 4–8 c.
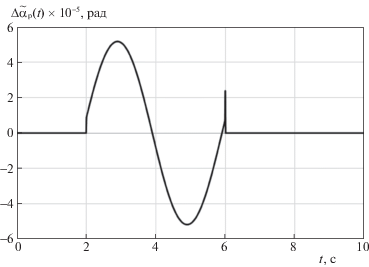
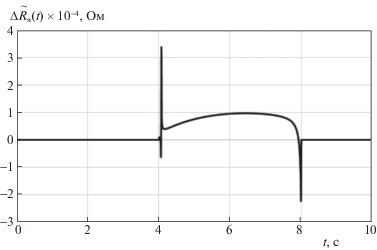
На рис. 1 представлены графики функции ${{\tilde {\alpha }}_{{\text{р}}}}(t)$ и ее оценки, на рис. 2 – график ошибки идентификации $\Delta {{\tilde {\alpha }}_{{\text{р}}}}(t)$ этой функции, на рис. 3 и 4 – аналогичные графики функции ${{\tilde {R}}_{{\text{я}}}}(t)$, ее оценки и ошибки идентификации $\Delta {{\tilde {R}}_{{\text{я}}}}(t)$ при отсутствии возмущения. Из рисунков можно видеть, что построенные наблюдатели позволяют своевременно определить моменты времени появления ошибок ${{\tilde {\alpha }}_{{\text{р}}}}$ и ${{\tilde {R}}_{{\text{я}}}}$, а также обеспечить достаточно точную оценку величин этих ошибок.
Рис. 1.
Функция ${{\tilde {\alpha }}_{{\text{р}}}}(t)$ (кривая 1) и результат ее идентификации (кривая 2) при $\rho (t) = 0$
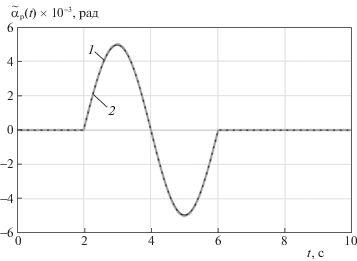
Рис. 3.
Функция ${{\tilde {R}}_{{\text{я}}}}(t)$ (кривая 1) и результат ее идентификации (кривая 2) при $\rho (t) = 0$
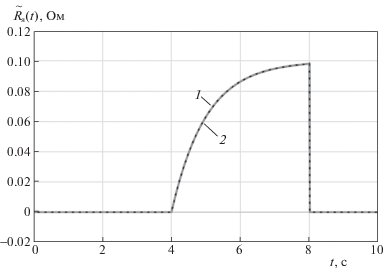
На рис. 5 приведен график оценки ${{\tilde {R}}_{{\text{я}}}}$ при наличии возмущения и отсутствии первого дефекта; график соответствующей ошибки идентификации совпадает с графиком рис. 4. Поскольку на интервалах 0–4 c и 8–10 c значения оценки равны нулю, ясно, что построенный наблюдатель не чувствителен к возмущению ρ(t).
Рис. 5.
Функция ${{\tilde {R}}_{{\text{я}}}}(t)$ (кривая 1) и результат ее идентификации (кривая 2) при $\rho (t) \ne 0$
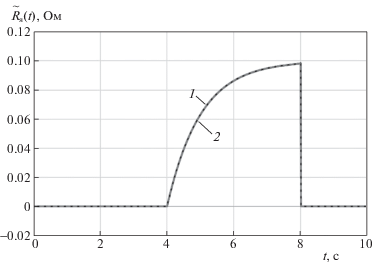
Таким образом, результаты моделирования на примере идентификации типовых дефектов, возникающих в следящем электроприводе, показали работоспособность и высокую эффективность предложенного в статье метода робастного поиска и идентификации дефектов на основе скользящих наблюдателей.
Заключение. С использованием метода на основе скользящих наблюдателей в работе решаются задачи обнаружения, поиска и идентификации дефектов. Предложенная модификация этого метода на основе редуцированной модели исходной системы дала возможность отказаться от условия, чтобы система была минимально фазовой, и уменьшить размерность скользящего наблюдателя. Использование редуцированной модели исходной системы позволило с единых позиций рассмотреть три варианта реализации средств диагностирования в зависимости от избирательных свойств модели к дефектам и возмущению. Результаты проведенного моделирования подтвердили правильность теоретических предпосылок.
Список литературы
Мироновский Л.А. Функциональное диагностирование динамических систем. М.–СПб.: МГУ-ГРИФ, 1998.
Шумский А.Е., Жирабок А.Н. Методы и алгоритмы диагностирования и отказоустойчивого управления динамическими системами. Владивосток: ДВГТУ, 2009.
Simani S., Fantuzzi C., Patton R. Model-based Fault Diagnosis in Dynamic Systems Using Identification. Berlin, Heidelberg: Springer-Verlag, 2002.
Blanke M., Kinnaert M., Lunze J., Staroswiecki M. Diagnosis and Fault-Tolerant Control. Berlin: Springer-Verlag, 2006.
Ding S. Data-driven Design of Fault Diagnosis and Fault-tolerant Control Systems. London: Springer-Verlag, 2014.
Уткин В.И. Скользящие режимы и их применение в системах с переменной структурой. М.: Наука, 1974.
Edwards C., Spurgeon S. On the Development of Discontinuous Observers // International J. Control. 1994. V. 59. P. 1211–1229.
Edwards C., Spurgeon S., Patton R. Sliding Mode Observers for Fault Detection and Isolation // Automatica. 2000. V. 36. P. 541–553.
Floquet T., Barbot J., Perruquetti W., Djemai M. On the Robust Fault Detection via a Sliding Mode Disturbance Observer // International J. Control. 2004. V. 77. P. 622–629.
Yan X., Edwards C. Nonlinear Robust Fault Reconstruction and Estimation Using Sliding Mode Observers // Automatica. 2007. V. 43. P. 1605–1614.
Sharma R., Aldeen A. Fault and Disturbance Reconstruction Nonlinear Systems Using a Network of Interconnecting Sliding Mode Observer // IET Control Theory and Applications. 2011. V. 5. № 6. P. 751–763.
He J., Zhang C. Fault Reconstruction Based on Sliding Mode Observer for Nonlinear Systems // Mathematical Problems in Engineering. 2012. V. 2012. ID 451843. P. 1–22.
Chan J., Tan C., Trinh H. Robust Fault Reconstruction for a Class of Infinitely Unobservable Descriptor Systems // International J. Systems Science. 2017. V. 48. № 8. P. 1646–1655.
Alwi H., Edwards C. Fault Tolerant Control Using Sliding Modes with On-line Control Allocation // Automatica. 2008. V. 44. P. 1859–1866.
Chandra K., Alwi H., Edwards C. Fault Reconstruction for a Quadrotor Using an LPV Sliding Mode Observer // Proc. 9th IFAC Symp. Safeprocess. Paris, France, 2015. P. 374–379.
Zhang K., Jiang B., Yan X., Mao Z. Sliding Mode Observer Based Incipient Sensor Fault Detection with Application to High-speed Railway Traction Device // ISA Transactions. 2016. V. 63. P. 49–59.
Жирабок А.Н., Шумский А.Е., Зуев А.В. Подход к диагностированию линейных систем на основе скользящих наблюдателей // Мехатроника, автоматизация, управление. 2017. Т. 18. № 11. С. 728–733.
Жирабок А.Н., Шумский А.Е., Соляник С.П., Суворов А.Ю. Метод построения нелинейных робастных диагностических наблюдателей // АиТ. 2017. № 9. С. 34–48.
Жирабок А.Н., Шумский А.Е., Павлов С.В. Диагностирование линейных динамических систем непараметрическим методом // АиТ. 2017. № 7. С. 3–21.
Low X., Willsky A., Verghese G. Optimally Robust Redundancy Relations for Failure Detection in Uncertain Systems // Automatica. 1996. V. 22. P. 333–344.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления