Известия РАН. Теория и системы управления, 2019, № 6, стр. 63-72

Ведение. В [1] функциональные характеристики сетевых систем общего вида изучались в рамках формализма математической модели передачи многопродуктового (МП) потока в сети. Основное внимание уделялось способности сети сохранять связи между пользователями после удаления ряда ее элементов. При этом структура информационных потоков не конкретизировалась и оценки строились, исходя из априорного наличия полного графа тяготений. Для более тонкого анализа уязвимости МП-сети требуется конструктивное описание множества достижимых МП-потоков. В данной работе ставится именно такая задача: для системы ограничений МП-модели изучается множество достижимых векторов потоков, которые могут передаваться одновременно между всеми парами узлов. Вычисляются граничные и угловые точки, соответствующие предельным значениям, достижимым при передаче максимального потока в монопольном режиме для соответствующих пар узлов.

При исследовании функциональных возможностей системы решаются различные задачи поиска распределения потоков в МП-сети. В итоге предложен ряд способов формирования внутреннего опорного каркаса множества достижимых значений МП-потока. Построение предлагается проводить итеративно. На каждом шаге строится конус возможных направлений для поиска оптимального распределения потоков. Направляющие лучи (ребра) конуса определяются на основе решения задач о передаче максимального потока для каждой (одной) пары узлов при сохранении достигнутых значений для всех остальных, т.е. в ограниченно-монопольном режиме.

1. Многопродуктовая потоковая модель. Рассмотрим стандартную математическую запись модели передачи МП-потока в сети с многими источниками и стоками [2]. МП-сеть $\langle V,R,P\rangle $ задается множествами:

вершин/узлов сети $V = \{ {{v}_{1}},{{v}_{2}},...,{{v}_{N}}\} $ ($N$ – общее число узлов);

ребер $R = \{ {{r}_{1}},{{r}_{2}},...,{{r}_{e}}\} \subset V \times V$ физического графа $G(d) = \langle V,R\rangle $ сети с пропускной способностью, равной вектору d, компоненты которого ${{d}_{k}}$ ограничивают суммарные потоки по ребру ${{r}_{k}}$, $k = \overline {1,e} $ ($e$ – общее число физических ребер), где граф $G(d)$ без петель и сдвоенных ребер;

дуг логического графа сети $P = \{ {{p}_{1}},{{p}_{2}},...,{{p}_{M}}\} \subset V \times V$, соответствующих тем парам вершин сети (далее – тяготеющим парам), между которыми передается поток определенного вида (продукта) с учетом направления передачи ($M$ – общее число тяготеющих пар).

Далее будем говорить об МП-сети, в которой между тяготеющими парами вершин из $P \subset V \times V$ передаются информационные потоки (свои для каждой упорядоченной пары).

Для упрощения обозначений предположим, что все физические ребра – неориентированные. При этом для спецификации потоков на ребрах $G(d)$ назовем прямым направление от вершины с меньшим номером к вершине с большим и каждое ребро ${{r}_{k}}$ физического графа сети будем представлять двумя ориентированными дугами с номерами k и $k + e$ для прямого и обратного направлений соответственно. (В случае ориентированного ребра физического графа формально можно ограничить нулем поток по дуге, направленной противоположно ориентации ребра.) Для любой вершины ${{v}_{j}} \in V$ обозначим через $S({{v}_{j}})$ множество номеров выходящих из нее дуг:

а через $T({{v}_{j}})$ – множество номеров входящих дуг:

Для каждой i-й тяготеющей пары ${{p}_{i}}$ введем обозначение ${{p}_{i}} = ({{v}_{{{{s}_{i}}}}},{{v}_{{{{t}_{i}}}}})$, где вершина ${{v}_{{{{s}_{i}}}}}$ называется источником, а ${{v}_{{{{t}_{i}}}}}$ – стоком i-го вида продукта и/или информационного потока. Вершины источник и сток определяются согласно ориентации дуги логического графа сети. Распределение потоков одного вида по дугам будет задаваться матричной переменной $x = {\text{\{ }}{{x}_{{ik}}}{\text{\} }}$ размерности $m \times 2e$. Каждый элемент ${{x}_{{ik}}}$ обозначает количество продукта i-го вида (i-го информационного потока) по ребру ${{r}_{k}} \in R$ в прямом направлении для $k \leqslant e$ или по ребру ${{r}_{{k - e}}} \in R$ в обратном направлении, если $k > e$. Все ${{x}_{{ik}}} \geqslant 0$. Кроме неотрицательности для возможных значений переменной $x$ должны выполняться условия сохранения потока любого вида в транзитных для него узлах, т.е. $\forall v \in V$:

Значение ${{z}_{i}} \geqslant 0$ равно величине входного информационного потока, который пропускается по сети от источника к стоку i-й тяготеющей пары при распределении потоков ${{x}_{{ik}}}$ по физическим ребрам сети. Вектор $z = z(x)$, определяемый из (1.1), называется МП-потоком.

На ребрах графа $G(d)$ МП-сети потоки не смешиваются, но, тем не менее, подчиняются единым ограничениям. Каждому ребру ${{r}_{k}} \in R$ физического графа $G(d)$ МП-сети приписано число ${{d}_{k}}$, названное пропускной способностью ребра ${{r}_{k}}$ и измеряемое в условных единицах потоков, для передачи которых предназначена данная сеть. Тем самым различные виды потоков должны измеряться в сопоставимых единицах. Как правило, речь идет об однотипных потоках, которые различаются лишь адресатами и отправителями, но не являются взаимозаменяемыми, например пассажиропотоки. Компоненты вектора $d = ({{d}_{1}},{{d}_{2}},...,{{d}_{e}})$ известны, фиксированы и неотрицательны. Вектор d задает ограничения-неравенства на распределение потоков в сети:

которые совместно с ограничениями (1.1) формируют многогранник допустимых распределений потоков:

Введем множество достижимых значений МП-потока

т.е. векторов величин потоков, которые удается одновременно передать между всеми тяготеющими парами (заданными дугами логического графа сети). Как правило, всем дугам логического графа МП-сети заранее приписаны числа $f_{i}^{0}$ и ставится задача о допустимости, состоящая в исследовании возможности пропускать по сети потоки величины $f_{i}^{0}$ для тяготеющих пар ${{p}_{i}} \in P$. Если ${{f}^{0}} \in Z(d)$, то МП-сеть называется допустимой для передачи вектора требований ${{f}^{0}}$, а вектор потоков ${{f}^{0}}$ – достижимым в данной МП-сети.

2. Предельные величины потоков и сечения множества достижимых значений МП-потока. Рассмотрим сначала модельную ситуацию, когда все ресурсы сети задействованы для передачи единственного потока между выделенной парой тяготеющих узлов ${{p}_{i}} \in P$, а для всех остальных потоки полагаются равными нулю или просто определяются по остаточному принципу. Указанный способ управления сетью назван в [1] монопольным режимом передачи потока z_i (далее –М-режимом). Максимальный поток, который можно передать для тяготеющей пары в М-режиме, является решением стандартной (однопродуктовой) задачи о максимальном потоке.

Задача 1. Найти

Поток величины $z_{i}^{0}$ назван в [1] МРМ-потоком, т.е. максимальным потоком для $i$-й тяготеющей пары, передаваемым в М-режиме.

Решим задачу 1 для всех ${{p}_{i}} \in P$ и вычислим значения $z_{i}^{0}\;{\text{для}}\;{\kern 1pt} i = \overline {1,M} $. Векторы ${{z}^{i}} = (0,...,0,z_{i}^{0}$, 0, ..., 0), $i = \overline {1,M} $, являются угловыми точками множества $Z(d)$, которые лежат на пересечении с соответствующими координатными осями границы множества достижимых значений в задаче многокритериальной максимизации МП-потока. Множество векторов

определяет угловые точки симплекса в $M$-мерном пространстве значений МП-потока. Этот симплекс назовем С-сечением 1-го уровня для множества $Z(d)$. Вектор с компонентами, равными МРМ-потокам, будем называть МРМ-вектором.

В общем случае u⁰ (2.2) не принадлежит множеству достижимых значений $Z(d)$, а является идеальной точкой [3] в указанной выше задаче многокритериальной оптимизации на максимум вектора z по всем $z \in Z(d)$. (Далее, говоря о границе Парето и Слейтера множества $Z(d)$, будем иметь в виду именно такую задачу.) Рассмотрим луч $(0,{{u}^{0}})$, направленный из начала координат в идеальную точку u⁰, как множество векторов $\{ 0,\beta {{u}^{0}}\} $ и найдем значение $\beta {\text{*}}$ в точке его пересечения с С-сечением.

Задача 2. Найти $\beta {\text{*}}(1)$, $\gamma _{i}^{*}(1) \geqslant 0$ такие, что

Для решения задачи представление вектора $\beta {\text{*}}(1){{u}^{0}}$ в виде выпуклой комбинации угловых точек zⁱ запишем покомпонентно:

Таким образом, величина

определяет искомую точку пересечения с координатами равными величинам потоков, которые можно одновременно передать по всем информационным направлениям ${{p}_{i}} \in P$ (т.е. всем тяготеющим парам). Вектор z*(1) принадлежит С-сечению и задает априорно допустимое распределение потоков и достижимое значение МП-потока, равно-пропорциональное МРМ-потокам.

Теперь найдем предельный вектор достижимых значений МП-потока z*(0) на луче, ведущем в идеальную точку, из решения следующей задачи.

Задача 3. Найти

Оптимум в задаче 3 определяет точку пересечения луча $(0,{{u}^{0}})$ с границей Парето множества достижимых значений МП-потока:

Тем самым вектор z*(0) лежит на границе множества $Z(d)$ и является парето-оптимальным МП-потоком, пропорциональным МРМ-потокам.

Сравним значения $\beta {\text{*}}(0),\beta {\text{*}}(1)$.

1. Если $\beta {\text{*}}(0) = \beta {\text{*}}(1) = 1{\text{/}}M$, то в этом случае граница Парето множества $Z(d)$ совпадает с С-сечением и любая точка этой границы может быть представлена в виде выпуклой комбинации угловых точек zⁱ. В частности, когда все пути соединения всех тяготеющих пар проходят через некоторое “узкое место” (“bottle neck”) физического графа $G(d)$ сети, а источники и стоки всех тяготеющих пар (элементы логического графа) находятся по разные стороны этого условного “моста”, тогда использование С-сечения 1-го уровня позволяет полностью описать все максимальные из достижимых значений МП-потока.

2. Рассмотрим другой крайний случай – паретовская точка совпадает с идеальной, т.е. $\beta {\text{*}}(0)$ = 1, $z{\text{*}}(0) = {{u}^{0}}$. Тогда множество $Z(d)$ – параллелепипед, а луч $(0,{{u}^{0}})$ – его главная диагональ. Например, исходная система – сеть “сигнального” управления, а соответствующий физический граф $G(d)$ и логический граф P представляют собой “звезду”, из центра которой получают управляющие сигналы и/или осуществляется информационный обмен лица, принимающего решения, с подчиненными, относящимися к “висячим” вершинам физического графа $G(d)$. Любая слейтеровская точка [4] из $Z(d)$ может быть представлена в виде выпуклой комбинации вектора $z{\text{*}}(0)$ и векторов из множества Z⁰ – угловых точек С-сечения (2.1).

3. В промежуточном случае $1 > \beta {\text{*}}(0) > \beta {\text{*}}(1)$. (Такие случаи возникают уже в двухуровневых сигнальных сетях, когда граф $G(d)$ имеет структуру типа “дерево”.) Построим для него С-сечение 2-го уровня из решения набора следующих задач для каждой тяготеющей пары ${{p}_{i}} \in P$.

Задача 4. Найти

при условиях

Понятно, что значение максимума в задаче 4 не превышает максимума в задаче 1. При этом вектор – решение задачи 4:

является граничной точкой множества достижимых значений МП-потока $Z(d)$. Множество всех таких векторов образует угловые точки симплекса, который определяет С-сечение 2-го уровня. Указанный симплекс будет не ближе к началу координат, чем С-сечение 1-го уровня. Найдем точку пересечения луча $(0,{{u}^{0}})$, ведущего в идеальную точку, с С-сечением 2-го уровня.

Задача 5. Найти $\beta {\text{*}}(2)$, $\gamma {\text{*}}(2) \geqslant 0$ такие, что

Перейдя к покомпонентной записи

с учетом сделанных обозначений получим, что и на основе найденного решения сформируем искомый вектор с компонентами $z_{i}^{*}(2) = {{\beta }^{*}}(2)z_{i}^{0}$, $i = \overline {1,M} $.

Значение $\beta {\text{*}}(2)$ не меньше, чем $\beta {\text{*}}(1)$, и не больше, чем $\beta {\text{*}}(0)$. Далее проверим условие $\beta {\text{*}}(0) - \beta {\text{*}}(2) \leqslant \delta $, где $\delta $ – заранее заданное малое положительное число – оценка достаточной близости к границе $Z(d)$. Если условие выполнено, то происходит останов. При этом запоминаем множество ${{Z}^{0}}(2)$ (2.3), задающее С-сечение 2-го уровня, для возможности быстрого поиска других оптимальных векторов МП-потока, например, на пересечении с лучом, ведущим в точку ${{u}^{0}}(2)$ с координатами $z_{i}^{0}(2)$, которая тоже, как правило, недостижима.

Если $\beta {\text{*}}(0) - \beta {\text{*}}(2) > \delta $, то исходя из достигнутого значения вектора МП-потока $z{\text{*}}(2)$ формируем С-сечение 3-го уровня на базе решения следующих задач.

Задача 6. Найти

при дополнительных условиях

Решаем задачу 6 для всех ${{p}_{i}} \in P$ и получаем векторы, соответствующие граничным точкам $Z(d)$, на основе найденных $z_{i}^{0}(3)$:

Формируем множество угловых точек С-сечения 3-го уровня:

Находим $\beta {\text{*}}(3)$ как аналитическое решение очередной задачи типа 5 поиска коэффициентов разложения $\gamma _{i}^{*}(3)$ по угловым точкам симплекса:

Проверяем выполнение $\beta {\text{*}}(0) - \beta {\text{*}}(3) \geqslant \delta $ и либо продолжаем аналогично построение С-сечений, либо останавливаемся на очередном шаге.

Задачи 4 и 6 похожи на стандартную задачу 2 на максимум однопродуктового потока, но только с дополнительным ограничением снизу на потоки остальных тяготеющих пар. Соответствующие значения $z_{i}^{0}(q)$ будем называть построенными для ${{p}_{i}} \in P$ в ограниченно-монопольном режиме (ОМ-режиме) управления потоками. Чем больше q, тем ближе $z_{i}^{0}(q)$ к $z_{i}^{*}(q)$, а составленный из них вектор ОМРМ-потоков ${{u}^{0}}(q)$ – к достижимому. Векторы, направленные из $z{\text{*}}(q)$ в угловые точки С-сечения уровня $(q + 1)$, определяют конус возможных направлений улучшения достигнутых значений $z_{i}^{*}(q)$, а ребра, соединяющие указанные угловые точки с $z{\text{*}}(0)$, относятся к внутреннему опорному каркасу $K(q)$, построение которого будет описано ниже. Послойное описание множества $Z(d)$ на основе С-сечений позволяет эффективно решать многие стандартные задачи распределения информационных потоков в МП-сетях даже безотносительно к вектору требований на их передачу.

3. Построение системы каркасов. Теперь вспомним, что, согласно разд. 1, в МП-модели задан вектор требований f ⁰ (или, другими словами, заявок) на величину информационного потока, передаваемого между источником и стоком, для всех тяготеющих пар. Для упрощения дальнейших вычислений рассмотрим случай, когда требования тяготеющих пар равны между собой (произвольный вектор требований исследуется аналогично) и превышают предельные функциональные возможности исходной сети по любому информационному направлению, в частности, речь может идти о сети после аварии.

Пусть ${{f}_{0}} > 0$ – величина потока, которую требуется передать для каждой тяготеющей пары ${{p}_{i}} \in P$, ${{f}^{0}} = \{ {{f}_{0}}, \ldots ,{{f}_{0}}\} $. Будем обозначать через

уровень выполнения требований i-й тяготеющей пары при передаче в сети потока ${{z}_{i}}$ для нее. Множеству достижимых значений МП-потока $Z(d)$ (1.3) поставим в соответствие множество достижимых уровней выполнения требований для всех тяготеющих пар:

Вернемся к определению (2.2) и на основе вектора из МРМ-потоков u⁰ вычислим значения:

В сделанных предположениях $0 < \theta _{i}^{0} < 1$ $\forall i = \overline {1,M} $ , так как требования на передачу информационных потоков больше соответствующих МРМ-потоков. Величина $\theta _{i}^{0}$ задает предельно достижимый уровень выполнения требований для тяготеющей пары ${{p}_{i}} \in P$ при условии передачи потока в М-режиме. Для данного вектора требований ${{f}^{0}} = ({{f}_{0}},...,{{f}_{0}})$ решим следующую задачу.

Задача 7. Найти

при условии

Вектор-решение ${{z}^{{**}}}(0) = (z_{1}^{{**}}(0),z_{2}^{{**}}(0),...,z_{M}^{{**}}(0))$ с равными компонентами $z_{i}^{{**}}(0) = {{\tau }^{{**}}}(0){{f}_{0}},$ $i = \overline {1,M} $, определяет точку пересечения луча $(0,{{f}^{0}})$ с внешней границей множества $Z(d)$. Здесь и далее под внешней границей множества достижимых значений МП-потока будем подразумевать замыкание той части границы, которая не лежит в координатных плоскостях. Внешняя граница не вся является паретовской, но состоит из слейтеровских точек множества $Z(d)$.

В общем случае $z{\text{**}}(0) \ne z{\text{*}}(0)$, примем такое предположение для дальнейшего. Определим множество векторов

как опорный внутренний каркас 1-го уровня для множества $Z(d)$. Каркас $K$(1) можно рассматривать как приближенное описание внешней границы множества $Z(d)$, он представляет собой набор (сетку) точек на внешней границе $Z(d)$, а z*(0) – одна из таких “реперных” точек, лежащая на главной диагонали $Z(d)$. Плоскость, в которой лежат векторы z*(0) и z**(0), будем называть рассекающей плоскостью, а сами векторы z*(0) и z**(0) – направляющими опорными векторами рассекающей плоскости (далее также – uf-плоскости, поскольку рассекающая плоскость определяется вектором, ведущим в идеальную точку, и вектором требований).

Для формирования граничных точек многоугольника, лежащего в пересечении множества достижимых значений МП-потока и uf-плоскости, сначала определим точку пересечения луча $(0,{{f}^{0}})$ с С-сечением 1-го уровня. Рассмотрим выпуклую комбинацию угловых точек из Z⁰:

или покомпонентно

Таким образом,

и координаты точки пересечения являются компонентами вектора

Следуя рассуждениям о соотношении значений $\beta {\text{*}}(0)$ и $\beta {\text{*}}(1)$, можно утверждать, что относительная разность коэффициентов $\tau {\text{**}}(0)$ и $\tau {\text{**}}(1)$ показывает, насколько можно увеличить потоки сразу для всех тяготеющих пар при “уравнительной” стратегии управления потоками. (В случае произвольного ${{f}^{0}}$ вместо уравнительной стратегии можно говорить о пропорциональной стратегии, которая является уравнительной в смысле равенства уровней ${{\theta }_{i}}$ выполнения требований тяготеющих пар.) Если возможное увеличение значимо для системы, то будем искать точку пересечения $z{\text{**}}(2)$ (сначала пусть существует) луча $(0,{{f}^{0}})$ с С-сечением 2-го уровня и т.д. (для этого уже все построено в разд. 2). Множество векторов

– опорный внутренний каркас 2-го уровня для множества $Z(d)$.

Прямая между точками z*(1) и $z{\text{**}}(1)$ принадлежит $uf$-плоскости, образованной лучами из начала координат в точки z*(0) и $z{\text{**}}(0)$ (и в идеальные точки ${{u}^{0}}$ и ${{f}^{0}}$). В той же плоскости будет лежать и прямая, соединяющая точки $z{\text{*}}(2)$ и $z{\text{**}}(2)$, образованные пересечением $(0,{{u}^{0}})$ и $(0,{{f}^{0}})$ с С-сечением 2-го уровня. Таким образом, в $uf$-плоскости получили приближение к отрезку, соединяющему $z{\text{*}}(0)$ и $z{\text{**}}(0)$.

В рассекающей плоскости для $Z(d)$ видны все С-сечения, они как бы “нанизаны” на луч $(0,{{u}^{0}})$, ведущий в идеальную точку. Однако С-сечения выше 1-го уровня не обязательно будут “протыкаться” вектором требований. В ситуации, когда луч $(0,{{f}^{0}})$ не пересекается с С-сечением 2-го уровня (если следующих уровней, то для них процедура аналогична), выберем для построения z**(2) точку ${{z}^{ + }}(2)$ его пересечения с плоскостью указанного сечения. Затем найдем точку пересечения с внешней границей множества $Z(d)$ луча с направляющим вектором $z{\text{*}}(2) - {{z}^{ + }}(2)$, исходящего из точки z*(2) (в сторону точки ${{z}^{ + }}(2)$, которая не является достижимой).

Задача 8. Найти

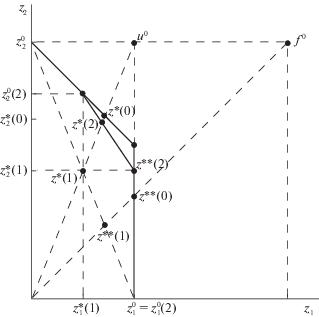
при условии

Решение задачи 8 определяет внешнюю граничную точку $z{\text{**}}(2) = z{\text{*}}(2) + \alpha {\text{*}}({{z}^{ + }}(2) - z{\text{*}}(2))$ множества $Z(d)$ и принадлежит uf-плоскости. Полученное решение может не быть равнопропорциональным вектору требований, но увеличивает уровень выполнения требований для тех тяготеющих пар, для которых это возможно без снижения достигнутого на предыдущем шаге значения $\tau {\text{**}}(1)$ по остальным информационным направлениям. На рисунке изображена описанная ситуация для примера, когда uf-плоскость совпадает с координатной плоскостью $(0,{{z}_{1}}) \times (0,{{z}_{2}})$. В этом случае $z_{1}^{{**}}(2)$ совпадает с $z_{1}^{0}(2)$.

В общем случае задачи типа 8 имеет смысл решать для получения дополнительных точек пересечения uf-плоскости с внешней границей множества $Z(d)$, которые не находятся на осях координат. В частности, кроме задачи 8, можно поставить симметричную ей задачу.

Задача 9. Найти

при условии

Решение задачи 9 определяет иную внешнюю граничную точку z^–(2) = z⁺(2) – $\alpha {\text{**}}({{z}^{ + }}(2) - z{\text{*}}(2))$ множества $Z(d)$, принадлежащую uf-плоскости. Для примера с рисунка эта точка совпадает с ${{z}^{2}}(2)$, но в общем случае позволяет получить еще один вектор в uf-плоскости на границе $Z(d)$. Аналогичные задачи для уточнения внутренних опорных каркасов ставятся и на остальных шагах процедуры агрегированного описания $Z(d)$ вместе с построением С-сечений. После того, как построено С-сечение уровня $q$ и найдены точки $z{\text{*}}(q)$ и $z{\text{**}}(q)$ его пересечения с лучами $(0,{{u}^{0}})$ и $(0,{{f}^{0}})$, лежащие в uf-плоскости, предлагается следующее. Отрезок, соединяющий найденные точки (и тоже лежащий в uf-плоскости), продляется в обе стороны до пересечения с внешней границей множества $Z(d)$ с помощью решения двух приведенных далее задач 10 и 11. Понятно, что в случае, когда вектор требований не пересекает рассматриваемое С-сечение и точка $z{\text{**}}(q)$ получена с помощью решения задачи типа описанной выше задачи 8, то соответствующую задачу 10 решать уже не надо – новая граничная точка не появится.

Задача 10. Найти

при условии

Задача 11. Найти

при условии

Если на очередном шаге $Q \geqslant 2$ разность $\tau {\text{**}}(Q) - \tau {\text{**}}(Q - 1)$ оказывается незначительной так же, как и разность $\beta {\text{*}}(0) - \beta {\text{*}}(Q)$, то на основе всех найденных к этому шагу точек внешней границы $Z(d)$ и множеств ${{Z}^{0}},\;{{Z}^{0}}(q)$ угловых точек С-сечений, $q \leqslant Q$, формируем $K(Q)$ – опорный внутренний каркас $Q$-го уровня для множества $Z(d)$. Любой вектор, представимый выпуклой комбинацией векторов из $K(Q)$, принадлежит $Z(d)$, т.е. является достижимым значением МП-потока. Последний построенный вектор $z{\text{**}}(Q)$ дает определенное приближение к такому распределению потоков в МП-сети, при котором нельзя повысить уровень выполнения требований ${{f}_{0}}$ ни одной тяготеющей пары без снижения указанного уровня для другой.

Замечание. Если вектор требований ${{f}^{0}}$ состоит из различных компонент, то указанные выше построения можно применять к множеству $\Theta ({{f}^{0}})$ вместо $Z(d)$ и определять аналоги С-сечений и систему опорных внутренних каркасов для множества достижимых уровней выполнения требований на потоки в МП-сети.

Заключение. Задачи потокового программирования [5, 6] имеют свою специфику, существенно отличающую их от общих задач линейного программирования в силу упрощенной структуры матрицы ограничений даже в наиболее общем случае МП-сети. Поэтому задача описания множества достижимых значений МП-потока стоит отдельно. В данной работе предложена процедура построения сечений указанного множества, приближающих изнутри те его грани, которые представляют интерес с точки зрения того или другого целевого вектора потоков, в частности, вектора требований и вектора, соответствующего идеальной точке в задаче максимизации вектора МП-потока. Показано, как перейти от М-режима управления потоками к ОМ-режиму, постепенно подходя к справедливому [7, 8] распределению потоков в МП-сети.