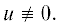Известия РАН. Теория и системы управления, 2020, № 1, стр. 168-176

Введение. Движение локомоционных систем, движущихся в среде с сопротивлением за счет изменения конфигурации (относительного положения тел системы), изучалось во многих работах, в том числе в [1–8]. Как правило, рассматривалось периодическое возбуждение системы, при котором конфигурация, или сила взаимодействия тел, изменяются периодически во времени. При этом предполагалось, что перемещение локомоционной системы за период постоянно и скорости тел системы периодичны. Такое движение является предпочтительным для локомоционной системы с практической точки зрения. Однако для периодического режима движения локомоционной системы начальные условия (начальная скорость одного из тел при заданном законе изменения конфигурации системы или начальные скорости всех тел при заданных силах взаимодействия) должны быть выбраны соответствующим образом, что, как правило, не удается точно осуществить при движении реального локомоционного робота. При произвольных же начальных условиях скорости тел системы не будут описываться периодическими функциями и перемещение за период каждого из тел, входящих в систему, не будет постоянной величиной. При численном моделировании и в экспериментах для различных систем с изменяемой конфигурацией было установлено, что периодический режим движения является устойчивым по отношению к начальным условиям и что произвольное движение сходится к периодическому. В небольшом количестве работ [5, 6] для конкретных механических систем и законов возбуждения вопрос о сходимости решения к периодическому был разрешен аналитически, причем было показано, что сходимость может осуществляться за конечное время или быть экспоненциальной. Неясно, является ли сходимость к периодическому режиму движения общим результатом или она верна лишь для некоторых классов динамических систем, законов возбуждения и законов сопротивления среды и какова скорость сходимости. Более того, проблема существования и единственности периодического режима движения системы тел с изменяемой конфигурацией при ее периодическом возбуждении также является открытой. В данной работе исследуются вопросы существования и единственности периодического режима движения, а также оценивается скорость сходимости к нему для простейшей системы двух взаимодействующих тел, движущихся вдоль прямой при периодическом возбуждении. Ранее в [7] авторами было показано, что для такой механической системы периодический режим существует в случае степенной зависимости сопротивления среды от скорости. В настоящем исследовании изучены широкие классы различных законов возбуждения и законов сопротивления среды, позволяющие утверждать существование, единственность и экспоненциальную устойчивость периодического режима движения, даны оценки скорости сходимости.

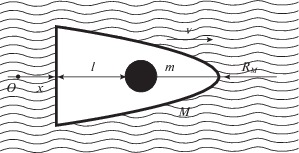
1. Постановка задачи. Рассмотрим прямолинейное движение локомоционной системы, состоящей из герметичного корпуса и массы, движущейся внутри корпуса. Корпус движется в сопротивляющейся среде. При взаимодействии внутреннего тела и корпуса изменяется скорость корпуса, что приводит к изменению силы сопротивления среды, являющейся внешней силой по отношению к системе. Таким образом, управляя движением внутреннего тела относительно корпуса, можно управлять движением системы. Оба тела моделируются точечными массами, через $M$ обозначим массу корпуса, а через $m$ – массу внутреннего тела. В дальнейшем будем называть корпус телом M, а внутреннее тело – массой $m$.

Масса $m$ движется вдоль горизонтальной направляющей внутри тела M, и тело $M$ движется вдоль параллельной ей прямой (см. рисунок). На массу $m$ действует сила со стороны тела M, внутренняя по отношению к системе, и не действует сила сопротивления среды, а тело $M$ подвержено влиянию и силы взаимодействия со стороны внутренней массы, и силы сопротивления среды. Обозначим координату и скорость тела $M$ через $x$ и $v(t) = \dot {x}(t)$, координату массы $m$ относительно тела $M$ – через $l$ и силу сопротивления среды – через ${{R}_{M}}$.

Движение корпуса подчиняется уравнению

Это равенство описывает движение центра масс системы; его левая часть представляет собой суммарную массу системы двух тел, умноженную на ускорение центра масс, а правая равна внешней силе (единственной внешней силе, действующей на систему). Предполагается, что сопротивление среды описывается строго убывающей непрерывной функцией скорости тела M, обращающейся в ноль в состоянии покоя тела:

Обозначим взятое с противоположным знаком нормированное ускорение массы $m$ относительно корпуса через $u$:

Введем также обозначение для нормированной силы сопротивления среды:

Предполагается, что масса $m$ движется периодически относительно тела M с периодом, равным T:

Исключим из рассмотрения случай, когда внутренняя масса не движется, т.е. положим, $l \ne {\text{const}}$. Отсюда следует, что

С учетом введенных обозначений уравнение движения системы принимает вид

где сопротивление R непрерывно зависит от скорости и удовлетворяет соотношениям

Будем предполагать, что функции $R(v)$ и $u(t)$ таковы, что решение уравнения (1.3) существует и единственно для любых начальных условий. В частности, достаточным условием существования и единственности решения является то, что функция $R(v)$ дифференцируема и ее производная ограничена на любом конечном интервале $[{{v}_{1}},{{v}_{2}}]$, а функция $u(t)$ – кусочно-непрерывна [9].

В силу периодичности движения (1.1) массы $m$ относительное ускорение $u$ является периодической функцией времени и удовлетворяет интегральному равенству

Это равенство – необходимое условие периодичности движения $l(t)$. Оно также достаточно для периодичности движения, поскольку скорость $\dot {l}(t)$ при этом условии периодична и существует величина $\dot {l}(0)$, при которой смещение $l(t)$ также периодично. Наложим дополнительное ограничение на функцию $u(t)$. Будем считать, что она принадлежит классу кусочно-непрерывных функций. В этом случае относительная скорость $\dot {l}(t)$ массы $m$, а также скорость корпуса $v(t)$ являются непрерывными функциями времени. С учетом периодичности $u$ ограничена:

Изучим движение тела M, подчиняющееся соотношениям (1.3)–(1.6), с начальной скоростью $v(0)$. Будем называть режим движения системы периодическим, если периодическое движение массы $m$ порождает движение тела $M$ с периодически изменяющейся скоростью, так что

Задача. Для системы, подчиняющейся соотношениям (1.3)–(1.6), исследовать существование и единственность решения, удовлетворяющего условию периодичности (1.7), и сходимость непериодических решений к нему.

Обозначим периодическое решение задачи (1.3)–(1.6) как ${{v}_{*}}(t)$. Поскольку функция $u$ периодична, тождество (1.7) эквивалентно условию

Таким образом, исследуется возможность выбора начальных условий для системы двух тел, движущейся вдоль прямой в сопротивляющейся среде, при котором периодическое изменение расстояния между телами приводит к периодическому изменению скорости тела M. В таком движении смещение обоих тел за период одинаково и постоянно. Кроме того, рассматривается вопрос об устойчивости такого движения по отношению к начальным условиям и вопрос о скорости сходимости к нему, если сходимость имеет место.

2. Периодические режимы движения системы. Исследуем поведение решений задачи (1.3)–(1.6). Покажем, что все решения монотонно стремятся к некоторому интервалу значений, за конечное время попадают в него и затем в нем остаются.

Лемма 1. Если $\mathop {lim}\limits_{v \to \pm \infty } \left| {R(v)} \right| > A$, то для каждого решения $v(t)$ задачи (1.3)–(1.6) существует момент времени $\tau \geqslant 0$, такой, что для всех $t \geqslant \tau $ выполнено неравенство

при этом если $\tau > 0$, то функция $\left| {v(t)} \right|$ монотонно убывает на отрезке $[0,\tau ]$.

Покажем сначала, что существует момент времени $\tau \geqslant 0$, такой, что $v(\tau ) \in [{{R}^{{ - 1}}}(A),{{R}^{{ - 1}}}( - A)]$. Если $v(0) \in [{{R}^{{ - 1}}}(A),{{R}^{{ - 1}}}( - A)]$, то это верно и $\tau = 0$. Предположим теперь, что $v(0) > {{R}^{{ - 1}}}( - A)$. Тогда существует такой момент времени ${{\tau }_{ + }}$, для которого $v({{\tau }_{ + }}) = {{R}^{{ - 1}}}( - A)$. Действительно, если такого момента времени не существует, то с учетом непрерывности $v(t)$ получаем

и, следовательно, $R(v) < - A$ для всех $t \geqslant 0$. Интегрируя уравнение движения (1.3) на интервале $[0,nT]$ и используя (1.5), находим для всех $n \in \mathbb{N}$. Это противоречит неравенству (2.2) для достаточно больших $n$. Следовательно, ${{\tau }_{ + }}$ существует. Обозначим через ${{D}_{ + }}$ множество всех таких ${{\tau }_{ + }}$. Положим $\tau = inf{{D}_{ + }}$. Поскольку $v({{\tau }_{ + }}) = {{R}^{{ - 1}}}( - A)$ для всех ${{\tau }_{ + }}$, а решение $v(t)$ непрерывно, то $v(\tau ) = {{R}^{{ - 1}}}( - A)$. Более того, $v(t)$ > R^–1(–A) на интервале $[0,\tau )$. Поэтому в силу уравнения (1.3), ограничения (1.6) на функцию $u(t)$ и монотонного убывания (1.4) сопротивления $R(v)$ имеем т.е. решение $v(t)$ убывает на отрезке $[0,\tau ]$.

Если $v(0) < {{R}^{{ - 1}}}(A)$, можно аналогично показать, что существует момент времени ${{\tau }_{ - }}$, для которого $v({{\tau }_{ - }}) = {{R}^{{ - 1}}}(A)$. Положим $\tau = inf{{D}_{ - }}$, где ${{D}_{ - }} = \{ {{\tau }_{ - }}\} $. При таком $\tau $ будет выполнено равенство $v(\tau )$ = R^–1(A), а на интервале $[0,\tau )$ – неравенство $v(t) < {{R}^{{ - 1}}}(A)$. Отсюда

т.е. решение $v(t)$ возрастает на отрезке $[0,\tau ]$.

Таким образом, получено, что для любого начального условия существует момент времени $\tau $, такой, что $v(\tau ) \in [{{R}^{{ - 1}}}(A),{{R}^{{ - 1}}}( - A)]$ и что модуль решения $\left| {v(t)} \right|$ монотонно убывает, а само решение монотонно приближается к отрезку $[{{R}^{{ - 1}}}(A),{{R}^{{ - 1}}}( - A)]$ при $t \in [0,\tau ]$.

Покажем теперь, что $v(t) \in [{{R}^{{ - 1}}}(A),{{R}^{{ - 1}}}( - A)]$, $t \geqslant \tau $. Покажем для этого, что $v(t) \in [{{R}^{{ - 1}}}(A) - \varepsilon $, R^–1(–A) + ε], $\varepsilon > 0$, $t \geqslant \tau $. Действительно, при $v = {{R}^{{ - 1}}}(A) - \varepsilon $ выполнено $\dot {v} > 0$ и при $v = {{R}^{{ - 1}}}( - A) + \varepsilon $ выполнено $\dot {v} < 0$, поэтому решение не выйдет из интервала $[{{R}^{{ - 1}}}(A) - \varepsilon ,{{R}^{{ - 1}}}( - A) + \varepsilon ]$. Поскольку $\varepsilon > 0$ может быть выбрано сколь угодно малым, то $v(t) \in [{{R}^{{ - 1}}}(A),{{R}^{{ - 1}}}( - A)]$, $t \geqslant \tau $. Лемма доказана.

Изучим теперь свойства периодических решений ${{{v}}_{ * }}$ задачи (1.3)–(1.6).

Утверждение 1 (cуществование). Для любого закона сопротивления среды, такого, что $\mathop {lim}\limits_{v \to \pm \infty } \left| {R(v)} \right|$ > A, периодическое решение ${{{v}}_{ * }}(t)$ задачи (1.3)–(1.6) существует и

Докажем сначала существование периодического решения ${{v}_{*}}(t)$. Для всех решений $v(t)$ задачи (1.3)–(1.6) с начальным условием $v(0) > {{R}^{{ - 1}}}( - A)$ выполнено $v(T) < v(0)$. Это следует из леммы 1, так как на интервале $[0,\tau ]$ решение $v(t)$ монотонно убывает, и при $t \geqslant \tau $ принадлежит интервалу $[{{R}^{{ - 1}}}(A),{{R}^{{ - 1}}}( - A)]$. Обозначим через B множество начальных значений, на которых $v(T) < v(0)$, и пусть ${{v}_{*}}$ – точная нижняя грань этого множества. Она существует, потому что множество B ограничено снизу, так как для всех решений $v(t)$ с начальным условием $v(0) < {{R}^{{ - 1}}}(A)$ выполнено $v(T) > v(0)$ (также следует из леммы 1).

Докажем, что для решения ${{v}_{*}}(t)$ с начальным значением ${{v}_{*}}$ выполнено ${{v}_{*}}(T) = {{v}_{*}}(0) = {{v}_{*}}$. Для доказательства от противного рассмотрим две другие возможности. Предположим, что ${{v}_{*}}(T) > {{v}_{*}}$. Рассмотрим решение $\tilde {v}(t)$ c начальным условием $\tilde {v}(0)$, таким, что ${{v}_{*}} < \tilde {v}(0) < {{v}_{*}}(T)$ и $\tilde {v}(0) \in B$, т.е. $\tilde {v}(T) < \tilde {v}(0)$. Такое $\tilde {v}(0)$ существует, поскольку ${{v}_{*}}$ – нижняя грань $B$ и ${{v}_{*}} \notin B$. Тогда решения ${{v}_{*}}(t)$ и $\tilde {v}(t)$ пересекаются, что противоречит допущению о единственности решения дифференциального уравнения. Аналогично можно показать, что если ${{v}_{*}}(T) < {{v}_{*}}$, то, положив $\tilde {v}(0) = ({{v}_{*}}(T) + {{v}_{*}}){\text{/}}2$, получим, что решение $\tilde {v}(t)$ с начальным значением $\tilde {v}(0)$ будет удовлетворять неравенству $\tilde {v}(T) > \tilde {v}(0)$ и будет пересекаться с решением ${{v}_{*}}(t)$, что также противоречит допущению о единственности решения. Поэтому ${{v}_{*}}(T) = {{v}_{*}}(0) = {{v}_{*}}$.

Покажем теперь, что ${{v}_{*}}(t) \in [{{R}^{{ - 1}}}(A),{{R}^{{ - 1}}}( - A)]$, $t \geqslant 0$. В лемме 1 было показано, что любое решение удовлетворяет соотношению (2.1), следовательно, и для периодического решения выполнено включение ${{v}_{*}}(t) \in [{{R}^{{ - 1}}}(A),{{R}^{{ - 1}}}( - A)]$, $t \geqslant \tau $ для некоторого $\tau $. В силу периодичности ${{v}_{ * }}(t)$ это включение верно для всех $t$, начиная с $t = 0$, т.е. ${{v}_{*}}(t) \in [{{R}^{{ - 1}}}(A),{{R}^{{ - 1}}}( - A)]$, $t \geqslant 0$. Утверждение доказано.

Утверждение 2 (единственность). Периодическое решение задачи (1.3)–(1.6) единственно.

Предположим противное и пусть ${{v}_{i}}(t)$, $i = 1,2$, – два различных периодических решения задачи (1.3)–(1.6). Проинтегрировав уравнение движения (1.3) на интервале $[0,T]$, получим

Из условия ${{v}_{i}}(0) = {{v}_{i}}(T)$ следует

что вместе с равенством (1.5) дает необходимое и достаточное условие периодического изменения скорости

Пусть ${{v}_{1}}(0) > {{v}_{2}}(0)$. В силу единственности решения дифференциального уравнения (1.3) выполнено неравенство ${{v}_{1}}(t) > {{v}_{2}}(t)$ для всех $t \in [0,T]$. Из монотонного убывания сопротивления (1.4) следует, что $R({{v}_{1}}(t)) < R({{v}_{2}}(t))$ для всех $t \in [0,T]$, откуда

Последнее противоречит равенству (2.4). Аналогично рассматривается случай ${{v}_{1}}(0) < {{v}_{2}}(0)$. Таким образом, доказано, что не существует двух различных периодических решений.

Утверждение 3 (сходимость). Любое решение задачи (1.3)–(1.6) экспоненциально сходится к периодическому.

Доказательство приведем для случая, когда функция $R(v)$ дифференцируема. Обозначим периодическое и произвольное решения уравнения (1.3) через ${{v}_{*}}(t)$ и $v(t)$ соответственно. Будем считать, что для $v(t)$ неравенство (2.1) выполнено при всех $t \geqslant 0$. В противном случае можно сделать замену переменной $\tilde {t} = t - \tau $, где $\tau $ определяется в лемме 1. Введем следующее обозначение:

В силу леммы 1 выполнено неравенство

В силу утверждения 1 периодическое решение удовлетворяет такому же неравенству

Обозначим через w разность периодического и произвольного решений:

Величина w подчиняется уравнению $\dot {w} = R({{v}_{*}}) - R(v)$, которое может быть представлено в виде

Из условия (1.4) монотонного убывания функции $R(v)$ следует, что

Укажем такой интервал $[{{t}_{1}},{{t}_{2}}]$, на котором выполнено

для некоторого $\varepsilon > 0$ и всех значений $v$, таких, что $\left| v \right| \leqslant {{V}_{{max}}}$. На интервале $[0,T]$ непрерывная функция ${{v}_{*}}(t)$ принимает все значения из некоторого интервала, обозначим этот интервал $[{{v}_{{min}}},{{v}_{{max}}}]$. Отметим, что ${{v}_{{min}}} \ne {{v}_{{max}}}$. Действительно, если ${{v}_{*}} \equiv {{c}_{1}}$, то из критерия периодичности решения (2.4) следует равенство $R({{c}_{1}}) = 0$ и с учетом (1.4) ${{c}_{1}} = 0$. Тогда в силу уравнения (1.3) имеем $u \equiv 0$, что противоречит условию движения внутренней массы (1.2). Таким образом, выполнено соотношение ${{v}_{{min}}} \ne {{v}_{{max}}}$.

Из-за монотонного убывания $R(v)$ не существует интервала значений ${v}$, на котором $R{\kern 1pt} '(v) \equiv 0$. Следовательно, существует интервал $[{{v}_{ - }},{{v}_{ + }}] \subset [{{v}_{{min}}},{{v}_{{max}}}]$, где

для некоторого $\delta > 0$. Существует временной интервал $[{{t}_{0}},{{t}_{3}}] \subset [0,T]$, на котором функция ${{v}_{*}}(t)$ строго возрастает и $[{{v}_{*}}({{t}_{0}}),{{v}_{*}}({{t}_{3}})] \subset [{{v}_{ - }},{{v}_{ + }}]$. Пусть ${{t}_{1}}$, ${{t}_{2}}$ – моменты времени, удовлетворяющие неравенствам

Тогда

где ${{v}_{i}} = {{v}_{*}}({{t}_{i}})$, $i = 0, \ldots ,3$. Отсюда, принимая во внимание (2.5), получаем

Выполнено неравенство

В силу монотонного возрастания ${{v}_{*}}(t)$ верно

Докажем, что неравенство (2.8) выполнено на отрезке $[{{t}_{1}},{{t}_{2}}]$ для всех $v$, таких, что $\left| v \right| \leqslant {{V}_{{max}}}$. Возможны следующие три случая.

Если $v \in [{{v}_{0}},{{v}_{3}}]$, то, используя теорему Лагранжа, получим

для некоторого $\tilde {v} \in [{{v}_{0}},{{v}_{3}}]$. Отсюда с учетом (2.9) следует, что и неравенство (2.8) выполнено для $\varepsilon = \delta $.

Если $v > {{v}_{3}}$, то для всех $v$, таких, что $\left| v \right| \leqslant {{V}_{{max}}}$, при условии (2.10), верна оценка

Следовательно, неравенство (2.8) выполнено для

Если $v < {{v}_{0}}$, то для всех $v$, таких, что $\left| v \right| \leqslant {{V}_{{max}}}$, при условии (2.10) верна оценка

и неравенство (2.8) выполнено для

Возьмем

Для такого $\varepsilon $ неравенство (2.8) верно при всех $t \in [{{t}_{1}},{{t}_{2}}]$ и любых ${v}$, таких, что $\left| v \right| \leqslant {{V}_{{max}}}$. Более того, из-за периодичности решения ${{v}_{*}}$ оно будет выполнено на всех отрезках

Тогда, из уравнения (2.6) следует, что разность решений w на отрезках (2.11) экспоненциально стремится к нулю. Более того, модуль разности $\left| w \right|$ вне этих отрезков убывает в силу (2.7). Поэтому верна оценка

где {⋅} обозначает целую часть числа. Таким образом, произвольное решение сходится к периодическому, а скорость этой сходимости не меньше экспоненциальной с некоторым показателем. Утверждение доказано.

Итак, в утверждениях 1–3 доказаны существование и единственность периодического решения задачи и показано, что любое решение этой задачи сходится к периодическому не медленнее, чем экспоненциально. Заметим, что сходимость произвольного решения к периодическому за конечное время невозможна при условии единственности решения дифференциального уравнения (1.3). Это условие выполнено для широкого класса законов сопротивления $R(v)$, например линейного или степенного, в случае, если функция $u(t)$ кусочно-непрерывна. Однако сходимость к периодическому решению за конечное время возможна, например, в случае, когда сопротивление среды описывается законом Кулона.

3. Построение периодических режимов в частных случаях. Доказанные выше результаты верны для большого количества законов сопротивления среды, например: для линейного или кусочно-линейного законов, для квадратичного закона $R(v) = - {{v}^{2}}{\text{sgn}}v$, для кубического закона $R(v) = - {{v}^{3}}$, для степенного закона $R(v) = - {{\left| v \right|}^{\alpha }}{\text{sgn}}v$, $\alpha > 0$. В настоящем разделе мы подробнее изучим случаи линейного и кусочно-линейного законов сопротивления среды, для них явно построим периодическое решение и укажем скорость экспоненциальной сходимости.

Рассмотрим линейный закон сопротивления $R = - Cv$, где C > 0. В этом случае уравнение (1.3) принимает форму

а его общее решение имеет вид

Из равенства ${{v}_{*}}(T) = {{v}_{*}}(0)$ можно найти начальную скорость периодического режима движения:

Любое решение $v(t)$ экспоненциально сходится к периодическому решению ${{v}_{*}}(t)$ с константой $C$ в экспоненте:

Заметим, что при линейном сопротивлении смещение системы за период для периодического режима движения равно нулю. Действительно,

Это соотношение получается интегрированием уравнения движения (3.1) на периоде [0, T] и использованием (1.5) и (1.7).

Рассмотрим теперь кусочно-линейное сопротивление окружающей среды:

где ${{C}_{1}},{{C}_{2}} > 0.$ В этом случае общее решение задачи (1.3)–(1.6) невозможно выписать в простой форме. В соответствии с утверждениями 1–3 периодическое решение ${{v}_{*}}(t)$ существует и единственно и любое решение экспоненциально сходится к нему. Для кусочно-линейного сопротивления возможно явно указать показатель экспоненциальной сходимости, т.е. выписать значение константы в экспоненте:

В частном случае кусочно-постоянного относительного ускорения внутренней массы

показано, что значение начальной скорости ${{v}_{*}} = {{v}_{*}}(0)$, определяющее периодический режим движения, удовлетворяет неравенству и является решением уравнения

Решение (3.5), удовлетворяющее (3.4), существует и единственно.

Результаты настоящего раздела могут быть использованы при моделировании движения [8]. Явные решения (3.2) для линейного сопротивления полезны для отладки соответствующих компьютерных программ, а формулы и соотношения (3.3)–(3.5) – для определения начальной скорости периодического режима для линейного и кусочно-линейного сопротивлений.

Заключение. В настоящей статье изучено прямолинейное движение системы, состоящей из корпуса и внутренней массы. Предполагается, что корпус испытывает сопротивление среды, а внутренняя масса движется периодически относительно корпуса и не взаимодействует со средой, и ее скорость относительно корпуса непрерывна. Изучены вопросы существования, единственности и устойчивости периодического режима движения системы, т.е. такого движения, при котором скорость корпуса периодична. Показано, что периодический режим движения существует в случае, когда сопротивление среды строго монотонно убывает с ростом скорости и при достаточно больших значениях скорости, модуль сопротивления превышает максимальную силу, действующую на тело со стороны внутренней массы. Линейные, кусочно-линейные, степенные и большинство известных законов сопротивления, за исключением сухого трения, удовлетворяют этим условиям. Получена двусторонняя оценка скорости периодического движения корпуса. Доказано, что периодический режим движения единственен при любом монотонно убывающем законе сопротивления среды, и в этом случае показана его экспоненциальная устойчивость. Для случаев линейного и кусочно-линейного сопротивления указана скорость экспоненциальной сходимости.

В рамках настоящего исследования планируется продолжить изучение периодических режимов движения и сходимости произвольного движения к периодическому для других законов сопротивления среды, например для закона Кулона. Следует изучить случай, когда второе тело тоже испытывает сопротивление окружающей среды. Планируется также рассмотреть случай, когда относительная скорость внутренней массы является разрывной функцией времени.