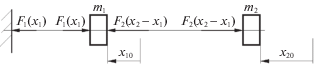Известия РАН. Теория и системы управления, 2020, № 1, стр. 161-167

Введение. Рассматривается система с двумя степенями свободы. Имеются две массы, соединенные упругими элементами. Первый упругий элемент соединяет первую массу системы с неподвижным основанием. Второй упругий элемент соединяет первую и вторую массы. Движение происходит в горизонтальной плоскости. Силы тяжести, как и силы трения, не учитываются. Величины масс выбираются достаточно произвольно. В начальный момент времени оба тела смещены из их нейтральных положений. Необходимо найти такие аналитические, в частности тригонометрические функции, определяющие законы движения каждой массы от времени, чтобы в терминальный момент времени оба упругих элемента были не напряжены и, кроме того, скорость первого тела при этом должна быть равна нулю. С точки зрения физики это означает, что энергия, сообщенная системе в начальный момент времени, равна кинетической энергии второго тела в терминальный момент времени, т.е. в заданный терминальный момент времени второе тело приобретает максимально возможную скорость при энергии, определяемой начальными условиями. Задается условие, чтобы восстанавливающие силы упругих элементов на протяжении всего времени движения, по возможности, были направлены в сторону разгона второго тела. По времени движение системы рассматривается от начала движения (время равно нулю) до терминального момента времени, когда оба тела находятся в нейтральном положении.

Из двух дифференциальных уравнений, описывающих движение рассматриваемой системы, возможно определение зависимостей восстанавливающих сил упругих элементов от времени. После исключения времени из функций, определяющих законы движения тел и восстанавливающие силы упругих элементов, можно получить зависимости восстанавливающих сил упругих элементов от координат. Для первого упругого элемента – это зависимость от координаты первого тела; для второго упругого элемента – зависимость от разности координат второго и первого тел. Требуется подобрать такие аналитические функции, описывающие движение тел системы, чтобы одному значению координаты каждого тела соответствовало одно значение соответствующей восстанавливающей силы.

Для создания упругих элементов с полученными аналитически восстанавливающими силами предполагается рассмотреть пружины, перемещающиеся между направляющими расчетной формы перпендикулярно их оси симметрии. Расчет формы направляющих сводится к решению квадратного уравнения, полученного из условия, что восстанавливающая сила каждого упругого элемента определяется как частная производная от потенциальной энергии соответствующей пружины по ее координате.

Рассматриваемый в статье подход к определению восстанавливающих сил упругих элементов в системе с двумя степенями свободы при заданном законе движения может найти широкое применение в технике, например, для создания конструкций, где требуется получать большие скорости рабочих элементов без больших перегрузок. Это могут быть различные катапульты и ударники. В частности, для катапульт беспилотных летательных аппаратов (БПЛА) использование дополнительного инерционного элемента позволило уменьшить длину направляющих стартового устройства на 30% без превышения нагрузки на БПЛА, что обеспечивает плавное безударное ускорение летательного аппарата и снижает требования к его прочности [1, 2]. В [3] рассмотрена задача разгона крайней массы цепочки (бойка) тел, соединенных пружинами, подчиняющимися закону Гука. В этих случаях задача получить заданный закон движения тел системы с несколькими степенями свободы путем решения дифференциальных уравнений при изменении параметров системы очень сложна. Предлагаемый способ управления системами с двумя степенями свободы посредством потенциальных сил позволит получать широкий класс желаемых законов движения тел.

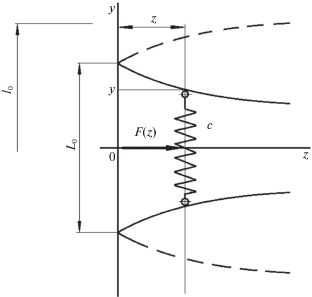
1. Постановка задачи. Рассматривается система с двумя степенями свободы. Принимаем, что восстанавливающая сила ${{F}_{1}}({{x}_{1}})$ упругого элемента, расположенного между неподвижным основанием и телом массой m₁ (рис. 1), зависит от координаты первого тела; восстанавливающая сила ${{F}_{2}}({{x}_{2}} - {{x}_{1}})$ упругого элемента, расположенного между первым телом и вторым телом массой m₂, зависит от разности координат второго и первого тел.

Движение системы задается выбранными определенным образом зависимостями координат первого и второго тел от времени ${{x}_{1}}\left( t \right)$ и ${{x}_{2}}\left( t \right)$. По этим функциям определяются зависимости сил, действующих на тела массой m₁ и m₂, от времени: $F_{1}^{/}\left( t \right)$ и $F_{2}^{/}\left( t \right)$. Исключая время из функций ${{x}_{1}}\left( t \right)$, ${{x}_{2}}\left( t \right)$, $F_{1}^{/}\left( t \right)$ и $F_{2}^{/}\left( t \right)$, получаются зависимости ${{F}_{1}}({{x}_{1}})$ и ${{F}_{2}}({{x}_{2}} - {{x}_{1}})$.

Создание упругих элементов с полученными восстанавливающими силами ${{F}_{1}}({{x}_{1}})$ и ${{F}_{2}}({{x}_{2}} - {{x}_{1}})$ предлагается осуществить при помощи пружин, перемещающихся между направляющими расчетной формы перпендикулярно их оси симметрии.

2. Метод решения. Рассматривается задача нахождения таких тригонометрических функций, определяющих законы движения каждой массы от времени, чтобы в терминальный момент времени ${{t}_{k}}$ оба упругих элемента были не напряжены при скорости первого тела, равной нулю, что приведет к максимально возможной скорости второго тела при заданной энергии системы.

Заданы граничные условия:

где ${{\dot {x}}_{{10}}};\;~{{\dot {x}}_{{20}}}$ – начальные скорости первого и второго тела; ${{x}_{{10}}}$, ${{x}_{{20}}}$ – начальные смещения первого и второго тела соответственно.

Условие ${{\dot {x}}_{{20}}} \approx 0$ принято из-за сложности получения точного равенства. Функции x₁(t) и x₂(t) были выбраны из условия, что правые части – монотонные функции времени, что позволяет выразить t как однозначные функции переменных x₁ и ${{x}_{2}} - {{x}_{1}}$:

где A, B, t_k, k – постоянные величины.

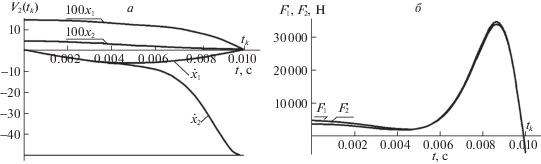
Такой выбор функций обеспечивает выполнение граничных условий (2.1) (рис. 2, а). В общем, исходные соотношения (2.1) и (2.2) могут быть и другими.

Постоянные, входящие в систему уравнений (2.2) с учетом условий (2.1), выбраны достаточно произвольно: В = 0.02 м; A = 0.10 м; ${{t}_{k}}$ = 0.01 c; $k = 500~$ с^–1; ${{x}_{{10}}} = 0.04~$ м; ${{x}_{{20}}} = 0.14~$ м. Эти величины будут использованы во всех дальнейших вычислениях и характеризуют типичные процессы, которые могут возникать при работе различных ударников и катапульт с двумя степенями свободы.

Дифференциальные уравнения, описывающие движение системы, изображенной на рис. 1, следующие:

Подставив в (2.3) производные ${{\ddot {x}}_{1}}\left( t \right)$ и ${{\ddot {x}}_{2}}\left( t \right)$, полученные из (2.2), определяем зависимости сил $F_{1}^{/}\left( t \right)$ и $F_{2}^{/}(t){\text{:}}$

где

Массы первого и второго тела выбраны следующие: ${{m}_{1}} = 0.5~$ кг; ${{m}_{2}} = 2~$ кг. На рис. 2, а изображены зависимости координат и скоростей тел системы с двумя степенями свободы от времени, полученные по формулам (2.2) и их производным. На рис. 2, б приведены силы $F_{1}^{/}\left( t \right)$ и $F_{2}^{/}\left( t \right)$, действующие на первое и второе тело системы соответственно, определенные по системе (2.4). Для перехода к зависимостям ${{F}_{1}}\left( {{{x}_{1}}} \right)$ и ${{F}_{2}}\left( {{{x}_{2}} - {{x}_{1}}} \right)$ подставляем вместо времени t в ${{\ddot {x}}_{1}}\left( t \right)$ функцию ${{t}_{1}} = {\text{arccos}}\left( {{{x}_{1}}{\text{/}}B - 1} \right){\text{/}}\left( {\pi {\text{/}}{{t}_{k}}} \right)$, полученную из первого уравнения системы (2.2), а вместо времени в ${{\ddot {x}}_{2}}(t)$ – функцию ${{t}_{2}} = {\text{arcth}}\left( {\left( {{{x}_{1}} - {{x}_{2}}} \right){\text{/}}A} \right){\text{/}}k + {{t}_{k}}$, полученную из второго уравнения системы (2.2). После упрощения находим систему дифференциальных уравнений (2.5), в которых силы ${{F}_{1}}\left( {{{x}_{1}}} \right)$ и ${{F}_{2}}\left( {{{x}_{2}} - {{x}_{1}}} \right)$ зависят от координат:

где

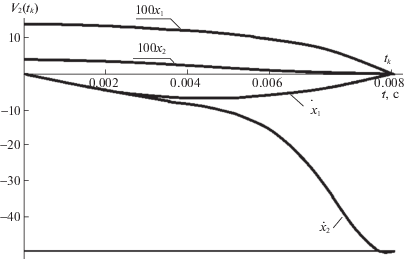
На рис. 3 представлены функции ${{x}_{1}}\left( t \right)$; ${{x}_{2}}\left( t \right)$; ${{\dot {x}}_{1}}\left( t \right)$; ${{\dot {x}}_{2}}\left( t \right)$, полученные численным решением системы дифференциальных уравнений (2.5). Как видно из рис. 3, зависимости ${{x}_{1}}\left( t \right)$; ${{x}_{2}}\left( t \right)$; ${{\dot {x}}_{1}}\left( t \right)$; ${{\dot {x}}_{2}}\left( t \right)$ практически совпадают с теми же зависимостями, представленными на рис. 2, а, что можно считать проверкой предыдущих вычислений.

Для определения аналитической зависимости ${{F}_{1}}\left( {{{x}_{1}}} \right)$ достаточно в функцию $F_{1}^{/}\left( t \right)$ (2.4) подставить вместо времени t функцию ${{t}_{1}}$, полученную выше. После упрощения имеем

Для определения аналитической зависимости ${{F}_{2}}\left( {{{x}_{2}} - {{x}_{1}}} \right)$ в функцию $F_{2}^{/}\left( t \right)$ (2.4) подставляем вместо времени t функцию ${{t}_{2}}$, полученную выше. После упрощения имеем

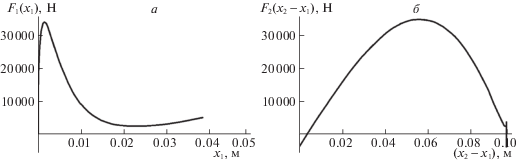
На рис. 4 представлены зависимости ${{F}_{1}}\left( {{{x}_{1}}} \right)$ и ${{F}_{2}}\left( {{{x}_{2}} - {{x}_{1}}} \right)$, найденные по уравнениям (2.6) и (2.7). Эти восстанавливающие силы, полученные аналитически, могут быть управляющими функциями для осуществления заданного движения, например, при изменении максимальной скорости второго тела ${{V}_{{2{\text{max}}}}}$ при тех же выбранных функциях ${{x}_{1}}\left( t \right)$ и ${{x}_{2}}\left( t \right)$ (рис. 2, а), т.е. при других значениях постоянных k, B, A, ${{t}_{k}}$, входящих в систему уравнений (2.1).

3. Способ технической реализации результатов. Для получения восстанавливающих сил ${{F}_{1}}\left( {{{x}_{1}}} \right)$ и ${{F}_{2}}\left( {{{x}_{2}} - {{x}_{1}}} \right)$ рассмотрена система, схема которой изображена на рис. 5 [4]. В ней пружина жесткостью “с” перемещается между направляющими расчетной формы перпендикулярно их оси симметрии.

Силу, c которой система “сопротивляется” перемещению пружины вдоль оси z (рис. 5, она будет противоположна F(z)), можно определить следующим образом (силы трения не учитываются) [5]:

где ${\text{П}} = с\Delta {{\ell }^{2}}{\text{/}}2$ – потенциальная энергия пружины; с – коэффициент жесткости пружины; $\Delta \ell = {{\ell }_{0}} - 2y$ – изменение длины пружины (рис. 5); ${{\ell }_{0}}$ – длина ненапряженной пружины; y – координата функции, определяющей направляющие.

Дифференциальное уравнение в частных производных (3.1) можно свести к обыкновенному дифференциальному уравнению:

Начальные условия для данного дифференциального уравнения следующие:

где 0.5${{L}_{0}}$ – начальная координата направляющей (рис. 5).

В дифференциальном уравнении (3.2) разделяем переменные и берем определенные интегралы, учитывая начальные условия (3.3):

Опуская выкладки, получаем квадратное уравнение для y(z), решение которого представлено ниже:

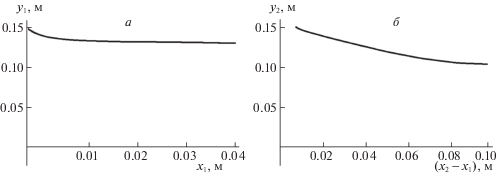
где $D = 0.5{{\ell }_{0}}{{L}_{0}} - 0.25L_{0}^{2} - \frac{1}{{2с}}\int_0^z {F\left( {\text{u}} \right)du} .$

Знаку “+” уравнения (3.5) соответствует пунктирная линия – пружина растягивается, знаку “–” соответствует сплошная линия – пружина сжимается (рис. 5) [5]. Рассмотрим вариант сжатия пружины – знак “–”. На рис. 6 представлены формы направляющих, определенные по формуле (3.5) (${{\ell }_{0}} = 0.3~$ м; ${{L}_{0}} = 0.3~$ м; $c = 1000000~$ Н/м). Для рис. 6, а:

где ${{F}_{1}}\left( w \right)$ находится по формуле (2.6). Для рис. 6, бгде ${{F}_{2}}\left( v \right)$ определяется по формуле (2.7).

Как видно из рис. 6, б, на начальном участке от $({{x}_{2}} - {{x}_{1}}) = 0$ до $({{x}_{2}} - {{x}_{1}}) \approx 0.005~$ м зависимость отсутствует. Это объясняется тем, что зависимость ${{F}_{2}}\left( {{{x}_{2}} - {{x}_{1}}} \right)$ на этом участке имеет отрицательные значения и для его нахождения требуется рассмотреть его отдельно. Из-за малости этого участка данный расчет здесь не приводится.

Требуемое изменение функций ${{F}_{1}}\left( {{{x}_{1}}} \right)$, ${{F}_{2}}\left( {{{x}_{2}} - {{x}_{1}}} \right)$ при управлении рассматриваемой системы с двумя степенями свободы можно осуществить изменением формы направляющих, которые определяются функциями ${{y}_{1}}\left( {{{x}_{1}}} \right)$ и ${{y}_{2}}\left( {{{x}_{2}} - {{x}_{1}}} \right)$ (рис. 6).

Заключение. Преимуществом предлагаемого подхода к заданию заданного движения каждого тела системы с двумя степенями свободы является то, что не требует решения системы нелинейных дифференциальных уравнений, это связано с известными трудностями. Фактически, решается первая задача динамики для системы с двумя степенями свободы.