Известия РАН. Теория и системы управления, 2020, № 1, стр. 44-53
ДИНАМИЧЕСКИЕ МОДЕЛИ СОГЛАСОВАНИЯ ЧАСТНЫХ И ОБЩЕСТВЕННЫХ ИНТЕРЕСОВ ПРИ ЭКОНОМИЧЕСКОЙ КОРРУПЦИИ
Г. А. Угольницкий a, *, А. Б. Усов a, **
a Южный федеральный ун-т
Ростов-на-Дону, Россия
* E-mail: ougoln@mail.ru
** E-mail: tol151968@yandex.ru
Поступила в редакцию 03.10.2017
После доработки 27.08.2019
Принята к публикации 30.09.2019
Аннотация
Рассматриваются динамические теоретико-игровые модели борьбы с коррупционным поведением субъектов в моделях согласования частных и общественных интересов. Исследован случай экономического воздействия субъекта верхнего уровня на субъектов нижнего. Указан алгоритм нахождения равновесий при побуждении. Приведены примеры расчетов для различных наборов входных данных. Обсуждается содержательная интерпретация результатов.
Введение. В работах по математическому моделированию эффективных способов борьбы с коррупцией используется в основном аппарат статических игр в нормальной форме или многошаговых игр. Например, способы организации инспекций в статической постановке изучаются в статьях [1, 2].
Существенно меньшее число публикаций посвящено динамическим моделям коррупции, основанным на моделях оптимального управления или дифференциальных играх. Некоторые примеры можно найти в учебном пособии [3], а также работах [4–14]. Так, авторы [4] показали, что эволюция коррупции в экономике может самопроизвольно привести к состоянию взрыва так называемой “революции честности”, в результате которой управляющий вектор системы переходит в новое состояние. В модели [12] показывается существование ситуаций, в которых экономики с одинаковыми параметрами развития находятся на разных уровнях коррупции. Работа [9] посвящена моделированию цикличности в политической коррупции, где наблюдаются смены кампаний по борьбе с коррупцией и периодов ее молчаливого поощрения на макроэкономическом уровне. Организация инспекций как эволюционная игра представлена в статье [14], этот же подход применен в [11] для описания борьбы с незаконной вырубкой леса. В [13] изучена дихотомия между общественным контролем и коррупционным давлением чиновников на рост экономики. В статье [10] используется подход “игр среднего поля” (mean-field games), описывающих взаимодействие очень большого числа рациональных агентов, в том числе под воздействием выделенного “основного” игрока.
Настоящая статья логически продолжает и обобщает целый ряд работ авторов [15–21]. В [17] описана авторская концепция моделирования коррупции и методов борьбы с ней в динамике, основные положения которой состоят в следующем.
1. Базовой схемой моделирования служит иерархическая система “принципал–супервайзер(ы)–агент(ы)–объект” в различных модификациях. Ее исследование проводится средствами теории оптимального управления и динамических игр. Принципал выбирает свою стратегию поведения (делает ход) первым и сообщает ее супервайзеру и агенту. При этом он максимизирует свой целевой функционал с учетом их оптимальных ответов на множестве тех стратегий, которые позволяют поддерживать систему в заданном состоянии. Супервайзер выбирает свою стратегию, когда выбор принципала известен, а агента еще нет. Агент выбирает стратегию, когда выбор остальных субъектов известен, и стремится только к оптимизации своего целевого функционала. Предполагается, что коррумпирован средний уровень управления (супервайзер), верхний уровень управления (принципал) считается не подверженным коррупции и выполняет функции борьбы с ней.
2. Действуя как ведущий, игрок (исходно принципал или супервайзер) для достижения своих целей использует методы принуждения и побуждения. При математической формализации принуждение означает воздействие ведущего на множество допустимых стратегий ведомого, обычно без обратной связи по управлению (игры Гермейера Г1,t, Г1,x), а побуждение – на функцию выигрыша ведомого с обратной связью по управлению (игры Гермейера Г2,t , Г2,x). Предполагается, что всем субъектам управления точно известны их целевые функционалы и целевые функционалы остальных субъектов.
3. Различаются административная коррупция, при которой за взятку ослабляются административные требования, и экономическая, при которой взятка позволяет ослабить экономические требования субъекта верхнего уровня управления. При моделировании административная коррупция означает принуждение с обратной связью по величине взятки, а экономическая – побуждение с дополнительной обратной связью по взятке.
4. Исследование коррупции в системе “принципал–супервайзер–агент–объект” возможно с трех позиций. Если функция взяточничества известна, то с позиции агента коррупция может быть описана моделью оптимального управления. С позиции супервайзера возникает иерархическая параметрическая игра Гермейера Г2,t . Наконец, с позиции принципала задача борьбы с коррупцией заключается в нахождении таких значений параметров управления, при которых оптимальная игровая стратегия супервайзера удовлетворяет требованиям устойчивого развития для управляемой динамической системы.
В [19, 20] построена система динамических моделей административной коррупции и методов борьбы с ней. Рассмотрение ведется на примере моделей оптимальной эксплуатации биоресурсов с учетом административной коррупции. В [21] предложены и исследованы модели экономической коррупции в системах контроля качества поверхностных вод. В [16] приведены подходы к исследованию задачи согласования частных и общественных интересов в статической постановке.
Настоящая статья посвящена динамическим моделям борьбы с экономической коррупцией в моделях согласования частных и общественных интересов (СОЧИ-моделях) при условии обязательного выполнения требований устойчивого развития системы. В развитие [16] ниже исследуются СОЧИ-модели в динамической постановке и, более того, с учетом наличия экономической коррупции в системе. Кроме того, в отличие от [19, 20], изучен случай нескольких агентов, что принципиально для СОЧИ-моделей и находит отражение в использовании равновесия Нэша.
1. Математическая постановка задачи. Рассмотрим СОЧИ-модель, описывающую трехуровневую систему управления с безразличным субъектом верхнего уровня. Исследуемая СОЧИ-модель включает субъекты управления верхнего (принципал), среднего (супервайзер) и нижнего (агенты) уровней, а также управляемую динамическую систему (УДС). Предполагается, что принципал не преследует частных целей и в системе имеется n агентов, которые действуют индивидуально. В роли принципала может выступать, например, государство, в роли супервайзера – местные органы государственного управления, агентов – промышленные предприятия, а в роли УДС – эколого-экономическая система. Условия устойчивого развития УДС состоят в выполнении некоторых требований к переменным ее состояния в динамике. Причем на УДС непосредственно воздействуют только агенты, а поддержание системы в заданном состоянии является основной целью принципала, которую он в силу ограниченности возможностей делегирует супервайзеру. Таким образом, фактически в системе целенаправленно действуют только супервайзер и агенты. Дальнейшее рассмотрение проведем при побуждении, т.е. считается, что супервайзер воздействует на целевые функционалы агентов.
В СОЧИ-моделях предполагается, что каждый из агентов $i\,,\,i = \overline {1,n} ,$ распределяет свой бюджет ${{r}_{i}} = {{r}_{i}}(t)$ между двумя направлениями: часть бюджета ${{u}_{i}}(t)$ (управление игрока) ассигнуется на выполнение общественных задач, а оставшаяся часть ${{r}_{i}}(t) - {{u}_{i}}(t)$ используется для финансирования частной деятельности [16, 17]. Соответственно текущий выигрыш игрока складывается из доходов от частной деятельности и доли в общественном благе. Когда агент дополнительно выделяет часть ${{b}_{i}}(t)$ своего бюджета на взятку, супервайзер завышает его долю полезности в распределении общественного блага (функция ${{s}_{i}}(t) = {{s}_{i}}({{b}_{i}}(t))$), что дает еще одно управление и завершает баланс (теперь на финансирование частной деятельности выделяется ${{r}_{i}}(t) - {{u}_{i}}(t) - {{b}_{i}}(t)$). Целевой функционал i-го агента берется в виде
(1.1)
${{J}_{i}}({{s}_{i}}( \cdot ),{{u}_{i}}( \cdot ),{{b}_{i}}( \cdot ),x( \cdot )) = \int\limits_0^T {{{e}^{{ - \rho t}}}\left[ {{{p}_{i}}({{r}_{i}}(t) - {{b}_{i}}(t) - {{u}_{i}}(t)) + {{s}_{i}}(t)c(x(t))} \right]dt + } {{s}_{i}}(T)c(x(T)) \to \max .$Здесь ${{J}_{i}}$ – выигрыш i-го агента; T – период рассмотрения; $t$ – время; $\rho $ – коэффициент дисконтирования; функции ${{u}_{i}}(t)$, ${{b}_{i}}(t)$ – управления i-го агента; x(t) – скалярная переменная состояния системы, выраженная в условных единицах; ${{p}_{i}}({{r}_{i}}(t) - {{u}_{i}}(t) - {{b}_{i}}(t))$ – вогнутые функции, отражающие доходы агентов от частной деятельности с учетом взятки ($i = \overline {1,n} $); c(x) – вогнутая возрастающая функция, дающая финансовое выражение общественной полезности в зависимости от состояния системы; ${{s}_{i}}(t)$ – доля i-го субъекта в этой полезности. Отметим, что функции ${{p}_{i}}$ убывают по переменной управления ${{u}_{i}}$, но возрастают по полному аргументу ${{r}_{i}} - {{b}_{i}} - {{u}_{i}}$. Под переменной состояния системы понимается некоторая общественная полезность, например, качество окружающей среды, здоровье населения, уровень культуры и т.п. Поскольку эта полезность в большинстве случаев носит нематериальный характер, для ее “монетизации” используется функция c(x).
Функционалы (1.1) рассматриваются со следующими ограничениями на управления агентов ($i = \overline {1,n} $):
(1.2)
$0 \leqslant {{b}_{i}}(t) + {{u}_{i}}(t) \leqslant {{r}_{i}}(t);\quad {{u}_{i}}(t),{{b}_{i}}(t) \geqslant 0;\quad t \in [0,T].$Уравнение динамики системы возьмем в виде
Здесь ${{{х}_{{\text{0}}}}}$ – значение состояния системы в начальный момент времени; f – непрерывная функция, зависящая от состояния системы и ассигнований агентов на выполнение общественных целей; $u(t) = ({{u}_{1}}(t),{{u}_{2}}(t),...,{{u}_{n}}(t))$ – управление агентов как вектор-функция времени. От супервайзера требуется, чтобы система находилась в заданном состоянии, т.е.
(1.4)
${{x}_{{\min }}} \leqslant x(t) \leqslant {{x}_{{\max }}},\quad {{x}_{{\min }}},{{x}_{{\max }}} = {\text{const}}.$Неравенства (1.4) определяют гомеостаз УДС как необходимое условие устойчивого развития. Величины ${{x}_{{\min }}},\;{{x}_{{\max }}}$ заданы.
Выигрыш супервайзера складывается из полученных взяток и доли в распределении общественного блага за минусом возможного наказания за взятку. Целевой функционал супервайзера возьмем в виде
(1.5)
${{J}_{0}}({{s}_{0}}( \cdot ),b( \cdot ),x( \cdot )) = \int\limits_0^T {{{e}^{{ - \rho t}}}\left( {{{s}_{0}}(t)c(x(t)) + \alpha ((1 - z) - Mz)\sum\limits_{i = 1}^n {{{b}_{i}}} (t)} \right)dt} + {{s}_{0}}(T)c(x(T)) \to \max .$Здесь ${{J}_{0}}$ – выигрыш супервайзера; ${{s}_{0}}$ – доля супервайзера в распределении общественного блага (заданная функция); $z \in [0,1]$ – вероятность поимки взяточника; $M \gg 1$ – коэффициент штрафа взяточника в случае поимки; $\alpha $ – коэффициент перевода части ресурса, идущего на взятки, в стоимость, выраженную в условных единицах (у.е.); $b(t) = ({{b}_{1}}(t),{{b}_{2}}(t),...,{{b}_{n}}(t))$ – управление агентов как вектор-функция времени.
Супервайзер управляет долями агентов в распределении общественного блага. Ограничения на его управления имеют вид
Если рассмотрение ведется с точки зрения агентов, то получается дифференциальная неантагонистическая игра n лиц (1.1)–(1.4), в которой строится равновесие Нэша. При этом функции ${{s}_{i}}(t) = {{s}_{i}}(b(t))$ заданы ($i = \overline {1,n} $).
При рассмотрении с точки зрения супервайзера решается задача (1.1)–(1.6), в которой функции ${{s}_{i}}(t) = {{s}_{i}}(b(t))$ ищутся как решение игры типа Г2,t между супервайзером и агентами [17, 22]. В этом случае соотношения (1.1)–(1.6) описывают в общем виде СОЧИ-модель в условиях коррупции и определяют дифференциальную иерархическую игру (n + 1)-го лица вида Г2,t при побуждении с учетом условий устойчивого развития системы (1.4).
Отметим, что при побуждении коррупция носит характер попустительства [15]. Минимально установленные доли агентов в распределении общественного блага гарантируются, а их увеличение предоставляется в обмен на взятку. Игра между супервайзером и агентом рассматривается в виде Г2,t [17, 22], поскольку при описании коррупции принципиально наличие обратной связи по величине взятки.
2. Одноуровневая модель. Вначале проведем исследование модели с точки зрения агентов. В этом случае решается дифференциальная неантагонистическая игра n лиц (1.1)–(1.4), в которой строится равновесие Нэша. Функции ${{s}_{i}}(t) = {{s}_{i}}(b(t))$ при этом заданы.
Для аналитического решения рассмотрим упрощенную версию модели (1.1)–(1.4) с линейными по состоянию и управлениям функциями $f(x,u)$ и $c(x(t))$:
а также степенными функциями частного доходаЗдесь $c,a,{{d}_{i}},\,i = \overline {1,n} ,$ – заданные константы; c > 0 – коэффициент перевода состояния системы в общественную полезность в финансовой форме, выраженную в у.е.; ${{d}_{i}} > 0$ – доля вклада инвестиций i-го игрока в улучшение состояния системы; $s_{i}^{0}(t)$ – заданные функции, описывающие доли агентов в распределении общественного блага при отсутствии коррупции.
Модель (1.1)–(1.4) в этом случае примет вид
(2.1)
$\begin{gathered} {{J}_{i}}({{u}_{i}}( \cdot ),{{b}_{i}}( \cdot ),x( \cdot )) = \\ = \int\limits_0^T {{{e}^{{ - \rho t}}}\left( {{{p}_{i}}\sqrt {{{r}_{i}}(t) - {{b}_{i}}(t) - {{u}_{i}}(t)} + сx(t)\frac{{s_{i}^{0}(t) + {{b}_{i}}(t)}}{{1 + \sum\limits_{j = 1}^n {{{b}_{j}}(t)} }}} \right)dt + \,} с\frac{{s_{i}^{0}(T) + {{b}_{i}}(T)}}{{1 + \sum\limits_{j = 1}^n {{{b}_{j}}(T)} }}x(T) \to \max . \\ \end{gathered} $(2.2)
$0 \leqslant {{b}_{i}}(t) + {{u}_{i}}(t) \leqslant {{r}_{i}}(t);\quad {{u}_{i}}(t),{{b}_{i}}(t) \geqslant 0;\quad i = \overline {1,n} ,$(2.3)
$\frac{{dx}}{{dt}} = - ax(t) + \sum\limits_{i = 1}^n {{{d}_{i}}{{u}_{i}}(t);\quad x(0) = {{x}_{0}}.} $Условие (1.4) при построении равнoвесия Нэша не учитывается. В (2.1)–(2.4), по сравнению с моделью (1.1)–(1.3), используются линейные функции $f(x(t),u(t))$ и $c(x(t))$, что делает модель линейной по состоянию. Кроме того, без существенного ограничения общности взята степенная функция дохода от частной деятельности.
Для решения задачи (2.1)–(2.4) применим принцип максимума Понтрягина. Функция Гамильтона i-го агента имеет вид
(2.4)
${{H}_{i}}({{u}_{i}}(t),{{\lambda }_{i}}(t),x(t),t) = {{e}^{{ - \rho t}}}\left( {{{p}_{i}}\sqrt {{{r}_{i}}(t) - {{b}_{i}}(t) - {{u}_{i}}(t)} + cx(t)\frac{{s_{i}^{0}(t) + {{b}_{i}}(t)}}{{1 + \sum\limits_{j = 1}^n {{{b}_{j}}(t)} }}} \right) + {{\lambda }_{i}}(t)( - ax(t) + \sum\limits_{j = 1}^n {{{d}_{j}}{{u}_{j}}} (t)),$Из необходимых условий экстремума (2.4)
Следовательно, внутри области (2.2) точки, “подозрительные” на максимум, определяются как решения системы уравнений
(2.5)
$\begin{gathered} {{u}_{i}} + {{b}_{i}} = {{r}_{i}} - \frac{{{{e}^{{ - 2\rho t}}}p_{i}^{2}}}{{4\lambda _{i}^{2}d_{i}^{2}}}, \\ - {{\lambda }_{i}}{{d}_{i}} + {{e}^{{ - \rho t}}}cx\frac{{1 + \sum\limits_{j = 1}^n {{{b}_{j}} - s_{i}^{0} - {{b}_{i}}} }}{{{{{\left( {1 + \sum\limits_{j = 1}^n {{{b}_{j}}} } \right)}}^{2}}}} = 0,\quad i = \overline {1,n} . \\ \end{gathered} $Кроме того, для определения сопряженных функций и состояния системы имеем уравнения
(2.6)
$\begin{gathered} - \frac{{\partial {{H}_{i}}}}{{\partial x}} = \frac{{d{{\lambda }_{i}}}}{{dt}} = - {{e}^{{ - \rho t}}}c\frac{{s_{i}^{0}(t) + {{b}_{i}}(t)}}{{1 + \sum\limits_{j = 1}^n {{{b}_{j}}} (t)}} + a{{\lambda }_{i}};\quad {{\lambda }_{i}}(T) = c\frac{{s_{i}^{0}(T) + {{b}_{i}}(T)}}{{1 + \sum\limits_{j = 1}^n {{{b}_{j}}(T)} }},\quad i = \overline {1,n} , \\ \frac{{dx}}{{dt}} = - ax(t) + \sum\limits_{i = 1}^n {{{d}_{i}}{{u}_{i}}(t)} ;\quad x(0) = {{x}_{0}}. \\ \end{gathered} $Таким образом, в общем случае при исследовании модели с точки зрения агентов решается задача (2.5), (2.6). Рассмотрим два частных случая.
1. Пусть все агенты симметричны, т.е. входные функции и параметры для всех агентов одинаковы и все они предлагают супервайзеру одинаковую взятку, другими словами, ${{b}_{i}}(t) = b(t);\,{{u}_{i}}(t)$ = u(t). Тогда $s_{i}^{0}(t) = 1{\text{/}}n$; $i = \overline {1,n} $, а функции ${{s}_{i}}(t)$ примут вид
Следовательно, если все агенты одинаковы и дают одинаковую взятку, то для них ничего не меняется по сравнению с отсутствием коррупции. Поэтому если бы все агенты знали стратегии остальных агентов, то взятку не дал бы ни один агент. Но агенты не знают выбор других агентов, кроме собственного. Поэтому они предлагают взятку, но никаких дополнительных льгот за это не получают. Их стратегии определяются из решения задачи (индекс i у всех функций далее опустим)
(2.7)
$\begin{gathered} u = r - b - \frac{{{{e}^{{ - 2\rho t}}}{{p}^{2}}}}{{4{{\lambda }^{2}}{{d}^{2}}}},\quad - \lambda d + {{e}^{{ - \rho t}}}cx\frac{{1 + (n - 1)b - 1{\text{/}}n}}{{{{{(1 + nb)}}^{2}}}} = 0, \\ \frac{{d\lambda }}{{dt}} = - {{e}^{{ - \rho t}}}\frac{c}{n} + a\lambda ,\quad \lambda (T) = \frac{c}{n},\quad \frac{{dx}}{{dt}} = - ax(t) + ndu,\quad x(0) = {{x}_{0}}. \\ \end{gathered} $Отсюда
(2.8)
$\lambda (t) = \frac{c}{n}\left( {{{e}^{{ - aT}}} - \frac{1}{\rho }({{e}^{{ - \upsilon T}}} - {{e}^{{ - \rho t}}})} \right){{e}^{{at}}},$2. Пусть все агенты симметричны, но взятку ${{b}_{k}}$ может предложить только один (k-й). Тогда
Количество ресурса у супервайзера ограничено, поэтому если взятку дает только один агент, то он от этого выигрывает, а остальные теряют. Для агентов, которые взятку не дают (j = = $\overline {1,n} ;j \ne k$), и k-го агента возникает в отличие от прошлого случая связанная задача вида
(2.9)
$ - {{\lambda }_{k}}d + {{e}^{{ - \rho t}}}cx\frac{{1 - 1{\text{/}}n}}{{{{{(1 + {{b}_{k}})}}^{2}}}} = 0,\quad {{\lambda }_{j}}(t) = {{e}^{{at}}}\frac{c}{n}\left( {{{e}^{{ - aT}}}\frac{1}{{(1 + {{b}_{k}}(T))}} + \int\limits_t^T {{{e}^{{ - \rho \tau }}}\frac{{d\tau }}{{(1 + {{b}_{k}}(\tau ))}}} } \right),$Так как все агенты, кроме k-го, симметричны, то обозначим ${{b}_{j}} \equiv b$; ${{u}_{j}} = u$; ${{\lambda }_{j}} = \lambda $; $j = \overline {1,n} $; $j \ne k$. В результате решения (2.9) определяется семь неизвестных функций: $u(t),\;\lambda (t),\;b(t),$ ${{u}_{k}}(t),\;{{\lambda }_{k}}(t),\;{{b}_{k}}(t),\;x(t)$.
3. Двухуровневая модель согласования частных и общественных интересов. Теперь проведем расмотрение с точки зрения супервайзера. В этом случае решается задача (1.1)–(1.6), где функции ${{s}_{i}}(t) = {{s}_{i}}(b(t))$ ищутся как решение игры типа Г2,t при побуждении между супервайзером и агентами с учетом условий устойчивого развития системы (1.4). Исходные множества допустимых стратегий супервайзера и агентов
Поскольку функции выигрыша игроков определены на исходных множествах допустимых стратегий, вводится проекция [22] $\pi :\tilde {S} \times \tilde {U}\tilde {B} \times X \to S \times UB \times X$, которая учитывает информационный регламент игры и получается подстановкой в функции $\tilde {s}$, $\tilde {u},\;\tilde {b}$ соответствующих аргументов.
Предлагается алгоритм построения равновесия в игре Гермейера Г2,t для модели (1.1)–(1.6), который состоит в следующем [18, 22].
1. Вычислим максимальный гарантированный выигрыш k-го агента при использовании супервайзером стратегии наказания в случае, когда решением игры между агентами считается равновесие Нэша ($k = \overline {1,n} $):
2. Определим множество
3. Вычислим максимальный гарантированный выигрыш супервайзера при учете интересов всех агентов:
4. Супервайзер предъявляет всем агентам стратегию с обратной связью по управлению
5. Равновесие в игре Гермейера Г2,t имеет вид $\{ s_{i}^{R}(t),u_{i}^{R}(t),b_{i}^{R}(t)\} _{{i = 1}}^{N}$.
Реализация алгоритма возможна только в случае ${{D}_{0}} \ne \emptyset $.
Поясним приведенный выше алгоритм. Стратегия наказания $k$-го агента супервайзером (п. 1 алгоритма) состоит в выборе минимально возможной доли полезности $k$-го агента из (1.6) ($s_{k}^{P} = 0$). В этом случае взятка агентом не предлагается ($b_{k}^{p} = 0$) и на общественные цели агенты средства из бюджета не выделяют, т.е. $u_{k}^{p} = 0$. При этом каждый из них получает гарантированный доход:
Для определения стратегии поощрения агентов супервайзер проводит оптимизацию функционала (1.5) сразу по 3n функциям ${{s}_{i}},\,\,{{u}_{i}},{{b}_{i}},\,i = \overline {1,n} ,$ при ограничениях на управления (1.2), (1.6) и условии $i = \overline {1,n} $:
4. Примеры расчетов. Решения построенных математических моделей в общем случае строятся численно, согласно предложенному в [18] методу дискретизации областей допустимых управлений субъектов. Расчеты проводились в случае:
$n = 3,$ ${{p}_{i}}({{r}_{i}}(t) - {{b}_{i}}(t) - {{u}_{i}}(t)) = {{p}_{i}}\sqrt {{{r}_{i}}(t) - {{b}_{i}}(t) - {{u}_{i}}(t)} ,$ $f(x,u) = - ax(t) + \sum\limits_{i = 1}^n {{{d}_{i}}{{u}_{i}}(t)} ,$ $\alpha = 1,$ $c(x(t)) = cx(t),$ ${{d}_{i}} = 0.00002$ сут–1, i = 1, 2, 3 ${{x}_{0}} = 1,$ $T = 730$ сут, $\rho = 0.00001,$ ${{x}_{{\min }}} = 0.5,$ ${{x}_{{\max }}} = 10,$ $a = 0.0003$ сут–1. В разных примерах менялись величины c, M, ${{p}_{i}}$, ${{r}_{i}}$ i = 1, 2, 3.
В примерах 1, 5 и 2, 6 из таблицы $M = 1,$ $c = 100$ у.е./сут, ${{p}_{i}} = 100$ у.е./сут, а ${{r}_{i}} = \,\,1300$ и 400 соответственно, i = 1, 2, 3. В примерах 3, 7 $c = 100$ у.е./сут, ${{p}_{i}} = 1$ у.е./сут, ${{r}_{i}} = \,\,1300,$ i = 1, 2, 3, M = 1, а в примере 8 при тех же входных данных M = 1000. В примерах 4, 9 M = 1, $c = 1000$ у.е./сут, ${{p}_{i}} = 100$ у.е./сут, ${{r}_{i}} = \,\,1300,$ i = 1, 2, 3. В примерах 10–14 $c = 100$ у.е./сут, ${{r}_{1}} = 400,$ ${{r}_{2}} = 800,$ ${{r}_{3}} = 1300$. Кроме того, в примерах 10, 11 M = 1, а ${{p}_{i}} = 1$ у.е./сут и 100 у.е./сут, i = 1, 2, 3 соответственно; в примере 12 $M = 1000,$ ${{p}_{i}} = 1$ у.е./сут; в примерах 13, 14 ${{p}_{1}} = 0.1$ у.е./сут, ${{p}_{2}} = 1$ у.е./сут, ${{p}_{3}} = 10$ у.е./сут, а M = 1 и 1000 соответственно.
В примерах 1–9 агенты симметричны. В примерах 1–4 предполагается, что взятку никто из агентов не предлагает, т.е. ${{b}_{i}} \equiv 0,$ ${{s}_{i}} \equiv (1 - {{s}_{0}}){\text{/}}3,$ i = 1, 2, 3, а в примерах 5–9 – что взятку может давать только первый агент, т.е. ${{b}_{1}} \ne 0,$ ${{b}_{2}} = {{b}_{3}} \equiv 0$. В примерах 10–14 агенты различны и каждый из них может предлагать взятку.
Если агенты симметричны и ни один из них не предлагает взятку, то для оценки степени системной согласованности приведенной модели введем индекс системной согласованности [17]. Он дает количественную характеристику общесистемных потерь от некооперативного поведения и вычисляется по формуле $PA = {{J}_{0}}{\text{/}}J$, где J есть максимальное значение функционала (1.5) при отсутствии коррупции (${{b}_{i}} \equiv 0$). Оптимизация (1.5) при этом проводится по шести функциям ${{s}_{i}},{{u}_{i}}$, $i = 1,2,3$, с учетом условий (1.2), (1.4), (1.6).
Доход субъектов и индекс системной согласованности (при отсутствии коррупции) для разных входных данных приведены в таблице.
Для входных данных примеров 1 и 2 возможен значительный доход агентов от частной деятельности (коэффициенты ${{p}_{i}}$ велики по сравнению с другими входными данными). Поэтому предлагать им взятку невыгодно как при небольших значениях своего бюджета (пример 2), так и с его увеличением (пример 1). Результаты счета для примеров 1, 5 и 2, 6 соответственно совпадают. При небольшом же доходе от частной деятельности (небольших коэффициентах ${{p}_{i}}$ в примере 3) и входных данных примера 1 агенту становится выгодным предложить взятку супервайзеру, который при небольшом штрафе при поимке ее принимает (пример 7), а при значительном – нет (пример 8).
Результаты счета в примерах 3 и 8 совпадают и отличаются от результатов счета в примере 7. Причем в случае входных данных примера 7 доходы супервайзера и агента, давшего взятку, возрастают по сравнению с примером 3, доходы остальных агентов падают. При увеличении коэффициента перевода состояния системы в общественную полезность по сравнению с примером 1 (пример 4) агент предлагает, а супервайзер принимает взятку (пример 9). Входные данные примеров 10, 13 похожи на данные примера 3, но в этих случаях супервайзер знает, что все агенты могут дать ему взятку. Используя особенности информационного регламента игры Гермейера Г2,t, он побуждает агентов предлагать взятки, за счет чего доход супервайзера значительно возрастает. Агентам невыгодно предлагать взятку, их доход значительно падает по сравнению со случаем отсутствия коррупции. С ростом доходов агентов от частной деятельности их зависимость от супервайзера уменьшается, давать взятку им становится невыгодно и коррупции в системе нет (пример 11). Аналогичная ситуация возникает при более жестком наказании супервайзера за взятки (примеры 12, 14).
Анализ величины индекса системной согласованности в модели при отсутствии коррупции показывает, что в рамках предложенной модели направленность интересов агентов и супервайзера сильно зависит от входных данных модели. Для одних входных данных их интересы полностью совпадают, система согласована и необходимости в иерархическом управлении нет (индекс системной согласованности равен единице). Для других входных данных интересы агентов и супервайзера могут быть прямо противоположными. Индекс системной согласованности близок к нулю. Для достижения общесистемных целей в этом случае иерархическая организация системы управления просто необходима.
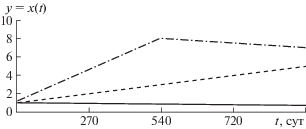
На рисунке приведено изменение состояния системы с течением времени. Сплошная линия соответствует данным примеров 1, 2, 5, 6, 10, 11; штрихпунктирная – примера 4, а пунктирная – примера 3. Изменение переменной состояния в примерах 12–14 аналогично ее изменению в примере 3. Характер поведения переменной состояния в примерах 7–9 совпадает с поведением в примере 4. Переменная, характеризующая состояние системы, с течением времени колеблется в заданном диапазоне (1.4).
Отметим, что в примерах 10, 11, 13 интересы супервайзера и агентов противоположны. В примерах 10, 13 агентам невыгодно давать взятку, но супервайзеру выгодно ее получить, а в примере 11 для агентов, в отличие от супервайзера, частная деятельность предпочтительнее вклада в общественное благосостояние. Только под угрозой наказания (п. 1 алгоритма построения равновесия) агенты в примерах 10, 13 дают взятки, а в примере 11 вкладывают ресурсы в общественное благосостояние. Супервайзер в силу условия на свои управления (1.6) выбирает в этих случаях одного агента и определяет доли агентов как ${{s}_{1}} \equiv 1 - {{s}_{0}} - \alpha ,$ ${{s}_{2}} = {{s}_{3}} \equiv \alpha {\text{/}}2,$ $\alpha \ll 1$ . В результате для двух из трех агентов доход отличается от дохода при наказании на некоторую малую величину $\delta $. При расчетах бралось значение $\alpha = 0.1$.
Заключение. В статье в игровой постановке исследуется динамическая СОЧИ-модель при наличии коррупции. Изменение состояния системы описывается обыкновенным дифференциальным уравнением. Исследование проведено с точки зрения агентов и супервайзера. При рассмотрении с точки зрения агентов строится равновесие Нэша, а рассмотрение с точки зрения супервайзера ведется в рамках информационного регламента игры Гермейера Г2,t . Указан алгоритм построения равновесия в игре Гермейера Г2,t . Отличительные особенности статьи состоят в учете нескольких агентов и возможной коррумпированности супервайзера. Первое вызвало необходимость построения равновесия Нэша, второе – применение информационного регламента игры Гермейера Г2,t .
Анализ результатов проведенных аналитических и численных расчетов позволил сделать ряд предварительных качественных выводов, основной из которых следующий. Для эффективной борьбы с экономической коррупцией в рамках предложенной модели необходимо или усиливать наказание супервайзера за взятки (увеличивать вероятность поимки и жесткость наказания), или увеличивать материальное поощрение агентов за их вклад в общественное благо с одновременным уменьшением их доходов от частной деятельности (например, при помощи налогов).
Таблица.
Доходы субъектов
| Пример | $J$ | ${{J}_{0}}$ | ${{J}_{1}}$ | ${{J}_{2}}$ | ${{J}_{3}}$ | PA |
|---|---|---|---|---|---|---|
| у.е. | ||||||
| 1, 5 | 16 659 | 3609 | 1 344 881 | 1 344 881 | 1 344 881 | 0.22 |
| 2, 6 | 11 687 | 3609 | 750 827 | 750 827 | 750 827 | 0.31 |
| 3, 8 | 16 659 | 16 659 | 61 365 | 61 365 | 61 365 | 1 |
| 4 | 166 596 | 166 596 | 1 638 476 | 1 638 476 | 1 638 476 | 1 |
| 7 | – | 25 718 | 66 913 | 53 014 | 53 014 | – |
| 9 | – | 155 515 | 1 949 741 | 1 381 026 | 1 381 026 | – |
| 10 | – | 64 894 | 13 966 | 15 124 | 16 595 | – |
| 11 | – | 3609 | 740 360 | 1 046 878 | 1 365 813 | – |
| 12 | – | 20 340 | 86 128 | 47 463 | 65 076 | – |
| 13 | – | 32 014 | 795 | 16 911 | 134 443 | – |
| 14 | – | 20 340 | 2404 | 87 660 | 165 305 | – |
Список литературы
Васин А.А., Картунова П.А., Уразов А.С. Модели организации государственных инспекций и борьбы с коррупцией // Математическое моделирование. 2010. Т. 22. № 4. С. 67–89.
Васин А.А., Николаев П.В., Уразов А.С. Механизмы подавления коррупции // Журнал новой экономической ассоциации. 2011. № 10. С. 10–30.
Grass D., Caulkins J., Feichtinger G. et al. Optimal Control of Nonlinear Processes: With Applications in Drugs, Corruption, and Terror. Berlin-Heidelberg: Springer-Verlag, 2008.
Bicchieri C., Rovelli C. Evolution and Revolution: The Dynamic of Corruption // Rationality and Society. 1995. № 7 (2). P. 201–224.
Blackburn K., Bose N., Hague M.E. The Incidence and Persistence of Corruption in Economic Development // J. of Economic Dynamic and Control. 2006. № 30. P. 2447–2467.
Blackburn K., Forgues-Puccio G.F. Financial Liberalization, Bureaucratic Corruption and Economic Development // J. of International Money and Finance. 2010. № 29. P. 1321–1339.
Blackburn K., Powell J. Corruption, Inflation and Growth // Econ. Letters. 2011. № 113. P. 225–227.
Caulkins J.P., Feichtinger G., Grass D. et al. Leading Bureaucracies to the Tipping Point: An Alternative Model of Multiple Stable Equilibrium Levels of Corruption // European J. of Operational Research. 2013. № 225. P. 541–546.
Feichtinger G., Wirl F. On the Stability and Potential Cyclicity of Corruption in Governments Subject to Popularity Constraints // Mathematical Social Sciences. 1994. № 28. P. 215–236.
Kolokoltsov V.N., Malafeev O.A. Mean-Field-Game of Corruption // Dynamic Games and Applications. 2017. № 7. P. 34–47.
Lambsdorff J.G. The Institutional Economics of Corruption and Reform. Cambridge: Cambridge University Press, 2007.
Levin M.I., Satarov G.A. Russian Corruption // The Oxford Handbook of Russian Economy. NY : Oxford University Press, 2013. P. 286–309.
Myerson R. Effectiveness of Electoral Systems for Reducing Government Corruption: a Game-theoretic Analysis // Game and Economic Behavior. 1993. № 5. P. 118–132.
Nikolaev P.V. Corruption Suppression Models: the Role of Inspectors’ Moral Level // Computer Math. Model. 2014. № 25 (1). P. 87–102.
Антоненко А.В., Угольницкий Г.А., Усов А.Б. Статические модели борьбы с коррупцией в иерархических системах управления // Изв. РАН. ТиСУ. 2012. № 4. С. 164–176.
Горбанева О.И., Угольницкий Г.А. Механизмы согласования интересов в модели распределения ресурсов // Системы управления и информационные технологии. 2014. № 3.2 (57). С. 225–231.
Угольницкий Г.А. Управление устойчивым развитием активных систем. Ростов-на-Дону: Изд-во Южного федерального ун-та, 2016. 940 с.
Угольницкий Г.А., Усов А.Б. Исследование дифференциальных моделей иерархических систем управления путем их дискретизации // АиТ. 2013. № 2. С. 109–122.
Угольницкий Г.А., Усов А.Б. Динамические модели коррупции в иерархических системах управления при эксплуатации биоресурсов // Изв. РАН. ТиСУ. 2014. № 6. С. 168–176.
Угольницкий Г.А., Усов А.Б. Модели борьбы с административной коррупцией в иерархических системах управления // Математическая теория игр и ее приложения. 2014. Т. 6. Вып. 1. С. 73–90.
Угольницкий Г.А., Усов А.Б. Моделирование коррупции в трехуровневых системах управления // Проблемы управления. 2014. № 1. С. 53–62.
Горелик В.А., Горелов М.А., Кононенко А.Ф. Анализ конфликтных ситуаций в системах управления. М.: Радио и связь, 1991. 288 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления