Известия РАН. Теория и системы управления, 2020, № 3, стр. 126-147
ОПРЕДЕЛЕНИЕ ОРБИТЫ НА БОРТУ КОСМИЧЕСКОГО АППАРАТА
Д. А. Тучин *
ИПМ им. М.В. Келдыша РАН
Москва, Россия
* E-mail: den@kiam1.rssi.ru
Поступила в редакцию 18.10.2019
После доработки 06.11.2019
Принята к публикации 25.11.2019
Аннотация
Рассматриваются методы и алгоритмы определения орбиты космического аппарата на его борту с использованием измерений глобальных систем спутниковой навигации. Описаны методы и алгоритмы получения радионавигационных измерений при высокой динамике орбитального движения. Приведена небесно-механическая интерпретация измерений. Предложены алгоритмы трехэтапной обработки траекторных измерений, позволяющие повысить надежность и точность определения орбиты. Разработана математическая модель имитатора сигналов спутниковой навигации. Приведены результаты вычислительных экспериментов.
Введение. Создание методов, алгоритмов и программ бортовой автономной навигационной системы (АНС) для околоземных космических аппаратов (КА) [1] потребовало привлечения опыта обработки траекторных измерений в Баллистическом центре ИПМ им. М.В. Келдыша РАН. Разработанные бортовые алгоритмы АНС позволяют проводить определение параметров движения КА по сигналам глобальных навигационных спутниковых систем ГЛОНАСС (Глобальная навигационная спутниковая система) и GPS (Global Positioning System) на геостационарных орбитах (ГСО), орбитах с большим эксцентриситетом (ВЭО11) и низкоорбитальных космических объектах (НОКО) [2, 3].
Надежность работы АНС строится на независимости получения измерений навигационных спутников от результатов определения орбиты КА [4]. При этом получение измерений и определение орбиты выполняются на двух разных специализированных процессорах. АНС включает два аппаратно-программных блока без обратной связи между ними: блок поиска сигналов навигационных КА (НКА) и получения измерений, блок обработки измерений и определения орбиты [1].
Алгоритмы поиска и слежения за сигналами навигационных систем для наземного пользователя изложены в [5, 6]. Реализация алгоритмов для бортовых систем КА в случае применения аппаратного и программного корреляторов – части аппаратуры приемных устройств спутниковых сигналов для НОКО изложена в [7]. Высокая динамика полета КА на орбите с большим эксцентриситетом и большая дальность до НКА потребовали разработки новых методов и алгоритмов поиска и слежения за радионавигационными сигналами с использованием аппаратного коррелятора. Повышенные требования к надежности приема сигналов заставили отказаться от алгоритмов поиска сигнала по априорному значению доплеровского смещения сигнала НКА, зависящего от точности знания орбиты.
В работе представлены алгоритмы поиска и слежения за сигналом НКА и математическая модель коррелятора. Приведена небесно-механическая интерпретация первичных измерений, т.е. соотношения связи физических величин и радиотехнических параметров, описывающих дальномерные и скоростные измерения. Предложена методика оценки точности измерений коррелятора без решения навигационной задачи.
Традиционная схема обработки одновременных измерений с более чем четырех НКА на орбитах ВЭО и ГСО является проблематичной из-за малого числа одновременно видимых навигационных спутников и противоречия между наилучшим геометрическим расположением НКА и ионосферными ошибками измерений [8]. Использование вектора кинематических параметров положения и скорости в качестве начальных условий для интегрирования уравнений движения не дает хороших результатов по точности даже на низкой околокруговой орбите [9]. Применение схемы с определением вектора положения и скорости в перицентре орбиты ВЭО с последующим прогнозом в апоцентр при наличии орбитальных маневров является проблематичным.
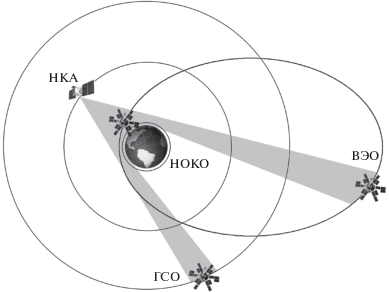
В работе представлены алгоритмы трехэтапного метода определения орбиты КА на его борту [2]. При отсутствии априорных данных об орбите КА на его борту решается задача первоначального определения орбиты. На первом этапе первоначального определения вместе с кинематическими параметрами движения КА находятся уход частоты опорного генератора и рассинхронизации шкал времени КА и спутниковой системы, эти искомые параметры называются служебными параметрами приемника радионавигационных сигналов [1]. Первоначальное определение орбиты происходит с учетом полного отсутствия априорной информации. Задача осложнена неоднозначностью дальномерного измерения псевдодальности. В основу алгоритмов первоначального определения орбиты положено геометрическое решение при избыточном числе принимаемых НКА не менее пяти. Избыточность необходима для использования остаточных невязок измерений при анализе достоверности первоначального определения. Применение специальной остронаправленной антенны [10], способной принимать сигнал, излученный с другой стороны Земли (рис. 1 ), позволяет проводить первоначальное определение в районе апоцентра ВЭО или на ГСО.
При наличии на борту КА данных об его орбите, переданных с Земли или полученных после решения задачи первоначального определения, происходит уточнение восьмимерного фазового вектора, состоящего из шести кинематических параметров начальных условий (НУ), ухода частоты опорного генератора и рассинхронизации шкалы времени КА и навигационной системы. Восьмимерный искомый фазовый вектор НУ строится на момент последнего измерения. Этот второй этап называется определением орбиты на короткой дуге. Обработка происходит на интервалах времени от одной минуты до получаса, которые зависят от числа видимых НКА.
Динамическая модель, описывающая поведение кинематических и служебных параметров, состоит из уравнений динамики полета КА и уравнений авторегрессии ухода частоты опорного генератора и рассинхронизации шкал времени [1–3] с возбуждающим белым шумом. Обработка измерений по короткой дуге производится итерационным фильтром Калмана. После решения навигационной задачи сохраняется вектор положения НУ с весом, равным обратной величине среднего квадратичного отклонения (СКО) остаточной невязки дальномерных измерений. Эти сохраненные векторы положения с весами являются по сути нормальными местами [11] и на третьем этапе определения параметров рассматриваются как измерения. Высокая эффективность алгоритмов определения орбиты по короткой дуге обеспечивается использованием законов динамики движения КА и модели поведения частоты опорного генератора непосредственно при обработке первичных скоростных и дальномерных измерений.
На заключительном третьем этапе обработки нормальных мест по измерениям, сформированным на этапе определения по короткой дуге, происходит окончательное определение орбиты КА. Проведенные вычислительные эксперименты показали высокую эффективность обработки нормальных мест на интервале полутора витков КА вокруг Земли.
Обработка нормальных мест и определение орбиты КА производится методом наименьших квадратов (МНК). Метод используется в Баллистическом центре ИПМ им. М.В. Келдыша РАН при оперативном определении орбит КА [9]. Проблема построения орбиты КА с помощью вычислительной машины была решена в конце ноября 1957 г. [12, 13]. Позже предложенный метод был существенно улучшен [14].
Высокоточное определение орбиты КА в АНС невозможно без методов отбраковки аномальных измерений. В работе описаны методы локальной обработки измерений и отбраковки с использованием построения гистограммы невязок в логарифмической шкале [2].
Для отработки алгоритмов получения измерений от НКА ГЛОНАСС и GPS создана математическая модель, которая обеспечивает: формирование орбит навигационных группировок; формирование параметров численно-аналитических моделей движения НКА [15]; формирование суперкадров НКА; расчет доплеровских и дальномерных измерений.
В работе приведены результаты численного моделирования и экспериментальной отработки алгоритмов на макете АНС [1, 4] с использованием имитатора навигационных сигналов на ВЭО с периодом около 12 ч и с высотой апоцентра 38.6 тыс. км.
1. Математическая модель коррелятора. Специализированное устройство для вычисления корреляционных функций принимаемых сигналов, соответствующих определенному интервалу измерения временных задержек, называют коррелятором. Приведем математическую модель одночастотного коррелятора и опишем управляющие и измеряемые параметры, а также алгоритмы поиска, захвата и слежения за радионавигационными сигналами ГЛОНАСС и GPS.
Рассмотрим одночастотный коррелятор, который способен обрабатывать сигналы радионавигационных систем на гражданской частоте пониженной точности ГЛОНАСС и гражданской частоте C/A (Coarse Acquisition) кода GPS. Современные корреляторы способны вести прием навигационных сигналов разных НКА по независимым каналам. Коррелятор обладает несколькими независимыми каналами для решения задач поиска, захвата и слежения за радионавигационным сигналом. Коррелятор способен одновременно обрабатывать сигналы с нескольких НКА, привязывая измерительную информацию к некорректируемой шкале времени, определяемой опорным генератором частоты.
Принимаемый в корреляторе гармонический радионавигационный сигнал ${{s}_{t}}$ в момент времени $t$ можно представить в виде [5]: ${{s}_{t}} = A{{J}_{s}}\left( t \right)\cos \left( {2\pi {{\omega }_{s}}t + {{\varphi }_{s}}} \right)$, где $A$ – амплитуда сигнала, ${{J}_{s}}$ – модулирующая функция, ${{\omega }_{s}}$ – несущая частота принимаемого сигнала, Гц, ${{\varphi }_{s}}$ – смещение фазы несущей частоты принимаемого сигнала.
Модулирующая функция ${{J}_{s}}$ принимает значения ±1 в зависимости от кода псевдошумовой последовательности (ПСП) и информационного кода НКА. Частота смены принимаемых символов определяется поднесущей излучаемой частотой ${{\Omega }_{0}}$ НКА. Для принимаемой поднесущей частоты $\Omega $ справедливо, что
где ${{\omega }_{0}}$ – несущая частота излучаемого сигнала.Для гражданского кода стандартной точности навигационной системы ГЛОНАСС на несущей частоте $f_{{{{{\text{L}}}_{1}}}}^{{{\text{ГЛН}}}} = 1602$ МГц определены следующие значения поднесущих частот излучаемых сигналов: ${{\Omega }_{0}} = 511$ кГц, ${{\omega }_{0}} = f_{{{{{\text{L}}}_{1}}}}^{{{\text{ГЛН}}}}{\text{ + }}{{n}_{{{\text{лит}}}}} \cdot \Delta f_{{{{{\text{L}}}_{1}}}}^{{{\text{ГЛН}}}}$, $\Delta f_{{{{{\text{L}}}_{1}}}}^{{{\text{ГЛН}}}} = 562.5$ кГц, где ${{n}_{{{\text{лит}}}}}$ – литер (номер частоты) НКА, принимающий целые значения от –7 до 6 [16].
Для гражданского кода навигационной системы GPS на несущей частоте ${{\omega }_{0}} = 1575.42$ МГц определено значение для поднесущей частоты излучаемого сигнала ${{\Omega }_{0}} = 1023$ кГц [17].
Пусть $\Delta t$ – длительность интервала накопления сигнала в корреляторе, тогда время генерации ПСП-кода для корреляции, называемое длительностью эпохи, определяется соотношением
Для обработки сигнала коррелятор имеет управление по: несущей частоте $\omega $ принимаемого сигнала; времени ${{\tau }_{{{\text{ПСП}}}}}$ начала генерации ПСП и смещению фазы несущей частоты принимаемого сигнала ${{\varphi }_{s}}$. По заданным значениям параметров управления коррелятор формирует сигнал и производит вычисления двух интегралов (корреляционных функций):
(1.2)
${{I}_{{\text{д}}}} = \int\limits_0^{{{t}_{{{\text{эп}}}}}} {{{s}_{t}}J\left( {t - {{\tau }_{{{\text{ПСП}}}}}} \right)} \cos \left( {2\pi \omega t + {{\varphi }_{s}}} \right)dt,\quad {{I}_{{\text{м}}}} = \int\limits_0^{{{t}_{{{\text{эп}}}}}} {{{s}_{t}}J\left( {t - {{\tau }_{{{\text{ПСП}}}}}} \right)} \sin \left( {2\pi \omega t + {{\varphi }_{s}}} \right)dt,$Наряду с интегралами (1.2), коррелятор вычисляет разности, называемые дискриминаторами по задержке, действительной ${{\Delta }_{{\text{д}}}}$ и мнимой ${{\Delta }_{{\text{м}}}}$ части сигнала между опережающей и задерживаемой ПСП:
(1.3)
$\begin{gathered} {{\Delta }_{{\text{д}}}} = \int\limits_0^{{{t}_{{{\text{эп}}}}}} {{{s}_{t}}\left( {J\left( {t - {{\tau }_{{{\text{ПСП}}}}} + \Delta \tau } \right) - J\left( {t - {{\tau }_{{{\text{ПСП}}}}} - \Delta \tau } \right)} \right)} \cos \left( {2\pi \omega t + \Phi } \right)dt, \\ {{\Delta }_{{\text{м}}}} = \int\limits_0^{{{t}_{{{\text{эп}}}}}} {{{s}_{t}}\left( {J\left( {t - {{\tau }_{{{\text{ПСП}}}}} + \Delta \tau } \right) - J\left( {t - {{\tau }_{{{\text{ПСП}}}}} - \Delta \tau } \right)} \right)} \sin \left( {2\pi \omega t + \Phi } \right)dt, \\ \end{gathered} $Целью слежения за сигналом НКА с использованием коррелятора является вычисление неизвестных параметров $\omega $, ${{\tau }_{{{\text{ПСП}}}}}$, ${{\varphi }_{s}}$ и $\Delta \tau $ при истечении эпохи, при которых значения ${{I}_{{\text{м}}}}$, ${{\Delta }_{{\text{д}}}}$, ${{\Delta }_{{\text{м}}}}$ обращаются в ноль [4]. Точность измерений псевдодальности и псевдоскорости определяется качеством подстройки параметров управления.
Кодовое измеренное значение псевдодальности ${{\tilde {\Psi }}^{{{\text{пд}}}}}$ в момент t приема сигнала задается параметром управления ${{\tau }_{{{\text{ПСП}}}}}$ по времени начала генерации ПСП и описывается соотношением:
(1.4)
${{\tilde {\Psi }}^{{{\text{пд}}}}} = c{{\tau }_{{{\text{ПСП}}}}} + {{\lambda }_{{{\text{зн}}}}}n,$Пусть ${{\omega }_{{{\text{доп}}}}} = \omega - {{\omega }_{0}}$ есть доплеровское смещение частоты сигнала, тогда измеренное значение псевдоскорости описывается соотношением
где $\lambda = {c \mathord{\left/ {\vphantom {c {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$ – длина волны излучаемого сигнала. Отметим, что для систем ГЛОНАСС и GPS длина волны составляет величину около 19 см.Фаза несущей частоты сигнала ${{\varphi }_{s}}$ есть интегральный параметр управления по смещению фазы несущей частоты $\Delta {{\varphi }_{i}}$ с момента начала слежения за НКА:
где $n$ – число управлений по смещению фазы несущей частоты, $i$ – номер эпохи с начала работы с радионавигационным сигналом.Время начала генерации ПСП ${{\tau }_{{{\text{ПСП}}}}}$ также является интегральным параметром и определяется соотношением
Для идентификации НКА навигационная система служебной информации принимает биты информационных сообщений, определяемые модулирующей функцией $\operatorname{J} $ (1.2).
В соответствии с интерфейсным документом ГЛОНАСС [16] информационная строка принимается в корреляторе для 2000 эпох
при длительности интервала накопления Δt = 1 мс. За время $\Delta {{t}_{{{\text{стр}}}}}$ принимается 85 информационных бит, при этом длительность каждого k-го бита составляет $\sum\limits_{i = k}^{k + 20} {t_{{{\text{эп}}}}^{i}} $. Если модулирующая функция J в течение первых 10 эпох равна 1, а в течение последующих 10 равна –1, то информационный бит равен 1. Если модулирующая функция $J$ в течение первых 10 эпох равна –1, а в течение последующих 10 эпох равна 1, то информационный бит равен 0. После 85 информационных битов следуют 30 битов метки времени длительностью по 10 эпох каждый: $\sum\limits_{i = k}^{k + 10} {t_{{{\text{эп}}}}^{i}} $. Значения 30 битов метки времени фиксированы и содержат значения “111110001101110101000010010110”. Эта последовательность используется для синхронизации приема информационного кода. Если модулирующая функция $J$ в течение первых 5 эпох равна 1, а в течение последующих 5 эпох равна –1, то бит метки времени равен 1, а если модулирующая функция J в течение первых 5 эпох равна –1, а в течение последующих 5 эпох равна 1, то бит метки времени равен 0.Информационная строка сообщения НКА GPS [17] принимается в корреляторе для 6000 эпох
при длительности интервала накопления Δt = 1 мс. За время $\Delta t_{{{\text{стр}}}}^{{{\text{GPS}}}}$ принимается 300 информационных бит, при этом длительность каждого k-го бита составляет $\sum\limits_{i = k}^{k + 20} {t_{{{\text{эп}}}}^{i}} $. Если модулирующая функция J в течение 20 эпох равна 1, то информационный бит равен 1, а если функция J в течение 20 эпох равна –1, то информационный бит равен 0. В информационном сообщении GPS нет метки времени, для синхронизации приема информации используют 8 первых фиксированных из 24 бит, передающихся с началом каждого 300-битного кадра: “10001011”.Знаки действительной части сигнала ${{I}_{{\text{д}}}}$ определяют значение модулирующей функции J, по которым находят значения принимаемых информационных битов. Отметим, что прием может осуществляться и в инверсном виде, что определяется только после приема 30 бит прямого или инверсного кода метки времени ГЛОНАСС или 8 фиксированных бит информационного кадра GPS.
2. Измерения. Рассмотрим небесно-механическую интерпретацию измерений [18], т.е. сопоставим измеряемые величины с параметрами движения КА, параметрами измерительной аппаратуры и систематическими ошибками распространения сигнала НКА в ионосфере Земли [8].
В АНС для определения орбиты КА применяют два типа радиотехнических измерений: псевдодальность и псевдоскорость.
Для описания процесса ухода шкалы времени опорного генератора от идеальной шкалы навигационной системы служит параметр рассинхронизации $\varphi \left( {{{t}_{{{\text{прм}}}}}} \right)$ в момент регистрации измерений, выраженный в единицах длины.
ПСП в приемнике генерируется так, что ее начало совпадает с началом каждой миллисекунды. Так как период передачи ПСП НКА ГЛОНАСС и GPS составляет 1 мс, то возникает неоднозначность измерения псевдодальности, обусловленная конечным числом зон однозначного измерения ${{\lambda }_{{{\text{зн}}}}} = {{10}^{{ - 3}}}$ с, где c – скорость света в м/с. Измеренное значение псевдодальности определено формулой (1.4), а расчетное значение $\Psi _{t}^{{{\text{пд}}}}$ измерения псевдодальности связано с векторами положения ${{{\mathbf{r}}}_{{{\text{КА}}}}}$ КА в момент приема сигнала $t$ и ${{{\mathbf{r}}}_{{{\text{НКА}}}}}$ НКА в момент излучения ${{t}_{{{\text{изл}}}}}$ следующим соотношением [2]:
(2.1)
$\Psi _{t}^{{{\text{пд}}}} = \left| {\Delta {\mathbf{r}}\left( t \right)} \right| + \varphi \left( t \right) - \Delta {{t}_{{{\text{НКА}}}}}с - {{\lambda }_{{{\text{зн}}}}}n - \Delta \rho + {{\delta }_{{{\text{пд}}}}},$Именно наличие неизвестного параметра $\varphi \left( t \right)$ в (2.1) повлияло на внесение в название дальномерного измерения приставки псевдо.
Эффективное устранение ионосферной задержки $\Delta \rho $ возможно при приеме в корреляторе АНС второй частоты сигнала НКА. Ионосферная задержка сигнала $\Delta \rho = \Delta {{\rho }_{{{\text{L1}}}}}$ на первой частоте ${{{\text{L}}}_{1}}$ устраняется с помощью двух измерений псевдодальности $\tilde {\Psi }_{{{\text{L1}}}}^{{{\text{пд}}}}$ и $\tilde {\Psi }_{{{\text{L2}}}}^{{{\text{пд}}}}$ на разных частотах ${{f}_{{{\text{L1}}}}}$ и ${{f}_{{{\text{L2}}}}}$ [17]:
Уход времени НКА $\Delta {{t}_{{{\text{НКА}}}}}$ относительно эталонного времени передается в навигационном сообщении [16, 17]. Оценка дисперсии $\sigma _{{{\text{пд}}}}^{2}$ случайной величины аппаратурной ошибки ${{\delta }_{{{\text{пд}}}}}$ измерения псевдодальности происходит на этапе калибровки коррелятора [4]. Нахождение числа зон однозначного измерения $n$ происходит на этапе приема измерений. Точность определения $n$ зависит от величины рассинхронизации шкал времени АНС и спутниковой навигационной системы.
Уход частоты опорного генератора $\Delta f$ описывается авторегрессией первого порядка. Значение ухода на момент времени ${{t}_{i}}$ представимо в виде временного ряда
(2.2)
$\Delta f\left( {{{t}_{i}}} \right) = \Delta f\left( {{{t}_{{i - 1}}}} \right) + \varepsilon _{{{{t}_{i}}}}^{{\Delta f}},$(2.3)
$\varphi \left( {{{t}_{i}}} \right) = \varphi \left( {{{t}_{{i - 1}}}} \right) + \Delta f\left( {{{t}_{i}}} \right)\left( {{{t}_{i}} - {{t}_{{i - 1}}}} \right) + \varepsilon _{{{{t}_{i}}}}^{\varphi },\quad \varepsilon _{{{{t}_{i}}}}^{\varphi } = \varphi \left( {{{t}_{i}}} \right) - \varphi \left( {{{t}_{{i - 1}}}} \right) - \Delta f\left( {{{t}_{i}}} \right)\left( {{{t}_{i}} - {{t}_{{i - 1}}}} \right),$Случайная величина $\varepsilon _{t}^{\varphi }$ имеет нулевое математическое ожидание. Оценка дисперсии $\sigma _{\varphi }^{2}$, определяется по большой выборке измерений на этапе калибровки коррелятора.
Расчетное значение псевдоскорости $\Psi _{t}^{{{\text{пc}}}}$ связано с кинематическими векторами ${{{\mathbf{r}}}_{{{\text{КА}}}}}$, ${{{\mathbf{v}}}_{{{\text{КА}}}}}$ КА в момент приема сигнала t и НКА (${{{\mathbf{r}}}_{{{\text{НКА}}}}}$, ${{{\mathbf{v}}}_{{{\text{НКА}}}}}$) в момент излучения ${{t}_{{{\text{изл}}}}}$ следующим соотношением:
(2.4)
$\Psi _{t}^{{{\text{пc}}}} = \frac{{\Delta {\mathbf{r}}\left( t \right) \cdot \Delta {\mathbf{v}}\left( t \right)}}{{\left| {\Delta {\mathbf{r}}\left( t \right)} \right|}} + \Delta f\left( t \right) + {{\delta }_{{{\text{пс}}}}},$Итак, измерения псевдодальности и псевдоскорости описываются соотношениями (2.1) и (2.4), неизвестными искомыми параметрами являются три компоненты вектора положения ${{{\mathbf{r}}}_{{{\text{КА}}}}}$, три компоненты вектора скорости ${{{\mathbf{v}}}_{{{\text{КА}}}}}$, значения ухода шкалы времени $\varphi $ и смещение частоты $\Delta f$ опорного генератора относительно эталонного значения навигационной системы. Время излучения сигнала ${{t}_{{{\text{изл}}}}}$ определяется по номеру ПСП относительно битов информационного кадра [4], а время приема $t$ вычисляется с использованием светового уравнения итерационным методом, при котором на нулевом шаге итерации ${{t}^{{\left( 0 \right)}}} = {{t}_{{{\text{изл}}}}}$, а на s-м шаге итерации:
(2.5)
${{t}^{{\left( s \right)}}} = {{t}_{{{\text{изл}}}}} + \frac{1}{с}{\text{|}}{{{\mathbf{r}}}_{{{\text{КА}}}}}({{t}^{{\left( {s - 1} \right)}}}) - {{{\mathbf{r}}}_{{{\text{НКА}}}}}\left( {{{t}_{{{\text{изл}}}}}} \right){\text{|}}{\kern 1pt} {\kern 1pt} .$Итерации продолжают до тех пор, пока ${\text{|}}{{t}^{{\left( s \right)}}} - {{t}^{{\left( {s - 1} \right)}}}{\text{|}} > \varepsilon $, полагая обычно $\varepsilon = {{10}^{{ - 10}}}$ с. Для расчета ${{{\mathbf{r}}}_{{{\text{КА}}}}}$ используется модель движения по априорным НУ.
Отметим, что при совместной обработке измерений псевдодальности и псевдоскорости систем ГЛОНАСС и GPS возникает проблема рассинхронизации шкал времени этих навигационных систем между собой. Поправка ${{\tau }_{{{\text{GPS}}}}}$ на расхождение системных шкал времени ГЛОНАСС и GPS передается в эфемеридном сообщении [16] и не превышает значения $1.9 \times {{10}^{{ - 3}}}$ c. Расхождение шкал ГЛОНАСС и GPS влияет только на точность относительной привязки времени излучения измерений ${{t}_{{{\text{изл}}}}}$ с борта НКА. Так как скорость КА не более 8 км/с, то предельная ошибка по дальности составляет 15.2 м и сопоставима с точностью измерения псевдодальности [4], вследствие чего можно пренебречь ${{\tau }_{{{\text{GPS}}}}}$. Гораздо бо́льшая ошибка в задержке сигнала GPS относительно ГЛОНАСС возникает в корреляторе АНС в связи с разными задержками прохождения сигналов в микросхемах делителей частот. Эта задержка, выраженная в единицах длины, составляет несколько сотен метров и определяется экспериментально в процессе настройки и калибровки аппаратуры АНС.
Для решения навигационной задачи необходимы частные производные псевдодальности и псевдоскорости по искомым параметрам ${{{\mathbf{r}}}_{{{\text{КА}}}}}$, ${{{\mathbf{v}}}_{{{\text{КА}}}}}$, $\Delta f$ и $\varphi $:
(2.6)
$\begin{gathered} \frac{{\partial \Psi _{t}^{{{\text{пд}}}}}}{{\partial {{{\mathbf{r}}}_{{{\text{КА}}}}}}} = \frac{{\partial \Psi _{t}^{{{\text{пc}}}}}}{{\partial {{{\mathbf{v}}}_{{{\text{КА}}}}}}} = \frac{{\Delta {\mathbf{r}}}}{{\left| {\Delta {\mathbf{r}}} \right|}},\quad \frac{{\partial \Psi _{t}^{{{\text{пд}}}}}}{{\partial {{{\mathbf{v}}}_{{{\text{КА}}}}}}} = {\mathbf{0}},\quad \frac{{\partial \Psi _{t}^{{{\text{пд}}}}}}{{\partial \Delta f}} = \frac{{\partial \Psi _{t}^{{{\text{пc}}}}}}{{\partial \varphi }} = 0, \\ \frac{{\partial \Psi _{t}^{{{\text{пc}}}}}}{{\partial {{{\mathbf{r}}}_{{{\text{КА}}}}}}} = \frac{{\Delta {\mathbf{v}}}}{{\left| {\Delta {\mathbf{r}}} \right|}} - \frac{{\Delta {\mathbf{r}}}}{{{{{\left| {\Delta {\mathbf{r}}} \right|}}^{3}}}}\left( {\Delta {\mathbf{r}} \cdot \Delta {\mathbf{v}}} \right),\quad \frac{{\partial \Psi _{t}^{{{\text{пд}}}}}}{{\partial \varphi }} = \frac{{\partial \Psi _{t}^{{{\text{пд}}}}}}{{\partial \Delta f}} = 1. \\ \end{gathered} $Отметим, что расчетные значения измерений (2.1), (2.4) и их производные (2.6) приведены для инерциальной системы координат (СК). Использование инерциальной СК необходимо для корректной небесно-механической интерпретации прохождения сигнала от НКА до КА.
Коррелятор способен измерить количество полных циклов несущей частоты $m_{{\text{ц}}}^{i}$ и остаток фазы несущей частоты $m_{\varphi }^{i}$ за время регистрации i-й принимаемой ПСП. Величины $m_{{\text{ц}}}^{i}$ и $m_{\varphi }^{i}$ связаны с измеренным значением $\omega _{{{\text{изм}}}}^{i}$ принимаемой несущей частоты $\omega $ на интервале ${{t}_{{{\text{эп}}}}}$:
(2.7)
$\omega _{{{\text{изм}}}}^{i} = \frac{1}{{t_{{{\text{эп}}}}^{i}}}\left( {m_{{\text{ц}}}^{i} + \frac{1}{{2\pi }}(m_{\varphi }^{i} - m_{\varphi }^{{i - 1}})} \right).$По фиксации эпохи коррелятор измеряет время ${{m}_{{{\text{эп}}}}}$ ее прихода в своей шкале времени и остаток фазы поднесущей частоты ${{m}_{\Omega }}$. Эти величины связаны с временем начала генерации ПСП:
(2.8)
${{\tau }_{{{\text{ПСП}}}}} = {{m}_{{{\text{эп}}}}} - \frac{1}{{2\pi }}\frac{{{{m}_{\Omega }}}}{\Omega }.$Для времени $t_{{{\text{эп}}}}^{i}$ на i-м такте измерения справедливо:
(2.9)
$t_{{{\text{эп}}}}^{i} = \left( {m_{{{\text{эп}}}}^{i} - \frac{1}{{2\pi }}\frac{{m_{\Omega }^{i}}}{{{{\Omega }^{i}}}}} \right) - \left( {m_{{{\text{эп}}}}^{{i - 1}} - \frac{1}{{2\pi }}\frac{{m_{\Omega }^{{i - 1}}}}{{{{\Omega }^{{i - 1}}}}}} \right) + \Delta t,$Подставляя (2.8) в (1.4), получим соотношение для измеренного значения псевдодальности в момент приема $t$:
(2.10)
${{\tilde {\Psi }}^{{{\text{пд}}}}} = c\left( {{{m}_{{{\text{эп}}}}} - \frac{1}{{2\pi }}\frac{{{{m}_{\Omega }}}}{\Omega }} \right) + {{\lambda }_{{{\text{зн}}}}}n.$Коррелятор позволяет идентифицировать ПСП, излучение которой было начато с НКА в момент времени, совпадающий с целой секундой бортовой шкалы этого спутника. Это позволяет соотнести измеренные значения псевдодальности ${{\tilde {\Psi }}^{{{\text{пд}}}}}$ и псевдоскорости ${{\tilde {\Psi }}^{{{\text{пс}}}}}$ к моментам времени излучения по шкалам времени навигационных систем ГЛОНАСС и GPS. Целочисленная секунда излучения определяется исходя из принятой битовой последовательности информационного кадра НКА.
Определение зоны однозначного измерения или целого числа $n$ происходит с использованием решения светового уравнения (2.5).
Отметим, что измеренное значение псевдоскорости ${{\tilde {\Psi }}^{{{\text{пc}}}}}$ (1.5) определяется сдвигом доплеровской частоты сигнала при управлении по несущей частоте сигнала $\omega $. Доплеровский сдвиг есть результат обработки измеренных мгновенных значений ${{\omega }_{{{\text{изм}}}}}$ (2.7). Измеренное значение кодовой псевдодальности ${{\tilde {\Psi }}^{{{\text{пд}}}}}$ приведено в (2.10). Небесно-механическая интерпретация дальномерного и скоростного измерения представлены в (2.1) и (2.4) соответственно.
3. Поиск сигнала и слежение за ним. Для получения измерений на борту КА необходимо сначала найти радионавигационный сигнал, а потом его отслеживать, учитывая доплеровское смещение частоты, вызванное изменением относительной радиальной скорости КА – НКА. Для эффективного поиска радионавигационного сигнала при большой динамике движения относительно НКА коррелятор должен содержать поисковую машину. Поисковая машина (ПМ) способна воспринимать упорядоченный по возрастанию массив значений несущей частоты sω = = $\{ s_{\omega }^{1}, \ldots ,s_{\omega }^{{{{n}_{{{\text{пм}}}}}}}\} $ размерности ${{n}_{{{\text{ПМ}}}}}$, для каждого элемента которого ищется сигнал НКА. Также для поиска сигналов ГЛОНАСС задается литер ${{n}_{{{\text{лит}}}}}$, а для GPS – номер НКА от 1 до 32. ПМ по значениям задаваемого массива ${{{\mathbf{s}}}_{\omega }}$ в каждой точке частоты производит корреляционную обработку и для каждой частоты вычисляет амплитуду, задержку и время фиксации. Из этих значений формируются упорядоченные по амплитуде массивы ${{{\mathbf{f}}}_{A}}$, ${{{\mathbf{f}}}_{\tau }}$ и ${{{\mathbf{f}}}_{{{\text{эп}}}}}$.
Стратегия поиска сигнала с использованием ПМ основывается на поиске максимума амплитуды сигнала $k = \mathop {\arg \max }\limits_{1 \leqslant i \leqslant {{n}_{{{\text{пм}}}}}} (f_{A}^{i})$, соответствующей несущей частоте $s_{\omega }^{k}$. Уменьшением интервала $(s_{\omega }^{1},s_{\omega }^{{{{n}_{{{\text{пм}}}}}}})$ достигаются необходимые точности нахождения ${{{\mathbf{f}}}_{\tau }}$ и ${{{\mathbf{f}}}_{{{\text{эп}}}}}$ для их использования в определении управления $\omega $ по несущей частоте и времени ${{\tau }_{{{\text{ПСП}}}}}$ начала генерации ПСП. Поиск сигнала разбивается на три этапа. На каждом этапе сигнал НКА считается найденным в k-м диапазоне, если $f_{A}^{k} > {{A}_{{\text{0}}}}$, где ${{A}_{{\text{0}}}}$ – пороговое значение амплитуды.
При поиске радионавигационного сигнала на первом этапе ищется диапазон частот, в котором может находиться НКА. Последовательно перебираются диапазоны частот с шагом около 20 кГц или 3.6 км/с [4]. Диапазон поиска перекрывает все возможные значения радиальной скорости от КА до НКА в диапазоне ±10 км/с. Отметим, что для наземного пользователя этот диапазон составляет ±0.8 км/с. Каждый диапазон перебираемых частот равномерно покрывается массивом ${{{\mathbf{s}}}_{\omega }}$.
На втором этапе в ПМ происходит поиск сигнала НКА для центральной несущей частоты найденного диапазона на первом этапе и шириной 128 Гц или 23 м/c. Ширина полосы поиска определяется предельными величинами радиальной скорости от КА до НКА на низкой околокруговой, геостационарной или орбите с большим эксцентриситетом.
На третьем этапе ищется радиосигнал для центральной несущей частоты диапазона, найденного на втором этапе. Ширина интервала при поиске на третьем этапе составляет 21 Гц или 4 м/c. После нахождения $f_{\tau }^{k}$ и $f_{{{\text{эп}}}}^{k}$ на третьем этапе при выполнении критерия $f_{A}^{k} > {{A}_{{\text{0}}}}$ подается управление на каналы коррелятора. Несущая частота сигнала рассчитывается по формуле $\omega = s_{\omega }^{k}$.
Учитывая уход задержки за время, прошедшее от времени $f_{{{\text{эп}}}}^{k}$ завершения работы ПМ и начала слежения ${{t}_{{{\text{эп}}}}}$ в канале коррелятора, можем записать:
(3.1)
${{\tau }_{{{\text{ПСП}}}}}\left( {{{t}_{{{\text{эп}}}}}} \right) = ({{\tau }_{{{\text{ПСП}}}}}\left( {{{t}_{{{\text{эп}}}}}} \right) - {{\tau }_{{{\text{ПСП}}}}}(f_{{{\text{эп}}}}^{k})) + {{\tau }_{{{\text{ПСП}}}}}(f_{{{\text{эп}}}}^{k}).$Используя (1.7) при n = 1, ${{\tau }_{{{\text{ПСП}}}}}(f_{{{\text{эп}}}}^{k}) = - f_{\tau }^{k}$ и оценивая ${{\tau }_{{{\text{ПСП}}}}}\left( {{{t}_{{{\text{эп}}}}}} \right) - {{\tau }_{{{\text{ПСП}}}}}(t_{{{\text{эп}}}}^{{{\text{ПМ}}}}) = \Omega ({{t}_{{{\text{эп}}}}} - t_{{{\text{эп}}}}^{{{\text{ПМ}}}})$, можем переписать соотношение (3.1) в виде $ - \tau = \Omega ({{t}_{{{\text{эп}}}}} - t_{{{\text{эп}}}}^{{{\text{ПМ}}}}) - f_{\tau }^{k}$. Учитывая (1.1), для расчета задержки сигнала $\tau $ получаем
При поиске сигнала смещение фазы несущей частоты $\Delta \varphi $ задается равным нулю.
Для алгоритма слежения за сигналом подставим (2.9) в (2.7) и получим соотношение для измеренной величины несущей частоты сигнала:
(3.2)
$\omega _{{{\text{изм}}}}^{i} = \frac{{m_{{\text{ц}}}^{i} + \frac{1}{{2\pi }}(m_{\varphi }^{i} - m_{\varphi }^{{i - 1}})}}{{\left( {m_{{{\text{эп}}}}^{i} - \frac{{m_{\Omega }^{i}}}{{{{\Omega }^{i}}}}} \right) - \left( {m_{{{\text{эп}}}}^{{i - 1}} - \frac{{m_{\Omega }^{{i - 1}}}}{{{{\Omega }^{{i - 1}}}}}} \right) + \Delta t}}.$На самом деле, параметр $\omega _{{{\text{изм}}}}^{i}$ можно интерпретировать как мгновенное измеренное значение $\omega $ управления по несущей частоте.
При слежении за сигналом вместо значений несущей частоты $\omega $, сдвига фазы несущей $\Delta \varphi $ и задержки $\tau $ используются мгновенные измерения $\omega _{{\text{ц}}}^{i}$ (3.2), измерения фазы несущей
Вычисление каждого из трех параметров осуществляется в предположении линейной зависимости компонент ${{{\mathbf{q}}}_{i}} = {{(\hat {\omega }_{{\text{ц}}}^{i},\;\Delta \varphi _{{{\text{изм}}}}^{i},\;\tau _{{{\text{изм}}}}^{i})}^{{\text{Т}}}}$ измеренных значений от времени. Формируется линейная регрессия ${{{\mathbf{q}}}_{i}} = {\mathbf{b}} + {\mathbf{a}} \cdot i + {{{\mathbf{\varepsilon }}}_{i}}$ по множеству пар $\left( {{{{\mathbf{q}}}_{i}},\;i} \right)$, $i = 1,...,n$, где $n$ – окно линейного фильтра, уникальное для каждого из параметров. Значения компонент ${\mathbf{a}}$ и ${\mathbf{b}}$ определяются по формулам
(3.3)
$a = {{(n{{\Sigma }_{{tq}}} - {{\Sigma }_{t}}{{\Sigma }_{q}})} \mathord{\left/ {\vphantom {{(n{{\Sigma }_{{tq}}} - {{\Sigma }_{t}}{{\Sigma }_{q}})} {(n{{\Sigma }_{{{{t}^{2}}}}} - \Sigma _{t}^{2})}}} \right. \kern-0em} {(n{{\Sigma }_{{{{t}^{2}}}}} - \Sigma _{t}^{2})}},\quad b = {{({{\Sigma }_{{{{t}^{2}}}}}{{\Sigma }_{q}} - {{\Sigma }_{t}}{{\Sigma }_{{tq}}})} \mathord{\left/ {\vphantom {{({{\Sigma }_{{{{t}^{2}}}}}{{\Sigma }_{q}} - {{\Sigma }_{t}}{{\Sigma }_{{tq}}})} {(n{{\Sigma }_{{{{t}^{2}}}}} - \Sigma _{t}^{2})}}} \right. \kern-0em} {(n{{\Sigma }_{{{{t}^{2}}}}} - \Sigma _{t}^{2})}},$(3.4)
$\sigma = \sqrt {\frac{{{{\Sigma }_{{{{q}^{2}}}}} + {{a}^{2}}{{\Sigma }_{{{{t}^{2}}}}} + n{{b}^{2}} + 2\left( {ab{{\Sigma }_{t}} - a{{\Sigma }_{{tq}}} - b{{\Sigma }_{q}}} \right)}}{{n - 2}}} ,$Для фильтрации измеренных значений несущей частоты $\hat {\omega }_{{\text{ц}}}^{i}$ окно линейного фильтра составляет $n = 100$, для измерения сдвига фазы несущей $\Delta \varphi _{{{\text{изм}}}}^{i}$ и измерений задержки сигнала $\tau _{{{\text{изм}}}}^{i}$ принимается $n = 10$.
Следует обратить внимание, что $\Delta \varphi _{{{\text{изм}}}}^{i}$ и $\tau _{{{\text{изм}}}}^{i}$ являются поправками к фазе несущей частоты (1.6) и задержке (1.7) соответственно, поэтому после выдачи управлений необходимо скорректировать соответствующие массивы измерений.
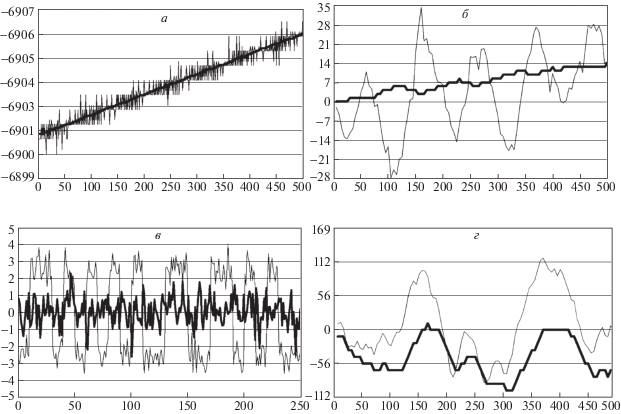
На рис. 2 , а–в изображены результаты фильтрации параметров управления: несущей (в м/с), накопления фазы и накопления задержки (в градусах). Тонкими линиями отмечены мгновенные измеренные значения, а жирной – результат фильтрации.
На рис. 2 , г изображены действительная ${{I}_{{\text{д}}}}$ (тонкая линия) и мнимая ${{I}_{{\text{м}}}}$ (жирная линия) (1.2) части сигнала на интервале длительностью приема 250 ПСП (ось абсцисс) при слежении за сигналом ГЛОНАСС в условных единицах накопления коррелятора (ось ординат). Изменение знака действительной части сигнала ${{I}_{{\text{д}}}}$ говорит о смене значения информационного бита.
4. Априорная оценка точности измерений. Для априорной оценки точности измерений псевдодальности ${{\tilde {\Psi }}^{{{\text{пд}}}}}$ (2.10) и псевдоскорости ${{\tilde {\Psi }}^{{{\text{пс}}}}}$ (1.5) в АНС без решения навигационной задачи с последующей оценкой невязки используются следующие методы приема и моделирования измерений с помощью имитатора: проведение измерений одного НКА по нескольким каналам коррелятора и проведение измерений разных НКА, находящихся в одной точке.
При проведении сеансов измерений одного НКА по нескольким каналам СКО рассогласования измерений псевдодальности составило 2 м, а СКО измерений псевдоскорости соответствует дискретной единице управления по несущей частоте сигнала и равно 6 см/с.
Метод оценки точности измерений от разных НКА, находящихся в одной точке, позволил оценить СКО псевдодальности в 6.4 м. Эксперимент позволил оценить СКО измерений псевдоскорости в 3 см/с, что соответствует дискретной единице управления по несущей частоте сигнала.
5. Модель движения КА. В бортовых алгоритмах АНС реализована модель движения КА, учитывающая силы центрального тяготения Земли, притяжения Луны и Солнца и нецентральности гравитационного поля Земли. Также возможен учет сил, связанных с торможением в верхней атмосфере Земли и работы двигательной установки (ДУ) КА. В прямоугольной инерциальной геоцентрической СК J2000 дифференциальные уравнения движения КА для ${\mathbf{x}} = {{({\mathbf{r}}_{{{\text{КА}}}}^{{\text{T}}},\;{\mathbf{v}}_{{{\text{КА}}}}^{{\text{T}}})}^{{\text{T}}}}$ записываются в форме
(5.1)
${{{\mathbf{x}}}_{0}} = {\mathbf{x}}\left( {{{t}_{0}}} \right),\quad {\mathbf{\dot {x}}} = {\mathbf{F}}\left( {\mathbf{x}} \right) = {{({\mathbf{v}}_{{{\text{КА}}}}^{{\text{T}}},\;{\mathbf{\dot {v}}}_{{{\text{КА}}}}^{{\text{T}}})}^{{\text{T}}}},\quad {{{\mathbf{\dot {v}}}}_{{{\text{КА}}}}} = {{{\mathbf{f}}}_{{\text{з}}}} + {{{\mathbf{f}}}_{{\text{л}}}} + {{{\mathbf{f}}}_{{\text{с}}}} + {\mathbf{M}}_{{{\text{ПЗ90}}}}^{{{\text{J2000}}}}\left( {{{{\mathbf{f}}}_{{{\text{гр}}}}} + {{{\mathbf{f}}}_{{{\text{атм}}}}}} \right) + {{{\mathbf{f}}}_{{{\text{ДУ}}}}},$При обработке измерений на интервале времени полутора витков давлением сил солнечной радиации и влияниями твердых приливов на Земле, обусловленных влиянием Луны и Солнца, в бортовых алгоритмах АНС пренебрегается.
Обозначим m×n-матрицу Якоби частных производных вектора ${\mathbf{q}} = {{\left( {{{q}_{1}},\; \ldots ,{{q}_{n}}} \right)}^{{\text{T}}}}$ по вектору ${\mathbf{p}} = {{\left( {{{p}_{1}},\; \ldots ,{{p}_{m}}} \right)}^{{\text{T}}}}$ через $\frac{{\partial {\mathbf{q}}}}{{\partial {\mathbf{p}}}}$ и запишем уравнение в вариациях:
(5.2)
$\frac{{\partial {\mathbf{\dot {x}}}}}{{\partial {{{\mathbf{x}}}_{0}}}} = \frac{{\partial {\mathbf{\dot {x}}}}}{{\partial {\mathbf{x}}}}\frac{{\partial {\mathbf{x}}}}{{\partial {{{\mathbf{x}}}_{0}}}} = \frac{{\partial {\mathbf{F}}\left( {\mathbf{x}} \right)}}{{\partial {\mathbf{x}}}}\frac{{\partial {\mathbf{x}}}}{{\partial {{{\mathbf{x}}}_{0}}}}.$Дифференциальные уравнения в вариациях всегда интегрируются совместно с уравнениями движения КА, поскольку для расчета правых частей системы уравнений в вариациях используется вектор состояния КА на текущий момент времени.
Соотношения для расчета правых частей приведены в [2]. Следовательно, в блочном представлении матрица $\frac{{\partial {\mathbf{F}}\left( {\mathbf{x}} \right)}}{{\partial {\mathbf{x}}}}$ имеет вид (5.3), и если возмущения атмосферы Земли ${{{\mathbf{f}}}_{{{\text{атм}}}}}$ не учитываются, то $\frac{{\partial {{{{\mathbf{\dot {v}}}}}_{{{\text{КА}}}}}}}{{\partial {{{\mathbf{v}}}_{{{\text{КА}}}}}}} = 0$:
(5.3)
$\frac{{\partial {\mathbf{F}}\left( {\mathbf{x}} \right)}}{{\partial {\mathbf{x}}}} = {{\left( {\begin{array}{*{20}{c}} {\frac{{\partial {{{{\mathbf{\dot {v}}}}}_{{{\text{КА}}}}}}}{{\partial {{{\mathbf{r}}}_{{{\text{КА}}}}}}}}&{\frac{{\partial {{{{\mathbf{\dot {v}}}}}_{{{\text{КА}}}}}}}{{\partial {{{\mathbf{v}}}_{{{\text{КА}}}}}}}} \\ {\mathbf{0}}&{\mathbf{E}} \end{array}} \right)}^{{\text{Т}}}}.$Отметим, что в бортовых алгоритмах АНС для учета возмущений от Луны и Солнца следует использовать соотношение, которое компенсирует вычислительную ошибку [20]:
В АНС положения Луны и Солнца рассчитывают по конечным формулам аналитических теорий движения конца XIX в., созданных Е.В. Брауном и С. Ньюкомом [21]. Погрешность вычисления положения Луны составляет не более 10 км, а Солнца – 100 км. Для оптимизации вычислений в АНС производится расчет коэффициентов полинома Чебышева на ближайшие 32 сут с использованием аналитических моделей для последующего применения в алгоритмах решения навигационной задачи [2].
Интегрирование уравнений движения КА (5.1) и уравнений в вариациях (5.2) при отключенной ДУ на борту КА происходит методом Рунге–Кутты 4-го порядка с шагом $h = 20$ с по времени. Для компенсации численной ошибки интегрирования в АНС необходимо применять метод пошагового интегрирования [2], в котором общий интервал интегрирования $t - {{t}_{0}}$ разбивается на k более мелких интервалов длиной Δ0: $t - {{t}_{0}} = k{{\Delta }_{0}} + {{\Delta }_{t}}$.
Для каждого s-го интервала длиной Δ0 и остаточного Δt происходит инициализация начальных условий уравнений (5.1) и (5.2):
При проведении баллистических расчетов на борту КА константно-эфемеридное обеспечение АНС определяется составом используемых моделей и постоянных. Для решения навигационной задачи в АНС применяются две подвижные гринвичские СК: ПЗ-90.2 для расчетов положения и скорости НКА ГЛОНАСС, WGS-84 для расчетов, связанных с навигационной системой GPS. Для интегрирования уравнений движения КА используются константы ПЗ-90.2.
Для расчета матрицы ${\mathbf{M}}_{{{\text{ПЗ90}}}}^{{{\text{J2000}}}}$ (5.1) применяется величина расхождения $\Delta U{{T}_{1}}$ времени начального меридиана и всемирного координированного времени UTC, которое постоянно обновляется и передается в информационном сообщении ГЛОНАСС [16]. Данные о движении полюсов Земли ${{x}_{{\text{п}}}}$, ${{y}_{{\text{п}}}}$ передаются в навигационном сообщении геостационарных спутников дифференциальных поправок SBAS. Данные о состоянии активности Солнца при расчете плотности атмосферы должны передаваться в АНС с Земли из наземного комплекса управления. Отметим, что если АНС выдает орбиту во вращающейся СК ПЗ-90.2 или WGS-84, то значениями $\Delta U{{T}_{1}}$, ${{x}_{{\text{п}}}}$ и ${{y}_{{\text{п}}}}$ можно пренебречь, используя СК J2000 только для интегрирования уравнений КА.
6. Первоначальное определение орбиты. Определение орбиты КА по измерениям псевдодальности (2.10) и псевдоскорости (1.5) состоит в нахождении неизвестных параметров уравнений движения КА (5.1) и расчетных значений измерений (2.1) и (2.4). Восьмимерный фазовый вектор неизвестных параметров состоит из кинематических векторов положения и скорости x0 = = ${{({\mathbf{r}}_{0}^{{\text{T}}},{\mathbf{v}}_{0}^{{\text{T}}})}^{{\text{T}}}}$, рассинхронизации шкал времени $\varphi \left( {{{t}_{0}}} \right)$ и ухода частоты опорного генератора $\Delta f$ на момент времени ${{t}_{0}}$. Априорные данные о НУ параметрах движения КА могут быть заложены на его борт с Земли или получены в результате решения автономной задачи первоначального определения орбиты.
Первоначальное определение орбиты [2] ищется в гринвичской вращающейся СК ПЗ-90.2 или СК WGS-84 без учета их различия. В основу алгоритма начального определения орбиты положено геометрическое решение по группе измерений псевдодальности и псевдоскорости от пяти НКА, излученных в один момент времени генерации ПСП. Другими словами, выбирается минимум пять пар измерений псевдодальности и псевдоскорости, отнесенных к одному моменту ${{t}_{{{\text{изл}}}}}$ и принятых, вообще говоря, в разные моменты в силу различия расстояний от КА до навигационных спутников.
Для получения измерений от пяти НКА при решении задачи первоначального определения в районе апоцентра ВЭО или на ГСО требуется наличие в АНС специальной остронаправленной антенны [10], способной принимать сигнал через просвет Земли (рис. 1 ). В случае невозможности приема необходимого числа измерений в апоцентре ВЭО для первоначального определения необходимо дождаться прохождения ближайшего перицентра орбиты. Для ускорения процесса первичного определения на ГСО можно передавать априорный вектор положения и скорости с Земли. Алгоритм расчета начальных значений служебных параметров $\Delta f$ и $\varphi $ основан на вычислении разности между измеренными значениями псевдодальности, псевдоскорости и расчетными значениями дальности, скорости соответственно.
При первоначальном определении орбиты находятся разности измеренных значений псевдодальности и псевдоскорости для исключения неизвестных значений $\Delta f$ и $\varphi $, пренебрегая ионосферной задержкой $\Delta \rho $ (2.1). Задача решается МНК [22] в два этапа: на первом определяется ${{{\mathbf{r}}}_{{{\text{КА}}}}}$ и $\varphi $, а на втором – ${{{\mathbf{v}}}_{{{\text{КА}}}}}$ и $\Delta f$. Веса измерений в МНК полагаются равными. На каждом из двух этапов размерность фазового вектора неизвестных параметров равна четырем. Однако алгоритм требует минимум пять пар измерений псевдодальности и псевдоскорости от разных НКА для избыточности, необходимой при оценке качества первичного определения по остаточным невязкам. Кинематические векторы ${{{\mathbf{r}}}_{{{\text{КА}}}}}$ и ${{{\mathbf{v}}}_{{{\text{КА}}}}}$, служебные параметры приемника $\Delta f$ и $\varphi $ привязываются к моменту первого принятого измерения ${{t}_{1}}$.
После определения векторов положения ${{{\mathbf{r}}}_{{{\text{КА}}}}}$ и скорости ${{{\mathbf{v}}}_{{{\text{КА}}}}}$ оцениваются значения ухода частоты $\Delta f$ (2.4) и рассинхронизации шкал времени $\varphi $ (2.1) по соотношениям
Начальное определение ${{{\mathbf{r}}}_{{{\text{КА}}}}}$, ${{{\mathbf{v}}}_{{{\text{КА}}}}}$, $\Delta f$ и $\varphi $ отбраковывается, если модули остаточных невязок (после последней итерации МНК) после определения ${{{\mathbf{r}}}_{{{\text{КА}}}}}$ или ${{{\mathbf{v}}}_{{{\text{КА}}}}}$ больше определенных пороговых значений. В случае неудовлетворительного решения задачи первоначального определения количество измерений $n \geqslant 6$ позволяет производить исключение одного измерения из обработки с последующим анализом результатов сходимости. Аномальные измерения могут возникать вследствие прохождения сигнала через атмосферу и ионосферу Земли и вследствие сбоев в корреляторе.
7. Определение орбиты на короткой дуге. Второй этап определения орбиты в АНС подразумевает нахождение восьмимерного фазового вектора, состоящего из кинематических параметров орбиты КА, ухода частоты опорного генератора и рассинхронизации шкалы времени КА с навигационными системами. Алгоритм основан на использовании законов динамики движения КА и применяется непосредственно при обработке первичных измерений псевдодальности и псевдоскорости по протяженной мерной базе [1]. Искомый фазовый вектор строится на момент последнего измерения. Обработка происходит на интервалах времени от одной минуты до получаса и зависит от числа видимых НКА.
В основу алгоритма определения по короткой мерной дуге положен итерационный фильтр Калмана [23]. Динамическая система, описывающая поведение фазового вектора, приведена в [1–3].
Обозначим искомый восьмимерный фазовый вектор через ${\mathbf{q}} = {{({\mathbf{r}}_{{{\text{КА}}}}^{{\text{T}}},{\mathbf{v}}_{{{\text{КА}}}}^{{\text{T}}},\Delta f,\varphi )}^{{\text{T}}}}$. Будем обрабатывать только парные измерения, т.е. дальномерное и скоростное измерение на один момент от одного НКА. Пусть имеется $n$ парных измерений. Найдем оценку вектора ${{{\mathbf{q}}}_{{{{t}_{n}}}}}$ на момент последнего измерения ${{t}_{n}}$.
Расчетные значения псевдодальности $\Psi _{t}^{{{\text{пд}}}}$ и псевдоскорости $\Psi _{t}^{{{\text{пc}}}}$ на момент времени $t$ приведены в (2.1) и (2.4) соответственно. Вектор невязок составлен из разностей между измеренными ${{\tilde {\Psi }}_{{{\text{пд}}}}}$, ${{\tilde {\Psi }}_{{{\text{пc}}}}}$ и расчетными ${{\Psi }_{{{\text{пд}}}}}$, ${{\Psi }_{{{\text{пc}}}}}$ значениями и описывается матрицей n × 2:
(7.1)
$\xi = ({{\xi }^{{{\text{пд}}}}},{{\xi }^{{{\text{пc}}}}}) = ({{\tilde {\Psi }}_{{{\text{пд}}}}} - {{\Psi }_{{{\text{пд}}}}},{{\tilde {\Psi }}_{{{\text{пc}}}}} - {{\Psi }_{{{\text{пc}}}}}).$Компоненты матрицы n × 16 частных производных
(7.2)
${\mathbf{W}}_{{{\text{пд}}}}^{{{\text{пс}}}} = \left( {\begin{array}{*{20}{c}} {1{\text{/}}\sigma _{{{\text{пд}}}}^{2}}&0 \\ 0&{1{\text{/}}\sigma _{{{\text{пс}}}}^{2}} \end{array}} \right)$Динамическая модель, описывающая поведение кинематических параметров КА и служебных параметров приемника, состоит из уравнений движения КА (5.1) и уравнений авторегрессии с весовой матрицей ${\mathbf{W}}_{{\Delta f}}^{\varphi }$:
Пусть матрица 2 × (n – 1), описывающая поведение ухода частоты опорного генератора (2.2) и рассинхронизации шкал времени (2.3), задается в виде
Обозначим априорный фазовый вектор на момент последнего измерения через ${{{\mathbf{q}}}_{{\text{а}}}}$. Пусть соответствующему весовая 8 × 8-матрица имеет вид
При последующих определениях орбиты по короткой дуге в разрывном навигационном поле с высотами орбиты КА более 2 тыс. км оценка расширенного вектора состояния не может быть получена без использования априорной информации. В качестве такой информации используется расширенный вектор состояния, полученный по измерениям на предшествующем интервале времени. В качестве начального значения ковариационной матрицы ${{{\mathbf{\tilde {K}}}}^{{ - 1}}}$ подставляется значение, определенное на предыдущем интервале. Затем диагональный элемент, соответствующий уходу частоты, умножается на величину $\Delta t({{{{{10}}^{2}}} \mathord{\left/ {\vphantom {{{{{10}}^{2}}} {3600}}} \right. \kern-0em} {3600}})$, а соответствующий уходу времени – на $\Delta t({{{{{25}}^{2}}} \mathord{\left/ {\vphantom {{{{{25}}^{2}}} {3600}}} \right. \kern-0em} {3600}})$, где $\Delta t$ – интервал времени, прошедший с предыдущего конца интервала на начало текущего.
Оценка фазового вектора ${{{\mathbf{q}}}_{{{{t}_{n}}}}}$ на момент времени последнего измерения ${{t}_{n}}$ получается в результате минимизации функционала, содержащего взвешенные квадраты невязок измеренных и расчетных значений, взвешенные приращения значений служебных параметров на интервале между измерениями (2.2), (2.3) и квадрат взвешенного отклонения априорно заданного фазового вектора от его расчетного значения. Минимизируемый функционал имеет вид
(7.3)
$\Phi = \xi {\mathbf{W}}_{{{\text{пд}}}}^{{{\text{пс}}}}{{\xi }^{{\text{Т}}}} + \varepsilon {\mathbf{W}}_{{\Delta f}}^{\varphi }{{\varepsilon }^{{\text{Т}}}} + {{\left( {{{{\mathbf{q}}}_{{\text{а}}}} - {{{\mathbf{q}}}_{{{{t}_{n}}}}}} \right)}^{{\text{Т}}}}{{{\mathbf{W}}}_{{\text{а}}}}\left( {{{{\mathbf{q}}}_{{\text{а}}}} - {{{\mathbf{q}}}_{{{{t}_{n}}}}}} \right).$Уравнения (2.2), (2.3), (5.1) описывают динамическую систему, в которой шум влияет на поведение этой системы. Алгоритм оценки фазового вектора для динамических систем такого типа рассмотрен в [23].
Минимум квадратичной формы (7.3) ищется методом последовательных приближений. На шаге $s$ итерационного процесса определяется минимум квадратичной формы следующего вида:
Для $i = 1, \ldots ,n$ последовательно переносится ковариационная матрица с момента ${{t}_{{i - 1}}}$ на ${{t}_{i}}$:
Матрица ${\mathbf{K}}_{i}^{{{\text{пс}}}}$ формируется переносом ковариационной матрицы с момента ${{t}_{{i - 1}}}$ на момент ${{t}_{i}}$; ${\mathbf{K}}_{i}^{{{\text{пд}}}}$ – усечение ${\mathbf{K}}_{i}^{{{\text{пс}}}}$ за счет измерения псевдоскорости на момент времени ${{t}_{i}}$. Матрица частных производных $\frac{{\partial {\mathbf{x}}}}{{\partial {{{\mathbf{x}}}_{{{{t}_{n}}}}}}}$ находится интегрированием уравнений в вариациях (5.2) с начальными условиями на момент ${{t}_{n}}$.
Поправка к фазовому вектору на момент ${{t}_{i}}$ вычисляется по формуле
Для $\Delta {\mathbf{q}}_{i}^{{пс}}$ справедливо
(7.4)
$\Delta {\mathbf{q}}_{i}^{{пс}} = \frac{1}{{{{\chi }_{{{\text{пс}}}}}}}(\xi _{i}^{{пс(s)}} - ({\mathbf{h}}_{i}^{{пс}}\Delta {{{\mathbf{q}}}_{{i - 1}}})){\mathbf{K}}_{i}^{{{\text{пс}}}}{\mathbf{h}}_{i}^{{пс}},\quad {\mathbf{h}}_{i}^{{пс}} = \frac{{\partial \xi _{i}^{{пс(s)}}}}{{\partial {\mathbf{q}}}},\quad {{\chi }_{{{\text{пс}}}}} = {{({\mathbf{h}}_{i}^{{пс}})}^{{\text{Т}}}}{\mathbf{K}}_{i}^{{{\text{пс}}}}{\mathbf{h}}_{i}^{{пс}} + \sigma _{{{\text{пс}}}}^{2}.$Рассчитывается или усекается новая ковариационная матрица ${\mathbf{K}}_{i}^{{{\text{пд}}}}$ для обработки измерения псевдодальности:
Аналогично рассчитывается поправка в (7.4) с использованием измерения псевдодальности:
Наконец,
Поправка к фазовому вектору $\Delta {{{\mathbf{q}}}^{{\left( s \right)}}}$ на шаге s при минимизации квадратичной формы (7.3) полагается $\Delta {{{\mathbf{q}}}^{{\left( s \right)}}} = \Delta {{{\mathbf{q}}}_{n}}$ на каждой из пяти фиксированных итераций. При этом контролируются значения компонент поправки $\Delta {{{\mathbf{q}}}^{{\left( s \right)}}}$ на последней итерации.
Реализация алгоритмов бортовой АНС показалa высокую эффективность применения метода Гаусса для обращения матриц.
На этапе накопления измерений происходит определение значения интервала для их обработки. Временной интервал $[{{t}_{1}},{{t}_{n}}]$ сеанса $n$ измерений считается завершенным, если $({{t}_{n}} - {{t}_{1}})\, \geqslant \,{{t}_{{{\text{инт}}}}}(\bar {n})$, где $\bar {n}$ – среднее число измерений. Значения функции ${{t}_{{{\text{инт}}}}}$ в зависимости от $\bar {n}$ приведены в табл. 1.
Таблица 1.
Интервал накопления измерений
| Среднее количество измерений $\bar {n}$ | Интервал ${{t}_{{{\text{инт}}}}}$, с |
|---|---|
| 0 – 2 | 1800 |
| 3 | 420 |
| 4 | 120 |
| 5 и более | 60 |
При определении орбит КА существенную роль играет этап локальной обработки измерений [9, 24]. Локальная обработка псевдодальности и псевдоскорости на короткой мерной дуге состоит в выявлении и отбраковке аномальных измерений и требует наличия начального приближения орбиты, которое позволяет анализировать не сами измерения ${{\tilde {\Psi }}_{{{\text{пд}}}}}$ и ${{\tilde {\Psi }}_{{{\text{пс}}}}}$, а их рассогласования ${{\xi }^{{{\text{пд}}}}}$ и ${{\xi }^{{{\text{пс}}}}}$ (7.1) с расчетными аналогами, математическое ожидание которых свободно от значительных нелинейностей.
На первом этапе локальной обработки отбраковываются аномальные измерения, связанные со сбоями в аппаратуре. Простым способом проверки является отбраковка по значению невязки с проверкой условий:
модуль значения псевдоскорости $\left| {\Psi _{t}^{{{\text{пc}}}}} \right|$ должен быть меньше $\Psi _{{\max }}^{{{\text{пc}}}} = 20$ м/с: $\left| {\Psi _{t}^{{{\text{пc}}}}} \right| < \Psi _{{\max }}^{{{\text{пc}}}}$;
рассогласование приращения псевдодальности от одного НКА на секундном интервале $\Delta t = 1$ с от значения псевдоскорости, умноженного на 1 с, должно быть меньше порогового значения: ${\text{|}}(\Psi _{t}^{{{\text{пд}}}} - \Psi _{{t - \Delta t}}^{{{\text{пд}}}}) - \Psi _{t}^{{{\text{пc}}}}{\text{|}} < 3{{\sigma }_{{{\text{пд}}}}}$, где ${{\sigma }_{{{\text{пд}}}}}$ – априорная точность измерения псевдодальности (7.2);
модуль приращения псевдоскорости на секундном интервале должен быть меньше априорного радиального ускорения ${{a}_{{\max }}} = 15$ м/с2: $\left| {\Psi _{t}^{{{\text{пc}}}} - \Psi _{{t - \Delta t}}^{{{\text{пc}}}}} \right| < {{a}_{{\max }}}$.
На втором этапе локальной обработки обеспечивается автоматическое выявление аномальных измерений, при котором определяются коэффициенты линейной функции от времени для аппроксимации невязок (7.1) между измеренными и ожидаемыми расчетными значениями. Анализируется СКО ${{\sigma }_{{{\text{лок}}}}}$ построенной аппроксимации. Если ${{\sigma }_{{{\text{лок}}}}}$ построенной аппроксимации больше предельного значения, то измерение исключается из дальнейшей обработки.
Для каждой группы измерений псевдодальности и псевдоскорости строится линейная регрессия невязок измерений ${{\xi }_{i}} = b + a{{t}_{i}} + {{\varepsilon }_{i}}$ по множеству пар $\left( {{{\xi }_{i}},{{t}_{i}}} \right)$, где ${{t}_{i}} = {{T}_{i}} - {{T}_{m}}$, $i = 1, \ldots ,n$, $n$ – количество измерений в сеансе, ${{T}_{i}}$ – момент измерения, ${{T}_{m}}$ – момент середины интервала. Значения a и b определяются по формулам (3.6). Квадрат СКО σ2 величин ${{\varepsilon }_{i}}$, $i = 1, \ldots ,n$ вычисляется по формуле (3.4).
Из обработки измерений последовательно исключаются измерения, для которых
(7.5)
$\left| {{{\xi }_{i}} - a{{t}_{i}} - b} \right| > 3\sqrt {\sigma _{{{\text{лок}}}}^{2} + \sigma _{{{\text{пд}}}}^{2}} .$Постоянное априорное значение $\sigma _{{{\text{пд}}}}^{2}$ (7.2) в подкоренном выражении (7.5) вводит ограничение на минимальный порог для отбраковки. Удаление измерений прекращается, если количество удаленных измерений более 10% от общего числа.
Итак, результатом определения орбиты КА по короткой дуге является восьмимерный фазовый вектор ${\mathbf{q}} = {{({\mathbf{r}}_{{{\text{КА}}}}^{{\text{T}}},\;{\mathbf{v}}_{{{\text{КА}}}}^{{\text{T}}},\;\Delta f,\;\varphi )}^{{\text{T}}}}$.
Значения кинематических векторов положения ${{{\mathbf{r}}}_{{{\text{КА}}}}}$ и скорости КА ${{{\mathbf{v}}}_{{{\text{КА}}}}}$ проверяются на порядок величин и на их соответствие орбите искусственного спутника Земли методом сравнения эксцентриситета, высоты апоцентра и перицентра с допустимыми значениями.
Значения ухода частоты опорного генератора $\Delta f$ и рассинхронизации шкал времени $\varphi $ могут использоваться при формировании сигнала точного времени в АНС на интервале накопления следующего интервала измерений.
Вектор положения в гринвичской вращающейся СК сохраняется как нормальное место ${{{\mathbf{r}}}^{{\text{н}}}} = {{{\mathbf{r}}}_{{{\text{КА}}}}}$ с весом $w = 1{\text{/}}{{\sigma }_{{{{\xi }^{{{\text{пд}}}}}}}}$, который соответствует обратному значению квадрата СКО остаточной невязки псевдодальности на последней итерации определения орбиты на короткой дуге. Осуществляется переход на третий этап определения орбиты в АНС. Компоненты вектора скорости в определении орбиты по нормальным местам не используются. Это обусловлено нехваткой вычислительных ресурсов.
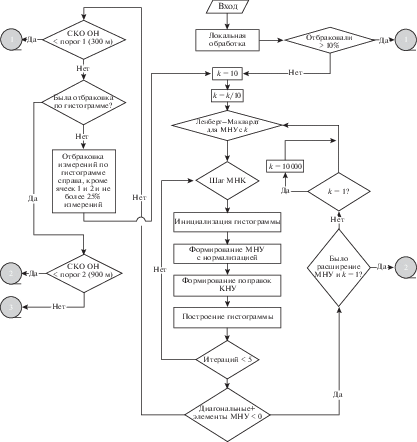
8. Обработка нормальных мест. Нормальные места рассматриваются как трехмерные измерения, результатом обработки которых является вектор начальных условий на момент последнего измерения. Нормальные места обрабатываются МНК с фиксированным числом итераций, схема алгоритма определения орбиты представлена на рис. 3 . Алгоритм обработки нормальных мест, как и алгоритм определения по короткой дуге, начинается с локальной обработки (разд. 7).
Алгоритм обработки нормальных мест учитывает численную ошибку формирования матрицы нормальных уравнений (МНУ) ${\mathbf{A}}$ в МНК:
Вследствие ошибки может возникнуть ситуация, при которой ковариационная матрица ${{{\mathbf{K}}}_{\Phi }}$ имеет отрицательные диагональные элементы после обращения ${\mathbf{A}}$. В [25] приведен метод Левенберга–Марквардта, являющийся альтернативой градиентного метода Гаусса–Ньютона, суть которого заключается в увеличении диагональных элементов матрицы ${\mathbf{A}}$ с определением поправок к начальным условиям. Другими словами, на каждом шаге модифицированного метода Левенберга–Марквардта вместо нормального уравнения МНК решается уравнение
Также в АНС для минимизации численных ошибок при формировании матрицы нормальных уравнений ${\mathbf{A}}$, состоящей из матрицы, имеющей размерность (3×6), частных производных $\frac{{\partial {\mathbf{\xi }}}}{{\partial {\mathbf{q}}}}$ i-го трехмерного измерения (2.6), выполняется операция нормализации. Элементы первых трех столбцов $\frac{{\partial {\mathbf{\xi }}}}{{\partial {\mathbf{q}}}}$ умножаются на ${{\omega }_{i}}{{k}_{{{\text{норм}}}}}$, а элементы следующих трех столбцов – на ${{\omega }_{i}}k_{{{\text{норм}}}}^{2}$. Невязка измерения умножается на ${{\omega }_{i}}{{k}_{{{\text{норм}}}}}$.
Для отбраковки нормальных измерений на каждой итерации МНК строится гистограмма $n$ остаточных невязок ${{\xi }_{i}}$ нормальных мест и их расчетных значений в логарифмической шкале. Строятся величины ${{\eta }_{i}} = {{\log }_{2}}\left( {{{\xi }_{i}}{{\omega }_{i}}} \right)$, где ${{\omega }_{i}}$ – вес соответствующей компоненты нормального места. Пусть ${{\eta }_{{{\text{макс}}}}} = \mathop {\max }\limits_{i = 1, \ldots ,n} {{\eta }_{i}}$, тогда для элемента ${\mathbf{\gamma }} = {{\left( {{{\gamma }_{0}},{{\gamma }_{1}}, \ldots ,{{\gamma }_{{{{n}_{{{\text{гст}}}}}}}}} \right)}^{{\text{T}}}}$ гистограммы, состоящего из ${{n}_{{{\text{гст}}}}}$ карманов, выполняется процедура
Полученный после МНК функционал сравнивается с пороговым значением (порог 1) (рис. 2 ), при превышении которого требуется отбраковка аномальных измерений с построением гистограммы. Проводится анализ начальных условий, по результатам которого выдается решение о принятии результата определения орбиты. С использованием гистограммы ${\mathbf{\gamma }}$ последовательно отбраковываются измерения, попавшие в карманы, начиная с последнего, но при этом нельзя исключать более 25% измерений. В табл. 2 приведены параметры работы алгоритма бортовой АНС при обработке нормальных мест.
Таблица 2.
Параметры алгоритма обработки нормальных мест
| Параметр | Описание | Значение |
|---|---|---|
| Порог 1 | Пороговое значение оценки остаточной невязки | 300 м |
| Порог 2 | Пороговое значение оценки остаточной невязки для инициализации отбраковки по гистограмме | 300–900 м |
| Итерации | Число итераций МНК | 5 |
| ${{k}_{{{\text{норм}}}}}$ | Коэффициент нормализации | 0.001 |
| ${{k}_{4}}$ | Начальный коэффициент метода Левенберга–Марквардта | 1000 |
| ${{n}_{{{\text{гст}}}}}$ | Число карманов при построении гистограммы | 10 |
| Порог 3 | Пороговое значение для отбраковки НУ методом сравнения | 3 км |
На рис. 3 кружками обозначены аварийные выходы алгоритма обработки нормальных мест в АНС, а квадратиками – штатное завершение программы. Диспетчер АНС, анализирующий работу алгоритма, выставляет счетчики возникновения аварийных ситуаций 1, 2, 3 и счетчик штатного завершения с плохой точностью (квадратик 2). При превышении значения счетчиков диспетчер принимает решение о сбросе измерений или начальной инициализации работы программ АНС. При штатном завершении алгоритма обработки нормальных мест (на рис. 2 – квадратики 1 и 2) производится анализ определенных начальных условий КА методом сравнения с начальными условиями, полученными на предыдущем шаге. Для этого предыдущие начальные условия прогнозируются на момент текущих и производится сравнение кинематического вектора положения с пороговым значением.
После решения навигационной задачи в АНС ежесекундно рассчитывается вектор положения и скорости КА с ковариационной матрицей, соответствующие времени выдаваемой секундной метки.
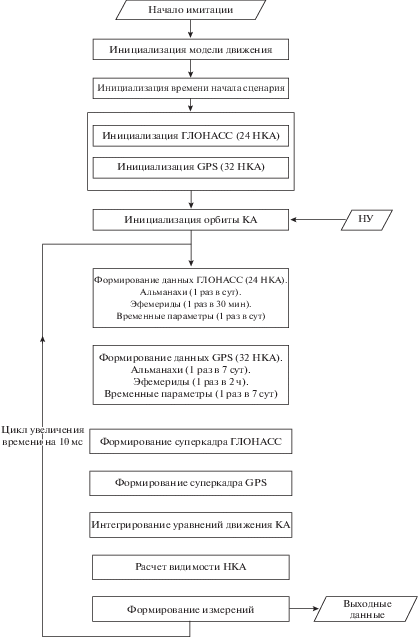
9. Математический стенд отработки. Для тестирования алгоритмов, рассмотренных в разд. 1–8, разработана имитационная математическая модель функционирования навигационных систем ГЛОНАСС и GPS, которая функционирует в реальном масштабе времени и обеспечивает:
формирование орбит НКА с учетом точной модели: нецентральности гравитационного поля Земли; возмущений Луны, Солнца, Юпитера; сил солнечного давления, сил приливных эффектов, неравномерности движения Земли, движения полюсов Земли и расхождения шкал времени UTC и $U{{T}_{1}}$;
формирование параметров численно-аналитических моделей движения НКА ГЛОНАСС [16] и GPS [17];
формирование суперкадров информационной последовательности, передаваемой с борта НКА;
расчет доплеровских измерений, дальномерных измерений с учетом скорости распространения сигнала от навигационных спутников. Учет задержек распространения сигнала в ионосфере Земли [8];
обновление выдаваемой информации с частотой 100 Гц.
На рис. 4 представлена схема моделирования измерений навигационных систем ГЛОНАСС и GPS. Моделирование построено на использовании единой модели движения КА и навигационных спутников. Это означает, что на КА и НКА действуют одни и те же силы в рамках единой модели движения.
Для работы имитационной модели производится инициализация группировок глобальных навигационных спутниковых систем ГЛОНАСС и GPS. Группировка ГЛОНАСС насчитывает 24 НКА, а группировка GPS – 32 рабочих НКА. Система моделирования инициализирует три орбитальных плоскости ГЛОНАСС и шесть плоскостей GPS. Определяются векторы положения и скорости НКА ГЛОНАСС и GPS на момент начального времени работы имитационной модели. Для любого класса орбиты КА: ВЭО, ГCО и НОКО формируются начальные условия.
Основной цикл вычислений имитационной модели составляет 10 мс. Это связанно с тем, что длина бита информационного кадра ГЛОНАСС составляет 10 или 20 мс в зависимости от типа передаваемой информации, а время передачи бита GPS составляет 20 мс. В основном цикле длиной 10 мс происходит интегрирование уравнений движения КА, интегрирование уравнений движения 24 НКА ГЛОНАСС, 32 НКА GPS. Формируются данные альманахов, эфемерид, временные параметры навигационных систем, суперкадры. Цикл реализуется по времени излучения сигнала, так как ПСП излучается синхронно со всех НКА, а приходит на коррелятор в разные моменты времени. В зависимости от взаимного расположения принимающей антенны КА и излучающих НКА ГЛОНАСС и GPS определяются видимые навигационные спутники.
Для каждого из 12 каналов АНС формируются измерения псевдодальности (2.10), псевдоскорости (1.5) и бит информационного кадра. Далее имитационная модель переходит к следующему такту длиной 10 мс.
10. Численное моделирование. Приведем результаты экспериментальной отработки алгоритмов и программ АНС с использованием модельных измерений. Для проведения вычислительного эксперимента смоделирована орбита КА на ВЭО с оскулирующими параметрами, приведенными в табл. 3.
Таблица 3.
Элементы орбиты
| Параметр | Значение |
|---|---|
| Период | 11:57:33 |
| Полуось | 26 550 км |
| Эксцентриситет | 0.69663 |
| Долгота восходящего узла | –70°42' |
| Наклонение | 63°42' |
| Высота апоцентра | 38 668 км |
| Высота перицентра | 1676 км |
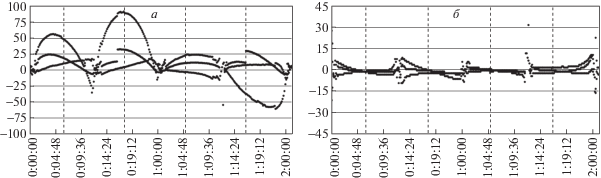
Точность (СКО) определения положения при определении орбиты составила 24 м, а точность определения скорости – 3 мм/c, На рис. 5 , а и б изображены графики невязок в определении положения и скорости по радиусу орбиты; вдоль направления движения, перпендикулярно радиусу (трансверсаль); в направлении, перпендикулярном плоскости орбиты (бинормаль) на интервале 2 сут (4 витков) соответственно. По оси абсцисс показано время в формате “сут чч:мм”.
Рис. 2.
Фильтрация управляющих параметров: а – несущая частота; б – накопление фазы сигнала; в – накопление задержки сигнала; г – действительная и мнимая части сигнала
Заключение. Созданные в ИПМ им. М.В. Келдыша РАН методы и алгоритмы АНС определения орбиты КА с использованием законов динамики движения могут применяться непосредственно при обработке псевдодальности и псевдоскорости по протяженной мерной базе. Представленные методы и алгоритмы обеспечивают получение и обработку первичных измерений навигационных систем ГЛОНАСС и GPS. Алгоритмы поиска радионавигационного сигнала не используют априорных данных об орбите КА и орбитах НКА и позволяют принимать измерения при радиальной скорости до НКА ±10 км/с с первоначальным шагом поиска 20.5 кГц. Предложены методики оценки точности псевдодальности и псевдоскорости без решения навигационной задачи.
Надежность построения АНС основана на независимости получения измерений навигационных спутников от их обработки, т.е. для получения измерений не требуется никаких целеуказаний по задержке и доплеровскому смещению частоты сигнала. Обработка измерений проходит на специализированном процессоре по трехэтапному алгоритму, включающему первоначальное определение орбиты, определение орбиты по короткой дуге с нахождением рассинхронизации шкал времени и окончательное определение параметров движения КА на интервале времени более периода.
Вычислительные эксперименты показали высокую точность определения параметров движения КА на ВЭО: 24 м по положению и 3 мм/с по скорости. Точности в определении орбиты КА позволяют создать бортовую АНС определения орбиты КА, превосходящую по оперативности и сравнимую по точности с наземным измерительным комплексом.
Список литературы
Аким Э.Л., Астахов А.П., Бакитько Р.В., Польщиков В.П., Степаньянц В.А., Тучин А.Г., Тучин Д.А. Автономная навигационная система околоземного космического аппарата // Изв. РАН. ТиСУ. 2009. № 2. С. 139–158.
Тучин Д.А. Автономное определение орбиты на борту космического аппарата // Препринты ИПМ им. М.В. Келдыша. 2019. № 7. 36 с.
Аким Э.Л., Капралов М.А., Степаньянц В.А., Тучин А.Г., Тучин Д.А. Определение параметров движения космического аппарата бортовой навигационной системой по измерениям псевдоскорости и псевдодальности спутниковых навигационных систем // Препринты ИПМ им. М.В. Келдыша. 2004. № 25. 24 с.
Тучин Д.А. Алгоритмы приема сигналов навигационных спутников на борту космического аппарата с использованием коррелятора // Препринты ИПМ им. М.В. Келдыша. 2018. № 4. 32 с.
ГЛОНАСС. Принципы построения и функционирования / Под ред. А.И. Перова, В.Н. Харисова. Изд. 4-е., перераб. и доп. М.: Радиотехника, 2010. 800 с.
Кудрявцев И.В., Мищенко И.Н., Волынкин А.И. и др. Бортовые устройства спутниковой радионавигации / Под ред. В.С. Шебшаевича. М.: Транспорт, 1988. 201 с.
Михайлов Н.В. Автономная навигация космических аппаратов при помощи спутниковых радионавигационных систем. СПб.: Политехника, 2014. 362 с.
Аким Э.Л., Тучин Д.А. Ионосферная составляющая измерений псевдодальности околоземных космических аппаратов // Препринты ИПМ им. М.В. Келдыша. 2004. № 4. 18 с.
Гордиенко Е.С., Ильин И.С., Мжельский П.В., Михайлов Е.А., Паламарчук Е.А., Погодин А.В., Тучин А.Г., Тучин Д.А., Филиппова Е.Н., Худорожков П.А., Ярошевский В.С. Баллистико-навигационное обеспечение полета малых космических аппаратов “Зонд-ПП” и “Рэлек” // Вестник НПО им. С.А. Лавочкина. 2016. № 2. С. 31–43.
Многофункциональная космическая платформа “Навигатор” / Автор-составитель Ефанов В.В.; под ред. Лемешевского С.А. Химки: ФГУП НПО им. С.А. Лавочкина, 2017. 360 с.
Дубяго А.Д. Определение орбит. М.–Л.: Тактико-техническая литература, 1949. 444 с.
Платонов А.К., Казакова Р.К. Создание проектного и оперативного баллистического обеспечения полетов космических аппаратов. Оперативные работы на первых ЭВМ // Препринты ИПМ им. М.В. Келдыша, 2014. № 38. 29 с.
Энеев Т.М., Платонов А.К., Казакова Р.К. Определение параметров орбиты искусственного спутника по данным наземных измерений // Искусственные спутники Земли. Вып. 1, 1960. С. 43–55.
Аким Э.Л., Энеев Т.М. Определение параметров движения космического летательного аппарата по данным траекторных измерений // Космич. исслед. 1963. Т. 1. Вып. 1. С. 5–50.
Сергеева Ю.Р., Тучин Д.А. Алгоритм определения параметров аналитической модели движения навигационных спутников // Препринты ИПМ им. М.В. Келдыша. 2016. № 109. 16 с.
Глобальная навигационная спутниковая система ГЛОНАСС. Интерфейсный контрольный документ, редакция 5.1. М.: Российский научно-исследовательский институт космического приборостроения, 2002.
Global Position System Wing (GPSW) Systems Engineering & Integration. Interface Specification IS-GPS-200. Revision E. Navstar GPS Space Segment / Navigation User Interfaces, 2010.
Комовкин С.В., Лавренов С.М., Тучин А.Г., Тучин Д.А. и др. Небесно-механическая интерпретация запросных радиотехнических измерений радиальной скорости космических аппаратов научного назначения // Вестник НПО им. С.А. Лавочкина. 2015. № 4. С. 77–80.
URL: http://www.morion.com.ru/rus/.
Бэттин Р. Наведение в космосе. М.: Машиностроение, 1966. 448 с.
Монтенбрук О., Пфлегер Т. Астрономия на персональном компьютере. СПб.: Питер, 2002. 320 с.
Идельсон Н. Способ наименьших квадратов. Л.: КУБУЧ, 1932. 200 с.
Тучин А.Г. Определение параметров движения КА по результатам измерений при наличии шума в динамической системе // Препринты ИПМ им. М.В. Келдыша. 2004. № 2. 32 с.
Тучин А.Г., Горохова А.А. Локальная обработка измерений дальности для околоземных орбит космических аппаратов // Препринты ИПМ им. М.В. Келдыша. 1990. № 99. 18 с.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация / Пер. с англ. М.: Мир, 1985. 509 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления