Известия РАН. Теория и системы управления, 2020, № 3, стр. 81-94
АНАЛИЗ ДВУХУРОВНЕВЫХ ПОТОКОВЫХ СЕТЕЙ РЕСУРСООБЕСПЕЧЕНИЯ
Ю. Е. Малашенко a, И. А. Назарова a, *, Н. М. Новикова a, **
a ФИЦ ИУ РАН
Москва, Россия
* E-mail: irina-nazar@yandex.ru
** E-mail: N_Novikova@umail.ru
Поступила в редакцию 19.11.2019
После доработки 20.12.2019
Принята к публикации 27.01.2020
Аннотация
Рассмотрена задача управления потоками ресурса в двухуровневых сетях со структурой типа дерева, упрощенно моделируемой веерной на каждом уровне. В качестве максимизируемой функциональной характеристики принят вектор потоков ресурса к конечным потребителям. Проанализированы две стратегии управления потоками для получения оптимального по Парето решения на базе взвешенного лексиминного правила. Первая стратегия, названная равнодолевым распределением ресурса, строится исходя из идеи уравнивания отношения доставляемого объема ресурса к максимально возможному для данного узла по условиям пропускной способности сети. Вторая стратегия, названная равнообеспечивающим распределением ресурса, строится исходя из идеи уравнивания отношения доставляемого объема ресурса к требуемому. В случае неизвестных требований предложено ориентироваться на уравнительное распределение. Обе стратегии описаны в двух вариантах: оптимизация на магистральном уровне с последующей дооптимизацией в каждой распредсети и прямая оптимизация без промежуточного уровня. Показано, что решения различаются и изучены их свойства. Исследована возможность комбинирования разных правил. Изложение сопровождается модельным примером.
0. Введение. Сетевые потоковые системы характеризуются специфической (и сложной) структурой совместных ограничений. Если говорить о протяженных, территориально-разветвленных таких системах распределения ресурсов, допустим энергоресурсов, в частности подсистем топливно-энергетического комплекса [1], то они как раз дают соответствующий пример. Укажем еще на более локальные сети: тепло- и водоснабжения, бензопроводные, газораспределительные. Подобные системы удобно представлять орграфом, который упрощенно (если не учитывать резервирование) имеет структуру типа дерева или леса. Далее, для определенности, ограничимся первой. Более того, сократим ее до двух содержательно различных уровней.
Существенным свойством изучаемых систем является наличие транспортной составляющей (как правило, трубопроводной). Это моделируется заданием ограничений по пропускной способности ребер графа сети. Транспортная подсистема, предопределяющая возможности процесса ресурсообеспечения, на деле оказывается наименее гибким фактором, практически неизменяемым, что отличает сети передачи ресурсов от, к примеру, современных сетей передачи данных. Потому, хотя исходно сеть проектировали под заданное потребление, с годами структура потребления могла довольно сильно отклониться (особенно структура конечного потребления) как в ту, так и в другую сторону.
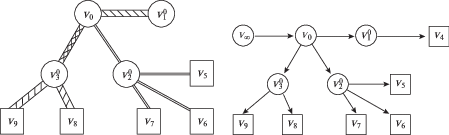
Цель настоящей работы – попытаться оцифровать влияние фиксированной инфраструктуры системы ресурсообеспечения на ее функциональные характеристики. Что до управления потоками в сети, то будем, ориентируясь на большинство ресурсных сетей, учитывать их принципиальную двухуровневость – разделение на магистральные и распределительные сети. В этой связи будем сравнивать два вида управления: двухуровневое, когда отдельно оптимизируется распределение потоков на магистральной сети, а затем от региональных узлов-агрегаторов к их потребителям, и без промежуточного уровня – непосредственно до конечных потребителей. В качестве иллюстративного примера рассмотрим модельную сеть с графом, изображенным на рис. 1.
Слева на рис. 1 показана схема сети, где толщины связующих линий отражают возможности передачи ресурса между соединяемыми пунктами. Справа на рис. 1 дано ее представление орграфом. Здесь фиктивная вершина ${{{v}}_{\infty }}$ добавлена для моделирования мощности источника ${{{v}}_{0}}$ ресурса путем задания ограничения величины ${{d}_{{\infty 0}}}$ на пропускную способность дуги (${{{v}}_{\infty }}$, ${{{v}}_{0}}$). Узел ${{{v}}_{0}}$ является также центром передачи ресурса по магистралям (${{{v}}_{0}}$, ${v}_{i}^{0}$), имеющим ограничения ${{d}_{{0i}}}$ по пропускной способности, в региональные центры распределения ресурса ${v}_{i}^{0}$, i = 1, 2, 3, из которых в свою очередь уходит ресурс конечным потребителям. Верхний индекс узла всюду в работе служит дополнительным (для выделения уровня управления) и будет опускаться, когда это не приводит к разночтениям.
В данном примере распределительные сети упрощенно одноуровневые, в общем случае сложных систем они характеризуются многозвенной структурой ветвлений. Как уже указывалось, предполагаем, что подграфы, соединяющие с конечными потребителями узлы ${v}_{i}^{0}$, $i = \overline {1,n} $, имеют тип “дерево”, и дополнительно можем помечать верхним индексом распредузла вершину такого потребителя: ${v}_{j}^{i}$, j > n. Пусть $J_{i}^{0}$ – множество индексов узлов-последователей вершины ${v}_{i}^{0}$, тогда $j \in J_{i}^{0}$ для любых ${v}_{j}^{i}$. На правом графе с рис. 1 такие узлы-потребители обозначены квадратиками и верхний индекс i опущен, поскольку понятно, от какого ${v}_{i}^{0}$ каждый из них “запитывается”.
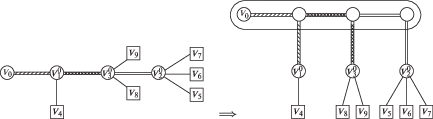
Также и магистральные сети могут содержать не только параллельные, но и последовательно соединенные ребра. Дальнейший анализ от этого несильно изменится. Для простоты считаем, что сеть верхнего уровня имеет веерную структуру (или тип “звезда”). Для того, чтобы привести к ней структуру дерева, можно выполнить следующее. Узлы ${v}_{i}^{0}$, $i = \overline {1,n} $, являющиеся вершинами распределительных подсетей, сделаем концевыми в магистральной сети, дублируя их при необходимости. Затем склеим все остальные узлы, кроме ${{{v}}_{\infty }}$, не являющиеся концевыми, с узлом ${{{v}}_{0}}$ в единый узел ${{{v}}_{0}}$ с уменьшением пропускной способности дуг, ведущих в концевые распредузлы, если она больше пропускной способности предшествующих дуг в дереве. Процесс такой “склейки” с корректировкой пропускной способности осуществляем начиная с ${{{v}}_{0}}$ по порядку ориентации дуг дерева. Получим сеть верхнего уровня, у которой все ее вершины, кроме ${{{v}}_{\infty }}$ и ${{{v}}_{0}}$, т.е. все ${v}_{i}^{0}$ для $i = \overline {1,n} $, оказываются концевыми в магистральной сети и начальными для распредсетей (для выполнения последнего условия на графе с рис. 1 справа добавлена вершина ${{{v}}_{4}}$ с подсоединением к узлу ${v}_{1}^{0}$ сети с рис. 1 слева). В частности, сеть с рис. 1 может получиться в результате подобной процедуры из графа локальной системы теплоподачи или отрезка газопроводной сети с рис. 2 слева, как схематично продемонстрировано на этом рисунке справа (замкнутым контуром обведены склеиваемые узлы).
С точки зрения управления потоками будем рассматривать всего два уровня. Верхний задан орграфом G0 на вершинах, помеченных “ноликом”, а нижний – набором орграфов Gi с вершинами ${v}_{i}^{0}$ распредсетей (т.е. идущих из ${v}_{i}^{0}$ деревьев на ${{{v}}_{j}}$ с $j \in J_{i}^{0}$). Весь граф исследуемой сети обозначим через $G = \left\langle {V,A} \right\rangle $, где V – множество вершин графа (узлов сети), а
– множество направленных дуг (ребер) графа G, объединяющего G 0 и все Gi, $i = \overline {1,n} $.На каждой дуге ${{a}_{{rk}}} \in A$ зададим ограничения пропускной способности ${{d}_{{rk}}}$, где r, k – нижние индексы вершин, соединяемых дугой, по порядку их следования в орграфе. Далее предположим, что пропускная способность ребер распредсети не превышает максимальной пропускной способности ребер сети верхнего уровня, а у последних не превышает ${{d}_{{\infty 0}}}$. Обозначим d = $({{d}_{{rk}}}\,|\,{{a}_{{rk}}} \in A)$. Введем также “укороченные” векторы: ${{d}^{0}} = ({{d}_{{0i}}}\,|\,i = \overline {1,n} )$ для пропускной способности ребер магистральной сети и ${{d}^{i}} = ({{d}_{{lj}}}\,|\,j \in J_{i}^{0},{{a}_{{lj}}} \in {{A}^{i}})$ – для пропускной способности ребер графов Gi, моделирующих распредсети, $i = \overline {1,n} $.
Добыча (или выкачка, производство), передача и распределение ресурса в сети описывается вектором $x$ потоковых переменных ${{x}_{{rk}}}$, каждая из которых обозначает объем потока ресурса по дуге ${{a}_{{rk}}}$ (из ${{{v}}_{r}}$ в ${{{v}}_{k}}$ без учета верхних индексов) в единицу времени. Указанные переменные подчинены ограничениям
(0.2)
${{x}_{{lr}}} = \sum\limits_{k:\;{{a}_{{rk}}} \in A} \,{{x}_{{rk}}}\quad \forall {{a}_{{lr}}} \in A,\quad {{{v}}_{r}} \in V{\backslash }R,$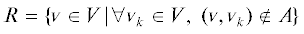 – множество концевых вершин графа G (конечных потребителей ресурса). Множество векторов x с действительными компонентами, удовлетворяющими (0.1) и (0.2), обозначим через X(d). Таким образом, управление потоками в сети соответствует выбору x из X(d) – множества допустимых управлений.
– множество концевых вершин графа G (конечных потребителей ресурса). Множество векторов x с действительными компонентами, удовлетворяющими (0.1) и (0.2), обозначим через X(d). Таким образом, управление потоками в сети соответствует выбору x из X(d) – множества допустимых управлений.
Введем переменную ${{y}_{r}} = {{x}_{{lr}}}$ (где ${{a}_{{lr}}} \in A$) для потока ресурса к конечному потребителю в узле ${{{v}}_{r}} \in R$ при управлении потоками $x \in X(d)$. Вектор $y = ({{y}_{r}}\,|\,{{{v}}_{r}} \in R)$, задающий целевой функционал сетевой системы, линейно зависит от x. Множество
Аналогично на верхнем уровне введем для ${{a}_{{0i}}} \in A$, $i = \overline {1,n} $, ${{z}_{i}} = {{x}_{{0i}}}$ – значения потоков в распредузлы при управлении потоками $x \in X(d)$, и определим
(0.3)
${{z}_{1}} + {{z}_{2}} + {{z}_{3}} \leqslant 6,\quad 0 \leqslant {{z}_{1}} \leqslant 6,\quad 0 \leqslant {{z}_{2}} \leqslant 1,\quad 0 \leqslant {{z}_{3}} \leqslant 4.$Для сети нижнего уровня с рис. 1 (см. граф справа) выберем ${{d}_{{1,4}}} = 6$, ${{d}_{{2,5}}} = {{d}_{{2,6}}} = {{d}_{{2,7}}}$ = 1, ${{d}_{{3,8}}} = {{d}_{{3,9}}}$ = 6. Это накладывает на распределение ресурсов $y \in Y(d)$ для нее условия:
(0.4)
$y \geqslant 0,\quad {{y}_{4}} \leqslant 6,\quad {{y}_{5}} \leqslant 1,\quad {{y}_{6}} \leqslant 1,\quad {{y}_{7}} \leqslant 1,\quad {{y}_{8}} \leqslant 6,\quad {{y}_{9}} \leqslant 6$(0.6)
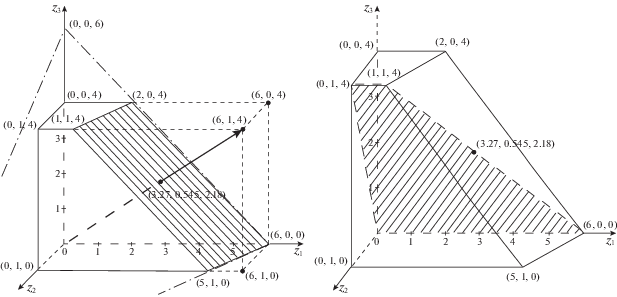
${{z}_{1}} = {{y}_{4}} \leqslant 6,\quad {{z}_{2}} = {{y}_{5}} + {{y}_{6}} + {{y}_{7}} \leqslant 1,\quad {{z}_{3}} = {{y}_{8}} + {{y}_{9}} \leqslant 4,$1. Двухуровневое управление потоками. Задачи верхнего уровня. Для исследования функциональных возможностей управления потоками на уровне магистральной сети воспользуемся методологией из [2]. Обозначим через $u_{i}^{0}$ максимально достижимый для данной сети поток в вершину ${v}_{i}^{0}$, $i = \overline {1,n} $. Указанные величины названы в [2] максимальными потоками в режиме монопольного управления (далее – МРМ-потоками), поскольку они достигаются при условии, что потоки из остальных распредузлов равны нулю (${{z}_{k}} = 0$ $\forall k \ne i$). Вычислим $u_{i}^{0}$ для $i = \overline {1,n} $. (Для примера сети $S$ МРМ-потоки на верхнем уровне: $u_{1}^{0} = 6,$ $u_{2}^{0} = 1,$ $u_{3}^{0} = 4$.) Вектор ${{u}^{0}} = (u_{i}^{0}\,|\,i = \overline {1,n} )$, составленный из этих максимально возможных значений, будем называть МРМ-вектором. Так в сети $S$ МРМ-вектор ${{u}^{0}}(S)$ = (6, 1, 4).
Для любой сетевой системы МРМ-вектор, как правило, недостижим, т.е. 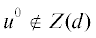 . Обозначим через z(i) достижимый вектор $(0, \ldots ,0,u_{i}^{0},0, \ldots ,0)$ с МРМ-потоком на i-м месте. Векторы z(i) являются угловыми точками множества Z(d), которые находятся на координатных осях, $i = \overline {1,n} $. В сети S (см. на рис. 3) $z(1) = (6,0,0),$ $z(2) = (0,1,0),$ $z(3) = (0,0,4).$
. Обозначим через z(i) достижимый вектор $(0, \ldots ,0,u_{i}^{0},0, \ldots ,0)$ с МРМ-потоком на i-м месте. Векторы z(i) являются угловыми точками множества Z(d), которые находятся на координатных осях, $i = \overline {1,n} $. В сети S (см. на рис. 3) $z(1) = (6,0,0),$ $z(2) = (0,1,0),$ $z(3) = (0,0,4).$
Заметим, что если рассмотреть задачу многокритериальной (МК) максимизации [3, 4] вектора z потоков ресурсов в региональные центры, поставленную в [5], то точку u0 в критериальном пространстве вряд ли следует считать целевой. Действительно, как уже отмечалось выше, структура потребления могла сильно измениться со времени создания сетевой инфраструктуры системы ресурсоснабжения. Тем не менее, для магистральных сетей это не столь характерно, как для распределительных (хотя и для них тоже надо различать старые и новые системы). Так что, оценивая сеть в общем, например, с прицелом на задачи развития и обеспечения роста потребления, естественно начинать с построения вектора МРМ-потоков, которое не требует больших вычислительных затрат.
Кроме того введем m0 – максимальную величину МРМ-потока, которую удается передать в сети верхнего уровня для хотя бы одного регионального распределительного узла:
В сети $S$ рекордное значение ${{m}^{0}}(S)$ = 6. На рис. 3 слева штрихпунктирной линией показаны границы пересечения с неотрицательным ортантом гиперплоскости, заданной ограничением
Формально уравнение (1.2) задает плоскость, определяющую симплекс на опорных векторах (6, 0, 0), (0, 6, 0), (0, 0, 6). Фактически значение (1.1) для этой сети равно максимальному суммарному потоку ресурса, который можно одновременно передать всем региональным распредузлам (и всем потребителям). Однако указанное свойство выполняется не всегда. На исходных данных сети $S$ получилось, что ${{m}^{0}} = {{d}_{{\infty 0}}}$. В общем случае веерной сети на верхнем уровне ${{m}^{0}} \leqslant {{d}_{{\infty 0}}}$, поэтому максимум суммы потоков может быть больше m0 (но не превышает ${{d}_{{\infty 0}}}$). Ниже рассмотрим преимущества случая равенства ${{m}^{0}} = {{d}_{{\infty 0}}}$ отдельно.
Слева на рис. 3 заштрихована грань множества ${{Z}_{S}}(d)$, лежащая в плоскости (1.2) и оказавшаяся для сети S множеством оптимальных по Парето распределений потока в МК-задаче поиска
(заглавная буква в записи максимума в (1.3) и далее служит для того, чтобы подчеркнуть, что значением МК-оптимума является все множество недоминируемых по Парето [3, 4] векторов). По определению(1.4)
$(1.3) = \{ z{\text{*}} \in Z(d)\,|\,\forall z \in Z(d){\backslash }\{ z{\text{*}}\} \;\exists i \in \{ 1, \ldots ,n\} {\kern 1pt} :\;{{z}_{i}} < z_{i}^{*}\} .$Для сети верхнего уровня с веерной структурой, если ${{m}^{0}} = {{d}_{{\infty 0}}}$, то
(1.5)
$(1.3) = Z(d) \cap \{ ({{z}_{1}}, \ldots ,{{z}_{n}})|{{z}_{1}} + \ldots + {{z}_{n}} = {{m}^{0}}\} .$Действительно, ${{z}_{1}} + \ldots + {{z}_{n}} \leqslant {{d}_{{\infty 0}}}$ и для случая веерной структуры равенство достигается. Так что значение ${{d}_{{\infty 0}}}$ дает максимум суммы потоков, который реализуется на векторе $z({{i}^{0}})$ для i 0 из (1.1) по условию равенства ${{m}^{0}} = {{d}_{{\infty 0}}}$. Отсюда по свойствам линейной свертки критериев [4] правая часть (1.5) состоит из точек Парето в задаче (1.3). Для любых других точек
$z \in Z(d)$ выполнено ${{z}_{1}} + \ldots + {{z}_{n}} < {{m}^{0}}$, следовательно, ${{z}_{{{{i}^{0}}}}} < {{m}^{0}}$ и существует возможность добавить к потокам ${{x}_{{\infty 0}}}$ и ${{x}_{{0{{i}^{0}}}}}$ на дугах ${{a}_{{\infty 0}}}$ и ${{a}_{{0{{i}^{0}}}}}$ количество ресурса ${{d}_{{\infty 0}}} - {{z}_{{{{i}^{0}}}}}$ с сохранением достижимости вектора распределения потоков верхнего уровня. Полученный
вектор будет доминировать $z$, т.е. 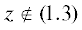 , согласно (1.4).
, согласно (1.4).
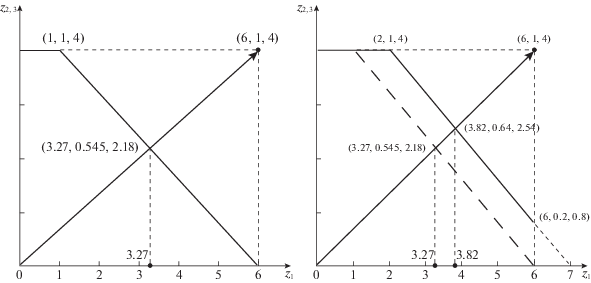
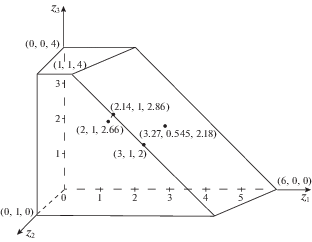
Теперь для анализа множества Z(d) найдем точку $z{\text{*}}(0)$ пересечения его границы лучом, выходящим из начала координат в точку u0. Построенный вектор будет входить в решение задачи (1.3). Для сети S $z{\text{*}}(0) = (36{\text{/}}11,6{\text{/}}11,24{\text{/}}11)$ (см. на рис. 3, там же даны численные значения координат в десятичном приближении). Плоскость, проходящая через начало координат, в которой лежат векторы $z{\text{*}}(0)$ и $z(1) = (6,0,0)$, изображена на рис. 3 справа (заштрихована), и пунктиром отмечены линии ее пересечения с границей множества ${{Z}_{S}}(d)$. На основании указанных плоскости и векторов сформирована двумерная (в этой плоскости) z-диаграмма, приведенная на рис. 4 слева (похожую диаграмму см. в [2, рис. 1]). Ось z2, 3 на диаграмме соответствует диагонали прямоугольника $[0,u_{2}^{0}] \times [0,u_{3}^{0}]$, являющегося проекцией ${{Z}_{S}}(d)$ на координатную плоскость z1 = 0. (Эта диагональ показана пунктиром на заднем плане правой фигуры с рис. 3.)
Векторы (1, 1, 4) и (6, 0, 0) на рис. 4 слева – угловые точки выпуклого множества ${{Z}_{S}}(d)$, лежат на одной прямой с $z{\text{*}}(0)$ и определяют на ней отрезок, принадлежащий (1.3). Данный отрезок – диагональ паретовской грани ${{Z}_{S}}(d)$ (см. пунктирную линию на переднем плане правой фигуры с рис. 3). Таким образом, выпуклая комбинация векторов (1, 1, 4) и (6, 0, 0) представляет собой однопараметрическое семейство допустимых паретовских распределений ресурса на верхнем уровне сети S. В качестве примера приведем запись $z{\text{*}}(0)$ через эти векторы:
Аналогичная диаграмма может быть построена и для общей веерной сети верхнего уровня на базе векторов $z{\text{*}}(0)$ и $z({{i}^{0}})$, однако в отсутствие равенства ${{m}^{0}} = {{d}_{{\infty 0}}}$ второй вектор не будет оптимальным по Парето. Поиск всех угловых точек границы Парето как пересечения Z(d) с гиперплоскостью ${{z}_{1}} + \ldots + {{z}_{n}} = {{d}_{{\infty 0}}}$ предполагает их перебор. С учетом веерной структуры граница Парето для $Z(d)$ задается пересечением указанной гиперплоскости с параллелепипедом {0 ≤ zi ≤ ≤ $u_{i}^{0}\,|\,i = \overline {1,n} \} $. Поэтому отрезки прямых, соединяющие z*(0) с недостижимыми точками z'(i) = = $(0, \ldots ,0,{{d}_{{\infty 0}}}$, 0, ..., 0) на осях координат, лишь отчасти лежат в $Z(d)$. Руководствуясь той же идеей, что и выше, в качестве второго репера для построения z-диаграммы можно использовать недостижимый вектор $z{\kern 1pt} '({{i}^{0}})$ с ${{d}_{{\infty 0}}}$ на i 0-м месте. Тогда и достижимый вектор $z({{i}^{0}})$ будет находиться в плоскости z-диаграммы (но уже не будет паретовским). Например, при ${{d}_{{\infty 0}}} = 7$ для сети S получим z-диаграмму, показанную на рис. 4 справа. Ее граница Парето (выделена жирным), как прежде, задает прямую на паретовской грани $Z(d)$, но поиск ее крайних точек чуть более сложен (см. в [2]). Тем не менее, таких точек всего две. Возможность перехода к плоской “картине” предоставляет удобный способ визуализации процесса принятия решений.
Вектор z*(0), являясь оптимальным по Парето в задаче (1.3), дает значимую характеристику сети верхнего уровня. В [2] соответствующее распределение ресурса названо равнодолевым в силу пропорциональности МРМ-вектору u0. Еще один вариант оптимального по Парето распределения строится на базе лексиминного правила [6] управления потоками. Построение начинается с поиска уравнительного распределения
(1.6)
${{z}^{ = }} \in {\text{Arg}}\mathop {max}\limits_{z \in Z(d)} \mathop {min}\limits_{i = \overline {1,n} } {{z}_{i}}.$Произвольный вектор ${{z}^{ = }}$ из (1.6) может не принадлежать (1.3). Для сети $S$ таким будет, к примеру, вектор (1, 1, 1). Ясно, что его вторую компоненту нельзя увеличить в рамках ${{Z}_{S}}(d)$, но остальные компоненты допускают увеличение без снижения достигнутого уровня $z_{2}^{ = }$. Решив для этой сети задачу (1.6) с дополнительным ограничением ${{z}_{2}} \geqslant 1$, получим оптимальный по Парето вектор ${{z}^{{ + = }}} = $ (2.5, 1, 2.5). В общем случае для построения лексиминного вектора из (1.3) надо решать задачу типа (1.6) с дополнительными ограничениями несколько раз (не больше n – 1). Результирующий вектор z0 считается справедливым дележом ограниченного ресурса, в том числе сетевого (см., например, в [7]).
В [2] подробно обсуждается возможность построения z-диаграммы на основе обоих характеризующих векторов: лексиминного и равнодолевого. Понятно, что в случае веерной структуры, когда $z{\text{*}}(0) \in $ (1.3), любая их выпуклая комбинация дает паретовское распределение потоков на верхнем уровне, хотя параметризовать все множество (1.3) таким образом не удастся. В частности, на одной прямой с этими векторами для сети $S$ не лежит точка (6, 0, 0), рассмотренная выше.
Отметим, что равнодолевое распределение потоков соответствует уравнительному, если справедливый дележ рассматривать в относительных величинах (по отношению к максимально возможным). Тогда в целевой функции (1.6) будет минимум из относительных значений. Для рассматриваемой веерной структуры оптимум по Парето при этом получается сразу на первой итерации (взвешенный таким образом лексимин оказывается равнодолевым). В принципе, о пропорциональности МРМ-значениям можно вспомнить на любом шаге процедуры поиска справедливого дележа. Так, решив задачу (1.6) и перейдя к относительным переменным для компонент, допускающих улучшение, при абсолютных ограничениях снизу на достигнутые значения по z с индексами, реализующими минимум в (1.6), уже на следующей итерации найдем паретовский вектор. В частности, для сети S придем к распределению потоков (3, 1, 2), тоже имеющему содержательный смысл. Далее посмотрим, как решения на магистральном уровне влияют на возможности распределения ресурса конечным потребителям.
2. Двухуровневое управление потоками. Задачи нижнего уровня. Задачи для распредсетей формально не отличаются от задачи верхнего уровня. Однако на практике в региональных распредузлах скорее ожидается информация о требуемых объемах конечного поузлового потребления ресурса. Обозначим через $f = ({{f}_{j}}\,|\,j > n)$ соответствующий вектор. На верхнем уровне он зачастую неизвестен. Если предположить дефицит ресурса (как при ${{m}^{0}} = {{d}_{{\infty 0}}}$), то территориальные центры его распределения заинтересованы в завышении требований при информировании лица, принимающего решения (ЛПР) в центре управления магистральными потоками. В итоге ЛПР будет склоняться к уравнительному распределению ресурса между узлами $v_{i}^{0}$, $i = \overline {1,n} $. Вместе с тем при дальнейшем перераспределении ресурса территориальные органы должны ориентироваться на пропорциональное ресурсообеспечение абонентов своей подсети. По крайней мере, передача потока больше, чем понадобится потребителю, экономически не выгодна. В случае тотального дефицита ресурса в распредузле последней проблемы не возникает и возможно использование всех способов, описанных выше. В общем случае добавим такой способ.
Рассмотрим произвольную вершину $v_{i}^{0}$ (для остальных $v_{k}^{0}$ рассуждения аналогичны). Допустим для простоты, что распредсеть для нее имеет веерную структуру. Поставим задачу поиска
(2.1)
${{y}^{i}}({{z}_{i}},f) \in {\text{Arg}}\mathop {max}\limits_{{{y}^{i}} \in {{Y}_{i}}({{z}_{i}},d)} \mathop {min}\limits_{j \in J_{i}^{0}} {{y}_{j}}{\text{/}}{{f}_{j}},$Возьмем, к примеру, вершину ${v}_{2}^{0}$ для сети S и пусть к ней приходит поток величины 1 (z2 = 1). Тогда равнодолевое управление потоками равносильно уравнительному и дает ${{y}_{5}} = {{y}_{6}} = {{y}_{7}} = 1{\text{/}}3$. Предположим, что требования конечных потребителей в этих узлах следующие: ${{f}_{5}} = 1,$ ${{f}_{6}} = 2,$ ${{f}_{7}} = 3$. Равнообеспечивающее распределение ресурса, согласно (2.1), приводит к решению (1/6, 1/3, 1/2) для потоков из второго магистрального узла. (В силу веерной структуры и дефицита ресурса в сравнении с пропускной способностью ребер второй распредсети лексимин достигнут за один шаг – по принципу уравнивания Гермейера [4].)
Подчеркнем, что применение идеи равнодолевого распределения к величинам ${{y}_{j}}{\text{/}}{{f}_{j}}$ обеспеченности требований в конечных узлах распредсети не адекватно постановке задачи ресурсоснабжения в условиях дефицита. Для предыдущего примера такой подход привел бы к вектору потоков (6/11, 3/11, 2/11) из второго магистрального узла, что представляется совсем несправедливым. Эти виды управления потоками не совмещаются. По сути равнодолевое распределение реализует равномерную загрузку трубопроводов, а равнообеспечивающее – пропорциональное удовлетворение требований. И тот, и другой векторы являются оптимальными по Парето в задаче на
для сети S при $i = 2$, ${{z}_{i}} = 1$.В общем случае равнообеспечивающее распределение потоков (2.1) необязательно будет решением (2.2). Тогда следует искать взвешенный лексимин с весами fj. Так, если бы вектор пропускной способности ${{d}^{i}} = ({{d}_{{ij}}}\,|\,j \in J_{i}^{0})$ для i-й распредсети был бы в рассматриваемой второй подсети сети $S$ равен (1, 1, 1/3), то равнообеспечивающий требования (1, 2, 3) вектор ${{y}^{{2 = }}} = (1{\text{/}}9,\;2{\text{/}}9$, 1/3) как непаретовский потребовал бы второй итерации решения задачи типа (2.1) с дополнительным ограничением ${{y}_{7}} \geqslant 1{\text{/}}3$, т.е. ${{x}_{{2,7}}} \geqslant 1{\text{/}}3$, что в итоге даст распределение ресурса (2/9, 4/9, 1/3), принадлежащее (2.2), для z2 = 1. Укажем также, что в ситуации, когда во втором узле-агрегаторе сети S оказалось ресурса в количестве, меньшем 1 (например, при равнодолевом управлении потоками на магистральном уровне), обеспеченность требований потребителей данного распредузла еще сильнее снизится. В силу условий (0.3) потоки ресурса во второй распредсети заметно меньше, чем в остальных подсетях сети S.
С целью, по возможности, уравнять условия снабжения всех конечных потребителей, в разд. 3 обсудим варианты одноуровневого управления конечными потоками – непосредственно с верхнего уровня. При этом чтобы не вводить дополнительные числовые характеристики для сети $S$, далее для простоты будем полагать в ней $f(S) = (1, \ldots ,1)$ и опускать зависимость от f у равнообеспечивающих распределений ресурса. Обозначение $y(z)$ в силу симметричности потребителей в подсетях нижнего уровня сети $S$ будем понимать как результат уравнительного управления потоками в этих подсетях, т.е. $\forall z \in {{Z}_{S}}(d)$
3. Прямое управление потоками. Сравнение для сети S. Следуя методологии разд. 1, вычислим МРМ-потоки, направленные на конечное использование в соответствующие узлы-потребители. Обозначим их через w с индексом рассматриваемого узла. Для сети S из соотношений (0.4)–(0.6)
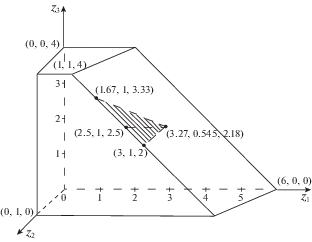
МРМ-вектор в терминах конечных потоков – $w(S) = (6,1,1,1,4,4)$; достижимое равнодолевое распределение ресурса между конечными потребителями – y*(0) = $(2,1{\text{/}}3,1{\text{/}}3,1{\text{/}}3,4{\text{/}}3,4{\text{/}}3)$. При этом обслуживающий указанное потребление на магистральном уровне вектор $z(y{\text{*}}(0)) = (2,1,8{\text{/}}3)$. Здесь и далее с помощью z(y) для $y \in Y(d)$ обозначается распределение ресурсов $z \in Z(d)$ (на верхнем уровне) с компонентамиУказанный вектор $z(y{\text{*}}(0))$ магистральных потоков лежит на боковой грани множества ${{Z}_{S}}(d)$ (см. рис. 5) и не является паретовским распределением в ${{Z}_{S}}(d)$. Из-за двухъярусности дерева графа сети до конечных потребителей вектор $y{\text{*}}(0)$ также оказался для сети S не из решения задачи на ${\text{Max}}\{ y\,|\,y \in Y(d)\} $. Взвешенный лексиминный вектор для этой сети с весами wj (значениями МРМ-потоков) –
Соответствующее оптимальное по Парето распределение ресурса на магистральном уровне $z(y{\text{*}}(1)) = (15{\text{/}}7,1,20{\text{/}}7)$ отмечено на рис. 5. При этом вектор из долей получаемых объемов ресурса от МРМ-потоков
(В данном случае, когда для сети S попытались передать во все узлы конечных потребителей ресурс равными долями от МРМ-потоков, то, поскольку пропускная способность дуги в узел $v_{2}^{0}$ минимальна (${{d}_{{02}}} = 1$), а число потребителей из этого узла максимально, решение $y{\text{*}}(0)$ получилось не оптимальным по Парето.)
С другой стороны, можно было бы зафиксировать поток $z_{2}^{*} = 1$ и перераспределить оставшиеся потоки в распредузлы $v_{i}^{0},\;i = 1,3$, согласно взвешенному лексиминному правилу с весами – МРМ-потоками $u_{i}^{0}$. Тогда пришли бы не к вектору $z(y{\text{*}}(1))$, а к $z{\text{*}} = (3,1,2)$, уже упоминавшемуся в разд. 1, который тоже является оптимальным по Парето для магистрального уровня сети $S$, но не совпадает с $z(y{\text{*}}(1))$. Более того, в $z(y{\text{*}}(1))$ третий распредузел получает ресурса меньше первого, а в z* – наоборот. В этом проявляется свойство равнодолевых (пропорциональных МРМ-потокам) векторов. Совпадение $z(y{\text{*}}(1))$, построенного на базе взвешенного с МРМ-потоками лексиминного вектора $y{\text{*}}(1)$, с аналогичным максимином долей от МРМ-потоков в распредузлы возможно лишь при равном числе конечных потребителей в этих узлах. В общем случае, нельзя равномерно “занять” ребра сразу на первом и на втором уровнях двухуровневых потоковых сетей, если величины пропускной способности дуг на разных ярусах не согласованы (что естественно в силу долгосрочности инфраструктуры). Подробнее разберем данный факт ниже на исследуемом примере модельной сети с рис. 1.
На рис. 5 для ${{Z}_{S}}(d)$ изображены: граничная точка $z(y{\text{*}}(0))$ и оптимальное по Парето решение $z(y{\text{*}}(1))$, которое соответствует $y{\text{*}}(1)$, построенному на основе равнодолевого $y{\text{*}}(0)$ с помощью взвешенного лексиминного правила для весов – МРМ-потоков к конечным потребителям. (Для удобства сравнениях на рисунках и в таблицах используется десятичное приближение дробей – с точностью до сотых). Еще на рис. 5 показаны вектор $z{\text{*}}(0)$, который подробно анализировался в разд. 1 (см. рис. 3), и вектор z*. Точка $z(y{\text{*}}(1))$, полученная путем прямого управления всеми потоками, лежит на паретовской грани множества достижимых распределений ресурса верхнего уровня и наряду с $z{\text{*}}(0)$ и z* может быть применена для представления и анализа других точек Парето из множества ${{Z}_{S}}(d)$.
На примере сети $S$ проведем сравнительный анализ двух равнодолевых стратегий управления потоками: напрямую с верхнего уровня и с использованием промежуточного звена. Применим табличную форму. В табл. 1 даны векторы распределения потоков для концевых узлов магистральной сети, а в табл. 2 – для конечных потребителей. Ожидаемо видно, что прямое управление (правые столбцы) приводит к более адекватным результатам в случае наличия на верхнем уровне нужной информации.
Таблица 1.
Сравнение двух равнодолевых решений на верхнем уровне
| Точки | z*(0) | $ \vee $ | z*(y*(1)) |
|---|---|---|---|
| z1 | 3.27 | > | 2.14 |
| z2 | 0.545 | < | 1 |
| z3 | 2.18 | < | 2.86 |
Таблица 2.
Сравнение двух вариантов равнодолевых решений на уровне потоков к потребителям
| Точки | y(z*(0)) | $ \vee $ | y*(1) |
|---|---|---|---|
| y4 | 3.27 | > | 2.14 |
| y5 | 0.18 | < | 0.33 |
| y6 | 0.18 | < | 0.33 |
| y7 | 0.18 | < | 0.33 |
| y8 | 1.09 | < | 1.43 |
| y9 | 1.09 | < | 1.43 |
Дополнительно сравним загрузку дуг ${{a}_{{rk}}}$ как отношение передаваемого по дуге потока ресурса ${{x}_{{rk}}}$ к ее пропускной способности ${{d}_{{rk}}}$ в процентах. На рис. 6, 7 показана загрузка сети S для полученных векторов $y{\text{*}}(0),$ $y{\text{*}}(1)$, $y(z{\text{*}}(0))$ и $y(z{\text{*}})$ (в десятичном приближении).
Рис. 6.
Загрузка сети для прямого равнодолевого распределения (слева) и его доведения до оптимального по Парето (справа)
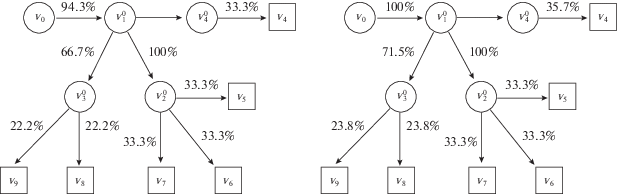
Рис. 7.
Загрузка сети для магистрального равнодолевого распределения (слева) и для распределения z*, совмещающего его с лексиминным (справа)
На рис. 6 слева – загрузка для исходного равнодолевого распределения при $\Delta {{y}_{j}} = 1{\text{/}}3$ $\forall j > 3$, которое не является паретовским:
На рис. 6 справа – загрузка сети для оптимального по Парето распределения ресурса конечным потребителям на базе указанного слева равнодолевого для них:
Здесь уже возможности источника ресурса использованы полностью (100% занятости дуги ${{f}_{{\infty 0}}}$).
На рис. 7 слева – загрузка сети для оптимального по Парето равнодолевого распределения агрегированных суммарных объемов ресурса в распредузлы:
Здесь равномерная загрузка – на верхнем уровне, но у абонентов узлов $v_{2}^{0}$ и $v_{3}^{0}$ гораздо меньше ресурса, чем у ${{v}_{4}}$. На рис. 7 справа – загрузка для паретовского вектора z* (равнодолевое распределение ресурса на втором этапе лексикографии в магистральной подсети сети S). Здесь тоже логичная картина в процентах (50, 100, 50) загрузки ребер на верхнем уровне привела к перекосу $(50,\;33,\;33,\;33,$ 17.5, 17.5) на нижнем, по-видимому, в силу несоответствия пропускной способности дуг нижнего уровня из распредузла $v_{3}^{0}$ возможностям передать ресурс в данный узел.
Векторы $y{\text{*}}(0)$, $y{\text{*}}(1)$, $y(z{\text{*}})$ и $y(z{\text{*}}(0))$ являются граничными точками множества ${{Y}_{S}}(d)$. Три последних определяют оптимальные по Парето решения. Их выпуклая комбинация представляет собой двухпараметрическое семейство оптимальных по Парето распределений объемов ресурса, которые допускается одновременно передать в узлы потребителям, но, естественно, не описывает это множество полностью. Тем не менее, основываясь на характеристиках загрузки ребер и обеспечения потребителей ресурсом, можно подобрать комбинации указанных векторов для достижения желательного ЛПР эффекта, например, компромисса между равномерностью загрузки на разных уровнях или между снабжением потребителей на разных территориях.
Векторы ${{u}^{0}}(S) = (6,1,4)$ и $w = (6,1,1,1,4,4)$ можно рассматривать как аналоги векторов требований на передачу ресурса в концевые узлы сети $S$ на соответствующем уровне. Приведенные выше построения останутся применимыми. Однако содержательные трактовки полученных результатов могут сильно отличаться. Если считать, что пропускная способность дуг отражает пожелания потребителей к объемам ресурса (возможностям потребления) и их величины между уровнями согласованы, то равнодолевое распределение потоков вполне адекватно. Если нет оснований для подобных предположений и у ЛПР на верхнем уровне нет иной информации, кроме как о drk, а информации с нижнего уровня он не очень доверяет, то кроме рассмотренных выше двух вариантов равнодолевого управления он может придерживаться уравнительных правил. Как будет показано далее, в таком случае решения, полученные с помощью двухуровнего управления, и решения, полученные путем прямого управления с верхнего уровня, тоже будут заметно отличаться.
Итак предположим, что ЛПР верхнего уровня использует уравнительное правило “всем поровну”. Формально можно задать вектор требований на поставки ресурса:
либо правилом: ${{f}^{0}} = (1,1,1)$ для узлов-распределителей $v_{1}^{0},\;v_{2}^{0},\;v_{3}^{0}$,
либо правилом: ${{f}_{j}} = 1$ $\forall j > n$, т.е. для узлов-потребителей ${{v}_{4}}{\kern 1pt} - {\kern 1pt} {{v}_{9}}$.
Снабжение распределительных узлов по правилу 1 рассматривалось в разд. 1 (см. (1.6)) и привело к лексиминному уравнительному распределению ${{z}^{{ + = }}} = (2.5,1,2.5)$. Соответствующий вектор распределения потоков ресурса в узлах потребителей
Проанализируем решение для правила 2. Прямое уравнительное распределение потока во все узлы конечных потребителей дает объемы ресурса, заданные вектором y= = $(1{\text{/}}3,1{\text{/}}3,1{\text{/}}3,1{\text{/}}3,1{\text{/}}3,1{\text{/}}3)$. При этом $z({{y}^{ = }}) = (1{\text{/}}3,1,2{\text{/}}3)$ лежит на боковой вертикальной грани ${{Z}_{S}}(d)$. Лексиминное распределение с верхнего уровня до конечных потребителей в сети $S$:
Сравним оптимальные по Парето распределения потоков ресурса при различных лексиминных стратегиях (по правилу 1 или 2) управления потоками (табл. 3).
Таблица 3.
Сравнение лексиминных решений
| Магистральный уровень | z+= | $ \vee $ | z(y*) |
|---|---|---|---|
| z1 | 2.5 | > | 1.67 |
| z2 | 1 | = | 1 |
| z3 | 2.5 | < | 3.33 |
| Распределительный уровень | y(z+=) | $ \vee $ | y* |
| y4 | 2.5 | > | 1.67 |
| y5 | 0.33 | = | 0.33 |
| y6 | 0.33 | = | 0.33 |
| y7 | 0.33 | = | 0.33 |
| y8 | 1.25 | < | 1.66 |
| y9 | 1.25 | < | 1.66 |
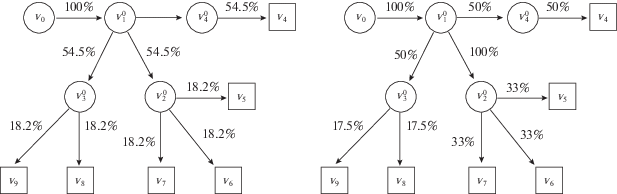
Видно, что с точки зрения конечных потребителей правый столбец – более “справедливый” (в том числе и в сравнении с табл. 2). Также более равномерна загрузка ребер распредсети для правила 2 (см. рис. 8). На рис. 8 слева показана загрузка сети при лексиминном распределении ресурса между территориальными центрами (правило 1). Загрузка сети при лексиминном распределении ресурса между конечными потребителями (правило 2) показана на рис. 8 справа.
Рис. 8.
Загрузка сети для лексиминного распределения ресурса: на магистральном уровне (слева) и напрямую конечным потребителям (справа)
Оба найденные с помощью лексиминного правила управления потоками оптимальные по Парето распределения ресурса лежат на ребре между точками (1, 1, 4) и (5, 1, 0). В этом простейшем случае интересующие ЛПР решения представимы в виде выпуклой комбинации, которая будет совмещать их свойства с соответствующими коэффициентами. Если выйти в плоскость паретовской грани множества ${{Z}_{S}}(d)$, то можно рассмотреть выпуклую комбинацию z*, $z(y{\text{*}})$ и $z{\text{*}}(0)$, т.е. взвесь лексиминных равнообеспечивающих распределений с равнодолевыми. Такой участок множества Парето уже целесообразно рекомендовать в качестве основы для использования в системах поддержки принятия решений по управлению потоками в ресурсоснабжающих сетях. Он содержит и ${{z}^{{ + = }}}$, и $z(y{\text{*}}(1))$ (см. на рис. 9).
Еще более широкий (но менее значимый) набор точек Парето получается с помощью выпуклой комбинации трех из четырех угловых точек паретовской грани достижимого множества ${{Z}_{S}}(d)$ как
Соответствующее управление потоками xij может быть найдено при фиксированном $\tilde {z}$, к примеру, как оптимальное решение задачи о передаче потока минимальной стоимости. Программное обеспечение, позволяющее его найти для общего случая, описано в [1].
Заключение. Сетевая потоковая модель топливно-энергетического комплекса [1] позволяет свести задачу управления потоками энергоресурсов в больших многопользовательских системах и территориальных объединениях к оптимизации однопродуктового потока в сети. На основе такого подхода в данной работе поставлена задача анализа и сравнения различных стратегий распределения энергоресурсов среди невзаимозаменяемых (равноправных) пространственно отдаленных потребителей с учетом наличия региональных центров управления и доставки энергоресурсов. В упрощенном виде задача была сформулирована как двухуровневая. При этом на верхнем уровне принятия решений возникла МК-проблема максимизации потоков для узлов сети, которые в модели соответствуют территориальным центрам управления. Предложены методы, как на границе множества достижимости построить оптимальные по Парето распределения, соответствующие векторам потоков энергоресурсов, которые можно одновременно передать всем региональным агрегаторам. Показано, что паретовские решения при распределении “напрямую” к потребителям и при “иерархической” схеме управления через территориальные центры различаются, но дают возможность описать представительный набор решений.
Аналогичное исследование может быть проведено и на более агрегированной сетевой потоковой модели, рассматривающей межрегиональные центры управления и распределение ресурсов между регионами. Например, модельная сеть $S$ соответствует агрегированной схеме поставок газа в три региональных объединения. В дальнейшем планируется распространить полученные результаты на многоуровневую модель управления потоками энергоресурсов. Второе направление будущих исследований предполагает учет в МК-постановке еще одной группы критериев, связанной с загрузкой ребер сети, т.е. с таким эффективным использованием их пропускной способности, которое позволяет избежать критических режимов передачи [8]. Проведенный выше анализ показал, что в общем случае не удается обеспечить равномерность загрузки одновременно для магистральных сетей и для распределительных. Так что здесь тоже надо изучать возможности компромисса.
Список литературы
Козлов М.В., Малашенко Ю.Е., Назарова И.А. и др. Управление топливно-энергетической системой при крупномасштабных повреждениях. I. Сетевая модель и программная реализация // Изв. РАН. ТиСУ. 2017. № 6. С. 50–73.
Малашенко Ю.Е., Назарова И.А., Новикова Н.М. Экспресс-анализ и агрегированное представление множества достижимых потоков многопродуктовой сетевой системы // Изв. РАН. ТиСУ. 2019. № 6. С. 63–72.
Лотов А.В., Поспелова И.И. Многокритериальные задачи принятия решений. М.: Макс Пресс, 2008.
Гермейер Ю.Б. Введение в теорию исследования операций. М.: Наука, 1971.
Malashenko Y.E., Nazarova I.A., Novikova N.M., Pospelova I.I. A Network Flow Model for Power and Energy System with Changing Capabilities // Int. J. of Public Administration. 2019. V. 42. Iss. 15–16. C. 1323–1332.
Мулен Э. Теория игр с примерами из математической экономики. М.: Мир, 1985.
Ogryczak W., Luss H., Pioro M., Nace D., Tomaszewski A. Fair Optimization and Networks: a Survey // J. Applied Mathematics. 2014. V. 25. P. 1–25.
Малашенко Ю.Е., Назарова И.А., Новикова Н.М. Управление топливно-энергетической системой при крупномасштабных повреждениях. III. Критические и стационарные режимы // Изв. РАН. ТиСУ. 2018. № 4. С. 60–72.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления