1. На главную
  2. Электронные версии
  3. Известия РАН. Теория и системы управления
  4. № 3, 2020

Известия РАН. Теория и системы управления, 2020, № 3, стр. 3-13

КЛАСТЕРНОЕ ДВИЖЕНИЕ В ДВУХКОНТУРНОЙ СИСТЕМЕ С ПРИОРИТЕТНЫМ ПРАВИЛОМ РАЗРЕШЕНИЯ КОНФЛИКТА

П. А. Мышкис a, b, А. Г. Таташев a, c, *, М. В. Яшина a, c

a Московский автомобильно-дорожный государственный технический ун-т (МАДИ)
Москва, Россия

b Национальный исследовательский университет “Высшая школа экономики” (НИУ ВШЭ)
Москва, Россия

c Московский технический университет связи и информатики (МТУСИ)
Москва, Россия

* E-mail: a-tatashev@yandex.ru

Поступила в редакцию 26.08.2019
После доработки 10.01.2020
Принята к публикации 27.01.2020

Полный текст (PDF)

Аннотация

Рассматривается детерминированная динамическая система, представляющая собой контурную сеть. Число контуров равно двум. На каждом контуре имеется движущийся с постоянной скоростью отрезок, который называется кластером, так как в дискретном варианте системы ему соответствует кластер частиц, т.е. группа частиц, занимающая соседние ячейки и перемещающиеся одновременно. Длины контуров и длины кластеров заданы. Имеется общая точка контуров, называемая узлом. Кластеры не могут проходить через узел одновременно. Кластер останавливается и ожидает освобождения узла, если этот кластер подошел к узлу в момент, когда другой кластер проходит через узел. Если кластеры подошли к узлу одновременно, то преимуществом всегда пользуется один и тот же кластер, считающийся приоритетным (приоритетное правило разрешения конфликта). Доказаны теоремы о средних скоростях движения кластеров с учетом задержек при различных типах поведения системы. Установлено, что средняя скорость движения каждого кластера в системе не зависит от расположения кластеров в начальный момент времени в отличие от рассматривавшийся ранее аналогичной системы с другим правилом разрешения конфликта, где такая зависимость в общем случае имеется. Дается возможная практическая интерпретация исследуемой системы. Представленная система относится к классу динамических систем, введенному и исследовавшемуся А.П. Буслаевым. Полученные результаты могут применяться при решении вопросов автоматизации движения непрерывной массы, использоваться при моделировании движения транспорта и иметь другие приложения.

Введение. Исследуется динамическая система, носитель которой образован двумя контурами с общей точкой. На каждом контуре перемещается масса, представленная кластером постоянной длины. Основная характеристика системы – скорости движения кластеров с учетом задержек, обусловленных невозможностью одновременного прохождения кластеров через общую точку. Рассматриваемая динамическая система относится к классу контурных сетей, введенному А.П. Буслаевым.

В известной дискретной транспортной модели, введенной в [1] (Nagel, Schreckenberg, 1992), на бесконечной или замкнутой одномерной решетке, представляющей собой последовательность клеток, движутся частицы в соответствии с заданными правилами. В общем случае эта модель исследовалась с помощью имитационного моделирования.

Для частных случаев модели Нагеля–Шрекенберга были получены аналитические результаты. Назовем некоторые работы по этой тематике. В [2] (препринт этой статьи был опубликован в 1999 г.) получены аналитические результаты для движения частиц на контуре. Здесь также предполагалось, что на каждом шаге любая частица перемещается вперед на одну ячейку, если ячейка впереди свободна, и остается на месте, если эта ячейка занята. Аналогичные результаты получены независимо в [3]. Как доказано в [2, 3], в случае если плотность частиц (число частиц, деленное на число ячеек) не больше 1/2, то для любого начального состояния все частицы перемещаются после некоторого момента на каждом шаге. Если плотность больше 1/2, то средняя скорость частиц (среднее число перемещений частиц в единицу времени) равна (1 – ρ)/ρ, где ρ – плотность. В [4] получены аналитические результаты для более общей транспортной модели. В этой модели частица перемещается из ячейки i в свободную ячейку i + 1 с вероятностью, зависящей от состояния ячеек i – 1, i + 2 (ячейки нумеруются в направлении движения). В [4] поведение системы исследовалось в частных случаях и для общего случая формула для скорости частиц не была получена. В [5] выведена формула для средней скорости частиц в стохастической версии транспортной модели. В этой системе на каждом шаге частица движется на ячейку вперед, если ячейка впереди свободна. Некоторые обобщения результатов [2–4] представлены в [6]. В частном случае система эквивалентна дискретной системе, рассматривавшийся в [2, 3].

Двухмерная транспортная модель (модель BML) с движением частиц на тороидальной решетке введена в [7]. В этой модели имеются два типа частиц, движущихся в перпендикулярных направлениях. В [8–10] для модели BML получены условия самоорганизации (при любом начальном расположении частиц система за конечное время попадает в состояние, такое, что частицы перемещаются на каждом шаге без задержек в текущий момент и в будущем) и попадания в состояние коллапса (с некоторого момента времени ни одна частица не перемещается).

В [11] введено понятие модели трафика с кластерным движением. Существует один или несколько контуров. В дискретном варианте кластерной модели контур содержит заданное число ячеек. На контуре имеются кластеры частиц. Кластер содержит частицы, находящиеся в соседних ячейках. Частицы одного кластера перемещаются одновременно в соответствии с заданным правилом. Общие точки контуров называются узлами. Частицы не могут проходить через узлы одновременно, вследствие чего могут возникать задержки кластеров у узлов. Кластеры одного контура могут сливаться в один кластер. В непрерывном варианте модели кластер представляет собой отрезок, движущийся по контуру с постоянной скоростью в заданном направлении.

В [12] введено понятие контурной сети (контурные сети Буслаева). Носитель контурной сети представляет собой систему контуров, образующих сетевую структуру. Частицы (кластеры) движутся на контурах по заданному правилу. На систему накладываются ограничения, которые позволяют исследовать систему аналитически.

В [13] введено понятие спектра контурной системы для детерминированной динамической системы с конечным множеством состояний. В такой системе некоторая последовательность состояний с определенного момента повторяется периодически. Эта последовательность состояний названа спектральным циклом. Рассматриваемая в [13] система представляет собой замкнутую цепочку контуров. На каждом контуре имеется единственный кластер. Спектром контурной системы называется множество спектральных циклов и соответствующих значений средних скоростей. Длина контура и длина кластера одинаковы для всех контуров. Частный случай приведенной в [13] системы исследовался в [14]. В [14] предполагалось, что на каждом контуре имеются две ячейки и одна частица. Непрерывный аналог системы, рассматривавшийся в [13], изучался в [15]. В [16] описывалась система, аналогичная [14], но с носителем, представляющим собой открытую цепочку контуров.

В [17–19] исследовались контурные сети на системах колец с тороидальной или сотовой структурой.

В [20, 21] рассматривалась дискретная двухконтурная система, а в [20] – также следующее обобщение. Имеется N контуров с единственной общей точкой (цветок или букет). В [20, 21] доказаны утверждения о поведении системы при различных правилах движения по контурам частиц, объединенных или не объединенных в кластеры. Здесь описывались преимущественно контуры с одинаковой длиной. Для различающихся по длине контуров в [17] получены условия самоорганизации (попадание системы в состояние свободного движения из любого начального состояния).

В [22, 23] рассматривалась непрерывная динамическая система с различными по длине контурами и кластерами. По каждому контуру движется единственный кластер. Имеется единственная общая точка контуров (узел), возле которой могут происходить задержки кластеров. Действует специальное правило разрешения конфликта. Доказано, что при этом правиле в общем случае средние скорости кластеров зависят от начального состояния. При заданных длинах контуров и кластеров и различных начальных расположениях кластеров может быть одна или две пары значений скоростей кластеров. Найден подход к нахождению значений средних скоростей кластеров.

В настоящей работе описывается система, отличающаяся от рассматривавшейся в [22, 23] правилом разрешения конфликта. Полагаем, что если кластеры подошли к узлу одновременно преимущество всегда предоставляется одному и тому же кластеру, считающемуся приоритетным. Доказано, что при данном правиле разрешения конфликта в отличие от правила из [22, 23], средние скорости кластеров не зависят от начального состояния.

Рассматриваемая система содержит два контура. На каждом контуре находится кластер, движущийся в заданном направлении с постоянной скоростью, принимаемой за единицу. Длина контура i равна ci, а длина кластера на этом контуре равна li < ci, i = 1, 2. Контуры имеют общую точку, называемую узлом. Состояние системы считается допустимым, если при этом состоянии узел накрывается не более чем одним кластером. Начальное состояние задается и должно быть допустимым. Два кластера не могут пересекать узел одновременно. Кластер останавливается, если подходит к узлу в момент, когда другой кластер проходит через узел. Если кластеры подходят к узлу одновременно, то первым через узел проходит кластер, выбираемый в соответствии с правилом разрешения конфликта. Замкнутую траекторию в пространстве состояний называем спектральным циклом. Говорим, что система находится в состоянии свободного движения, если оба кластера перемещаются без задержек в настоящий момент и в будущем. Свойство системы при заданных параметрах попадать в состояние свободного движения называется самоорганизацией.

В работе доказано, что при рассматриваемом правиле разрешения конфликта, в отличие от системы с правилом из [22, 23] средние скорости кластеров не зависят от начального состояния. Доказано, что если при заданном наборе значений c1, c2, l1, l2 условия самоорганизации не выполняются, то при этих значениях имеется единственный спектральный цикл, проходимый системой с некоторого момента времени. Доказаны теоремы о значениях средних скоростей кластеров, периоде спектрального цикла, условии самоорганизации, общем характере поведения системы.

Результаты работы могут применяться при автоматизации движения непрерывной массы и иметь другие приложения. Дадим возможную практическую интерпретацию рассматриваемой системы. Предположим, что к двум подразделениям некоторого предприятия с некоторого склада подвозится сырье или топливо. Имеются два транспортных средства, например вагонетки, перемещающиеся по узкоколейным путям. Каждое транспортное средство доставляет груз к одному из двух подразделений. Пути, по которым движутся эти транспортные средства, пересекаются в точке, в которой находится склад. Если одно из транспортных средств подошло к складу в промежутке времени, когда осуществляется загрузка второго транспортного средства, первое средство ожидает окончания загрузки и затем сразу само начинает загружаться. Пусть i-е транспортное средство проходит путь от склада к подразделению, к которому подвозится груз, и обратно за ci – li единиц времени, а загрузка этого транспортного средства длится li единиц времени, i = = 1, 2. Тогда процесс перемещения транспортных средств моделируется динамической системой, рассматриваемой в настоящей работе.

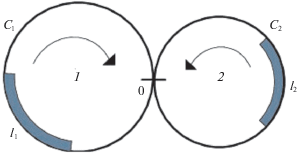
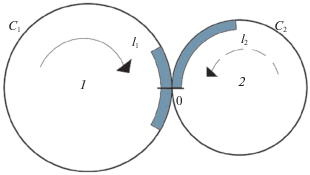
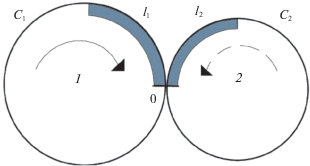
1. Описание системы. Динамическая система содержит два контура 1 и 2 (рис. 1). На i-м контуре находится движущийся отрезок (кластер i) длиной li, i = 1, 2. Контуры имеют общую точку (узел). В любой момент времени кластер движется с единичной скоростью в заданном направлении, если нет задержки в движении этого кластера. Введем систему координат [0, ci) на i-м контуре, i = 1, 2. Направление координатной оси противоположно направлению движения кластера. Точка расположения узла имеет координату 0. Система находится в момент t в состоянии (α1(t), α2(t)), если αi(t)– координата передней точки кластера i в момент t, т.е. αi(t) – расстояние, которое осталось пройти передней точки i-го кластера до достижения узла, i = 1, 2. Будем говорить, что кластер i в момент времени t накрывает узел i, если ci – li < αi(t) < ci, i = 1, 2, а также, что кластер i в момент t находится перед узлом, если αi(t) = 0, i = 1, 2. Допустимыми состояниями системы считаются только те состояния, при которых узел накрывается не более одним кластером. Если в некоторый момент кластер i находится перед узлом, а другой кластер накрывает узел, то осуществляется задержка кластера i, i = 1, 2 (рис. 2). Если оба кластера располагаются перед узлом, т.е. система находится в состоянии (0, 0), то имеет место конфликт, (рис. 3). В случае конфликта первым проходит через узел кластер, выбираемый в соответствии с правилом разрешения конфликта. Считаем, что действует левоприоритетное правило разрешение конфликта, при котором преимущество имеет кластер 1, который находится на контуре, расположенном слева от узла. Начальное состояние системы задается. Это состояние должно быть допустимым.

Рис. 1.

Двухконтурная система

Рис. 2.

Задержка кластера 2

Рис. 3.

Конфликт

2. Понятия спектрального цикла, скорости, свободного движения и самоорганизации. Докажем, что состояния системы начиная с некоторого момента времени будут периодически повторяться. Система будет с этого момента проходить замкнутую траекторию в пространстве состояний, которую назовем спектральным циклом. Обозначим через T период спектрального цикла, т.е. длительность интервала времени, через который состояние системы повторяется.

Пусть Si – суммарное расстояние, проходимое кластером i за спектральный цикл. Значение

${{{v}}_{i}} = \frac{{{{S}_{i}}}}{T}$
назовем средней скоростью кластера i, i = 1, 2.

Будем говорить, что система находится в момент времени t0 в состоянии свободного движения, если оба кластера перемещаются в этот момент и в будущем, т.е. в любой момент t ≥ t0. Свойство системы попадать из любого начального состояния в состояние свободного движения за некоторое время называем самоорганизацией.

3. Утверждение о решениях уравнений в целых числах, [24]. Рассмотрим линейное уравнение в целых числах с двумя переменными.

(3.1)
$ax + by + c = 0,$
где a и b – целые числа, не равные 0, c – целое число.

Целые решения системы (3.1) существуют в том и только в том случае, если c делится на наибольший общий делитель чисел a и b, [24]. Пусть x = x0, y = y0 – решение уравнения (3.1). Тогда все решения уравнения (3.1) вычисляются по формулам

$x = {{x}_{0}} - bt,\quad y = {{y}_{0}} + at,\quad t = 0, \pm 1, \pm 2.$

4. Условие самоорганизации. Обозначим через GCD(c1, c2) наибольший общий делитель (НОД) длин контуров c1, c2 в предположении, что отношение c1/c2 – рациональное число. Если это отношение длин – число иррациональное, будем считать их НОД равным нулю. Обозначим через LCM(c1, c2) наименьшее общее кратное (НОК) длин кластеров c1, c2.

Лемма 1. В момент времени t0 начинается или продолжается задержка кластера i, или имеет место конфликт одновременно подошедших к узлу кластеров в том и только в том случае, если выполняется условие

(4.1)
${{\alpha }_{i}}({{t}_{0}}) = 0,\quad {{\alpha }_{j}}({{t}_{0}}) \in ({{c}_{j}} - {{l}_{j}},{{c}_{j}}) \cup \{ 0\} ,\quad j \ne i.$

Доказательство. Если условие (4.1) выполняется, то в момент t0 кластер i находится перед узлом, а кластер  j накрывает узел или находится перед узлом и, таким образом, осуществляется задержка этого кластера или имеет место конфликт.

С другой стороны, если в момент t0 осуществляется задержка кластера i или имеет место конфликт, то этот кластер находится перед узлом, а кластер j проходит через узел и, следовательно, условие (4.1) выполняется. Лемма 1 доказана.

Следующая теорема дает необходимое и достаточное условие самоорганизации системы. В соответствии с этой теоремой оказывается, что только от значений c1, c2, l1, l2 зависит, попадет ли система в состояние свободного движения или нет, но не от начального расположения кластеров.

Теорема 1. Если отношение c1/c2 – рациональное число и выполняется условие

(4.2)
${{l}_{1}} + {{l}_{2}} \leqslant {\text{GCD}}({{c}_{1}},{{c}_{2}}),$
то из любого начального система попадает за некоторое время в состояние свободного движения, причем может иметь место не более чем одна задержка одного из кластеров, с момента окончания которой система находится в состоянии свободного движения и состояния системы повторяются с периодом T = LCM(c1, c2).

Если отношение c1/c2 – рациональное число и выполняется неравенство

(4.3)
${{l}_{1}} + {{l}_{2}} > {\text{GCD}}({{c}_{1}},{{c}_{2}})$
или это отношение – иррациональное число, то система не может находиться в состоянии свободного движения.

Доказательство. Предположим, что числа c1 и c2 рационально соизмеримы. Обозначим через ki значение ci/GCD(c1, c2), i = 1, 2. Предположим, что в момент времени t0 система находится в состоянии (α1(t0), α2(t0)). Задержка одного из кластеров произойдет при некотором t ≥ t0, если существуют неотрицательные целые числа x, y и действительное число b, удовлетворяющие условию

(4.4)
${{k}_{1}}x - {{k}_{2}}y = \frac{{{{\alpha }_{2}}({{t}_{0}}) - {{\alpha }_{1}}({{t}_{0}}) + b}}{{{\text{GCD}}({{c}_{1}},{{c}_{2}})}},\quad - {\kern 1pt} l < b < {{l}_{2}}.$

Тогда либо в момент t0 + c1x + α1(t0) начнется задержка кластера 1, либо в момент t0 + c2y + α2(t0) начнется задержка кластера 2. Действительно, если в интервале времени [t0, t0 + c1x + α1(t0)) задержек кластеров не происходит и b > 0, то в момент t1 = t0 + c1x + α1(t0) кластер 1 находится перед узлом и α2(t1) = c2 – b < c2 – l2, т.е. кластер 2 накрывает узел. Поэтому в момент t0 + k1x + α1(t0) начинается задержка клaстера 1. Если в интервале времени длительностью c1x + α1(t0) + |b| задержек не происходит и b < 0, то кластер 2 находится у узла и, таким образом, α1(t0) = c1 – |b| < c1 – l1 или α1(t0) = 0. Следовательно, в момент времени t0 + c1x + α1(t0) + |b| начинается задержка кластера 2. Числа k1, k2 – взаимно простые числа, так как GCD(c1, c2) – наибольший общий делитель чисел c1 и c2. Таким образом, в соответствии с теорией линейных уравнений в целых числах уравнение (4.4) имеет решение при условии, что правая часть (4.4) представляет собой целое число. Если выполняется (4.3), то существует значение b ∈ (–l1, l2), такое, что правая часть (4.4) является целым числом. Таким образом, неравенство (4.2) представляет собой необходимое условие самоорганизации при рациональном значении c2/c1, причем система не может попасть в состояние свободного движения ни из какого начального состояния.

Пусть значение c2/c1 – рациональное число и выполняется неравенство (4.3). Если в момент t0 заканчивается задержка кластера 1, то в момент t0 система находится в состоянии (0, c2 – l2), если в некоторый момент t1 > t0 начинается следующая задержка в движении одного из кластеров, то при некоторых неотрицательных целых числах x, y выполняется условие

(4.5)
${{k}_{1}}x - {{k}_{2}}y = \frac{{{{c}_{2}} - {{l}_{2}} + a}}{{{\text{GCD}}({{c}_{1}},{{c}_{2}})}},$
где a должно удовлетворять условию –l1 < a < l2. Так как GCD(c1, c2) – делитель c2 и выполняется (4.2), правая часть (4.5) не может быть целым числом при –l1 < a < l2.

Если в момент t0 заканчивается задержка кластера 2, то в момент времени t0 система находится в состоянии (c1 – l1, 0), если в момент t1 > t0 начинается новая задержка кластера, то при некоторых неотрицательных целых x и y выполняется условие

(4.6)
${{k}_{2}}y - {{k}_{1}}x = \frac{{{{c}_{1}} - {{l}_{1}} + a}}{{{\text{GCD}}({{c}_{1}},{{c}_{2}})}},$
где a удовлетворяет неравенству –l2 < a < l1. Так как GCD(c1, c2) – делитель c1 и выполняется (4.2), правая часть (4.6) не может быть целым числом при –l2 < a < l1.

Таким образом, выполнение неравенства (4.2) является достаточным условием самоорганизации при рационально соизмеримых c1 и c2.

Предположим, что значение

$\alpha = \frac{{{{c}_{2}}}}{{{{c}_{1}}}}$
является иррациональным числом.

Пусть начальное состояние системы задано. Рассмотрим последовательность значений отношения к c1 координаты передней точки кластера 1 в моменты пересечения узла передней точкой кластера 2 узла. Эта последовательность может рассматриваться как последовательность итераций поворотов

${{R}_{\alpha }}(x) = x + \alpha (x),\quad \bmod (1)$
единичной окружности на угол 2πα. Эти итерации, имеющие вид
$R_{\alpha }^{n}(x) = x + n\alpha ,\quad n = 1,2,...,$
образуют всюду плотное подмножество окружности (доказательство этого факта приводится в [25, с. 108–110]). Отсюда и из леммы 1 следует, что при значениях c1 и c2, не являющихся рационально соизмеримыми, система не может попасть в состояние самоорганизации. Теорема 1 доказана.

5. Леммы и вспомогательные параметры. Предположим, что условия самоорганизации не выполняются.

Пусть A – множество состояний системы, таких, что при нахождении системы в этих состояниях один из кластеров не движется; A1 – множество состояний, таких, что не перемещается кластер 1; A2 – множество состояний, таких, что не перемещается кластер 2. В соответствии с леммой 1 множество A1 содержит состояния (0, α2), c2 – l2 < α2 < c2, а множество A2, содержит состояния (α1, 0), c1 – l1 < α1 < c1 или α1 = 0. Имеем A = A1 ∪ A2.

Лемма 2. Если выполняется неравенство (4.3), то существует момент, когда система находится в состоянии (0, c2 – l2) или в состоянии (c1 – l1, 0).

Доказательство. Так как выполняется неравенство (4.3), система в соответствии с теоремой 1 попадает за некоторое время в множество состояний A из любого начального состояния и выходит из этого множества через состояние (0, c2 – l2) или (c1 – l1, 0).

Лемма 3. Пусть в момент времени t0 система находится в состоянии (0, c2 – l2), причем целые числа k11 ≥ 0, k12 ≥ 1 и действительное число d1(k11, k12) ∈ (0, l1 + l2) удовлетворяют условию

(5.1)
${{k}_{{11}}}{{c}_{1}} = {{k}_{{12}}}{{c}_{2}} - {{d}_{1}}({{k}_{{11}}},{{k}_{{12}}}).$

Тогда имеет место следующее.

1. Если d1(k11, k12) ∈ (0, l2), то в момент времени t0 + k11c1 начнется задержка кластера 1, если в промежутке времени [t0, t0 + k11c1) других задержек не произойдет. Длительность этой задержки равна d1(k11, k12).

2. Если d1(k11, k12) ∈ [l2, l1 + l2), то в момент времени t0 + k12c2 – l2 начнется задержка кластера 2, которая длится в течение l1 + l2 – d1(k11, k12) единиц времени.

Доказательство. Если выполняется условие d1(k11, k12) ∈ (0, l2) и в промежутке времени [t0, t0 + k11c1) задержек не происходит, то в момент времени [t0, t0 + k11c1) система оказывается в состоянии (0, c2 – l2 + d1(k11, k12)). В этом состоянии системы начинается задержка кластера 1, которая длится в течение времени d1(k11, k12) до попадания системы в состояние (0, c2 – l2).

Если выполняется условие d1(k11, k12) ∈ [l2, l1 + l2) и в промежутке времени [t0, t0 + k12c2 –l2) задержек нет, то в момент времени t0 + k12c2 – l2 система попадает в состояние (c1 – d1(k11, k12) + l2, 0). В этот момент начинается задержка кластера 2, которая длится до момента, когда система попадает в состояние (c1 – l1, 0), т.е. в течение l1 + l2 – d1(k11, k12) единиц времени. Лемма 3 доказана.

Лемма 4. Пусть в момент времени t0 система находится в состоянии (c1 – l1, 0), причем целые числа k21 ≥ 1, k22 ≥ 0 и действительное число d2(k21, k22) ∈ (0, l1 + l2) удовлетворяют условию

(5.2)
${{k}_{{22}}}{{c}_{2}} = {{k}_{{21}}}{{c}_{1}} - {{d}_{2}}({{k}_{{21}}},{{k}_{{22}}}).$

Тогда имеет место следующее.

1. Если d2(k21, k22) ∈ (0, l1], то в момент времени t0 + k22c2 начнется задержка кластера 2, если в промежутке времени [t0, t0 + k22c2) других задержек не произойдет. Длительность этой задержки равна d2(k21, k22).

2. Если d2(k21, k22) ∈ (l1, l1 + l2), то в момент времени t0 + k21c1 – l1 начнется задержка кластера 1, которая длится в течение l1 + l2 – d2(k21, k22) единиц времени.

Лемма 4 доказывается так же, как лемма 3.

Введем вспомогательные параметры ${{\hat {g}}_{1}}$, ${{\hat {g}}_{2}}$, b1, b2 и опишем способ вычисления этих параметров. Как будет доказано, при невыполнении условия самоорганизации существует единственный спектральный цикл и будут получены формулы, выражающие средние скорости кластеров через значения этих параметров.

Пусть значения c1, c2, l1, l2 заданы. Для каждого набора, состоящего из целых чисел k11 ≥ 0, k12 ≥ 1, и действительного числа d1(k11, k12) ∈ (0, l1 + l2), такого, что выполняется условие (5.1), определим величины g1(k11, k12) следующим образом:

${{g}_{1}}({{k}_{{11}}},{{k}_{{12}}}) = \left\{ \begin{gathered} {{k}_{{11}}}{{c}_{1}},\quad {\text{если}}\quad {{d}_{1}}({{k}_{{11}}},{{k}_{{12}}}) \in (0,{{l}_{2}}), \hfill \\ {{k}_{{12}}}{{c}_{2}} - {{l}_{2}},\quad {\text{если}}\quad {{d}_{1}}({{k}_{{11}}},{{k}_{{12}}}) \in [{{l}_{2}},{{l}_{1}} + {{l}_{2}}). \hfill \\ \end{gathered} \right.$

Пусть

${{\hat {g}}_{1}} = \min {{g}_{1}}({{k}_{{11}}},{{k}_{{12}}}),$
где минимум берется по всем наборам k11, k12, для которых определена функция g1(k11, k12). Этот минимум существует. Действительно, в соответствии с условием (4.3) наборы чисел k11, k12, d1(k11, k12), удовлетворяющие условию (5.1), существуют. Пусть задан один из таких наборов. Имеется не более чем конечное число наборов, для которых значение g1(k11, k12) меньше, чем при заданном наборе. Если таких наборов нет, то значение g1(k11, k12) достигается на заданном наборе. Если множество наборов с меньшими значениями g1(k11, k12) не пусто, то минимум достигается на одном из значений этого конечного множества. Пусть ${{\hat {d}}_{1}}$ = d1(k11, k12), где (k11, k12) – набор, на котором достигается минимум g1(k11, k12).

Определим значение b1 следующим образом. Пусть k11, k12 – набор, на котором достигается минимум g1(k11, k12). Тогда полагаем

${{b}_{1}} = \left\{ \begin{gathered} {{{\hat {d}}}_{1}},\quad {\text{если}}\quad {{{\hat {d}}}_{1}} \in (0,{{l}_{2}}], \hfill \\ {{l}_{1}} + {{l}_{2}} - {{{\hat {d}}}_{1}},\quad {\text{если}}\quad {{{\hat {d}}}_{1}} \in ({{l}_{2}},{{l}_{1}} + {{l}_{2}}), \hfill \\ \end{gathered} \right.$
b1 = ${{\hat {d}}_{1}}$, если ${{\hat {d}}_{1}}$ ∈ (0, l2), и b1 = l1 + l2 – ${{\hat {d}}_{1}}$, если ${{\hat {d}}_{1}}$ ∈ [l2, l1 + l2).

Значение ${{\hat {g}}_{1}}$ представляет собой длительность промежутка времени от момента нахождения системы в состоянии (0, c2 – l2) до начала первой после этого момента задержки одного из кластеров, а b1 – длительность этой задержки.

Аналогично для каждого набора, состоящего из целых чисел k21 ≥ 0, k22 ≥ 1, и действительного числа d2(k21, k22) ∈ (0, l1 + l2),, таких, что выполняется условие (5.2), определим величины g2(k21, k22), следующим образом:

${{g}_{2}}({{k}_{{21}}},{{k}_{{22}}}) = \left\{ \begin{gathered} {{k}_{{22}}}{{c}_{2}},\quad {\text{если}}\quad {{d}_{2}}({{k}_{{21}}},{{k}_{{22}}}) \in (0,{{l}_{1}}), \hfill \\ {{k}_{{21}}}{{c}_{1}} - {{l}_{1}},\quad {\text{если}}\quad {{d}_{2}}({{k}_{{21}}},{{k}_{{22}}}) \in [{{l}_{1}},{{l}_{1}} + {{l}_{2}}). \hfill \\ \end{gathered} \right.$
Пусть

${{\hat {g}}_{2}} = \min {{g}_{2}}({{k}_{{21}}},{{k}_{{22}}}).$

Минимум берется по всем наборам k21, k22, для которых функция g2(k21, k22) определена.

Пусть k21, k22 – набор, на котором достигается минимум g2(k21, k22). Полагаем ${{\hat {d}}_{2}}$ = d2(k21, k22);

${{b}_{2}} = \left\{ \begin{gathered} {{{\hat {d}}}_{2}},\quad {\text{если}}\quad {{{\hat {d}}}_{2}} \in (0,{{l}_{1}}], \hfill \\ {{l}_{1}} + {{l}_{2}} - {{{\hat {d}}}_{2}},\quad {\text{если}}\quad {{{\hat {d}}}_{2}} \in ({{l}_{1}},{{l}_{1}} + {{l}_{2}}). \hfill \\ \end{gathered} \right.$

Значение ${{\hat {g}}_{2}}$ представляет собой длительность промежутка времени от момента нахождения системы в состоянии (c1 – l1, 0) до начала первой после этого момента задержки одного из кластеров; b2 – длительность этой задержки.

6. Поведение системы при невыполнении условия самоорганизации. Докажем теоремы о поведении системы в случае, когда условие самоорганизации не выполняется, т.е. верно условие (4.3).

Теорема 2. Ни при каких значениях c1, c2, l1, l2 не могут одновременно выполняться условия ${{\hat {d}}_{1}}$ ∈ (0, l2), ${{\hat {d}}_{2}}$ ∈ (0, l1].

Доказательство. Предположим, что для k11 ≥ 0, k12 ≥ 1, k21 ≥ 1, k22 ≥ 0 верны условия (5.1), (5.2), причем ${{\hat {d}}_{1}}$ = d1(k11, k12) ∈ (0, l2), ${{\hat {d}}_{2}}$ = d2(k21, k22) ∈ (0, l1). Тогда ${{\hat {g}}_{1}}$ = g1(k11, k12) = k11c1, ${{\hat {g}}_{2}}$ = = g2(k21, k22) = k22c2.

Коэффициенты k11, k12 положительны, так как k11c1 = k12c2 – ${{\hat {d}}_{1}}$ > k12l2 – ${{\hat {d}}_{1}}$ > 0, k22c2 = k21c1 – ${{\hat {d}}_{2}}$ > > k21l1 – ${{\hat {d}}_{2}}$ ≥ 0. Из соотношений (5.1), (5.2) вытекает следующее:

(6.1)
$({{k}_{{11}}} - {{k}_{{21}}}){{c}_{1}} = ({{k}_{{12}}} - {{k}_{{22}}}){{c}_{2}} - d,\quad d = {{\hat {d}}_{1}} + {{\hat {d}}_{2}} \in (0,{{l}_{1}} + {{l}_{2}}).$

1. Предположим, что k11 – k21 > 0. Тогда k12 – k22 > 0.

Если d ∈ (0, l2), то за время (k11 – k21)c1 < k11c1 = ${{\hat {g}}_{1}}$ система из состояния (0, c2 – l2) система переходит в множество состояний A1, что противоречит тому, что система не попадает в множество A1 ранее через ${{\hat {g}}_{1}}$ единиц времени.

Если d ∈ [l2, l1 + l2), то имеем переход системы из состояния (0, c2 – l2) в множество состояний A2 за промежуток времени длительностью

$\begin{gathered} ({{k}_{{12}}} - {{k}_{{22}}}){{c}_{2}} - {{l}_{2}} = ({{k}_{{11}}} - {{k}_{{21}}}){{c}_{1}} + (d - {{l}_{2}}) = \\ = {{{\hat {g}}}_{1}} - {{k}_{{21}}}{{c}_{1}} + (d - {{l}_{2}}) \leqslant {{{\hat {g}}}_{1}} - {{c}_{1}} + (d - {{l}_{2}}) < {{{\hat {g}}}_{1}} + d - ({{l}_{1}} + {{l}_{2}}) < {{{\hat {g}}}_{1}}. \\ \end{gathered} $

2. Пусть k11 = k21. Из (6.1) следует, что k12 – k22 > 0. Тогда d = (k12 – k22)c2 > l2 и получаем переход из состояния (0, c2 – l2) в множество состояний A2. Неравенство (k12 – k22)c2 – l2 < ${{\hat {g}}_{1}}$ доказывается так же, как и при k11 – k21 > 0. Снова получаем противоречие с тем, что время перехода ${{\hat {g}}_{1}}$ из состояния (0, c2 – l2) в множество состояний A минимально.

3. Пусть k11 – k21 < 0. Из (6.1) следует, что

$({{k}_{{21}}} - {{k}_{{11}}}){{c}_{1}} + ({{k}_{{12}}} - {{k}_{{22}}}){{c}_{2}} = d < {{c}_{1}} + {{c}_{2}}.$

Учитывая, что k21 – k11 ≥ 1, получаем k12 – k22 < 1, а значит, k22 – k12 ≥ 0. Перепишем теперь (6.1) в виде

$({{k}_{{22}}} - {{k}_{{12}}}){{c}_{2}} = ({{k}_{{21}}} - {{k}_{{11}}}){{c}_{1}} - d,\quad d \in (0,{{l}_{1}} + {{l}_{2}})$
и повторим оценки времени возвращения в множество A, полученные при k11 – k21 > 0 и при k11 – – k21 = 0. Теорема 2 доказана.

Теорема 3. Пусть выполняются неравенство (4.3) и условия

${{\hat {d}}_{1}} \in (0,{{l}_{2}}),\quad {{\hat {d}}_{2}} \in ({{l}_{1}},{{l}_{1}} + {{l}_{2}}).$

Тогда имеется единственный спектральный цикл. Этому циклу принадлежит состояние (0, c2 – l2). Период спектрального цикла равен ${{\hat {g}}_{1}}$ + b1. Средние скорости кластеров равны

(6.2)
${{{v}}_{1}} = \frac{{{{{\hat {g}}}_{1}}}}{{{{{\hat {g}}}_{1}} + {{b}_{1}}}},\quad {{{v}}_{2}} = 1.$

Доказательство. Так как выполняется неравенство (4.3), система в некоторый момент времени попадает в множество состояний A. Если система попадает в множество состояний A2, то она выходит из этого множества через состояние (c1 – l1, 0). Так как ${{\hat {d}}_{2}}$ ∈ (l1, l1 + l2), в соответствии с леммой 4 система, попав снова в множество состояний A, окажется в множестве состояний A1 и выйдет из этого множества через состояние (0, c2 – l2). В соответствии с леммой 3 система будет возвращаться в множество состояний A1 через промежутки времени длительностью ${{\hat {g}}_{1}}$ и находиться в множестве A1 в течение времени b1. Теорема 3 доказана.

Пример 1. Пусть c1 = 3, l1 = 2, c2 = 5, l2 = 3. Наибольший общий делитель чисел c1 и c2 равен 1. Таким образом, верно неравенство (4.3). Следовательно, условие самоорганизации не выполняется.

Положим k11 = 0. Тогда не существует целого числа k12 ≥ 1 и неотрицательного числа ${{\hat {d}}_{1}}$ ∈ ∈ (0, l1 + l2), удовлетворяющего условию (5.1). При k11 = 1 условию (5.1) удовлетворяют значения k12 = 1, ${{\hat {d}}_{1}}$ = 2 ∈ (0, 3). Таким образом, ${{\hat {g}}_{1}}$ = 3, b1 = 2. Набор k21 = 0, k22 = 1, ${{\hat {d}}_{2}}$ = 3 ∈ (2, 5). Следовательно,

${{{v}}_{1}} = \frac{3}{5},\quad {{{v}}_{2}} = 1.$

Теорема 4. Пусть выполняются неравенство (4.3) и условия

${{\hat {d}}_{1}} \in [{{l}_{2}},{{l}_{1}} + {{l}_{2}}),\quad {{\hat {d}}_{2}} \in (0,{{l}_{1}}].$

Тогда имеется единственный спектральный цикл. Этому циклу принадлежит состояние (c1 – l1, 0). Период спектрального цикла равен ${{\hat {g}}_{2}}$ + b2. Средние скорости частиц равны

${{{v}}_{1}} = 1,\quad {{{v}}_{2}} = \frac{{{{{\hat {g}}}_{2}}}}{{{{{\hat {g}}}_{2}} + {{b}_{2}}}}.$

Пример 2. Пусть c1 = 10, l1 = 9, c2 = 2, l2 = 1. Наибольший общий делитель чисел c1 и c2 равен 2, и, таким образом, неравенство (4.3) верно. Значит, условие самоорганизации не выполняется.

Набор k11 = 0, k12 = 1, ${{\hat {d}}_{1}}$ = 2 ∈ [1, 10) удовлетворяет условию (5.1).

При k21 = 0 нельзя подобрать целое число k22 ≥ 1 и число ${{\hat {d}}_{2}}$ ∈ (0, l1 + l2), удовлетворяющие условию (5.2). Числа k22 = k21 = 1, ${{\hat {d}}_{2}}$ = 8 ∈ (0, 9] удовлетворяют условию (5.2).

Таким образом, ${{\hat {g}}_{2}}$ = 2, b2 = 8,

${{{v}}_{1}} = 1,\quad {{{v}}_{2}} = \frac{1}{5}.$

Теорема 5. Пусть выполняется неравенство (4.3) и условия ${{\hat {d}}_{1}}$ ∈ [l2, l1 + l2), ${{\hat {d}}_{2}}$ ∈ (l1, l1 + l2). Тогда существует единственный спектральный цикл. Этому циклу принадлежат состояния (0, c2 – l2) и (c1 –l1, 0). Период цикла равен ${{\hat {g}}_{1}}$ + ${{\hat {g}}_{2}}$ + b1 + b2. Скорости кластеров

${{{v}}_{1}} = \frac{{{{{\hat {g}}}_{1}} + {{{\hat {g}}}_{2}} + {{b}_{1}}}}{{{{{\hat {g}}}_{1}} + {{{\hat {g}}}_{2}} + {{b}_{1}} + {{b}_{2}}}},\quad {{{v}}_{2}} = \frac{{{{{\hat {g}}}_{1}} + {{{\hat {g}}}_{2}} + {{b}_{2}}}}{{{{{\hat {g}}}_{1}} + {{{\hat {g}}}_{2}} + {{b}_{1}} + {{b}_{2}}}}.$

Доказательство. Так как условие самоорганизации не выполняется, система не попадает в состояние свободного движения. Следовательно, в соответствии с леммой 1 система попадает в некоторый момент в множество состояний A. Если система попадает в состояние, принадлежащее множеству A1, то впоследствии она выходит из этого множества через состояние (0, c2 – l2). Через промежуток времени длительностью ${{\hat {g}}_{1}}$ после пребывания в этом состоянии система в соответствии с леммой 3 попадает в множество состояний A2 и задержка кластера 2 длится b1 единиц времени. Через ${{\hat {g}}_{2}}$ единиц времени после выхода из множества A2 через состояние (c1 – l1, 0) система попадает в состояние множества A1 и в соответствии с леммой 4 задержка кластера 1 длится в течение промежутка времени длительностью b2. Из изложенного следует утверждение теоремы 5.

Теорема 6. При фиксированных значениях c1, c2, l1, l2 средняя скорость частиц не зависит от начального состояния системы.

Доказательство. Если выполняется неравенство (4.2), то в соответствии с теоремой 1 из любого начального состояния система попадает в состояние свободного движения и, таким образом, скорость частиц равна 1. Если верно неравенство (4.3), то в соответствии с теоремами 3–5 имеется единственный спектральный цикл и, таким образом, средняя скорость частиц одинакова для всех начальных состояний. Теорема 6 доказана.

Заключение. Исследуется двухконтурная система с контурами различной длины. Длина контура i равна ci, i = 1, 2. На каждом контуре имеется движущийся отрезок (кластер) длиной li, i = 1, 2. Существует общая точка контуров, называемая узлом. Задержки в движении кластеров обусловлены ограничениям, заключающимся в том, что кластеры не могут проходить через узел одновременно. Кластер останавливается, если он подошел к узлу в момент, когда другой кластер проходит через узел. Если кластеры подошли к узлу одновременно, то первым через узел проходит кластер контура 1. Состояние системы в текущий момент времени определяется координатами передних точек кластеров.

Доказано следующее. При любом начальном состоянии системы, начиная с некоторого момента времени, состояния периодически повторяются. Если длины контуров c1 и c2 рационально соизмеримы и сумма длин кластеров l1 + l2 не превышает наибольший общий делитель длин контуров, то начиная с некоторого момента времени оба кластера перемещаются без задержек. Если длины контуров c1 и c2 рационально несоизмеримы или сумма длин кластеров больше их общего делителя, то при заданных значениях c1, c2, l1, l2 система проходит одну и ту же циклическую траекторию (спектральный цикл) в пространстве состояний системы, причем эта траектория не зависит от начального состояния системы. Найден алгоритм для вычисления средних скоростей движения частиц на спектральном цикле.

Список литературы

  1. Nagel K., Schreckenberg M.A. Cellular Automation Models for Freeway Traffic // J. Phys. I. France 1992. V. 2. № 12. P. 2221–2229.

  2. Belitsky V., Ferrari P.A. Invariant Measures and Convergence Properties for Cellular Automation 184 and Related Processes // J. Stat. Phys. 2005. V. 118. № 3/4. P. 589–523.

  3. Бланк М.Л. Точный анализ динамических систем, возникающих в моделях транспортных потоков // УМН. 2000. Т. 55. № 3 (333). С. 167–168.

  4. Gray L., Griffeath D. The Ergodic Theory of Traffic Jams // J. Stat. Phys. 2001. V. 105. № 3/4. P. 413–452.

  5. Kanai M., Nishinary K., Tokihiro T. Exact Solution and Asymptotic Behavior of the Asymmetric Behavior of the Asymmetric Simple Exclusion Process on a Ring. arXiv.0905.2795v1 [cond-mat-stat-mech] 18 May 2009.

  6. Blank M. Metric Properties of Discrete Time Exclusion Type Processes in Continuum // J. Stat. Phys. 2010. V. 140. № 1. P. 170–197.

  7. Biham O., Middleton A.A., Levine D. Self-organization and a Dynamic Transition in Traffic-flow Models // Phys. Rev. A. The American Physical Society. 1992. V. 46. № 10. R6124–R6127.

  8. D’Souza R.M. Coexisting Phases and Lattice Dependence of a Cellular Automaton Model for Traffic Flow // Phys. Rev. E. The American Society. 2005. V. 71. № 6. 066112.

  9. Angel O., Horloyd A.E., Martin J.B. The Jammed Phase of the Biham-Middelton-Levine Traffic Model for Traffic Flow Model // Electronic Communication in Probability. 2005. V. 10. P. 167–178.

  10. Austin T., Benjamini I. For what Number of Cars Must Self Organization Occur in the Biham-Middleton-Levine Traffic Model From Any Possible Starting Configuration? 2006. arXiv:math/0607759.

  11. Bugaev A.S., Buslaev A.P., Kozlov V.V., Yashina M.V. Distributed Problems of Monitoring and Modern Approaches to Traffic Modeling // 2011. 14th International IEEE Conference on Intelligent Transactions Systems (ITSC 2011). Washington, USA, 2011. P. 477–481.

  12. Kozlov V.V., Buslaev A.P., Tatashev A.G. On Energy of  Totally Connected Flow on Chainmails // CMMSE-2013. Cadis, Spain, 2013. V. 3. P. 861–873.

  13. Buslaev A.P., Fomina M.Yu., Tatashev A.G., Yashina M.V. On Discrete Flow Networks Model Spectra: Statement, Simulation, Hypotheses // J. Phys: Conf. Ser. 2018. V. 1053. № 012034.

  14. Kozlov V.V., Buslaev A.P., Tatashev A.G. Monotonic Walks on a Necklace and a Coloured Dynamic Vector // Int. J. Comput. Math. 2015. V. 92. № 9. P. 1910–1920.

  15. Buslaev A.P., Tatashev A.G., Yashina M.V. Flows Spectrum on Closed Trio of Contours with Uniform Load // Eur. J. Pure Appl. Math. 2018. V. 11. № 1. P. 260–283.

  16. Buslaev A.P., Tatashev A.G. Spectra of Local Cluster Flows on Open Chain of Contours with Uniform Load // Eur. J. Pure Appl. Math. 2018. V. 11. № 3. P. 628–644.

  17. Бугаев А.С., Буслаев А.П., Козлов В.В., Таташев А.Г., Яшина М.В. Обобщенная транспортно-логистическая модель как класс динамических систем // Математическое моделирование. 2015. Т. 27. № 12. С. 65–87.

  18. Buslaev A.P., Tatashev A.G., Yashina M.V. Qualitative Properties of Dynamical System on Toroidal Chainmail // AIP Conf. Proc. V. 1558. Rhodes, Greece, 2013. P. 1144–1147.

  19. Kozlov V.V., Buslaev A.P., Tatashev A.G., Yashina M.V. Dynamical systems on honeycombs // Traffic and Granular Flow’13. 2015. P. 441–452.

  20. Buslaev A.P., Tatashev A.G. Flows on Discrete Traffic Flower // J. Mathematics Research. 2017. V. 9. № 1. P. 98–108.

  21. Buslaev A.P., Tatashev A.G. Exact Results for Discrete Dynamical Systems on a Pair of Contours // Math. Appl. Sci. 2018. V. 41. № 17. P. 7283–7294.

  22. Tatashev A.G., Yashina M.V. Spectrum of Continuous Two-Contours system // ITM Web of  Conferences. 2019. V. 24. № 01014.

  23. Tatashev A.G., Yashina M.V. Behavior of Continuous Two-contours System // WSEAS Transactions on Mathemmatics. 2019. V. 18. № 5. P. 28–36.

  24. Бухштаб А.А. Теория чисел. М.: Просвещение, 1966. 384 с.

  25. Каток А.Б., Хассельблатт Б. Введение в теорию динамических систем с обзором последних достижений / Пер. с англ. М.: Изд-во МЦНМО, 2005. 466 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал