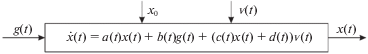Известия РАН. Теория и системы управления, 2020, № 3, стр. 14-29
МОДЕЛИРОВАНИЕ И АНАЛИЗ ВЫХОДНЫХ ПРОЦЕССОВ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ НА ОСНОВЕ ОРТОГОНАЛЬНЫХ РАЗЛОЖЕНИЙ СЛУЧАЙНЫХ ФУНКЦИЙ
К. А. Рыбаков *
МАИ (национальный исследовательский ун-т)
Москва, Россия
* E-mail: rkoffice@mail.ru
Поступила в редакцию 22.02.2019
После доработки 18.03.2019
Принята к публикации 27.01.2020
Аннотация
Рассматривается задача моделирования и анализа выходных процессов линейных непрерывных стохастических систем и предлагается метод ее решения, основанный на спектральной форме математического описания систем управления. Предложенный подход дает явное представление выходного сигнала системы в виде функционального ряда со случайными коэффициентами либо при приближенном решении в виде частичной суммы, что отличает этот метод от других подходов, когда результатом решения задачи являются детерминированные характеристики выходного сигнала: первые два момента или плотность распределения вероятностей. В качестве приложения рассмотрена задача моделирования ветровых воздействий с помощью формирующего фильтра Драйдена.
Введение. Представление функций с помощью рядов широко применяется для решения самых разных прикладных задач, в том числе задач теории управления. Один из подходов к решению задачи анализа выходных процессов линейных детерминированных систем, основанный на представлении функций рядами по произвольным полным ортонормированным системам функций (базисным системам), т.е. обобщенными рядами Фурье, породил спектральную форму математического описания систем управления и спектральный метод анализа и синтеза [1, 2]. Эта форма предполагает переход от операций с функциями к операциям с их спектральными характеристиками – упорядоченными наборами коэффициентов разложения по базисной системе, которые могут быть представлены в виде матриц-столбцов. Элементарным и типовым звеньям линейных систем, например усилительному, дифференцирующему, интегрирующему, апериодическому, колебательному и др., ставятся в соответствие матрицы, а преобразования сигналов сводятся к линейным преобразованиям спектральных характеристик. Спектральная форма математического описания использовалась и для нелинейных систем управления различных классов.
Хорошо известно, что для линейных непрерывных стохастических систем управления можно получить замкнутую систему обыкновенных дифференциальных уравнений для моментных характеристик ее вектора состояния. Если выходной сигнал имеет нормальное распределение (гауссовская случайная функция), то его можно описать первыми двумя моментами. Это свойство линейных систем учитывалось и для спектрального метода: он применялся для анализа линейных систем при случайных воздействиях в рамках корреляционной теории, т.е. задача анализа выходных процессов решалась как детерминированная, где входные и выходные сигналы задавались своими математическими ожиданиями и ковариационными функциями [1, 3, 4]. Анализ нелинейных систем при случайных воздействиях сводился к детерминированной задаче нахождения плотности распределения вероятностей вектора состояния [5].
В статье предлагается расширить спектральную форму математического описания для представления случайных функций, что позволит решать задачу анализа выходных процессов линейных стохастических систем, не переходя от случайных функций к их моментным характеристикам или плотностям распределения вероятностей. Предложенный метод дает возможность рассматривать линейные системы как с аддитивным, так и с мультипликативным шумом и находить явный вид выходного сигнала как случайной функции, т.е. не ограничиваться детерминированными характеристиками вектора состояния. Это особенно важно при моделировании систем управления.
Опишем простейший пример двумерной системы с мультипликативным шумом, модель которой задается двумя стохастическими дифференциальными уравнениями [6]:
Исследование этой случайной функции составляет отдельную проблему [7–11]. Она не является гауссовской, знание моментных характеристик (нулевое математическое ожидание и дисперсия t2/2) не позволяет моделировать ее траектории или сечения, в то время как такое моделирование, например, обеспечивает построение численных методов решения стохастических дифференциальных уравнений с порядком сильной или среднеквадратической сходимости выше, чем у стохастического метода Эйлера.
В общем нелинейном случае для решения задачи моделирования и анализа выходных процессов основной метод, используемый на практике, заключается в применении разностных схем [10–12]. В результате процедура моделирования состоит в том, что строится дискретная аппроксимация выходного сигнала шаг за шагом по времени, т.е. с применением рекуррентных формул, и переход от текущего узла дискретизации к следующему связан с добавлением случайной величины, а именно приращения случайной функции. Для моделирования стохастического интеграла, приведенного выше, в [7] был предложен метод, основанный на разложении процесса броуновского моста по собственным функциям его ковариационного оператора, причем этот метод оказался эффективнее дополнительной дискретизации по времени (в пределах выбранного шага дискретизации). Далее в [8, 9] были предложены разложения в виде обобщенных рядов Фурье по различным базисным системам, причем в [8] – сразу для стохастических интегралов, которые связаны с более сложными нестационарными системами, размерность которых больше двух. Численные методы, описанные в [7, 8, 10, 11], используют как дискретизацию по времени, так и представление случайных функций обобщенными рядами Фурье между узлами дискретизации.
В результате применения разностных схем накапливается ошибка, характерная для численных методов, и приближенное решение определено только в узлах дискретизации. Предлагаемый в статье подход позволяет отказаться от дискретизации по времени, получить непрерывную аппроксимацию выходного сигнала сразу на всем заданном промежутке времени для линейных систем с аддитивным и мультипликативным шумом и найти явный вид выходного сигнала как случайной функции. Он обеспечивает моделирование линейных систем, причем свойства траекторий выходного сигнала могут варьироваться с помощью подбора базисной системы, и нахождение в явном виде выходного сигнала системы как случайной функции. В дальнейшем такой подход может быть применен для решения задач оптимизации линейных систем и оценивания сигналов (фильтрации, интерполяции и экстраполяции). В основе метода кроме спектральной формы математического описания систем управления лежат известные факты о представлении случайных функций с помощью функциональных рядов со случайными коэффициентами, обсуждаются связи с разложением Карунена–Лоэва [13] и каноническим представлением случайных функций [14, 15].
Статья помимо введения содержит два раздела и Приложение. В разд. 1 рассматривается задача моделирования и анализа выходных процессов линейных одномерных непрерывных стохастических систем и предлагается спектральный метод для ее решения. В разд. 2 результаты разд. 1 обобщаются для решения задачи моделирования и анализа выходных процессов линейных многомерных непрерывных стохастических систем. Приложение содержит теоретические основы предлагаемого метода.
Апробация метода моделирования и анализа выходных процессов проведена на примере формирующего фильтра Драйдена и его двумерной модификации, которые позволяют моделировать продольные ветровые воздействия на летательный аппарат в неспокойной атмосфере [16–19].
1. Моделирование и анализ выходных процессов одномерных линейных стохастических систем. 1.1. Постановка задачи. Рассмотрим одномерные линейные системы, которые описываются стохастическим дифференциальным уравнением (структурная схема системы приведена на рис. 1):
(1.1)
$\dot {x}(t) = a(t)x(t) + b(t)g(t) + \left( {c(t)x(t) + d(t)} \right){v}(t),\quad x(0) = {{x}_{0}},$Уравнение модели системы записано в форме Ланжевена, под решением этого уравнения будем понимать случайный процесс x(t), удовлетворяющий интегральному соотношению
Задача анализа выходных процессов состоит в нахождении выходного сигнала x(t) как случайной функции по заданной модели (1.1) и входному сигналу g(t).
1.2. Спектральный метод моделирования и анализа выходных процессов. Воспользуемся для решения задачи анализа выходных процессов спектральным методом (все необходимые сведения приведены в Приложении), представляя все входящие в уравнение (1.1) функции спектральными характеристиками (см. Приложение, разд. А). Для этого нужно применить спектральное преобразование $\mathbb{S}$ (см. Приложение, формула (П.4)) к левой и правой частям (1.1):
(1.2)
$\begin{gathered} \mathbb{S}\left[ {\dot {x}(t){{{\text{|}}}_{{x(0) = {{x}_{0}}}}}} \right] = \mathbb{S}\left[ {a(t)x(t) + b(t)g(t) + \left( {c(t)x(t) + d(t)} \right){v}(t)} \right] = \\ = \;\mathbb{S}\left[ {a(t)x(t)} \right] + \mathbb{S}\left[ {b(t)g(t)} \right] + \mathbb{S}\left[ {\left( {c(t)x(t) + d(t)} \right){v}(t)} \right]. \\ \end{gathered} $Подробно записывать все шаги представляется излишним, поскольку в целом они не отличаются от применения спектрального метода к анализу выходных процессов линейных детерминированных систем [1, 3, 4]. Однако нужно ввести обозначения для спектральных характеристик относительно выбранной базисной системы $\{ q(i,t)\} _{{i = 0}}^{\infty }$ на отрезке $\mathbb{T}$ (см. Приложение, разд. А и Д, формулы (П.2), (П.6), (П.9)): $G$, $X$ и $D$ – спектральные характеристики входного, выходного сигналов и функции $d(t)$ соответственно; $\mathcal{V}$ – спектральная характеристика стандартного гауссовского белого шума ${v}(t)$; A, B и C – спектральные характеристики операторов умножения на функции a(t), b(t) и c(t) соответственно; $\mathcal{P}$ – спектральная характеристика оператора дифференцирования; $\Delta $ – спектральная характеристика дельта-функции $\delta (t)$, т.е. матрица-столбец значений функций базисной системы $\{ q(i,t)\} _{{i = 0}}^{\infty }$ в точке t = 0. Отличие от детерминированного случая состоит в том, что одна из спектральных характеристик, а именно $\mathcal{V}$, образована случайными величинами, начальное значение x0 также случайно. Кроме того, в уравнении модели имеется произведение $x(t){v}(t)$ при $c(t) \ne 0$.
Если условие $c(t) \ne 0$ выполнено, то требуется определить спектральную характеристику множительного звена или трехмерную нестационарную передаточную функцию множительного звена – бесконечную пространственную матрицу $V$ с элементами
С помощью этой матрицы можно преобразовать спектральные характеристики функций в спектральные характеристики операторов умножения на эти функции [1, 5]:
В результате из соотношения (1.2) получаем
где $P = \mathcal{P} + \Delta {{\Delta }^{{\text{т}}}}$ – спектральная характеристика оператора дифференцирования с учетом начального условия [1, 3, 4]. Действительно,Таким образом,
и(1.4)
$X = {{\left( {P - A - (V\mathcal{V})C} \right)}^{{ - 1}}}\left( {{{x}_{0}}\Delta + BG + (V\mathcal{V})D} \right).$При $c(t) = 0$ целесообразно определить спектральную характеристику оператора умножения на функцию d(t), обозначив ее $\tilde {D}$, а спектральную характеристику D, определенную ранее, не использовать. Тогда можно обойтись без пространственной матрицы V, а уравнение (1.3) примет вид
его решение представляется следующим образом:Применяя обратное спектральное преобразование, находим решение задачи анализа выходных процессов, согласно формуле обращения (см. Приложение, разд. А, формула (П.2)), в виде ряда
коэффициенты Xi которого зависят от элементов спектральной характеристики $\mathcal{V}$ стандартного гауссовского белого шума ${v}(t)$, т.е. от счетного числа независимых случайных величин, имеющих стандартное нормальное распределение, а также от случайной величины x0.Выполнение операций с бесконечными матрицами затрудняет нахождение выходного сигнала точно, особенно это касается умножения и обращения бесконечных матриц. Поэтому перейдем к приближенному решению, используя тот же подход, что и при анализе выходных процессов линейных детерминированных систем, а именно усечение всех спектральных характеристик до некоторого выбранного порядка L [1, 3, 5]. Это означает, что все матрицы, входящие в соотношение (1.4), являются конечными размера L по каждому измерению, т.е. L для матриц-столбцов, L × L для квадратных и L × L × L для пространственных матриц. В этом случае будет получено приближенное решение задачи анализа выходных процессов в виде частичной суммы:
где коэффициенты Xi зависят от элементов усеченной спектральной характеристики $\mathcal{V}$ стандартного гауссовского белого шума ${v}(t)$, т.е. от конечного числа L независимых случайных величин, имеющих стандартное нормальное распределение, а также от случайной величины x0.В качестве базисной системы $\{ q(i,t)\} _{{i = 0}}^{\infty }$ могут использоваться различные полные ортонормированные системы функций, успешно применяемые при решении задач в спектральной форме математического описания, например, полиномы Лежандра, косинусоиды, функции Уолша и функции Хаара [1, 3]. Для всех перечисленных базисных систем разработано алгоритмическое обеспечение (элементарные и специализированные алгоритмы динамического расчета), включающее алгоритмы расчета спектральных характеристик типовых входных воздействий, спектральных характеристик операторов умножения на типовые функции, операторов дифференцирования и интегрирования, а также спектральную характеристику множительного звена [1, 3, 5]. Все эти алгоритмы реализованы в виде пакетов программ для систем компьютерной математики и отдельных приложений [21].
Приведем методику решения задачи анализа выходных процессов одномерных линейных стохастических систем.
1. Выбрать отрезок $\mathbb{T} = [0,T]$, на котором нужно найти решение задачи анализа выходных процессов, а также соответствующую базисную систему $\{ q(i,t)\} _{{i = 0}}^{\infty }$.
2. Найти спектральную характеристику G входного сигнала $g(t)$; спектральную характеристику $\mathcal{V}$ стандартного гауссовского белого шума ${v}(t)$; спектральные характеристики $A$, $B$ и $C$ операторов умножения на функции $a(t)$, $b(t)$ и $c(t)$ соответственно; спектральную характеристику $\mathcal{P}$ оператора дифференцирования; матрицу-столбец $\Delta $ значений функций базисной системы $\{ q(i,t)\} _{{i = 0}}^{\infty }$ в точке t = 0. Дополнительно определить при $c(t) \ne 0$ спектральную характеристику D функции $d(t)$, спектральную характеристику V множительного звена, а при $c(t) = 0$ – спектральную характеристику $\tilde {D}$ оператора умножения на функцию $d(t)$.
3. При $c(t) \ne 0$ записать уравнение (1.3) для спектральной характеристики X выходного сигнала $x(t)$ и найти его решение (1.4). При $c(t) = 0$ записать уравнение (1.5) для спектральной характеристики X и найти его решение (1.6).
4. Применить обратное спектральное преобразование: найти выходной сигнал $x(t)$ по спектральной характеристике X, используя формулу обращения (1.7).
При приближенном решении задачи анализа выходных процессов дополнительно задается порядок усечения спектральных характеристик $L$ и на шаге 4 методики применяется формула (1.8) вместо (1.7). Для получения выборочной траектории выходного сигнала достаточно воспользоваться методикой для реализаций спектральной характеристики $\mathcal{V}$ и случайной величины x0.
Получив явный вид выходного сигнала как случайной функции, можно оценить моментные характеристики любого порядка и плотность распределения вероятностей состояния системы, описываемой уравнением (1.1), т.е. решить задачу статистического анализа стохастической системы. Использовать этот прием для моментных характеристик вряд ли оправдано, поскольку для линейных непрерывных стохастических систем управления можно записать замкнутую систему обыкновенных дифференциальных уравнений для моментных характеристик, ее решение с вычислительной точки зрения значительно проще. Для плотности распределения вероятностей $p(t,x)$ состояния, если она не является гауссовской, можно предложить следующую ядерную оценку [22]:
(1.9)
$p(t,x) \approx \frac{1}{{M{{h}_{x}}}}\sum\limits_{j = 1}^M {K\left( {\frac{{x - {{x}^{j}}(t)}}{{{{h}_{x}}}}} \right)} ,$Пример 1. Рассмотрим формирующий фильтр Драйдена для моделирования продольного турбулентного ветра [19]. Он задается линейным стохастическим дифференциальным уравнением
(1.10)
$\dot {x}(t) = - \mu x(t) + \sigma {v}(t),\quad x(0) = {{x}_{0}},\quad \mu = \frac{{{{V}_{t}}}}{{{{L}_{t}}}},\quad \sigma = \sqrt {2\mu } {{\sigma }_{0}},$На основе формулы (1.6) запишем выражение для спектральной характеристики X процесса $x(t)$, удовлетворяющей уравнению (1.5):
пользуясь свойством спектрального преобразования операторов умножения, а именно равенством спектральной характеристики оператора умножения на константу произведению этой константы на единичную матрицу E, т.е. $A = - \mu E$, $B = O$, $C = O$, $\tilde {D} = \sigma E$ (O – нулевая матрица).В выражении (1.11) $P = \mathcal{P} + \Delta {{\Delta }^{{\text{т}}}}$ – спектральная характеристика оператора дифференцирования с учетом начального условия; $\Delta $ – матрица-столбец значений функций базисной системы $\{ q(i,t)\} _{{i = 0}}^{\infty }$ в точке $t = 0$; $\mathcal{V}$ – спектральная характеристика стандартного гауссовского белого шума ${v}(t)$. Тогда точное решение уравнения (1.10) задается формулой (1.7), а приближенное решение – формулой (1.8) с учетом усечения всех спектральных характеристик до некоторого выбранного порядка L.
Далее приведем результаты моделирования на основе соотношений (1.8) и (1.11) для базисной системы косинусоид:
Для выбранной базисной системы элементы спектральной характеристики P оператора дифференцирования с учетом начального условия задаются в виде [1, 3, 4]
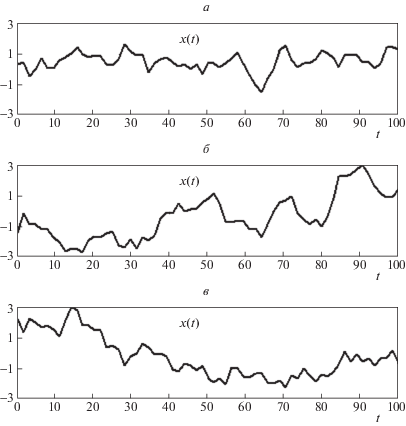
Пример трех траекторий выходного сигнала (скорости ветра) приведен на рис. 2, а–в. Максимальное отклонение выборочной дисперсии выходного сигнала на рассматриваемом промежутке времени, рассчитанной по ансамблю 106 траекторий, от точного значения $\sigma _{0}^{2} = 2.25$ составляет 2.07%, при увеличении порядка усечения до $L = 128$ и 256 максимальные отклонения составляют 1.10 и 0.69% соответственно, т.е. увеличение порядка усечения в 2 раза примерно в 2 раза сокращает погрешность расчетов для дисперсии. Данные приведены для узловых точек, которые получены следующим образом: отрезок [0, T] был разбит на 20 отрезков одинаковой длины и взяты центры этих отрезков. Для базисной системы косинусоид выборочная дисперсия меньше точного значения в узловых точках. Здесь нужно принять во внимание, что помимо методической погрешности спектрального метода, связанной с усечением спектральных характеристик, есть еще и статистическая погрешность, обусловленная моделированием конечного числа траекторий.
2. Моделирование и анализ выходных процессов многомерных линейных стохастических систем. 2.1. Постановка задачи. Рассмотрим систему стохастических дифференциальных уравнений, записанную в матричной форме:
(2.1)
$\dot {x}(t) = a(t)x(t) + b(t)g(t) + \sum\limits_{k = 1}^s {({{c}^{k}}(t)x(t) + {{d}^{k}}(t)){{{v}}_{k}}(t)} ,\quad x(0) = {{x}_{0}},$Решение этой системы следует понимать как случайный процесс x(t), удовлетворяющий интегральному соотношению (см. одномерный случай), в котором стохастический интеграл – интеграл Стратоновича. Решение такой системы существует, единственно и удовлетворяет условию ${\text{E}}{{\left| {x(t)} \right|}^{2}} < \infty $ [20].
Задача анализа выходных процессов, как и для одномерного случая, состоит в нахождении сигнала x(t) как случайной вектор-функции по заданной модели (2.1) и входному сигналу g(t).
2.2. Спектральный метод моделирования и анализа выходных процессов. Перепишем систему (2.1) в координатной форме:
(2.2)
$\begin{gathered} {{{\dot {x}}}_{l}}(t) = \sum\limits_{m = 1}^n {{{a}_{{lm}}}(t){{x}_{m}}(t)} + \sum\limits_{r = 1}^q {{{b}_{{lr}}}(t){{g}_{r}}(t)} + \\ + \;\sum\limits_{k = 1}^s {\left( {\sum\limits_{m = 1}^n {c_{{lm}}^{k}(t){{x}_{m}}(t)} + d_{l}^{k}(t)} \right){{{v}}_{k}}(t)} ,\quad {{x}_{l}}(0) = {{x}_{{l0}}},\quad l = \overline {1,n} , \\ \end{gathered} $Применим спектральное преобразование $\mathbb{S}$ (см. Приложение, формула (П.4)) к левой и правой частям (2.2):
(2.3)
$\begin{gathered} \mathbb{S}[{{\left. {{{{\dot {x}}}_{l}}(t)} \right|}_{{{{x}_{l}}(0) = {{x}_{{l0}}}}}}] = \mathbb{S}\left[ {\sum\limits_{m = 1}^n {{{a}_{{lm}}}(t){{x}_{m}}(t)} + \sum\limits_{r = 1}^q {{{b}_{{lr}}}(t){{g}_{r}}(t)} + } \right.{\mkern 1mu} \\ + \;\left. {\sum\limits_{k = 1}^s {\left( {\sum\limits_{m = 1}^n {c_{{lm}}^{k}(t){{x}_{m}}(t)} + d_{l}^{k}(t)} \right){{{v}}_{k}}(t)} } \right] = \sum\limits_{m = 1}^n {\mathbb{S}\left[ {{{a}_{{lm}}}(t){{x}_{m}}(t)} \right]} + \sum\limits_{r = 1}^q {\mathbb{S}\left[ {{{b}_{{lr}}}(t){{g}_{r}}(t)} \right]} + \\ + \;\sum\limits_{k = 1}^s \mathbb{S} \left[ {\left( {\sum\limits_{m = 1}^n {c_{{lm}}^{k}(t){{x}_{m}}(t)} + d_{l}^{k}(t)} \right){{{v}}_{k}}(t)} \right], \\ \end{gathered} $(2.4)
$P{{X}_{l}} - {{x}_{{l0}}}\Delta = \sum\limits_{m = 1}^n {{{A}_{{lm}}}{{X}_{m}}} + \sum\limits_{r = 1}^q {{{B}_{{lr}}}{{G}_{r}}} + \sum\limits_{k = 1}^s {(V{{\mathcal{V}}_{k}})} \left( {{\mkern 1mu} \sum\limits_{m = 1}^n {C_{{lm}}^{k}{{X}_{m}}} + D_{l}^{k}} \right),$Как и в одномерном случае, при $c(t) = 0$ полученные соотношения можно упростить, определив $\tilde {D}_{l}^{k}$ как спектральные характеристики операторов умножения на функции $d_{l}^{k}(t)$ вместо спектральных характеристик $D_{l}^{k}$. Тогда систему уравнений (2.4) можно записать в виде
(2.5)
$P{{X}_{l}} - {{x}_{{l0}}}\Delta = \sum\limits_{m = 1}^n {{{A}_{{lm}}}{{X}_{m}}} + \sum\limits_{r = 1}^q {{{B}_{{lr}}}{{G}_{r}}} + \sum\limits_{k = 1}^s {\tilde {D}_{l}^{k}} {{\mathcal{V}}_{k}}.$Решение задачи анализа выходных процессов в многомерном случае может быть получено в результате нахождения спектральных характеристик Xl, удовлетворяющих линейной системе (2.4) или (2.5), и применения обратного спектрального преобразования, или формулы обращения (см. Приложение, разд. А, формула (П.2)):
(2.6)
${{x}_{l}}(t) = {{\mathbb{S}}^{{ - 1}}}[{{X}_{l}}] = \sum\limits_{i = 0}^\infty {X_{i}^{l}q(i,t)} ,\quad l = \overline {1,n} ,$Приближенное решение задачи анализа выходных процессов выражается в виде частичных сумм:
(2.7)
${{x}_{l}}(t) \approx \sum\limits_{i = 0}^{L - 1} {X_{i}^{l}q(i,t)} ,\quad l = \overline {1,n} ,$Опишем подробнее частный случай: n = 2 (размерность $x(t)$), $q = s = 1$ (входной сигнал $g(t)$ и белый шум ${v}(t)$ скалярные), т.е. системы уравнений (2.2) и (2.4) имеют вид
Решение последней системы матричных уравнений несложно получить методом исключения неизвестных:
(2.8)
${{X}_{l}} = {{({{Z}_{{ll}}} - {{Z}_{{lj}}}Z_{{jj}}^{{ - 1}}{{Z}_{{jl}}})}^{{ - 1}}}({{Q}_{l}} - {{Z}_{{lj}}}Z_{{jj}}^{{ - 1}}{{Q}_{j}}),$Если размерность $n$ больше двух и матричные функции a(t) и ${{c}^{k}}(t)$ имеют специальный вид, например это треугольные или трехдиагональные матрицы, то решение систем (2.2) и (2.4) также несложно получить методом исключения неизвестных. В случае матричных функций a(t) и ${{c}^{k}}(t)$ общего вида при использовании спектрального метода можно применить специальные операции для матриц: агрегирование и декомпозицию [5].
Приведем методику решения задачи анализа выходных процессов многомерных линейных стохастических систем.
1. Выбрать отрезок $\mathbb{T} = [0,T]$, на котором нужно найти решение задачи анализа выходных процессов, а также соответствующую базисную систему $\{ q(i,t)\} _{{i = 0}}^{\infty }$.
2. Найти спектральные характеристики ${{G}_{r}}$ координат входного сигнала ${{g}_{r}}(t)$; спектральные характеристики ${{\mathcal{V}}_{k}}$ стандартных гауссовских белых шумов ${{{v}}_{k}}(t)$; спектральные характеристики ${{A}_{{lm}}}$, ${{B}_{{lr}}}$ и $C_{{lm}}^{k}$ операторов умножения на функции ${{a}_{{lm}}}(t)$, ${{b}_{{lr}}}(t)$ и $c_{{lm}}^{k}(t)$ соответственно; спектральную характеристику $\mathcal{P}$ оператора дифференцирования; матрицу-столбец $\Delta $ значений функций базисной системы $\{ q(i,t)\} _{{i = 0}}^{\infty }$ в точке t = 0. Дополнительно определить при $c(t) \ne 0$ спектральные характеристики $D_{l}^{k}$ функций $d_{l}^{k}(t)$, спектральную характеристику V множительного звена, а при $c(t)$ = 0 – спектральные характеристики $\tilde {D}_{l}^{k}$ операторов умножения на функции $d_{l}^{k}(t)$.
3. При $c(t) \ne 0$ записать систему уравнений (2.4) для спектральных характеристик Xl координат выходного сигнала ${{x}_{l}}(t)$ и решить эту систему (при n = 2 воспользоваться формулой (2.8)). При $c(t) = 0$ записать систему уравнений (2.5) для спектральных характеристик Xl и найти решение этой системы.
4. Применить обратное спектральное преобразование: найти координаты выходного сигнала ${{x}_{l}}(t)$ по спектральным характеристикам Xl, используя формулу обращения (2.6).
При приближенном решении задачи анализа выходных процессов дополнительно задается порядок усечения спектральных характеристик L и на шаге 4 методики применяется формула (2.7) вместо (2.6).
Здесь, как и для одномерного случая, используя явный вид выходного сигнала как случайной функции, можно оценить моментные характеристики любого порядка и плотность распределения вероятностей вектора состояния системы, описываемой уравнением (2.1). Ядерная оценка плотности распределения вероятностей $p(t,x)$ вектора состояния имеет вид, аналогичный (1.9):
Пример 2. Рассмотрим двумерный формирующий фильтр Драйдена [19]. Он задается системой линейных стохастических дифференциальных уравнений:
(2.9)
$\begin{array}{*{20}{c}} {{{{\dot {x}}}_{1}}(t) = {{x}_{2}}(t),\quad {{x}_{1}}(0) = {{x}_{{10}}},} \\ {{{{\dot {x}}}_{2}}(t) = - \lambda \mu {{x}_{1}}(t) - (\lambda + \mu ){{x}_{2}}(t) + \sigma {\text{*}}{v}(t),\quad {{x}_{2}}(0) = {{x}_{{20}}},} \end{array}$Воспользуемся соотношением (2.8), в котором
Решение системы матричных уравнений можно представить в виде
(2.10)
$\begin{array}{*{20}{c}} {{{X}_{1}} = {{{({{P}^{2}} + (\lambda + \mu )P + \lambda \mu E)}}^{{ - 1}}}\left[ {{{x}_{{10}}}(P + (\lambda + \mu )E)\Delta + {{x}_{{20}}}\Delta + \sigma {\text{*}}\mathcal{V}} \right],} \\ {{{X}_{2}} = P{{X}_{1}} - {{x}_{{10}}}\Delta ,} \end{array}$Далее приведем результаты моделирования на основе соотношений (2.7) и (2.10) для той же базисной системы косинусоид и тех же числовых параметров. Дисперсии координат x1(t) и x2(t), которые соответствуют установившемуся режиму, равны $\sigma _{0}^{2}$ и $\lambda \mu \sigma _{0}^{2}$ соответственно, поэтому начальные значения x10 и x20 зададим как случайные величины, имеющие нормальное распределение с нулевым математическим ожиданием и дисперсиями для установившегося режима. Другими словами, дисперсии координат ${{x}_{1}}(t)$ и ${{x}_{2}}(t)$ не зависят от времени для рассматриваемой модели, а их математические ожидания нулевые. Порядок усечения не меняется: L = 64.
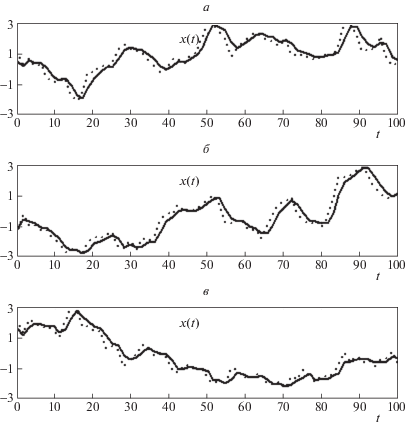
Пример трех траекторий выходного сигнала (скорости ветра) приведен на рис. 3, а–в, дополнительно на этом рисунке пунктиром показаны траектории из примера 1 для сравнения. Максимальное отклонение выборочной дисперсии выходного сигнала на рассматриваемом промежутке времени, рассчитанной по ансамблю 106 траекторий, от точного значения $\sigma _{0}^{2} = 2.25$ составляет 0.82%, при увеличении порядка усечения до L = 128 и 256 максимальные отклонения составляют 0.35 и 0.22% соответственно, т.е. наблюдается такая же зависимость погрешности расчетов для дисперсии от порядка усечения спектральных характеристик. Знак отклонения выборочной дисперсии от точного значения для базисной системы косинусоид в этом примере зависит от узловых точек (узловые точки формируются так же, как и в примере 1). Меньшая погрешность по сравнению с результатами примера 1 объясняется сглаженностью траектории выходного сигнала.
Рис. 3.
Пример трех траекторий выходного сигнала для двумерного формирующего фильтра Драйдена и их сравнение с рис. 2
Заключение. Предложен спектральный метод решения задачи моделирования и анализа выходных процессов линейных непрерывных стохастических систем. При его применении выходной сигнал системы представляется в виде функционального ряда или частичной суммы со случайными коэффициентами, которые выражаются через независимые случайные величины, имеющие стандартное нормальное распределение, а также через начальные данные, т.е. получается непрерывная аппроксимация выходного сигнала на всем заданном промежутке времени. В дальнейшем этот метод можно развивать в нескольких направлениях. Первое из них – применение спектральной формы математического описания для общего пуассоновского процесса и решение задачи моделирования и анализа выходных процессов линейных стохастических систем с пуассоновской составляющей [24], второе – оптимизация линейных стохастических систем, третье – решение задачи оценивания сигналов (фильтрации, интерполяции и экстраполяции) в линейных стохастических системах по косвенным измерениям, предполагающее совместное применение спектральной формы математического описания и фильтров частиц [25].
Список литературы
Солодовников В.В., Семенов В.В. Спектральная теория нестационарных систем управления. М.: Наука, 1974.
Семенов В.В. Формы математического описания линейных систем. М.: МАИ, 1980.
Рыбин В.В. Моделирование нестационарных непрерывно-дискретных систем управления спектральным методом в системах компьютерной математики. М.: Изд-во МАИ, 2011.
Пантелеев А.В., Бортаковский А.С. Теория управления в примерах и задачах. М.: Инфра-М, 2016.
Пантелеев А.В., Рыбаков К.А., Сотскова И.Л. Спектральный метод анализа нелинейных стохастических систем управления. М.: Вузовская книга, 2015.
Clark J.M.C., Cameron R.J. The Maximum Rate of Convergence of Discrete Approximations for Stochastic Differential Equations // Stochastic Differential Systems. Filtering and Control (ed. by Grigelionis B.). Springer-Verlag, 1980. P. 162–171.
Мильштейн Г.Н. Численное интегрирование стохастических дифференциальных уравнений. Свердловск: Изд-во Уральского ун-та, 1988.
Кузнецов Д.Ф. Метод разложения и аппроксимации повторных стохастических интегралов Стратоновича, основанный на кратных рядах Фурье по полным ортонормированным системам функций // Дифференциальные уравнения и процессы управления. 1997. № 1. С. 18–77.
Пригарин С.М., Белов С.М. Об одном применении разложений винеровского процесса в ряды // Препринт 1107. Новосибирск: ИВМиМГ СО РАН, 1998.
Milstein G.N., Tretyakov M.V. Stochastic Numerics for Mathematical Physics. Springer-Verlag, 2004.
Кузнецов Д.Ф. Стохастические дифференциальные уравнения: теория и практика численного решения. С программами в среде MATLAB // Дифференциальные уравнения и процессы управления. 2018. № 4. С. А.1–А.1073.
Graham C., Talay D. Stochastic Simulation and Monte Carlo Methods. Berlin: Springer-Verlag, 2013.
Фукунага К. Введение в статистическую теорию распознавания образов. М.: Наука, 1979.
Лапин С.В., Егупов Н.Д. Теория матричных операторов и ее приложение к задачам автоматического управления. М.: Изд-во МГТУ им. Н.Э. Баумана, 1997.
Синицын И.Н. Канонические представления случайных функций и их применение в задачах компьютерной поддержки научных исследований. М.: Торус Пресс, 2009.
Доброленский Ю.П. Динамика полета в неспокойной атмосфере. М.: Машиностроение, 1969.
Парышева Г.В., Ярошевский В.А. Проблема формирования расчетных ветровых возмущений для задач динамики полета // Уч. зап. ЦАГИ. 2001. Т. 32. № 1–2. С. 102–118.
Бобылев А.В., Ярошевский В.А. Применение вероятностных методов к задачам динамики полета // Уч. зап. ЦАГИ. 2008. Т. 39. № 1–2. С. 111–119.
Куликов В.Е. Формирующий фильтр дифференцируемого турбулентного ветра // Тр. МИЭА. 2013. Вып. 7. С. 36–42.
Øksendal B. Stochastic Differential Equations. An Introduction with Applications. Berlin: Springer-Verlag, 2000.
Рыбаков К.А., Рыбин В.В. Алгоритмическое и программное обеспечение расчета систем автоматического управления в спектральной форме математического описания // Современная наука: теоретические, практические и инновационные аспекты развития. Т. 2. Ростов-на-Дону: Научное сотрудничество, 2018. С. 171–199.
Silverman B.W. Density Estimation for Statistics and Data Analysis. London: Chapman & Hall/CRC, 1986.
Пантелеев А.В., Якимова А.С., Рыбаков К.А. Обыкновенные дифференциальные уравнения. Практикум. М.: Инфра-М, 2016.
Rudenko E.A. Continuous Finite-Dimensional Locally Optimal Filtering of Jump Diffusions // J. Computer and Systems Sciences International. 2018. V. 57. № 4. P. 505–528.
Rybakov K.A. Solving the Nonlinear Problems of Estimation for Navigation Data Processing Using Continuous Particle Filter // Gyroscopy and Navigation. 2019. V. 10. № 1. P. 27–34.
Липцер Р.Ш., Ширяев А.Н. Статистика случайных процессов (нелинейная фильтрация и смежные вопросы). М.: Наука, 1974.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления