Известия РАН. Теория и системы управления, 2020, № 3, стр. 64-74

Введение. В работе приведена задача граничного управления колебаниями двумерной пластины. При этом на управляющие воздействия наложены ограничения на максимум абсолютной величины. Рассмотрим возможность приведения пластины в состояние покоя. Точные математические определения будут даны ниже.

Возможность полной остановки за конечное время в случае распределенного управления доказывается в монографии [1]. Там же дана оценка сверху для оптимального времени управления.

Ранее вопрос об управлении колебаниями пластин и мембран c помощью граничных сил исследовался многими авторами (например, [2] и приведенная в ней литература). В [3] рассматривается задача об остановке колебаний ограниченной струны с помощью граничного управления, доказывается, что возможно за конечное время полностью остановить колебания струны при ограничении на абсолютную величину управляющего воздействия и дается оценка времени, необходимого для полной остановки колебаний. В [4] содержится исследование задач оптимального управления системами с распределенными параметрами и формулируются условия оптимальности, аналогичные принципу максимума Л.С. Понтрягина для систем с конечным числом степеней свободы. При этом указанные условия далеко не всегда приводят к конструктивному способу построения оптимального управления. В обзорной работе [2] рассматривается задача о полной остановке движения мембраны, доказывается существование такого граничного управления и оценивается время, необходимое для полной остановки колебаний. Здесь авторы во многих постановках задач отказываются от требований оптимальности управления и изучают только проблему управляемости, что существенно облегчает исследование; в работе не рассматриваются задачи с ограничением на абсолютную величину управляющих сил, а также не приводится явных выражений для управляющих воздействий, а только доказываются теоремы существования.

Ограниченное управление (приложенное к границе) для мембран и пластин описывалось ранее, например в [5–7].

Помимо приведения в полный покой, для распределенных колебательных систем существует так называемая задача стабилизации решения. Эта задача состоит в задании на границе области некоторого управления по обратной связи, которое “стабилизирует” решение, т.е. энергия системы стремится к нулю, когда время t стремится к бесконечности. Например в [8] рассматривается задача стабилизации энергии мембраны посредством трения, введенного на границе. Более точно, граница области, занимаемой мембраной, состоит из двух частей: Γ₀ и Γ₁, удовлетворяющих некоторым дополнительным геометрическим условиям. На Γ₀ вводится условие Дирихле, т.е. эта часть границы жестко фиксируется, а на Γ₁ вводится краевое условие вида

где $\nu $ – внешняя единичная нормаль к Γ₁, $k > 0$. Заданное таким образом трение приводит к диссипации энергии системы, а следовательно, к стабилизации ее колебаний. Так как часть границы зафиксирована, то энергия системы совпадает с квадратом нормы прямого произведения пространств: ${{H}^{1}} \times {{L}_{2}}$. Следовательно, при $t \to + \infty $ решение задачи и его первая производная по t (скорость) стремятся к нулю по нормам пространств H¹ и ${{L}_{2}}$ соответственно. Заметим, что в указанной постановке начальные данные задачи должны быть выбраны достаточно гладкими и удовлетворяющими условиям согласования.

Похожая постановка рассматривалась и для задачи граничной стабилизации поперечных колебаний тонкой пластины [9]. Эта проблема нами будет изложена подробно далее.

В целом методы граничной стабилизации достаточно эффективны, так как позволяют привести колебания системы за конечное время в сколь угодно малую окрестность нуля, что на практике, как правило, равносильно приведению в покой. Тем не менее, у этих методов есть и недостаток. Время, затрачиваемое на стабилизацию, может оказаться более длительным, чем в задачах точного управления. Например, для пластины известны способы, позволяющие приводить колебания системы в покой за сколь угодно малое время.

1. Описание основных методов. Нерешенные проблемы. Среди большого числа различных подходов в управлении распределенными колебательными системами (мембраны, пластины) можно выделить три основных метода: метод моментов, метод продолжения решения на неограниченную область и Hilbert uniqueness method.

Метод моментов, предложенный А.Г. Бутковским, оказывается эффективным для одномерных задач (таких, как задачи о струне и стержне). Этот метод состоит в декомпозиции исходной задачи на счетное число задач управления гармоническими осцилляторами. К сожалению, данный метод мало применим для областей размерности больше единицы.

Для двумерных областей гораздо более эффективными оказываются два последних метода. Д.Л. Расселлом было предложено продолжить решение задачи на неограниченную область. Суть метода состоит в следующем. Вместо исходной задачи управления рассматривается начально-краевая задача (с нулевыми граничными условиями Дирихле) в неограниченной области, состоящей из плоскости без некоторой звездной области. Далее исходные начальные данные продолжаются на эту неограниченную область так, чтобы соответствующее новым (продолженным) начальным данным решение (вместе со скоростью) пришло в нулевое состояние в исходной (ограниченной) области в некоторый момент времени. Тогда управление определяется как ограничение решения задачи в неограниченной области на границу мембраны. В данном случае главной проблемой является определение способа продолжения начальных условий. Для построения этого продолжения определяющую роль играет важное физическое свойство: в неограниченной области на выбранном компакте с течением времени происходит экспоненциальная стабилизация к нулю колебаний волн, если начальное возмущение было выбрано финитным.

Hilbert uniqueness method был предложен Ж.Л. Лионсом и основан на операторном подходе. Задача сводится к доказательству обратимости некоторого линейного оператора. С помощью этого метода многими авторами были исследованы вопросы управляемости за часть границы для мембран и пластин. При этом на геометрию границ налагались некоторые существенные условия.

Заметим, что в данном исследовании мы будем в том числе пользоваться (с существенными изменениями) методом Д.Л. Расселла.

Метод моментов применялся А.Г. Бутковским для доказательства ограниченной управляемости, т.е. управляющее воздействие, приложенное к одному концу струны, должно быть ограничено по абсолютной величине. В методах Д.Л. Расселла и Ж.Л. Лионса ставилась только задача управляемости, ограничения на модуль функции управления не накладывались. Заметим, что подобного рода ограничение существенно усложняет задачу.

В данной работе мы исследуем возможность приведения в покой поперечных колебаний тонкой пластины именно в случае, когда граничные управляющие воздействия ограничены по абсолютной величине. При этом на геометрию границы области, заполненной пластиной, будут наложены существенные ограничения. Кроме того, на начальные данные задачи также будут наложены некоторые условия, а именно условия гладкости и согласования. Остаются открытыми вопросы управляемости, связанные с ослаблением данных ограничений. Например, в представленном исследовании граница области, занимаемой пластиной, должна состоять из двух частей. А именно, рассматривается пластина с отверстием (подробности см. ниже). Остается неясным, можно ли привести в покой колебания (ограниченным граничным воздействием), если отверстия нет и область односвязна. Также возникает задача по снижению степени гладкости начальных данных, в данном исследовании на начальное возмущение накладываются достаточно сильные условия гладкости. Но это задачи для будущих исследований.

2. Постановка задачи управления. Пусть ${\Omega }$ – ограниченная область на плоскости R² с бесконечно гладкой границей Γ, состоящей из двух связных частей: Γ₀ и Γ₁, т.е. ${\Gamma } = {{{\Gamma }}_{0}} \cup {{{\Gamma }}_{1}}$ и $\nu = ({{\nu }_{1}},{{\nu }_{2}})$ – внешняя единичная нормаль к границе области ${\Omega }$ (мы считаем, что $\nu $ определено в каждой точке Γ). Пусть дополнительно выполнено условие:

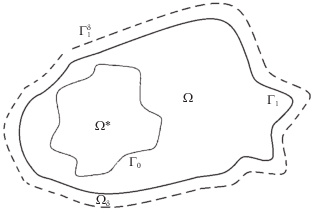
Предположим, что Γ₀ должна быть также границей некоторой ограниченной области Ω*, такой что ${\Omega } \cap {\Omega *} = \emptyset $ (рисунок).

Рассмотрим начально-краевую задачу для уравнения поперечных колебаний тонких пластин:

где $\mu $ – постоянная Пуассона ($0 < \mu < 1{\text{/}}2$), $\tau = \left( { - {{\nu }_{2}},{{\nu }_{1}}} \right)$ – касательный вектор, а B₁, B₂ – граничные операторы, определяемые формулами:

Здесь и далее будем считать, что на границе Γ выполнены неравенства:

Пусть ε > 0 – произвольное число. Ставится задача построить такие управляющие воздействия ${{u}_{1}}$ и ${{u}_{2}}$, удовлетворяющие неравенствам:

что соответствующее решение $w$ и его производная по $t$ обращаются в нуль в некоторый момент времени T, т.е. $w\left( {T,x} \right) = 0,$ ${{w}_{t}}\left( {T,x} \right) = 0$ для всех $x \in {\Omega }$. Нулевое смещение и нулевую скорость будем называть состоянием покоя рассматриваемой системы.

Следующая теорема является главным результатом данной работы.

Теорема. Пусть функции $\varphi \left( x \right) \in {{H}^{6}}\left( {\Omega } \right)$ и $\psi \left( x \right) \in {{H}^{4}}\left( {\Omega } \right)$, такие что они равны нулю вблизи границы Γ (т.е. являются финитными в области Ω). Тогда найдутся момент T и управляющие воздействия ${{u}_{1}}\left( {t,x} \right)$ и ${{u}_{2}}\left( {t,x} \right)$, удовлетворяющие ограничению (2.5), такие, что система (2.1)–(2.4) приводима в покой.

Доказательство теоремы разбивается на два этапа и будет проведено в разд. 3 и 4.

Замечание. Условия, наложенные на границу области ${\Omega }$, важны для доказательства убывания “энергии” некоторой вспомогательной системы (см. ниже). Данный факт будет нами существенно использоваться в дальнейшем.

3. Первый этап управления. На первом этапе управления рассмотрим задачу стабилизации к нулю решения по норме некоторого соболевского пространства. Для этого будем использовать результаты монографии [9]. Опишем вспомогательную задачу, а именно уравнение (2.1), начальные условия (2.2) и новые краевые условия:

где λ – фиксированное положительное число.

Определим “энергию” системы (2.1), (2.2), (3.1), (3.2):

Введем обозначения:

где

Определим билинейные формы:

Заметим, что $a\left( {w,w} \right)$ является квадратом нормы пространства $H_{{{{{\Gamma }}_{0}}}}^{2}\left( {\Omega } \right)$ [10], которая эквивалентна обычной норме соболевского пространства ${{H}^{2}}\left( {\Omega } \right)$ (для элементов из $H_{{{{{\Gamma }}_{0}}}}^{2}\left( {\Omega } \right)$).

Пусть $W{\text{'}}$ – сопряженное к W пространство. С помощью данных форм определим линейные непрерывные операторы $A \in \mathcal{L}\left( {W,W{\text{'}}} \right)$, $B \in \mathcal{L}\left( {W,W{\text{'}}} \right)$:

Пусть также I – тождественый оператор, действующий из H в себя.

Умножим уравнение (1) скалярно слева и справа на функцию $v \in W$ и формально, “перебросив” соответствующие производные (используя краевые условия), получим интегральное тождество:

Используя определение операторов A, B и I, интегральное тождество (3.4) можно переписать в виде системы уравнений:

где $\bar {w} = ({{w}_{1}},{{w}_{2}})$, причем

Известно, что оператор $\mathfrak{A}$ порождает непрерывную полугруппу, при этом норма в пространстве $D\left( \mathfrak{A} \right)$ может быть задана следующим образом [9]:

Более того, оператор $\mathfrak{A}$ – производящий оператор сжимающей полугруппы ${{e}^{{t\mathfrak{A}}}}$, т.е. такой полугруппы, для которой

Согласно теории непрерывных полугрупп, если пара начальных данных $\left( {\varphi ,\psi } \right)$ является элементом пространства $D({{\mathfrak{A}}^{k}})$, $k = 0,1,2,...$, то для соответствующего решения системы (2.3) верно включение

С помощью теории эллиптических граничных задач пространство $D\left( \mathfrak{A} \right)$ можно описать эффективно. Для этого рассмотрим краевую задачу (относительно неизвестной w₁) в следующей форме:

Формально используя формулу Грина, можно доказать, что (3.7) это вариационная формулировка задачи [9]:

где ${{w}_{2}} \in W$. Задача (3.8)–(3.10) является регулярной эллиптической задачей в смысле определения, данного в [11]. В [9] показано, что решение w₁ задачи (3.8)–(3.10) принадлежит пространству ${{H}^{4}}({\Omega })$. Следовательно, уравнение (3.8) и краевые условия (3.9), (3.10) выполнены в классическом смысле.

Суммируя все вышеизложенное, получаем, что пространство $D\left( \mathfrak{A} \right)$ состоит из всех пар $({{w}_{1}},{{w}_{2}}) \in {{H}^{4}}({\Omega })$ × W, удовлетворяющих краевым условиям (3.9) и (3.10), а оператор $\mathfrak{A}$ над элементами $D\left( \mathfrak{A} \right)$ может быть представлен как

Рассмотрим теперь линейный оператор $\mathcal{B}$, действующий из пространства H⁴(Ω) в пространство ${{L}_{2}}\left( {\Omega } \right) \times {{H}^{{\frac{3}{2}}}}\left( {\Gamma } \right) \times {{H}^{{\frac{1}{2}}}}\left( {\Gamma } \right)$ по правилу:

где $\alpha \left( x \right) \equiv 1$, если $x \in {{{\Gamma }}_{0}}$, $\alpha \left( x \right) \equiv 0$, если $x \in {{{\Gamma }}_{1}}$, и $\beta \left( x \right) \equiv 0$, если $x \in {{{\Gamma }}_{0}}$, $\beta \left( x \right) \equiv 1$, если $x \in {{{\Gamma }}_{1}}$. Как было сказано выше, (3.8)–(3.10) является регулярной эллиптической задачей в терминах [11, гл. 2]. Тогда оператор $\mathcal{B}$ фредгольмов. Следовательно, мы попадаем в область применения теории разрешимости эллиптических граничных задач, рассмотренной в [12].

Предположим, что $\left( {\varphi ,\psi } \right) \in W \times H$. Доказано, что для “энергии” системы верно неравенство [9]

где положительные постоянные M и $\gamma $ не зависят от начальных данных.

Пусть $\left( {\varphi ,\psi } \right) \in D\left( \mathfrak{A} \right)$ и $\left( {{{w}_{1}}\left( t \right),{{w}_{2}}\left( t \right)} \right)$ – соответствующее этим начальным данным решение. Подействуем на уравнение (3.5) и начальные условия (2.2) оператором $\mathfrak{A}$. Следовательно, получим

Заметим, что

Тогда из (3.11) и (3.12) имеем

Объединяя (3.11), (3.12) и (3.13), запишем:

Так как $({{w}_{2}}\left( t \right), - {{{\Delta }}^{2}}{{w}_{1}}\left( t \right)) \in W \times H$, то, используя теорию эллиптических граничных задач [12, с. 98], получим

Из последней оценки, очевидно, следует эквивалентность нормы пространства $D\left( \mathfrak{A} \right)$ и нормы пространства ${{H}^{4}} \times {{H}^{2}}$ (для элементов из $D\left( \mathfrak{A} \right)$).

Перейдем теперь к рассмотрению пространства $D({{\mathfrak{A}}^{2}})$. Как и прежде, используя теорию разрешимости эллиптических краевых задач, данное пространство можно эффективно описать, а именно $D({{\mathfrak{A}}^{2}})$ состоит из всех пар:

удовлетворяющих краевым условиям (3.9), (3.10) и дополнительно краевым условиям:

Пусть $\left( {{{w}_{1}}\left( t \right),{{w}_{2}}\left( t \right)} \right)$ – решение задачи (2.1)–(2.3), (3.2), тогда оно принадлежит пространству $C([0,T];D({{\mathfrak{A}}^{2}}))$. Имеем

Из (3.11) и [9] следует:

Объединяя (3.11) и (3.18), получим

Применяя теорию эллиптических граничных задач [12, с. 98], можно написать

где константы N₂, N₃, N₄ и N₅ не зависят от выбора $\left( {{{w}_{1}},{{w}_{2}}} \right)$.

Из (3.18) следует, что ${{{\Delta }}^{2}}{{w}_{1}}\left( t \right)$ стремится к нулю (при $t \to + \infty $) по норме W (или ${{H}^{2}}\left( {\Omega } \right)$). Следовательно, по теореме С.Л. Соболева о следах ${{{\Delta }}^{2}}{{w}_{1}}\left( t \right)$ будет стремиться к нулю и по норме ${{H}^{{\frac{1}{2}}}}\left( {{{{\Gamma }}_{1}}} \right)$. Тогда, используя также (3.11) и снова (3.18), получаем, что w₂(t) стремится к нулю (при $t \to + \infty $) по норме в ${{H}^{4}}\left( {\Omega } \right)$. Таким образом, из оценки (3.20) вытекает, что w₁(t) стремится к нулю при $t \to + \infty $ по норме в ${{H}^{6}}\left( {\Omega } \right)$, так как w₁ закреплено на части границы вместе со своей производной по нормали.

Следствием этих оценок и рассуждений является эквивалентность норм в пространствах $D({{\mathfrak{A}}^{2}})$ и ${{H}^{6}} \times {{H}^{4}}$ (для элементов из $D({{\mathfrak{A}}^{2}})$).

Из оценки (3.20), очевидно, следует, что величина

стремится к нулю при $t \to + \infty $.

Пусть $\varphi \left( x \right)$ и $\psi \left( x \right)$ удовлетворяют условиям теоремы. Используя теорию полугрупп операторов, получим, что в этом случае существует решение системы (2.1)–(2.3), (3.2), такое, что

Решаем вспомогательную задачу (2.1)–(2.3), (3.2) с заданными начальными условиями, затем это решение подставляется только в правую часть второго равенства (3.2). Тем самым получаем краевые условия (2.3) и (2.4) для начально-краевой задачи (2.1)–(2.4). Другими словами, управляющие воздействия в задаче (2.1)–(2.4) определяются по формулам

где w₀ – решение вспомогательной задачи (2.1)–(2.3), (3.2).

Таким образом, доказано, что, управляя достаточно долгое время, мы можем сделать значение

сколь угодно малым в некоторый достаточно большой момент времени t = T₁. А в силу доказанной эквивалентности норм сколь угодно малой будет и величина где

Более точно, благодаря эквивалентности норм верна оценка:

Покажем теперь, что граничное управляющее воздействие $u_{2}^{{\left( 1 \right)}}\left( {t,x} \right)$ можно сделать также достаточно малым, т.е. удовлетворить ограничению (2.5). Для этого заметим, что так как полугруппа ${{e}^{{t\mathfrak{A}}}}$ сжимающая, следует

В последней оценке выражение, стоящее в правой части, зависит только от начальных данных и не зависит от коэффициента λ. Используя последнее неравенство и теорему С.Л. Соболева о вложении, получим ограниченность модуля ${{w}_{t}}\left( {t,x} \right)$ на замыкании цилиндра

константой, зависящей только от начальных данных. Выбирая коэффициент λ достаточно близким к нулю, получим, что условие (2.5) выполнено.

4. Второй этап управления. Поставим теперь задачу привести описанную систему в полный покой. Функции $w{{{\text{|}}}_{{t = 0}}} = w\left( {{{T}_{1}},x} \right)$ и ${{w}_{t}}{{{\text{|}}}_{{t = 0}}} = {{w}_{t}}\left( {{{T}_{1}},x} \right)$ будем считать новыми начальными данными в задаче (2.1)–(2.4). Напомним, что, согласно доказанному выше, эти начальные условия (пара функций) достаточно малы по норме пространства $\mathcal{H}_{0}^{6}\left( {\Omega } \right)$.

Рассмотрим область Ω_δ, которая по определению является $\delta $-окрестностью области Ω без точек множества $\overline {{\Omega *}} $ (рисунок). Область Ω_δ построим так, чтобы внешний контур ее границы (назовем его ${\Gamma }_{1}^{\delta }$) удовлетворял условиям, которые были наложены ранее на Γ₁. Пусть также ${{\nu }_{\delta }}$ – внешняя единичная нормаль к границе области Ω_δ.

Определим пространства

Рассмотрим также произвольную пару функций

из пространства $\mathcal{H}_{0}^{6}\left( {\Omega } \right)$. Продолжим эту пару к тождественному нулю (линейный оператор продолжения существует и ограничен) на область Ω_δ с сохранением гладкости. В данном случае продолженная на Ω_δ пара будет тождественно равна нулю в “узкой” полосе, примыкающей изнутри к границе ${\Gamma }_{1}^{\delta }$. Конструкция оператора продолжения E хорошо известна и подробно описана в [11].

Продолженные таким образом функции начальных данных будем, следуя Д.Л. Расселу, обозначать соответственно ${{f}^{e}}(x)$ и ${{g}^{e}}(x)$.

Рассмотрим начально-краевую задачу для уравнения колебания пластины в области ${{{\Omega }}_{\delta }}$:

Для решения задачи (1)–(4) аналогично предыдущему разделу имеет место оценка

где ${{H}_{\delta }} = {{L}_{2}}\left( {{{{\Omega }}_{\delta }}} \right)$ и ${{\gamma }_{1}} > 0$.

Далее будем использовать метод (в измененном виде), описанный в [8] и примененный в задачах граничного управления для волнового уравнения.

Пусть имеются некоторые начальные условия f(x) и $g(x)$, $x \in {\Omega }$. Продолжим их на Ω_δ с помощью линейного ограниченного оператора E. Тогда $({{f}^{e}},{{g}^{e}}) = E\left( {f,g} \right)$. Получаем начально-краевую задачу (4.1)–(4.4). Пусть ${{w}^{s}}(t,x)$ – решение данной задачи. Для области Ω_δ рассмотрим оператор ${{\mathfrak{A}}_{\delta }}$, который строится совершенно аналогично оператору $\mathfrak{A}$ для области ${\Omega }$. Тогда выполнена оценка

Рассмотрим некоторый достаточно большой момент времени t = T₂ и ограничение решения и его производной по времени в момент T₂ на область Ω. Очевидно, что для t = T₂ в силу (4.6) и непрерывности оператора E верна оценка

Пусть по определению

Приведем теперь начально-краевую задачу в обратном времени (т.е. при $t \leqslant {{T}_{2}}$) для уравнения (остается неизменным)

с краевым условием на ${\Gamma }_{1}^{\delta }$: условием (4.3) на Γ₀ и начальными условиями

Пусть $(w_{{{\kern 1pt} 1}}^{{{\kern 1pt} i}}\left( t \right),w_{{{\kern 1pt} 2}}^{{{\kern 1pt} i}}\left( t \right))$ – решение начально-краевой задачи (4.3), (4.8), (4.9) (4.10) в обратном времени. Аналогично предыдущему выполнена оценка

Рассмотрим сумму решений в прямом и обратном времени, ограниченную на область ${\Omega }$:

Эта сумма удовлетворяет уравнению (2.1), краевым условиям на Γ, которые определяются значением самой функции и ее производных на границе области Ω.

Очевидно, что решение (4.12) с начальными условиями вида

(индекс r означает ограничение на Ω) тождественно равно нулю в Ω вместе со своей первой производной по t в момент времени $t = {{T}_{2}}$. Заметим, что значение соответствующего решения начально-краевой задачи с начальными условиями (4.13) на границе области Ω и определяет искомое управление.

Пара $(w_{{{\kern 1pt} 1}}^{{{\kern 1pt} i,{\kern 1pt} r}}(0,x),w_{{{\kern 1pt} 2}}^{{{\kern 1pt} i,{\kern 1pt} r}}(0,x))$ получается из пары $\left( {f\left( x \right),g\left( x \right)} \right)$ применением некоторого линейного непрерывного оператора, назовем его L с нормой, меньшей единицы, если T₂ достаточно велико (следствие оценок (4.7) и (4.11)). Очевидно, что суммы в правых частях (4.13) дают все элементы пространства $\mathcal{H}_{0}^{6}\left( {\Omega } \right)$. Действительно, (4.13) можно записать как

где I – тождественный оператор. Следовательно, так как $\left\| L \right\| < 1$, то оператор I + L, действующий из $\mathcal{H}_{0}^{6}\left( {\Omega } \right)$ в себя, обратим.

Теперь представим искомые функции управления (на втором этапе) в следующем виде:

$x \in {{{\Gamma }}_{1}}$, где R – оператор ограничения из ${{{\Omega }}_{\delta }}$ на область Ω, ${{S}_{ + }}\left( t \right)$, ${{S}_{ - }}\left( {{{T}_{2}} - t} \right)$ – разрешающие операторы диссипативной задачи в прямом и обратном времени соответственно, $P$ – проекция: $\left( {a,b} \right) \mapsto a$ и

Таким образом, доказана возможность приведения в покой системы с произвольными гладкими начальными данными. Покажем теперь, что, выбирая начальные данные достаточно малыми, можно привести систему в покой малым по модулю граничным управлением.

Пусть пара $\left( {w{{{\text{|}}}_{{t = 0}}},{{w}_{t}}{{{\text{|}}}_{{t = 0}}}} \right)$ достаточно мала по норме пространства $\mathcal{H}_{0}^{6}\left( {\Omega } \right)$. Из формул (4.15)–(4.17) автоматически следует достаточная малость управляющих воздействий:

так как все операторы, входящие в формулу (4.17), непрерывны. Следовательно, применяя теорему С.Л. Соболева о вложении, нетрудно показать, что эти управляющие воздействия будут меньше наперед заданного $\varepsilon $ по абсолютной величине, если время управления на первом этапе выбрать достаточно большим. Последнее и означает, что выполнено требуемое ограничение на функции управления. Теорема доказана.

Заключение. В представленной работе доказано существование граничного управления, приводящего колебания тонкой пластины в покой за конечное время. При этом на управляющие воздействия наложено ограничение по абсолютной величине. В формулировке основной теоремы начальное смещение, начальная скорость и геометрия границы пластины удовлетворяют некоторым условиям.