Известия РАН. Теория и системы управления, 2020, № 4, стр. 169-176
КЛАССИФИКАЦИЯ ТРАЕКТОРИЙ СКРЫТНОГО ДВИЖЕНИЯ ВОЗДУШНОГО ОБЪЕКТА В ЗОНЕ ОБНАРУЖЕНИЯ БОРТОВОЙ ДОПЛЕРОВСКОЙ РАДИОЛОКАЦИОННОЙ СТАНЦИИ
А. П. Кирсанов *
Национальный исследовательский ун-т “Высшая школа экономики”
Москва, Россия
Поступила в редакцию 10.01.2020
После доработки 28.02.2020
Принята к публикации 30.03.2020
Аннотация
Показано, что из-за особенностей зоны обнаружения бортовой радиолокационной станции системы дальнего радиолокационного обнаружения, работающей в импульсно-доплеровском режиме, существуют скрытные траектории, при движении по которым воздушные объекты не обнаруживаются бортовой радиолокационной станцией. Найдены решения дифференциальных уравнений, описывающих скрытные траектории. Выполнена классификация скрытных траекторий. Построены фазовые портреты, соответствующие различным видам скрытных траекторий. Найдены условия на параметры движения воздушного объекта и самолета дальнего радиолокационного обнаружения, при выполнении которых реализуется скрытная траектория того или иного вида.
Введение. Одним из факторов, уменьшающих дальность обнаружения наземными радиолокационными станциями (РЛС) воздушных объектов (ВО), летящих на малых высотах, является ограниченность радиогоризонта. Поэтому для увеличения дальности обнаружения низколетящих ВО антенны РЛС стараются размещать на возвышенностях или специальных мачтах. Это позволяет в какой-то мере увеличить радиогоризонт. Однако наиболее радикальным решением проблемы ограниченности радиогоризонта наземных РЛС является размещение РЛС на летательных аппаратах. Наибольшее распространение получили многофункциональные авиационные системы дальнего радиолокационного обнаружения (ДРЛО) или авиационные комплексы радиолокационного дозора и наведения (АК РЛДН) в отечественной терминологии. Основу таких систем составляют РЛС кругового обзора, установленные на специальных самолетах [1, 2].
Размещение РЛС на самолете решает проблему ограниченности радиогоризонта, но, как это часто бывает, приводит к появлению другой проблемы. В данном случае возникает необходимость обнаруживать низколетящие ВО на фоне подстилающей поверхности, что приводит к появлению особенностей в зоне обнаружения бортовой РЛС самолета ДРЛО. Эти особенности связаны с использованием импульсно-доплеровского режима работы бортовой РЛС самолета ДРЛО [1–3] и заключаются в появлении в каждой точке зоны обнаружения направлений движения ВО, при которых радиальные составляющие скорости ВО и подстилающей поверхности совпадают, и поэтому ВО не могут быть обнаружены РЛС с доплеровской фильтрацией сигналов. Более подробно особенности зоны обнаружения доплеровской РЛС рассмотрены в [4]. Из-за таких особенностей в зоне обзора могут быть построены скрытные траектории, т.е. такие траектории, при движении по которым воздушный объект не обнаруживается бортовой РЛС системы ДРЛО.
В [5] выведены дифференциальные уравнения, решениями которых являются скрытные траектории, для важного частного случая найдены и описаны различные виды так называемых ортогональных скрытных траекторий. Однако исследованными в [5] ортогональными скрытными траекториями не исчерпывается все множество траекторий скрытного движения.
В статье решены дифференциальные уравнения, описывающие траектории скрытного движения для более общих значений входящих в них параметров движения ВО и самолета ДРЛО. В результате чего найден более обширный набор скрытных траекторий, не являющихся ортогональными. Выполнена классификация таких траекторий и исследованы их свойства. Проведено сравнение найденных скрытных траекторий с ортогональными.
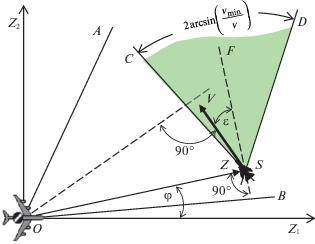
1. Секторы резекции и невидимых направлений движения. Далее будет рассматриваться ситуация, когда самолет ДРЛО (носитель) движется прямолинейно с постоянной скоростью ${{{v}}_{{\text{н}}}}$. С самолетом ДРЛО связывается подвижная прямоугольная система координат на плоскости, в которой описывается движение ВО в горизонтальной плоскости. Центр этой подвижной системы находится в месте расположения самолета ДРЛО, а координатная ось OZ1 направлена вдоль вектора скорости самолета ДРЛО, как это показано на рис. 1 . Наряду с подвижной системой координат будет использоваться неподвижная земная система, оси которой удобно считать параллельными осям подвижной системы. Несмотря на то, что движение ВО рассматривается как движение на плоскости, предполагается, что ВО летит на достаточно малой высоте и его обнаружение бортовой доплеровской РЛС самолета ДРЛО производится на фоне подстилающей поверхности. В [4] показано, что ВО не обнаруживается доплеровской РЛС самолета ДРЛО из-за близости радиальных составляющих скоростей ВО и подстилающей поверхности, если выполняется неравенство
Во-первых, множество точек, в которых ВО не обнаруживается доплеровской РЛС на фоне подстилающей поверхности (при фиксированном векторе скорости ВО V), имеет вид секторов, образованных пересекающимися прямыми линиями OA и OB. Точка пересечения этих прямых (общая вершина двух секторов) находится в месте положения бортовой РЛС самолета ДРЛО (точка O на рис. 1 ). Далее в тексте эти секторы будут называться зонами резекции. Ориентация и размер зоны резекции зависит от вектора скорости ВО V. Общая биссектриса секторов резекции всегда перпендикулярна вектору скорости ВО V. Угловой размер α каждого сектора зависит от величины ${v} = \left| {\mathbf{V}} \right|$ скорости ВО и определяется по формуле:
Во-вторых, для каждого возможного положения ВО (вектора z) имеется сектор направлений, двигаясь в котором ВО не будет обнаруживаться доплеровской РЛС самолета ДРЛО. Этот сектор называется сектором невидимых направлений движения (СННД) ВО. Расположение СННД полностью определяется положением ВО. Вершина СННД находится в месте текущего положения ВО (точка S на рис. 1 ). Биссектриса (ось симметрии) SF сектора невидимых направлений движения перпендикулярна линии визирования OS “самолет ДРЛО – ВО”. Угловой размер СННД совпадает с угловым размером сектора резекции и равен α.
Из условия невидимости и определений сектора резекции и СННД следует, что расположение ВО в секторе резекции эквивалентно нахождению вектора скорости ВО в СННД.
ВО не обнаруживается РЛС самолета ДРЛО, если в процессе движения ВО находится в СННД. Случай, когда вектор скорости V совпадает с биссектрисой СННД и, следовательно, ортогонален линии визирования “самолет ДРЛО – ВО”, рассмотрен в [5]. Получающиеся при таком движении скрытные траектории названы ортогональными и представляют собой в подвижной системе координат конические сечения. Если рассмотреть движение ВО, когда его вектор скорости V направлен не по биссектрисе СННД, а отличается на некоторый постоянный угол ε, то множество ортогональных скрытных траекторий может быть дополнено другими (неортогональными) скрытными траекториями.
2. Уравнения траекторий скрытного движения ВО в зоне обзора доплеровской РЛС. Будем отсчитывать положительный угол ε от биссектрисы СННД против часовой стрелки так, как это показано на рис. 1 . Тогда вектор скорости ВО описывается выражением
Через $\varphi $ обозначен угол между вектором z и осью OZ1, отсчитываемый против часовой стрелки. Для простоты аналитических выражений была выбрана земная система координат, у которой первая ось параллельна вектору скорости самолета ДРЛО. В такой системе координат вектор скорости самолета ДРЛО имеет вид ${{{\mathbf{V}}}_{{\text{н}}}} = {{({{{v}}_{{\text{н}}}},0)}^{{\text{T}}}}$.
В подвижной системе координат, связанной с самолетом ДРЛО, движение ВО описывается уравнением ${\mathbf{\dot {z}}} = {\mathbf{V}} - {{{\mathbf{V}}}_{{\text{н}}}}$ или
В прямоугольной системе координат ${{Z}_{1}}O{{Z}_{2}}$ это выражение может быть записано в виде системы дифференциальных уравнений:
(2.1)
$\left\{ {\begin{array}{*{20}{l}} {{{{\dot {z}}}_{1}} = - \frac{{v}}{{\sqrt {z_{1}^{2} + z_{2}^{2}} }}\left( {{{z}_{1}}\sin \varepsilon + {{z}_{2}}\cos \varepsilon } \right) - {{{v}}_{{\text{н}}}},} \\ {{{{\dot {z}}}_{2}} = \frac{{v}}{{\sqrt {z_{1}^{2} + z_{2}^{2}} }}\left( {{{z}_{1}}\cos \varepsilon - {{z}_{2}}\sin \varepsilon } \right).} \end{array}} \right.$Обозначим правые части первого и второго уравнений этой системы через ${{{v}}_{1}}({{z}_{1}},{{z}_{2}},\varepsilon )$ и ${{{v}}_{2}}({{z}_{1}},{{z}_{2}},\varepsilon )$ соответственно. Правые части уравнений (2.1) для каждого значения угла ε задают на плоскости ${{Z}_{1}}O{{Z}_{2}}$ векторное поле
Можно проверить, что
Это означает, что фазовые траектории, соответствующие векторному полю ${\mathbf{v}}({\mathbf{z}},\pi - \varepsilon )$, симметричны относительно оси OZ1 фазовым траекториям, соответствующим векторному полю v(z, ε).
Можно также проверить, что
Следовательно, фазовые траектории, соответствующие векторному полю ${\mathbf{v}}({\mathbf{z}}, - \varepsilon )$, симметричны относительно оси OZ2 фазовым траекториям, соответствующим векторному полю v(z, ε).
Таким образом, фазовые траектории (скрытные траектории ВО) для произвольных значений угла ε могут быть получены из траекторий векторного поля для $0 < \varepsilon < \pi {\text{/}}2$ путем отражений от координатных осей и изменения на противоположное направлениe движения по траектории (в некоторых случаях). Поэтому далее будет рассматриваться только случай, когда $0 < \varepsilon < \pi {\text{/}}2$.
В полярной системе координат система уравнений (2.1) имеет вид [5]
(2.2)
$\left\{ \begin{gathered} \dot {\rho } = - {v}\sin \varepsilon - {{{v}}_{{\text{н}}}}\cos \phi , \hfill \\ \dot {\phi } = \frac{1}{\rho }\left( {{v}\cos \varepsilon + {{{v}}_{{\text{н}}}}\sin \phi } \right). \hfill \\ \end{gathered} \right.$Эта система уравнений эквивалентна дифференциальному уравнению
Решение этого уравнения описывается выражением
(2.3)
$\rho = \left| {\frac{1}{{\mu + \sin \phi }}} \right|\exp \left( { - \mu \cdot {\text{tg}}\varepsilon \int {\frac{{d\phi }}{{\mu + \sin \phi }}} } \right),\quad {\text{где}}\quad \mu = \left( {{v}{\text{/}}{{{v}}_{{\text{н}}}}} \right){\text{cos}}\varepsilon .$В зависимости от значения параметров μ и ε, входящих в это выражение, скрытные траектории имеют различный вид.
3. Виды и особенности траекторий скрытного сближения. Рассмотрим траектории при различных значениях параметров движения ВО и самолета ДРЛО. В табл. 1 представлены принципиально отличающиеся семейства скрытных траекторий в подвижной (связной с самолетом ДРЛО) системе координат. Эти семейства соответствуют указанным в тех же ячейках значениям угла ε, скоростям ${v}$ и ${{{v}}_{{\text{н}}}}$. В последнем столбце показаны семейства неортогональных (при ε > 0) траекторий, а в соседнем столбце для сравнения приведены семейства ортогональных (ε = 0) траекторий. В двух ячейках таблицы семейства траекторий не представлены, поскольку соответствующие этим ячейкам условия ε = 0, ${v} > {{{v}}_{{\text{н}}}}$, $\mu < 1$ несовместны.
Таблица 1.
Виды скрытных траекторий
| Значения параметров | Скрытные траектории при ε = 0 | Скрытные траектории при ε > 0 | |||
|---|---|---|---|---|---|
| μ > 1 | ε = 0° | 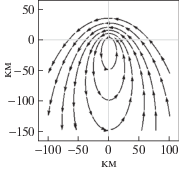 |
ε = 15° | 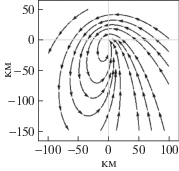 |
|
| ${v}$ = 800 км/ч | ${v}$ = 800 км/ч | ||||
| ${{{v}}_{{\text{н}}}}$ = 700 км/ч | ${{{v}}_{{\text{н}}}}$ = 700 км/ч | ||||
| μ = 1.14 | μ = 1.1 | ||||
| μ = 1 | ε = 0° | 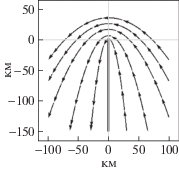 |
ε = 15° | 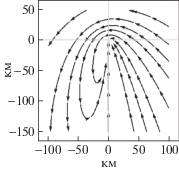 |
|
| ${v}$ = 700 км/ч | ${v}$ = 800 км/ч | ||||
| ${{{v}}_{{\text{н}}}}$ = 700 км/ч | ${{{v}}_{{\text{н}}}}$ = 772.7 км/ч | ||||
| μ = 1.0 | μ = 1.0 | ||||
| μ < 1 | ${v}$ > ${{{v}}_{{\text{н}}}}$ | Несовместимые значения параметров | ε = 20° | 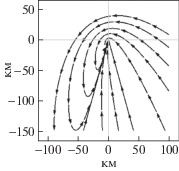 |
|
| ${v}$= 800 км/ч | |||||
| ${{{v}}_{{\text{н}}}}$ = 780 км/ч | |||||
| μ = 0.96 | |||||
| ${v}$ = ${{{v}}_{{\text{н}}}}$ | Несовместимые значения параметров | ε = 20° | 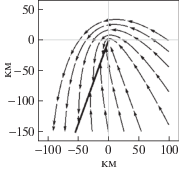 |
||
| ${v}$ = 750 км/ч | |||||
| ${{{v}}_{{\text{н}}}}$ = 750 км/ч | |||||
| μ = 0.94 | |||||
| ${v}$ < ${{{v}}_{{\text{н}}}}$ | ε = 0° | 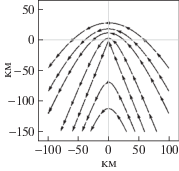 |
ε = 15° | 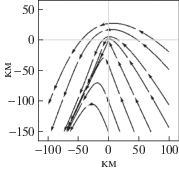 |
|
| ${v}$ = 650 км/ч | ${v}$ = 750 км/ч | ||||
| ${{{v}}_{{\text{н}}}}$ = 700 км/ч | ${{{v}}_{{\text{н}}}}$ = 800 км/ч | ||||
| μ = 0.929 | μ = 0.91 | ||||
При $0 < \varepsilon < \pi {\text{/}}2$ и $\mu = \left( {{v}{\text{/}}{{{v}}_{{\text{н}}}}} \right){\text{cos}}\varepsilon > 1$ уравнение семейства скрытных траекторий имеют вид
(3.1)
$\rho = \frac{{{{c}_{o}}}}{{\mu + \sin \phi }}\exp \left[ { - \frac{{2\mu \cdot {\text{tg}}\varepsilon }}{{\sqrt {{{\mu }^{2}} - 1} }}{\text{arctg}}\left( {\frac{{\mu \cdot {\text{tg}}\frac{\phi }{2} + 1}}{{\sqrt {{{\mu }^{2}} - 1} }}} \right)} \right].$Постоянная интегрирования co находится из начальных условий $\rho (0) = {{\rho }_{0}},\varphi (0) = {{\varphi }_{0}}$ по формуле
Формула (3.1) отличается от уравнения эллипса экспоненциальным членом, из-за которого семейство эллипсов превращается в семейство спиралей. Траектории такого типа имеет смысл называть псевдоэллиптическими. Вид траекторий в рассматриваемом случае показан в табл. 1 в ячейке, соответствующей значению ε > 0, μ > 1. Стрелками на этом и других рисунках в табл. 1 показаны направления движения по скрытным траекториям из различных начальных положений.
По траекториям такого типа можно быстрее сблизиться с носителем доплеровской РЛС, чем при движении по эллиптическим скрытным траекториям при одних и тех же скоростях ${{v}_{{\text{н}}}}$ и $v$ и начальном положении наводимого самолета. Кроме того, минимальное расстояние до носителя РЛС на первом витке траектории также меньше минимального расстояния до РЛС, достижимого при движении по эллиптическим траекториям, изображенным левее в той же строке табл. 1. На рис. 2 , а для сравнения с эллиптическими скрытными траекториями (ε = 0) показаны две псевдоэллиптические траектории, соответствующие ε = 3 и 6° в подвижной (связанной с носителем РЛС) системе координат, на рис. 2 , б – эти же траектории в земной системе координат.
Рис. 2.
Скрытные траектории с различным угловым отклонением ($ \bullet $ – 0°, ▲ – 3°, $*$ – 6°) вектора скорости от биссектрисы СННД: а – в подвижной системе координат; б – в земной системе координат
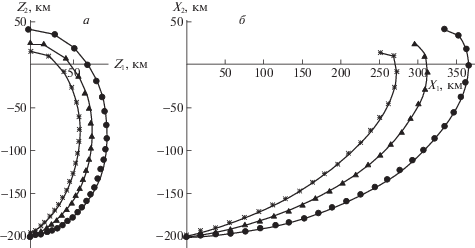
Время движения по эллиптической траектории из максимально удаленной от носителя РЛС точки в минимально удаленную точку составляет около 31 мин [5]. Аналогичное время движения для неэллиптических траекторий и другие параметры приведены в табл. 2.
Таблица 2.
Параметры скрытных траекторий сближения с носителем РЛС
| Тип траектории | Минимальное расстояние до носителя РЛС, км | Длина траектории, км | Время движения по траектории, мин |
|---|---|---|---|
| Эллиптическая, ε = 0° | 40.00 | 507.00 | 31.08 |
| Псевдоэллиптическая, ε = 3° | 25.36 | 433.88 | 26.70 |
| Псевдоэллиптическая, ε = 6° | 15.38 | 382.20 | 23.52 |
| Прямолинейная в точку встречи | 0.00 | 268.33 | 16.51 |
В этой таблице представлены для сравнения характеристики сближения ВО с самолетом ДРЛО по кратчайшей прямолинейной траектории в упреждающую точку встречи (методом “Перехват”). Однако при движении по данной прямолинейной траектории не гарантируется скрытность движения ВО в зоне обнаружения доплеровской РЛС вдоль всей траектории.
Приведенные данные показывают, что отклонения от биссектрисы СННД на 3–6° позволяют сократить на 15–32% время сближения с подвижной доплеровской РЛС и минимальное расстояние до нее.
При $\mu = \left( {{v}{\text{/}}{{{v}}_{н}}} \right){\text{cos}}\varepsilon = 1$ решение (2.2) имеет вид
(3.2)
$\rho = \frac{{{{c}_{o}}}}{{1 + \sin \phi }}\exp \left( {\frac{{2\mu \cdot {\text{tg}}\varepsilon }}{{1 + {\text{tg}}\frac{\phi }{2}}}} \right).$Если известны начальные условия (${{\rho }_{o}},{{\phi }_{o}}$), то постоянная интегрирования co находится по формуле
Семейство траекторий, определяемое выражением (3.2), представлено в ячейке табл. 1, соответствующей значениям μ = 1 и ε > 0. Это семейство имеет некоторое сходство (особенно вдали от начала системы координат и полупрямой $\phi = - \pi {\text{/}}2$) с семейством ортогональных параболических траекторий, показанном в соседней слева ячейке табл. 1. Поэтому это семейство можно назвать квазипараболическим. Следует отметить, что все квазипараболические траектории, в отличие от ортогональных параболических траекторий, оканчиваются в начале системы координат.
Из (2.1) видно, что полупрямая $\phi = - \pi {\text{/}}2$ (z1 = 0, z2 < 0) является решением данной системы. Скорость движения к началу координат (скорость сближения с самолетом ДРЛО) по этой прямолинейной траектории равна ${v}\sin \varepsilon $. Это является еще одним отличием данного семейства скрытных траекторий от семейства ортогональных параболических траекторий. В семействе ортогональных параболических траекторий вся полупрямая ϕ = –π/2 состоит из особых точек. Каждой такой точке (в земной системе координат) соответствует скрытное движение ВО по прямолинейной траектории, параллельной траектории движения самолета ДРЛО с углом визирования на самолет ДРЛО, равным π/2 относительно вектора скорости ВО.
При $\mu = \left( {{v}{\text{/}}{{{v}}_{{\text{н}}}}} \right){\text{cos}}\varepsilon < 1$ решение (2.2) преобразуется к виду
(3.3)
$\rho = \frac{{{{с}_{o}}}}{{\left| {\mu + \sin \phi } \right|}}{{\left| {\frac{{\mu \cdot {\text{tg}}\frac{\phi }{2} + 1 - \sqrt {1 - {{\mu }^{2}}} }}{{\mu \cdot {\text{tg}}\frac{\phi }{2} + 1 + \sqrt {1 - {{\mu }^{2}}} }}} \right|}^{{\frac{{\mu \cdot {\text{tg}}\varepsilon }}{{\sqrt {1 - {{\mu }^{2}}} }}}}}.$Постоянная интегрирования co находится из начальных условий по формуле
Вид семейства траекторий, определяемый этой формулой, зависит от соотношения скоростей ${{{v}}_{{\text{н}}}}$ и ${v}$. Однако при μ < 1 и любом соотношении скоростей имеются две прямолинейные траектории, представляющие собой лучи, которые исходят из начала подвижной системы координат. При движении по этим траекториям полярный угол не изменяется и $\dot {\phi } = 0$. В этом случае из второго уравнения системы (2.2) следует, что постоянное значение угла φ, при котором возможно прямолинейное скрытное движение, удовлетворяет условию $\sin \phi = - \mu $. Этому условию удовлетворяют также два значения полярного угла ${{\phi }_{1}} = - \arcsin \mu $ и ${{\phi }_{2}} = \pi + \arcsin \mu $. Движение по прямолинейным скрытным траекториям, соответствующим этим углам, может быть направлено как к центру подвижной системы координат, так и от него, либо движение ВО (в подвижной системе координат) может отсутствовать вовсе. Направление скрытного движения определяется значением производной $\dot {\rho } = - {v} \cdot {\text{sin}}\varepsilon \pm \sqrt {{v}_{{\text{н}}}^{2} - {{{v}}^{2}}{\text{co}}{{{\text{s}}}^{2}}\varepsilon } $, которое получается после подстановки в первое уравнение системы (2.2) полярных углов ϕ1 и ϕ2. Нетрудно установить, что при ε > 0 и ${v} > {{{v}}_{{\text{н}}}}$ радиальная скорость $\dot {\rho }$ для обоих углов ϕ1 и ϕ2 будет отрицательной. Иными словами, по обеим прямолинейным скрытным траекториям ВО будет приближаться к центру подвижной системы координат (самолету ДРЛО). По одной из этих траекторий сближение будет происходить с постоянной скоростью $\dot {\rho } = - {v}\sin \varepsilon - {{{v}}_{{\text{н}}}}\sqrt {1 - {{\mu }^{2}}} $, а по другой – с постоянной скоростью $\dot {\rho } = - {v}\sin \varepsilon $ + ${{{v}}_{{\text{н}}}}\sqrt {1 - {{\mu }^{2}}} $. Вид семейства невидимых траекторий, определяемых уравнением (3.3), при ε > 0, $\mu < 1$ ${v} > {{{v}}_{{\text{н}}}}$ показан в соответствующей ячейке табл. 1.
При ${v} = {{{v}}_{{\text{н}}}}$ вид траекторий меняется. Полупрямая $\phi = {{\phi }_{2}} = \pi + \arcsin \mu $ в этом случае вся составлена из особых точек, в которых $\dot {\phi } = 0\;$ и $\dot {\rho } = 0$, а другие траектории не входят в начало координат, а оканчиваются на этой прямой. В каждой точке данной полупрямой оканчиваются две траектории. Полупрямая $\phi = {{\phi }_{2}} = \pi + \arcsin \mu $ аналогична полупрямой $\phi = - \pi {\text{/}}2$ для семейства ортогональных параболических скрытных траекторий, которая также состоит из особых точек (см. ячейку табл. 1, соответствующую значениям ε = 0 и $\mu = {v}{\text{/}}{{{v}}_{{\text{н}}}} = 1$). Отличие заключается в том, что в ортогональном случае в особых точках на полупрямой $\phi = - \pi {\text{/}}2$ не заканчиваются другие траектории. Вид траекторий для ε > 0, μ = 1 и ${v} = {{{v}}_{{\text{н}}}}$ показан в соответствующей ячейке табл. 1.
Если при μ < 1 скорость ВО ${v}$ меньше скорости самолета ДРЛО ${{{v}}_{{\text{н}}}}$, то по прямолинейной скрытной траектории $\phi = \pi + \arcsin \mu $ ВО будет удаляться от центра подвижной системы координат со скоростью $\dot {\rho } = - {v}\sin \varepsilon + {{{v}}_{{\text{н}}}}\sqrt {1 - {{\mu }^{2}}} > 0$. По другой скрытной прямолинейной траектории $\phi = - \arcsin \mu $ ВО будет приближаться к центру с постоянной скоростью $\dot {\rho } = - {v}\sin \varepsilon - {{{v}}_{{\text{н}}}}\sqrt {1 - {{\mu }^{2}}} $ < 0. Скрытные траектории в данном случае становятся похожи на гиперболические ортогональные траектории при ε = 0 и ${v} < {{{v}}_{{\text{H}}}}$. Небольшое отличие заключается в том, что точки траекторий, расстояние от которых до начала координат минимально, располагаются теперь не на вертикальной оси, а на двух полупрямых, определяемых уравнением ${\text{cos}}\phi = - \left( {{v}{\text{/}}{{{v}}_{{\text{н}}}}} \right){\text{sin}}\varepsilon $.
Вид семейства скрытных траекторий при μ < 1 и ${v} < {{{v}}_{{\text{H}}}}$ показан в соответствующей ячейке табл. 1.
Заключение. Проведенные исследования позволили найти все неортогональные скрытные траектории движения ВО в зоне обзора РЛС самолета ДРЛО с постоянным угловым отклонением вектора скорости ВО от биссектрисы СННД. Выполнена классификация различных вариантов неортогональных скрытных траекторий. Найдены условия на параметры движения ВО и самолета ДРЛО, при выполнении которых реализуется скрытная траектория того или иного вида. Построены фазовые портреты, соответствующие различным видам траекторий в связной с самолетом ДРЛО системе координат. Установлено существование прямолинейных скрытных траекторий и описано их расположение относительно самолета ДРЛО.
Использование неортогональных скрытных траекторий увеличивает число возможных вариантов скрытного движения между заданными пунктами и, в частности, позволяет выбрать вариант с минимальным временем полета. Поэтому знание специфики различных неортогональных скрытных траекторий может быть полезно при формировании траекторий наискорейшего скрытного выхода в заданную точку (подвижную или неподвижную) при ограничениях, накладываемых условиями невидимости. Такие траектории могут состоять из фрагментов рассмотренных неортогональных скрытных траекторий.
Полученные результаты справедливы не только для РЛС кругового обзора самолетов ДРЛО, но и для других самолетных РЛС, имеющих секторную зону обзора и использующих доплеровский принцип обнаружения целей на фоне отражений от подстилающей поверхности.
Список литературы
Авиационные комплексы радиолокационного дозора и наведения. Принципы построения, проблемы разработки и особенности функционирования. М.: Радиотехника, 2014. 528 с.
Long Maurice W. Airborne Early Radar Warning System Concepts. N.Y.: SciTech, 2004. 519 p.
Справочник по радиолокации. В 2 кн. / Под ред. М.И. Сколника. Пер. с англ. под общ. ред. В.С. Вербы. М.: Техносфера, 2014.
Гандурин В.A., Кирсанов А.П. Особенности зоны обнаружения низколетящих воздушных объектов доплеровской радиолокационной станции // Радиотехника. 2007. № 10. С. 42–46.
Кирсанов А.П. Траектории скрытного движения воздушного объекта в зоне обнаружения бортовой доплеровской радиолокационной станции // АиТ. 2014. № 9. С. 144–155.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления