Известия РАН. Теория и системы управления, 2020, № 4, стр. 3-17

Введение. Анализ свойств математических моделей систем, выявление аналогий и вообще каких-то связей между свойствами разных моделей, сведение анализа моделей к анализу более простых зачастую выполняются с привлечением тех или иных дополнительных объектов, связывающих эти модели, например, преобразований переменных одной модели в переменные другой. Эти и другие межмодельные объекты связи (МОС), будучи согласованы с собственными структурами исследуемых моделей, могут обеспечивать следование того или иного свойства P, изучаемого на предмет его наличия в одной модели $\mathfrak{M}$, из факта наличия некоторого свойства P ' в другой модели $\mathfrak{M}'$, связанной с $\mathfrak{M}$ этими МОС. Данная статья посвящена алгоритмизации формирования условий X, обеспечивающих эту импликацию свойств P ' → P в терминах МОС и объектов самих моделей.

В литературе известны результаты об импликации свойств математических моделей, именуемые сохранением свойств; при этом определения свойств P ', P получаются одно из другого заменой объектов одной модели соответствующими объектами другой, но однотипной модели. Сами такие свойства будем тоже называть однотипными. Этот частный случай импликации свойств соответствует наличию прямой аналогии в свойствах P ', P рассматриваемой пары моделей. Например, известным условием сохранения так называемых позитивных свойств однотипных алгебраических систем является сюръективный гомоморфизм этих моделей [1, 2]. При этом направления действия гомоморфизма и сохранения этих свойств совпадают, а однотипность свойств состоит в том, что определения свойств P ' и P записаны в одной сигнатуре, интерпретируемой объектами алгебраических систем $\mathfrak{M}'$ и $\mathfrak{M}$ одного типа. Объектами каждой модели являются ее операции и отношения, а межмодельным объектом связи – упомянутый гомоморфизм.

В динамике систем для некоторого класса динамических свойств математических моделей, удовлетворяющих аксиоматике системы процессов, в [3, 4] был предложен метод гибкого формирования условий сохранения X по виду определения изучаемого свойства P. При этом в качестве одного из МОС выступало отображение из пространства позиций изучаемой системы процессов $\mathfrak{M}$ в пространство состояний системы процессов $\mathfrak{M}'$ и в дополнение к формируемому набору условий X априорно задавалось условие M как условие межмодельной связи. Оно означало мажорирование значений этого отображения, названного вектор-функцией сравнения (ВФС), на процессах системы $\mathfrak{M}$ состояниями соответствующих процессов системы $\mathfrak{M}'$. Получаемые теоремы о сохранении (с условиями X, M) и сам метод стали именоваться теоремами и соответственно методом сравнения. Направления сохранения свойств и действия ВФС противоположны, а однотипность моделей $\mathfrak{M}'$ и $\mathfrak{M}$ как наличие взаимного соответствия объектов этих моделей обусловлена подчиненностью объектов обеих моделей единой аксиоматике системы процессов. Класс свойств, охватываемых методом сравнения [3, 4], был ограничен некоторыми требованиями, одним из которых является требование согласованности условий M мажорирования ВФС с определениями свойств P и P '. В частности, порядки квантификации переменных P и P ' должны соответствовать порядку квантификации переменных того же смысла в M.

Выход за рамки систем процессов и этого класса их свойств был достигнут рассмотрением задачи формирования условий импликации свойств как задачи построения содержательных решений логических уравнений X&M → (P ' → P) [5, 6]. При этом известные члены уравнения M, P ', P записываются в языке L позитивно-образованных формул [5, 6], т.е. составленных из заключительных формул с помощью ти́повых кванторов [7] и бинарных логических связок &, ∨ (упоминавшиеся позитивные свойства являются весьма частным случаем позитивно-образованных формул). Свойства P и P ' не обязательно однотипные, но имеют одинаковую структуру. Под структурой позитивно-образованной формулы будем здесь и далее понимать древовидный граф ее строения, помеченный соответственно его структурным элементам: висячие вершины – номерами i ∈ $\overline {1,m} $ (m ≥ 1), вершины ветвления – метками &, ∨, а кванторные вершины – метками ∀, ∃. Если Var(F) – множество обозначений всех кванторных переменных ти́повых кванторов в позитивно-образованной формуле F, то Var(P) ∩ Var(P ') = ∅. Формулы M, P ', P имели одинаковую степень m, т.е .образованы из одинакового количества m своих заключительных формул. Переменные одного смысла из M и P (соответственно из M и P ') имеют одинаковые обозначения, т.е. Var(M) ⊆ Var(P) ∪ Var(P '). При этом то или иное условие межмодельной связи M должно было задаваться априорно и быть согласованным с P и P '. В частности, из условий этой согласованности следует существование такого надграфа, в который изоморфно, с сохранением меток, можно вложить схемы формул M, P ', P, если под схемой понимать результат удаления из структуры формулы меток &, ∨ и замены меток ∀, ∃ на обозначения соответствующих кванторных переменных. Этот надграф являлся начальной схемой решения X, подлежащего построению.

Необходимость задания условия межмодельной связи, отличного от условия мажорирования ВФС, может вызываться как переходом к другим моделям и их свойствам, так и желанием исследования задействовать МОС из некоторого конкретного класса объектов, отличных от ВФС. Но требование априорного указания отдельного условия межмодельной связи с обеспечением его согласованности с P и P ' снижает алгоритмичность метода в целом и усложняет формирование как уравнения, так и искомого решения X.

Формирование условий сохранения свойств алгебраических систем по виду изучаемого свойства P без априорного задания условия межмодельной связи в случае многоосновных алгебраических систем было выполнено в [8]. Охватываемый при этом класс однотипных свойств ограничен тем, что в определениях свойств P и P ' в качестве областей изменения кванторных переменных могут быть только множества, построенные над носителями системы $\mathfrak{M}$ и соответственно $\mathfrak{M}{\kern 1pt} '$ как ступени в смысле Н. Бурбаки [7] или их некоторые обобщения.

В данной статье в развитие [9–11] предлагается метод построения содержательных решений логических уравнений X → (P ' → P) для произвольных математических моделей систем. При формировании уравнений не требуется его эвристическое наращивание дополнительными априорными посылками, согласованными с P и P '. Вместо этого в состав формируемого решения X встраиваются относительно простые и обычно бескванторные подформулы связи: условие каждого ти́пового квантора существования (ТКС) решения X конъюнктивно наращивается подформулой, связывающей кванторную переменную этого ТКС с некоторыми из переменных, ранее квантифицированных в структуре X. Благодаря этому, упрощается варьирование задействуемых МОС. Однотипностью свойств P и P ' обеспечивается согласованность известных членов исходного логического уравнения, а в случае неоднотипности свойств P и P ' структура свойства P ' должна совпадать со структурой свойства P хотя бы частично, т.е. с точностью до замены некоторых меток ∃ или ∨ структуры свойства P на ∀ и & соответственно. В отличие от других известных работ по решению логических уравнений (например, [12, 13], спецификой рассматриваемого класса уравнений и правил его решения обеспечивается содержательность искомого решения уравнения.

Рассматриваются примеры, детально иллюстрирующие применение метода. Метод обеспечивает получение теорем, которые, как правило, являются новыми или модификациями известных, а в других случаях – следствиями или, наоборот, обобщениями известных. Сказанное относится, например, к теоремам о сохранении свойств алгебраических и динамических систем при морфизмах (в частности, типа теорем из [2, 7, 8]) и к теоремам сравнения в терминах ВФС и вектор-функций Ляпунова в динамике систем и в теории управления (например, типа теорем из [3–6, 11, 14, 15]).

1. Исходные определения. Используется язык L позитивно-образованных формул (ПОФ) в частично-формализованном варианте. В древовидном графе строения всякой ПОФ F висячими вершинами являются некоторые заключительные утверждения F_i, i = $\overline {1,m} $, а вершинами ветвления – бинарные логические связки ${{\ell }_{j}}$ ∈ {(& (“и”), ∨ (“или”)} (j = $\overline {1,m - 1} $). Остальные вершины – это ти́повые кванторы (ТК) w(z_α) [7] (в частности, ограниченные). Эти ТК w(z_α) ∈ {$\hat {w}$(z_α), 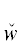(z_α)} являются либо ТК всеобщности (ТКВ) $\hat {w}$(z_α) $\mathop = \limits^{{\text{def}}} $ ∀z_α(${{W}^{{{{z}_{\alpha }}}}}$ → _) (“для всякого значения переменной z_α, удовлетворяющего условию ${{W}^{{{{z}_{\alpha }}}}}$, следует …”), либо ТК существования (ТКС) 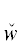(z_α) $\mathop = \limits^{{\text{def}}} $ ∃z_α(${{W}^{{{{z}_{\alpha }}}}}$ & _) (“существует такое значение переменной z_α, что выполняется условие ${{W}^{{{{z}_{\alpha }}}}}$ и …”). Здесь z_α – кванторные переменные, α = 1, 2, …, а условия ${{W}^{{{{z}_{\alpha }}}}}$, ограничивающие область их допустимых значений, именуются ти́повыми условиями соответствующих переменных. Разумеется, что условия ${{W}^{{{{z}_{\alpha }}}}}$ могут зависеть не только от переменных z_α, но и других, а именно кванторных переменных, связанных в F ти́повыми кванторами, в области действия которых находится ТК w(z_α).

Выражения R ∈ {F_i, ${{W}^{{{{z}_{\alpha }}}}}$} допускают любые вольности записи обычных математических текстов, но в их отношении предполагается известным, от каких кванторных переменных z_β кванторов w(z_β) (включая w(z_α)) они зависят. Число m называется степенью формулы.

Пример 1. Пусть модель $\mathfrak{M}$ суть кортеж (A, B,  f, ≤) с функцией f : A → B, где множество B частично упорядочено отношением ≤. Свойство P ограниченности сверху функции f в языке L запишется как свойство степени 1:

где F₁$\mathop = \limits^{{\text{def}}} $ z ≤ x, или в метаязыке:

Пример 2. Пусть $\mathfrak{M}$ – обыкновенное дифференциальное уравнение (ОДУ)

f  удовлетворяет некоторым условиям существования классических решений x при некоторых u ∈ $\mathcal{U}$ и начальных данных (t₀, x₀) ∈ Ω, x(t₀) = x₀ (u(t, x) – функциональный параметр из семейства функций $\mathcal{U}$, например, управление). Через $\mathcal{X}$(t₀, x₀, u(t, x)) обозначим множество всех решений x(⋅, t₀, x₀, u) уравнения (1.2) при фиксированных (t₀, x₀, u). Пусть также S(u) = = {(t₀, x₀) ∈ Ω : $\mathcal{X}$(t₀, x₀, u) ≠ ∅}.

Пусть A ⊂ R ^r – подмножество состояний системы (1.2), интересующее нас с точки зрения динамического свойства P типа инвариантности множества A относительно решений ОДУ (1.2):

где A₀ ⊆ A, R¹ × A ⊆ Ω, T₀ ⊆ R¹. Это свойство означает существование такого u ∈ $\mathcal{U}$, что:

а) решения x(⋅, t₀, x₀, u) с любыми начальными данными из R¹ × A₀ остаются в A,

б) существует такой начальный момент времени t₀ из T₀, при котором решения также остаются в A для любых начальных состояний из A,

в) решения x(⋅, t₀, x₀, u) при (t₀, x₀) ∈ T₀ × A, по крайней мере, “посещают” множество A в сколь угодно далекие моменты времени.

Назовем свойство (1.3) “инвариантностью с посещением”. Иначе говоря, свойство (1.3) состоит в том, что имеет место обычное свойство (A₀, A)-оценки (оценки множеством A решений ОДУ (1.2) с начальными состояниями x₀ ∈ A₀) в сочетании со свойствами слабой (A, A)-оценки (т.е. при некотором t₀ ∈ T₀) и посещения множества A из T₀ × A в сколь угодно далекие моменты времени. Ясно, что при A₀ = A из а) следуют б) и в).

Степень m свойства (1.3) равна 3. Его определение записано в метаязыке, но оно (как и (1.1)) будет рассматриваться как формула языке L:

где w(z_αi) понимается как ТК w(z_α) из i-ветви формулы P, i = $\overline {1,3} $.

Далее под структурными элементами (или просто элементами) ПОФ F понимаются ее части F_i, ТК w(z_α) и связки ${{\ell }_{j}}$, а под структурой – граф ее строения с метками вершин i = $\overline {1,m} $, ∀, ∃, &, ∨. Будем говорить, что структура ПОФ F частично повторяет структуру ПОФ G, если структура F получается из структуры G заменой некоторых меток ∃ и/или ∨ на метки ∀ и & соответственно. Будем предполагать, что F не содержит переменных, одновременно связанных кванторами и свободных (т.е. не связанных кванторами), и что кванторные переменные всех ТК попарно различны, хотя в примерах переменные близкого смысла могут обозначаться одинаково, если контекст или используемые приемы исключают возможные коллизии.

Позитивность структуры ПОФ F обеспечивает применимость к ним дополнительных логических правил обработки, неприменимых, например, к произвольным формулам первопорядковой логики.

В языке L заключительные формулы F_i и формулы $\tilde {F}$, возникающие в процессе образования F из F_i, называем главными подформулами (ГП) из F и обозначаем $\tilde {F}$ $ \sqsubseteq $ F. Если $\tilde {F}$ и w(z_α)$\tilde {F}$ – ГП из F и в $\tilde {F}$ отсутствуют вхождения z_α, то ТК w(z_α) называем независимым в F (ТКН). Из двух элементов ветви структуры формулы F называем старшим более близкий к корню и, если w(z_β) старше, чем w(z_α), то говорим, что переменная z_β старше, чем z_α.

2. Метод получения условий импликации свойств математических моделей. Пусть $\mathfrak{M}$ и $\mathfrak{M}'$ – пара произвольных математических моделей, а P и P ' – определения их некоторых свойств соответственно, причем структуры свойств P и P ' одинаковые (хотя при этом свойства P и P ' могут быть неоднотипными) или структура P ' лишь частично совпадает со структурой P (см. Введение). Рассматриваются логические уравнения

где X – неизвестный набор нетривиальных условий импликации свойств, подлежащий формированию по виду свойств P, P '.

Условимся кванторные переменные z_α формулы F в случае P (соответственно P ') обозначать через y_α (соответственно $y_{\alpha }^{'}$), а заключительные формулы – через P_i (соответственно $P_{i}^{'}$), i = $\overline {1,m} $. ТКС и связки ∨, входящие в P и отвечающие заменяемым меткам при переходе к структуре P ', будем называть особыми в отличие от остальных – неособых.

Для каждой пары (y_α, $y_{\alpha }^{'}$) кванторных переменных из P и P ' введем в рассмотрение формулу связи ${{\Phi }^{{{{y}_{\alpha }}}}}$ как пока неопределенную формулу, которая может содержать, помимо (y_α, $y_{\alpha }^{'}$), также старшие переменные. Для некоторых пар (y_α, $y_{\alpha }^{'}$) эти формулы могут быть тождественно-истинными предикатами, т.е. отсутствовать. При конкретизации формул ${{\Phi }^{{{{y}_{\alpha }}}}}$ в них могут входить вспомогательные объекты, в конечном счете подчиняемые формируемым условиям X и тем самым ответственные за импликацию изучаемых свойств. Такими объектами могут быть, например, координатные преобразования, преобразования шкалы времени и прочие (не обязательно функциональные) отношения связи на декартовых произведениях множеств допустимых значений кванторных переменных из числа y_α, $y_{\alpha }^{'}$ и более старших переменных.

Процесс формирования условий импликации X состоит в применении описываемых далее правил I–IV.

Правило I (переработка ТК). Определение свойства P перерабатывается в формулу D^I заменой каждого ТКВ $\hat {w}$(y_α) на пару

каждого неособого ТКС 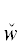(y_α) – на пару

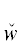и каждого особого ТКС (y_α) – на пару

Деление структурных связок ∨ в P на неособые и особые переносится с формулы P на построенную на ее базе формулу D^I.

Правило II (переработка структурных логических связок и заключительных формул). Формула D^I перерабатывается в D^II заменой всех неособых структурных связок ∨ на & и всех формул P_i на $D_{i}^{{II}}$ = ($P_{i}^{'}$ → P_i). Особые структурные связки ∨ остаются без изменения.

Пример 1а (продолжение примера 1). Пусть модель $\mathfrak{M}'$ = (A', B', f   ' ≤') однотипна модели $\mathfrak{M}$ = (A, B, f, ≤) и ее свойство P ' аналогично свойству P:

По правила I и II получим

Пример 2а (продолжение примера 2). Пусть $\mathfrak{M}'$ – ОДУ:

где g : Ω' × R^q → R ^s удовлетворяет условиям существования классических решений x' ∈ $\mathcal{X}'$(⋅, $t_{0}^{'}$, ${\mathbf{x}}_{0}^{'}$, u') для некоторых u' ∈ $\mathcal{U}'$ и начальных данных ($t_{0}^{'}$, ${\mathbf{x}}_{0}^{'}$) ∈ Ω', x'($t_{0}^{'}$) = ${\mathbf{x}}_{0}^{'}$. Пусть S '(u') = {($t_{0}^{'}$, ${\mathbf{x}}_{0}^{'}$) ∈ ∈ Ω' : $\mathcal{X}'$(⋅, $t_{0}^{'}$, ${\mathbf{x}}_{0}^{'}$, u') ≠ ∅}.

Введем свойство P ' решений уравнения (2.4) относительно некоторых множеств $A_{0}^{'}$, A', $A_{0}^{'}$ ⊆ A', R¹ × A' ⊆ Ω' и $T_{0}^{'}$ ⊆ R¹, аналогичное свойству P вида (1.3) для ОДУ (1.2):

По правилам I и II получим

Лемма 1. D^II → (P ' → P).

Доказательство. Пусть свойства P и P ' имеют одинаковую структуру. Если P = P₁, то доказываемое является тавтологией вида ($P_{1}^{'}$ → P₁) → ($P_{1}^{'}$ → P₁). Пусть Q $ \sqsubseteq $ P и для собственных ГП из Q лемма справедлива (индуктивное предположение), а для самой Q ее надо доказать. Тогда имеет место один из четырех случаев: а) Q = $\hat {w}$(y_α)$\tilde {P}$, б) Q = 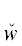(y_α)$\tilde {P}$, в) Q = $\tilde {P}$ ∨ $\tilde {\tilde {P}}$, г) Q = $\tilde {P}$ & $\tilde {\tilde {P}}$.

В случае (а) формуле Q в P ' отвечает Q' = $\hat {w}$($y_{\alpha }^{'}$)P ', а в D^II после шагов I, II применения соответствующих правил переработки Q будет соответствовать формула

Надо доказать, что D^II(Q) → ($\hat {w}$($y_{\alpha }^{'}$)$\tilde {P}'$ → $\hat {w}$(y_α)$\tilde {P}$). Пусть справедливы D^II(Q) и $\hat {w}$($y_{\alpha }^{'}$)$\tilde {P}'$, а y_α – произвольное, подчиненное условию ${{W}^{{{{y}_{\alpha }}}}}$. Надо доказать, что верно $\tilde {P}$. В силу (2.7) существует такое $y_{\alpha }^{'}$, что имеют место ${{W}^{{y_{\alpha }^{'}}}}$, ${{\Phi }^{{{{y}_{\alpha }}}}}$ и D^II($\tilde {P}$). Так как при этом $y_{\alpha }^{'}$ верно $\tilde {P}'$, то по предположению из D^II($\tilde {P}$) и $\tilde {P}'$ следует $\tilde {P}$, что и требовалось доказать в случае а). Случай б) доказывается аналогично случаю а).

В случае в)

и, если справедливо $\tilde {P}{\kern 1pt} '$ или $\tilde {\tilde {P}}{\kern 1pt} '$, то в силу (2.8) и индуктивного предположения верно $\tilde {P}$ или соответственно $\tilde {\tilde {P}}$, что и требовалось доказать. Случай (г) доказывается аналогично случаю в).

Если структура свойства P ' лишь частично совпадает со структурой свойства P, то при тех же четырех случаях а)–г), разобранных выше при доказательстве индуктивного шага, доказательство случаев а) и г) не изменится. В случаях б) (соответственно в)) с особыми структурными элементами ∃ (соответственно ∨) в определении свойства P каждому особому ТКС 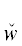(y_α) (соответственно каждой особой логической связке ∨) из P в P ' отвечает ТКВ $\hat {w}$($y_{\alpha }^{'}$) (соответственно логическая связка &), а в D^II – пара ТК 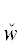($y_{\alpha }^{'}$)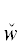*(y_α) (соответственно логическая связка ∨). Таким образом, инверсии в P ' некоторых структурных элементов из P соответствует обратная инверсия в D^II. Поэтому доказательство леммы в случае частичной одинаковости структуры свойств P и P ' аналогично вышеприведенному доказательству для структурно одинаковых P и P '.

Правило III (расщепление по ТКС). Рассмотрим случай одинаковости структур свойств P и P '. Расщепление осуществляется в порядке перехода в D^II от ТКС по старшим переменным к ТКС по младшим. Этот шаг может не выполняться для ТКС с тождественно-истинными формулами связи ${{\Phi }^{{{{y}_{\alpha }}}}}$.

В формуле D^II через ${{u}_{{{{\alpha }_{1}}}}}$ обозначим ту из переменных ${{y}_{{{{\alpha }_{1}}}}}$, $y_{{{{\alpha }_{1}}}}^{'}$, которая является кванторной переменной квантора 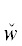*(${{u}_{{{{\alpha }_{1}}}}}$) ∈ {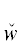*(${{y}_{{{{\alpha }_{1}}}}}$), 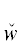*($y_{{{{\alpha }_{1}}}}^{'}$)}. На базе D^II расщепление по первому ТКС 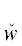*(${{u}_{{{{\alpha }_{1}}}}}$) приводит к формулам

Здесь условие D^II[*(${{u}_{{{{\alpha }_{1}}}}}$)] формируется вначале как последовательность ${{{v}}_{1}}$ … ${{{v}}_{n}}$ 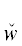*(${{u}_{{{{\alpha }_{1}}}}}$) (n ≥ 1) ТК из D^II, в области действия которых находится 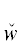*(${{u}_{{{{\alpha }_{1}}}}}$), и самого этого квантора, выписываемая в порядке от старших ТК к младшим. Затем из префикса ${{{v}}_{1}}$ … ${{{v}}_{n}}$ вычеркиваются все ТКН и получается формула ${{D}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ = ${{{\tilde {v}}}_{1}}$ … ${{{\tilde {v}}}_{{{{n}_{1}}}}}$ 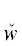*(${{u}_{{{{\alpha }_{1}}}}}$), n₁ ≤ n. Через ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ обозначен результат инверсии в D^II ТКС, входящих в ${{D}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$, в соответствующие ТКВ. Заметим, что те ТКС, которые входили в префикс ${{{v}}_{1}}$ … ${{{v}}_{n}}$ как независимые и не вошли в ${{D}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$, войдут в ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ без инверсии. Через S₁/S₂ здесь и далее обозначается подстановка выражения S₁ вместо S₂.

Далее в ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ ищется очередной старший ТКС 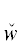*(${{u}_{{{{\alpha }_{2}}}}}$), с которым аналогично предыдущему осуществляется построение ${{D}^{{{{u}_{{{{\alpha }_{2}}}}}}}}$ = ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$[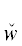*(${{u}_{{{{\alpha }_{2}}}}}$)] и ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{2}}}}}}}}$ = ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$($\hat {w}$*(${{u}_{{{{\alpha }_{2}}}}}$)/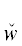*(${{u}_{{{{\alpha }_{2}}}}}$); $\hat {w}$(u_β)/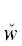(u_β), если (u_β) ∈ ${{D}^{{{{u}_{{{{\alpha }_{2}}}}}}}}$), и т.д., в результате чего будет получен набор формул D^III $\mathop = \limits^{{\text{def}}} $ $\& _{{i = 1}}^{k}$ ${{D}^{{{{u}_{{{{\alpha }_{i}}}}}}}}$ & ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{k}}}}}}}}$.

Если структура свойства P ' лишь частично совпадает со структурой свойства P, то при расщеплении по особым ТКС кванторы 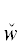*(y_α) рассматриваются в парах 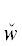($y_{\alpha }^{'}$)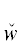*(y_α), а шаги расщепления аналогичны вышеописанным.

Лемма 2. D^III → D^II.

Доказательство. Пусть структуры свойств P и P ' одинаковы. Убедимся сначала, что ${{D}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ & ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ → D^II. Восстановим в условии ${{D}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ все ТКН, вычеркнутые при его построении, но при этом те восстанавливаемые ТКН ${{{v}}_{i}}$, i = $\overline {1,n} $, которые являлись кванторами существования и без инверсии вошли в ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$, инвертируем в ТКВ. Получим некоторое условие $D_{ + }^{{{{u}_{{{{\alpha }_{1}}}}}}}$ = ${{{\tilde {v}}}_{1}}$ … ${{{\tilde {v}}}_{n}}$ 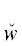*(${{u}_{{{{\alpha }_{1}}}}}$).

Индукцией по структуре формулы $D_{ + }^{{{{u}_{{{{\alpha }_{1}}}}}}}$ нетрудно убедиться в том, что ${{D}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ → $D_{ + }^{{{{u}_{{{{\alpha }_{1}}}}}}}$. Пусть ГП G из $D_{ + }^{{{{u}_{{{{\alpha }_{1}}}}}}}$ в ${{D}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ соответствует ГП $\bar {G}$ и для всех ГП G₁ из G и соответствующих ГП ${{\bar {G}}_{1}}$ из $\bar {G}$ справедливо ${{\bar {G}}_{1}}$ → G₁. Это заведомо так в простейшем случае, когда $\bar {G}$ = G = 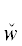*(${{u}_{{{{\alpha }_{1}}}}}$). Если H = ${{{\tilde {v}}}_{i}}$G $ \sqsubseteq $ $D_{ + }^{{{{u}_{{{{\alpha }_{1}}}}}}}$, то этой ГП в ${{D}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ по построению будет соответствовать ГП $\bar {H}$ вида либо а) ${{{\tilde {v}}}_{i}}\bar {G}$, либо б) $\bar {G}$. Поскольку $\bar {G}$ → G, то ${{{\tilde {v}}}_{i}}\bar {G}$ → ${{{\tilde {v}}}_{i}}G$, т.е. в случае а) $\bar {H}$ → H. В случае б) ${{{\tilde {v}}}_{i}}$ – независимый ТКВ ${{{\hat {v}}}_{i}}$ и поэтому G → ${{{\hat {v}}}_{i}}$G. Поскольку $\bar {G}$ → G, снова получаем, что $\bar {H}$ → H. Это завершает обоснование индуктивного перехода. Поэтому с учетом простейшего случая получаем, что ${{D}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ → $D_{ + }^{{{{u}_{{{{\alpha }_{1}}}}}}}$.

Докажем теперь, что $D_{ + }^{{{{u}_{{{{\alpha }_{1}}}}}}}$ & ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ → D^II.

Линейные участки формулы ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ отличаются от соответствующих линейных участков структуры формулы $D_{ + }^{{{{u}_{{{{\alpha }_{1}}}}}}}$ только инверсией некоторых ТКС: если в один из них входит ТКС, то в другой – его инверсия, причем места вхождения ТК существования соответствуют их местам в структуре исходной формулы D^II, а местам вхождения в D^II ТК всеобщности в обеих формулах $D_{ + }^{{{{u}_{{{{\alpha }_{1}}}}}}}$ и ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ одновременно соответствуют ТКВ.

Пусть A, B, C – соответствующие друг другу ГП из $D_{ + }^{{{{u}_{{{{\alpha }_{1}}}}}}}$ True, ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ и D^II, имеющие вид 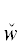*(${{u}_{{{{\alpha }_{1}}}}}$) True, $\hat {w}$*(${{u}_{{{{\alpha }_{1}}}}}$)G, 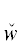*(${{u}_{{{{\alpha }_{1}}}}}$)G, где G – область действия кванторов по переменной ${{u}_{{{{\alpha }_{1}}}}}$ в B и C. Очевидно, что A & B → C (база индуктивного доказательства по сложности структуры формулы D^II).

Предположим теперь, что A, B, C – произвольные, но соответствующие друг другу ГП из тех же формул, причем в силу индуктивного предположения верно, что A & B → C.

Пусть A₁, B₁, C₁ – такие соответствующие друг другу ГП из той же тройки формул, что A $ \sqsubseteq $ A₁, B $ \sqsubset $ B₁, C $ \sqsubset $ C₁ и при этом C₁ – минимальная ГП из D^II. Тогда а) C₁ = ${{{v}}_{1}}$C $ \sqsubseteq $ D^II или б) C₁ = C & $\bar {C}$ $ \sqsubseteq $ D^II (заметим, что именно в случае б) A = A₁). Если C₁ = ${{{v}}_{1}}$C, то A₁ = ${{{v}}_{2}}$A $ \sqsubseteq $ $D_{ + }^{{{{u}_{{{{\alpha }_{1}}}}}}}$, B₁ = ${{{v}}_{3}}$B $ \sqsubseteq $ ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{1}}}}}}}}$ и в случае а) возможны только следующие сочетания ТК: ${{{v}}_{1}}$, ${{{v}}_{2}}$, ${{{v}}_{3}}$ : (${{{v}}_{1}}$, ${{{v}}_{2}}$, ${{{v}}_{3}}$) ∈ {(${\hat {v}}$, ${\hat {v}}$, ${\hat {v}}$), (${\hat {v}}$, 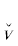, 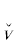), (, 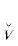${\hat {v}}$, 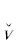)}. Отсюда с учетом того, что A & B → C, верно, что A₁ & B₁ → C₁. В случае б) C₁ = C & $\bar {C}$, A₁ = A, B₁ = B & $\bar {C}$ и поэтому снова A₁ & B₁ → C₁, что завершает обоснование справедливости индуктивного перехода, а с учетом предыдущего и доказательства леммы при одинаковости структур свойств P и P '.

В случае лишь частичной одинаковости структур свойств P и P' и расщепления по особым ТКС обоснование правила III аналогично.

Пример 1б. По правилу III в применении к (1.1) расщеплением условия (2.3) по ТКС ∃x ∈ ∈ B : Φ^x получим два условия:

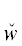(использованная здесь подстановка понимается как инверсия ТКС *(x)).

Расщеплением ${{\tilde {D}}^{{\mathbf{x}}}}$ по ТКС ∃y' ∈ A' : Φ^y получим:

(здесь и далее запись блока одноименных ТКВ ∀${{y}_{{{{\alpha }_{1}}}}}$ : ${{W}^{{{{y}_{{{{\alpha }_{1}}}}}}}}$  ∀${{y}_{{{{\alpha }_{2}}}}}$ : ${{W}^{{{{y}_{{{{\alpha }_{2}}}}}}}}$ ... ∀${{y}_{{{{\alpha }_{n}}}}}$ : ${{W}^{{{{y}_{{{{\alpha }_{n}}}}}}}}$ сокращаем до ∀${{y}_{{{{\alpha }_{1}}}}}$ : ${{W}^{{{{y}_{{{{\alpha }_{1}}}}}}}}$, ${{y}_{{{{\alpha }_{2}}}}}$ : ${{W}^{{{{y}_{{{{\alpha }_{2}}}}}}}}$, ..., ${{y}_{{{{\alpha }_{n}}}}}$ : ${{W}^{{{{y}_{{{{\alpha }_{n}}}}}}}}$; аналогично далее для ТКС);

При расщеплении ${{\tilde {D}}^{{{\mathbf{y}}'}}}$ по ТКС 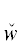*(z) получаются условия

Набор условий D^III будет иметь вид

По леммам 1 и 2 из (2.9) следует, что (2.2) → (1.1).

Пример 2б. Применим правило III к (2.6). Как и в разд. 1 (см. 1.4)) при возможной одинаковости обозначений некоторых кванторных переменных в P (что возможно лишь в случае непересекающихся областей действия их т${\text{и}}'$повых кванторов) условимся, рассматривая ТКС 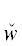*(u_α) (u_α ∈ {y_α, $y_{\alpha }^{'}$}), для различения формулируемых условий обозначать их ${{D}^{{{{u}_{\alpha }}i}}}$, ${{\tilde {D}}^{{{{u}_{\alpha }}i}}}$. Здесь i – номер ветви, в которой находится рассматриваемый ТКС 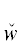*(u_α), i = $\overline {1,m} $ (m – степень свойства P). При этом сам ТКС, а также его т${\text{и}}'$повое условие ${{W}^{{{{u}_{\alpha }}}}}$ будем обозначать тоже с указанием этого номера: 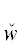*(u_αi), ${{W}^{{{{u}_{\alpha }}i}}}$.

В соответствии с ранее сказанным о том, что некоторые формулы связи ${{\Phi }^{{{{y}_{\alpha }}}}}$ могут быть тождественно-истинными (иначе говоря, отсутствовать), выберем Φ^xi = True, i = $\overline {1,3} $, для сохранения возможности использования ТКС по x' в других условиях из D^III.

По правилу III на базе D^II вида (2.6) расщеплением D^II по ТКС ∃u ∈ $\mathcal{U}$ : Φ ^u формируются два условия:

Аналогично расщеплением ${{\tilde {D}}^{u}}$ по ТКС ∃$t_{0}^{'}$ ∈ R¹ : ${{\Phi }^{{{{t}_{0}}1}}}$ формируются два условия:

Расщеплением ${{\tilde {D}}^{{t_{0}^{'}1}}}$ по ТКС ∃${\mathbf{x}}_{0}^{'}$ ∈ $A_{0}^{'}$ : ${{\Phi }^{{{{{\mathbf{x}}}_{0}}1}}}$ формируются

Расщеплением ${{\tilde {D}}^{{{\mathbf{x}}_{0}^{'}1}}}$ по ТКС ∃t' ≥ $t_{0}^{'}$ : Φ^t1 формируются

Здесь и далее для краткости некоторые ти́повые условия ${{W}^{{{{u}_{\alpha }}}}}$ при ∀u_α, ∃u_α не выписываются, если их вид ясен из контекста. Так в формуле D^t'1 вид этих условий для всех u_α ∈ {u', u, t₀, $t_{0}^{'}$, x₀, ${\mathbf{x}}_{0}^{'}$, x, x', t} представлен в первой ветви из (2.6). Продолжение расщепления приводит к следующим условиям:

(здесь и далее не выписанные для краткости ТК легко восстановить из предыдущего);

В результате получится условие

при выполнении которого по леммам 1 и 2 из (2.5) следует (1.3).

Правило IV (упрощение условий леммы 2). Это упрощение обеспечивается, во-первых, путем полной или частичной конкретизации выбора формул связи ${{\Phi }^{{{{y}_{\alpha }}}}}$, а во-вторых, – путем сокращения наборов свободных переменных в некоторых условиях ${{W}^{{{{y}_{\alpha }}}}}$ и ${{W}^{{y_{\alpha }^{'}}}}$ ти́повых кванторов.

Конкретизация состоит в ограничении наборов свободных переменных, входящих в формулу связи. Это сужает классы формул связи, возможных для использования в синтезируемом условии X, т.е. сужает допустимые к применению МОС. Удаление части свободных переменных из формул связи, как правило, приводит к появлению независимых ТКВ в условиях D^III$\mathop = \limits^{{\text{def}}} $ $\& _{{i = 1}}^{k}{{D}^{{{{u}_{{{{\alpha }_{i}}}}}}}}$ & ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{k}}}}}}}}$, а удаление этих ТК из D^III приводит к более простым достаточным условиям $D_{*}^{{{{u}_{{{{\alpha }_{i}}}}}}}$, $\tilde {D}_{*}^{{{{u}_{{{{\alpha }_{k}}}}}}}$, i = $\overline {1,k} $. Далее ${{\Phi }^{{{{y}_{\alpha }}}}}$(${{y}_{{{{\alpha }_{1}}}}}$, …, ${{y}_{{{{\alpha }_{l}}}}}$) обозначает тот факт, что в формуле ${{\Phi }^{{{{y}_{\alpha }}}}}$ множество свободных переменных не шире списка (${{y}_{{{{\alpha }_{1}}}}}$, …, ${{y}_{{{{\alpha }_{l}}}}}$).

Пример 1в. Сузим в (2.9) классы двух из трех формул связи, выбрав Φ^y(y, y') и Φ^z(z, z'). Набор условий из (2.9) примет вид

где $D_{*}^{{{\mathbf{y}}'}}$ = ∀y ∈ A ∃y' ∈ A' : Φ^y, $D_{*}^{{\mathbf{z}}}$ = ∀y ∈ A, y' ∈ A' : Φ^y, z' = f   '(y') ∃z = f(y) : Φ^z.

Пример 2в. Сузим классы следующих формул связи, ограничив наборы их аргументов:

Например, формулы связи Φ^xi(t, t', x, x') (в ТК 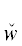*(xi), i = $\overline {1,2} $, и 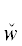*(x'3)) могут задавать частные связи уравнений (1.2) и (2.4) по переменным x, x' с возможным привлечением старших переменных t, t', но не шире, т.е. возможны варианты:

где φ₁ : R¹ × R ^r → R ^s, φ₂ : R¹ × R ^s → R ^r и т.д.

Тогда, применив к D^III сужение наборов свободных переменных в формулах связи ${{\Phi }^{{{{y}_{\alpha }}}}}$ и вычеркивание ТКН, возникающих после этого сужения, придем к следующему набору условий $D_{*}^{{III}}$:

Набор условий (2.11) обеспечивает следование свойства (1.3) из (2.5).

Как было выше отмечено, упрощение посылок из леммы 2 или условий из $D_{*}^{{III}}$ в виде (2.10), (2.11) можно обеспечить также сокращением наборов свободных переменных в некоторых условиях ${{W}^{{{{y}_{\alpha }}}}}$ и ${{W}^{{y_{\alpha }^{'}}}}$ ти́повых кванторов. Здесь мы рассмотрим упрощение загрублением ти́повых условий в некоторых ТКВ, т.е. ослаблением этих условий с одновременным уменьшением разнообразия входящих в этих условия кванторных переменных. При этом некоторые ТКВ $\hat {w}$(y_α), $\hat {w}$($y_{\alpha }^{'}$), $\hat {w}$*(u_α) становятся независимыми и тоже удаляются.

Пусть, например, F – одно из условий леммы 2, $\hat {w}$(z_β)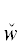(z_α)G $ \sqsubseteq $ F, где ${{W}^{{{{z}_{\alpha }}}}}$ зависит не только от z_α, но и от старших переменных, например z_β, а область G действия квантора $\hat {w}$(z_α) не зависит хотя бы от z_β. Пусть также ${{\tilde {W}}^{{{{z}_{\alpha }}}}}$ не зависит от z_β и ${{W}^{{{{z}_{\alpha }}}}}$ → ${{\tilde {W}}^{{{{z}_{\alpha }}}}}$, т.е. область значений переменной z_α, вообще говоря, расширится в формуле $\tilde {F}$ = F($\hat {w}$(z_α)/$\hat {w}$(z_β)$\hat {w}$(z_α), ${{\tilde {W}}^{{{{z}_{\alpha }}}}}$/${{W}^{{{{z}_{\alpha }}}}}$), но сама формула упростится вычеркиванием независимого ТКВ $\hat {w}$(z_β). Так как оба типа подстановок приводят к достаточным условиям, то справедлива следующая лемма.

Лемма 3. При сформулированных условиях $\tilde {F}$ → F.

Модификация подобными преобразованиями нацелена прежде всего на исключение нежелательных переменных и других объектов, о которых у исследователя меньше информации (например, может не доставать информации о самих движениях динамической системы). Эта модификация с заменами вида $\tilde {F}$ → F осуществима не только на логическом уровне, но и на уровнях более богатых теорий (теории множеств и др.). Такая модификация часто применяется к обычно наиболее сложному поначалу условию ${{\tilde {D}}^{{{{u}_{{{{\alpha }_{k}}}}}}}}$, которое преобразуется в некоторое более простое условие $\tilde {D}$ с получение на шаге IV результата D^IV $\mathop = \limits^{{\text{def}}} $ $\& _{{i = 1}}^{k}{{D}^{{{{u}_{{{{\alpha }_{i}}}}}}}}$ & $\tilde {D}$, где в силу вышеупомянутого D^IV → D^III.

Таким образом, с учетом лемм 1–3 справедлива теорема.

Теорема 1. D^IV → (P ' → P).

Получаемые наборы условий D^IV, как правило, являются новыми (особенно для новых свойств P) либо модификациями известных теорем, а в других случаях обобщают известные теоремы или, наоборот, следуют из них.

Пример 1г. В ти́повых условиях кванторных переменных z' и z из ${{\tilde {D}}^{{\mathbf{z}}}}$ можно выполнить подстановки

и удалить независимые ТКВ по переменным y и y'. Получится достаточное для ${{\tilde {D}}^{{\mathbf{z}}}}$ условие:

Дальнейшее упрощение условий D^IV возможно при полной конкретизации формул связи как частных межмодельных связей. Эта конкретизация осуществима переходом с логического уровня на уровень более богатых теорий (теории множеств и др.).

Выберем формулы связи: Φ^x$\mathop = \limits^{{\text{def}}} $ (φ(x) = x'), Φ^z$\mathop = \limits^{{\text{def}}} $ (φ(z) = z'), где φ : B → B', и Φ^y$\mathop = \limits^{{\text{def}}} $ (ψ(y) = y'), где ψ : A → A'. Тогда набор условий импликации (2.2) → (1.1) примет вид

где

1) D ^x означает сюръективность φ,

2) $D_{*}^{{{\mathbf{y}}'}}$ равносильно просто определению ψ : A → A',

3) $D_{*}^{{\mathbf{z}}}$ ⇔∀y ∈ A φ(f(y)) = f '(ψ(y)),

4) $\tilde {D}_{*}^{{}}$ ⇔∀x ∈ B, z ∈ B (z ≰ x → φ(z) ≰' φ(x)).

По теореме 1 из этих условий следует импликация (2.2) → (1.1).

Пусть, например, A = A' = B = B' = (–∞, 0], f(y) = y³,  f '(y') ≡ y', φ(y) = y^1/3, ψ(y') ≡ y'. В этой интерпретации условия из D^IV выполнены, а функция  f, как и  f  ', обладает свойством ограниченности сверху.

Пример 1д. При рассмотрении по-прежнему свойства P вида (1.1) в качестве P ' можно привлечь не однотипное свойство (2.2), а свойство, структура которого частично повторяет структуру свойства P:

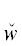где f   ' : (A') → B ', т.е. f  ' – теперь частичная функция. Свойство P – результат инверсии ТК (z') в определении свойства (2.2). Этот ТК является особым. По правилам I–IV запишем набор условий, отличающихся от ранее полученного только некоторым ослаблением условия $D_{*}^{{\mathbf{z}}}$, которое примет вид

Пример 1е. Если изучается обратная импликация свойств (1.1) → (2.2) и направления действия отображений φ и ψ совпадают с направлением импликации, то набор условий D^IV будет следующим:

1) D^x, равносильное определению φ : B → B',

2) $D_{*}^{{{\mathbf{y}}'}}$, означающее сюръективность ψ : A → A',

3) $D_{*}^{{\mathbf{z}}}$ ⇔ ∀y ∈ A φ(f(y)) = f  '(ψ(y)),

4) $\tilde {D}_{*}^{{}}$ ⇔ ∀x ∈ B, z ∈ B (z ∈ x → φ(z) ≤' φ(x)).

Если при этом A = B, A' = B', то свойство P можно рассматривать как свойство алгебраической системы $\mathfrak{M}$ = (A, f, ≥). При его формализации в языке первопорядковой логики оно примет вид

Это выражение принадлежит классу позитивных свойств в смысле [1, 2], т.е. образованных из атомов с помощью связок &, ∨ и кванторов по предметным переменным (без отрицаний и импликаций). Поэтому при сюръективном гомоморфизме должна иметь место импликация P → P '. Условия 1–4 при φ = ψ имеют тоже смысл сюръективного гомоморфизма.

Пример 2г. В примере 2, 2а–2в условие ${{\tilde {D}}^{{{\mathbf{x}}3}}}$ сформулировано в терминах решений x, x' и является наиболее сложным для проверки. Переменные x и x' входят также в условия $D_{*}^{{{\mathbf{x}}{\kern 1pt} '{\kern 1pt} 1}}$, $D_{*}^{{{\mathbf{x}}{\kern 1pt} '{\kern 1pt} 2}}$ и $D_{*}^{{{\mathbf{x}}3}}$, которые связывают решения x и x' уравнений (1.2) и (2.4) между собой, но могут быть сведены к условиям типа траекторного гомоморфизма, например φ(t, x(t, t₀, x₀, u)) = x'(ψ(t), ψ(t₀), φ(t₀, x₀), s(u)), φ : Ω → R^s, или мажорирования (с неравенствами ≤, ≥). Однако условие ${{\tilde {D}}^{{{\mathbf{x}}3}}}$ требует трудно проверяемого на выполнимость некоторого согласованного поведения этих решений относительно пары множеств (A, A'), поэтому желательно упростить ${{\tilde {D}}^{{{\mathbf{x}}3}}}$, что и сделаем по правилу IV.

Поскольку в этом примере в области действия ТК ($\hat {w}$(xi), $\hat {w}$(x'i) переменные x и x' входят в ${{\tilde {D}}^{{{\mathbf{x}}3}}}$ только в ти́повые условия W^xi, W^x'i кванторов всеобщности по x, x' в виде равенств W^xi$\mathop = \limits^{{\text{def}}} $ (x = x(t)) и W^x'i$\mathop = \limits^{{\text{def}}} $ (x' = x'(t')), то возможна замена этих условий на следствия x ∈ R ^r и x' ∈ R ^s соответственно. После этой замены и удаления независимых ТКВ получим постоянное для ${{\tilde {D}}^{{{\mathbf{x}}3}}}$ условие

с новыми ти́повыми условиями в ТК по переменным x, x'.

На базе условий (2.11) заменой ${{\tilde {D}}^{{{\mathbf{x}}3}}}$ на $\tilde {D}$ получим набор условий D^IV.

Конкретизируем формулы связи в двух вариантах:

На основе подстановки в выше полученный набор условий D^IV формул связи (2.12) получается набор условий, упрощение которых с применением как логических, так и нелогических преобразований приводит к следующим достаточным условиям соответственно:

1) s – сюръекция,

2) ψ(R¹) ⊆ R¹ (выполнено по определению ψ),

3) φ(R¹ × A₀) ⊆ $A_{0}^{'}$,

4) ψ – монотонно (выполнено в силу тождественности отображения ψ),

5) ∀u ∈ $\mathcal{U}$ ∀u' ∈ $\mathcal{U}'$ : s(u) = u' ∀(t₀, x₀) ∈ (R¹ × A₀) ∩ S(u) : (ψ(t₀), φ(t₀, x₀)) ∈ S '(u'),

R¹(t₀) ∩ domx(⋅, t₀, x₀, u) ⊆ domx'(⋅, ψ(t₀), φ(t₀, x₀), s(u)),

∀t ≥ t₀ φ(t, x(t, t₀, x₀, u)) $ \prec $ x'(ψ(t), ψ(t₀), φ(t₀, x₀), s(u)),

где R¹(t₀) = {t ∈ R¹ : t ≥ t₀}, $ \prec $ – равенство и тогда ОДУ (1.2) и (2.4) должны обладать единственностью решений или же “≤” и тогда x – любое решение из $\mathcal{X}$(t₀, x₀, u), а x'(⋅, ψ(t₀), φ(t₀, x₀), s(u)) – соответствующее верхнее решение, существующее, например, при квазимонотонной по x' правой части уравнения (2.4),

6) $T_{0}^{'}$ ⊆ ψ(T₀),

7) φ(T₀ × A) ⊆ A',

8) ∀(t, t₀) ∈ R¹ × T₀ (t ≥ t₀ → ψ(t) ≥ ψ(t₀)) (следует из 4),

9) условие 5 с подстановкой (T₀ × A)/(R¹ × A₀),

10) ψ(T₀) ⊆ $T_{0}^{'}$,

11) повтор условия 7,

12) повтор условия 8,

13) ∀t₁ ∈ $\bigcup\limits_{{{t}_{0}} \in {{T}_{0}}}^{} {{{R}^{1}}} $(t₀), t' ≥ ψ(t₁) ∃t ≥ t₁ : ψ(t) = t' (выполнено, если, например, ψ – монотонная биекция),

14) условие 5 с подстановками (T₀ × A)/(R¹ × A₀), dom x/dom x', dom x'/dom x,

15) φ(R¹ × (R ^r\A)) ⊆ R ^s\A'.

Таким образом, для ОДУ (1.2) и его свойства (1.3) с помощью правил I–IV получена следующая теорема.

Теорема 2. Если для ОДУ (1.2) существуют ОДУ (2.4) и отображения ψ : R¹ → R¹, φ : R¹ × × R ^r → R ^s, такие, что выполняются условия 1, 3, 5–7, 9, 10, 13–15, то из свойства (2.5) решений ОДУ (2.4) следует аналогичное свойство (1.3) решений уравнения (1.2).

Пусть, например, ОДУ (1.2) имеет вид

Если в (2.13) преобразование φ : Ω → R¹ выбрать вида φ(t, x) = x/(2 + cost), то полная производная φ(t, x) по t в силу (2.13)

будет равна 0 при u(x) = –x. Поэтому, выбрав ОДУ (2.4) в виде получим, что в (2.14) имеет место свойство (2.5) при любых $T_{0}^{'}$ ⊆ R¹, $A_{0}^{'}$ = A' ⊂ R¹, где A' = (–α, α'), ∀α' > 0. Если выбрать $\mathcal{U}$ = {–x} – singl, $\mathcal{U}{\kern 1pt} '$ = {0} – singl, то условие 1 выполнено. Так как ψ : R¹ × × R¹ – тождественное отображение, то при выбранном u на решениях (2.13) и (2.14) выполняются условия 5, 9, 14 с S(u) = S'(u') = R¹ × R¹ при любых A₀ и A, а также условие 13 и при T₀ = $T_{0}^{'}$ – условия 6, 10. Наконец, если к тому же A₀ = (–1, 1), A = (–3, 3), T₀ = {t₀ : ∃k ∈ {0, 1, 2, …} t₀ = 2kπ}, то будут выполнены и последние упоминаемые в теореме 2 условия 3, 7, 15 при A' = $A_{0}^{'}$ = (–1, 1). Поэтому в (2.13) при выбранных u, T₀, A₀, A имеет место свойство (1.3) ((A₀, A)-оценки и слабой (A, A)-оценки с посещением A из T₀ × A).

В примере 2, 2а–2г определение (2.5) свойства P ' получается из P путем подстановки в (1.3) вместо каждого объекта модели $\mathfrak{M}$ вида (1.2) соответствующего объекта модели $\mathfrak{M}'$ вида (2.4), т.е. P и P ' – однотипные свойства. Если же в (2.5) заменить $A_{0}^{'}$ на A', то полученное свойство станет усилением прежнего (2.5), не будучи уже однотипным свойству P. При этом ослабятся условия D^II, 3 и несколько усилится условие 5. При прежних МОС этим новым набором условий снова будет обеспечено наличие в (1.2) свойства (1.3). Заметим, что новое условие P ', полученное заменой $A_{0}^{'}$ на A', эквивалентно свойству степени 1 обычной инвариантности множества A'.

Пример 2д. Свойство (1.3) неформализуемо в языке первопорядковой логики ввиду наличия в формализованном определении этого свойства кванторов по функциональным переменным x. В качестве примера свойства, в определение которого при формализации вошли бы кванторы по предметным, функциональным и предикатным переменным, приведем определение свойства отдаленности решений ОДУ (1.2) друг от друга при разных начальных состояниях:

где $\mathcal{W}$ – семейство окрестностей диагонали множества R ^r × R ^r (иначе говоря, $\mathcal{W}$ – фильтр окружений равномерной структуры в пространстве R ^r). Неформализуемость (2.15) в первопорядковом языке не препятствует получению условий сохранения этого свойства при переходе от (2.4) к (1.2), например с межмодельными связями:

Применением правил I–IV к свойству (2.15) и однотипному свойству P ' уравнения (2.4) получается следующая теорема.

Теорема 3. Свойство отдаленности (в смысле (2.15)) решений ОДУ сохраняется при переходе от (2.4) к (1.2), если выполняется следующий набор условий:

1) ψ(T₀) ⊆ $T_{0}^{'}$,

2) s – сюръекция,

3) φ(T₀ × A₀) ⊆ $A_{0}^{'}$ и сужение φ на множество A₀ инъективно при любом фиксированном t₀ ∈ T₀,

4) верхние решения ОДУ (2.4) существуют при любых начальных данных (ψ(t₀), φ(t₀, x₀), s(u)) и продолжимы вправо не менее, чем решения ОДУ (1.2) с начальными данными (t₀, x₀, u) ∈ T₀ × × A₀ × $\mathcal{U}$,

5) ψ(R¹(t₀)) ⊆ R¹(ψ(t₀)) для любых t₀ ∈ T₀,

6) на решениях x и соответствующих верхних решениях x' справедлива оценка φ(t, x(t, t₀, x₀, u)) ≤ ≤ x'(ψ(t), ψ(t₀), φ(t₀, x₀), s(u)),

7) ∀t₀ ∈ T₀ ∀$\mathcal{V}'$ ∈ $\mathcal{W}'$ ∃$\mathcal{V}$ ∈ $\mathcal{W}$ ∀t ∈ R¹(t₀) (φ(t, ⋅), φ(t, ⋅))($\mathcal{V}$) ⊆ $\mathcal{V}'$ (при каждом t₀ ∈ T₀ условие равномерной по t ∈ R¹(t₀) непрерывности канонического распространения отображения φ(t, ⋅) : R ^r → R ^s на произведение R ^r × R ^r).

В частности, для ОДУ (2.13) и (2.14), а также выбранных ранее отображений φ(t, x), ψ(t), u(x), u'(x') получим, что все условия теоремы 3 выполнены при том, что ОДУ (2.14) заведомо обладает свойством отдаленности. Поэтому в ОДУ (2.13) имеет место свойство (2.15).

Заключение. Предложен метод получения содержательных решений логических уравнений X → (P ' → P) для произвольных математических моделей связанных систем и их структурно близких свойств. Не требуется эвристического подбора и включения в уравнение того или иного априорно задаваемого условия межмодельной связи, формулируемого в терминах межмодельных объектов связи и объектов обеих моделей согласованно с P и P ' по порядку квантификации переменных. Вместо этого используется конъюнктивное встраивание в каждый ТКС формируемого решения X относительно простого и обычно бескванторного условия связи значения кванторной переменной этого ТКС со значениями некоторых ее старших переменных.

Метод обладает высокой алгоритмичностью и общностью. Он позволяет варьировать выбор межмодельных объектов связи для модификации условий X и упрощения их проверки на выполнимость. В случае неоднотипности свойств P и P ' структура свойства P ' должна совпадать со структурой свойства P хотя бы с точностью до замены некоторых меток ∃, ∨ на ∀, & соответственно.

Первые шаги применения метода выполняются на логическом уровне чисто алгоритмически, а последующие – на логической и теоретико-множественной основе с элементами довольно простых эвристик. Получаемые теоремы, как правило, являются новыми (особенно для новых свойств) или модификациями известных, а в других случаях – следствиями или, наоборот, обобщениями известных теорем. Все шаги применения метода детально проиллюстрированы на примерах с интерпретацией условий получаемых теорем.