Известия РАН. Теория и системы управления, 2020, № 5, стр. 157-176

Введение. Эффективность средств и методов управления движением космического аппарата (КА) непосредственно влияет на эффективность выполнения целевых программ – на объем решаемых задач, проведенных наблюдений и экспериментов, на точность полученных результатов, на время активного существования на орбите и целевого применения КА и т.д. К проблеме управляемых вращений твердого тела вокруг центра масс многие исследователи обращались неоднократно [1–19]. В данной работе решается задача приведения КА в положение заданной ориентации оптимальным образом. Большинство существующих решений задачи пространственного разворота соответствуют вращению вокруг неподвижной оси [1–4]. И хотя принципы оптимизации и алгоритмы управления различны (на основе нечеткой логики [1], обратных задач динамики [2] и др.), результирующее управление приводит к развороту вокруг оси, неподвижной относительно связанной системы координат. В то же время разворот в плоскости наименьшего угла разворота во многих практических случаях не является оптимальным, как бы точно он не исполнялся.

Большой практический интерес представляют аналитические решения задачи оптимального разворота в замкнутой форме, так как они позволяют применять на борту КА готовые законы программного управления и изменения оптимальной траектории движения КА. Некоторые решения известны для сферически-симметричного [4, 9] и осесимметричного КА [6, 8, 10]. Для КА с произвольным распределением масс при произвольных граничных условиях по угловому положению КА аналитическое решение задачи пространственного разворота не найдено; известны лишь некоторые особые случаи решения задачи разворота (например, [3, 4]). Вопросы создания высокоэффективных алгоритмов управления ориентацией КА остаются актуальными и сегодня. В частности, КА дистанционного зондирования Земли, мониторинга, а также астрофизические и другие научные КА требуют периодической смены ориентации для наведения научных приборов и целевой аппаратуры на интересующие участки земной поверхности или область небесной сферы. Минимизация длительности разворота увеличит время наблюдения и улучшит условия их выполнения (заметим, что задачи оптимального по времени разворота решались и раньше [4–8]).

Нередко управление ориентацией осуществляется инерционными исполнительными органами (системой силовых гироскопов или гиродинами) [11]. В этом случае разворот выполняется за счет перераспределения кинетического момента между системой гиродинов и корпусом КА. Маневренность таких КА определяется главным образом длительностью поворотного маневра; чем быстрее КА может совершать развороты, тем выше маневренность КА. Для исключения “насыщения” гиросистемы ее суммарный кинетический момент не должен превышать допустимого значения. Ниже исследуется задача определения оптимальной по времени программы переориентации КА, при которой запас кинетического момента системы гиродинов был бы достаточным для выполнения маневра без привлечения других (кроме гиродинов) средств управления ориентацией КА (время перехода в заданное конечное угловое положение должно быть минимальным). Подробно изучен случай разворота КА, управляемого силовыми гироскопами, с учетом действия возмущающих моментов.

1. Уравнения углового движения и постановка оптимизационной задачи. Под поворотным маневром понимают перевод связанных осей КА из одного известного углового положения в другое известное (обычно заданное) угловое положение за конечное время Т. Полагаем, что управление угловым положением КА осуществляется посредством исполнительных механизмов, создающих вращающие моменты относительно всех трех главных центральных осей инерции КА. Для описания пространственного движения КА используем математический аппарат кватернионов (параметров Родрига–Гамильтона). Движение связанного базиса Е относительно опорного базиса I будем задавать кватернионом Λ [4]. Для определенности базис I считается инерциальным. Поэтому справедливы следующие кинематические уравнения:

или в кватернионной форме: где ω_i , i = $\overline {1,\;3} $, – проекции вектора ω абсолютной угловой скорости КА на оси связанного базиса E, образованного главными центральными осями эллипсоида инерции аппарата; λ_j , j = $\overline {0,\;3} $, – компоненты кватерниона Λ (sqalΛ = λ₀ – скалярная часть кватерниона Λ; vectΛ = λ₁e₁+λ₂e₂+λ₃e₃ – векторная часть кватерниона Λ; e₁, e₂, e₃ – орты осей связанного базиса E), причем ||Λ|| = = $\lambda _{0}^{2} + \lambda _{1}^{2} + \lambda _{2}^{2} + \lambda _{3}^{2}$ = 1; символ “$ \circ $” – знак умножения кватернионов [4, с. 11–20]. Кватернион Λ, задающий текущую ориентацию КА, принят нормированным [4] для удобства. Здесь и далее операция кватернионного умножения на вектор понимается как умножение на кватернион с нулевой скалярной частью; в частности $\Lambda \circ \omega = \Lambda \circ \Omega $, где Ω – кватернион, у которого sqalΩ = 0, vectΩ = ω. Запишем граничные условия задачи разворота: где Т – время окончания поворотного маневра. Кватернионы Λ_н и Λ_к, задающие ориентацию связанных с КА осей в начальный и конечный моменты времени, имеют произвольные наперед заданные значения, удовлетворяющие условию ||Λ_н|| = ||Λ_к|| = 1 (полагаем, что Λ_к ≠ ±Λ_н).

Под маневренностью понимается способность КА совершать маневры вокруг центра масс за меньшее время. Чем быстрее мы можем перенацелить КА на новый объект наблюдения (в данном случае развернуть КА) или для проведения очередной коррекции орбиты, тем больше полезного времени будет для выполнения целевой задачи (для использования КА по целевому назначению – снимкам из космоса, для изучения интересующих объектов, получения метеоинформации и т.д.). Оптимизация способа переориентации (в смысле маневренности КА) повышает эффективность использования КА. Поскольку разворот выполняется с помощью силовых гироскопов [11], главной характеристикой становится кинетический момент L корпуса КА. С целью улучшения маневренности КА оптимальным будем считать движение, при котором длительность маневра Т минимальна.

При управлении ориентацией КА силовыми гироскопами кинетический момент G гиросистемы должен находиться внутри заданной ограниченной области S, выход за которую приводит к потере управляемости КА. При исследовании управляемых вращений КА с инерционными исполнительными органами принято считать допустимыми движения, которые удовлетворяют условию |G| ≤ R₀, где R₀ – радиус сферы, вписанной в область S возможных значений кинетического момента G гиросистемы [12–14]. Чтобы разворот произошел без “разгрузки” гиросистемы, в любой момент времени модуль кинетического момента системы гиродинов должен быть заведомо меньше радиуса R₀ сферы, вписанной в область возможных значений кинетического момента гиросистемы S (R₀ > 0) [11]. Если возмущающие моменты малы, то общий кинетический момент КА как твердого тела с вращающимися массами равен или близок нулю (L + G ≈ 0). Поэтому оптимальное движение КА должно удовлетворять условию

где L_max – максимально допустимая величина кинетического момента, такая, что 0 < L_max < R₀ (запас кинетического момента R₀ – |L| > 0 необходим для использования его на компенсацию предполагаемых возмущающих моментов М_в). Задачу оптимального управления сформулируем следующим образом: необходимо развернуть КА из положения (1.2) в положение (1.3) в соответствии с уравнениями (1.1) при ограничении (1.4) за минимальное время Т. Принципиальным отличием от известных задач оптимизации является то, что в задаче (1.1)–(1.4) правая часть неравенства (1.4) не постоянна (L_max – постоянная величина только в том случае, если какие-либо возмущения полностью отсутствуют и М_в = 0); в общем случае разворота значение L_max как неизвестная функция времени подлежит оптимизации (если иметь в виду действие на КА возмущающих моментов). Необходимо отметить, что принцип максимума напрямую применим, только если правая часть в ограничении (1.4) постоянна. В случае, когда ограничение на управление зависит от времени, требуется дополнительное исследование.

Особенность повышения маневренности КА, управляемого силовыми гироскопами (гиродинами), заключается в необходимости определения величины L_max и решении задачи максимального быстродействия как классической задачи оптимального управления (L_max должна быть как можно ближе к R₀, но при этом достаточной для компенсации возможных возмущений или отклонений). Когда возмущающие моменты пренебрежимо малы, значение L_max можем считать известным (например, L_max = 0.99R₀). В противном случае (когда действие возмущающих моментов необходимо учитывать) задача оптимального управления кинетическим моментом во время разворота включает две задачи – оптимизация ограничивающего уровня L_max для модуля кинетического момента |L| и построение оптимальной программы изменения кинетического момента при известном изменении L_max; изменение параметра L_max в условии (1.4) должно быть оптимальным, чтобы максимально полно использовать располагаемый кинетический момент гиросистемы для минимизации длительности маневра.

2. Решение задачи оптимального управления без учета возмущений. Изучение проблемы обеспечения разворота КА без “разгрузки” системы управляющих гиродинов начнем с ситуации, когда возмущающие моменты пренебрежимо малы и их влиянием можно пренебречь. В этом случае значение L_max известно, и в ограничении (1.4) L_max – постоянный параметр. Будем решать поставленную задачу (1.1)–(1.4), используя принцип максимума Л.С. Понтрягина [20]. Управляющими переменными принимаем угловые скорости ω_i относительно осей связанного базиса E. Наличие фазового ограничения ||Λ|| = 1 несущественно, так как оно всегда выполняется (при любых движениях КА вокруг центра масс). Переменные ${{\lambda }_{j}}$ имеют свойство – в силу уравнений (1.1) норма ||Λ|| кватерниона Λ есть величина постоянная, $\lambda _{0}^{2} + \lambda _{1}^{2} + \lambda _{2}^{2} + \lambda _{3}^{2}$ = const. В начальный момент времени ||Λ(0)|| = ||Λ_н|| = 1, поэтому ||Λ(t)|| = 1 в любой момент времени t ∈ [0, T]. Так как критерий оптимальности не включает позиционных координат λ_j , мы можем использовать универсальные переменные r_i, $i = \overline {1,3} $ [15], заменяющие сопряженные переменные. Для задачи максимального быстродействия (или максимальной маневренности КА) функция Гамильтона Н равна

Оптимальные функции r_i, как компоненты вектора r, удовлетворяют уравнениям

Вектор r неподвижен относительно инерциального базиса I, из-за чего |r| = const ≠ 0. Решение r(t) системы (2.2) определяется начальным Λ_н и конечным Λ_к положениями КА. Оптимальная функция r(t) вычисляется через кватернион Λ(t) [4, 15]:

(составляющие вектора c_E – проекции вектора r на оси инерциального базиса I). Так как время разворота Т не фиксировано, оптимальное решение должно удовлетворять условию Н(Т) = 0. Система (2.2) совместно с требованием максимальности гамильтониана H и условием Н(Т) = 0 являются необходимыми условиями оптимальности (заметим, что составленная краевая задача всегда имеет решение). Условия максимума функции H определяют искомое решение ω(t); граничные условия по положению (для Λ(0) и Λ(Т)) определяют решения Λ(t) и r(t).

Краевая задача принципа максимума заключается в нахождении значения r(0), при котором решение системы дифференциальных уравнений (1.1), (2.2) с одновременной максимизацией в каждый момент времени гамильтониана Н удовлетворяет условиям разворота Λ(0) = Λ_н, Λ(Т) = Λ_к и требованию Н(Т) = 0. В случае |L| ≤ L_max максимум гамильтониана Н достигается при |L| = L_max, поэтому оптимальные функции ω_i определяются выражением

Поскольку оптимальные угловые скорости ω_i не зависят от |r|, перейдем к нормированному вектору р = r/|r| и обозначим r₀ = |r| = const = |r(0)| ≠ 0. Для проекций p_i орта р на оси связанного базиса Е справедливы уравнения

и

В дальнейшем будем использовать компоненты p_i вектора р; переменные r_i = r₀p_i, где r₀ – константа, которую необходимо определить в процессе оптимизации. Необходимое условие оптимальности можно записать в виде

где $b = {{{{L}_{{\max }}}} \mathord{\left/ {\vphantom {{{{L}_{{\max }}}} {\sqrt {р_{1}^{2}{\text{/}}J_{1}^{2} + р_{2}^{2}{\text{/}}J_{2}^{2} + р_{3}^{2}{\text{/}}J_{3}^{2}} }}} \right. \kern-0em} {\sqrt {р_{1}^{2}{\text{/}}J_{1}^{2} + р_{2}^{2}{\text{/}}J_{2}^{2} + р_{3}^{2}{\text{/}}J_{3}^{2}} }} > 0$ – скалярная величина.

С учетом зависимостей (2.4) для оптимального движения гамильтониан равен

В случае отсутствия возмущающих моментов L_max = const, гамильтониан Н не зависит в явном виде от времени и длительность Т не фиксирована. Поэтому Н = 0 в любой момент времени t [21]. Подставив оптимальные значения функций ω_i , вычисленные по соотношениям (2.4), в выражение (2.1) для функции Н с учетом равенств r_i = r₀p_i , получим уравнение

из которого следует $p_{1}^{2}{\text{/}}J_{1}^{2} + p_{2}^{2}{\text{/}}J_{2}^{2} + p_{3}^{2}{\text{/}}J_{3}^{2}$ = const и r₀ = 1/(L_maxС) – оптимальное значение, где C = $\sqrt {p_{{10}}^{2}{\text{/}}J_{1}^{2} + p_{{20}}^{2}{\text{/}}J_{2}^{2} + p_{{30}}^{2}{\text{/}}J_{3}^{2}} $; р₁₀, р₂₀, р₃₀ – компоненты вектора р₀ = p(0).

Задача построения оптимального управления свелась к решению системы уравнений углового движения КА (1.1) и уравнений (2.3) при условии, что управление ω выбрано из требования (2.4). Сформулированная задача управления (1.1)–(1.4) решается до конца. Условия максимума функции H определяют оптимальное решение ω(t). На всем интервале движения 0 < t < Т КА должен вращаться с постоянным по модулю кинетическим моментом |L| = const (поэтому во время идеального по маневренности разворота b = const). Уравнения (1.1) и (2.3) совместно с соотношениями (2.5) образуют замкнутую систему уравнений. Значение параметра С зависит от вектора р(0), который в свою очередь определяется граничными значениями Λ(0), Λ(Т) и моментами инерции J₁, J₂, J₃.

Таким образом, задача построения оптимального управления ω(t) состоит главным образом в нахождении такого значения вектора р(0), при котором в результате движения КА в соответствии с уравнениями (1.1), (2.3), (2.5) и Λ(0) = Λ_н выполнялось равенство Λ(Т) = Λ_к. Общее решение приведенной системы уравнений найти практически невозможно. Трудность заключается в определении граничных значений p(0) и p(T), которые связаны выражением

где ${{\Lambda }_{{\text{р}}}} = {{\tilde {\Lambda }}_{{\text{н}}}} \circ {{\Lambda }_{{\text{к}}}}$ – кватернион разворота. Задача оптимального управления с учетом ограничения (1.4) будет решена, если мы найдем решение системы уравнений (1.1), (2.3), (2.4), удовлетворяющее граничным условиям (1.2) и (1.3). Оптимальная угловая скорость ω связана с кватернионом ориентации Λ зависимостью: где c_Р = const = Λ_н $ \circ $ p₀ $ \circ $ ${{\tilde {\Lambda }}_{{\text{н}}}}$ ; J_КА = diag(J₁, J₂, J₃) – тензор инерции КА (напомним, что р_i0 = р_i(0)). Ключевой искомой характеристикой является значение вектора р₀ = p(0).

Решение ω(t) во время кинематически оптимального разворота (без ограничений на силовые моменты) обладает свойствами (интегралами движения):

Поскольку управлением считается вектор ω угловой скорости КА, то поставленную кинематическую задачу оптимального разворота можно считать решенной – уравнения (1.1), (2.3) и (2.4) с учетом граничных условий (1.2), (1.3) полностью определяют искомое решение ω(t). Уравнения для управляющих функций ω_i формализуются так:

Допустимое многообразие для начальной угловой скорости описывается уравнением

Оптимальное управление пространственным разворотом заключается в сообщении КА начальных условий движения (расчетной угловой скорости в начале разворота), поддержании вращения КА с требуемым (программным) изменением угловой скорости ω(t), при котором модуль кинетического момента имеет постоянное значение |L| = const, и сбросе имеющегося кинетического момента до нуля в момент времени t = Т, когда Λ(t) = Λ_к (при достижении КА конечного положения Λ_к). Основная задача – нахождение закона изменения вектора p(t), чтобы в результате решения системы уравнений (1.1), (2.3), (2.4) с начальными условиями Λ(0) = Λ_н граничное условие Λ(T) = Λ_к на правом конце было выполнено (определение вектора p(0) – самостоятельная и достаточно непростая задача).

Однако построить управление в форме синтеза в рассматриваемой задаче будет сложно (например, из-за нелинейности краевой задачи принципа максимума). Также заметим, что в случае разворота КА из положения покоя в положение покоя указанное движение (импульсный разгон, вращение в соответствии с (2.6), импульсное торможение) является квазиоптимальным, так как оптимальность обеспечивается только на одном из трех временных участков при определенных условиях (ограничениях на угловую скорость) в начале среднего участка и при отсутствии возмущений. При этом бесконечно большие управляющие моменты для мгновенного разгона и торможения на первом и третьем участках соответственно недопустимы.

Важнейшей характеристикой для КА, управляемых гиродинами, является интеграл

Время разворота в соответствии с уравнениями (2.7) равно T_ид = Q₀/R₀, если ω(0) = $J_{{{\text{КА}}}}^{{ - 2}}$R₀p₀/C (такой разворот назовем идеальным, возмущения отсутствуют), где Q₀ – значение интеграла Q, когда вращение удовлетворяет уравнениям (2.3), (2.5) (независимо от характера изменения скалярной величины b). Ранее было показано [16], что для движений, удовлетворяющих уравнениям (2.3), (2.5), значение интеграла (2.8) минимально.

Для динамической системы (1.1) управление (2.6) является оптимальным по быстродействию при наличии ограничения (1.4). Так как время Т не ограничено, то такое вращение КА всегда можно осуществить. Для оптимального движения ω(t) выполняются уравнения (2.3) и (2.4). Определяющим в решении задачи оптимального разворота (при построении оптимального программного движения ω(t) и оптимальной траектории Λ(t)) станет нахождение начальных условий р(0) (вектор р(0) зависит исключительно от параметров разворота Λ_р и моментов инерции КА J₁, J₂, J₃ и не зависит от L_max). Оптимальное изменение функций p_i описывается уравнениями:

Для построения оптимального управления при развороте КА необходимо знать не только программу изменения координат р_i(t), но и характеристику L_max, определяющую не только длительность маневра, но и запас кинетического момента гиросистемы. Особенностью управления угловой скоростью КА во время разворота за минимальное время является то, что при наличии возмущающих моментов (когда М_в≠0) значение ключевого параметра L_max алгоритма оптимального управления заранее не известно. Поэтому при практическом проектировании требуется предварительно решить задачу определения оптимального значения модуля кинетического момента КА во время номинального вращения, соответствующего закону (2.6).

3. Решение задачи оптимального разворота с учетом возмущений. Рассмотренное выше управление угловым положением КА может быть реализовано с помощью способа [17]. Действие возмущающего момента М_в приводит к тому, что |G| ≠ |L(t)|. Для КА с инерционными исполнительными органами (силовыми гироскопами) крайне важно определить такое значение параметра L_max, чтобы во время движения КА вокруг центра масс эволюция вектора G суммарного кинетического момента системы гиродинов не привела к выходу его за пределы области S возможных значений (тогда “насыщения” системы гиродинов не наступит) и “разгрузки”, т.е. снятия накопленного кинетического момента системы гиродинов за счет приложения момента сил иной природы (магнитного, включением реактивных двигателей ориентации и др.) не потребуется. Такие движения КА считаются допустимыми (в смысле управления ориентацией КА без “разгрузки” системы гиродинов). При этом запас кинетического момента системы гиродинов должен быть максимальным, что позволит уменьшить вероятность задействования других (кроме гиродинов) средств управления ориентацией (например, реактивных двигателей) даже при действии на КА возмущающего момента.

При разработке, анализе, отработке и моделировании алгоритмов управления ориентацией КА с силовыми гироскопами принимается, что область располагаемого кинетического момента системы силовых гироскопов ограничена сферой (такое утверждение используется многими разработчиками и конструкторами [12–14]). В случае отсутствия возмущающих моментов можем считать |G| = |L(t)|, и выполнение ограничения (1.4) гарантирует удовлетворение условия |G| ≤ R₀, из-за чего вектор G останется внутри области S (без “разгрузки” гиросистемы). Чтобы время Т было минимальным, L_max должно быть максимально близким к R₀.

В реальных условиях полета М_в ≠ 0, поэтому L + G ≠ 0, а значит на участке номинального вращения (когда удовлетворяются (2.3), (2.4)) в общем случае d|G|/dt ≠ 0. При наличии возмущающих моментов М_в ≠ 0 возникает проблема – каким должно быть значение L_max, чтобы до окончания маневра возможное увеличение величины |G| было меньше R₀ – L_max. Хотя возмущения М_в могут “помогать” развороту КА (при этом d|G|/dt < 0), но гарантировать, что такое положение вещей будет продолжаться на всем отрезке времени [0, T], никак нельзя. Поэтому при выборе оптимального значения L_max необходимо учитывать наихудший сценарий – считать возмущения М_в максимально возможными по величине и направленными против кинетического момента L корпуса КА. Тогда d|G|/dt = |М_в| и $\mathop {\max }\limits_{0 < t < T} d\left| {\mathbf{G}} \right|{\text{/}}dt$ = М_рас, если оставить |L| = const, где М_рас – расчетное значение (полученное, например, по экспертным оценкам) максимально возможной величины возмущающего момента М_в (т.е. |М_в| ≤ М_рас). Если принять постоянным |L|, то наихудший сценарий поведения модуля кинетического момента G гиросистемы, когда d|G|/dt ≥ 0, можно оценить по выражению

Мы заинтересованы в том, чтобы L_max было как можно больше (для минимизации времени Т). Однако с увеличением L_max запас ΔR = R₀ – L_max уменьшается, что в свою очередь повышает вероятность наступления “насыщения” гиросистемы (т.е. выполнения равенства |G| = R₀). Здесь становится актуальной задача максимального использования запаса кинетического момента R₀ – |L| для компенсации предполагаемых возмущающих моментов.

Чтобы максимально полно использовать запас ΔG = R₀ – |G| кинетического момента гиросистемы, необходимо оптимизировать изменение модуля |L(t)| и сделать зависящей от времени величину L_max. Для гарантированного исключения “насыщения” гиросистемы достаточно принять следующую программу изменения параметра L_max:

или (при известном значении М_рас для возмущающего момента М_в). Нетрудно показать, что для вращений твердого тела, удовлетворяющих уравнениям (2.3), (2.5), справедливо равенство где величина Q₀ не зависит от характера изменения модуля |L| кинетического момента и определяется исключительно кватернионом разворота ${{\Lambda }_{{\text{р}}}} = {{\tilde {\Lambda }}_{{\text{н}}}} \circ {{\Lambda }_{{\text{к}}}}$ и инерционными характеристиками КА J₁, J₂, J₃ [16]. Время оптимального разворота, соответствующего уравнениям (2.3), (2.4), в которых величина L_max изменяется согласно закону (3.1), составляет

Зависимость T_opt от Q₀ есть монотонно возрастающая функция. Время T_opt минимально, так как для движений, удовлетворяющих уравнениям (2.3), (2.4), значение интеграла (2.8) минимально [16].

Управляющие переменные рассчитываются в соответствии с законом (2.4), (3.1), для реализации которого необходимо в каждый момент времени t знать все три переменные р₁, р₂, р₃ . При оптимальном движении компоненты р_i вектора р подчиняются уравнениям (2.9), в которых L_max рассчитывается в соответствии с (3.1). Общее решение системы уравнений (1.1), (2.3), (2.4) получить практически невозможно; трудность заключается в определении граничных значений p(0) и p(T), которые связаны между собой выражением

или р(Т) = ${{\tilde {\Lambda }}_{{\text{Р}}}} \circ {\mathbf{р}}\left( 0 \right) \circ {{\Lambda }_{{\text{Р}}}}$, где ${{\Lambda }_{{\text{р}}}} = {{\tilde {\Lambda }}_{{\text{н}}}} \circ {{\Lambda }_{{\text{к}}}}$ – кватернион разворота.

Приведенная система имеет аналитическое решение только для динамически симметричного и сферического тел. Для сферически-симметричного КА (J₁ = J₂ = J₃) решение такое:

где ${{\nu }_{1}},\;{{\nu }_{2}},\;{{\nu }_{3}}$ – компоненты векторной части кватерниона разворота Λ_р; Q₀ = 2J₁arccos (sqalΛ_р).

Для динамически симметричного КА (например, когда J₂ = J₃) задача оптимального управления разворотом решается до конца (не умаляя общности рассуждений, за ось симметрии принята ось ОХ КА). Оптимальное движение в этом частном, но достаточно распространенном случае представляет собой одновременное вращение КА как твердого тела вокруг своей продольной оси ОХ и вокруг некоторого направления η, неподвижного в инерциальном пространстве и составляющего с продольной осью КА определенный постоянный угол ϑ. Угловые скорости относительно осей ОХ и η пропорциональны с постоянным коэффициентом пропорциональности, и поэтому справедливо соотношение

где р₀ = р(0); е₁ – орт продольной оси КА; α – угол поворота КА вокруг продольной оси ОХ; β – угол поворота КА вокруг вектора р (углы α и β удовлетворяют неравенствам |α| ≤ π, 0 ≤ β ≤ π); вектор в показателе степени кватернионной экспоненты понимается как кватернион с нулевой скалярной частью. Решение p(t) системы уравнений (1.1), (2.3), (2.4) представим так: где p_{i 0} = р_i(0); J = J₂ = J₃; ϑ – угол отклонения продольной оси КА от вектора p; ($\dot {\alpha } = {{\omega }_{1}} - {{\sqrt {\omega _{2}^{2} + \omega _{3}^{2}} {{p}_{{10}}}} \mathord{\left/ {\vphantom {{\sqrt {\omega _{2}^{2} + \omega _{3}^{2}} {{p}_{{10}}}} {\sqrt {1 - p_{{10}}^{2}} }}} \right. \kern-0em} {\sqrt {1 - p_{{10}}^{2}} }}$ – скорость собственного вращения); угловые скорости ω_i(t) определяются из равенств (2.4) с учетом р₁ = const = р₁₀ и $p_{2}^{2} + p_{3}^{2} = {\text{const}} = p_{{20}}^{2} + p_{{30}}^{2}$. Зависимость параметров p_i0, α, β от граничных значений Λ_Н и Λ_К определяется системой уравнений: где ${{\nu }_{0}},\;{{\nu }_{1}},\;{{\nu }_{2}},\;{{\nu }_{3}}$ – компоненты кватерниона разворота Λ_р; –π ≤ α ≤ π, 0 ≤ β ≤ π.

Программные значения угловых скоростей ω_i изменяются в соответствии с уравнениями:

где σ₀ = arctg(p₂₀/p₃₀); $\dot {\alpha }$ – угловая скорость собственного вращения (вокруг продольной оси); $\dot {\beta }$ – угловая скорость прецессии (вокруг вектора р). Траектория движения следующая: где χ = $\int\limits_0^t {\dot {\beta }dt} $; $\dot {\beta } = {{L}_{{\max }}}{\text{/}}(J_{2}^{2}\sqrt {p_{{10}}^{2}{\text{/}}J_{1}^{2} + (p_{{20}}^{2} + p_{{30}}^{2}){\text{/}}J_{2}^{2}} )$.

При наличии ограничения (1.4) время разворота T минимально, если минимально значение Q. Время кинематически оптимального разворота рассчитываeтся по формуле (3.2), где

Время T_opt – монотонно возрастающая функция аргумента Q₀. Отсюда отчетливо видно, что при оптимальном по быстродействию движении КА значения углов поворотов α, β и угла ϑ между продольной осью КА и вектором р должны удовлетворять системе (3.3) и условию

Оптимизация в этом частном случае сводится к нахождению таких значений параметров ϑ, α, β и вектора p₀, удовлетворяющих условиям разворота (1.2), (1.3) и соответственно системе (3.3), чтобы величина (3.4) была минимальной. Таким образом, кинематическую задачу переориентации КА (как твердого тела) можно считать решенной. Оптимальные значения углов α, β и ϑ и вектора p₀, удовлетворяющие заданным граничным значениям Λ_н и Λ_к в соответствии с уравнениями (3.3), могут быть определены с помощью устройства [22].

Для несимметричного КА (${{J}_{1}} \ne {{J}_{2}} \ne {{J}_{3}}$) решение системы уравнений (1.1), (2.3), (2.4) в квадратурах не представляется возможным и находится исключительно численными методами (например, методом последовательных приближений). Определение вектора p₀ производится путем решения краевой задачи р(0) = р₀, р(Т) = ${{\tilde {\Lambda }}_{{\text{Р}}}} \circ {{{\mathbf{р}}}_{0}} \circ {{\Lambda }_{{\text{Р}}}}$ с учетом накладываемых на движение связей (2.9). При решении краевой задачи в уравнениях (2.9) полагаем b = const (и соответственно |L| = const), так как искомое значение p₀ не зависит от характера изменения модуля |L| [16]. В результате получим значение кинетического момента в начальный момент времени L_рас, при котором обеспечивается перевод КА из состояния Λ(0) = Λ_н, L(0) = L_рас в состояние Λ(Т) = Λ_к в соответствии с уравнениями (1.1) в условиях закона движения (2.7) (L(Т) при этом принципиального значения не имеет). Значение вектора p₀ связано с найденным L_рас соотношениями

Значение интеграла Q рассчитывается моделированием движения в соответствии с уравнениями (1.1), (1.2), (2.5), (2.9) с начальным условием ω(0) = $J_{{{\text{КА}}}}^{{ - 1}}{{{\mathbf{L}}}_{{{\text{рас}}}}}$ и с учетом найденного вектора p₀.

4. Построение типовой программы оптимального разворота с учетом ограниченности управляющего момента. Практическое значение имеют задачи, в которых ω(0) = ω(Т) = 0 (такие условия разворота КА наиболее характерны). Разумеется, в моменты времени t = 0 и t = T угловая скорость для номинальной программы вращения КА, определяемая уравнениями (2.4), не равна нулю. Следовательно, неизбежны переходные участки: разгон – переход из состояния покоя (когда ω = 0) в режим вращения с кинетическим моментом максимальной величины L_max и торможение – гашение кинетического момента КА до нуля. Между разгоном и торможением выполняются уравнения (2.3) и (2.5), в которых b = L_max/С.

Если условия разворота Λ_н, Λ_к и время Т таковы, что времена разгона и торможения пренебрежимо малы (по сравнению с длительностью всего разворота), то сообщение КА необходимого кинетического момента L_max и гашение имеющегося кинетического момента до нуля можно считать импульсным и почти на всем развороте (между разгоном и торможением) |L(t)| = L_max с выполнением уравнений (2.6), (3.1). Определяющим при нахождении оптимальных решений p(t), ω(t) является значение вектора р на момент времени t = 0.

Если управляющий момент М ограничен, то сообщение требуемого кинетического момента до уровня |L| = L_max в начале разворота и гашение имеющегося кинетического момента до нуля в конце разворота занимают некоторое конечное (отличное от нуля) время. Время разворота T увеличится и станет больше, чем T_имп, которое соответствует импульсному управлению (даже при неизменном значении интеграла (2.8) длительность разворота увеличивается из-за наличия участков, когда |L(t)| < L_max). Интерес представляет общий случай, когда условия разворота Λ_н и Λ_к таковы, что переходными участками (разгоном и торможением) нельзя пренебречь. Для КА, управляемых силовыми гироскопами, обычно используют ограничение

В этом случае законы максимально быстрого набора и гашения кинетического момента известны [18]. Оптимальное по времени управление на участке разгона (пока |L| < L_max) такое:

При оптимальном движении кинетический момент КА не меняет своего направления относительно инерциальной системы координат, модуль кинетического момента изменяется по закону |L| = m₀t. На участке торможения оптимальное по времени управление имеет вид [18]

направление кинетического момента КА неизменно в инерциальной системе координат, а управляющий момент М составляет с кинетическим моментом 180°; величина кинетического момента КА изменяется по закону |L| = L_max – m₀(t – t_т), где t_т – момент начала остановки вращения. И при разгоне, и при торможении оптимальным по быстродействию является управление, при котором управляющий момент все время параллелен кинетическому моменту.

В момент времени t = 0 кинетический момент КА L = 0, и для быстрейшего достижения заданного уровня |L| = L_max необходимо управление (4.2). Пока |L(t)| < L_max, управляющий момент М = m₀L/|L| будет оптимальным. С момента времени t_р, когда |L(t_р)| = L_max, оптимальным будет движение (2.3), (2.4), при котором |L(t)| = L_max. Из-за наличия граничного условия ω(Т) = 0 существует такой момент времени t_т < Т, начиная с которого производят гашение кинетического момента с максимальным моментом управления М = –m₀L/|L| (момент времени t_т выбирается с таким расчетом, чтобы к моменту полной остановки ω = 0 КА занял требуемое угловое положение Λ_к). На интервалах разгона и торможения предельно максимальным является управляющий момент М (условие (4.1) переходит в строгое равенство), а на отрезке между разгоном и торможением выполняются уравнения (2.3) и равенства (2.4) и |L| = L_max. В результате траектория вращения КА Λ(t) разделяется на три составляющие: Λ(0) – Λ(t_р), Λ(t_р) – Λ(t_т) и Λ(t_т) – Λ(Т). Кватернион разворота представим так:

где $\Delta {{\Lambda }_{{\text{р}}}} = {{\tilde {\Lambda }}_{{\text{н}}}} \circ \Lambda ({{t}_{{\text{p}}}})$ – кватернион поворота КА за время разгона; $\Delta {{\Lambda }_{{\text{T}}}} = \tilde {\Lambda }($t_т)$ \circ {{\Lambda }_{{\text{к}}}}$ – кватернион поворота КА за время торможения; $\Delta {{\Lambda }_{{{\text{ном}}}}} = \tilde {\Lambda }({{t}_{{\text{р}}}}) \circ \Lambda ({{t}_{{\text{т}}}})$ – кватернион поворота за время вращения КА с кинетическим моментом, модуль которого равен L_max. Начальная и конечная угловые скорости равны нулю, и длительность этапов разгона и торможения будет одинакова только, если М_в ≡ 0 (в силу того, что на этих этапах величина управляющего момента постоянна |M| = const = m₀). Если М_в ≠ 0, то длительность торможения τ меньше длительности разгона t_р (так как на начало торможения модуль кинетического момента будет меньше, чем в момент окончания разгона). Оптимальное решение L(t) на участке номинального движения (между разгоном и торможением) обладает свойствами (2.3), (2.4), величина кинетического момента максимально допустимая |L| = L_max, а L_max – линейно уменьшающаяся функция времени.

Главное условие разворота КА без “разгрузки” гиросистемы – в каждый момент времени |G| ≤ R₀ (G – суммарный кинетический момент системы гиродинов), для чего необходимо удовлетворить условию

в любой момент времени t от t = 0 до t = t_т (t_т – момент начала торможения). На участке торможения (гашения угловой скорости до нуля) производная d|G|/dt < 0 из-за существенного превышения управляющего момента над возмущающим моментом М_в.

В случае нулевых граничных условий ω(0) = ω(Т) = 0 реализуется только один единственный тип движения: первый участок – разгон КА с максимальным управляющим моментом |M| = m₀ до наступления равенства |L| = L_max, далее участок движения КА с программно уменьшающимся по модулю кинетическим моментом с выполнением уравнений (2.3), (2.4), (3.1) и далее участок торможения КА с максимальным управляющим моментом |M| = m₀ до полной остановки КА (М||L). Изменение модуля кинетического момента G системы силовых гироскопов во время разворота таково, что на участках разгона и торможения d|G|/dt ≈ const (так как момент М управляющих сил намного больше возмущающего момента M_в). Причем в большинстве случаев можно считать |d|G|/dt|_t<tр = |d|G|/dt|_t>tт. В гипотетическом случае, когда М_в = 0, разгон КА можно осуществлять до наступления ситуации |L| = R₀, так как в этом идеальном случае |L| = |G| и в интервале между разгоном и торможением d|G|/dt = 0 из-за М_рас = 0 (напомним, что R₀ – радиус сферы, вписанной в область S возможных значений кинетического момента G системы силовых гироскопов). Как было показано выше, для выполнения маневра переориентации без “разгрузки” гиросистемы предпочтительно, чтобы параметр L_max оптимальной программы управления (2.4) изменялся по правилу L_max(t) = R₀ – М_расt. Ключевым является значение орта разгонного импульса l(0) = M(0)/m₀. Он определяет всю дальнейшую программу оптимального движения при известных R₀, М_рас, m₀, J₁, J₂, J₃. Повышение маневренности КА и уменьшение времени разворота Т достигается оптимизацией модуля кинетического момента в каждый текущий момент времени t внутри участка номинального вращения между разгоном и торможением. При непостоянном профиле изменения параметра L_max закона управления угловой скоростью КА требуемый запас R₀ – L₀ кинетического момента системы гиродинов окажется меньше, чем при постоянном значении L_max, а значит, разворот завершится быстрее (L₀ – модуль кинетического момента на момент окончания разгона).

Исходя из того, что на участках разгона и торможения модуль кинетического момента изменяется по линейному закону |d|L|/dt| = т₀, справедливы следующие соотношения:

где t_р – время окончания разгона; t_т – время начала торможения; L₀ – модуль кинетического момента на момент окончания разгона; L_т – модуль кинетического момента на начало торможения. Получили систему двух уравнений. Выпишем эти уравнения:

Так как вращение КА без “разгрузки” системы гиродинов возможно, если $\mathop {\max }\limits_{0 < t < T} \left| {\mathbf{G}} \right| < {{R}_{0}}$, то оптимальное значение параметра L₀ находим из уравнения L₀ = R₀ – M_расL₀/m₀. В результате

Решением системы уравнений (4.4) относительно переменной t_т является

где R₀ – априорно известная величина (значения Q и М_рас также известны). Чтобы время разворота Т было минимальным, оптимальным L_max будет наибольшее значение, удовлетворяющее условию L_max + М_расt < R₀ (очевидно, L_max < R₀). Ожидаемое время t_т начала торможения равно (4.5). При m₀ → ∞ величины t_р → 0, τ → 0 и Q = (R₀ – М_расТ/2)Т, L₀ → R₀, поэтому

Для нулевых граничных условий ω(0) = ω(Т) = 0 оптимальный по времени разворот КА включает две фазы, в течение которых величина момента М максимально возможная – разгон (увеличение модуля кинетического момента) и торможение (гашение кинетического момента до нуля), и фазу номинального движения, при котором справедливы уравнения (2.3), (2.4), (3.1). На участке разгона векторы М и L имеют одинаковое направление, а на участке торможения векторы М и L имеют противоположные направления; вектор кинетического момента L имеет постоянное направление в инерциальном пространстве, но меняется по величине (на участке разгона он увеличивается с нуля до максимального значения L_max, а на участке торможения уменьшается до нуля). Движение КА во время разворота происходит по следующей программе изменения кинетического момента: увеличение модуля вектора L с нуля до L_max с максимальной скоростью (|M| = m₀) при неизменном направлении относительно инерциального базиса I; далее вращение вектора L с линейно уменьшающейся величиной L_max по оптимальному закону, определяемому уравнениями (2.3), (2.4), (3.1), и, наконец, уменьшение модуля вектора L до нуля с максимальной скоростью (|M| = m₀) при неизменном направлении относительно инерциального базиса I. Эта программа полностью определяет движение КА в процессе перехода из состояния Λ = Λ_н, ω = 0 в состояние Λ = Λ_к, ω = 0.

У построенного управления модуль |L| кинетического момента – кусочно-линейная функция времени. Сначала модуль |L| максимально быстро возрастает (при этом |M| = m₀) до максимального значения L₀ (параметр L₀ рассчитывается с учетом предполагаемых возмущений), затем он линейно уменьшается в соответствии с правилом (3.1), а в заключительной стадии маневра он максимально быстро снижается до нуля (при этом |M| = m₀). Момент t_т начала интенсивного гашения кинетического момента выбирается из условия полной остановки вращения к моменту достижения равенства (1.3). Время оптимального разворота с учетом ограниченности управляющего момента находится из уравнений:

Из второго уравнения, которое является квадратным уравнением относительно неизвестной t_т, определяем t_т и, подставив его в первое уравнение, легко вычисляем время разворота T:

Главное отличие представленного решения от всех известных публикаций – учет возмущений М_в ≠ 0 при удовлетворении требования выполнить разворот только с помощью гиродинов, а также оптимизация ограничивающего уровня L_max(t) для модуля |L| (изменение параметра L_max должно быть оптимальным, чтобы максимально полно использовать располагаемый кинетический момент гиросистемы для минимизации длительности маневра). Дальнейшее уменьшение длительности разворота Т  возможно, если более точно спрогнозировать величину L_max. Понятно, что в каждый момент времени

(поскольку не всегда направления вектора G и суммарного возмущающего момента М_в одинаковы). Если информация о величине суммарного возмущающего момента доступна бортовой системе управления в каждый текущий момент времени t, то можно применить такой закон:

Так как при торможении КА управляющий момент М соответствует закону (4.3) и направлен строго против кинетического момента L, то момент начала торможения может быть спрогнозирован достаточно точно. Длительность остановки вращения равна τ = |L|/m₀. Если τ $ \ll $ Q₀/R₀, то торможение КА можно начать с момента выполнения равенства

или $4\arccos {{\delta }_{0}} = {{\omega }_{1}}K{\text{/}}{{m}_{0}}$, если $\omega _{2}^{2} + \omega _{3}^{2} = 0$, где J₁, J₂, J₃ – моменты инерции КА относительно связанных осей OX, OY, OZ; δ_j – компоненты кватерниона рассогласования $\tilde {\Lambda }(t) \circ {{\Lambda }_{{\text{к}}}}$ (j = $\overline {0,\;3} $); К = = |J_КАω| – величина кинетического момента КА. Момент начала участка торможения определяется условием (4.6), так как гашение кинетического момента на участке торможения происходит по линейному закону: |L(t)| = L_max – т₀(t – t_т), где t_т – момент начала торможения. Условие (4.6) позволяет повысить точность приведения КА в требуемое конечное состояние Λ(Т) = Λ_к, ω(Т) = 0 за счет возможности в бортовой системе управления формировать сигнал на остановку вращения по информации о текущей ориентации КА и измерениям его угловой скорости.

Мы исходили из того, что за время τ уменьшения кинетического момента с текущего значения до нуля КА повернется на кватернион ΔΛ_т в виде прецессии вокруг оси L ⋅ |L|^–1, неподвижной в инерциальной системе координат. При гашении угловой скорости направление кинетического момента L остается неизменным относительно инерциальной системы координат. Угол поворота ψ вокруг оси, параллельной вектору L, связан с кватернионом поворота из текущего углового положения Λ в заданное конечное угловое положение Λ_к соотношением

где θ – угол между кинетическим моментом L и продольной осью ОХ КА. За время гашения кинетического момента КА повернется вокруг вектора L на угол $\psi = {{\dot {\psi }}_{0}}\tau {\text{/}}2$, где ${{\dot {\psi }}_{0}} = \sqrt {\omega _{2}^{2} + \omega _{3}^{2}} {\text{/sin}}\theta $ – начальная угловая скорость вокруг оси, параллельной вектору L. Так как во время гашения угловой скорости до нуля управляющий момент М параллелен кинетическому моменту, то для полного гашения кинетического момента с уровня К = |L(t)| до нуля потребуется время τ = K/m₀, поэтому $\psi = K\sqrt {\omega _{2}^{2} + \omega _{3}^{2}} {\text{/}}(2{{m}_{0}}\sin \theta )$. Угол поворота вокруг L за время торможения должен быть равен углу ψ, который соответствует рассогласованию $\tilde {\Lambda } \circ {{\Lambda }_{{\text{к}}}}$. Приравнивая значение угла ψ, рассчитанного исходя из текущего рассогласования $\tilde {\Lambda } \circ {{\Lambda }_{{\text{к}}}}$, углу поворота КА вокруг вектора L кинетического момента за время торможения, получим соотношение

Очевидно, что $\sin \theta = \sqrt {J_{2}^{2}\omega _{2}^{2} + J_{3}^{2}\omega _{3}^{2}} {\text{/}}K$. Следовательно, момент t_т начала торможения (гашения угловой скорости) совпадает с моментом выполнения равенства (4.6). Если $\omega _{2}^{2} + \omega _{3}^{2} = 0$, то КА вращается вокруг продольной оси и $\psi = 2\arccos {{\delta }_{0}}$, а ${{\dot {\psi }}_{0}} = {{\omega }_{1}}$. Из равенства $\psi = {{\dot {\psi }}_{0}}K{\text{/}}(2{{m}_{0}})$ получаем условие начала торможения для случая $\omega _{2}^{2} + \omega _{3}^{2} = 0$.

Проблема минимизации длительности маневров обсуждалась многими авторами неоднократно [4–8, 19]. Отличие данного исследования состоит в необходимости совершить разворот КА исключительно с помощью управляющих силовых гироскопов (гиродинов) даже в условиях действия на КА возмущающих моментов. Повышение маневренности КА, оборудованных инерционными исполнительными органами (системой гиродинов), достигается максимальным использованием располагаемого кинетического момента гиросистемы за счет минимизации расчетного запаса кинетического момента гиросистемы, необходимого для компенсации возмущающих моментов. Предложенный метод управления ориентацией КА полезен для практики космических полетов тем, что позволяет совершать маневры переориентации без “разгрузки” системы гиродинов за минимальное время с учетом действия возмущающего момента. Разработанная программа управления вращением КА достаточно эффективна (с точки зрения маневренности), если оценка М_рас максимальной величины суммарного возмущающего момента M_в достоверна (т.е. практически совпадает с истинным значением). Однако при достаточно большом опыте эксплуатации конкретного класса КА (в том числе имея в виду тип рабочей орбиты КА) и имеющихся статистических данных, полученных ранее и основанных на результатах функционирования аналогичных КА, задача определения величины М_рас вполне решаема (и поэтому не столь актуальна и критична).

5. Результаты математического моделирования. Приведем численный пример решения задачи управления КА во время программного разворота и построения оптимальной программы вращения. Рассмотрим разворот КА на 150° из начального положения Λ_н, при котором оси КА совмещены (совпадают по направлению) с осями опорного базиса I, в заданное конечное положение Λ_к = Λ_зад за минимальное время Т без “разгрузки” системы гиродинов (с учетом действия возможных возмущающих моментов). При этом считалось, что начальная и конечная угловые скорости нулевые ω(0) = ω(Т) = 0. Значения элементов кватерниона Λ_зад, характеризующего требуемое угловое положение КА, были равны: λ₀ = 0.258819; λ₁ = 0.6830127; λ₂ = 0.3415064; λ₃ = = 0.5915064. Будем полагать, что инерционные характеристики КА имеют значения: J₁ = 12801 кг ⋅ м², J₂ = 44795 кг ⋅ м², J₃ = 43 032 кг ⋅ м², а управляющий момент ограничен условием (4.1). Мощность исполнительных органов характеризуется величиной m₀ = 42.7 Н ⋅ м. Для системы гиродинов константа R₀ = 364 Н ⋅ м ⋅ с. Предполагается, что максимальная величина возмущающего момента М_рас = 0.12 Н ⋅ м.

Определим оптимальную программу управления угловой скоростью КА ω(t) для перевода КА из состояния Λ(0) = Λ_н, ω(0) = 0 в состояние Λ(Т) = Λ_к, ω(Т) = 0. Нахождение расчетного значения вектора l(0) начинаем с решения той же краевой задачи для динамически симметричного КА с моментами инерции J₁, J и в предположении отсутствия возмущающих моментов М_в и ограничений на управляющий момент М, где J – момент инерции относительно поперечной оси, принимаемый равным J = (J₂ + J₃)/2. В результате из системы (3.3) получим начальное приближение вектора р₀.

Процедура расчета вектора l(0) и управляющего момента M(0), необходимого для разгонного импульса, состоит из двух этапов: а) нахождение значения l(0), соответствующего кинематической задаче разворота без учета ограничения (4.1) на силовой момент M, которое принимается за начальное приближение l⁽⁰⁾(0); б) уточнение вектора l(0) с учетом ограничения (4.1) для управляющего момента M и оптимального изменения параметра L_max (функции L_max(t)), рассчитанного исходя из имеющихся оценок М_рас максимальной величины возмущающего момента М_в. Начальное приближение l⁽⁰⁾(0) вычисляется с помощью формул

в которых р₀ – решение краевой задачи принципа максимума для задачи (1.1)–(1.4) с учетом L_max = const (например, L_max = R₀). Поиск расчетного значения р₀ выполняется методом наискорейшего спуска с использованием известных рекуррентных соотношений.

Краевая задача принципа максимума – определение вектора p₀ для оптимального движения в соответствии с (1.1), (2.6) – может быть решена методом последовательных приближений. За начальное приближение принимается решение той же задачи оптимального управления для динамически симметричного тела с моментами инерции J₁ вокруг продольной оси и J = (J₂ + J₃)/2 вокруг поперечной оси. Для начального приближения p₀⁽⁰⁾ решение находится из системы уравнений (3.3) с минимизацией величины $J_{1}^{2}{{(\alpha + \beta {{р}_{{10}}})}^{2}} + {{J}^{2}}{{\beta }^{2}}(1 - р_{{10}}^{2})$ по переменной р₁₀ (переменные α и β есть функции от р₁₀ и связаны друг с другом системой (3.3)). Поясним сказанное.

Для динамически симметричного тела кинематически оптимальное движение представляет собой одновременное вращение вокруг некоторой оси, неподвижной относительно инерциальной системы координат и составляющей с осью симметрии тела постоянный угол, и вокруг оси симметрии тела с угловыми скоростями $\dot {\beta }$ и $\dot {\alpha }$, сохраняющими постоянную пропорцию $\dot {\alpha }$/$\dot {\beta }$ = = const ($\dot {\beta }$ – угловая скорость вокруг оси, неподвижной относительно инерциальной системы координат, а $\dot {\alpha }$ – угловая скорость вокруг оси симметрии тела). Для такого движения интеграл (2.8) равен Q = $\sqrt {J_{1}^{2}{{{(\alpha + \beta {{p}_{{10}}})}}^{2}} + {{J}^{2}}{{\beta }^{2}}(1 - p_{{10}}^{2})} $. Значения углов α, β и р₁₀ = cosϑ должны удовлетворять системе (3.3). Ранее было показано, что время разворота минимально, если интеграл (2.8) имеет минимальное значение. Следовательно, оптимальными являются такие значения α, β, ϑ, при которых сумма $J_{1}^{2}{{(\alpha + \beta {{р}_{{10}}})}^{2}} + {{J}^{2}}{{\beta }^{2}}(1 - р_{{10}}^{2})$ минимальна.

Далее вектор p₀ уточняется путем моделирования кинематически оптимального движения в соответствии с уравнениями (1.1), (2.6) (оптимальное значение p₀ не зависит от величины L_max). Сначала производится интегрирование системы (1.1), (2.6) с начальными условиями

(константа С и постоянный вектор c_Р, участвующие в уравнении (2.6), вычисляются, исходя из принятого значения p₀, а L_max = R₀). На каждом шаге интегрирования вычисляется оценка

В момент времени Т, когда величина ε максимальна, параметры Λ(T) фиксируются и запоминаются: Λ_мод = Λ(T); Λ_мод – ожидаемое (прогнозируемое путем моделирования движения, т.е. смоделированное) положение, в которое перейдет КА, если не изменить значение вектора p₀. Целью процесса приближения вектора p₀ к искомому решению является сведение невязок λ_jк – λ_jмод к нулю. Для корректировки вектора p₀ используем функцию

Оптимальное (искомое) значение вектора p₀ соответствует минимуму функции F. Минимизация целевой функции F по аргументу p₀ производится градиентным методом [23] (или методом скорейшего спуска). Учитывая, что |p₀| = 1, удобно перейти к координатам ϑ = arccosр₁₀ и φ = = arctg(р₂₀/р₃₀). В сферических координатах

Варьируя значения переменных ϑ, φ, получаем вариацию функции F (через решение системы уравнений (1.1), (2.6), в которых начальные условия определяются выражениями (5.3) и (5.2), связывающими ω_i(0) и p_i0, и определение Λ_мод). Интегрирование системы уравнений (1.1), (2.6) и нахождение Λ_мод производится на каждом шаге приближения, при каждой коррекции параметров ϑ, φ (и соответственно вектора p₀). Для k-го приближения ϑ^(k), φ^(k) (а значит, ${\mathbf{p}}_{0}^{{(k)}}$) находится смоделированное положение $\Lambda _{{{\text{мод}}}}^{{(k)}}$ и значение минимизируемой функции F. Итерационный процесс прекращается, когда F < F_доп, где F_доп – некоторая близкая к нулю положительная величина (допуск). Заметим, что значение F_доп определяет точность решения краевой задачи Λ(0) = Λ_н, Λ(Т) = Λ_к по положению на правом конце. Действительно, точность разворота Δψ связана с функцией F выражением

откуда $\Delta {\psi } < 4\arcsin ({{\sqrt {{{F}_{{{\text{доп}}}}}} } \mathord{\left/ {\vphantom {{\sqrt {{{F}_{{{\text{доп}}}}}} } {2)}}} \right. \kern-0em} {2)}}$. В соответствии с последним неравенством выбираем приемлемую границу F_доп. Анализ системы уравнений (3.3) показывает, что составляющая р₁₀ не может выходить за пределы диапазона |р₁₀| ≤ ξ, где ξ = $\sqrt {\nu _{0}^{2} + \nu _{1}^{2}} $. Из первых двух уравнений системы (3.3) следует равенство из которого получаем выражение для р₁₀, откуда max|р₁₀| = ξ.

Стратегия поиска минимума функции $J_{1}^{2}{{(\alpha + \beta {{р}_{{10}}})}^{2}} + {{J}^{2}}{{\beta }^{2}}(1 - р_{{10}}^{2})$ на отрезке [–ξ, ξ] может быть разной (план Фибоначчи [23], метод деления отрезка пополам и т.д.). Наилучшим оказывается метод золотого сечения [23]. Задавшись точностью решения Δр₁₀, равной 10^–7, получим искомое значение ${\mathbf{p}}_{0}^{{(0)}}$ уже на n-й итерации, где $n \geqslant {{(7 + \lg {\xi })} \mathord{\left/ {\vphantom {{(7 + \lg {\xi })} {(\lg (\sqrt 5 + 1) - \lg 2)}}} \right. \kern-0em} {(\lg (\sqrt 5 + 1) - \lg 2)}} + 1$.

Отмечаем, что F(ϑ, φ) – выпуклая функция (в терминологии Ф.П. Васильева [23]). Обозначая через u = (ϑ, φ)^T – вектор аргумента, а через gradF = (F_ϑ, F_φ)^T – градиент функции F(ϑ, φ), запишем основное правило градиентного метода: u^{(k+ 1)} = u^(k) – ρ^(k)gradF(u^(k)), где ρ^(k) > 0. Используя свойство minF(ϑ, φ) = 0, принимаем следующую схему генерации последовательности приближений (ϑ^(k), φ^(k)) (минимизирующей последовательности [23]):

или в развернутом виде где F_ϑ и F_φ – частные производные функции F(ϑ, φ); F_ϑ = дF/дϑ; F_φ = дF/дφ.

Величина ρ выбрана с использованием условия ΔϑF_ϑ + ΔφF_φ = –F(ϑ, φ), и поэтому считалось, что ρ^(k) = F(u^(k))/|gradF(u^(k))|². При определении частных производных F_ϑ и F_φ (для расчета градиента функции F(ϑ, φ)) приращения независимых переменных ϑ, φ принимались порядка 5 × × 10^–4–10^–3. Порог точности F_доп установлен на уровне 2 × 10^–7, что соответствует ошибке ориентации Δψ не более 3 угл. мин. Сходимость процесса приближения к минимуму функции F обусловлена близостью начального приближения ${\mathbf{p}}_{0}^{{(0)}}$ к действительному экстремуму функции F. Даже для случая разворота на 180^о отклонение $\Delta р = {\text{|}}{\mathbf{p}}_{0}^{{(0)}} - {\mathbf{p}}_{0}^{*}{\text{|}}$ не превышает 2.2 × 10^–2, где ${\mathbf{p}}_{0}^{{(0)}}$ – начальное приближение, ${\mathbf{p}}_{0}^{*}$ – истинное значение вектора p₀, при котором F = 0 (т.е. $F({\mathbf{p}}_{0}^{*}) = 0$); а величина F⁽⁰⁾ = 6.5 × 10^–3.

Таким образом, процедура расчета искомого вектора p₀, определяющего начальные условия p(0) и ω(0) кинематически оптимального движения (начальные условия Λ(0) не меняются; они известны и равны Λ_н), состоит из двух последовательных этапов – нахождения начального приближения ${\mathbf{p}}_{0}^{{(0)}}$ процедурой поиска минимума функции одного переменного р₁₀ (углы α, β и значение минимизируемой функции $J_{1}^{2}{{(\alpha + \beta {{р}_{{10}}})}^{2}} + {{J}^{2}}{{\beta }^{2}}(1 - р_{{10}}^{2})$ рассчитываются из решения системы (3.3) при известном значении р₁₀) и уточнения вектора p₀ путем минимизации функции F невязок как функции двух переменных ϑ и φ одним из известных численных методов [23]. Значение функции F невязок для конкретного значения p₀ определяется интегрированием системы уравнений (1.1), (2.6) с начальными условиями (5.2) (моделированием движения КА) и получением прогнозируемого положения Λ_мод.

Полученное значение p₀ определяет начальное приближение l⁽⁰⁾(0) к истинному решению. Орт l⁽⁰⁾(0) рассчитывается по формулам (5.1). Далее он уточняется до тех пор, пока не будет удовлетворять накладываемым на движение КА ограничениям Λ(0) = Λ_н, Λ(T) = Λ_к, ω(0) = ω(Т) = 0 в результате вращения, согласно описанной выше программе изменения кинетического момента L, с учетом участков разгона, торможения и условия (3.1) для интервала между разгоном и торможением. Запишем орт l(0) в сферических координатах (здесь l₀ = l(0)):

Начальному приближению l⁽⁰⁾(0) соответствуют значения θ⁽⁰⁾ = $\arccos l_{{10}}^{{(0)}}$ и γ⁽⁰⁾ = ${\text{arctg}}(l_{{20}}^{{(0)}}{\text{/}}l_{{30}}^{{(0)}})$. Варьируя значения переменных θ, γ, получим вариацию функции F через моделирование движения с учетом участков разгона и торможения, а также закона (3.1) для оптимального изменения модуля кинетического момента КА на участке номинального вращения между разгоном и торможением, используя начальные условия, рассчитанные по выражениям (5.4) и M_i(0) = m₀l_i0, и определение Λ_мод, при котором ω = 0 . Момент начала торможения t_т определяется с использованием условия (4.6). Моделирование движения и нахождение Λ_мод производится на каждом шаге приближения, при каждой коррекции параметров θ, γ (и соответственно вектора l₀). Для k-го приближения θ^(k), γ^(k) (а значит, ${\mathbf{l}}_{0}^{{(k)}}$) находится смоделированное положение $\Lambda _{{{\text{мод}}}}^{{(k)}}$ и значение минимизируемой функции F. Итерационный процесс прекращается, когда F < F_доп; здесь F_доп – некоторая близкая к нулю положительная величина (допуск), которая определяет точность решения краевой задачи Λ(0) = Λ_н, Λ(Т) = Λ_к по положению на правом конце. Так как F(θ, γ) – выпуклая функция (в терминологии Ф.П. Васильева [23]), то, обозначив w = (θ, γ)^T – вектор аргумента, gradF = (F_θ, F_γ)^T – градиент функции F (θ, γ), запишем основное правило градиентного метода: w^{(k+ 1)} = w^(k) – $\rho _{0}^{{(k)}}$gradF(w^(k)), где $\rho _{0}^{{(k)}}$ > 0. Используя свойство minF(θ, γ) = 0 , принимаем следующую схему генерации последовательности приближений (θ^(k), γ^(k)) (минимизирующей последовательности [23]):

или в развернутом виде где F_θ и F_γ – частные производные функции F(θ, γ); F_θ = ∂F/∂θ; F_γ = ∂F/дγ.

Значение ρ₀ выбрано с использованием условия ΔθF_θ + ΔγF_γ = –F(θ, γ) и считалось равным $\rho _{0}^{{(k)}}$ = F(w^(k))/|gradF(w^(k))|². При нахождении частных производных F_θ и F_γ (для расчета градиента функции F(θ, γ)) приращения независимых переменных θ, γ принимались порядка 5 × 10^–4–10^–3. Порог точности F_доп установлен на уровне 2 × 10^–7, что соответствует ошибке ориентации Δψ не более 3 угл. мин. Сходимость процесса приближения к минимуму функции F обусловлена близостью начального приближения ${\mathbf{l}}_{0}^{{(0)}}$ к действительному экстремуму функции F. Даже для случая разворота на 180° отклонение $\Delta l = {\text{|}}{\mathbf{l}}_{0}^{{(0)}} - {\mathbf{l}}_{0}^{*}{\text{|}}$ не превышает 2.3 × 10^–2, где ${\mathbf{l}}_{0}^{{(0)}}$ – начальное приближение, ${\mathbf{l}}_{0}^{*}$ – истинное значение вектора l₀, при котором F = 0 (т.е. $F({\mathbf{l}}_{0}^{*})$ = 0), а величина F⁽⁰⁾ = 7.2 × × 10^–3.

Таким образом, процедура расчета искомого вектора l₀, определяющего начальный управляющий момент M(0) (начальные условия Λ(0) не меняются и равны Λ_н), состоит из трех последовательных этапов – нахождения начального приближения ${\mathbf{p}}_{0}^{{(0)}}$ процедурой поиска минимума функции одного переменного р₁₀ (углы α, β и значение минимизируемой функции $J_{1}^{2}{{(\alpha + \beta {{р}_{{10}}})}^{2}} + {{J}^{2}}{{\beta }^{2}}(1 - р_{{10}}^{2})$ рассчитываются из решения системы (3.3) при известном значении р₁₀), уточнения вектора p₀ путем минимизации функции F невязок как функции двух переменных ϑ и φ одним из известных численных методов [23] и расчета первого приближения ${\mathbf{l}}_{0}^{{(0)}}$, а затем уточнения вектора l₀ путем минимизации функции F невязок как функции двух переменных θ и γ одним из известных численных методов [23]. Значение функции F невязок для конкретного значения l₀ определяется моделированием движения КА и получением прогнозируемого положения Λ_мод. Заметим, что это лишь один из возможных (но далеко не единственный) итерационных алгоритмов поиска оптимального вектора l(0).

В результате решения краевой задачи разворота из положения Λ(0) = Λ_н в положение Λ(Т) = Λ_к получили расчетное значение вектора l(0) = {0.4040083; –0.4510156; 0.7958405} и интеграл Q = = 72517.4 Н ⋅ м ⋅ с². Время разгона t_р определяется из условия L₀ + М_расt_р = R₀ с учетом равенства L₀ = m₀t_р. Максимальная величина кинетического момента (модуль кинетического момента в момент окончания разгона) составляет L₀ = 363 Н⋅м⋅с, а длительность разгона t_р = 8.5 с. Поскольку длительность торможения τ < t_р (в силу закона (3.1)), а t_р ≪ Q/R₀, то начало остановки вращения t_т определяется из условия (4.6), и по результатам численного моделирования получилось t_т = 206.8 с. Определение момента времени t_т по фактическим (измеренным значениям) параметрам движения (угловому рассогласованию и угловой скорости ω) повышает точность приведения КА в требуемое состояние Λ = Λ_к, ω = 0. Общее время разворота составило T = 214.7 с. Оптимальная программа управления угловой скоростью КА формировалась из условия действия возмущающего момента М_в по наихудшему сценарию, когда в каждый момент времени t кинетический момент КА L и возмущающий момент М_в имеют противоположные направления, а модуль возмущающего момента равен максимальному значению М_рас. Поэтому с момента окончания разгона до начала торможения |L(t)| = R₀ – М_расt (на участках разгона и торможения модуль кинетического момента изменяется по линейному закону в соответствии с условием |d|L|/dt| = m₀).

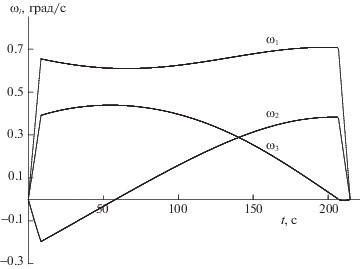
Результаты математического моделирования динамики оптимального по быстродействию разворота представлены рис. 1–3. На рис. 1 изображены графики изменения угловых скоростей в связанной с КА системе координат ω₁(t), ω₂(t), ω₃(t) по времени. Из соотношения моментов инерции J₁, J₂, J₃ следует, что ОХ – продольная ось КА. Отмечаем, что угловая скорость ω₁, соответствующая продольной оси КА, – знакопостоянна. На рис. 2 отображены графики изменения компонент кватерниона Λ(t), определяющего текущую ориентацию КА в процессе совершаемого поворотного маневра: λ₀(t), λ₁(t), λ₂ (t), λ₃ (t). Оптимальная траектория движения Λ(t ) получается из решения уравнений (1.1) с учетом начальных условий Λ(0) = Λ_н и известного закона изменения угловой скорости ω(t ). Оптимальное значение орта l(0) выбирается из условия выполнения равенства Λ(Т) = Λ_к для решения Λ(t), соответствующего оптимальной программе вращения ω(t ). Динамика изменения составляющих l₁(t), l₂(t), l₃(t) орта l кинетического момента по времени приведена на рис. 3. Характерным является незначительное изменение проекции l₁ (угловая скорость ω₁ относительно продольной оси КА на участке между разгоном и торможением также меняется гораздо меньше, чем угловые скорости ω₂ и ω₃ относительно поперечных осей КА). При оптимальном управлении в отличие от переменных ω_i переменные l_i и λ_j – гладкие функции времени. Для наглядности на рис. 4 показано изменение модуля кинетического момента во время оптимального разворота; на участках разгона и торможения |L| < L_max, а между разгоном и торможением (в интервале номинального вращения) изменение модуля кинетического момента |L| совпадает с оптимальным изменением функции L_max(t).

Если на всем протяжении разворота модуль кинетического момента КА не будет превышать уровня L_max, изменяющегося в соответствии с законом L_max = R₀ – М_расt, то можно с высокой степенью уверенности утверждать, что суммарный кинетический момент G гиросистемы не выйдет за пределы области располагаемого кинетического момента гиросистемы S и “насыщения” гиросистемы не наступит (для завершения маневра разворота “разгрузка” гиросистемы не потребуется), если конечно экспертная оценка верна и фактический возмущающий момент по величине не больше значения М_рас (т.е., если мы верно предположили, что |M_в| ≤ М_рас).

Заключение. В статье исследуется задача оптимального управления пространственным разворотом КА из произвольного начального в требуемое конечное угловое положение за минимальное время. Для решения поставленной задачи используются необходимые условия оптимальности в форме принципа максимума и кватернионы. Постановка задачи имеет традиционную форму, в которой управление считается кусочно-непрерывной функцией времени. Сформулированная задача управления достаточно актуальна. На основании принципа максимума и использования универсальных переменных r_i [15] получены выражения для оптимального управления, функции Гамильтона и сопряженной системы уравнений для исходной задачи. Найдены условия оптимальности и определена структура оптимального управления; получены формализованные соотношения для определения программного движения КА. Определены тип траектории и ключевые свойства оптимального движения. Подробно изучены вопросы обеспечения выполнения маневра переориентации КА, управляемого инерционными исполнительными органами (системой гиродинов), без “разгрузки” гиросистемы, в том числе с учетом действия возможных (или предполагаемых) возмущающих моментов.

Исследуется проблема повышения маневренности КА путем оптимизации управления угловой скоростью при разворотах в требуемое положение. Выписаны условия оптимальности режима переориентации без “разгрузки” гиросистемы и изучены свойства оптимального пространственного (трехмерного) разворота. Необходимые условия максимального быстродействия записаны в аналитическом виде. В общем случае оптимальный маневр делится на три характерных фазы: раскрутка КА до максимально допустимого кинетического момента L_max, вращение по номинальной траектории с программным изменением модуля кинетического момента, вызванным действием возмущающего момента, и гашение угловой скорости до нуля. Задача управления ориентацией сводится к решению трех задач – наискорейшему сообщению КА требуемого кинетического момента, вращению КА с расчетной скоростью движения и максимально быстрому торможению (успокоению) КА. На участках разгона и торможения управляющий момент максимально возможный и параллелен вектору кинетического момента.

Главным отличием от известных публикаций является то, что в задаче (1.1)–(1.4) значение L_max подлежит оптимизации, причем L_max рассчитывается в каждый текущий момент времени t, если требуется учитывать наличие возмущающих моментов. Даны ключевые соотношения и уравнения для оптимального движения, которые определяют программу изменения угловой скорости КА. Приводится условие для определения момента начала торможения по фактическим параметрам движения (текущим значениям кватерниона рассогласования и вектора угловой скорости) исходя из принципов терминального управления (используются информация об угловом положении и измерения угловой скорости КА), что существенно повышает точность приведения КА в требуемое конечное положение. Созданные алгоритмы управления позволяют совершать развороты КА с помощью гиродинов за минимальное время и без “разгрузки” гиросистемы. Подробно исследована проблема нахождения оптимального модуля кинетического момента в интервале между разгоном и торможением, если КА разворачивается в условиях возмущений. Получены формализованные уравнения и найдены расчетные выражения для вычисления значения L_max при известных условиях разворота – начального и конечного положений КА и его инерционных характеристик. Параметр L_max закона управления рассчитывается так, чтобы запас кинетического момента системы гиродинов позволил исключить привлечение других органов управления (кроме гиродинов) для совершения маневра и его завершения с учетом действующих возмущений. Представлены результаты численного моделирования движения КА в соответствии с разработанным способом управления. Предлагаемый алгоритм управления переориентацией КА с инерционными исполнительными органами позволяет уменьшить время разворота на 25–35%.