Известия РАН. Теория и системы управления, 2020, № 5, стр. 142-156
РАСЧЕТ УПРАВЛЕНИЙ, НЕ ПОРОЖДАЮЩИЙ СИНГУЛЯРНЫХ СОСТОЯНИЙ ЧЕТЫРЕХ ИСПОЛНИТЕЛЬНЫХ ГИРОДИНОВ
Э. И. Дружинин a, *, С. А. Ульянов a
a Институт динамики систем и теории управления им. В.М. Матросова СО РАН
Иркутск, Россия
* E-mail: druzh@icc.ru
Поступила в редакцию 10.09.2019
После доработки 04.02.2020
Принята к публикации 25.05.2020
Аннотация
Демонстрируется технология расчета программных законов ориентации космических аппаратов, не порождающая особых, сингулярных, состояний исполнительных гиросистем, состоящих из двух коллинеарных пар гиродинов. Расчет программных законов ориентации, не содержащих сингулярных состояний для двух пар гиродинов, оказывается возможным благодаря использованию в новой технологии расчета управлений космическим аппаратом кинематического конфигурирования системы исполнительных гиродинов, позволяющей при необходимости настраивать положение осей виртуальных маховиков для новых задач ориентации. Сегодня законы программной ориентации вычисляются как решение прямой задачи динамики. В этих законах содержатся сингулярные состояния гиросистемы, в которых космический аппарат остается неуправляемым. Восстановление управляемости осуществляется выводом гиросистемы из этих состояний, используя дополнительную гиросистему и дополнительное управление. При этом на время вывода процесс ориентации аппарата прерывается. Эти материальные и временные потери требуют поиска законов ориентации, не содержащих особых состояний гиросистемы. Расчет таких законов продемонстрирован в решении задачи ориентации космического телескопа двумя коллинеарными парами гиродинов.
Введение. Проблема использования однокарданных силовых гироскопов (гиродинов) изучается давно [1–3]. В [4] был впервые опубликован способ радикального решения так называемой “проблемы сингулярности” исполнительных гиродинов: предложен расчет законов управления ориентацией космического аппарата (КА), не порождающий сингулярных состояний исполнительных гиродинов.
Рабочим инструментом гиродинов является суммарный кинетический момент ${\mathbf{k}}\left( t \right)$ собственных кинетических моментов роторов гироскопов исполнительной гиросистемы. Механизм крепления ротора в корпусе гироскопа позволяет создавать нужной величины и направления суммарный кинетический момент гиросистемы в движении ее гироскопов относительно несущего корпуса КА. Этот кинетический момент ${\mathbf{k}}\left( t \right)$ исполнительной гиросистемы, определяющий ее управляющее воздействие на аппарат, для краткости будем называть гиростатическим моментом. В распространенной сегодня технологии расчета законов управления ориентацией в качестве управляющего воздействия принимается производная по времени ${\mathbf{\dot {k}}}\left( t \right)$ гиростатического момента, индуцированная заданным априори законом движения КА [5, 6]. При таком подходе к нахождению программных законов управления задача сводилась к более простой из двух задач динамики, в терминологии Ньютона – к прямой задаче динамики (в сегодняшней терминологии – первой задаче динамики): к задаче определения действующих сил по известному закону движения [7]. Решение, полученное таким способом, не гарантирует управляемость краевых условий поставленной задачи ориентации КА, т.е. вычисленное управление не гарантирует, что априори введенный в задачу закон движения КА будет решением двухточечной краевой задачи для уравнений динамики КА с подставленным в них этим управлением. При этом распространено мнение, что причиной существования в вычисленных управлениях сингулярных состояний гиросистемы, в которых нарушается управляемость аппаратом, является не способ их расчета, используемый расчетчиками, а некое особое свойство гиродинов.
Это утверждение опровергнуто в [4, 8, 9] для исполнительной гиросистемы из шести гиродинов, составляющих три коллинеарные пары. В предлагаемой сейчас вниманию статье решается задача расчета закона управления, не порождающего сингулярностей для гиросистемы из четырех гиродинов, образующих две коллинеарные пары. Выясняется, что решение этой задачи для гиросистемы из четырех гиродинов путем расчета по предлагаемой новой технологии возможно только при кинематическом конфигурировании исполнительной гиросистемы. Такое конфигурирование обеспечивает виртуальную (кинематическую) синхронизацию вращений гироузлов гиродинов с коллинеарными осями прецессии и позволяет при необходимости устанавливать нужное положение осей виртуальных маховиков для решения новой задачи ориентации. Для гиросистем же, имеющих механическую (редукторную – шестерёнчатую или ременную) синхронизацию вращений гироузлов гиродинов с коллинеарными осями прецессии изменение положения осей виртуальных маховиков невозможно. Так будет для гиросистем типа “Twin–Gyro” [2] или “Scissored pairs” [3] с синхронизацией, обеспеченной механическими средствами.
В этой статье так же, как и ранее в статьях, где рассмотрены три коллинеарные пары [4, 8, 9], вычислены законы управления, исполняющие ориентацию КА и не содержащие сингулярных состояний кинематически конфигурированной гиросистемы. Таким образом, и для гиросистемы, образованной двумя коллинеарными парами стандартных гиродинов, подтверждается возможность вычислять законы ориентации, не содержащие сингулярностей, и снимается ответственность только гиродинов за их наличие.
1. Формулировка задачи программной ориентации КА. Процесс ориентации заключается в переводе аппарата из заданного начального состояния x0$\mathop = \limits^\Delta $ (ω(t0), λ(t0)) в заданное конечное состояние xf $\mathop = \limits^\Delta $ ((ω(tf), λ(tf)), где $\omega $ – вектор угловой скорости, λ – кватернион ориентации КА, ${{t}_{0}}$ и ${{t}_{f}}$ – начальный и конечный моменты времени ориентации. При том процесс этого перевода является решением уравнений динамики КА, соответствующим найденному программному закону управления, за который принимаем закон изменения гиростатического момента в функции времени ${\mathbf{k}} \equiv {\mathbf{k}}(t)$, $t \in \left[ {{{t}_{0}},{{t}_{f}}} \right]$ .
В рассматриваемой новой технологии расчет закона управления k(t) процессом ориентации происходит в три этапа. Каждый этап представляет собой вращение КА $\omega \left( t \right) = \omega \left( t \right){\mathbf{n}}$ вокруг неподвижной оси, определяемой ортом ${\mathbf{n}}$, который направлен так, чтобы с его конца видеть направление вращения аппарата, происходящее в правой системе отсчета против часовой стрелки; ω(t) – проекция скорости на перманентную ось; ее величину будем обозначать через $\left| {\omega \left( t \right)} \right|$. На каждом этапе вращения априори фиксируется только ось этого вращения, т.е. структура траектории движения на этапе: ${\mathbf{n}} = {\mathbf{const}}$. Таким образом, в отличие от вычисления управления как решения прямой задачи динамики здесь закон вращения вокруг неподвижной оси ω(t) не задается. Это позволяет найти закон управления, согласованный в силу уравнений динамики с окончательным движением КА.
В общем невырожденном случае, т.е. когда ${\mathbf{n}}_{f}^{{}} \ne {\mathbf{n}}_{0}^{{}}$, каждому этапу отвечает своя неподвижная ось вращения. Заметим, что из указанных трех этапов только два этапа (этап гашения начальной скорости и этап разгона скорости вращения после конечного поворота Эйлера–Шаля) являются перманентными вращениями КА–гиростата как решения уравнений динамики. Однако на оси этих перманентных вращений утверждение Эйлера о том, что их оси должны быть главными осями эллипсоида инерции, не распространяется. Дело в том, что, как показано в [4], гиростатический момент в обоих этих случаях состоит из двух частей, сумма которых не является постоянным по направлению вектором, что необходимо, как показано в [10], для осуществления перманентного вращения гиростата. Что же касается конечного поворота Эйлера–Шаля, то неподвижная ось этого поворота строится из кинематических соображений и ее существование в связанной системе отсчета является чисто кинематическим фактом. Однако исполняется этот поворот гиродинами, законы прецессий гироузлов которых вычисляются из уравнений динамики гиростата, превращая этот поворот в их решение. Теорема из [10] о перманентных осях гиростата к этому повороту как решению уравнений динамики отношения не имеет по той же причине, что в случаях перманентных гашения и разгона.
Значения начального момента времени ${{t}_{0}}$ и начального состояния КА x0, используемые на первом этапе, заданы по постановке задачи. Начальное состояние аппарата ${\mathbf{x}}_{0}^{{\text{э}}}$ $\mathop = \limits^\Delta $ (0, λ($t_{0}^{{\text{э}}}$)) при повороте Эйлера–Шаля вычисляется в момент гашения начальной скорости ω($t_{0}^{{\text{э}}}$) = 0. Конечное состояние аппарата ${\mathbf{x}}_{f}^{{\text{э}}}$ $\mathop = \limits^\Delta $ (0, λ($t_{0}^{{\text{э}}}$)) при этом повороте вычисляется в момент численного гашения финальной скорости ω($t_{0}^{{\text{э}}}$) = 0. Это гашение реально не происходит, оно рассчитывается по математической модели и необходимо для определения времени перманентного разгона неподвижного КА после завершения поворота Эйлера–Шаля. Перманентный разгон до значения заданной величины финальной скорости $\left| {{{\omega }_{f}}} \right|$ и заданного финального положения аппарата, определяемого значением кватерниона ${{\lambda }_{f}}$, происходит за время, вычисленное в процессе численного гашении заданной величины $\left| {{{\omega }_{f}}} \right|$ финальной скорости до нулевого значения.
Считаем, что конечный момент времени ${{t}_{f}}$ достижения заданного конечного состояния определяется вычисленным законом перманентного вращения КА. Закон управления k(t) определяется такими параметрами процесса ориентации, как значения переменных состояния x0 и xf, значения инерционных характеристик аппарата КА и силовых (энергетических) характеристик исполнительной гиросистемы.
Все вычисления на этапах поставленной задачи ориентации КА производятся до начала реализации процесса ориентации. Как показали расчеты конкретных задач, суммарное время всех вычислений составляет десятые доли секунды. При этом процесс ориентации в виде последовательности вращений КА прерывается только в моменты времени начала и окончания поворота Эйлера–Шаля, вычисляемые по перечисленным выше заданным параметрам. При наличии же в найденном по традиционной технологии расчета законе управления сингулярных состояний гиросистемы моменты времени, когда гироузлы гиродинов попадают в них, и процесс ориентации прерывается, как правило, не предсказуемы.
Отметим, что настройка гирузлов исполнительной гиросистемы на выполнение очередного этапа переориентации проходит в виртуальных углах прецессий. Это новшество позволяет в процессе настройки обеспечить невозмущаемость состояния КА при движении настраиваемых гироузлов, что позволяет обойтись в процессе настройки без дополнительных исполнительных гироскопов, используемых для компенсации таких возмущений при реализации традиционных управлений ориентацией, имеющих сингулярности. Применяемый в новом методе расчета дополнительный трехстепенной гироскоп обеспечивает реализацию новой технологии расчета законов управления, а не их исполнение.
2. Уравнения перманентных вращений КА при не полностью разгруженном полном кинетическом моменте. Рассмотрим аппарат, состоящий из жесткого корпуса, несущего оборудование и систему гиродинов. Считаем, как и в [4], что после расстыковки аппарата с разгонным блоком (РБ) его кинетический момент полностью не разгружен, а момент внешних сил не действует.
В связанной с КА системе отсчета (ССО) его суммарный кинетический момент определим равенством ${\mathbf{K}}_{р}^{{ССО}}(t) = {\mathbf{I}}\omega (t) + {\mathbf{k}}(t)$, где I – тензор инерции КА. Уравнение движения КА в связанных осях имеет вид ${\mathbf{\dot {K}}}_{р}^{{ССО}}(t) + \omega (t) \times {\mathbf{K}}_{р}^{{ССО}}(t)$ = 0. Отметим, что в ССО величина ${\text{|}}{\mathbf{K}}_{р}^{{ССО}}(t){\text{|}} \equiv {\text{|}}{\mathbf{I}}\omega (t) + {\mathbf{k}}(t){\text{|}}$ ≡ const, т.е. сохраняет свое значение во все время движения аппарата [8]. В силу этого угловая скорость аппарата ω(t) определяется только гиростатическим моментом k(t). Из определения кинетического момента КА и установленного свойства угловой скорости ясно, что управлять вращением КА вокруг центра масс, которое описывается вектором угловой скорости ω(t), возможно только за счет изменения гиростатического момента k(t).
Сужая класс движений КА до перманентных вращений вокруг оси, определяемой постоянным ортом n0: ω(t) = ω(t)n0, преобразуем уравнение движения к виду:
(2.1)
${\mathbf{\dot {K}}}_{р}^{{{\text{ССО}}}} = - \omega (t)\langle {{{\mathbf{n}}}_{0}}\rangle {\mathbf{K}}_{р}^{{ССО}},\quad {\text{где}}\quad \langle {{{\mathbf{n}}}_{0}}\rangle \mathop = \limits^\Delta \left( {\begin{array}{*{20}{c}} 0&{ - {{n}_{{0z}}}}&{{{n}_{{0y}}}} \\ {{{n}_{{0z}}}}&0&{ - {{n}_{{0x}}}} \\ { - {{n}_{{0y}}}}&{{{n}_{{0x}}}}&0 \end{array}} \right).$Принимая ${\mathbf{K}}_{p}^{{{\text{ССО}}}}\left( t \right)$ за переменную состояния КА и рассматривая ω(t) в качестве независимого от ${\mathbf{K}}_{р}^{{{\text{ССО}}}}\left( t \right)$ параметра, определяемого гиростатическим моментом $k{\text{(}}t{\text{)}}$, проинтегрируем уравнение (2.1), матрица коэффициентов которого, будучи скалярной по времени, функционально коммутативна [11]. В результате интегрирования уравнения (2.1) и замены кинетического момента ${\mathbf{K}}_{p}^{{{\text{ССО}}}}\left( t \right)$ его составляющими Iω(t) и k(t) получим [8]:
(2.2)
$\omega {\text{(}}t{\text{)}}{\mathbf{I}}{{{\mathbf{n}}}_{0}} + {\mathbf{k}}{\text{(}}t{\text{)}} = L{\text{(}}\varphi {\text{(}}t{\text{))}}{\mathbf{K}}_{{p0}}^{{{\text{ССО}}}},$Разложим вектор k(t) на аддитивные составляющие, соответствующие векторам ω(t) и ${\mathbf{K}}_{p}^{{{\text{ССО}}}}\left( t \right)$: k(t) = kω(t) + kK(t). При этом разделении величину |kK(t)| вектора kK(t) выберем равной постоянному и в ССО, и в инерциальной системе отчета (ИСО) значению
Уравнение перманентного вращения (2.2) при этом примет вид:
При указанном выборе вектора kK(t) величина вектора ω(t)In0 + kω(t) будет тождественно равна нулю: |ω(t)In0 + kω(t)| ≡ 0, следовательно, во все время перманентного вращения аппарата будет иметь место векторное равенство:
Таким образом, по построению вектора kK(t) уравнение перманентного вращения (2.2) распалось на два уравнения: (2.3) и
Реализация кинетического момента kK(t), обеспечивающего выполнение равенства (2.4), осуществляется установкой в КА трехстепенного гироскопа с собственным кинетическим моментом ротора, равным величине |${\mathbf{K}}_{p}^{{{\text{ИСО}}}}$| неразгруженного кинетического момента ${\mathbf{K}}_{p}^{{{\text{ИСО}}}}$ в ИСО. Векторное равенство (2.4) обеспечивается безопорными кардановыми кольцами, несущими ротор, и управляемые электроприводами. Необходимый закон изменения перманентной угловой скорости ω(t) = = ω(t)n0 исполняется вектором kω(t) в силу уравнения (2.3). При известном законе вращения ССО ω(t) будет известен закон вращения неразгруженного кинетического момента аппарата L(φ(t))${\mathbf{K}}_{{p0}}^{{{\text{CCO}}}}$. Из (2.4) вычисляются компоненты момента kK(t), которые реализуются электроприводами картанновых колец. Осуществление всех перечисленных операций представляет чисто техническую проблему (подробности см. в [8, 9]).
3. Установление перманентного вращения КА вокруг главной оси тензора инерции с помощью РБ. В [8, 9] рассматривался вариант перманентного гашения начальной скорости исполнительной гиросистемой. Сохраняя намерение решать задачи ориентации КА в классе перманентных вращений, опишем установку перманентного вращения КА и его гашение, используя имеющийся в составе ракет-носителей среднего и тяжелого класса РБ, служащий для выведения КА на заданные рабочие орбиты.
В перечень задач, решаемых такими универсальными РБ, как “Фрегат”, наряду с задачей построения необходимой ориентации головного блока (ГБ), обеспечением его стабилизации на пассивных и активных участках полета по орбите входят и задачи обеспечения закрутки ГБ и разгрузки кинетического момента КА перед его отделением от РБ [12].
Используем технически предусмотренную для исполнения “Фрегатом” раскрутку КА для установления перманентного вращения аппарата вокруг главной оси тензора инерции. Для этого перед выводом КА на орбиту установим на аппарат трехстепенной гироскоп-компенсатор [4, 8] c предварительно обнуленным собственным кинетическим моментом его ротора. Гиростатический момент исполнительной гиросистемы аппарата перед раскруткой и разгрузкой КА также обнулим, устанавливая гироузлы каждой пары гиродинов с коллинеарными осями прецессий (в дальнейшем для краткости – каждой “спарки”) так, чтобы векторы собственных кинетических моментов роторов, несомых гироузлами, были направлены в противоположные стороны. Для полученного таким образом КА как твердого тела, согласно результатам Эйлера, перманентными осями устойчивого вращения могут служить только главные оси эллипсоида инерции аппарата с экстремальными значениями моментов инерции аппарата.
До раскрутки аппарата ось ротора компенсаторного гироскопа фиксируется кардановыми кольцами коллинеарно выбранной устойчивой главной оси эллипсоида инерции. Раскручивать аппарат РБ следует вокруг той главной оси инерции, коллинеарно которой закреплена ось ротора компенсаторного гироскопа с нулевым начальным собственным кинетическим моментом. Направление и величина в ССО вектора кинетического момента КА, неразгруженного после расстыковки с “Фрегатом”, определяется в случае перманентного вращения аппарата вектором угловой скорости. Поэтому в результате установления “Фрегатом” перманентного вращения КА вокруг его главной оси инерции вектор кинетического момента аппарата после расстыковки будет коллинеарен этой главной оси.
После установления перманентного вращения КА вокруг главной оси инерции и последующего отделения его от “Фрегата” уравнения движения общего вида в ССО следует привести к виду (2.3), (2.4), не содержащему производной гиростатического момента ${\mathbf{\dot {k}}}(t)$. После этого ротор гироскопа-компенсатора раскручивается до измеренной величины неразгруженного кинетического момента аппарата $\left| {I{{\omega }_{p}}} \right| = {{J}_{{{\text{гл}}}}}{{\omega }_{p}}$, оставшегося после отделения от “Фрегата” (где ${{J}_{{{\text{гл}}}}}$ – момент инерции КА). В результате этих действий неразгруженный кинетический момент КА будет “перекачен” в ротор гироскопа-компенсатора. Осуществление процесса компенсации неразгруженного кинетического момента КА в процессе его неустановившегося перманентного вращения гарантируется обеспечением коллинеарности двух векторов направлению выбранной главной оси инерции аппарата [10]. Этими двумя коллинеарными векторами являются: переменной величины вектор кинетического момента ротора гироскопа-компенсатора и постоянной величины вектор компенсируемого неразгруженного кинетического момента аппарата. Поскольку по оговоренному условию кинетические моменты исполнительной гиросистемы и компенсационного гироскопа во время разгрузки КА были обнулены, то величина неразгруженного кинетического момента КА равна $\left| {I{{\omega }_{p}}} \right|$ и является первым интегралом общих уравнений движения [8] и в ИСО, и в ССО. Как следствие компенсации неразгруженного кинетического момента КА, определяемого угловой скоростью, угловая скорость КА будет обнулена: ${{\omega }_{0}} = 0$. Гиростатический момент исполнительной гиросистемы, не участвующий в этой операции, как было указано выше, следует обнулять до раскрутки КА.
В дальнейшем при исполнении новой технологии ориентации, состоящей из последовательности перманентных вращений КА, собственный кинетический момент ротора гироскопа-компенсатора будет поддерживать компенсацию кинетического момента КА, неразгруженного после расстыковки с РБ. Кинетический момент КА, возникающий в процессе ориентации, компенсируется прецессированием гироузлов гиродинов при исполнении вычисленного закона перманентного вращения КА.
4. О кинематическом конфигурировании силовых гиросистем. Распространенное на сегодня конфигурирование системы однокарданных силовых безупорных гироскопов (гиродинов) заключается в жестком закреплении осей прецессии гироузлов в корпусе аппарата. Это конфигурирование можно назвать геометрическим конфигурированием. Используемое же в статье конфигурирование состоит в дополнении традиционного закрепления осей прецессии гироузлов в корпусе аппарата кинематическим синхронизированием прецессий пар гироузлов с коллинеарными осями прецессии. Подчеркнем, что синхронизирование производится не механическим (редукторным) способом, а кинематическим, программно реализуемым связыванием вращений гироузлов вокруг коллинеарных осей прецессирования. Характер таких кинематических связей определился при анализе результатов итерационных расчетов программных управлений с позиции обеспечения управляемости краевых условий в задаче переориентации для достаточно широкого класса динамических моделей КА [13–15] с инерционными исполнительными органами системы управления (СУ). Реализуется дополнительное конфигурирование виртуально: программные связи скоростей прецессий коллинеарных пар гироузлов численно “прошиваются” в законах вращения гироузлов предварительно и независимо от рабочих программ управления гироузлами, получаемых в результате расчетов. При пересчете рабочих законов для измененных постановок задач параметры кинематических связей могут настраиваться.
Идеология введения в рассмотрение кинематически конфигурированных гиросистем и их связь с проблемой управляемости краевых условий задачи ориентации описана в [8, 16]. Здесь рассмотрим конфигурирование гиросистемы, в котором геометрическое конфигурирование осей реальных прецессий гироузлов коллинеарных пар из четырех гиродинов дополнено программно исполняемой синхронизацией реально прецессирующих углов.
При формировании методом кинематического конфигурирования гиросистемы из четырех гиродинов с попарно коллинеарными осями прецессии гироузлов получим два виртуальных маховика. Собственный кинетический момент каждого маховика представлен диагональю ромба, построенного на прецессирующих гироузлах с постоянными величинами собственных кинетических моментов роторов коллинеарной пары гиродинов. Виртуальное прецессирование собственных кинетических моментов роторов, происходит сопряженно: сумма виртуальных углов прецессии, отсчитываемых от диагонали, в любой момент времени равна нулю. В результате такого прецессирования обеспечивается управление величиной кинетического момента виртуального маховика – целенаправленное изменение длины диагонали ромба.
Для возможности расчета законов управления по новой технологии при решении краевой задачи ориентации необходима компланарность трех векторов: угловой скорости аппарата и гиростатических моментов двух виртуальных маховиков. Для выполнения этого условия в общем случае значений вектора начальной скорости новой задачи требуется настройка положений осей виртуальных маховиков, обеспечивающая указанную компланарность.
Рассмотрим конфигурирование гиросистемы из четырех гиродинов с одинаковыми собственными кинетическими моментами роторов величиной ${\mathbf{h}}$ и углами прецессий ${{\delta }_{{i1}}}(t),{{\delta }_{{i2}}}(t)$ гироузлов, составляющих две коллинеарные пары с номерами гироузлов i = 1, 2.
Введем параметры ${{\alpha }_{i}}\left( t \right) = \left( {{{\delta }_{{i1}}}\left( t \right) + {{\delta }_{{i2}}}\left( t \right)} \right){\text{/}}2$, ${{\beta }_{{i\,j}}}\left( t \right) = \pm \left( {{{\delta }_{{i1}}}\left( t \right) - {{\delta }_{{i2}}}\left( t \right)} \right){\text{/}}2$ для коллинеарных гироузлов [3]. Гиростатический момент ${{{\mathbf{k}}}_{\omega }}\left( t \right)$, гасящий скорость $\omega \left( t \right) = \omega \left( t \right){{{\mathbf{n}}}_{0}}$, определим как сумму гиростатических моментов коллинеарных пар гиродинов: ${{{\mathbf{k}}}_{\omega }}\left( t \right) = {{{\mathbf{k}}}_{{\omega 1}}}\left( t \right) + {{{\mathbf{k}}}_{{\omega 2}}}\left( t \right)$. Здесь векторы ${{{\mathbf{k}}}_{{\omega 1}}}\left( t \right)$ и ${{{\mathbf{k}}}_{{\omega 2}}}\left( t \right)$ представлены диагоналями ${{{\mathbf{k}}}_{{\omega \,\,i}}} = {\mathbf{h}}_{i}^{ + } + {\mathbf{h}}_{i}^{ - } = 2{{{\mathbf{h}}}_{i}}\cos {{\beta }_{i}}$ параллелограммов со сторонами, образуемыми кинетическими моментами ${\mathbf{h}}_{i}^{ + }$ и ${\mathbf{h}}_{i}^{ - }$ роторов каждой пары гиродинов, ${\text{|}}{\mathbf{h}}_{i}^{ + }{\text{|}} = {\text{|}}{\mathbf{h}}_{i}^{ - }{\text{|}} = {\text{|}}{{{\mathbf{h}}}_{i}}{\text{|}}$, i = 1,2, а ${{\beta }_{i}}$ обозначает величину виртуальной прецессии βij: βi = $\mathop = \limits^\Delta $ |βij|. Направление этих диагоналей $2{{{\mathbf{h}}}_{i}}\cos {{\beta }_{i}}$ определено углами αi(t). Эти диагонали представляют кинетические моменты виртуальных маховиков. Построим одну из кинематических конфигураций гиросистемы, состоящей из четырех гиродинов с попарно коллинеарными осями прецессий.
Положение оси виртуальной прецессии гироузлов первой спарки – линии действия вектора суммарного кинетического момента первой спарки ${{{\mathbf{k}}}_{1}} = {\mathbf{h}}_{1}^{ + } + {\mathbf{h}}_{1}^{ - }$, определяемого углом α1(t), – зададим следующими поворотами осей Oxyz (см. рис. 1, а). Повернем систему Oxyz вокруг оси Oz на угол ${{{\gamma }}_{z}}$. Полученную систему координат обозначим Ox1y1z. Ось виртуального маховика получим, повернув Oy1 вокруг оси виртуальной прецессии Ox1 на угол ${{{\alpha }}_{{{{x}_{1}}}}}$.
Рис. 1.
Представление компонент гиростатического момента через углы виртуальных прецессий: a – для первой коллинеарной пары гиродинов, ${{k}_{{1x}}} = - 2h\cos {{\beta }_{{{{x}_{1}}}}}\cos {{\alpha }_{{{{x}_{1}}}}}\sin {{\gamma }_{z}}$, ${{k}_{{1y}}} = 2h\cos {{\beta }_{{{{x}_{1}}}}}\cos {{\alpha }_{{{{x}_{1}}}}}\cos {{\gamma }_{z}}$, k1z = = $2h{\text{cos}}{{\beta }_{{{{x}_{1}}}}}{\text{sin}}{{\alpha }_{{{{x}_{1}}}}}$; б – для второй коллинеарной пары гиродинов, ${{k}_{{2x}}} = 2h\cos {{\beta }_{{{{y}_{2}}}}}\sin {{\alpha }_{{{{y}_{2}}}}}$, k2y = = $ - 2h{\text{cos}}{{\beta }_{{{{y}_{2}}}}}{\text{cos}}{{\alpha }_{{{{y}_{2}}}}}{\text{sin}}{{\gamma }_{x}}$, ${{k}_{{2z}}} = 2h\cos {{\beta }_{{{{y}_{2}}}}}\cos {{\alpha }_{{{{y}_{2}}}}}\cos {{\gamma }_{x}}$
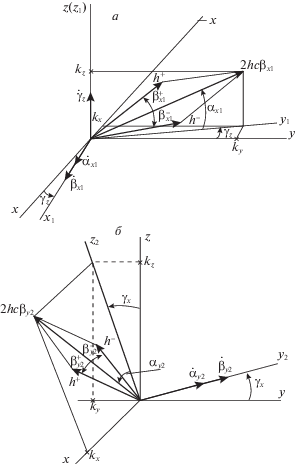
В формулах использованы обозначения: $\beta _{{{{x}_{1}}}}^{ + }$, $\beta _{{{{x}_{1}}}}^{ - }$ – углы виртуальной прецессии гироузлов первой спарки одинаковой величины $\beta _{{{{x}_{1}}}}^{{}} = \left| {\beta _{{x_{1}^{{}}}}^{ + }} \right| = \left| {\beta _{{x_{1}^{{}}}}^{ - }} \right|$, но отсчитываемые в противоположных направлениях от оси виртуального маховика.
Построим положение осей прецессии гироузлов второй спарки (см. рис. 1, б). Систему осей Ox2y2z2 получим поворотом ССО Oxyz вокруг оси Ox на угол γx. Затем поворотом вокруг оси Oy2 на угол ${{\alpha }_{{{{y}_{2}}}}}$(t) ось Oz2 переведем в диагональ ромба ${{{\mathbf{k}}}_{2}} = {\mathbf{h}}_{2}^{ + } + {\mathbf{h}}_{2}^{ - }$ − ось виртуального маховика.
Суммарный гиростатический момент k = k1 + k2 гиросистемы запишем как
(4.1)
$\left\{ \begin{gathered} {{k}_{x}} = 2h\left( { - \cos {{\beta }_{{{{x}_{1}}}}}\cos {{\alpha }_{{{{x}_{1}}}}}\sin {{\gamma }_{z}} + \cos {{\beta }_{{{{y}_{2}}}}}\sin {{\alpha }_{{{{y}_{2}}}}}} \right), \hfill \\ {{k}_{y}} = 2h\left( {\cos {{\beta }_{{{{x}_{1}}}}}\cos {{\alpha }_{{{{x}_{1}}}}}\cos {{\gamma }_{z}} - \cos {{\beta }_{{{{y}_{2}}}}}\cos {{\alpha }_{{{{y}_{2}}}}}\sin {{\gamma }_{x}}} \right), \hfill \\ {{k}_{z}} = 2h\left( {\cos {{\beta }_{{{{x}_{1}}}}}\sin {{\alpha }_{{{{x}_{1}}}}} + \cos {{\beta }_{{{{y}_{2}}}}}\cos {{\alpha }_{{{{y}_{2}}}}}\cos {{\gamma }_{x}}} \right). \hfill \\ \end{gathered} \right.$Выберем ${{\gamma }_{z}} = {{\gamma }_{x}} = \pi {\text{/}}4$. Уравнения (4.1) примут следующий вид:
(4.2)
$\left\{ \begin{gathered} {{k}_{x}} = 2h\left( { - \frac{{\sqrt 2 }}{2}\cos {{\beta }_{{{{x}_{1}}}}}\cos {{\alpha }_{{{{x}_{1}}}}} + \cos {{\beta }_{{{{y}_{2}}}}}\sin {{\alpha }_{{{{y}_{2}}}}}} \right), \hfill \\ {{k}_{y}} = 2h\left( {\frac{{\sqrt 2 }}{2}\cos {{\beta }_{{{{x}_{1}}}}}\cos {{\alpha }_{{{{x}_{1}}}}} - \frac{{\sqrt 2 }}{2}\cos {{\beta }_{{{{y}_{2}}}}}\cos {{\alpha }_{{{{y}_{2}}}}}} \right), \hfill \\ {{k}_{z}} = 2h\left( {\cos {{\beta }_{{{{x}_{1}}}}}\sin {{\alpha }_{{{{x}_{1}}}}} + \frac{{\sqrt 2 }}{2}\cos {{\beta }_{{{{y}_{2}}}}}\cos {{\alpha }_{{{{y}_{2}}}}}} \right). \hfill \\ \end{gathered} \right.$Подставляя выражения компонент kx, ky, kz вектора k из (4.2) в уравнение (2.3), предназначенное для расчета закона гашения угловой скорости ω(t), представим (2.3) как:
(4.3)
$\left( \begin{gathered} - \frac{{\sqrt 2 }}{2}\cos {{\alpha }_{{{{x}_{1}}}}} \\ \frac{{\sqrt 2 }}{2}\cos {{\alpha }_{{{{x}_{1}}}}} \\ \sin {{\alpha }_{{{{x}_{1}}}}} \\ \end{gathered} \right)\cos {{\beta }_{{{{x}_{1}}}}}(t) + \left( \begin{gathered} \sin {{\alpha }_{{{{x}_{2}}}}} \\ - \frac{{\sqrt 2 }}{2}\cos {{\alpha }_{{{{x}_{2}}}}} \\ \frac{{\sqrt 2 }}{2}\cos {{\alpha }_{{{{x}_{2}}}}} \\ \end{gathered} \right)\cos {{\beta }_{{{{y}_{2}}}}}(t) = - \frac{{\omega (t)}}{{2h}}\left( \begin{gathered} A{{n}_{{0x}}} \\ B{{n}_{{0y}}} \\ C{{n}_{{0z}}} \\ \end{gathered} \right).$Отметим, что необходимым условием существования решения (4.3) является условие компланарности векторов: In0, ${{{\mathbf{k}}}_{1}}(t) = 2h\cos {{{\beta }}_{1}}{{\kappa }_{1}}$, ${{{\mathbf{k}}}_{2}}(t) = 2h\cos {{{\beta }}_{2}}{{\kappa }_{2}}$. Без выполнения этого условия нельзя обеспечить гашение угловой скорости вращения аппарата двумя спарками гиродинов. Таким образом, условие существования решения системы (4.3) имеет вид: det(In0, κ1(t), κ2(t)) = 0, т.е.
При ${{\alpha }_{i}} \ne \pi {\text{/}}2$, где $i = {{x}_{1}}$, y2, оно примет вид:
(4.4)
$A{{n}_{{0x}}}(1 + \sqrt 2 \operatorname{tg} {{\alpha }_{{{{x}_{1}}}}}) + B{{n}_{{0y}}}(1 + 2\operatorname{tg} {{\alpha }_{{{{x}_{1}}}}}\operatorname{tg} {{\alpha }_{{{{y}_{2}}}}}) + C{{n}_{{0z}}}(1 - \sqrt 2 \operatorname{tg} {{\alpha }_{{{{y}_{2}}}}}) = 0.$Уравнение (4.4) содержит два настраиваемых параметра ${{\alpha }_{{{{x}_{1}}}}}$ и ${{\alpha }_{{{{y}_{2}}}}}$ для обеспечения компланарности векторов In0, ${{{\mathbf{k}}}_{1}}(t) = 2h\cos {{{\beta }}_{1}}{{\kappa }_{1}}$, ${{{\mathbf{k}}}_{2}}(t) = 2h\cos {{{\beta }}_{2}}{{\kappa }_{2}}$. Без компланарности указанных векторов перманентное гашение произвольной угловой скорости КА двумя виртуальными маховиками невозможно.
Условие компланарности позволяет построить векторы k1(t), k2(t) как стороны параллелограмма, диагональю которого при подборе необходимых для гашения скорости значений $\cos {{\beta }_{{{{x}_{1}}}}}\left( t \right)$ и $\cos {{\beta }_{{{{y}_{2}}}}}\left( t \right)$ будет служить вектор $\omega \left( t \right){\mathbf{I}}{{{\mathbf{n}}}_{0}}$. Предлагаемая новая технология расчета законов управления ориентацией, не порождающая сингулярностей исполнительных гиродинов, не реализуема для гиросистем типа “Twin–Gyro” или “Scissored pairs” с механической синхронизацией вращений гироузлов гиродинов с коллинеарными осями прецессии.
5. Необходимые построения для численной реализации метода. Введем следующие обозначения: ${{\beta }_{1}} \equiv {{\beta }_{{{{x}_{1}}}}},$ ${{\beta }_{2}} \equiv {{\beta }_{{{{y}_{2}}}}},$ ${{\alpha }_{1}} \equiv {{\alpha }_{{{{x}_{1}}}}},$ ${{\alpha }_{2}} \equiv {{\alpha }_{{{{y}_{2}}}}}.$ Пусть в начальный момент времени t0 для гироузлов двух спарок заданы значения углов виртуальных прецессий ${{\alpha }_{{10}}} \equiv {{\alpha }_{1}}({{t}_{0}})$, ${{\alpha }_{{20}}} \equiv {{\alpha }_{2}}({{t}_{0}})$, а также значения модулей ${{\beta }_{{10}}} \equiv {{\beta }_{1}}({{t}_{0}})$ и ${{\beta }_{{20}}} \equiv {{\beta }_{2}}({{t}_{0}})$ углов $\beta _{{{{x}_{1}}}}^{ \pm }$ и $\beta _{{{{y}_{2}}}}^{ \pm }$ соответственно.
Поскольку в статье предполагается устанавливать, а затем гасить перманентное вращение, используя разгонный блок (см. разд. 3), будем считать, что ${{\omega }_{0}} = 0$, ${{\beta }_{{10}}} = {{\beta }_{{20}}} = \pi {\text{/}}2$ (т.е. углы виртуальных прецессий $\beta _{{1j\,0}}^{{}} = \beta _{{2j0}}^{{}} = \pm \pi {\text{/}}2$), α10 и α20 фиксированы. Виртуальные прецессии $\beta _{{i\,j0}}^{{}}$ выбираем равными ±π/2 так, чтобы величина гиростатического момента равнялась нулю во время настройки гироузлов.
Решение задачи ориентации с применением перманентных вращений КА включает следующие последовательно выполняемые этапы.
I. Перестройка гиросистемы, обеспечивающая поворот Эйлера–Шаля.
II. Поворот Эйлера–Шаля.
III. Перестройка гиросистемы для разгона.
IV. Разгон аппарата до заданной угловой скорости и положения на оси.
Этапы II и IV будем называть основными, а этапы I и III – вспомогательными. В отличие от этапов процесса ориентации, упомянутых в разд. 1, здесь добавлены два вспомогательных этапа и исключен этап гашения начальной скорости, выполняемый РБ.
Кроме названных этапов имеется этап виртуального гашения заданной финальной скорости $\omega ({{t}_{f}})$, который совершается численно и служит для определения времени гашения и положения КА после поворота Эйлера–Шаля. Этот поворот совершается из одного неподвижного положения КА в другое неподвижное.
Ставится задача определения законов управления двумя спарками гиродинов, т.е. законов изменения углов виртуальных прецессий $\{ {{\alpha }_{1}}(t),{{\beta }_{{1j}}}(t)\} $ и $\{ {{\alpha }_{2}}(t),{{\beta }_{{2j}}}(t)\} $, обеспечивающих реализацию всех упомянутых этапов. Законы управления будем искать в предположении, что на основных этапах, включая этап численного гашения финальной скорости на динамической модели, углы ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$ являются постоянными, а изменяются лишь углы ${{\beta }_{{1j}}}$ и ${{\beta }_{{2j}}},$ в то время как на вспомогательных этапах наоборот – постоянны углы ${{\beta }_{{1j}}}$ и ${{\beta }_{{2j}}}$, а изменяются ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$. Начнем с вывода закона управления для этапа гашения финальной скорости.
6. Гашение заданной финальной скорости ${{\omega }_{f}} = \omega \,\,({{t}_{f}})$. В отсутствие требований к конфигурированию гиросистемы в конечный момент времени ${{t}_{f}}$ значение углов виртуальных прецессий, определяющих это состояние, целесообразно искать, исходя из минимизации временных затрат на выполнение всех этапов решения задачи переориентации.
Решение оптимизационной задачи
(6.1)
${{({{\beta }_{1}} - {{\beta }_{{10}}})}^{2}} + {{({{\beta }_{2}} - \beta _{{20}}^{{}})}^{2}} + {{({{\alpha }_{1}} - \alpha _{{10}}^{{}})}^{2}} + {{({{\alpha }_{2}} - \alpha _{{20}}^{{}})}^{2}} \to \min $(6.2)
$\left( {\begin{array}{*{20}{c}} { - \frac{{\sqrt 2 }}{2}\cos {{\alpha }_{1}}} \\ {\frac{{\sqrt 2 }}{2}\cos {{\alpha }_{1}}} \\ {\sin {{\alpha }_{1}}} \end{array}} \right)\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\beta }_{1}}\left( t \right) + \left( {\begin{array}{*{20}{c}} {\sin {{\alpha }_{2}}} \\ { - \frac{{\sqrt 2 }}{2}\cos {{\alpha }_{2}}} \\ {\frac{{\sqrt 2 }}{2}\cos {{\alpha }_{2}}} \end{array}} \right)\cos {{\beta }_{2}}\left( t \right) = - \frac{{{{\omega }_{f}}}}{{2h}}\left( \begin{gathered} A{{n}_{{0x}}} \hfill \\ B{{n}_{{0y}}} \hfill \\ C{{n}_{{0z}}} \hfill \\ \end{gathered} \right),$Следуя замечанию о структуре законов управления на основных этапах, для этапа гашения определим значения углов ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$ в виде
Пусть ${\text{|}}{{\beta }_{{10}}} - \beta _{1}^{*}{\text{|}} > {\text{|}}{{\beta }_{{20}}} - \beta _{2}^{*}{\text{|}}$. Тогда законы управления ${{\beta }_{1}}(t),\;{{\beta }_{2}}(t)$, обеспечивающие перманентное гашение скорости ${{\omega }_{f}}$, можно выбрать в виде
(6.4)
${{\beta }_{1}}(t) = {{k}_{{\dot {\beta }}}}t + \beta _{1}^{*},\quad {{\beta }_{2}}(t) = \arccos (\mu \cos {{\beta }_{1}}(t)),$(6.5)
$\omega (t) = \frac{{{{\omega }_{f}}}}{{\cos \beta _{1}^{*}}}\cos ({{k}_{{\dot {\beta }}}}t + \beta _{1}^{*}).$Проинтегрировав (6.5) на промежутке $[0,T]$, получим угол
(6.6)
$\varphi = \frac{{{{\omega }_{f}}}}{{{{k}_{{\dot {\beta }}}}\cos \beta _{1}^{*}}}(\sin ({{k}_{{\dot {\beta }}}}T + \beta _{1}^{*}) - \sin (\beta _{1}^{*})),$В случае ${\text{|}}{{\beta }_{{10}}} - \beta _{1}^{*}{\text{|}} \leqslant {\text{|}}{{\beta }_{{20}}} - \beta _{2}^{*}{\text{|}}$ законы управления, аналогичные (6.4), примут вид
Подобно (6.5) и (6.6) определяются закон ω(t) и угол φ.
7. Поворот Эйлера–Шаля. Сформируем закон управления для осуществления поворота КА, выполняемого на этапе II, из положения ${\mathbf{\lambda }}_{0}^{{{\text{II}}}}$ $\mathop = \limits^\Delta $ λ(t0) в положение ${\mathbf{\lambda }}_{f}^{{{\text{II}}}}$. Здесь и далее верхний индекс указывает на принадлежность величины соответствующему этапу (для этапа виртуального гашения будем использовать в верхнем индексе символ E). Величину ${\mathbf{\lambda }}_{f}^{{{\text{II}}}}$ определим как
Для расчета оси и угла перманентного поворота КА вычислим кватернион Эйлера–Шаля следующим образом [17]:
где символ $ \circ $ обозначает кватернионное умножение.Орт оси поворота Эйлера–Шаля 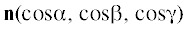 , задаваемый в ССО направляющими косинусами, и угол поворота χ определяются следующими
формулами [17]:
, задаваемый в ССО направляющими косинусами, и угол поворота χ определяются следующими
формулами [17]:
С целью определения “наилучших” значений углов виртуальных прецессий гиродинов для этапа поворота решается следующая задача:
(7.1)
$\begin{gathered} {{({{\beta }_{1}} - {{\beta }_{{01}}})}^{2}} + {{({{\beta }_{2}} - {{\beta }_{{02}}})}^{2}} + {{({{\alpha }_{1}} - {{\alpha }_{{01}}})}^{2}} + \\ \, + {{({{\alpha }_{2}} - {{\alpha }_{{02}}})}^{2}} + {{({{\alpha }_{1}} - \alpha _{1}^{{*E}})}^{2}} + {{({{\alpha }_{2}} - \alpha _{2}^{{*E}})}^{2}} \to \min \\ \end{gathered} $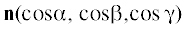 , а в качестве ωf можно взять любое положительное число, значительно меньшее, чем предельно возможная
скорость вращения КА. Обозначим это число через ω*. Такой выбор оправдан, так как
в данном случае значение имеет ориентация оси вращения, а не ее скорость. Углы $\alpha _{1}^{{*E}}$ и $\alpha _{2}^{{*E}}$ в (7.1) определены ранее из решения задачи (6.1).
, а в качестве ωf можно взять любое положительное число, значительно меньшее, чем предельно возможная
скорость вращения КА. Обозначим это число через ω*. Такой выбор оправдан, так как
в данном случае значение имеет ориентация оси вращения, а не ее скорость. Углы $\alpha _{1}^{{*E}}$ и $\alpha _{2}^{{*E}}$ в (7.1) определены ранее из решения задачи (6.1).
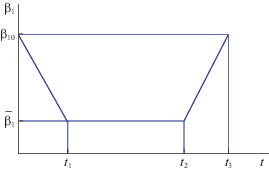
По аналогии с этапом гашения законы управления ${{\alpha }_{1}}(t)$ и ${{\alpha }_{2}}(t)$ определим как в (6.3), т.е. постоянными. Законы ${{\beta }_{1}}(t)$ и ${{\beta }_{2}}(t)$ будем искать в виде, представленном на рис. 2. В соответствии со структурой такого закона управления на первом временном промежутке
β1 линейно изменяется с β10 до некоторого значения  , на втором промежутке это значение удерживается и, наконец, на третьем промежутке
значение угла восстанавливается до β10. Рассмотрим только случай, когда ${\text{|}}{{\beta }_{{10}}} - \beta _{1}^{*}{\text{|}} > {\text{|}}{{\beta }_{{20}}} - \beta _{2}^{*}{\text{|}}$.
, на втором промежутке это значение удерживается и, наконец, на третьем промежутке
значение угла восстанавливается до β10. Рассмотрим только случай, когда ${\text{|}}{{\beta }_{{10}}} - \beta _{1}^{*}{\text{|}} > {\text{|}}{{\beta }_{{20}}} - \beta _{2}^{*}{\text{|}}$.
Как и в случае гашения, закон ${{\beta }_{2}}(t)$ возьмем в виде
где $\mu = \cos \beta _{1}^{*}{\text{/}}\cos \beta _{2}^{*}$.Вычислим угол, на который повернется КА при изменении угла β1 от β10 до 0 при использовании закона управления β1(t) = ${{k}_{{\dot {\beta }}}}$t + β10, с ${{k}_{{\dot {\beta }}}}$ $\mathop = \limits^\Delta $ $\bar {\dot {\delta }}$ sign($\beta _{1}^{*}$ – β10):
Если $\chi < 2{{\varphi }_{q}}$ (при изменении угла прецессии ${{\beta }_{1}}$ от начального значения $\beta _{1}^{*}$ до нуля, а потом обратно, корпус КА повернется на угол, больший, чем χ), то положим ${{t}_{1}} = {{t}_{2}} = {{T}_{a}}$, ${{t}_{3}} = 2{{T}_{a}}$,
(7.3)
${{\beta }_{1}}(t) = \left\{ \begin{gathered} {{k}_{{\dot {\beta }}}}t + {{\beta }_{{10}}},\quad t \in [0,{{t}_{1}}), \hfill \\ {{k}_{{\dot {\beta }}}}{{t}_{1}} + {{\beta }_{{10}}},\quad t \in [{{t}_{1}},{{t}_{2}}), \hfill \\ - {{k}_{{\dot {\beta }}}}(t - {{t}_{1}} - {{t}_{2}}) + {{\beta }_{{10}}},\quad t \in [{{t}_{2}},{{t}_{3}}]. \hfill \\ \end{gathered} \right.$В случае $\chi \geqslant 2{{\varphi }_{q}}$ будем иметь ${{t}_{1}} = {{T}_{q}}$, ${{t}_{2}} = {{t}_{1}} + {{T}_{h}}$, ${{t}_{3}} = {{t}_{2}} + {{T}_{q}}$, ${{\bar {\beta }}_{1}} = 0$, а закон управления ${{\beta }_{1}}(t)$ останется прежним. Время ${{T}_{h}}$ удержания угла ${{\beta }_{1}}$ в нуле определится из следующего соотношения:
8. Разгон до заданной угловой скорости ${{\omega }_{f}}$. Подходящие значения $\alpha _{1}^{*},$ $\beta _{1}^{*}$, $\alpha _{2}^{*}$, $\beta _{2}^{*}$ углов виртуальных прецессий для этого этапа не вычисляются, а берутся те, что были определены для этапа гашения из решения задачи (6.1) и (6.2). Таким образом, $\alpha _{1}^{*} = \alpha _{1}^{{*E}}$, $\beta _{1}^{*} = \beta _{1}^{{*E}}$, $\alpha _{2}^{*} = \alpha _{2}^{{*E}}$, $\beta _{2}^{*} = \beta _{2}^{{*E}}$.
Законы управления ${{\alpha }_{1}}(t)$ и ${{\alpha }_{2}}(t)$ для гашения возьмем как в (6.3), а законы управления ${{\beta }_{1}}(t)$ и ${{\beta }_{2}}(t)$ по аналогии с (6.4) определим следующим образом:
9. Перестроение гиросистемы. На этапах $J \in \{ {\text{I}},{\text{III}}\} $ перестроения гиросистемы решается задача изменения виртуальных углов прецессии ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$ c начальных значений $\alpha _{{10}}^{J}$, $\alpha _{{20}}^{J}$ до заданных конечных $\alpha _{{1f}}^{J}$, $\alpha _{{2f}}^{J}$ при условии постоянства значений углов β1$\mathop = \limits^\Delta $ β10 и β2$\mathop = \limits^\Delta $ β20. Решение задачи обеспечивается следующими законами управления:
(9.1)
${{\alpha }_{1}}(t) = {{k}_{{{{{\dot {\alpha }}}_{1}}}}}t + \alpha _{{10}}^{J},\quad {{\alpha }_{2}}(t) = {{k}_{{{{{\dot {\alpha }}}_{2}}}}}t + \alpha _{{20}}^{J},$(9.2)
${{\beta }_{1}}(t) = {{\beta }_{{10}}},\quad {{\beta }_{2}}(t) = {{\beta }_{{20}}},\quad t \in [0,T],$10. Численные расчеты. Численные расчеты выполнены для следующих исходных данных: ${\mathbf{I}} = {\text{diag}}(12 \times {{10}^{3}};\;21 \times {{10}^{3}};\;23 \times {{10}^{3}})$, кгм2, h = 100 нмс, $\bar {\dot {\delta }}$ = 0.6 град/с, ${{\lambda }_{0}} = [{\text{0}}{\text{.65328}}\,\,\, - {\kern 1pt} {\text{0}}{\text{.2706}}$ 0.65328 0.2706]T, ${{\omega }_{0}}$ = [0 0 0]T, град/c, ${{\alpha }_{{10}}} = {{\alpha }_{{20}}} = \pi {\text{/}}6,$ ${{\beta }_{{10}}} = {{\beta }_{{20}}} = \pi {\text{/}}2,$ ${{{\mathbf{\lambda }}}_{f}} = {{\left[ {\begin{array}{*{20}{c}} {{\text{0}}{\text{.5}}}&{{\text{0}}{\text{.5}}}&{ - {\text{0}}{\text{.5}}}&{{\text{0}}{\text{.5}}} \end{array}} \right]}^{T}}$, ${{\omega }_{f}}$ = [0.025 0.05 0.02]T, град/c.
Результаты расчета законов управления для этапов I–IV по приведенным выше алгоритмам сведены в таблице.
Таблица
| Этап | Законы управления | Время этапа, с | |||
|---|---|---|---|---|---|
| α1(t) | β1(t) | α2(t) | β2(t) | ||
| I | Формулы (9.1) и (9.2) с ${{k}_{{{{{\dot {\alpha }}}_{1}}}}}$ = 0.007455 | π/2 | Формулы (9.1) и (9.2) с ${{k}_{{{{{\dot {\alpha }}}_{1}}}}}$ = –0.010472 | π/2 | 63.772 |
| II | 0.99902 | arccos(μcosβ2(t)) μ = –0.37814 | –0.14423 | Формула (7.3) с t1 = 150, t2 = 320.52, t3 = 470.5, ${{\bar {\beta }}_{2}}$ = 0, ${{k}_{{\dot {\beta }}}}$ = 0.010472 | 470.52 |
| III | Формулы (9.1) и (9.2) с ${{k}_{{{{{\dot {\alpha }}}_{1}}}}}$ = 0.010472 | π/2 | Формулы (9.1) и (9.2) с ${{k}_{{{{{\dot {\alpha }}}_{1}}}}}$ = –0.0068436 | π/2 | 35.205 |
| IV | 0.7332 | ${{k}_{{\dot {\beta }}}}$t + π/2, ${{k}_{{\dot {\beta }}}}$ = 0.010472 | –0.0105 | arccos(μcos(β1(t)))μ = = –0.97301 | 11.24 |
Проверка рассчитанных с помощью описанной технологии законов управления для рассматриваемого примера осуществлялась путем интегрирования полной модели КА, заданной системой уравнений
(10.1)
${\mathbf{I\dot {\omega }}}(t) + {\mathbf{\dot {k}}}(t) = - {\mathbf{\omega }}(t) \times ({\mathbf{I\omega }}(t) + {\mathbf{k}}(t)),$(10.2)
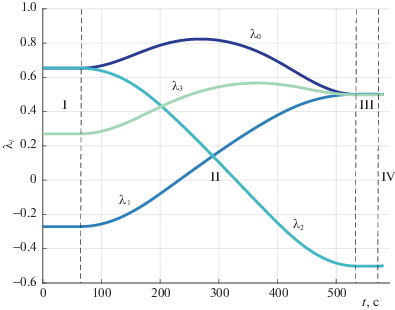
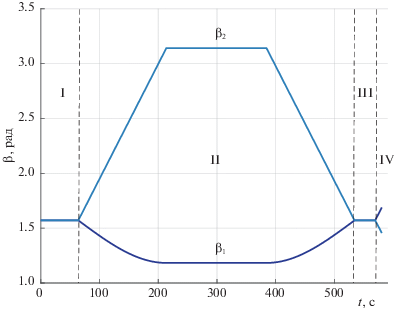
${\mathbf{\dot {\lambda }}} = \frac{1}{2}{\mathbf{\omega }} \circ {\mathbf{\lambda }}{\kern 1pt} ,$На рис. 3–7 представлены полученные в результате интегрирования модели (10.1), (10.2) графики изменения элементов кватерниона положения λ, компонент вектора угловой скорости ω, законов управления ${{\beta }_{i}}(t),$ ${{\alpha }_{i}}(t)$ и соответствующих им реальных прецессий ${{{\delta }}_{{i1}}}$ и ${{{\delta }}_{{i2}}}$. Римскими цифрами на рисунках обозначены соответствующие этапы переориентации.
Заключение. Исследования, проведенные в статье, показали возможность вычислять программные законы ориентации КА, не содержащие сингулярных состояний гиросистемы для двух коллинеарных пар четырех гиродинов, также, как и для трех таких пар [8, 9]. Выясняется, что вычисление законов управления по предлагаемой новой технологии расчетов, не порождающей сингулярных состояний исполнительной гиросистемы, возможно, в отличие от случая шести гиродинов, только при кинематическом конфигурировании гиросистемы. Такое конфигурирование обеспечивает кинематическую синхронизацию вращений гироузлов гиродинов с коллинеарными осями прецессии и позволяет при необходимости устанавливать нужное положение осей виртуальных маховиков. Такая коррекция положения одной из осей виртуальных маховиков необходима в общем случае для новой задачи ориентации, когда вектор новой начальной скорости не компланарен с осями виртуальных маховиков. Для гиросистем, имеющих механическую синхронизацию вращений гироузлов с коллинеарными осями прецессии, изменение положения осей виртуальных маховиков невозможно. Так будет для гиросистем типа “Twin–Gyro” [2] или “Scissored pairs” [3] с синхронизацией, обеспеченной механическими средствами. Таким образом, и для гиросистемы, образованной двумя коллинеарными парами стандартных гиродинов, подтверждается возможность вычислять законы ориентации, не содержащие сингулярностей.
Список литературы
Amster M.N., Anderson R.P., Williams H.M. Analysis of Twin–gyro Attitude Controller; Final Summary Report // EL–EOR–13005. Dallas Texas: Chance Vought Aircraft, Inc., 1960.
Lopez A.E., Ratcliff J.W., Havill J.R. Results of Studies on a Twin–Gyro Attitude Control System for Space Vehicles // J. Spacecraft. 1964. V. 1. № 4. P. 399–402.
Crenshaw J.W. 2–SPEED, A Single–Gimbal Control Moment Gyro Attitude Control System // AIAA Paper. 1973. № 895. P. 1–10.
Дружинин Э.И. Расчет программных управлений, безостановочно исполняемых гиродинами // ДАН. 2017. Т. 476. № 1. С. 22–25.
Токарь Е.Н., Легостаев В.П., Михайлов М.В., Платонов В.П. Управление избыточными гиросиловыми системами // Космич. исслед. 1980. Т. XVIII. Вып. 2. С. 147–156.
Kurokawa H. Survey of Theory and Steering Laws of Single–Gimbal Control Moment Gyros // J. Guidance, Control, and Dynamics. 2007. V. 30. № 5. P. 1331–1340.
Суслов Г.К. Теоретическая механика. Л.: Гостехтеоретиздат, 1946.
Дружинин Э.И. Расчет программных управлений, не порождающий сингулярных состояний гиросистемы. I // Изв. РАН. ТиСУ. 2019. № 2. С. 106–116.
Беляев Б.Б., Бычков И.В., Дружинин Э.И., Ульянов С.А. Расчет программных управлений, не порождающий сингулярных состояний гиросистемы. II // Изв. РАН. ТиСУ. 2019. № 3. С. 194–206.
Дружинин Э.И. О перманентных вращениях уравновешенного неавтономного гиростата // ПММ. 1999. Т. 63. № 5. С. 875–876.
Богданов Ю.С., Чеботарев Г.Н. О матрицах, коммутирующих со своей производной // Изв. вузов. Математика. 1959. № 4 (11). С. 27–37.
75 лет ФГУП. “НПО им. С.А. Лавочкина” 2012 г. www.laspase.ru.
Дружинин Э.И., Дмитриев А.В. Метод Ньютона–Канторовича в задаче управления конечным состоянием нелинейного объекта // Метод функций Ляпунова и его приложения. Новосибирск: Наука. СО, 1984. С. 251–254.
Дружинин Э.И., Дмитриев А.В. К теории нелинейных краевых задач управляемых систем // Дифференциальные уравнения и численные методы. Новосибирск: Наука. СО, 1986. С. 179–187.
Васильев С.Н., Воронов В.А., Дружинин Э.И. Новая вычислительная технология формирования программных управлений в нелинейных системах // Тр. XIII Санкт-Петербургской междунар. конф. по интегрированным навигационным системам. СПб.: ОАО “Концерн “ЦНИИ Электроприбор”, 2006. С. 48–56.
Бычков И.В., Дружинин Э.И., Огородников Ю.И., Беляев Б.Б., Ульяшин А.И. О кинематическом конфигурировании силовых гиросистем // Тр. XXII Санкт-Петербургской междунар. конф. по интегрированным навигационным системам. СПб.: ОАО “Концерн “ЦНИИ Электроприбор”, 2015. С. 234–239.
Бранец В.Н., Шмыглевский И.П. Применение кватернионов в задачах ориентации твердого тела. М.: Наука, 1973.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления