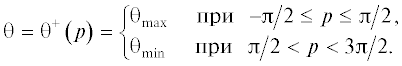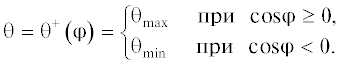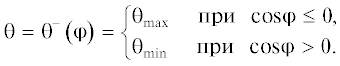Известия РАН. Теория и системы управления, 2020, № 5, стр. 89-105

Введение. Качели относятся к механическим объектам, в которых управляющие воздействия создаются человеком. Проблемы исследования таких объектов можно отнести к биомеханике, к теории управления и к теории колебаний. Математическое моделирование подобных систем актуально для многих прикладных задач. Среди классических задач динамики объектов, управляемых человеком, моделирование динамики качелей выделяется как проблема, имеющая не только прикладное, но и фундаментальное значение. Процесс раскачивания качелей не утрачивает актуальности как классический пример вынужденных колебаний [1]. Моделирование различных стратегий управления качелями позволяет исследовать эффективность этих стратегий, механические эффекты, влияющие на колебания качелей, и интересные с точки зрения теории колебаний.

При рассмотрении задачи о раскачивании качелей человеком, стоящим на них, часто изучается модель качелей в виде маятника переменной длины, поскольку человек, раскачивающий качели стоя, в какие-то моменты времени приседает на них, а в какие-то встает. Подобная модель рассматривается, например, в работах [2–7]. В [8–11] решается задача оптимального управления качелями, при котором достигается максимальное отклонение качелей от вертикали в конце каждого “полуколебания”, а также после любого конечного числа полуколебаний.

Принципиально отличной и более трудной является задача моделирования поведения человека, раскачивающего качели, сидя на них, что отмечено еще в работе [7]. Наиболее распространенный в литературе подход предполагает изучение двухзвенной системы, при этом человек моделируется одним твердым телом, раскачивание реализуется посредством изменения угла между человеком и качелями. Для такой модели выделяются два подхода к построению управления: 1) управление явно зависит от времени; тем самым задача организации колебаний качелей рассматривается как задача параметрического возбуждения колебаний; 2) используется обратная связь по углу и/или угловой скорости качелей (формирование автоколебательной системы). Можно более-менее точно указать работы, ставшие “отправными точками” в развитии этих подходов: [5, 12] для параметрического возбуждения и [13] для управления в виде обратной связи соответственно. Отметим, что в этих статьях, помимо всего прочего, получены оценки эффективности стратегий раскачивания, реализуемого путем изменения угла между человеком и качелями, и раскачивания посредством “приседаний”. При этом предложен критерий эффективности – скорость раскачивания (т.е. увеличение амплитуды за одно очередное колебание качелей), который затем используется при оценке качества управления в подавляющем большинстве работ в этой области.

Сравнение эффективности законов управления, построенных путем параметрического возбуждения колебаний и управления в виде обратной связи, проведено в [14, 15]. В этом сравнении рассматриваются, в частности, “базовые” законы управления, предложенные в [12, 13]. Управление в виде обратной связи оказывается более эффективным. В [16] ставится вопрос о том, близко ли “антропоморфное” управление в виде обратной связи (подобное рассмотренному в работе [13]) к оптимальному (критерий эффективности тот же). Cравнение проводится в некотором (достаточно узком) классе управлений, в котором “антропоморфная” стратегия оказывается максимально эффективной. В [17, 18] исследуется вопрос о переводе качелей в режим колебаний из состояния покоя.

В задаче о раскачивании качелей сидящим на них человеком остаются открытыми следующие вопросы: построение управления, близкого к оптимальному по скорости наращивания амплитуды колебаний, учет влияния ограничений на управляющие моменты, приложенные в шарнирах (в [14] значения момента обсуждаются, но ограничение не накладывается), анализ влияния трения в оси качелей (вопрос поставлен еще в [13]), выход колебаний на установившийся режим (вопросы единственности, устойчивости).

Отдельно следует отметить, что в научной литературе практически не обсуждаются многозвенные модели человека, сидящего на качелях, хотя известно об экспериментах по созданию многозвенных антропоморфных роботов, раскачивающих качели, для которых такие модели актуальны (см., например, [19]).

Задача синтеза управления качелями перекликается с задачей об управлении маятником при помощи маховика [9, 10, 20–22]. Она имеет также сходство с задачей о раскачивании гимнаста на перекладине [9, 10, 23, 24]. В отличие от последней в задаче о качелях целью управления является установившееся движение, которое представляет собой колебания с постоянной амплитудой.

В отличие от многих известных работ, в которых изучается только двухзвенная механическая модель человека на качелях, в настоящей статье рассматривается как двухзвенная модель, так и модель, представляющая собой трехзвенный шарнирный механизм. Первое звено трехзвенного механизма моделирует корпус человека (вместе с головой и руками), второе звено – два бедра, жестко соединенные с качелями, а третье – две голени (со стопами). Шарнир между первым звеном (корпус) и вторым (бедра) моделирует два тазобедренных сустава, шарнир между вторым звеном (бедра) и третьим (голени) – два коленных сустава. В этих шарнирах прикладываются ограниченные по абсолютной величине управляющие моменты.

Решаются задачи синтеза в виде обратной связи законов управления, обеспечивающих раскачивание или торможение качелей сидящим на них человеком. Обратная связь вначале строится для управления более простой моделью – двухзвенной. Затем построенный для двухзвенной модели закон управления “переносится” на трехзвенную модель. Показано, что реализуется выход на колебания с постоянной амплитудой. Если трение в точке подвеса относительно мало, то колебания переходят в ротацию и качели совершают вращение вокруг точки подвеса подобно гимнасту, выполняющему на перекладине упражнение “солнышко”. Таким образом, в настоящей статье возникновение колебаний качелей, а также их кругового вращения – ротации – трактуется не как результат параметрического возбуждения, а как результат целенаправленного управления с обратной связью.

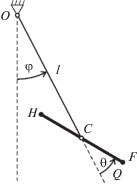
1. Трехзвенная механическая модель человека на качелях. На рис. 1 показана схема изучаемой плоской трехзвенной модели. Звено HP моделирует корпус человека вместе с руками и головой, звено PK – два бедра человека, которые жестко соединены с качелями, звено KF – обе голени. Шарнир P моделирует оба тазобедренных сустава человека, шарнир K – оба коленных, O – точка подвеса качелей.

Точки ${{C}_{b}}$, ${{C}_{h}}$ и ${{C}_{s}}$ – центры масс звеньев HP, PK и KF соответственно. Качели состоят из стержня OC_h и перпендикулярного ему сидения, жестко скрепленного со стержнем OC_h. Звено PK (бедра) располагается на сидении и жестко крепится на нем (на рис. 1 сидение не показано). Таким образом, звено PK ортогонально стержню OC_h и составляет с ним одно твердое тело. Массу качелей, т.е. стержня OC_h вместе с сидением, в дальнейшем учитывать не будем, считая ее пренебрежимо малой, по сравнению с массой человека (трехзвенника HPKF).

Рассматриваемая система имеет три степени свободы и соответственно три обобщенные координаты: угол $\varphi $ между вертикалью и качелями (стержнем OC_h), углы $\alpha $ и $\beta $ отклонения звеньев KF и HP от прямой, параллельной стержню OC_h. Таким образом, угол между звеном KF (голени) и вертикалью равен $\left( {\varphi + \alpha } \right)$, а между звеном HP (корпус) и вертикалью – $\left( {\varphi + \beta } \right)$. Направление против часовой стрелки выбрано положительным при отсчете углов.

В шарнире K (в коленных суставах) прикладывается управляющий момент L, а в шарнире P (в тазобедренных суставах) – управляющий момент M (см. рис. 1). Каждый из этих моментов считается ограниченным по абсолютной величине:

Моменты L и M могут поворачивать соответственно звено KF (голени) и звено HP (корпус) относительно звена PK (бедра).

Будем предполагать, что в точке O подвеса качелей действуют силы вязкого трения, момент которых $\mu \dot {\varphi }$ пропорционален угловой скорости $\dot {\varphi }$, а коэффициент $\mu = {\text{const}}$.

В силу анатомических свойств человека углы в его коленных и тазобедренных суставах могут изменяться лишь в ограниченных пределах. Эти ограничения обеспечиваются, в частности, связками и сухожилиями, а для корпуса – также руками. Будем моделировать соответствующие воздействия как моменты односторонних спиральных пружин в шарнирах K и P, обладающих “большой” жесткостью. Модель такого рода рассматривается в работе [25]. Когда углы $\alpha $ и $\beta $ достигают некоторых критических значений ${{\alpha }_{{{\text{min}}}}}$, ${{\alpha }_{{{\text{max}}}}}$ и ${{\beta }_{{{\text{min}}}}}$, ${{\beta }_{{{\text{max}}}}}$, в шарнирах K и P возникают моменты ${{L}_{S}}$ и ${{M}_{S}}$ сил упругости, направленные на возвращение углов $\alpha $ и $\beta $ в диапазоны, где они изменяются свободно:

Диапазоны, в которых влияние линейных пружин отсутствует, обозначены следующим образом:

Естественно считать, что

2. Математическая модель человека на качелях. Уравнения движения системы, показанной на рис. 1, составим, пользуясь вторым методом Лагранжа. Для этого необходимо выписать выражения для кинетической и потенциальной энергии, а также для виртуальной работы моментов L и M.

Выражение для кинетической энергии T имеет вид

Здесь

Выкладки, проведенные при выводе соотношений (2.1), (2.2), здесь опущены из-за их громоздкости.

Потенциальная энергия П описывается выражением

Здесь

В соотношениях (2.2)–(2.4) g – ускорение свободного падения, ${{m}_{b}}$, ${{m}_{h}}$ и ${{m}_{s}}$ – массы звеньев HP (корпуса), PK (обоих бедер) и KF (обеих голеней) соответственно, $I_{b}^{P}$, $I_{h}^{O}$ и $I_{s}^{K}$ – моменты инерции этих же звеньев HP, PK и KF соответственно относительно точек P (тазобедренных суставов), O (точки подвеса качелей) и K (коленных суставов); $\delta $ – угол между прямой OP и стержнем OC_h, $\gamma $ – угол между прямой OK и стержнем OC_h.

Выражение для виртуальной работы $\delta W$ моментов L и M имеет вид

где $\delta \alpha $ и $\delta \beta $ – возможные перемещения.

Используя выражения (2.1) и (2.3) для кинетической и потенциальной энергии, выражение (2.5) для обобщенной работы и общую форму уравнений Лагранжа, можно выписать три уравнения движения системы в следующем виде:

Уравнения (2.6)–(2.8) отвечают обобщенным координатам $\varphi $, $\alpha $ и $\beta $ соответственно. В этих уравнениях введены следующие обозначения:

Величины, определяемые выражениями (2.9)–(2.11), имеют размерность момента инерции (см. (2.2)).

В уравнениях (2.7) и (2.8), наряду с управляющими моментами L и M, учтены также моменты ${{L}_{S}}$ и ${{M}_{S}}$ (см. формулы (1.2)).

Для того чтобы построить управление (в виде обратной связи) в трехзвенной модели качелей, рассмотрим сначала вспомогательную (упрощенную) модель качелей, содержащую только два звена. Исследуя эту более простую модель, удается построить “квазиоптимальное” управление, которое затем используется и для управления более сложной трехзвенной моделью, изображенной на рис. 1.

3. Синтез программного управления в двухзвенной модели человека на качелях. На рис. 2 показана относительно простая модель качелей с человеком на них. Подобная модель, как указано выше, рассматривается во многих работах. Неподвижный шарнир O – точка подвеса качелей OC, которые будем считать невесомыми, l – их длина. Через $\varphi $ обозначается, как и в трехзвенной модели, угол отклонения качелей от вертикали. Человек моделируется абсолютно твердым однородным стержнем HF, центр масс C которого шарнирно закреплен на свободном конце качелей. Через $\theta $ обозначим угол между продолжением качелей OC и стержнем HF.

Длину стержня HF (рост человека) обозначим через r, массу – через m, тогда его момент инерции относительно центра масс ${{J}_{С}} = m{{r}^{2}}{\text{/}}12$. В шарнире C прикладывается момент Q, который поворачивает стержень HF относительно качелей OC (рис. 2). Этот момент Q, так же как моменты L и M (см. (1.1)), будем считать ограниченным по абсолютной величине: $\left| Q \right| \leqslant {{Q}_{0}}$, где ${{Q}_{0}}$ = const.

Уравнения движения описанного выше двухзвенного механизма имеют вид

Здесь ${{J}_{O}} = m{{l}^{2}} + {{J}_{C}}$ – момент инерции двухзвенника относительно точки подвеса O, а слагаемое $\mu \dot {\varphi }$ описывает, как и в уравнении (2.6), момент сил вязкого трения в точке O. В шарнире C, кроме управляющего момента Q, прикладывается также момент Q_S, который призван предотвратить нарушение условий:

Условия (3.2) связаны с тем, что человек совершает относительно качелей только ограниченные угловые перемещения. В отсутствие момента Q_S они описывали бы фазовые ограничения.

Выражение для этого момента Q_S имеет вид (подобно (1.2))

На интервале (3.2) момент Q_S равен нулю и в шарнире C прикладывается только управляющий момент. Вне интервала (3.2) момент Q_S отличен от нуля и линейно зависит от угла θ, коэффициент q_S выбирается “большим”.

Первое из уравнений (3.1) описывает изменение момента количества движения системы

относительно точки подвеса O под влиянием момента сил тяжести и момента сил вязкого трения $\mu \dot {\varphi }$.

Представляет интерес задача синтеза оптимального управления $Q(\varphi ,\dot {\varphi },\theta ,\dot {\theta })$, при котором на каждом полуколебании качелей достигается максимальное значение угла $\varphi $ отклонения их от вертикали. Однако решение такой задачи вызывает значительные трудности. Дело в том, что рассматриваемая система (3.1) имеет две степени свободы и является нелинейной, управляющий момент Q подчиняется условию $\left| Q \right| \leqslant {{Q}_{0}}$. Поэтому заменим указанную задачу другой – более простой, но приближенной. Управляющий момент Q изменяет угол $\theta $, поэтому попытаемся вместо момента Q использовать в качестве управляющего параметра этот угол $\theta $, ограниченный условиями (3.2). Для построения квазиоптимального управления углом $\theta $ применим методику, аналогичную предложенной в [9, 10] для задачи о гимнасте.

3.1. Новые переменные.  Разделим обе части равенства (3.4) на постоянную величину J_O. Тогда получим

Введем в рассмотрение новую переменную – “приведенный” угол p:

тогда (3.5) примет вид а первое из уравнений (3.1), описывающее изменение момента количества движения системы (3.4), –

В соотношении (3.8) опущен момент $\mu \dot {\varphi }$ сил вязкого трения в точке O подвеса качелей.

В соответствии с равенством (3.6) разность $\left( {p - {\varphi }} \right)$ между “приведенным” углом $p$ и углом $\varphi $ отклонения качелей характеризуется величиной $j\theta $. Чтобы оценить эту разность, рассмотрим величину j:

Если ${r \mathord{\left/ {\vphantom {r l}} \right. \kern-0em} l} \to 0$, то $j \to 0$. При $r = l$ из выражения (3.9) получаем, что $j = {1 \mathord{\left/ {\vphantom {1 {13}}} \right. \kern-0em} {13}} \approx 0.0769$. Если же $r = {l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}$, т.е. рост человека в 2 раза меньше длины качелей, тогда $j = {1 \mathord{\left/ {\vphantom {1 {49}}} \right. \kern-0em} {49}} \approx 0.0204$. Оценим в этом случае величину $j\theta $ при условии (3.2), где ${{\theta }_{{{\text{min}}}}} = - {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$, ${{\theta }_{{{\text{max}}}}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. Легко видеть, что при этих условиях величина $j\theta $ удовлетворяет неравенствам:

Из соотношений (3.10) видно, что приведенный угол p отличается от угла $\varphi $ на сотые доли радиана. При этом угол $\varphi $ в процессе колебаний качелей может изменяться на величину порядка $\pi $.

Система уравнений (3.7), (3.8) имеет в отличие от системы (3.1) второй порядок, и роль управляющего сигнала в ней уже играет угол θ, который должен удовлетворять неравенствам (3.2). Систему (3.7), (3.8) будем исследовать на фазовой плоскости $(p,K)$. При этом, наряду с этой системой двух уравнений, можно рассматривать одно уравнение первого порядка:

Пусть в начале движения (при t = 0)

Точка (3.12) располагается на оси абсцисс фазовой плоскости (p, K) (см. рис. 3). Из уравнения (3.7) следует, что горизонтальная составляющая $\dot {p}$ вектора фазовой скорости в точке (3.12), как и во всех других точках оси абсцисс, равна нулю. Вертикальная составляющая $\dot {K}$ вектора фазовой скорости в точке (3.12) направлена вверх, т.е. $\dot {K}\left( 0 \right) > 0$, тогда и только тогда, когда угол $\theta $ выбран из допустимого диапазона (3.2) таким образом, что

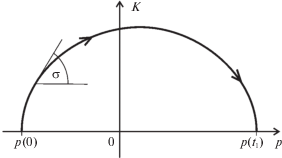
При условиях (3.12), наложенных на величину $p\left( 0 \right)$, такой выбор угла $\theta $ возможен.

3.2. Квазиоптимальное управление. Поставим задачу максимизации “приведенного” угла $p\left( {{{t}_{1}}} \right)$, где ${{t}_{1}} > 0$ – первое после t = 0 значение времени t, когда кинетический момент K обращается в нуль – $K\left( {{{t}_{1}}} \right) = 0$. Поставленную задачу в принятых обозначениях запишем следующим образом:

Заметим, что подобная задача максимизации рассматривается в [26].

На рис. 3 показана расположенная в полуплоскости $K > 0$ фазовой плоскости (p, K) часть траектории системы (3.7), (3.8) (или уравнения (3.11)), начинающаяся в точке (3.12). Нетрудно убедиться в том, что оптимальное управление $\theta (p,K)$, которое решает задачу (3.14) (доставляет максимум величине $p\left( {{{t}_{1}}} \right)$), имеет вид

Аналогичным выражением описывается оптимальное управление $\theta (p,K)$, которое на следующем полуколебании, при K < 0, доставляет минимум величине $p\left( {{{t}_{2}}} \right)$, где t₂ – первое после t₁ значение времени t, при котором $K\left( t \right) = 0$ (см. рис. 4).

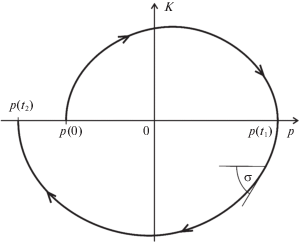
Введем обозначение ${{dK} \mathord{\left/ {\vphantom {{dK} {dp}}} \right. \kern-0em} {dp}} = {\text{tg}}\sigma $, где σ – угол между касательной к траектории системы (3.7), (3.8) в произвольной ее точке и горизонталью (см. рис. 3, 4). В каждой точке оптимальной траектории, на которой достигает максимума величина $p\left( {{{t}_{1}}} \right)$ и минимума величина $p\left( {{{t}_{2}}} \right)$, угол $\sigma $, как можно показать, должен быть максимально большим. Отсюда и вытекает равенство (3.15).

При K > 0 выражение (3.15) принимает вид

а при K < 0 –

Здесь и далее индексы “+” и “–” отвечают условиям K > 0 и K < 0 соответственно.

Анализ соотношения (3.16) (K > 0) показывает следующее:

1) на отрезке

имеет место равенство ${{\theta }^{ + }}(p) = {{\theta }_{{\min }}}$;

2) с ростом аргумента p на отрезке

величина ${{\theta }^{ + }}(p)$ монотонно возрастает от значения θ_min до значения θ_max;

3) на отрезке

сохраняется равенство ${{\theta }^{ + }}(p) = {{\theta }_{{\max }}}$;

4) с ростом аргумента p на отрезке

величина ${{\theta }^{ + }}(p)$ монотонно убывает от значения θ_max до значения θ_min;

5) на отрезке

как и на отрезке (3.18), имеет место равенство ${{\theta }^{ + }}(p) = {{\theta }_{{\min }}}$.

Из неравенств (3.10) следует, что сумма длин отрезков (3.18) и (3.22), на которых ${{\theta }^{ + }}(p) = {{\theta }_{{\min }}}$, близка к величине π, точнее говоря, эта сумма меньше значения π на величину, которая на 2 порядка меньше самого значения π. Аналогичное утверждение имеет место и для отрезка (3.20), на котором ${{\theta }^{ + }}(p) = {{\theta }_{{\max }}}$. Пользуясь “малостью” отрезков (3.19), (3.21), заменим функцию $\theta = {{\theta }^{ + }}(p)$ разрывной, считая, что ее разрывы происходят в точках $p = \pm {{\pi } \mathord{\left/ {\vphantom {{\pi } 2}} \right. \kern-0em} 2}$, лежащих внутри отрезков (3.19) и (3.21). Эта разрывная функция представляется в виде

Пользуясь тем, что разность $\left| {p - \varphi } \right|$ удовлетворяет неравенствам (3.10), т.е. “мала”, заменим в формуле (3.23) переменную p на $\varphi $ и, кроме того, упростим ее:

Переключения в релейном законе управления (3.24) происходят при $\varphi = \pm {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$.

В соответствии с формулой (3.24) величина $\theta $ принимает только постоянные значения θ_min и θ_max. Поэтому, как следует из выражения (3.4) для кинетического момента K, вместо неравенств K > 0 и K < 0 можно использовать неравенства ${\dot {\varphi }} > 0$ и ${\dot {\varphi }} < 0$ соответственно. Таким образом, выражение (3.24) имеет место при условии

Пусть теперь

Тогда, исходя из соотношения (3.17), можно получить выражение

Выражение (3.27) получается из соотношения (3.17) таким же путем, как и выражение (3.24) из соотношения (3.16).

Объединяя выражения (3.24), (3.25) с выражениями (3.26), (3.27), получаем окончательную формулу для управления ${\theta }\left( {{\varphi ,\dot {\varphi }}} \right)$ двухзвенным механизмом:

Закон управления (3.28) (если управлением считать угол $\theta $) является квазиоптимальным, поскольку при его выводе использован ряд упрощений. Переключения в релейном управлении (3.28) происходят при $\dot {\varphi } = 0$ или (и) $\varphi = \pm {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, т.е. когда угловая скорость качелей меняет знак или (и) когда качели оказываются в горизонтальном положении.

На рис. 5 показаны значения функции (3.28) в полосе $ - \pi \leqslant \varphi \leqslant \pi $ фазовой плоскости $(\varphi ,\dot {\varphi })$.

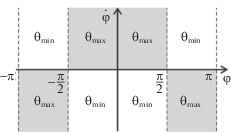
Вместо части $ - \pi \leqslant \varphi \leqslant \pi $ фазовой плоскости $\left( {\varphi ,\dot {\varphi }} \right)$ (рис. 5) можно рассматривать фазовый цилиндр, в котором прямые $\varphi = - \pi $ и $\varphi = \pi $ совмещены. Другими словами, на рис. 5 представлена развертка фазового цилиндра.

Выражение (3.28) и рис. 5 используются для вычисления программных значений ${{{\theta }}_{{{\text{prog}}}}}$ в законе управления двухзвенной моделью (3.1). Затем это выражение распространяется на случай трехзвенной модели для вычисления программных значений ${{{\alpha }}_{{{\text{prog}}}}}$ и ${{{\beta }}_{{{\text{prog}}}}}$.

4. Численные исследования двухзвенной модели. Численные исследования движения человека на качелях с использованием двухзвенной модели проводим путем решения полной системы уравнений (3.1) с двумя степенями свободы при ограниченном по абсолютной величине управляющем моменте Q. Закон управления моментом Q формируем, вычисляя программное значение ${{\theta }_{{{\text{prog}}}}}$ на основе формулы (3.28) и рис. 5:

В зависимости от значений фазовых переменных ${\varphi }$ и ${\dot {\varphi }}$ (от знака произведения ${\dot {\varphi }cos\varphi }$) вычисляется программное значение ${{\theta }_{{{\text{prog}}}}}$, равное θ_max или θ_min. Линейная обратная связь по фазовым переменным $\theta $ и $\dot {\theta }$ отслеживает значение θ_prog; постоянная величина ${{q}_{1}} > 0$ – коэффициент обратной связи по отклонению текущего значения угла θ от значения θ_prog, а ${{q}_{2}} > 0$ – постоянный коэффициент демпфирования.

При численном решении уравнений (3.1) используются следующие значения параметров:

При численном интегрировании системы с указанными значениями параметров задавались различные начальные условия (в том числе нулевые начальные значения угла отклонения и угловой скорости качелей). Показано, что из всех рассмотренных начальных состояний система выходит на орбитально асимптотически устойчивый режим периодических колебаний с постоянной амплитудой. Этот режим приведен на рис. 6. Слева продемонстрировано изменение во времени углов $\varphi $ и $\theta $ на этом периодическом решении уравнений (3.1), а справа – это же решение на плоскости конфигурационных переменных $\varphi $ и θ. Буквами A, B, C, D на левом и правом рисунках отмечены точки, соответствующие одна другой, стрелками справа показано направление движения.

Согласно численным исследованиям, при использовании момента (3.3) с коэффициентом ${{q}_{S}} = 10000$ Н ⋅ м нарушение условий (3.2) оказывается незначительным. Угол $\varphi $ в переходном процессе, а также и в установившемся движении остается внутри диапазона (рис. 6):

В интервале (4.2) имеет место неравенство $cos\varphi > 0$, и программное значение ${{\theta }_{{{\text{prog}}}}}$ меняется только тогда, когда меняет знак угловая скорость $\dot {\varphi }$ качелей (см. формулу (3.28) и рис. 5). В этом случае при вычислении значения ${{\theta }_{{{\text{prog}}}}}$ в законе управления (4.1) можно обойтись более простой формулой:

При условии (4.2) в течение одного “полного” колебания величина θ_prog меняется 2 раза: один раз со значения ${{\theta }_{{\max }}}$ на значение ${{\theta }_{{\min }}}$, а в другой раз, наоборот, со значения ${{\theta }_{{\min }}}$ на значение ${{\theta }_{{\max }}}$.

Амплитуда установившихся колебаний оказывается тем больше, чем меньше коэффициент вязкости $\mu $, что представляется естественным. Кроме того, при достаточно малом значении коэффициента $\mu $ возникает установившийся режим ротации качелей вокруг точки подвеса.

5. Синтез управления колебаниями в трехзвенной модели человека на качелях. Вернемся к основной трехзвенной модели. Рассмотрим задачу синтеза в виде обратной связи законов управления моментами L и M. При синтезе управления будем использовать программные значения α_prog и β_prog. Эти значения вычисляются в соответствии с выражением (3.28) и рис. 5, т.е. так же, как вычисляются программные значения θ_prog в законе управления (4.1) двухзвенной моделью качелей.

По аналогии с (4.1) законы управления моментами L и M построим в следующем виде:

Выражения для моментов ${{L}_{1}}$ и ${{M}_{1}}$ в формулах (5.1) и (5.2) описывают обратные связи в системе. Вычисление этих моментов производится в два этапа: на первом этапе в зависимости от знака произведения ${\dot {\varphi }cos\varphi }$ определяются значения α_prog и β_prog. Величина α_prog может быть равна ${{{\alpha }}_{{\max }}}$ или ${{{\alpha }}_{{\min }}}$, а величина β_prog может равняться ${{{\beta }}_{{\max }}}$ или ${{{\beta }}_{{\min }}}$. На втором этапе эти значения используются для формирования линейных обратных связей по фазовым переменным $\alpha $ и $\dot {\alpha }$, а также $\beta $ и $\dot {\beta }$. Постоянные ${{k}_{1}} > 0$ и ${{n}_{1}} > 0$ – коэффициенты обратной связи по отклонению текущих значений углов $\alpha $ и $\beta $ от вычисленных на первом этапе значений α_prog и β_prog соответственно; постоянные ${{k}_{2}} > 0$, ${{n}_{2}} > 0$ – коэффициенты демпфирования. Таким образом, при условии ${\dot {\varphi }cos\varphi } \geqslant 0$ обратные связи (5.1), (5.2) отслеживают максимальные значения ${{\alpha }_{{\max }}}$ и ${{\beta }_{{\max }}}$ углов $\alpha $ и $\beta $, а при условии ${\dot {\varphi }cos\varphi } < 0$ – минимальные ${{\alpha }_{{\min }}}$ и ${{\beta }_{{\min }}}$.

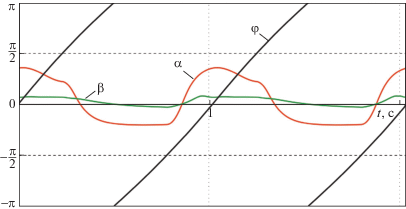
На рис. 7 графически показана схема вычисления программных значений α_prog и β_prog в зависимости от значений $\varphi $ и $\dot {\varphi }$, а также этапы процесса раскачивания качелей с различной амплитудой и в режимах ротации.

Переключение обоих программных значений α_prog и β_prog происходит одновременно – при смене знака произведения ${\dot {\varphi }cos\varphi }$. Поэтому моменты L и M “стремятся” поворачивать звенья KF (голени) и HP (корпус) относительно звена PK (бедра) синхронно – то в одну сторону (например, против часовой стрелки), то в другую (по часовой стрелке). Синхронное вращение голеней и корпуса у человека, раскачивающегося на качелях, наблюдается и в реальности. Движение, при котором голени и корпус вращаются против часовой стрелки и человек распрямляется, “похоже” на вращение корпуса человека как целого против часовой стрелки в двухзвенной модели. Движение человека, когда голени и корпус вращаются по часовой стрелке, напоминает вращение корпуса человека в двухзвенной модели по часовой стрелке. Эти наблюдения и наталкивают исследователей на мысль об использовании двухзвенной модели в качестве простейшей для синтеза закона управления раскачиванием качелей.

Для того чтобы построить управление, обеспечивающее торможение качелей, достаточно в приведенных выше законах управления (5.1) и (5.2) поменять местами неравенства $\dot {\varphi }\cos \varphi \geqslant 0$ и $\dot {\varphi }\cos \varphi < 0$ или же величины ${{\alpha }_{{\min }}}$ и ${{\alpha }_{{\max }}}$, а также ${{\beta }_{{\min }}}$ и ${{\beta }_{{\max }}}$.

6. Результаты численных исследований управляемого движения трехзвенного механизма. Численные исследования уравнений движения (2.6)–(2.8) трехзвенного шарнирного механизма, показанного на рис. 1, с моментами (1.2) и управлением (5.1), (5.2) проводились при следующих антропоморфных значениях параметров этого механизма, почерпнутых из работы [27]:

Параметры законов управления (5.1), (5.2) приняты следующими:

Значения ограничений на управляющий момент выбраны на основе экспериментальных данных, приведенных в [28].

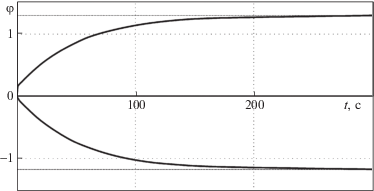
На рис. 8 показан при относительно большом значении коэффициента вязкого трения $\mu = 10\;{\text{Н}} \cdot {\text{м}} \cdot {\text{c}}$ процесс раскачивания, характеризующийся нулевыми начальными значениями угла отклонения и угловой скорости качелей. Верхняя кривая, показанная на рис. 8, проходит через точки, в которых угол $\varphi $ отклонения качелей от вертикали достигает локальных максимумов, нижняя соединяет точки локальных минимумов угла $\varphi $. Разность между значениями угла $\varphi $ на верхней и нижней кривых характеризует размах (амплитуду) колебаний качелей. Эта амплитуда с течением времени возрастает и асимптотически стремится к стационарному значению ≈2.5 рад.

На рис. 9 слева показаны графики функций $\varphi \left( t \right)$, $\alpha \left( t \right)$ и $\beta \left( t \right)$ в стационарном режиме, справа – соответствующий орбитально асимптотически устойчивый цикл в трехмерном пространстве конфигурационных переменных $\varphi $, $\alpha $, $\beta $. Период колебаний в стационарном режиме $T \approx 3.1$ с. При движении, рассмотренном на рис. 8, 9, угол $\varphi $ не выходит из диапазона (4.2), в котором ${\text{cos}}\varphi > 0$. При этом переключение программных значений α_prog и β_prog происходит как в переходном, так и в установившемся процессе лишь в моменты изменения знака скорости $\dot {\varphi }$, т.е. два раза за одно “полное” колебание (см. кривую ${{\Gamma }_{{\text{1}}}}$ на рис. 7).

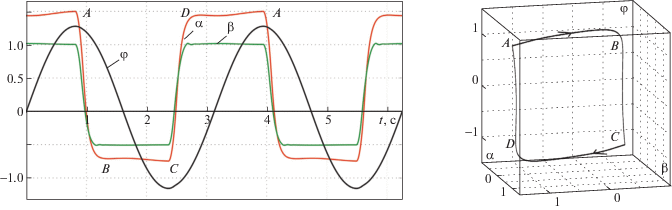
Буквами A, B, C, D на левом и правом рисунках обозначены точки, соответствующие одна другой.

Рассмотрим теперь случай, когда коэффициент вязкого трения относительно мал: $\mu = 0.5$ = 0.5 Н ⋅ м ⋅ с. Для этого случая на рис. 10 показаны две непрерывные кривые, ограничивающие сверху и снизу график функции φ(t), описывающей процесс раскачивания качелей при управлении (5.1), (5.2). Верхняя сплошная кривая соединяет точки, в которых функция $\varphi \left( t \right)$ достигает локального максимума, а нижняя – локального минимума. Нижняя кривая оканчивается на прямой $\varphi = - \pi $, верхняя – на прямой φ = π.

Опишем этапы процесса, представленного на рис. 10 сплошными кривыми. При $t \in \left( {0,{{t}_{a}}} \right)$ качели раскачиваются, не поднимаясь выше горизонтали. В это время имеют место неравенства (4.2) и ${\text{cos}}\varphi > 0$. Поэтому переключение программных значений ${{\alpha }_{{{\text{prog}}}}}$ и ${{\beta }_{{{\text{prog}}}}}$ происходит только при перемене знака угловой скорости $\dot {\varphi }$, т.е. дважды за полное колебание. Для этого этапа выбор программных значений ${{\alpha }_{{{\text{prog}}}}}$ и ${{\beta }_{{{\text{prog}}}}}$ на одном полном колебании иллюстрируется на рис. 7 кривой ${{\Gamma }_{{\text{1}}}}$. Точки ${{A}_{{\text{1}}}}$ и ${{C}_{{\text{1}}}}$ отвечают моментам переключения программных значений углов отклонения коленей и корпуса (подобно точкам $A$ и $C$ на рис. 9).

С ростом амплитуды качели начинают при каждом колебании пересекать горизонталь; при этом угол $\varphi $ выходит из диапазона (4.2). Сначала (при $t \in \left( {{{t}_{a}},{{t}_{b}}} \right)$) такие пересечения происходят только при $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. Затем, когда $t \in \left( {{{t}_{b}},{{t}_{c}}} \right)$, пересечение горизонтали происходит как при $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, так и при $\varphi = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}$. Этап раскачивания, отвечающий интервалу времени $t \in \left( {{{t}_{b}},{{t}_{c}}} \right)$, иллюстрируется на рис. 7 кривой ${{\Gamma }_{2}}$. Рассмотрим этот этап подробно. При пересечении горизонтали $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ (в точке ${{A}_{2}}$ на рис. 7) меняется знак величины ${\text{cos}}\varphi $, а с ним – и значения ${{\alpha }_{{{\text{prog}}}}}$ и ${{\beta }_{{{\text{prog}}}}}$. Затем (в точке $A_{2}^{{\text{/}}}$ на рис. 7) меняется знак скорости $\dot {\varphi }$, и качели начинают опускаться вниз. В момент смены знака скорости $\dot {\varphi }$ снова происходит переключение программных значений углов $\alpha $ и $\beta $. Опускаясь, качели в некоторый момент снова пересекают горизонталь $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ (в точке $A_{2}^{{//}}$ на рис. 7); при этом меняется знак величины ${\text{cos}}\varphi $, а с ним – и значения ${{\alpha }_{{{\text{prog}}}}}$, ${{\beta }_{{{\text{prog}}}}}$. При двукратном пересечении горизонтали $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ возникают два дополнительных переключения значений ${{\alpha }_{{{\text{prog}}}}}$, ${{\beta }_{{{\text{prog}}}}}$. В результате при $t \in \left( {{{t}_{b}},{{t}_{c}}} \right)$, т.е. когда на каждом полном колебании качели поднимаются выше горизонтали как слева, так и справа от точки подвеса, добавляются еще четыре переключения по сравнению с этапом, когда $t \in \left( {0,{{t}_{a}}} \right)$.

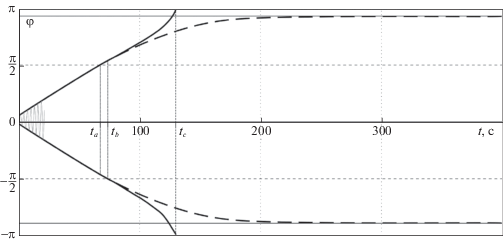
На следующем этапе колебаний ($t > {{t}_{c}}$) угол $\varphi $ при управлении (5.1), (5.2) доходит до значения $\varphi = \pi $ (отметим, что значения $\varphi = \pi $ и $\varphi = - \pi $ отождествляются, иными словами, на рис. 7 представлена развертка фазового цилиндра), после чего начинается процесс ротации качелей (см. кривую Γ₃ на рис. 7). Во время ротации угловая скорость $\dot {\varphi }$ не меняет знак, и переключения в законе управления происходят только при $\varphi = \pm {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ (в точках A₃ и C₃ на рис. 7), т.е. дважды за каждый полный оборот качелей вокруг точки подвеса. Постепенно движение стремится к установившемуся режиму ротации, изображенному на рис. 7 пунктирной кривой Γ₄. На рис. 11 показаны графики функций φ(t), α(t) и β(t) на этом установившемся режиме ротации. В этом режиме время полного оборота качелей T ≈ 2 c. Периодический режим ротации является орбитально асимптотически устойчивым.

Таким образом, если коэффициент трения $\mu $ достаточно мал, то при управлении (5.1), (5.2) качели после некоторого количества колебаний с увеличивающейся амплитудой выходят на стационарный режим движения, который представляет собой вращение вокруг точки подвеса – ротацию. При ротации, представленной на рис. 11, угловая скорость $\dot {\varphi } > 0$ и человек “делает солнышко” на качелях, вращаясь лицом вперед, т.е. против часовой стрелки (см. рис. 1). В зависимости от начальных условий возможен также выход и на режим ротации по часовой стрелке (пунктирная кривая $\Gamma _{4}^{/}$ на рис. 7).

Функция φ(t) претерпевает разрывы, если рассматривать ее в полосе $ - \pi \leqslant \varphi \leqslant \pi $ фазовой плоскости $(\varphi ,\dot {\varphi })$ (см. рис. 11). Если, однако, полосу $ - \pi \leqslant \varphi \leqslant \pi $ “свернуть” в цилиндр, совместив горизонтальные прямые $\varphi = - \pi $ и $\varphi = \pi $, то вместо фазовой плоскости получится фазовый цилиндр, на котором график функции φ(t) будет непрерывным и спиралевидным.

На рис. 10 показаны не только две сплошные кривые, которые относятся к процессу раскачивания качелей с последующим выходом их на режим ротации, но также и две пунктирные. Эти пунктирные кривые построены при “альтернативном” управлении, когда величины ${{\alpha }_{{{\text{prog}}}}}$ и ${{\beta }_{{{\text{prog}}}}}$ вычисляются по упрощенным формулам:

в течение всего времени раскачивания качелей, а не только при $t < {{t}_{a}}$. Значения ${{\alpha }_{{{\text{prog}}}}}$, ${{\beta }_{{{\text{prog}}}}}$, вычисленные по формулам (6.1), при $t < {{t}_{a}}$ совпадают с квазиоптимальными, а пунктирные кривые при этом совпадают со сплошными. В то же время значения ${{\alpha }_{{{\text{prog}}}}}$, ${{\beta }_{{{\text{prog}}}}}$, вычисленные по формулам (6.1), при $t > {{t}_{a}}$ квазиоптимальными не являются, и пунктирные кривые при $t > {{t}_{a}}$ не совпадают со сплошными.

Как следует из рассмотрения рис. 10, относительно “простой” способ (6.1) формирования программных значений ${{\alpha }_{{{\text{prog}}}}}$ и ${{\beta }_{{{\text{prog}}}}}$, в отличие от квазиоптимального, не выводит качели на режим ротации. Однако при управлении (6.1) реализуется стационарный режим колебаний с “довольно большой” амплитудой, которая составляет примерно 329.4° (5.75 рад.).

Заметим, что формулы (6.1) для вычисления программных значений ${{\alpha }_{{{\text{prog}}}}}$ и ${{\beta }_{{{\text{prog}}}}}$ аналогичны формуле (4.3) для вычисления программного значения ${{\theta }_{{{\text{prog}}}}}$ при синтезе управления двухзвенной моделью качелей в диапазоне (4.2).

Отметим, что на практике человек при раскачивании качелей, по-видимому, использует стратегию, близкую к (6.1), если только не ставит себе задачу выхода на ротацию. Если же человек хочет привести качели во вращение, то, как можно наблюдать (см., например, [29, 30]), при достижении достаточно больших амплитуд колебаний он начинает менять углы в суставах не при смене знака угловой скорости, а при $\varphi \approx \pm {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. Как правило, не видно, чтобы человек совершал более двух “переключений” за колебание/оборот. Иными словами, когда качели совершают колебания не только в диапазоне (4.2) (см. кривую ${{\Gamma }_{2}}$ на рис. 7), то человек пропускает по два переключения на каждом полуколебании. При этом его стратегия раскачивания становится более простой, но, вместе с тем, менее эффективной (с точки зрения скорости увеличения амплитуды), чем при квазиоптимальном управлении (5.1), (5.2). Последнее видно из сравнения сплошной и пунктирной кривых на рис. 10.

Помимо сказанного выше, можно заметить, что при ротации качелей человек, как правило, лишь незначительно меняет угол между качелями и корпусом [29, 30]. В связи с этим рассмотрим влияние диапазона отклонений корпуса на процесс ротации. На рис. 12 показаны графики функций $\varphi \left( t \right)$, $\alpha \left( t \right)$ и $\beta \left( t \right)$ в установившемся режиме ротации с управлением (5.1), (5.2), но при ${{\beta }_{{{\text{max}}}}} = 0.2$, ${{\beta }_{{{\text{min}}}}} = - 0.1$. В этом режиме $\dot {\varphi } > 0$, т.е. качели вращаются против часовой стрелки, как и при ротации, показанной на рис. 11.

Коэффициент вязкого трения $\mu $ в процессе, приведенном на рис. 12, равен 0.5 H ⋅ м ⋅ с, время полного оборота качелей $T \approx 1.01$ с, тогда как в режиме ротации, показанном на рис. 11, время полного оборота $T \approx 2$ с.

На рис. 13 помещены графики функций $\varphi \left( t \right)$, $\alpha \left( t \right)$ и $\beta \left( t \right)$ в установившемся режиме ротации по часовой стрелке $\left( {\dot {\varphi } < 0} \right)$ с управлением (5.1), (5.2) при ${{\beta }_{{{\text{max}}}}} = 0.2$, ${{\beta }_{{{\text{min}}}}} = - 0.1$ (μ = 0.5 H ⋅ м ⋅ с). Время одного полного оборота качелей $T \approx 2.1$ с.

Численное исследование показывает, что благодаря достаточно большой жесткости “пружин”, описываемых моментами ${{L}_{S}}$, ${{M}_{S}}$, происходит лишь незначительное нарушение условий (1.3) в процессе раскачивания качелей, а также на установившихся режимах. Отметим, что углы $\alpha $ и $\beta $ во все время движения не превосходят по модулю величины π/2. В отсутствие моментов ${{L}_{S}}$, ${{M}_{S}}$, указанное ограничение выполняется не всегда.

Заключение. В точке подвеса качелей отсутствует какой-либо “внешний” управляющий момент, т.е. соответствующая степень свободы является “пассивной”. Тем самым в механической модели качелей (рис. 1) есть три степени свободы и только два управляющих момента, т.е. имеет место “дефицит” числа управляющих воздействий. Сидящий на качелях человек, впрочем, как и стоящий, может прикладывать лишь внутренние силы – моменты в суставах и перемещать одни части (звенья) своего тела относительно других. Однако при таких перемещениях изменяется конфигурация человека, а с нею – расположение его центра масс, его момент инерции относительно точки подвеса качелей. При изменении положения центра масс системы изменяется момент относительно точки подвеса качелей силы тяжести, приложенной к системе, что влияет на угловую скорость качелей. Изменение момента инерции человека относительно точки подвеса качелей также приводит к изменению угловой скорости.

Таким образом, относительные перемещения звеньев системы позволяют организовать перемещение системы в целом желаемым образом. Другими словами, при построенном в статье управлении относительным перемещением частей тела человеку удается достичь желаемого результата – раскачивать качели (или тормозить).

В статье приведено аналитическое обоснование близости построенного закона управления к оптимальному (по скорости увеличения амплитуды колебаний), а также результаты численного сравнения скорости раскачивания со случаем альтернативного (более простого) управления.

Результаты проведенных численных исследований показывают, что выбор величин ${{\alpha }_{{{\text{min/max}}}}}$, а также ${{\beta }_{{{\text{min/max}}}}}$ влияет на процесс раскачивания качелей, что естественно.

В работе изучено влияние коэффициента вязкого трения в точке подвеса качелей на характер периодических движений. Как показывают численные исследования, если трение в точке подвеса достаточно велико, то амплитуда колебаний качелей вначале возрастает, а затем колебания “выходят” на установившийся режим с постоянной амплитудой, который представляет собой предельный орбитально асимптотически устойчивый цикл. Если трение в точке подвеса не слишком велико, то при построенном управлении качели после процесса раскачивания выходят на режим ротации – вращаются вокруг точки подвеса либо по часовой стрелке, либо против. Каждое из этих периодических движений является орбитально асимптотически устойчивым.

Отметим, однако, что утверждения о наличии предельных циклов и их устойчивости не доказаны в статье теоретически. Они вытекают лишь из численных исследований. Составленные программы позволяют наблюдать колебания качелей и их ротацию в режиме компьютерной анимации.

Результаты численных исследований показывают, что движения трехзвенника при описанном выше управлении (5.1), (5.2) согласуются с наблюдениями за людьми, качающимися на качелях, собственным опытом авторов и интуицией.

Заметим, что все животные могут перемещать лишь одни части своего тела относительно других. Однако животное организует эти относительные перемещения так, что возникающие при этом внешние силы перемещают его как целое желаемым для него образом. Так животные перемещаются по земле (ходят, бегают, прыгают, ползают), плавают в воде, летают в воздухе.