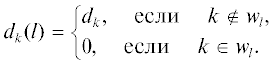Известия РАН. Теория и системы управления, 2020, № 5, стр. 106-115
АНАЛИЗ КРИТИЧЕСКИ ОПАСНЫХ ПОВРЕЖДЕНИЙ СЕТИ СВЯЗИ. I. МОДЕЛЬ И ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
Ю. Е. Малашенко a, *, И. А. Назарова a
a ФИЦ ИУ РАН
Москва, Россия
* E-mail: irina-nazar@yandex.ru
Поступила в редакцию 20.03.2020
После доработки 09.04.2020
Принята к публикации 25.05.2020
Аннотация
В рамках вычислительных экспериментов на потоковой модели сети связи и управления изучаются изменения системных функциональных характеристик при разрушающих воздействиях. В качестве критически опасного повреждения рассматривается подмножество ребер, при удалении которых хотя бы для одной пары узлов источник-приемник отсутствуют любые пути соединения. Для каждого повреждения определяется как общее число разъединенных пар-корреспондентов, так и все направления связи, пропускная способность которых оказывается меньше заданного нормативного значения. На основе полученных данных формируются многопараметрические диаграммы оценки изменения максимально возможных потоков для каждого разделяющего разреза и всех пар вершин. Граничные точки на диаграммах соответствуют наиболее опасным повреждениям, недоминируемым хотя бы по одному показателю ущерба. Анализируются результаты последствий разрушающих воздействий на сетевые системы с различными структурными особенностями.
Введение. В работе излагаются результаты вычислительных экспериментов на модели многопользовательской сети связи и управления. Анализируются изменения значений предельно-допустимых потоков между всеми парами узлов при разрушении ребер. Рассматриваются критически опасные повреждения, при которых хотя бы для одной пары источник-приемник отсутствует возможность установить связь.
Оценка последствий конкретного разрушения производится по двум критериям: число разъединенных пар источник-приемник и/или уменьшение пропускной способности каналов связи между всеми корреспондентами. Величина ущерба для каждой пары вычисляется как разность максимальных значений потока в исходной и поврежденной сети [1]. Расчеты по указанным критериям позволяют получить представительные векторные оценки, с помощью которых можно выделить наиболее опасные разрушающие воздействия.
Вычислительные эксперименты проводились для сетей с различными структурными особенностями. Для всех сетей сформированы соответствующие многопараметрические диаграммы, позволяющие сравнивать критически опасные повреждения с недоминируемыми векторными оценками ущерба.
Предложенный метод можно рассматривать как один из подходов к решению классической задачи исследования операций “оборона против нападения” [2–5]. Полученные диаграммы позволяют “обороняющейся стороне” в условиях неопределенности сравнивать возможные потери при разрушении ребер минимальных и вершинных разрезов.
Вершинные разрезы изучаются при поиске критически важных элементов (узлов) сети в [6–8], с использованием различных векторных критериев – в [9, 10]. При анализе уязвимости кластерных конгломератов обычно проводится агрегированная оценка потерь суммарного предельно-допустимого потока из центрального узла ко всем остальным [11, 12].
В последние годы возрос интерес к более предметному и комплексному анализу уязвимости сложных взаимосвязанных сетевых систем различного назначения, функционирующих как единое территориально-распределенное образование [13–15]. В [14] прослеживается эволюция моделей исследования уязвимости, отмечается необходимость специального анализа влияния человеческого фактора, а также террористических действий и/или спланированных хакерских атак. В [16] рассматривается влияние природных катастроф на региональные сети связи, в [17, 18] предлагаются технические решения по управлению сетевым трафиком в условиях чрезвычайных ситуаций, охватывающих большие территории. В [19] приводится одна из возможных классификаций различных повреждающих воздействий на сетевые информационные системы. В [20–23] основное внимание уделяется изучению уязвимости сетевых распределенных систем топливно-энергетического комплекса. Далее в данной работе предлагается вычислительная схема, использующая методы многокритериального анализа и потокового программирования, которая может быть применена при анализе уязвимости сетевых систем различного назначения [24, 25].
1. Математическая модель. Для анализа последствий повреждений многопользовательской сетевой системы связи и управления используется модель передачи многопродуктового (МП) потока. Граф сети G(d) без петель и сдвоенных ребер задается множествами $\left\langle {V,R} \right\rangle $: узлов (вершин графа) сети $V = \{ {{v}_{1}},{{v}_{2}},...,{{v}_{n}},...,{{v}_{N}}\} $; неориентированных ребер $R = \{ {{r}_{1}},{{r}_{2}},...,{{r}_{k}},...,{{r}_{E}}\} \subset V \times V$.
Пусть ребро rk соединяет узлы с номерами ${{n}_{k}},{{j}_{k}}$, ${{r}_{k}} = ({{v}_{{{{n}_{k}}}}},{{v}_{{{{j}_{k}}}}}) = ({{n}_{k}},{{j}_{k}})$. Для описания направления передачи потоков по сети каждому ребру rk, $k = \overline {1,E} $, ставятся в соответствие две ориентированные дуги uk, ${{u}_{{k + E}}}$, прямого и обратного направления из множества направленных дуг U = = $\{ {{u}_{1}},{{u}_{2}},...,{{u}_{k}},...,{{u}_{{2E}}}\} $ графа сети $G(d)$, ${{r}_{k}} \Leftrightarrow \{ {{u}_{k}},{{u}_{{k + E}}}\} $. Обозначим через $K({{v}_{n}})$ множество номеров ребер ${{r}_{k}} \in R$, инцидентных вершине ${{v}_{n}}$:
$S({{v}_{n}})$ – множество номеров исходящих дуг, по которым поток покидает узел ${{v}_{n}}$; $T({{v}_{n}})$ – множество номеров входящих дуг, по которым поток поступает в узел ${{v}_{n}}$.Множества $S({{v}_{n}})$, $T({{{v}}_{n}})$ однозначно определяются следующей процедурой. Пусть некоторое ребро ${{r}_{k}} \in R$ соединяет вершины с номерами $n$ и $j$, такими, что $n < j$. Тогда ориентированная дуга ${{u}_{k}} = ({{v}_{n}},{{v}_{j}})$ считается исходящей из вершины ${{v}_{n}}$ и ее номер k заносится в множество $S({{v}_{n}})$, а ориентированная дуга ${{u}_{{k + E}}} = ({{v}_{j}},{{v}_{n}})$ – входящей для ${{v}_{n}}$ и ее номер $k + E$ помещается в список $T({{v}_{n}})$. Соответственно дуга uk является входящей для ${{v}_{j}}$ и ее номер k попадает в $T({{v}_{j}})$, а дуга ${{u}_{{k + E}}}$ – исходящей и номер $k + E$ заносится в список $S({{v}_{j}})$ исходящих дуг.
В рамках модели предполагается, что между любой парой узлов передаются различные потоки, например, происходят телефонные разговоры или двигаются пассажиропотоки между станциями метро. Пара узлов-корреспондентов ${{p}_{m}}$ определяется упорядоченной парой вершин ${{p}_{m}} = ({{v}_{{{{s}_{m}}}}},{{v}_{{{{t}_{m}}}}})$, где вершина с номером ${{s}_{m}}$ называется источником, а с номером ${{t}_{m}}$ – стоком или приемником потока m-го вида. В настоящей работе в сети из N узлов рассматривалось $M = N(N - 1)$ независимых, невзаимозаменяемых и равноправных потоков различных видов, которые передаются между узлами-корреспондентами из множества $P = \{ {{p}_{1}},{{p}_{2}},...,{{p}_{M}}\} \subset V \times V$. Величины указанных потоков считаются функциональными характеристиками сети. В ходе вычислительных экспериментов изучаются изменения предельно-возможных потоков для каждой пары ${{p}_{m}}$ при разрушении ребер сети.
Пусть ${{x}_{{mk}}}$ – величина потока m-го вида, который передается в МП-сети по ребру ${{r}_{k}}$, ${{x}_{{mk}}} \geqslant 0$, $m = \overline {1,M} $, $k = \overline {1,E} $. Каждому ребру ${{r}_{k}} \in R$ приписывается число ${{d}_{k}}$, определяющее предельно-допустимый поток, который можно пропустить через ${{r}_{k}}$ в обоих направлениях. В исходной сети компоненты вектора пропускных способностей – $d = ({{d}_{1}},{{d}_{2}},...,{{d}_{k}},...,{{d}_{E}})$ – наперед заданные положительные числа ${{d}_{k}} > 0$. Вектором $d$ определяются следующие ограничения на потоки, передаваемые по ребру ${{r}_{k}}$:
(1.1)
$\sum\limits_{m = 1}^M \,({{x}_{{mk}}} + {{x}_{{m(k + E)}}}) \leqslant {{d}_{k}},\quad {{x}_{{mk}}} \geqslant 0,\quad {{x}_{{m(k + E)}}} \geqslant 0,\quad k = \overline {1,E} .$Обозначим через ${{z}_{m}}$, ${{z}_{m}} \geqslant 0$, величину потока m-го вида, который поступает в сеть в узле с номером ${{s}_{m}}$ и покидает ее из узла с номером ${{t}_{m}}$.
Во всех узлах ${{v}_{n}} \in V$, $n = \overline {1,N} $, сети для всех видов потоков должны выполняться условия сохранения потоков:
(1.2)
$\begin{gathered} \sum\limits_{i \in S({{v}_{n}})} \,{{x}_{{mi}}} - \sum\limits_{i \in T({{v}_{n}})} \,{{x}_{{mi}}} = \left\{ \begin{gathered} {{z}_{m}},\quad {\text{если}}\;{{v}_{n}} = {{v}_{{{{s}_{m}}}}}, \hfill \\ - {{z}_{m}},\quad {\text{если}}\;{{v}_{n}} = {{v}_{{{{t}_{m}}}}}, \hfill \\ 0\quad {\text{в}}\;{\text{остальных}}\;{\text{случаях}}, \hfill \\ \end{gathered} \right. \\ n = \overline {1,N} ,\quad m = \overline {1,M} ,\quad {{x}_{{mi}}} \geqslant 0,\quad {{z}_{m}} \geqslant 0. \\ \end{gathered} $Величина ${{z}_{m}}$ равна входящему потоку m-го вида, который пропускается от источника к стоку пары ${{p}_{m}}$ при распределении потоков ${{x}_{{mi}}}$ по дугам сети.
Ограничения (1.1), (1.2) задают множество достижимых векторов потоков $z = ({{z}_{1}},{{z}_{2}},...,{{z}_{m}}$, ..., zM):
при передаче в МП-сети для всех пар ${{p}_{m}} \in P$.В настоящей работе анализируются результаты вычислительных экспериментов и изучаются оценки изменения максимальных величин потоков для всех возможных пар узлов $M = N(N - 1)$ при структурных повреждениях ребер сети.
2. Формирование множества структурных повреждений. Рассмотрим некоторую произвольную пару узлов-корреспондентов ${{p}_{m}} \in P$ и определим максимально возможный поток, который можно передать в сети $G(d)$ из вершины с номером ${{s}_{m}}$ в вершину с номером ${{t}_{m}}$ без учета всех остальных потоков.
Задача 1. При некотором фиксированном m найти максимальный поток из узла с номером ${{s}_{m}}$ в узел с номером ${{t}_{m}}$:
Согласно [1], каждому максимальному значению $z_{m}^{0}$ соответствует некоторый набор ребер – минимальный разрез ${{R}_{m}}$, ${{R}_{m}} \subset R$. Множество номеров ребер, образующих разрез ${{R}_{m}}$, обозначим
Вектору ${{z}^{0}}$ ставится в соответствие множество
номеров ребер, найденных при решении последовательности задач 1 для всех ${{p}_{m}} \in P$.Для дальнейшего формирования множества повреждений рассматривается следующая модифицированная сеть. В графе сети G(d) пропускная способность всех ребер полагается равной единице:
полученный граф сети обозначается G(1), а соответствующее множество достижимых потоков – Z(x, 1):Для G(1) определяется максимальный поток для всех пар ${{p}_{m}} \in P$ как решение следующей задачи максимизации.
Задача 2. Для некоторой фиксированной пары ${{p}_{m}} \in P$ найти максимальный поток
Величина $z_{m}^{1}$ равна числу ребер в минимальном разрезе $R_{m}^{1}$ для максимального целочисленного потока из вершины с номером ${{s}_{m}}$ в вершину с номером tm, $z_{m}^{1} = {\text{|}}R_{m}^{1}{\text{|}}$. Обозначим через
По аналогии с множеством $H( \cdot )$ строится множество
номеров ребер, входящих в минимальные разрезы, найденные при решении задачи 2 для всех ${{p}_{m}} \in P$, $m = \overline {1,M} $, в сети $G(1)$.Рассмотрим подмножество
номеров ребер, инцидентных вершине ${{v}_{n}}$, и сформируем множество состоящее из списков номеров ребер, инцидентных каждой вершине сети.Для проведения вычислительного эксперимента и анализа возможных повреждений формируется множество уникальных повреждений сети
согласно следующей процедуре. В множествах $H( \cdot )$, $Q( \cdot )$, $Y( \cdot )$ могут содержаться одинаковые элементы. Тождественным спискам номеров ребер $h( \cdot ),\;q( \cdot ),\;y( \cdot )$ ставится в соответствие единственный элемент wl – список номеров ребер для совпадающих $h( \cdot ),q( \cdot )$ или $y( \cdot )$:3. Оценки повреждений. При проведении вычислительных экспериментов при некотором повреждении wl пропускная способность ребер сети $G(d(l))$ задается следующим образом:
В поврежденной сети $G(d\left\langle l \right\rangle )$ для всех ${{p}_{m}} \in P$, последовательно для каждого $m = \overline {1,M} $ определяется возможный максимальный поток.
Задача 3. При некоторых заданных $l$ и $m$ найти:
Задача 3 решается последовательно для всех ${{p}_{m}}$, ${{p}_{m}} \in P$, и всех ${{w}_{l}} \in W$. На основе найденных $z_{m}^{0}(l)$, $m = \overline {1,M} $, $l = \overline {1,L} $, вычисляются индикаторные показатели:
Для каждого ${{w}_{l}} \in W$ рассчитывается
– доля от общего числа пар узлов P, для которых максимальный поток становится равен нулю при данном повреждении wl.Для всех $m = \overline {1,M} $, $l = \overline {1,L} $, таких, что $z_{m}^{0}(l) > 0$, и наперед заданного значения γ вычисляется индикаторная функция
Значения параметра γ задаются априори в диапазоне $0 < \gamma < 1$. Индикатор $\eta (m,l,\gamma ) = 1$, если максимальный поток $z_{m}^{0}(l)$ для пары ${{p}_{m}}$ при повреждении wl оказывается не больше критического значения γ.
При заданном γ для некоторого повреждения ${{w}_{l}} \in W$ и $z_{m}^{0}(l) > 0$ вычисляется
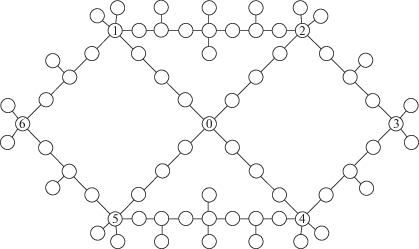
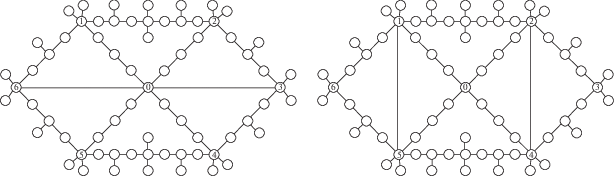
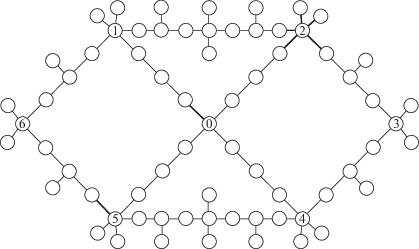
4. Вычислительный эксперимент. Вычислительный эксперимент проводился на моделях сетевых систем, представленных на рис. 1, 2 (на рис. 1 – базовая, на рис. 2 слева – рокадная, справа – фронтальная). В каждой из сетей 69 узлов. Пропускные способности ребер выбирались случайным образом из отрезка [900, 999] и совпадают для всех сетей. Пропускная способность каждого из двух дополнительных ребер на рис. 2 равна 900.
Для формирования множества критически опасных повреждений $W$ было найдено порядка 104 минимальных разрезов, из которых чуть более 102 разрезов вошло в $W$ (около 1%). Для целей анализа и отображения структурных повреждений на диаграммах каждому ${{w}_{l}} \in W$ ставится в соответствие “ маска” – тройка индикаторов $str({{w}_{l}}) = (a,b,c)$, значения которых определяются следующим образом:
a = 1, если повреждение ${{w}_{l}}$ совпадает с одним или более списком $h(j)$ в $H( \cdot )$, a = 0 – в противном случае;
b = 1, если список ${{w}_{l}}$ встречается в множестве $Q( \cdot )$ хотя бы один раз, b = 0 – в противном случае;
c = 1, если ${{w}_{l}}$ идентичен одному или более элементам в $Y( \cdot )$, c = 0 – в противном случае.
Для базовой сети (рис. 1) в множество $W$ было включено всего 125 различных повреждений. В табл. 1 для базовой сети представлены: семь возможных записей строк-индикаторов, соответствующее число повреждений и обозначение последних на диаграммах.
Таблица 1
| Маска | Число повреждений | Обозначение на диаграмме |
|---|---|---|
| 100 | 28 | Кольцо |
| 010 | 23 | Жирная точка |
| 001 | 17 | Треугольник |
| 111 | 35 | Крестик c указанием числа одинаковых повреждений |
| 011 | 17 | |
| 110 | 5 | |
| 101 | 0 |
Маска, содержащая только одну единицу, указывает на повреждение, принадлежащее к одному типу разрезов. Таких повреждений в множестве $W$ больше половины и именно эти разрушения приводят к самым большим потерям.
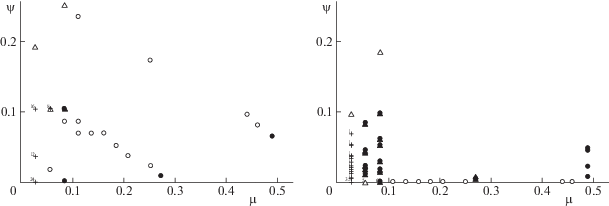
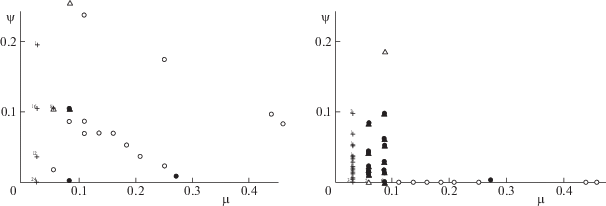
На рис. 3 представлены диаграммы $(\mu ,\psi )$ для базовой сети при $\gamma = 0.6$ и 0.5. “Жирные точки” у восточного края диаграмм определяют недоминируемые повреждения, разделяющие максимальное число пар-корреспондентов (значение $\mu $ = 1/48 по оси абсцисс). Маска (0, 1, 0) соответствует разрезам в сети с графом $G(1)$ при ${{d}_{k}} = 1$, $k = \overline {1,E} $. Согласно табл. 2, существует четыре различных недоминируемых разрушения ${{w}_{l}}$, приводящих к одинаковому ущербу.
Таблица 2
| Маска | γ | 100 | 010 | 001 | 111 | 011 | 110 | 101 |
|---|---|---|---|---|---|---|---|---|
| Число недоминируемых | γ = 0.6 | 4 | 4 | 4 | – | – | – | – |
| повреждений | γ = 0.5 | – | 1 | 1 | – | – | – | – |
На диаграммах для базовой сети (рис. 3) недоминируемые повреждения с максимальными значениями $\psi $ отмечены “треугольниками”. Указанные разрушения возникают при удалении вершины ${{v}_{2}}$, а точнее – инцидентных ей ребер. Таким образом удаление вершины приводит к заметному ухудшению качества связи, уменьшению пропускной способности, хотя не сильно влияет на связность графа сети. На диаграммах “треугольники” расположены ближе к оси ординат и имеют бóльшие значения $\psi $. В табл. 3 приводится максимальное число пар-корреспондентов с различными нарушениями связи для двух недоминируемых разрушений при $\gamma $ = 0.6.
Таблица 3
| Маска | 010 | 001 |
|---|---|---|
| Число разъединенных пар | 1150 | $ \gg $ 200 |
| Число пар с уменьшением потока ниже γ = 0.6 | 150 | $ \ll $ 600 |
Недоминируемые разрушения базовой сети с указанными масками приводят к повреждениям, ущерб от которых различается более чем в 4 раза. Недоминируемый разрез в сети с единичной пропускной способностью ребер разъединяет половину пар, но только у 7% оставшихся величина потока снижается ниже критического значения $\gamma $ = 0.6. Наихудший вершинный разрез – удаление вершины ${{v}_{2}}$ – разъединяет менее 9% пар, качество связи становится ниже допустимого у 25% пар.
Недоминируемые повреждения для базовой сети при γ = 0.6 лежат в северо-восточной части диаграммы на рис. 3 слева и обозначены кольцами и жирной точкой. Маска (1, 0, 0) соответствует минимальным разрезам из множества $H( \cdot )$. На рис. 3 справа для базовой сети и γ = 0.5 повреждения с недоминируемыми значениями ущерба и масками (0, 1, 0), (0, 0, 1) обозначены жирной точкой и остались в северо-восточной части диаграммы, а все кольца переместились в ее внутреннюю часть. Дело в том, что значение γ = 0.5 задает более жесткие ограничения на величины сохранившихся потоков, но не влияет на число разрывов для линий связи. В результате значения $\psi $ уменьшаются, $\mu $ – остается неизменным, а рассматриваемое повреждение перестает быть недоминируемым. На рис. 4 на графе базовой сети отмечены все ребра, входящие хотя бы в одно повреждение из табл. 3.
Базовая сеть и сети с рис. 2 имеют совпадающие множества узлов и пар-корреспондентов. Диаграммы оценки повреждений для сетей с добавленными ребрами приведены на рис. 5, 6. Добавление двух дополнительных ребер увеличивает число возможных путей соединения и максимальные потоки для большого числа корреспондентов. В табл. 4 помещены число разъединенных пар и число пар, для которых максимально возможные потоки оказываются ниже критического значения $\gamma $. Все величины приводятся для двух недоминируемых повреждений, при которых достигается либо максимум числа разъединенных пар (самая восточная точка на диаграммах), либо максимум числа пар, для которых максимальной поток ниже $\gamma $ (самая северная точка на диаграммах).
Таблица 4
| γ | Сеть | Базовая | Фронтальная | Рокадная | |||
|---|---|---|---|---|---|---|---|
| Маска | 010 | 001 | 100 | 001 | 010 | 001 | |
| 0.6 | Число разъединенных пар | 1150 | 200 | 1080 | 200 | 1010 | 200 |
| Число пар с уменьшением потока | 150 | 600 | 200 | 600 | 90 | 480 | |
| 0.5 | Число разъединенных пар | 1150 | 200 | 1080 | 200 | 1010 | 70 |
| Число пар с уменьшением потока | 110 | 435 | 0 | 435 | 60 | 235 | |
Анализ табл. 4 показывает, что базовая сеть более уязвима, поскольку при особо опасных разрушениях большее число корреспондентов (6%) оказываются разъединенными по сравнению с фронтальной и рокадной сетями. Наилучший показатель у рокадной сети – наименьший по ущербу. Полученный результат закономерен, поскольку шесть центральных ребер рокадной сети, инцидентных узлу ${{v}_{0}}$, затрудняют разделение графа сети на две связанные компоненты. В рокадной сети после повреждений также поддерживается более высокое качество связи – потери потоков меньше. Последнее связано с более мощным транзитным узлом ${{v}_{0}}$, который усилен двумя дополнительными ребрами. На диаграммах с рис. 5, 6 видно (и анализ табл. 4 это подтверждает), что разрушение минимального разреза из множеств $H( \cdot )$ или $Q( \cdot )$ влечет за собой более серьезные нарушения функционирования сети. Наличие всего двух дополнительных ребер в рокадной сети (по сравнению с базовой) позволяет снизить максимальное число разъединенных пар на 12%, однако не влияет на ухудшение качества связи. Действительно, при разрушении соответствующих вершинных разрезов падение потоков практически одинаково как в базовой, так и в рокадной сетях (см. табл. 4).
Заключение. При проведении вычислительных экспериментов используются алгоритмы потокового программирования. На первом этапе для каждой пары узлов решается задача поиска максимального потока и минимального разреза. Верхняя оценка числа операций для решения этой задачи составляет $O({{N}^{5}})$: всего пар узлов $O({{N}^{2}})$, а для определения максимального потока достаточно $O({{N}^{3}})$ [26]. На базе полученных минимальных разрезов формируется множество повреждений W, верхняя оценка числа элементов в котором $O({{N}^{2}})$. Для каждого повреждения ${{w}_{l}}$ вновь определяются максимальные потоки для всех пар узлов. Результирующая верхняя оценка вычислительных затрат полиномиально зависит от числа узлов в сети и составляет не более $O({{N}^{7}})$.
При проведении расчетов для больших сетей можно использовать простые схемы распараллеливания вычислений в гетерогенной вычислительной среде и программные реализации алгоритмов сетевой оптимизации для различных операционных систем. Указанные возможности позволяют производить модельные эксперименты как на кластерах из персональных компьютеров, так и в больших территориально-удаленных центрах.
Список литературы
Йенсен П., Барнес Д. Потоковое программирование. М.: Радио и связь, 1984.
Фрэнк Г., Фриш М. Сети, связь и потоки. М.: Связь, 1978.
Гермейер Ю.Б. Введение в теорию исследования операций. М.: Наука, 1971.
Dinh T.N., Thai M.T. Assessing Attack Vulnerability in Networks with Uncertainty // IEEE Conf. on Computer Communications (INFOCOM). Kowloon, 2015. P. 2380–2388.
Малашенко Ю.Е., Назарова И.А., Новикова Н.М. Один подход к анализу возможных структурных повреждений в многопродуктовых сетевых системах // ЖВМиМФ. 2019. Т. 59. № 9. С. 1626–1638.
Lalou M., Tahraoui M.A., Kheddouci H. The Critical Node Detection Poblem in Networks: a Survey // Computer Science Review. 2018. V. 28. P. 92–117.
Walteros J., Pardalos P. Selected Topics in Critical Element Detection // Optimization and its Applications. 2012. V. 71. P. 9–26.
Veremyev A., Prokipyev O.A., Pasiliao E.L. Critical Nodes for Distance-based Connectivity and Related Problems in Graphs // Networks. 2015. V. 66. Iss. 3. P. 170–195.
Ventresca M., Harrison K.R., Ombuki-Berman B.M. The Bi-objective Critical Node Detection Problem // European J. Oper. Res. 2018. V. 265. Iss. 3. P. 895–908.
Li J., Pardalos P.M., Xin B., Chen J. The Bi-objective Critical Node Detection Problem with Minimum Pairwise Connectivity and Cost: Theory and Algorithms // Soft Computing. 2019. V. 23. P. 1–16.
Kuhnle A., Nguyen N.P., Dinh T.N., Thai M.T. Vulnerability of Clustering under Nodes Failure in Complex Networks // Social Network Analysis and Mining. 2017. V. 7. Iss. 1. P. 8–24.
Малашенко Ю.Е., Назарова И.А., Новикова Н.М. Анализ кластерных повреждений в сетевых системах // ЖВМиМФ. 2020. Т. 60. № 2. С. 173–184.
Grubesic T.H., Matisziw T.C., Murray A.T. et al. Comparative Approaches for Assessing Network Vulnerability // Inter. Regional Sci. Review. 2008. V. 31.
Murray A.T. An Overview of Network Vulnerability Modeling Approaches // GeoJournal. 2013. V. 78. P. 209–221.
Johansson J. Risk and Vulnerability Analysis of Interdependent Technical Infrastructures. Addressing Socio-technical Systems. Doctoral Thesis in Industrial Automation. Department of Measurement Technology and Industrial Electrical Engineering. Lund: Lund University, 2010.
Gomes T., Esposito C., Hutchison D., Kuipers F., Rak J., Tornatore M. A Survey of Strategies for Communication Networks to Protect against Large-scale Natural Disasters // Int. Workshop on Reliable Networks Design and Modeling (RNDM). Halmstad, 2016. P. 11–22.
Величко В.В., Попков Г.В., Попков В.К. Модели и методы повышения живучести современных систем связи. М.: Горячая Линия – Телеком, 2017.
Леваков А.К. Особенности функционирования телекоммуникационных сетей следующего поколения в чрезвычайных ситуациях. М.: ИРИАС, 2012.
Носков С.И., Бутин А.А., Соколова Л.Е. Многокритериальная оценка уровня уязвимости объектов информатизации // Доклады ТУСУРа. 2014. № 2 (32). С. 137–142.
Wang S., Zhang J., Duana N. Multipleperspective Vulnerability Analysis of the Power Network // Physica A. 2018. V. 492. P. 1581–1590.
Фаддеев А.М. Оценка уязвимости энергосистем России, стран Ближнего зарубежья и Европы // Вестн. МГУ. Сер. 5. География. 2016. № 1. С. 46–53.
Malashenko Y.E., Nazarova I.A., Novikova N.M., Pospelova I.I. A Network Flow Model for Power and Energy System with Changing Capabilities // Int. J. of Public Administration. 2019. V. 42. Iss. 15–16. C. 1323–1332.
Malashenko Yu.E., Nazarova I.A., Novikova N.M. Fuel and Energy System Control at Large-scale Damages. IV. A Priori Estimates of Structural and Functional Vulnerability // J. Computer and Systems Sciences International. 2018.V. 57. № 6. P. 907–920.
Royset J.O., Wood R.K. Solving the Bi-objective Maximum-flow Network-interdiction Problem // INFORMS J. Comput. 2007. V. 19. Iss. 2. P. 175–184.
Nicholson C.D., KashBarker K., Ramirez-Marquez J.E. Flow-based Vulnerability Measures for Network Component Importance: Experimentation with Preparedness Planning // Reliability Engineering and System Safety. 2016. V. 145. P. 62–73.
Кормен Т.Х., Лейзерсон Ч.И., Ривест Р.Л. и др. Алгоритмы: построение и анализ. М.: Вильямс, 2005.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления