Известия РАН. Теория и системы управления, 2020, № 5, стр. 129-141
ЛИНЕЙНО-КУБИЧЕСКОЕ ЛОКАЛЬНО-ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЛИНЕЙНЫМИ СИСТЕМАМИ И ЕГО ПРИМЕНЕНИЕ ДЛЯ НАВЕДЕНИЯ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
В. С. Верба a, *, В. И. Меркулов a, Е. А. Руденко b, **
a АО “Концерн “Вега”,
Москва, Россия
b МАИ (национальный исследовательский ун-т)
Москва, Россия
* E-mail: vvs.msk@gmail.com
** E-mail: rudenkoevg@yandex.ru
Поступила в редакцию 25.03.2020
После доработки 28.04.2020
Принята к публикации 25.05.2020
Аннотация
Рассмотрены требования, предъявляемые к методам наведения летательных аппаратов. Отмечено, что существующие методы оптимизации линейных систем управления, базирующиеся в основном на минимизации квадратичных функционалов качества, не позволяют обеспечить совокупность требований, предъявляемых к системам перехвата воздушных объектов. Предложено использовать новые локальные квадратично-биквадратные функционалы качества, минимизация которых позволяет получить более общие линейно-кубические законы управления, адекватные современным требованиям. При этом биквадратная терминальная часть функционала содержит слагаемые четвертой степени. Рассмотрен пример синтеза конкретного метода наведения и проведен его анализ.
Введение. Основой совершенства любой авиационной системы перехвата целей является используемый в ней метод наведения, обеспечивающий формирование требуемой траектории [1], полет по которой позволяет поразить цель.
В настоящее время для синтеза методов наведения применяется представление процессов и систем в многомерном пространстве состояний, в рамках которого наибольшее распространение получили динамическое программирование Беллмана и принцип максимума Понтрягина [2, 3]. Общим недостатком для них является достаточно высокая сложность процедуры синтеза управления. Так, метод Беллмана даже в простейшем случае использования линейных моделей состояния и квадратичных функционалов качества сводится к решению в обратном времени уравнения Риккати для вычисления коэффициентов передачи ошибок управления [2–4], в том числе и в более сложных современных задачах [5, 6].
Необходимо отметить, что, манипулируя в них видами исходных моделей и функционалов качества, можно получить большой набор конкретных законов управления, адаптированных под решение конкретных задач [7–9]. В простейшем случае, увеличивая размерность исходных моделей объекта управления, можно получить более сложные законы управления, адаптированные для перехвата маневренных целей.
Однако изменения, произошедшие за последние десятилетия в военно-техническом противоборстве [10, 11], предъявляют к методам наведения более жесткие и часто противоречивые требования, в том числе и по расширению функциональных возможностей при работе по новым перспективным типам целей [12–14].
Далее будет проведен краткий анализ требований к процедурам синтеза методов наведения, предложен более универсальный способ их оптимизации, основанный на минимизации более сложных квадратично-биквадратных функционалов, и рассмотрен пример его использования.
1. Анализ требований к перспективным системам наведения и методам их синтеза. Анализ тенденций развития способов военно-технического противоборства [10, 11] позволяет выделить ряд направлений, непосредственно влияющих на информационно-управляющую сторону функционирования систем наведения (СН) [1].
К таким направлениям, прежде всего, относятся:
– качественное усложнение законов взаимного пространственного перемещения летательных аппаратов (ЛА);
– групповое применение как средств нападения, так и защиты;
– высокая динамичность и скоротечность боестолкновений;
– широкое использование режимов управления и информационного обеспечения на грани потери устойчивости, характерное для сверхманевренных ЛА и следящих систем.
В связи с этим для улучшения системных показателей совершенства СН [7]: эффективности, живучести, динамичности и информативности необходимо принимать специальные меры по совершенствованию методов наведения и алгоритмов их информационного обеспечения.
Усложнение траекторных эволюций ЛА требует учета в методах наведения производных старших порядков от дальности и угловых координат [15, 16]. Однако использование такого подхода приводит к существенному усложнению алгоритмов фильтрации, формирующих оценки производных старших порядков [17].
Групповое применение ЛА, в том числе и беспилотных, также приводит к усложнению законов управления, поскольку наряду с образованием сигнала траекторного управления всей группой необходимы дополнительные управляющие воздействия, формирующие ее требуемую топологию и предотвращающие столкновения ЛА внутри нее [18].
Специфической особенностью перспективных СН является необходимость кардинального увеличения управляющих воздействий, уводящих от границ устойчивой работы или опасных состояний.
Решить эту задачу в рамках традиционных подходов, основанных на минимизации квадратичных функционалов качества, которые обеспечивают линейную зависимость сигналов управления от ошибок функционирования, практически невозможно. Отсюда следует необходимость использования более совершенных приемов оптимизации, гарантирующих нелинейную зависимость сигналов управления от ошибок функционирования [19, 20].
Необходимо отметить, что целевое назначение СН обеспечивается совместной работой функционально связанных информационных и управляющих подсистем, решающих частные задачи. При этом, как правило, конечные результаты, полученные одной подсистемой, являются задающими для функционирования другой подсистемы, образуя последовательную информационно-управляющую цепь. В составе такой цепи в качестве подсистем можно выделить [1, 21]:
– цель;
– информационно-вычислительную подсистему (ИВПС);
– управляющую подсистему (УПС);
– ЛА-носитель;
– оружие.
В процессе функционирования СН ее ИВПС, используя измерители различной природы, оценивает координаты относительного и абсолютного движения цели и ЛА-носителя. Полученные оценки поступают на вход УПС, которая преобразует их в отклонение рулевых органов, предопределяя целенаправленное изменение пространственного положения ЛА, необходимое для эффективного применения оружия.
Следует подчеркнуть, что в общем случае различные подсистемы имеют различную динамичность, характеризующую их способность реагировать на изменение управляющих сигналов [22]. От того, насколько согласованы динамические свойства подсистем в процессе совместного функционирования, во многом зависит совершенство системы в целом. В связи с этим в процедурах синтеза законов управления системой наведения в целом необходимо принимать специальные меры по учету несоответствия динамических свойств ее подсистем, особенно на участке “цель–ИВПС”.
В процессе перехвата СН должна удовлетворять ряду противоречивых требований, обеспечивая:
– минимум промаха;
– минимум времени наведения;
– минимум затрат энергии на управление и т.д.;
– практическую реализуемость информационного обеспечения.
Удовлетворять этим требованиям в рамках традиционных методов наведения с постоянными коэффициентами передачи ошибок управления достаточно сложно. В связи с этим весьма актуальной становится задача разработки нестационарных законов управления, обеспечивающих перераспределение приоритетов в процессе наведения. В простейшем случае такие законы вначале должны устранять ошибки наведения по направлению, а на конечном – обеспечивать минимизацию линейного промаха.
Особую сложность представляет синтез методов наведения на цели, двигающиеся по траекториям со сменой знаков производных (в простейшем случае – по квазисинусоидальным траекториям), при которых теряет смысл использование традиционных методов наведения в упрежденную точку встречи [23, 24]. Вариант применения наведения в упрежденную точку встречи, иллюстрирующий невозможность перехвата цели, которая движется со сменой знака вертикальной составляющей производной скорости, показан на рис. 1.
Рис. 1.
Траектория движения цели (сплошная эпюра) и перехватчика (штрихпунктирная эпюра) при его наведении в упрежденную точку встречи
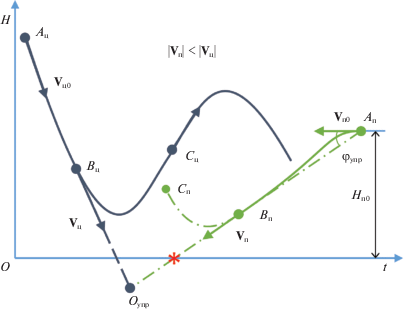
На этом рисунке ${{{\mathbf{V}}}_{{{\text{ц0}}}}}$ и ${{{\mathbf{V}}}_{{{\text{п0}}}}}$ – первоначальные векторы скорости цели Aц и перехватчика Aп соответственно, а ${{\varphi }_{{{\text{упр}}}}}$ – требуемый угол упреждения, реализуя который перехватчик движется в направлении вектора ${{{\mathbf{V}}}_{{\text{п}}}}$. Невозможность перехвата обусловлена либо недостаточной начальной высотой ${{H}_{{{\text{п0}}}}}$, приводящей к столкновению перехватчика с земной поверхностью (обозначено * на рис. 1) либо к его выходу в заднюю полусферу цели, догнать которую при $\left| {{{{\mathbf{V}}}_{{\text{п}}}}} \right| < \left| {{{{\mathbf{V}}}_{{\text{ц}}}}} \right|$ невозможно.
Одной из наиболее сложных задач при синтезе СН является снижение размерности векторов состояния, что особенно актуально при групповом наведении. Необходимость снижения размерности решаемой задачи синтеза обусловлена, как минимум, тремя причинами.
Во-первых, оно позволит снизить в законе управления число слагаемых, учитывающих производные старших порядков, что особенно актуально при перехвате сверхманевренных и гиперзвуковых целей [23, 24].
Во-вторых, это позволит упростить алгоритмы фильтров информационной системы за счет исключения старших производных координат состояния [15].
В-третьих, это обеспечит качественное упрощение самой процедуры формирования сигналов управления за счет снижения размерности задачи вычисления текущих коэффициентов передачи ошибок управления с помощью классических приемов оптимизации в постановке Летова–Калмана [2, 3].
Кардинальным приемом решения последней задачи является использование более простых вариантов локальной оптимизации в каждый текущий момент времени, а не за все время функционирования [1, 15].
Суммируя результаты проведенного анализа можно прийти к заключению, что при разработке СН математический аппарат оптимизации должен обеспечивать:
– эффективное наведение на цели, маневрирующие по сложным законам, желательно без учета старших производных, в том числе и со сменой их знаков;
– гарантированный увод от границ зон устойчивой (опасной) работы, в том числе для предотвращения столкновений при групповом применении;
– учет несоответствия динамических свойств подсистем в процессе их совместного функционирования, особенно на уровне “цель – ИВПС”;
– возможность перераспределения приоритетов управления в процессе наведения;
– существенное снижение сложности процедур синтеза как самих сигналов управления, так и алгоритмов их информационного обеспечения;
– универсальность синтеза методов наведения различного назначения.
Следует подчеркнуть, что классические способы оптимизации, основанные на минимизации квадратичных функционалов качества [2, 3], неспособны удовлетворить всей совокупности этих требований. В связи с этим необходимо найти новые, более универсальные приемы.
Целью статьи является разработка аппарата универсального метода синтеза управления, учитывающего перечисленные выше требования, на основе локальной оптимизации квадратично-биквадратных функционалов качества с учетом несоответствия динамических свойств цели и СН. Следует подчеркнуть, что в современной научно-технической литературе этой проблеме практически не уделяется должного внимания.
2. Локально-оптимальное позиционное управление динамическим объектом. Рассмотрим задачу управления детерминированным объектом:
(2.1)
${\mathbf{\dot {x}}}(t) = {\mathbf{f}}(t,{\mathbf{x}}(t),{\mathbf{u}}(t)){\text{,}}\quad {\mathbf{x}}(0) = {{{\mathbf{x}}}_{0}},$(2.2)
$\Delta {{I}_{{t,\Delta t}}} = {{I}_{{t + \Delta t}}} - {{I}_{t}} \to \mathop {\min }\limits_{{\mathbf{u}}(t) \in {{\mathbb{R}}^{r}}} ,\quad t \geqslant 0,\quad \,\,\Delta t \downarrow 0$(2.3)
${{I}_{t}}[{\mathbf{x}}( \cdot ),{\mathbf{u}}( \cdot )] = \int\limits_0^t {\varphi \left( {\tau ,{\mathbf{x}}(\tau ),{\mathbf{u}}(\tau )} \right)\,d\tau } + \psi \left( {t,{\mathbf{x}}(t)} \right),\quad t \geqslant 0.$Здесь $\varphi (t,{\mathbf{x}},{\mathbf{u}}),\psi (t,{\mathbf{x}})$ – подынтегральная (интегрант) и терминальная (терминант) функции потерь соответственно.
Как известно [25], требование (2.2) приводит к оптимизации сначала начального значения критерия (2.3), которое в данном случае от управления не зависит: ${{I}_{0}}[{\mathbf{x}}( \cdot ),{\mathbf{u}}( \cdot )] = \psi (0,{{{\mathbf{x}}}_{0}})$, а затем к минимизации, при каждом t ≥ 0, производной критерия (2.3), которая в силу нелинейного уравнения объекта (2.1) имеет вид
(2.4)
$\frac{{d{{I}_{t}}}}{{dt}} = \varphi \left( {t,{\mathbf{x}}(t),{\mathbf{u}}(t)} \right) + \frac{{\partial \psi \left( {t,{\mathbf{x}}(t)} \right)}}{{\partial t}} + \nabla _{{\mathbf{x}}}^{{\text{Т}}}\psi (t,{\mathbf{x}}(t)){\mathbf{f}}(t,{\mathbf{x}}(t),{\mathbf{u}}(t)) \to \mathop {\min }\limits_{{\mathbf{u}}(t) \in {{\mathbb{R}}^{r}}} .$Здесь ${{\nabla }_{{\mathbf{x}}}}\psi (t,{\mathbf{x}})$ – градиент терминанта из (2.3). Учитывая, что в (2.4) слагаемое ${{\partial \psi \left( {t,{\mathbf{x}}(t)} \right)} \mathord{\left/ {\vphantom {{\partial \psi \left( {t,{\mathbf{x}}(t)} \right)} {\partial t}}} \right. \kern-0em} {\partial t}}$ от оптимизируемой переменной не зависит, имеем следующую задачу на экстремум функции времени и двух векторных переменных по одной из них при любых значениях других ее аргументов:
(2.5)
$\theta (t,{\mathbf{x}},{\mathbf{u}}) = \varphi (t,{\mathbf{x}},{\mathbf{u}}) + \nabla _{{\mathbf{x}}}^{{\text{Т}}}\psi (t,{\mathbf{x}}){\mathbf{f}}(t,{\mathbf{x}},{\mathbf{u}}) \to \mathop {\min }\limits_{{\mathbf{u}} \in {{\mathbb{R}}^{r}}} \quad \forall t \geqslant 0,\quad {\mathbf{x}} \in {{\mathbb{R}}^{n}}.$Для решения этой задачи можно использовать соответствующие необходимое и достаточное условия экстремума функции. Так, точки ее стационарности определяются из уравнения
(2.6)
${{\nabla }_{{\mathbf{u}}}}\theta \left( {t,{\mathbf{x}},{\mathbf{u}}} \right) = {\mathbf{0}} \Rightarrow {\mathbf{u}} = {\mathbf{u}}{\kern 1pt} *(t,{\mathbf{x}}),$(2.7)
${{\nabla }_{{\mathbf{u}}}}\nabla _{{\mathbf{u}}}^{{\text{T}}}\theta \left( {t,{\mathbf{x}},{\mathbf{u}}} \right)\left| {_{{{\mathbf{u}} = {\mathbf{u}}{\text{*}}(t,{\mathbf{x}})}}} \right. \succ 0$.Далее будут рассмотрены варианты процедур синтеза для линейных моделей объекта управления в приложении к квадратичным и квадратично-биквадратным функционалам.
2.1. Линейный объект и квадратичный функционал качества. Рассмотрим частный случай, когда уравнение (2.1) является линейным:
(2.8)
${\mathbf{\dot {x}}}(t) = {\mathbf{F}}(t){\mathbf{x}}(t) + {\mathbf{B}}(t){\mathbf{u}}(t){\text{,}}$(2.9)
$\varphi (t,{\mathbf{x}},{\mathbf{u}}) = {{{\mathbf{x}}}^{{\text{T}}}}{\mathbf{L}}(t){\mathbf{x}} + {{{\mathbf{u}}}^{{\text{T}}}}{\mathbf{K}}(t){\mathbf{u}},\quad \psi (t,{\mathbf{x}}) = {{{\mathbf{x}}}^{{\text{T}}}}{\mathbf{R}}(t){\mathbf{x}}$,Тогда градиент терминанта линеен:
(2.10)
${{\nabla }_{{\mathbf{x}}}}\psi (t,{\mathbf{x}}) = {{\nabla }_{{\mathbf{x}}}}[{{{\mathbf{x}}}^{{\text{T}}}}{\mathbf{R}}(t){\mathbf{x}}] = [{\mathbf{R}}(t) + {{{\mathbf{R}}}^{{\text{T}}}}(t)]{\mathbf{x}} = 2{\mathbf{R}}(t){\mathbf{x}}$Поэтому условие ее стационарности (2.6) дает линейное матричное уравнение
(2.11)
${\mathbf{u}} = - {{{\mathbf{K}}}^{{ - 1}}}(t){{{\mathbf{B}}}^{{\text{T}}}}(t){\mathbf{R}}(t){\mathbf{x}}$.Достаточное же условие (2.7) в этом случае сводится к требованию положительной определенности матрицы
интегральных штрафов ${{{\mathbf{u}}}^{{\text{T}}}}(t){\mathbf{K}}(t){\mathbf{u}}(t)$ за величины элементов вектора управления.Отметим, что матрица F(t) из уравнения линейного объекта (2.8) и матрица L(t) интегральных штрафов критерия за величины элементов вектора состояния никакого влияния на полученный линейный закон локально-оптимального управления (2.11) не оказывают. Они определяют только скорость изменения (2.4) критерия оптимальности и, следовательно, его текущее значение. Поэтому в этом случае можно положить ${\mathbf{L}}(t) = {\mathbf{0}}$, так как в переменном критерии (2.3), (2.9) текущие величины переменных состояния ${\mathbf{x}}(t)$ уже штрафуются терминальным слагаемым ${{{\mathbf{x}}}^{{\text{T}}}}(t){\mathbf{R}}(t){\mathbf{x}}(t)$.
2.2. Линейный объект и квадратично-биквадратный функционал качества. Рассмотрим теперь более общий случай, когда в функционале (2.3) интегрант $\varphi (t,{\mathbf{x}},{\mathbf{u}})$ остался квадратичным как в (2.9), а терминант $\psi (t,{\mathbf{x}})$ получил дополнительное слагаемое
(2.13)
$\varphi (t,{\mathbf{x}},{\mathbf{u}}) = {{{\mathbf{u}}}^{{\text{T}}}}{\mathbf{K}}(t){\mathbf{u}},\quad \psi (t,{\mathbf{x}}) = {{{\mathbf{x}}}^{{\text{T}}}}{\mathbf{R}}(t){\mathbf{x}} + \xi (t,{\mathbf{x}})$(2.14)
$\xi (t,{\mathbf{x}}) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^n {\sum\limits_{l = 1}^n {{{с}_{{ijkl}}}(t){{x}_{i}}{{x}_{j}}{{x}_{k}}{{x}_{l}}} } } } .$В этом случае в предыдущих соотношениях изменится только градиент терминанта (2.10):
(2.15)
${\mathbf{u}} = - {{{\mathbf{K}}}^{{ - 1}}}(t){{{\mathbf{B}}}^{{\text{T}}}}(t)[{\mathbf{R}}(t){\mathbf{x}} + 0.5{{\nabla }_{{\mathbf{x}}}}\xi (t,{\mathbf{x}})].$Исследуем некоторые его частные виды.
2.2.1. Скалярный случай. Для простоты сначала рассмотрим объект (2.8) с одномерными состоянием ${\mathbf{x}} = x \in \mathbb{R}$ и управлением ${\mathbf{u}} = u \in \mathbb{R}$. Тогда по (2.14) имеем $\xi (t,x) = P(t){{x}^{4}}$ и функции потерь (2.13) выглядят следующим образом:
Отсюда легко находим градиент
так что локально-оптимальное управление (2.15) определяется по формулеОтсюда в явном виде следует, что сигнал управления наряду с линейной составляющей $R(t)x$ содержит и кубическую составляющую $2P(t){{x}^{3}}$.
2.2.2. Биквадратная форма. Пусть общая форма 4-й степени (2.14), содержащая большое число коэффициентов, представляет собой произведение двух в общем случае независимых квадратичных форм:
(2.16)
$\xi (t,{\mathbf{x}}) = ({{{\mathbf{x}}}^{{\text{T}}}}{\mathbf{S}}(t){\mathbf{x}})({{{\mathbf{x}}}^{{\text{T}}}}{\mathbf{P}}(t){\mathbf{x}}),$(2.17)
$\xi (t,{\mathbf{x}}) = ({{{\mathbf{x}}}^{{\text{T}}}}{\mathbf{x}})({{{\mathbf{x}}}^{{\text{T}}}}{\mathbf{P}}(t){\mathbf{x}}) = {{{\mathbf{x}}}^{{\text{T}}}}({\mathbf{x}}{{{\mathbf{x}}}^{{\text{T}}}}){\mathbf{P}}(t){\mathbf{x}} = {{{\mathbf{x}}}^{{\text{T}}}}{\mathbf{M}}({\mathbf{x}}){\mathbf{P}}(t){\mathbf{x}},$Например, для размерности n = 2 биквадратная форма (2.17) имеет лишь три параметра:
(2.18)
$\begin{gathered} \xi (t,{{x}_{1}},{{x}_{2}}) = \left[ {\begin{array}{*{20}{c}} {{{x}_{1}}}&{{{x}_{2}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {x_{1}^{2}}&{{{x}_{1}}{{x}_{2}}} \\ {{{x}_{1}}{{x}_{2}}}&{x_{2}^{2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{p}_{{11}}}(t)}&{{{p}_{{12}}}(t)} \\ {{{p}_{{12}}}(t)}&{{{p}_{{22}}}(t)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{x}_{1}}} \\ {{{x}_{2}}} \end{array}} \right] = \\ \, = {{p}_{{11}}}(t)x_{1}^{4} + 2{{p}_{{12}}}(t)(x_{1}^{3}{{x}_{2}} + {{x}_{1}}x_{2}^{3}) + ({{p}_{{11}}}(t) + {{p}_{{22}}}(t))x_{1}^{2}x_{2}^{2} + {{p}_{{22}}}(t)x_{2}^{4}. \\ \end{gathered} $Тогда, вычисляя градиент формы (2.16), можно использовать свойство производной от произведения, что приводит к удобному выражению
В частности, для случая (2.18) находим
В результате общий закон управления (2.15) в случае (2.16) в приложении к (2.8) определяется соотношением
(2.19)
${\mathbf{u}} = - {{{\mathbf{K}}}^{{ - 1}}}(t){{{\mathbf{B}}}^{{\text{T}}}}(t)({\mathbf{R}}(t){\mathbf{x}} + [{{{\mathbf{x}}}^{{\text{T}}}}{\mathbf{P}}(t){\mathbf{x}}]{\mathbf{S}}(t){\mathbf{x}}\, + [{{{\mathbf{x}}}^{{\text{T}}}}{\mathbf{S}}(t){\mathbf{x}}]{\mathbf{P}}(t){\mathbf{x}}).$Анализ (2.19) позволяет прийти к заключению, что сформированный сигнал управления содержит наряду с линейной составляющей $ - {{{\mathbf{K}}}^{{ - 1}}}{{{\mathbf{B}}}^{{\text{T}}}}{\mathbf{Rx}}$ и кубическую составляющую $ - {{{\mathbf{K}}}^{{ - 1}}}{{{\mathbf{B}}}^{{\text{T}}}}[{{{\mathbf{x}}}^{{\text{T}}}}{\mathbf{PxSx}}$ + + xTSxPx]. При этом, манипулируя элементами матриц R, P и S, можно изменять приоритеты управления между линейной и различными видами кубических составляющих.
3. Учет несоответствия динамических свойств цели и СН. Рассмотрим задачу управления n-мерным линейным объектом
(3.1)
${{{\mathbf{\dot {x}}}}_{{\text{у}}}}(t) = {{{\mathbf{F}}}_{{\text{у}}}}(t){{{\mathbf{x}}}_{{\text{у}}}}(t) + {{{\mathbf{B}}}_{{\text{у}}}}{\mathbf{u}}(t){\text{,}}\quad {{{\mathbf{x}}}_{{\text{у}}}}(0) = {{{\mathbf{x}}}_{{{\text{у}}0}}},$(3.2)
${{{\mathbf{\dot {x}}}}_{{\text{т}}}}(t) = {{{\mathbf{F}}}_{{\text{т}}}}(t){{{\mathbf{x}}}_{{\text{т}}}}(t) + {{{\mathbf{B}}}_{{\text{т}}}}{\mathbf{v}}(t){\text{,}}\quad {{{\mathbf{x}}}_{{\text{т}}}}(0) = {{{\mathbf{x}}}_{{{\text{т}}0}}}.$Здесь ${{{\mathbf{F}}}_{{\text{т}}}}(t)$, ${{{\mathbf{F}}}_{{\text{у}}}}(t)$ – в общем случае нестационарные матрицы, определяющие динамические свойства подсистем (3.1) и (3.2), ${\mathbf{u}}(t)$ – $r$‑мерный ($r \leqslant n$) вектор управления, ${{{\mathbf{B}}}_{{\text{у}}}}$ – стационарная матрица эффективности управления, ${{{\mathbf{B}}}_{{\text{т}}}}$ и ${\mathbf{v}}(t)$ – коэффициент передачи и управляющее воздействие системы (3.2), а подстрочные индексы “${\text{т}}$” и “y” соответствуют требуемым и управляемым координатам. Для упрощения записей зависимость векторов от времени далее будет опущена.
В общем случае несоответствие динамических свойств подсистем (3.1) и (3.2) можно оценить вектором возникающих ошибок функционирования
текущие значения которых удовлетворяют уравнению(3.4)
$\Delta {\mathbf{\dot {x}}} = {{{\mathbf{F}}}_{{\text{у}}}}(t)\Delta {\mathbf{x}} - {{{\mathbf{B}}}_{{\text{у}}}}{\mathbf{u}} + {{{\mathbf{s}}}_{{\text{у}}}}(t),\quad \Delta {\mathbf{x}}(0) = {{{\mathbf{x}}}_{{\text{т}}}}(0) - {{{\mathbf{x}}}_{{\text{у}}}}(0),$(3.5)
${{{\mathbf{s}}}_{{\text{у}}}}(t) = ({{{\mathbf{F}}}_{{\text{т}}}}(t) - {{{\mathbf{F}}}_{{\text{у}}}}(t)){{{\mathbf{x}}}_{{\text{т}}}} + {{{\mathbf{B}}}_{{\text{т}}}}{\mathbf{v}}(t)$Если динамические свойства объекта (3.1) соответствуют требуемым значениям ${{{\mathbf{F}}}_{{\text{у}}}} = {{{\mathbf{F}}}_{{\text{т}}}}$, то ${{{\mathbf{s}}}_{{\text{у}}}} = 0$ и ошибка Δx даже при отсутствии управлений u = 0 и v = 0 будет убывать вплоть до нуля со скоростью, определяемой собственными значениями заданной матрицы ${{{\mathbf{F}}}_{{\text{у}}}}$. В случае несоответствия динамических свойств ${{{\mathbf{F}}}_{{\text{у}}}} \ne {{{\mathbf{F}}}_{{\text{т}}}}$ в уравнении (3.4) появится вынужденная составляющая ${{{\mathbf{s}}}_{{\text{у}}}} \ne 0$, задаваемая характером изменения требуемой траектории ${{{\mathbf{x}}}_{{\text{т}}}}$ (3.2). Необходимо выбором сигнала управления u ускорить убывание ошибки $\Delta {\mathbf{x}}$ и скомпенсировать влияние на нее возмущения ${{{\mathbf{s}}}_{{\text{у}}}}$.
Для этого сформируем вектор u сигналов управления, обеспечивающий локальную оптимизацию переменного квадратично-биквадратного функционала качества, штрафующего большие значения не только элементов векторов состояния Δx и управления u системы (3.4), но и вектора несоответствия ${{{\mathbf{s}}}_{{\text{у}}}}$:
(3.6)
$\begin{gathered} {{I}_{t}}[\Delta {\mathbf{x}},{\mathbf{u}},{{{\mathbf{s}}}_{{\text{у}}}}] = \int\limits_0^t {{{{\mathbf{u}}}^{{\text{T}}}}(\tau ){\mathbf{Ku}}(\tau )d\tau } + \Delta {{{\mathbf{x}}}^{{\text{T}}}}(t){\mathbf{Q}}\Delta {\mathbf{x}}(t) + 2\Delta {{{\mathbf{x}}}^{{\text{T}}}}(t){\mathbf{G}}{{{\mathbf{s}}}_{{\text{у}}}}(t) + \\ \, + {\mathbf{s}}_{{\text{у}}}^{{\text{T}}}(t){\mathbf{P}}{{{\mathbf{s}}}_{{\text{у}}}}(t) + \Delta {{{\mathbf{x}}}^{{\text{T}}}}(t)\Delta {\mathbf{x}}(t)\Delta {{{\mathbf{x}}}^{{\text{T}}}}(t){\mathbf{P}}\Delta {\mathbf{x}}(t). \\ \end{gathered} $Здесь K – положительно определенная симметрическая матрица штрафов за величину сигналов управления, реализующая ограничения на их величину, G – матрица взаимовлияния $\Delta {\mathbf{x}}$ и ${{{\mathbf{s}}}_{{\text{у}}}}$, Q и P – симметрические матрицы, определяющие в законе управления (2.15) веса линейной и кубической составляющих, причем последняя обусловлена использованием частного вида (2.17) общей биквадратной формы (2.14).
Принципиальным отличием такой постановки задачи от классической [2–4] является наличие в (3.6) биквадратной части функционала и учет вектора (3.5) несоответствия динамических свойств систем (3.1) и (3.2).
Следует подчеркнуть, что в рамках квадратично-биквадратных представлений может быть получено большое количество самых разных функционалов, дающих решение задач оптимизации с разной степенью эффективности. Функционал (3.6) был выбран как вариант, обеспечивающий наибольшую полноту и наглядность дальнейшей процедуры синтеза управления.
Чтобы применить к рассматриваемой задаче (3.4), (3.6) результаты разд. 2, включим измеряемое возмущение ${{{\mathbf{s}}}_{{\text{у}}}}$ в расширенный 2n-мерный вектор состояния ${\mathbf{y}} = {{[\begin{array}{*{20}{c}} {\Delta {{{\mathbf{x}}}^{{\rm T}}}}&{{\mathbf{s}}_{{\text{у}}}^{{\rm T}}} \end{array}]}^{{\rm T}}}$, для которого получим уравнение
с блочными матрицами(3.8)
${\mathbf{F}}(t) = \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{F}}}_{{\text{у}}}}(t)}&{\mathbf{E}} \\ {{{{\mathbf{O}}}_{1}}}&{{{{\mathbf{O}}}_{2}}} \end{array}} \right],\quad {\mathbf{B}} = \left[ {\begin{array}{*{20}{c}} { - {{{\mathbf{B}}}_{{\text{у}}}}} \\ {{{{\mathbf{O}}}_{3}}} \end{array}} \right],$(3.9)
${{I}_{t}}[{\mathbf{y}},{\mathbf{u}}] = \int\limits_0^t {{{{\mathbf{u}}}^{{\rm T}}}(\tau ){\mathbf{Ku}}(\tau )d\tau } + {{{\mathbf{y}}}^{{\rm T}}}(t){\mathbf{Ry}}(t) + \xi (t,{\mathbf{y}}),\quad {\mathbf{R}} = \left[ {\begin{array}{*{20}{c}} {\mathbf{Q}}&{\mathbf{G}} \\ {\mathbf{G}}&{\mathbf{P}} \end{array}} \right],$(3.10)
$\xi (t,{\mathbf{y}}) = {{{\mathbf{y}}}^{{\text{T}}}}\left[ {\begin{array}{*{20}{c}} {{\mathbf{M}}(\Delta {\mathbf{x}}){\mathbf{P}}}&{\mathbf{O}} \\ {\mathbf{O}}&{\mathbf{O}} \end{array}} \right]{\mathbf{y}}.$Соотношения (3.7), (3.9) с точностью до замены переменной y на x соответствуют условиям задачи локальной оптимизации управления (2.1)–(2.3) применительно к линейному объекту (2.8) и критерию оптимальности с квадратично-биквадратными функциями потерь (2.13), (2.17). Поэтому, используя (2.19), получаем закон управления
(3.11)
${\mathbf{u}} = {{{\mathbf{K}}}^{{ - 1}}}{\mathbf{B}}_{{\text{у}}}^{{\rm T}}({\mathbf{Q}}\Delta {\mathbf{x}} + {\mathbf{G}}{{{\mathbf{s}}}_{{\text{у}}}} + (\Delta {{{\mathbf{x}}}^{{\text{T}}}}{\mathbf{P}}\Delta {\mathbf{x}})\Delta {\mathbf{x}} + (\Delta {{{\mathbf{x}}}^{{\text{T}}}}\Delta {\mathbf{x}}){\mathbf{P}}\Delta {\mathbf{x}}).$Анализ формулы (3.11) позволяет сделать следующие выводы:
– сигнал управления u зависит: от матрицы штрафов K за величину сигналов управления, от матрицы ${{{\mathbf{B}}}_{{\text{у}}}}$ восприимчивости к нему управляемой системы (3.1), а также от ошибок управления $\Delta {\mathbf{x}} = {{{\mathbf{x}}}_{{\text{т}}}} - {{{\mathbf{x}}}_{{\text{у}}}}$ и от несоответствия динамических свойств подсистем ${{{\mathbf{s}}}_{{\text{у}}}} = ({{{\mathbf{F}}}_{{\text{т}}}} - {{{\mathbf{F}}}_{{\text{у}}}}){{{\mathbf{x}}}_{{\text{т}}}}$;
– сигнал управления u содержит четыре слагаемых, из них первое и второе определяют его линейные составляющие по ошибке Δx и по возмущению ${{{\mathbf{s}}}_{{\text{у}}}}$, тогда как третье и четвертое – кубическую составляющую по ошибке Δx;
– при малых ошибках $\Delta {{x}_{i}} \to 0$, $i = \overline {1,n} $, кубическая составляющая практически не влияет на величину сигнала управления, обеспечивая высокую чувствительность линейного управления к малым ошибкам;
– при больших ошибках $\Delta {{x}_{i}}$, $i = \overline {1,n} $, превалирующей становится кубическая составляющая, за счет которой и осуществляется увод траектории от допустимых границ функционирования;
– влияние учета несоответствия динамических свойств проявляется тем сильнее, чем выше определяемая матрицей ${{{\mathbf{F}}}_{{\text{т}}}}$ скорость изменения требуемой траектории ${{{\mathbf{x}}}_{{\text{т}}}}$.
В итоге предложенный метод оптимизации позволяет обеспечить:
– возможность перераспределения приоритетов управления от ошибок наведения к ошибкам, минимизирующим текущий промах;
– снижение сложности формирования как самого сигнала управления, так и, что особенно важно при учете случайных погрешностей измерений, сложности алгоритмов фильтрации, обусловленное отсутствием необходимости формирования оценок третьей и четвертой производных координат состояния ввиду их отсутствия в законе управления.
Несомненным достоинством предложенного способа оптимизации, определяющего его простоту, является возможность формирования сигнала управления без решения сложной задачи вычисления коэффициентов передачи ошибок наведения, характерной для классических приемов оптимизации [2–4].
4. Пример. В общем случае рассмотренный способ локальной оптимизации по минимуму квадратично-биквадратных функционалов качества может быть использован для синтеза управления системами управления самого различного назначения. Однако для определенности в качестве примера дальнейшая процедура синтеза управления будет выполнена в приложении к системам самонаведения. В такой ситуации постановка задачи синтеза управления выглядит так.
Пусть ЛА, определяемый в траекторной плоскости типовой двумерной моделью
(4.1)
$\begin{gathered} {{{\dot {\varphi }}}_{{\text{у}}}} = {{\omega }_{{\text{у}}}},\quad {{\varphi }_{{\text{у}}}}(0) = {{\varphi }_{{{\text{у0}}}}}, \\ {{{\dot {\omega }}}_{{\text{у}}}} = - \frac{1}{{{{T}_{{\text{у}}}}}}{{\omega }_{{\text{у}}}} + \frac{b}{{{{T}_{{\text{у}}}}}}{{j}_{{\text{у}}}},\quad {{\omega }_{{\text{у}}}}(0) = {{\omega }_{{{\text{у0}}}}}, \\ \end{gathered} $(4.2)
$\begin{gathered} {{{\dot {\varphi }}}_{{\text{т}}}} = {{\omega }_{{\text{т}}}},\quad {{\varphi }_{{\text{т}}}}(0) = {{\varphi }_{{{\text{т0}}}}}, \\ {{{\dot {\omega }}}_{{\text{т}}}} = - \frac{{2\dot {D}(t)}}{{D(t)}}{{\omega }_{{\text{т}}}} + \frac{1}{{D(t)}}{{j}_{{\text{т}}}},\quad {{\omega }_{{\text{т}}}}(0) = {{\omega }_{{{\text{т0}}}}}. \\ \end{gathered} $Здесь ${{\varphi }_{{\text{у}}}}$ и ${{\omega }_{{\text{у}}}}$ – угол направления движения перехватчика и скорость его изменения; ${{\varphi }_{{\text{т}}}}$ – угол визирования цели в выбранной системе координат; ${{\omega }_{{\text{т}}}}$ – угловая скорость линии визирования; ${{T}_{{\text{у}}}}$ – постоянная времени перехватчика, характеризующая его динамические свойства (инерционность); $b$ – коэффициент передачи сигнала управления; $D$ и $\dot {D}$ – дальность от перехватчика до ИМЦ и ее производная; ${{j}_{{\text{у}}}}$, ${{j}_{{\text{т}}}}$ – поперечные ускорения перехватчика и цели, причем переменная ${{j}_{{\text{у}}}}$ выполняет роль синтезируемого управления.
Взаимное геометрическое расположение ЛА и ИМЦ показано на рис. 2, на котором ${{O}_{{\text{ц}}}}$, ${{O}_{{\text{п}}}}$ – точки текущего расположения цели и перехватчика; ${{{\mathbf{V}}}_{{\text{т}}}}$, ${{{\mathbf{V}}}_{{\text{у}}}}$ – векторы их скорости.
Вводя обозначения
(4.3)
${{{\mathbf{x}}}_{{\text{у}}}} = {{\left[ {\begin{array}{*{20}{c}} {{{\varphi }_{{\text{у}}}}}&{{{\omega }_{{\text{у}}}}} \end{array}} \right]}^{{\text{T}}}},\quad {\mathbf{u}} = {{j}_{{\text{у}}}},\quad {{{\mathbf{x}}}_{{\text{т}}}} = {{\left[ {\begin{array}{*{20}{c}} {{{\varphi }_{{\text{т}}}}}&{{{\omega }_{{\text{т}}}}} \end{array}} \right]}^{{\text{T}}}},\quad {\mathbf{v}} = {{j}_{{\text{т}}}},$(4.4)
 ${{{\mathbf{F}}}_{{\text{у}}}} = \left[ {\begin{array}{*{20}{c}} 0&1 \\ 0&{ - \frac{1}{{{{T}_{{\text{у}}}}}}} \end{array}} \right],\quad {{{\mathbf{B}}}_{{\text{у}}}} = \left[ {\begin{array}{*{20}{c}} 0 \\ {\frac{b}{{{{T}_{{\text{у}}}}}}} \end{array}} \right],\quad {{{\mathbf{F}}}_{{\text{т}}}}(t) = \left[ {\begin{array}{*{20}{c}} 0&1 \\ 0&{ - \frac{{2\dot {D}(t)}}{{D(t)}}} \end{array}} \right],\quad {{{\mathbf{B}}}_{{\text{т}}}} = \left[ {\begin{array}{*{20}{c}} 0 \\ {\frac{1}{{D(t)}}} \end{array}} \right].$
${{{\mathbf{F}}}_{{\text{у}}}} = \left[ {\begin{array}{*{20}{c}} 0&1 \\ 0&{ - \frac{1}{{{{T}_{{\text{у}}}}}}} \end{array}} \right],\quad {{{\mathbf{B}}}_{{\text{у}}}} = \left[ {\begin{array}{*{20}{c}} 0 \\ {\frac{b}{{{{T}_{{\text{у}}}}}}} \end{array}} \right],\quad {{{\mathbf{F}}}_{{\text{т}}}}(t) = \left[ {\begin{array}{*{20}{c}} 0&1 \\ 0&{ - \frac{{2\dot {D}(t)}}{{D(t)}}} \end{array}} \right],\quad {{{\mathbf{B}}}_{{\text{т}}}} = \left[ {\begin{array}{*{20}{c}} 0 \\ {\frac{1}{{D(t)}}} \end{array}} \right].$Тогда для вектора $\Delta {\mathbf{x}} = {{\left[ {\begin{array}{*{20}{c}} {\Delta \varphi }&{\Delta \omega } \end{array}} \right]}^{{\text{T}}}}$ ошибок функционирования $\Delta \varphi = {{\varphi }_{{\text{т}}}} - {{\varphi }_{{\text{у}}}}$, $\Delta \omega = {{\omega }_{{\text{т}}}} - {{\omega }_{{\text{у}}}}$ определено уравнение (3.4) с вектором несоответствия (3.5):
(4.5)
${\mathbf{s}} = {{\left[ {\begin{array}{*{20}{c}} 0&{{{s}_{2}}} \end{array}} \right]}^{{\text{T}}}},\quad {{s}_{2}} = \left( {{1 \mathord{\left/ {\vphantom {1 {{{T}_{{\text{у}}}}}}} \right. \kern-0em} {{{T}_{{\text{у}}}}}} - {{2\dot {D}(t)} \mathord{\left/ {\vphantom {{2\dot {D}(t)} {D(t)}}} \right. \kern-0em} {D(t)}}} \right){{\omega }_{{\text{т}}}} + {{{{j}_{{\text{т}}}}} \mathord{\left/ {\vphantom {{{{j}_{{\text{т}}}}} {D(t)}}} \right. \kern-0em} {D(t)}}.$Необходимо сформировать сигнал управления jy, локально-оптимальный по минимуму переменного функционала качества (3.6) с весовыми матрицами:
(4.6)
${\mathbf{K}} = {{k}_{u}},\quad {\mathbf{Q}} = \left[ {\begin{array}{*{20}{c}} {{{q}_{{11}}}}&{{{q}_{{12}}}} \\ {{{q}_{{12}}}}&{{{q}_{{22}}}} \end{array}} \right],\quad {\mathbf{G}} = \left[ {\begin{array}{*{20}{c}} {{{g}_{{11}}}}&{{{g}_{{12}}}} \\ {{{g}_{{21}}}}&{{{g}_{{22}}}} \end{array}} \right],\quad {\mathbf{P}} = \left[ {\begin{array}{*{20}{c}} {{{p}_{{11}}}}&{{{p}_{{12}}}} \\ {{{p}_{{12}}}}&{{{p}_{{22}}}} \end{array}} \right].$Используя соотношения (4.3)–(4.6) в общей формуле (3.11), получим закон управления объектом (4.1) сначала в матричной форме:
(4.7)
$\begin{gathered} {{j}_{{\text{у}}}} = \frac{b}{{{{k}_{u}}{{T}_{{\text{у}}}}}}[{{q}_{{12}}}\Delta \varphi + {{q}_{{22}}}\Delta \omega + {{p}_{{12}}}\Delta {{\varphi }^{3}} + ({{p}_{{11}}} + {{p}_{{22}}})\Delta {{\varphi }^{2}}\Delta \omega + \\ \, + 3{{p}_{{12}}}\Delta \varphi \Delta {{\omega }^{2}} + 2{{p}_{{22}}}\Delta {{\omega }^{3}} + {{g}_{{22}}}{{s}_{2}}]. \\ \end{gathered} $Анализ формулы (4.7) позволяет сделать следующие выводы.
1. Метод наведения характеризует многоконтурную систему с обратными связями только по углу Δφ и угловой скорости Δω. При этом в состав сигнала управления входят линейная составляющая, определяемая первыми двумя слагаемыми, нелинейная составляющая в виде слагаемых с третьего по шестое и нестационарная из-за переменности ${{s}_{2}}$ составляющая, задаваемая седьмым слагаемым.
2. Сигнал управления зависит не только от ошибок $\Delta \varphi $ и $\Delta \omega $, но и от их произведений $\Delta {{\varphi }^{2}}\Delta \omega $ и $\Delta \varphi \,\Delta {{\omega }^{2}}$.
3. Сигнал управления зависит не от абсолютных значений коэффициентов штрафов, а от отношений ${{{{q}_{{12}}}} \mathord{\left/ {\vphantom {{{{q}_{{12}}}} {{{k}_{u}}}}} \right. \kern-0em} {{{k}_{u}}}}$, ${{{{q}_{{22}}}} \mathord{\left/ {\vphantom {{{{q}_{{22}}}} {{{k}_{u}}}}} \right. \kern-0em} {{{k}_{u}}}}$, ${{{{p}_{{11}}}} \mathord{\left/ {\vphantom {{{{p}_{{11}}}} {{{k}_{u}}}}} \right. \kern-0em} {{{k}_{u}}}}$, ${{{{p}_{{12}}}} \mathord{\left/ {\vphantom {{{{p}_{{12}}}} {{{k}_{u}}}}} \right. \kern-0em} {{{k}_{u}}}}$, ${{{{p}_{{22}}}} \mathord{\left/ {\vphantom {{{{p}_{{22}}}} {{{k}_{u}}}}} \right. \kern-0em} {{{k}_{u}}}}$ и ${{{{q}_{{22}}}} \mathord{\left/ {\vphantom {{{{q}_{{22}}}} {{{k}_{u}}}}} \right. \kern-0em} {{{k}_{u}}}}$, что облегчает выбор их значений. При этом степень влияния нелинейных слагаемых на величину сигнала управления определяется значениями коэффициентов матрицы ${\mathbf{P}}$.
Особенно важно то, что для получения сигнала управления не требуется знания старших производных пространственных координат цели. Достаточно иметь полученные по результатам измерений оценки разности углов визирования цели и наводимого объекта $\Delta \hat {\varphi }$, разности угловых скоростей линии визирования $\Delta \hat {\omega }$, а также дальности цели от перехватчика и скорости ее изменения, что не накладывает ограничений на возможность его реализации. Различные способы формирования этих оценок подробно описаны в [27, 28] и здесь эта задача не рассматривается.
Характерной особенностью полученного метода является то, что, в отличие от традиционных методов, текущее направление полета перехватчика формируется не в упрежденную точку встречи, что при смене направления полета приводит к появлению дополнительных ошибок наведения (рис. 1), а непосредственно на цель, что особенно важно при наведении на цели, движущиеся со сменой знака производных координат состояния.
Специфика с третьего по шестое слагаемых состоит в их нелинейности, что предопределяет адаптацию чувствительности СН к ошибкам наведения. При малых ошибках, когда $\Delta \varphi \ll 1^\circ $ и $\Delta \omega \ll 1$ град/с, эти слагаемые практически не оказывают никакого слияния на процедуру наведения. Однако при увеличении ошибок они оказывают все возрастающее влияние, обеспечивая быструю реакцию перехватчика на приближение к опасным границам.
Особенностью нестационарного седьмого слагаемого с переменной (4.5) является его зависимость от условий применения, определяемых величинами $D$, $\dot {D}$, ${{\omega }_{{\text{т}}}}$. На больших расстояниях, когда ${{\omega }_{{\text{т}}}} \to 0$, оно практически не влияет на формирование сигнала управления. Однако на малых расстояниях с возрастанием значений ${{\omega }_{{\text{т}}}}$ его влияние существенно усиливается, обеспечивая минимизацию линейного промаха [8], определяемого соотношением $h \approx {{{{D}^{2}}{{\omega }_{{\text{т}}}}} \mathord{\left/ {\vphantom {{{{D}^{2}}{{\omega }_{{\text{т}}}}} {{{V}_{{\text{т}}}}}}} \right. \kern-0em} {{{V}_{{\text{т}}}}}}$.
Результаты моделирования такой ситуации приведены на рис. 3 и 4. На рис. 3, где ${{X}_{{\text{м}}}}$, ${{Z}_{{\text{м}}}}$ – масштабирующие коэффициенты по соответствующим координатам, показаны траектории цели (Ц), движущейся по квазисинусоидальной траектории, и перехватчика (П), наводимого по закону (4.7) без учета третьего слагаемого в переднюю полусферу с учетом и без учета их динамических свойств. На рис. 4, где ${{h}_{{\text{м}}}}$ и ${{t}_{{\text{м}}}}$ – масштабирующие коэффициенты по промаху и времени соответственно, приведена зависимость текущего относительного линейного промаха [1] от времени. Из рисунков видно, что учет этого несоответствия позволяет существенно повысить его точность на последнем участке.
Рис. 3.
Траектории движения цели (кривая 3) и перехватчика при наведении в переднюю полусферу без учета в (4.7) (кривая 1) и с учетом (кривая 2) несоответствия их динамических свойств
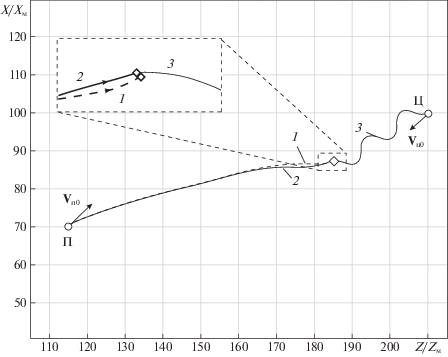
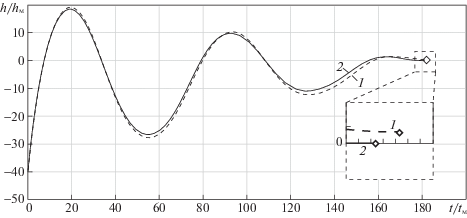
Рис. 4.
Зависимость текущих промахов от времени без учета в (4.7) (кривая 1) и с учетом (кривая 2) несоответствия динамических свойств цели и перехватчика
Для формирования сигнала управления (4.7) необходимо иметь фильтры, формирующие оптимальные оценки углов, угловой скорости линии визирования цели, а также дальности и скорости сближения. Разработанный способ наведения не накладывает принципиальных ограничений на возможность его реализации ни по требуемой вычислительной производительности, ни по возможности его информационного обеспечения. Определенные трудности его реализации обусловлены усложнением задачи выбора оптимальных значений коэффициентов матриц штрафов ${{q}_{{12}}}$, ${{q}_{{22}}}$, ${{p}_{{11}}}$, ${{p}_{{12}}}$, ${{p}_{{22}}}$ и g22. Однако эти усложнения не носят принципиального характера, поскольку могут быть решены на основе известных методик их выбора [15, 29].
Следует подчеркнуть высокую универсальность предложенного способа оптимизации, позволяющего получить широкий спектр различных методов наведения как частных случаев. Так, например, метод пропорционального наведения [1] определяется последним слагаемым из (4.7):
Заключение. Проведен анализ требований к СН, на основе которого предложен способ их оптимизации по минимуму локального квадратично-биквадратного функционала качества. Этот способ дает возможность обеспечить:
– синтез широкого спектра методов наведения на все типы целей, включая интенсивно маневрирующие цели, движущиеся со сменой знака производных за счет использования комбинации линейной и нелинейной зависимости от ошибок управления;
– гарантированный увод от границ устойчивой (опасной) работы за счет учета квадратичных и кубических ошибок функционирования;
– учет несоответствия динамических свойств цели и СН, что дает возможность осуществлять перехват ИМЦ с помощью ЛА, имеющих существенно худшую динамичность.
Список литературы
Авиационные системы радиоуправления: учебник для военных и гражданских вузов / Под ред. В.И. Меркулова. М.: Изд-во ВВИА им. проф. Н.Е. Жуковского, 2008.
Сейдж Э.П., Уайт Ч.С. Оптимальное управление системами. М.: Радио и связь, 1982.
Ройтенберг Я.Н. Автоматическое управление. М.: Наука, 1992.
Черноусько Ф.А., Колмановский В.Б. Оптимальное управление при случайных возмущениях. М.: Наука, 1978.
Халина А.С., Хрусталев М.М. Оптимизация облика и стабилизация управляемых квазилинейных стохастических систем, функционирующих на неограниченном интервале времени // Изв. РАН. ТиСУ. 2017. № 1. С. 65–88.
Бортаковский А.С. Теорема разделения в задачах управления пучками траекторий детерминированных линейных переключаемых систем // Изв. РАН. ТиСУ. 2020. № 2. С. 37–63.
Авиационные системы радиоуправления / Под ред. В.С. Вербы и В.И. Меркулова. М.: Радиотехника, 2014.
Авиационные системы радиоуправления. Т. 2. Радиоэлектронные системы самонаведения / Под ред. А.И. Канащенкова и В.И. Меркулова. М.: Радиотехника, 2003.
Радиоэлектронные комплексы навигации, прицеливания и управления вооружением летательных аппаратов. Т. 1. Теоретические основы / Под ред. М.С. Ярлыкова. М.: Радиотехника, 2012.
Попов И.М., Хамзатов М.М. Война будущего. Концептуальные основы и практические выводы. М.: изд. Кучково поле, 2017.
Федосов Е.А. Реализация сетецентрической технологии ведения боевых действий потребует создания БРЛС нового поколения // Фазотрон. 2007. № 1, 2. С. 11–14.
Siouris G.M. Missile Guidance and Control Systems. N.Y.: Springer-Verlag, 2004.
Yanushevsky R. Modern missile guidance. N.Y., London: CRC Press, 2018.
Zarchan P. Tactical and Strategic Missile Guidance. Reston: AIAA, 2013.
Меркулов В.И., Верба В.С., Ильчук А.Р. Автоматическое сопровождение целей в РЛС интегрированных авиационых комплексов. Т. 1. Теоретические основы. РЛС в составе интегрированных авиационных комплексов / Под ред. В.С. Вербы. М.: Радиотехника, 2018.
Харьков В.П., Меркулов В.И. Синтез закона управления системы перехвата высокоскоростных высокоманевренных воздушных целей // Информационно-измерительные и управляющие системы. 2017. Т. 15. № 10. С. 3–8.
Меркулов В.И., Соколов Д.А. Многоступенчатый фильтр для системы автосопровождения // Информационно-измерительные и управляющие системы, 2016. Т. 14. № 2. С. 3–9.
Верба В.С., Меркулов В.И., Самодов И.О. Оптимизация группового управления беспилотными летательными аппаратами // Динамика сложных систем. 2016. Т. 10. № 3. С. 3–9.
Меркулов В.И. Оптимизация систем управления по локальным квадратично-биквадратным функционалам качества // Информационно-измерительные и управляющие системы. 2016. Т. 14. № 11. С. 27–33.
Меркулов В.И., Гусаров С.Б. Оптимизация систем управления по квадратично-биквадратным функционалам качества в постановке Летова–Калмана // Информационно-измерительные и управляющие системы. 2017. Т. 15. № 3. С. 3–7.
Blakelock J.H. Automatic Control of Aircraft and Missile. N.Y.: John Wiley & Sons, 1991.
Меркулов В.И. Динамичность авиационных комплексов и бортовые радиоэлектронные системы // Радиотехника. 2010. № 1. С. 88–96.
Меркулов В.И., Дрогалин В.В., Миляков Д.А. Проблемы перехвата гиперзвуковых летательных аппаратов // Фазотрон. 2012. № 3. С. 52–54.
Верба В.С. Теоретические и прикладные проблемы разработки систем перехвата гиперзвуковых летательных аппаратов // Полет. 2014. № 2. С. 14–22.
Казаков И.Е. Статистическая теория систем управления в пространстве состояний. М.: Наука, 1975.
Меркулов В.И. Учет измеряемых возмущений при локальной оптимизации систем управления // Информационно-измерительные и управляющие системы. 2016. Т. 14. № 2. С. 61–64.
Руденко Е.А. Оптимальная структура непрерывного нелинейного фильтра Пугачева пониженного порядка // Изв. РАН. ТиСУ. 2013. № 6. С. 25–51.
Меркулов В.И., Верба В.С., Ильчук А.Р., Колтышев Е.Е. Автоматическое сопровождение целей в РЛС интегрированных авиационых комплексов. Т. 2. Сопровождение одиночных целей / Под ред. В.С. Вербы. М.: Радиотехника, 2018.
Крутько П.Д., Максимов А.И., Скворцов Л.М. Алгоритмы и программы проектирования автоматических систем. М.: Радио и связь, 1988.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления



