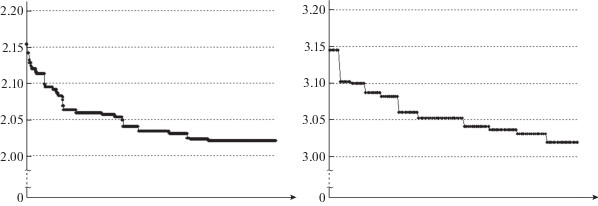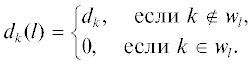Известия РАН. Теория и системы управления, 2020, № 6, стр. 109-119

Введение. Данная работа продолжает исследования, начатые в [1]. Здесь излагались результаты вычислительных экспериментов, анализирующие последствия целенаправленных разрушающих воздействий на функционирование сети связи. Для оценки ущерба каждого повреждения определялось как общее число разъединенных пар-корреспондентов, так и все направления связи, пропускная способность которых оказывалась меньше заданного нормативного значения. Расчеты по указанным критериям позволили найти представительные векторные оценки наиболее опасных разрушающих воздействий, а также построить соответствующие многопараметрические диаграммы.

В настоящей работе основное внимание уделено получению гарантированных оценок [2] уязвимости сети. В качестве основной функциональной характеристики изучается вектор предельно-допустимых потоков между всеми парами узлов при разрушении ребер. Исследуется множество повреждений, при которых хотя бы для одной пары источник–приемник предельно возможный поток оказывается равен нулю [3]. При анализе каждого конкретного повреждения вычисляются максимальные потоки для всех пар вершин источник–приемник. Полученные значения располагаются по невозрастанию, перенумеровываются и формируется вектор упорядоченных максимальных потоков всех пар-корреспондентов при данном повреждении. Оценка последствий конкретного разрушения производится по векторному критерию: число разъединенных пар источник–приемник и уменьшение максимально-допустимых потоков между корреспондентами. Для определения гарантированных оценок векторы максимальных потоков сравниваются по указанным критериям. По результатам вычислительных экспериментов находятся гарантированные оценки и строится результирующая диаграмма, отражающая изменения функциональных характеристик при повреждениях из заданного множества.

Получение гарантированных оценок ущерба и потерь для пар-корреспондентов можно рассматривать как способ исследования уязвимости [4] сетей связи. При любом повреждении нижние оценки допустимых потоков можно считать показателем неуязвимости и устойчивости системы к разрушающим воздействиям. Вычислительные эксперименты проводились для сетей с различными структурными особенностями. Сформированы соответствующие характеристические диаграммы, позволяющие сравнивать уязвимость и возможный ущерб.

1. Математическая модель. Для описания многопользовательской сетевой системы используется математическая запись модели передачи многопродуктового потока [5]. Структура сети G(d) задается множествами $\left\langle {V,R,U} \right\rangle $: узлов (вершин) сети $V = \{ {{v}_{1}},{{v}_{2}},...,{{v}_{n}},...,{{v}_{N}}\} $; неориентированных ребер $R = \{ {{r}_{1}},{{r}_{2}},...,{{r}_{k}},...,{{r}_{E}}\} \subset V \times V$. Ребро ${{r}_{k}} = ({{v}_{{{{n}_{k}}}}},{{v}_{{{{j}_{k}}}}})$ соединяет вершины ${{v}_{{{{n}_{k}}}}}$, ${{v}_{{{{j}_{k}}}}}$ (инцидентно вершинам ${{v}_{{{{n}_{k}}}}}$, ${{v}_{{{{j}_{k}}}}}$), которые для него являются концевыми. Предполагается, что в сети отсутствуют петли и сдвоенные ребра. Ребру r_k ставятся в соответствие две ориентированные дуги u_k, ${{u}_{{k + E}}}$ прямого и обратного направления из множества ориентированных дуг $U = \{ {{u}_{1}},{{u}_{2}},...,{{u}_{k}},...,{{u}_{{2E}}}\} $. Дуги $\{ {{u}_{k}},{{u}_{{k + E}}}\} $ определяют направление передачи потока по ребру r_k между концевыми вершинами ${{v}_{{{{n}_{k}}}}}$, ${{v}_{{{{j}_{k}}}}}$. Обозначим через $S({{v}_{n}})$ множество номеров исходящих дуг, по которым поток покидает узел ${{v}_{n}}$; $T({{v}_{n}})$ – множество номеров входящих дуг, по которым поток поступает в узел ${{v}_{n}}$.

Состав множеств $S({{v}_{n}})$, $T({{v}_{n}})$ однозначно определяется в ходе выполнения следующей процедуры. Пусть некоторое ребро ${{r}_{k}} \in R$ соединяет вершины с номерами n и  j, такими, что $n < j$, тогда ориентированная дуга ${{u}_{k}} = ({{v}_{n}},{{v}_{j}})$ считается исходящей из вершины ${{v}_{n}}$ и ее номер k заносится в множество $S({{v}_{n}})$, а ориентированная дуга ${{u}_{{k + E}}} = ({{v}_{j}},{{v}_{n}})$ – входящей для ${{v}_{n}}$ и ее номер k + E помещается в список $T({{v}_{n}})$. Соответственно дуга ${{u}_{k}}$ является входящей для ${{v}_{j}}$ и ее номер k попадает в $T({{v}_{j}})$, а дуга ${{u}_{{k + E}}}$ – исходящей и номер k + E вносится в список исходящих дуг $S({{v}_{j}})$.

Предполагается, что в сети между любой парой узлов могут передаваться потоки различных видов. Пара узлов корреспондентов ${{p}_{m}}$ определяется упорядоченными вершинами $({{v}_{{{{s}_{m}}}}},{{v}_{{{{t}_{m}}}}})$, где вершина с номером s_m называется источником, а с номером ${{t}_{m}}$ – стоком или приемником потока m-го вида. Далее в сети из N узлов рассматривается $M = N(N - 1)$ независимых, невзаимозаменяемых и равноправных потоков различных видов, которые передаются между узлами корреспондентами из $P = \{ {{p}_{1}},{{p}_{2}},...,{{p}_{M}}\} $.

Пусть ${{x}_{{mk}}}$ – величина потока m-го вида, который передается по ребру r_k, ${{x}_{{mk}}} \geqslant 0$, $m = \overline {1,M} $, $k = \overline {1,E} $. Каждому ${{r}_{k}} \in R$ приписывается неотрицательное число d_k, определяющее суммарный предельно-допустимый поток, который можно передать по ребру r_k в обоих направлениях. В исходной сети компоненты вектора пропускных способностей – $d = ({{d}_{1}},{{d}_{2}},...,{{d}_{k}},...,{{d}_{E}})$ – наперед заданные положительные числа ${{d}_{k}} > 0$. Вектором $d$ определяются следующие ограничения на все потоки, передаваемые по ребру r_k:

Обозначим через z_m, величину потока m-го вида, который поступает в сеть в узле с номером s_m и покидает из узла с номером t_m.

Во всех узлах ${{v}_{n}} \in V$, $n = \overline {1,N} $, сети для всех видов потоков должны выполняться условия сохранения потоков:

Величина z_m равна, входному потоку m-го вида, который пропускается от источинка к стоку пары ${{p}_{m}}$ при распределении потоков ${{x}_{{mi}}}$ по дугам сети.

Ограничения (1.1), (1.2) задают множество достижимых значений компонент векторов потоков $z = ({{z}_{1}},{{z}_{2}},...,{{z}_{m}},..,{{z}_{M}})$:

Рассмотрим произвольную пару узлов ${{p}_{m}} \in P$ и определим максимальный поток, который можно независимо передать в сети из вершины с номером s_m в вершину с номером ${{t}_{m}}$ без учета всех остальных потоков.

Задача 1. Для некоторой фиксированной пары p_m найти максимальный поток из узла с номером ${{s}_{m}}$ в узел с номером t_m:

Согласно [5], максимальному значению $z_{m}^{*}$, найденному при решении задачи 1, соответствует некоторый минимальный разрез $R(z_{m}^{*}) \subset R$, такой, что суммарная пропускная способность ребер ${{r}_{k}} \in R(z_{m}^{*})$ равна величине $z_{m}^{*}$. При удалении из сети ребер минимального разреза $R(z_{m}^{*})$ вершины с номерами ${{s}_{m}}$ и ${{t}_{m}}$ окажутся в разных фрагментах сети, а максимально возможный поток из ${{{v}}_{{{{s}_{m}}}}}$ в ${{{v}}_{{{{t}_{m}}}}}$ станет равным нулю. Обозначим через

множество номеров ребер, которые образуют минимальный разрез $R(z_{m}^{*})$:

2. Характеристические диаграммы неповрежденной сети. В результате последовательного решения цепочки задач 1 для каждой пары узлов ${{p}_{m}} \in P$ определяются максимальные потоки $z_{m}^{*}$, $m = \overline {1,M} $. Найдем величину максимального

и минимального потоков для всех пар из $P$. Вычислим и обозначим нормированные значения максимальных потоков. Набор $z_{m}^{*}( \cdot )$ сортируется по убыванию (невозрастанию). Элементы полученной упорядоченной последовательности переобозначаются и нумеруются подряд в соответствии с установленным порядком от большего $z{\kern 1pt} *(1) = {{(z{\kern 1pt} *{\kern 1pt} *{\text{/}}{{z}_{*}})}_{1}}$ к меньшему $z{\kern 1pt} *(M) = {{({{z}_{*}}{\text{/}}{{z}_{*}})}_{M}}$ = 1. Для элементов последовательности выполняются следующие условия:

Полученные значения $z{\kern 1pt} {\text{*}}(j)$, $j = \overline {1,M} $, далее рассматриваются как компоненты вектора нормированных упорядоченных максимальных потоков (далее – вектор NM-потока):

Компоненты z* – нормированные упорядоченные по величине максимальные потоки всех узлов корреспондентов в исходной неповрежденной сети.

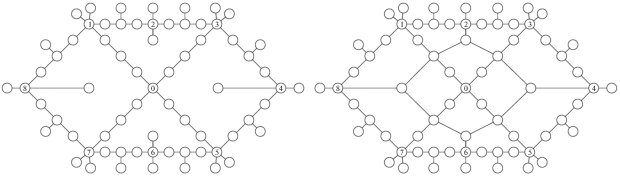
Вычислительные эксперименты проводились на моделях сетевых систем, представленных на рис. 1 (слева – базовая, справа – кольцевая). В каждой сети 69 узлов. Пропускные способности ребер – значения d_k, выбирались случайным образом из отрезка [1, 1.11] и совпадают для ребер, общих для обеих сетей. В кольцевой сети пропускная способность всех добавленных ребер равна 1. Статистика проведенных экспериментов подробно изложена в [1]. В настоящей работе для различных сетей на первом этапе для всех ${{p}_{m}} \in P$, $m = \overline {1,M} $, решалась задача 1 и формировался вектор z*. Значения компонент вектора z* использовались для построения диаграмм, изображенных на рис. 2–4.

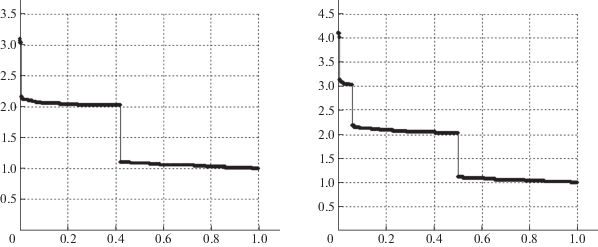
На рис. 2 по горизонтальной оси откладываются величины

по вертикальной – значения нормированного максимального потока $z{\kern 1pt} {\text{*}}(j)$, соответствующие каждой j-й компоненте вектора z* (2.1).

Диаграмма на рис. 2 слева относится к базовой сети, справа – к кольцевой. Диаграммы характеризуют предельные возможности исходной неповрежденной сети по передаче максимально-достижимых потоков между всеми парами источник–приемник. Диаграмму можно рассматривать как построенную эмпирическим путем функцию распределения NM-потоков при случайно заданных пропускных способностях ребер сети. Почти горизонтальные “ступени” на рис. 2 соответствуют парам ${{p}_{m}} \in P$, для которых минимальный разделяющий разрез содержит одно, два или три ребра.

Значения максимальных потоков, вернее компонент вектора NM-потоков, указанные по вертикали в диапазоне:

$1 \leqslant z{\kern 1pt} {\text{*}}(j) < 2$ относятся к парам, для которых минимальный разрез содержит только одно ребро;

$2 \leqslant z{\kern 1pt} {\text{*}}(j) < 3$ – парам с минимальным разрезом из двух ребер;

$3 \leqslant z{\kern 1pt} {\text{*}}(j) < 4$ – парам с минимальным разрезом с тремя ребрами.

Из анализа диаграмм на рис. 2 следует, что для половины всех пар-корреспондентов минимальный разрез содержит единственное ребро.

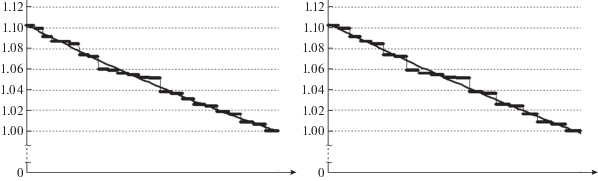
На рис. 3 представлены детализированные диаграммы распределения NM-потоков, соответствующих минимальному разрезу из одного ребра. Согласно исходным данным пропускная способность любого ребра является случайной величиной, равномерно распределенной на отрезке [1, 1.11]. Далее для обозначения узлов с одним, двумя или k инцидентными ребрами (вершин со степенью 1, 2, …, k) будем использовать обозначения $deq(1)$, $deq(2)$, …, $deq(k)$. Рассмотрим пару узлов корреспондентов ($deq(1)$, $deq(k)$), где $k \geqslant 2$. Для таких пар пропускная способность минимального разреза определяется пропускной способностью ребра для узла $deq(1)$ и имеет равномерное распределение. Доля таких пар составляет 80% при $1 \leqslant z{\kern 1pt} *(j) < 2$. Эти NM-потоки образуют основу линейной составляющей графика на диаграмме. Для пар узлов ($deq(1)$, $deq(1)$) функция распределения минимума пропускной способности из двух независимых случайных величин является квадратичной. Доля таких пар составляет 20% от общего числа разрезов, состоящих из одного ребра. Результирующая функция распределения пропускной способности минимальных разрезов ближе к линейной, но с небольшой квадратичной составляющей. Изображенная на диаграмме квазилинейная линия трендов для распределения NM-потоков соответствует указанному почти равномерному распределению пропускных способностей минимальных разрезов из одного ребра.

На рис. 4 слева для базовой сети представлена детализированная диаграмма распределения NM-потоков для минимальных разрезов из двух ребер; справа – для кольцевой сети с минимальным разрезом из трех ребер.

3. Множество повреждений. Вычислительные эксперименты проводились для оценки последствий разрушений специально выбранных ребер сети [1]. В настоящей работе рассматривались повреждения различных типов. Элементами множества повреждений первого типа

являются наборы номеров ребер $h(m)$ минимальных разрезов (см. (1.4)), найденных при решении последовательности задач 1 для всех ${{p}_{m}} \in P$. В ходе выполнения вычислительных экспериментов при решении задачи 1 для некоторой фиксированной пары p_a максимальному потоку $z_{a}^{*}$ ставится в соответствие единственный минимальный разрез $R(z_{a}^{*})$ и набор ребер $h(a)$.

В качестве критически опасных повреждений второго типа рассматриваются минимальные разрезы в сети с единичными пропускными способностями. В ходе вычислительного эксперимента пропускные способности всех ребер исходной сети полагаются равными единице:

Граф сети с единичными пропускными способностями обозначим $G(1)$, а соответствующее множество достижимых потоков – $Z(x,1)$:

Минимальный разрез для каждой пары ${{p}_{m}} \in P$ в такой сети определяется в ходе решения задачи о максимальном потоке.

Задача 2. Для некоторой фиксированной пары p_m найти максимальный поток

Величина $z_{m}^{1}$ равна числу ребер в минимальном разрезе $R(z_{m}^{1})$ для максимального целочисленного потока из вершины с номером s_m в вершину с номером t_m, $z_{m}^{1} = {\text{|}}R(z_{m}^{1}){\text{|}}$. В ходе решения задачи 2 максимальному потоку $z_{m}^{1}$ ставится в соответствие единственный список номеров ребер

при удалении которых максимальный поток из ${{v}_{{{{s}_{m}}}}}$ в ${{v}_{{{{t}_{m}}}}}$ становится равным нулю. Элементами множества повреждений второго типа являются номера ребер, входящих в минимальные разрезы, найденные при решении последовательности задач 2 для всех пар узлов ${{p}_{m}},m = \overline {1,M} $.

Повреждения третьего типа возникают в исходной сети при удалении всех ребер ${{r}_{k}} \in R({{v}_{k}})$, инцидентных некоторой вершине ${{v}_{k}}$. Элементами множества повреждений третьего типа

являются подмножества номеров ребер, инцидентных вершине ${{v}_{n}}$:

В множествах $H( \cdot )$, $Q( \cdot )$, $Y( \cdot )$ могут содержаться тождественные элементы. Для сокращения объема необходимых вычислений производится сравнение, сортировка и удаление повторяющихся повреждений любого типа. Из оставшихся формируется множество уникальных повреждений

которое не содержит одинаковых элементов.

Для каждого ${{w}_{l}} \in W$ рассматривается поврежденная сеть, в которой пропускная способность ребер ${{d}_{k}}(l)$ полагается равной:

В поврежденной сети для некоторой пары узлов p_m определяется допустимый максимальный поток $z_{m}^{0}(l)$.

Задача 3. При некоторых заданных w_l и p_m найти:

Для $z_{m}^{0}(l)$ и минимального значения ${{z}_{ * }}$ для неповрежденной сети вычисляется нормированная величина

Задача 3 решается для фиксированного w_l, всех ${{p}_{m}}$, $m = \overline {1,M} $, и определяются наборы $\{ z_{1}^{0}(l),z_{2}^{0}(l),...,z_{m}^{0}(l),....z_{M}^{0}(l)\} $ и $\{ \mathop {\tilde {z}}\nolimits_1^0 ( \cdot ,l),\mathop {\tilde {z}}\nolimits_2^0 ( \cdot ,l),...,\mathop {\tilde {z}}\nolimits_m^0 ( \cdot ,l),...,\mathop {\tilde {z}}\nolimits_M^0 ( \cdot ,l)\} $. Следуя процедуре, описанной в разд. 2, для выбранного w_l  формируется вектор NM-потоков

компоненты которого упорядочены по убыванию (невозрастанию) и равны нормированным максимальным потокам при данном повреждении ${{w}_{l}}$.

Цепочка задач 3 решается последовательно для всех ${{p}_{m}}$, $m = \overline {1,M} $, и всех w_l, $l = \overline {1,L} $, вычисляются нормированные величины максимальных потоков и строятся все векторы NM-потоков ${{z}^{0}}(l)$, $l = \overline {1,L} $.

4. Анализ повреждений. Для покомпонентного анализа NM-векторов z⁰(l) рассчитываются верхние и нижние оценки значений компонент, согласно следующей процедуре. Для всех компонент с некоторым фиксированным номером j вычисляются максимальное и минимальное значение потока для всех повреждений из множества $W$:

Для выделения ненулевых значений ${{z}^{0}}(j,l)$ вводится индикаторная функция:

Среднее значение ${{\bar {z}}_{ + }}(j,W)$ ненулевых величин ${{z}^{0}}(j,l)$ для  j-й компоненты и всех повреждений ${{w}_{l}} \in W$ определяется в соответствии с правилом:

Доля нулевых величин ${{z}^{0}}(j,l)$ для некоторого j составляет

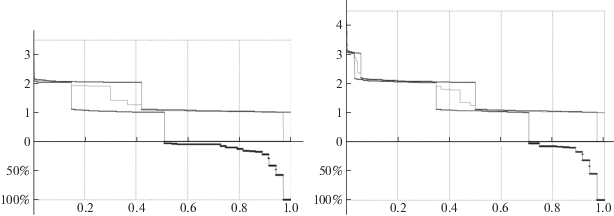
В разд. 2 был определен вектор z* и описан способ построения диаграмм, представленных на рис. 2. Указанные диаграммы были дополнены значениями $z{\kern 1pt} {\text{*}}(j,W)$, ${{z}_{*}}(j,W)$, ${{\bar {z}}_{ + }}(j,W)$, ${{\bar {z}}_{ - }}(j,W)$ для поврежденных сетей и изображены на рис. 5 (слева – для базовой сети, справа – для кольцевой).

Внешняя огибающая линия на диаграмме рис. 5 проходит через точки $z{\kern 1pt} {\text{*}}(j)$ – NM-потоки в исходной, неповрежденной сети и является частью исходных диаграмм, изображенных на рис. 2. Линию, проходящую через $z{\kern 1pt} *(j,W)$, можно рассматривать как выпуклую оболочку максимальных значений $j$-х компонент вектора NM-потоков для всех повреждений ${{w}_{l}} \in W$. Последовательность минимальных значений ${{z}_{*}}(j,W)$ определяет нижнюю огибающую и набор гарантированных значений j-х компонент векторов NM-потоков для всех повреждений ${{w}_{l}} \in W$.

Из анализа диаграммы следует, что максимальные потоки в неповрежденной сети $z{\kern 1pt} {\text{*}}(j)$ и верхние оценки $z{\kern 1pt} {\text{*}}(j,W)$ в поврежденной практически совпадают для 97% пар-корреспондентов. При этом доля пар-корреспондентов, для которых допустимый максимальный поток больше нуля при любом повреждении ${{w}_{l}} \in W$, составляет для базовой сети не менее 50%, а для кольцевой – не менее 70%. Доля пар, для которых при любом повреждении ${{w}_{l}} \in W$ сохраняются значения максимальных потоков, достижимых в исходной неповрежденной сети, составляет для базовой сети не менее 25%, а для кольцевой – не менее 50%. Доля пар, для которых верхние оценки максимально-допустимых потоков строго больше нуля, при любом повреждении ${{w}_{l}} \in W$ – 97% для обеих сетей.

Нижние значения ${{z}_{*}}(j,W)$ можно рассматривать как гарантированные оценки неуязвимости системы, понимая под этим показатели сети, которые сохраняются при любом повреждении. Из диаграммы следует, что нижние оценки компонент NM-векторов становятся равными нулю:

для базовой сети ${{z}_{*}}(j,W) = 0$ для всех $\pi (j) \geqslant 0.5$;

для кольцевой сети ${{z}_{*}}(j,W) = 0$ для всех $\pi (j) \geqslant 0.7$.

Однако для компонент с теми же номерами  j значения $z{\kern 1pt} {\text{*}}(j)$ в неповрежденной сети практически совпадают с верхними оценками ${{z}_{*}}(j,W)$ и средними величинами ${{\bar {z}}_{ + }}(j,W)$ в поврежденной сети. Соответствующие кривые изображены на рис. 5 одной жирной линией. В целом диаграммы свидетельствуют о том, что ненулевые компоненты векторов NM-потоков при повреждениях близки к исходным значениям функциональных характеристик в неповрежденной сети. Таким образом, для всех неразъединенных пар-корреспондентов при повреждениях сохраняются исходные показатели допустимых потоков. Таким образом, если рассматривать лексикографически упорядоченные оценки уязвимости, основываясь на NM-векторах потоков, то при фиксированных показателях числа разъединенных пар анализ сохранившихся значений допустимых потоков показывает, что сеть является неуязвимой по отношению к повреждениям из множества W.

На рис. 5 часть диаграмм, лежащая ниже осевой линии, построена на основе расчетных данных о нулевых компонентах векторов NM-потоков для всех повреждений из W. Величины ${{\bar {z}}_{ - }}(j,W)$ позволяют количественно оценить влияние каждого повреждения на число разъединенных пар, для которых максимальный поток становится равным нулю. На рис. 5 для каждого $\pi (j)$ соответствующее значение ${{\bar {z}}_{ - }}(j,W)$ откладывается по вертикальной оси, направленной сверху вниз. Величина ${{\bar {z}}_{ - }}(j,W)$ равна доле от общего числа повреждений, при которых  j-е компоненты векторов NM-потоков окажутся равным нулю. Таким образом ${{\bar {z}}_{ - }}(j,W)$ можно рассматривать как гарантированные оценки числа разъединенных пар при повреждениях из $W$. Например, нижнее значение ${{\bar {z}}_{ - }}(M,W)$ для последней ступеньки (для $j = M$) равно 100%, поскольку при любом повреждении ${{w}_{l}} \in W$ найдутся разъединенные пары. Следовательно, последняя, M-я компонента любого из NM-потоков всегда равна нулю. Для обеих сетей при любом повреждении ${{w}_{l}} \in W$ не менее 3% пар узлов корреспондентов окажутся разъединенными. Формально на диаграмме ширина последней нижней ступеньки по горизонтали равна 0.03 – доле разъединенных пар от их общего числа M.

В разд. 3 при решении задачи 3 для выбранной пары узлов ${{p}_{m}}$ и некоторого повреждения w_l был определен максимальный поток $z_{m}^{0}(l)$. Введем индикаторную функцию

и вычислим долю общего числа пар, разъединенных при повреждении w_l:

Следуя процедуре сортировки из разд. 2, полученный набор чисел $\eta (l,M)$, $l = \overline {1,L} $, упорядочивается по убыванию (невозрастанию), элементы полученной последовательности нумеруются подряд и обозначаются ${{\bar {z}}_{0}}(i) = {{[\eta (l,M)]}_{i}}$, где $i = \overline {1,M} $ – порядковые номера. По построению

Каждому номеру i ставится в соответствие нормированная величина

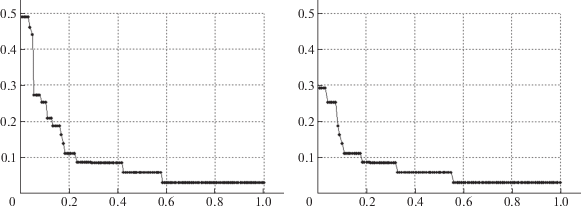
На рис. 6 изображены диаграммы: слева для базовой сети, справа – для кольцевой. По горизонтальной оси откладываются значения $\omega {\kern 1pt} {\kern 1pt} (i)$, а по вертикальной – ${{\bar {z}}_{0}}(i)$. Анализ диаграммы на рис. 6 показывает, что для обеих сетей не более 10% пар-корреспондентов окажутся разъединенными при четырех повреждениях из пяти. Только каждое пятое повреждениe разделяет более 10% пар. Однако в базовой сети 30-е повреждение приводит к разрыву связи для почти половины пар-корреспондентов. В кольцевой сети менее 3% повреждений из W могут привести к разрыву всех путей соединения для не более 30% пар. Каждое десятое повреждение разъединяет не менее 20% пар в базовой сети, а каждое второе – не более чем 6%. Любое повреждение из W разъединяет не менее 3% пар-корреспондентов как в базовой, так и в кольцевой сетях. Каждое второе повреждение приводит к отсутствию связи между не менее чем 6% пар. И только каждое десятое повреждение разъединяет более 10% пар в базовой сети.

Приведенный выше анализ диаграммы рис. 6 показывает, что они могут быть использованы для изучения уязвимости специальных сетей связи и управления, например, при чрезвычайных ситуациях и/или природных бедствиях, охватывающих большие территории.

Заключение. В данной работе при получении гарантированных оценок и формирования множества повреждений используются методы потокового программирования. Как уже было отмечено в [1], суммарные вычислительные затраты при решении цепочек задач о максимальном потоке и минимальном разрезе (задачи 1–3) полиномиально зависят от числа узлов в сети и не превышают $O({{N}^{7}})$.

Для построения диаграмм и формирования векторов NM-потоков многократно используется программа сортировки, при реализации которой стандартная оценка числа требуемых операций для набора из M элементов составляет $MlnM$ [6]. В рассматриваемом случае $M = {{N}^{2}}$ – числу компонент одного вектора NM-потоков. Поскольку на этапе формирования W каждому значению максимального потока для пары p_m ставится в соответствие один минимальный разрез в качестве кандидата на включение в множество повторений, то максимально возможное число повреждений $L = {{N}^{2}}$. При этом суммарные затраты на сортировку компонент векторов потоков для всех пар узлов при всех повреждениях составят ${{N}^{4}}2lnN$, а верхняя оценка будет порядка $O({{N}^{4}})$. Для построения диаграмм на рис. 6 требуется $LlnL$ операций, где $L = {{N}^{2}}$ – возможное число повреждений в множестве W, а вычислительные затраты составят ${{N}^{2}}2lnN$. Таким образом выполнение процедур сортировки данных не влияет на общую оценку суммарных затрат, величина которых не превысит $O({{N}^{7}})$.

При использовании данного подхода при исследовании уязвимости больших сетей можно задействовать простые процедуры распараллеливания в гетерогенной вычислительной среде. Предложенные методы позволяют проводить модельные эксперименты на кластерах из персональных компьютеров с различными операционными системами.