Известия РАН. Теория и системы управления, 2021, № 1, стр. 91-113

Введение. Статья посвящена разработке методики моделирования для описания случаев нестационарного развития экологических процессов и прогнозирования их резких качественных изменений. Методика основывается на различных реальных примерах.

Современные экосистемы функционируют без балансового равновесия их составляющих, соответственно усложняется задача рационального использования биоресурсов. Наблюдаются резкие переходные процессы, и эти явления не укладываются в регулярные флуктуации численности видов. Изменения выравненности показателя видового разнообразия экосистем под антропогенным давлением происходят стремительными скачками. Астатичность новых условий среды не мешает адаптации видов-вселенцев [1]. Для анализа ситуаций резких изменений не применимы традиционные модели математической биологии. Стремительные сдвиги популяционных трендов для разных видов обладают сходством [2], что даст математикам возможность классифицировать эти трансформации с точки зрения теории динамических систем. В статье мы сосредоточим внимание на формировании специфических вычислительных модельных сценариев, куда включим факторы стадий жизненного цикла и изменений популяционных характеристик при адаптации. Рассмотрим аспект релевантности принятия решений экспертами при управлении эксплуатацией биоресурсов и долгосрочном регулировании промысла при попытках достичь оптимального изъятия.

Цель статьи заключается в разработке способа организации гибридной вычислительной структуры, который позволит в компьютерных экспериментах описывать переходы к нестационарной динамике различных форм и учесть нелинейные эффекты в значимых экологических процессах. Разработку математического аппарата проведем поэтапно и отметим вариативность выбора функций. В результате серии модификаций и выработки практического обоснования по реальным данным идеи методики моделирования станут применимы к широкому кругу проблем экодинамики. Интересен подход, который даст специалистам алгоритм для расширения моделей в целях описания других особых ситуаций и экстремальных явлений помимо рассмотренных нами случаев – вспышки с единичным пиком и коллапса популяции.

Эпизодические экстремальные явления влекут существенные последствия для эволюции экосистем. Агрессивный хищник без биотического сопротивления одной вспышкой уничтожает свой новый ареал, как ядовитая морская звезда Acanthaster planci опустошает на долгие годы коралловые рифы [3]. По логистическому закону рост численности должен замедлиться у равновесия, но в реальности полная гибель экосистемы иногда случается, как в хрестоматийном примере вымирания оленей на острове Беринга. Пороговые эффекты в регуляции эффективности воспроизводства – важная причина подобных экстремальных явлений как в стремительном распространении одних видов, так и в быстром исчезновении других. Существуют интересные примеры, когда нежелательные вторжения видов были успешно остановлены средствами биологического подавления, выпуском эффективных естественных врагов.

Традиционные методы моделирования популяционных инвазий сталкиваются с рядом проблем, когда нужно достичь адекватного описания экстремальных состояний в биосистемах. Особи неидентичны по репродуктивным характеристикам. В малой группе дисперсия проявляется сильнее. Проблема разнородности особей в моделях отчасти решалась в [4]. Вторая сложность в том, что отдельные особи насекомых и рыб претерпевают изменения в жизненном цикле. Популяция в целом адаптируется и к биотической среде, и к изъятию промыслом самых крупных особей. Проблема моделирования сложного жизненного цикла фундаментальна и связана с коэволюцией популяций [5]. Противодействие хищников и паразитов в новой среде рассматривается теоретически как стимулирующий фактор для адаптации и дальнейшего видообразования [6]. Прогнозировать моменты переходов в неоптимальные условия взаимодействия биологических видов с помощью моделей мы сможем, если будем проводить сравнения модельных сценариев, в том числе с разной стратегией управления биоресурсами.

Мы обсудим преимущества подхода к расчетам основных характеристик популяций, где будем использовать вспомогательные и эволюционные факторы для прогнозирования выживаемости поколения и его итоговой репродуктивной эффективности. Методика отличается способом организации предикативных изменений на базе традиционных дифференциальных уравнений с гибридным кадрированным временем. Новизна заключается в идее конструирования переопределяемой вычислительной структуры отдельно из базового варьирующего форму уравнения и нескольких вспомогательных. Примером реализации новых идей станет формирование структуры из дифференциальных уравнений динамики поколений в трех формах для всех стадий развития. Переходы контролируются скоростью индивидуального роста организмов поколения. Дополняется структура модели особыми функциями, такими, что в разных практических задачах их “триггерное” действие включается на разных стадиях онтогенеза. Практический результат состоит в моделировании предложенными нами методами двух актуальных сценариев биологической кибернетики – коллапса запасов крупных рыб и неожиданной вспышки численности опасных насекомых, уничтожающих гектары ценного вечнозеленого леса.

В результате покажем, что ситуация коллапса обусловлена трудно преодолимой проблемой выработки релевантной стратегии управления при эксплуатации биоресурсов. Экспертам решение по квотированию объема добычи необходимо принимать сейчас, а получить достоверную оценку о реакции биосистемы на новое воздействие возможно только несколько лет спустя. Обоснуем причины того, что выбираемые для одной задачи управления две модели популяций часто оказываются противоречивы и несовместимы друг с другом по важным свойствам качественных изменений поведения их траекторий.

1. Методология построения гибридных структур в экодинамике. Системно или спорадически, но происходит смена превалирующих в регуляции выживания поколения факторов. Сложный жизненный цикл – это приспособление видов, потому формирование гибридной (непрерывно-событийной) структуры вычислений следует эволюционно заданным экологическим механизмам. Актуальная задача первого этапа нашей работы – достичь целенаправленного математического описания пороговых эффектов, тех внутренних критических состояний, которые определяют качественную перемену характера развития биологического процесса. Пороговые явления мы можем наблюдать только в узких диапазонах характеристик состояния самого экосистемного процесса.

К важным пороговым эффектам относим резкое увеличение эффективности воспроизводства, наблюдаемое у видов при эволюционной адаптации к среде размножения и ослаблении подавляющего биотического фактора. Альтернативный пороговый эффект – падение выживаемости на ранних стадиях онтогенеза в малой группе. “Пороговость” явления состоит в том, что при сокращении популяции в 3 раза численность новых поколений упадет в 5 раз, что становится причиной проблем восстановления популяций. По мере того, как группы становятся больше, их количество становится меньше, как показано в [7]. Частота встреч между хищником и добычей уменьшается с агрегацией добычи. Обеспеченность пищей и защищенность у ранних стадий развития в группе повышается. Наблюдается положительный эффект агрегированной группы, когда для эффективного выращивания потомства нужно поддерживать большую численность коллектива. Нельзя искусственными методами снова воссоздать сразу большие стаи. Эффект группы может стать симметрично отрицательным из-за факторов конкуренции.

Методику анализа нелинейных процессов лучше строить на основе математического описания выживаемости поколений популяций в раннем онтогенезе. На прогнозировании выживаемости личинок и молоди строится теория оптимального нерестового запаса [8]. Согласно концепции “критического периода” сэра Р. Мэя [9] у видов рыб с большой плодовитостью колебания выживаемости на личиночной стадии играют ощутимую роль в появлении флуктуаций общей численности. Средняя выживаемость от икры до малька севрюги по данным Т. Усовой составляет 1% при оптимальном режиме паводка [10], значит, доля дожития 1.5% становится существенным успехом вида в воспроизводстве.

В вычислительной структуре нам нужно рассчитать формирование половозрелого поколения, задав сильно различающиеся темпы убыли стадий развития. Актуально для новых моделей явно выделять по ходу расчетов переходы между непрерывными уравнениями для всех стадий онтогенеза, сделав систему гибридной и событийной [11].

Применительно к меняющимся условиям и факторам в эколого-физиологическом развитии видов вычислительные модели обосновано формировать в виде структур с переключениями. Под термином “гибридная система” понимается большое разнообразие всех структур с переключениями, разными разрывами и регулярными импульсами [12]. К гибридным относятся логико-динамические системы, в которых дискретная часть описывается логическими переменными [13]. О наших вычислениях мы предпочитаем говорить как о предикативно-переопределяемых изменениях состояния системы.

Разрабатываемый нами комплекс уравнений и правил как логических функций будем далее рассматривать как группу сценариев в итерационной форме. Дискретная составляющая модели обладает более удобными возможностями по смене поведения при бифуркациях. Можно получить равновесие, циклическую динамику или хаотическое движение разных типов. Форма границы областей притяжения разных аттракторов влияет на поведение траектории [14]. При анализе моделей мы должны понимать, что именно будем считать обоснованным поведением гибридной модели, а какие нелинейные эффекты нам необходимо исключить из итогового обсуждения результатов.

Используем форму времени как с дискретной, так и с непрерывной составляющими для построения модели популяции с выраженными стадиями развития в жизненном цикле. Этот известный в моделировании подход со сложным временем нам нужно адаптировать для биологических проблем. Дискретные эффекты в моделируемом процессе проявляются в течение онтогенеза уже существующего поколения, потом происходит событие – появление нового поколения. Соответственно разные события присутствуют как внутри интервала онтогенеза поколения, так и происходят межинтервальные переключения. Структура отрезков времени важна, так как некоторые интервалы – это биологические характеристики популяций, другие – адаптационные промежутки, зависящие от условий развития поколений. Потому мы используем и разбиение времени на кадры жизни поколений, и расчеты событий внутри интервала онтогенеза вида.

Дискретные элементы событий нужно пронумеровать, согласно их положению, в последовательности кадров в непрерывном течении видимого наблюдателю общего модельного времени. Для построения модели популяций с выраженными стадиями развития жизненного цикла разработаем форму времени более сложным способом, чем просто чередующиеся интервалы у гибридных систем. Используем разбиение – кадрирование иерархии непрерывных отрезков времени, внутри больших кадров оставим место для пронумерованных событий tⁱ. Гибридно-событийное время, которое используется при расчетах нашей программной средой, формализуем в виде мультимножества – объединения кортежей из упорядоченных элементов:

где $i$ – порядковый номер внутрикадрового события $0 < i \leqslant I < \infty $, n – номер кадра времени в вычислительном эксперименте, I – количество событий, которое возможно внутри кадра, T – точка завершения расчетов в кадре в единицах модельного времени, биологически событие T интерпретируется как достижение половозрелым поколением сезона размножения, $Gap\_Lef$ – техническая щель у левой границы кадра, $Gap\_Right$ – аналогичная щель у правой границы непрерывного кадра, соседствующая с левой щелью следующего кадра. Для гибридных автоматов с обычными событийными переходами между состояниями число событий не обязательно должно быть жестко фиксировано или ограничиваться, но в нашей программной реализации действует именно кадрированное время с внутренними событиями. Потому число I должно быть ограничено, так как невозможно деление интервала онтогенеза на бесконечное число составляющих. Между t^I и завершающим кадр моментом $T$ не может быть событий. В этом отличие нашего метода с иерархией событий от теории классических гибридных моделей, как, например, известной задачи расчета траектории после отскоков мячика от упругой поверхности.

Момент, отмеченный в (1.1) как ${{t}_{0}}$, – специальное событие инициализации модели, присутствующее всегда по умолчанию независимо от существования других событий, это замечание относится и к моменту T, как априори присутствующему в программной реализации кадрированного времени. Форма времени с непрерывной и дискретной компонентой оставляет щели-границы (от слова “gap” – щель) $Gap\_Left[N(0) = f(\lambda ,q)$; w(0) = w₀]; $Gap\_Right[t = 0]$ справа и слева от непрерывного кадра. К кадру примыкают аналогично пронумерованные щели между соседними кадрами времени, правая щель кадра n станет смежной для левой щели кадра n + 1. Щели, не входящие в кадр, понадобились нам, так как края каждого отрезка времени входят в сам кадр. Нужны технические моменты для обнуления переменных-счетчиков и для выполнения перестроений в выделенных точках переходов к расчету развития уже следующего смежного поколения с t = 0. В экспериментах с внешним управлением щели необходимы для учета изъятия или выпуска партии особей – при расчете величины N(0).

В работах по гибридным моделям мало уделяют внимания интервалам времени при управлении изменением непрерывного процесса, но формализация существенно помогает настройке и отладке работы переходов. C (1.1) составим иерархию событий: ${{t}^{1}},{{t}^{2}},...,{{t}^{I}}$, которые указываются расчетами. Внешнее управление процессом в сценариях отнесем к межкадровым переходам. Таким методом осуществим простую фиксацию момента для перехода к расчету динамики следующего поколения в популяционной возрастной структуре и определим начальное состояние для количества особей поколения.

Первая идея нашего метода состоит в том, что модель популяционного процесса формируется на основе динамически переопределяемой системы. Факторы убыли численности существенно колеблются между тремя стадиями онтогенеза. В задачах о рыбах или насекомых ключевой биологический аспект стадийность их жизни позволяет нам рассматривать последствия изменений в их жизненном цикле как фактор нелинейной динамики. Разные стадии жизни видов с глубоким преобразованием строения организма имеют различную и экологию, и физиологию, они становятся хищниками или жертвами.

Биологическое обоснование метода строится на теории формирования пополнения промысловых популяций “stock–recruitment relationship” из знаменитой работы [15] в современном ее истолковании в [16]. Представления о роли функциональной связи в эффективности воспроизводства использовались для прогнозирования уровня эксплуатации многих запасов ценных видов рыб, но не всегда управление ресурсами было успешно на основе статистического анализа данных [17]. Традиционно используют принятые обозначения для показателей запаса S “stock”, пополнения R “recruitment”. Пусть в начальный момент существует достаточно значительный родительский запас популяции S₀ со средней плодовитостью $\lambda $. Задача прогнозирования состоит в том, чтобы установить по данным наблюдений функциональную связь для величины ожидаемого пополнения R к моменту Т – достижения половозрелого состояния поколением. Далее необходимо исследовать влияние этой функциональной связи на положение равновесия или флуктуаций численности, в том числе для сложных случаев – явлений коллапса и вспышки. Задача регулирования промысла требует применения теории бифуркаций.

Важность стадийного онтогенеза отмечалась многими авторами в анализе восполнения запасов [18]. Вторая идея нашей методики – устанавливать события по набору соотношений между величинами модели, не обязательно связанными с модельным временем. За данными событиями следуют изменения процедуры расчета уравнений. Для построения модели мы предлагаем предикативно переопределяемую вычислительную структуру с тремя последовательными режимами изменениями состояния поколения: от $N\left( 0 \right) = \lambda S$ до $R = N(T)$. Модель убыли численности от исходного значения N(0) записывается дифференциальным уравнением с набором последовательно действующих форм для его изменяемой правой части. Дополнительно в составе базовой модели укажем множество предикатов для смены режима расчетов, перехода к иной форме правой части уравнения. Сами логические функции определим отдельно.

Пусть ограничение на количество стадий I = 3 и внутрикадровых событий $i \in \{ 1,2,3\} $ действует для соответствия отрезков внутри кадра с количеством стадий онтогенеза. Представим основную “скелетную” модель с тремя неспецифичными обобщенными стадиями развития онтогенеза, вычисляемую на склеенном из плавающих субинтервалов фиксированном интервале времени – в череде пронумерованных кадров:

Для ясности изложения следующая базовая модель включает два внутрикадровых события и определяется тремя формами правой части одного дифференциального уравнения:

с включением запаздывания $\eta < \tau $, связанного с исчерпанием ресурсов предыдущими стадиями, $w(\tau )$ – важный показатель достигнутого размера к моменту окончания первой стадии развития особей. В (1.2) основная величина N(t) – текущая численность поколения: $N(t) < N(0),$ $\forall t > 0$. Убывающие коэффициенты ${{\alpha }_{1}} > {{\alpha }_{2}} > {{\alpha }_{3}}$ и $\beta $ – различно трактуемые показатели ювенильной смертности в зависимости от численности. Величина субинтервала времени $\tau $ – длительность самой первой эмбриональной стадии развития без внешнего питания до активной личинки.

В нашем методе перестроения в (1.2) совершаются между режимами изменения состояния (меняются темпы убыли). Способ отличается от организации прямых переходов между самими состояниями, как программировалось в дискретно-событийных моделях. Формой для алгоритмической реализации модели в вычислительной среде служит гибридный автомат [19]. Такой автомат с переходами представим в среде AnyLogic как граф с ориентированными дугами – направлениями трансформации правой части от начального положения посредством очередности активации вершин графа. Имеющая минимум одну входную дугу активная вершина гибридного автомата соответствует текущему режиму изменения состояния, заданного нами одной из трех форм уравнений в (1.2). В вычислительной среде мы можем выполнять изменения и при входе в вершину автомата, и при выходе. Контролируют старт и завершение активности каждой формы правой части предикаты, логические функции дуг, которые принимают значения истина / ложь в зависимости от выполнения соотношений между включенными в предикаты переменными. Для каждой формы организованы соотношения для ее запуска ${{A}_{1}},\;{{A}_{2}},\;{{A}_{3}}$ и для остановки расчетов ${{Z}_{1}},{{Z}_{2}},{{Z}_{3}}$. Пары предикатов ${{A}_{i}},{{Z}_{i}}$ вместе мы назовем правилами активации переходов между режимами изменения состояния:

Предикаты в (1.3) используют пороговый уровень w_k для выхода поколения из-под давления ювенильных “квадратичных” факторов смертности. Наличие порога w_k исходит из динамики показателя размерного развития $w(t) = f(N(t))$. В (1.3) предикаты для завершения мы записали с логическим отрицанием, так как переход к следующей форме (или остановка автомата и реинициализация внутренних переменных) станет возможным при нарушении соотношений, так как расчет формы правой части происходит по принципу “до тех пор, пока выполняются условия”. Для каждой формы правой части (1.2) в переходах проводится перерасчет промежуточных начальных условий: ${{N}_{1}}(0){{{\text{|}}}_{{t = t_{{}}^{1}}}} = N{{{\text{|}}}_{{t = \tau }}}$.

Выполняется сопряжение с предшествующими конечными значениями на каждом субинтервале. Последнее событие фиксирует состояние в момент окончания расчетов. В простом случае остановка происходит на правом краю заданного интервала [0, T]. Строгая последовательность переключений внутри [0, T], как показано в случае модели переходов между стадиями онтогенеза, для автоматов – не обязательное условие [20]. Можно реализовать произвольный порядок выбора правых частей из множества возможных.

Для реализации гибридных систем при аппроксимации решений краевых задач используются модификации схемы Годунова [21]. Методология развивается, и для таких систем обобщена даже теория функций Ляпунова [22]. При реализации вычислительных систем с переключениями следует учесть средства для избегания режима с вырождением непрерывного времени – известного “эффекта Зенона” [23]. Численный алгоритм может блуждать в окрестности условий разрыва, а длины непрерывных отрезков будут стремиться к нулю при бесконечном количестве таких тактов, потому гибридные системы используют способы доопределения состояний [24] и сшивания траекторий.

Истинность для стартовых и завершающих предикатов проверяется по отсчетам кадров времени (назовем такие переходы таймированными “time-forced”) либо определяется внутренними зависимостями – реляционными “relation-forced” переходами. Более интересно, когда переход происходит после сравнения соотношений значений у внутренних модельных переменных, чем от времени. Далее опишем величины, связанные с расчетами вспомогательных уравнений и способы моделирования для темпов роста w(t).

2. Связь вспомогательных уравнений и предикатов. Третья идея методики – расчет сокращения численности необходимо дополнить вычислением других биологических показателей, чтобы получить возможность применять наборы предикатов из (1.3). Вспомогательные показатели модели должны быть легко измеримыми.

Важнейшим из всех возможных является темп среднего весового прироста поколений, что показано для разных биологических объектов [25]. В работе [26] проводилось исследование зависимости смертности личинок рыб от их среднего веса. Влияние на выживаемость фактора, связанного с конкуренцией за ресурсы между особями поколения, установлено экспериментально для скорости развития гусениц вредителей и божьих коровок в [27]. Базовую гибридную структуру (1.2) будем решать численно во взаимосвязи со вспомогательным показателем размерных характеристик поколения. Дополнительное уравнение системы для темпов индивидуального развития $w(t)$ запишем так:

где δ – поправочный показатель, $w(0) = {{w}_{0}}$, $\rho \gg \delta $ фиксировано отражает доступность пищевых ресурсов, что можно применять в большинстве случаев, когда скорость восполнения кормовых объектов велика, как для случая крупных морских рыб. Обосновано, что существует достижимый пороговый уровень веса организма $\bar {w}$. При достижении такого состояния особи поколения перестают испытывать давление факторов смертности, которые квадратично зависят от численности и которые называют “компенсационными”. Особи становятся способны передвигаться, избегать встреч с хищниками или уже недоступны для атак паразитов, поражающих личиночные стадии.

Вариант (2.1) полагает статичность условий. Параметр доступных пищевых ресурсов в числителе можно задать динамически $\rho (t)$ – третьим уравнением. Если полагается, что кормовая база стремится к стационарному равновесию $\rho (t) \to \Upsilon $, то можно использовать простые уравнения кибернетической саморегуляции. Подойдет модель Ферхюльста с самой популярной “квадратичной формой” саморегуляции численности в такой форме:

где $\vartheta $ – репродуктивный параметр, сравнимый с коэффициентом потребления корма $\varsigma $, а параметр $\Upsilon $ – балансовая величина равновесия, означающая емкость насыщения экологической ниши. Условия экологической задачи управления биоресурсами могут быть связаны с климатическими или сезонными изменениями, где важна колебательная динамика кормовых ресурсов. Для моделирования вместо (2.2) можно использовать уравнение с одним запаздыванием $\dot {\rho } = \vartheta f(N(t - \xi ))$. Например, прямо ввести запаздывание ξ в уравнение (2.2) и применить свойства модели “Hutchinsоn equation” с коэффициентом изъятия корма $\varsigma $:

Поведение (2.3) зависит от значения произведения модельных параметров $\vartheta \xi $, что показано в [28]. При увеличении $\vartheta \xi $ наблюдаем обычную бифуркацию Андронова–Хопфа с возникновением вместо затухающих колебаний орбитально устойчивой циклической траектории, которую обозначают ${{\rho }_{*}}(t;\vartheta \xi )$. Звездочкой внизу принято обозначать циклическую траекторию, а наверху – стационарную точку итераций. С возрастанием значения $\vartheta \xi $ траектория цикла ${{\rho }_{*}}(t;\vartheta \xi )$ приобретет негармоническую (релаксационную) форму с увеличением амплитуды колебаний при чрезвычайно низких $\min {{\rho }_{*}}(t;\vartheta \zeta ) \to 0 + \varepsilon $.

Можно использовать вместо квадратичной более сложную функцию саморегуляции:

В уравнение (2.4) введен показатель независимой смертности $\chi ,\chi < \varsigma $, который будет отражать целенаправленное изъятие доступного для популяции ресурса. Запаздывание $\xi $ тут не несет сущностной интерпретации, но нужно для феноменологического описания невынужденных колебаний обилия ресурсов. Однако самые очевидные варианты уравнений с запаздыванием при численном моделировании демонстрируют существенный недостаток. При необходимости увеличить период между максимумами колебаний с ростом $\vartheta \xi $ происходит быстрое увеличение амплитуды цикла ${{\rho }_{*}}(t)$. Минимумы становятся чрезвычайно малыми: $\mathop {\lim }\limits_{\xi \vartheta \to \infty } \min {{\rho }_{*}}(t) = 0$. Низкие значения ресурсов ρ недопустимы для расчетов (2.2). Такая модель не соотносится с экологической реальностью – тогда погибало бы все поколение сразу, потому в некоторых небольших реках Канады нет “четных” (или нечетных) популяций горбуши, у которой жизненный цикл строго 2 года.

Предложим новое, специальное уравнение для колебательного варианта модели динамики развития ресурсов для показателя индивидуального среднего роста особей поколения, где важным фактором будет текущая разность величин $\Upsilon - {{N}^{2}}(t - \xi )$:

В (2.5) после бифуркации рождения цикла получим релаксационные колебания – Λ-образные пики значительной амплитуды негармонической формы с масштабирующим коэффициентом μ < 1, начинающиеся от ненулевого порогового значения около потерявшего устойчивость равновесия. Ситуация соответствует осеннему минимуму корма, что обычно для планктона. Вариант (2.5) без недостатка глубоких минимумов флуктуаций будет актуален для ряда задач с сезонной изменчивостью $\rho $, когда генерируется несколько поколений в разных условиях. Впрочем, метод позволит задать вариации обеспечения ресурсами простым средством. Можно табличной функцией при смене кадров менять значение величины кормовой базы $\rho $ для разных поколений.

В результате численного решения задачи Коши (1.2) c (2.1) для всех значимых $N(0)$ (натуральных чисел) получим функциональную зависимость $N(0) \to N(T) \equiv \varphi (N(0))$ от начальной (яиц или икры) группы особей. Потом снова сможем вычислить для следующей итерации величину $N(0) = \lambda S$, где S – традиционно численность половозрелого запаса. Биологическое обоснование вычисления $R = N(T) = \varphi (N(0))$ в виде оператора эволюции для анализа итераций ${{R}_{{n + 1}}} = \varphi ({{R}_{n}})$ строится на принципах теории формирования пополнения промысловых запасов и роли нелинейного характера зависимостей $R = f(S)$ при экспертном управлении промыслом биоресурсов, описанной в работе [29].

Поведение итераций подчиняется фундаментальным теоремам, но нам для описания актуальных примеров из динамики насекомых и рыб будет недостаточно известных свойств возникновения циклов четных и нечетных периодов. В гладкие зависимости необходимо добавить возможности для описания скачкообразных изменений траектории. Обязательно избегать скачкообразных изменений во внутренних параметрах гибридной системы для сохранения теоретической обоснованности всей методики. Совершенно нереалистичны изменения ключевых характеристик: $\lambda ,{{w}_{0}},\tau $. В сложных биологических системах меняются не скачками вдруг отдельные параметры популяции, а подстраиваются функции регуляции, они определяют направленность эволюционного тренда [30].

3. Вариативность метода моделирования. Описывать темпы роста поколений можно различным образом: классическим уравнением баланса анаболизма и катаболизма Л. фон Берталанфи или другой предикативной структурой из набора форм правой части уравнения c таймированными переходами между ними. Задача таких уравнений описывать факторы опосредованной регуляции численности поколения, тогда как в базовой модели – непосредственные факторы убыли. В гибридную систему можно включать специфические формы регуляции выживаемости помимо типичной квадратичной формы. Метод, который позволяет расширять базовую модель, сделал идею актуальной для экстремальной динамики многих видов с большой плодовитостью λ, например, для вспышек насекомых с неполным циклом превращений. Численность многих вредных насекомых фитофагов регулируют паразиты. Наездники и осы атакуют обычно одну из стадий развития, чаще всего яйца [31]. Реакция паразитов обусловлена наличием массовых доступных жертв, которых им легче обнаружить именно в скоплениях, чем в однородном распределении. В моделировании темпов убыли эффект массовой атаки можно учесть, включив в уравнение N(0), но только на первой стадии:

Данным методом учтем особенности регуляции выживаемости яиц для насекомых вредителей. Уровень выживаемости мелких насекомых обусловлен скученностью неподвижных жертв при атаке их врагов, что используется при целенаправленном выпуске паразитов для искусственного биологического подавления многих бабочек.

Моделирование с гибридным временем обладает реалистичностью при описании эволюции стадий жизни и вариативностью числа вспомогательных уравнений. Покажем, как точечно учесть критический фактор, который важен только для одной из стадий.

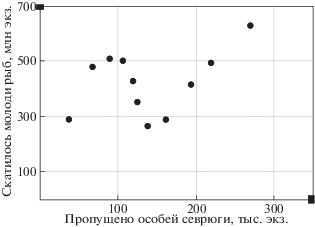
4. Метод включения триггерных функций. Из практики наблюдений известно, что при малой численности многократно возрастает роль неблагоприятных факторов среды в воспроизводстве популяций. Непропорциональное сокращение восполнения запасов рыб невозможно заранее предвидеть корреляционными методами. Внезапно снизилась эффективность естественного нереста севрюги Acipenser stellatus, что видно по показателю численности молоди, мигрировавшей из реки в Каспийское море. Снижение произошло резко, когда численность нерестового запаса севрюги стала меньше пороговой (420 тыс. особей) из-за систематического перелова. На рис. 1 представлены обработанные нами методом “скользящей средней” данные о воспроизводстве севрюги на нерестилищах Нижней Волги из [32].

На графике приведены ценные и редкие данные, которые позволяют непосредственно оценить форму зависимости в эффективности пополнения до 2007 г., имеющую тут два явных максимума. Для других случаев у нас нет способов решить обратную задачу — однозначно восстановить функциональную зависимость по данным наблюдений. Если популяция стабильно пребывает в состоянии равновесия, то на графике увидим только сгущения точек у равновесия, но севрюге Acipenser stellatus Каспийского моря сейчас угрожает полное вымирание, так как промысел в Волге не был остановлен своевременно и незаконный вылов продолжается в море.

Необходимость учета пороговых изменений параметров важна в объяснении проблемы низкой эффективности искусственного воспроизводства осетровых рыб Каспия. Гидрологический режим реки Волги нарушен в 1960-е годы. С конца 1970-х годов применялось искусственное воспроизводство с целью увеличить уловы осетровых до 30 тыс. т, но уловы с 1979 г. продолжали только неуклонно снижаться вплоть до запрета промысла. Столь низкий процент возврата созревших для нереста рыб из Каспийского моря обратно в Волгу от объема исходного выпуска молоди рыб не могли объяснить ихтиологи [33]. Завышение ожидания промыслового возврата от искусственного воспроизводства стало одной из причин деградации ценных популяций. При прогнозировании объема запаса и доли уловов ихтиологи исходят из ожидаемого показателя “промвозврата”, который считают по корреляционным зависимостям [34].

Проблема прогнозирования судьбы осетровых рыб Каспия привела к другой идее нашего подхода – внедрение в базовую предикативно переопределяемую динамическую систему с гибридным временем триггерных функций. По своей сути – это динамические коэффициенты для итераций: ${{\varphi }^{n}}({{x}_{0}};{{\Psi }_{t}}),{{\Psi }_{t}} \ne const$, но только с ограниченной областью воздействия на допустимом множестве значений аргумента. Функции будут сохранять свое значение на всем объединенном интервале кадра модельного времени поколения, но меняться на следующих пронумерованных элементах множества ${{\{ [{{t}_{0}},...,{{t}^{i}},{{t}^{{i + 1}}},...,T]\} }_{n}}$ от кадра к кадру. Триггеры необходимо отдельно из условий каждой экологической задачи подбирать в модель на нужную стадию развития. Для стадии нужен только один триггер.

В нашем уравнении убыли численности поколения есть два коэффициента смертности: зависящий от внутривидового взаимодействия квадратично $\alpha {{N}^{2}}$ и независимый линейный $\beta N$. Для третьей стадии квадратичный фактор убыли в (1.2) мы не используем. Сомножитель $\alpha w$ учитывает быстрейшее исчерпание необходимых для развития ресурсов по мере повышения биомассы рыб. Оказалось, что имеет смысл учитывать потери воспроизводства для мигрирующих рыб при низкой плотности зашедших на нерест в реку половозрелых особей севрюги в момент ${{t}_{0}}$. Эффект потерь репродуктивной активности рыб реализован в модели дополнительным динамическим коэффициентом $\Psi [S]$, функционально зависящим от состояния запаса S. Он включен при сомножителе $\beta N$, где учитывается независимая от плотности смертность поколения:

В (4.1) запись $\Psi [S]$ дана в квадратных скобках, потому как величина родительского запаса неизменна при расчете убыли пополнения: $S = {\text{const}},$ $t \in [0,T]$. Действие эффекта демографической ямы у севрюги (рис. 1) ограничено в модели диапазоном для принимаемых функцией Ψ следующих значений: $\forall S \in {{{\mathbf{Z}}}^{ + }}$, $\Psi (S) \in [2,1)$. По условию задачи можно ограничить значения родительской популяции S подмножеством из натуральных чисел $S < {{S}_{{\max }}}$. Положим, что Ψ(S) = = $1 + \exp ( - \sigma {{S}^{2}})$ зависит от величины родительской популяции S. Из текущей величины S рассчитаем начальные условия N(0).

Область допустимых значений функций-триггеров для первой стадии справа должна, согласно нашей идее, иметь единичный предел. Триггер Ψ должен становиться нейтральным, если в нем нет больше необходимости:

где параметр σ < 1 непосредственно отражает степень выраженности порогового эффекта. Биологическая причина проявления описываемого методом эффекта наступает из-за снижения вероятности образования нерестовых пар на большом протяжении нерестилищ. Далее покажем примеры применения метода гибридных структур и триггерных функций для моделирования двух критических ситуаций для управления биоресурсами. Данный эффект ведет к наличию критической численности, которая необходима для стабильного существования популяции. Гипотеза о существовании такой минимальной численности подтверждается все чаще. В 2020 г. сообщено в новостных агентствах, что крупнейшая пресноводная рыба – лопатонос вида Psephurus gladius официально признан вымершим.

5. Практика применения гибридной структуры и разновидности аттракторов. Численное решение объединенной модели позволяет вычислять итоговое $N(T) = R$ для допустимых исходных величин запаса. Мы используем эту зависимость φ как оператор эволюции для функциональных итераций: ${{R}_{{n + 1}}} = \varphi ({{R}_{n}}) - {{q}_{n}}{{R}_{n}}$, $n = 1,2,3...{{n}_{\infty }}$, где $q \in [0,1)$ – доля промыслового изъятия. При регулируемом промысле вылов q рассчитывается на каждый сезон n. Величина ${{n}_{\infty }}$ тут указана как число итераций, при котором мы будем считать асимптотическим состояние траектории в вычислительных экспериментах, для большинства расчетов достаточно ${{n}_{\infty }} = {{10}^{4}}$, для установления признаков хаотичности поведения итераций по факту экспоненциального разбегания близких траекторий – известного физического критерия возникновения хаоса [35] нами используется ${{n}_{\infty }} = {{10}^{6}}$.

В гибридной модели расчет убыли последовательных поколений с промысловым изъятием задается с выражением для начальных условий первой стадии развития: ${{N}_{{n + 1}}}{{{\text{|}}}_{{t = 0}}} = (1 - {{q}_{n}})\lambda {{N}_{n}}{{{\text{|}}}_{{t = Tn}}}$. Изменения управляющего воздействия стратегии промысла q_n не составит труда варьировать в специальных щелях по ходу вычислительного эксперимента.

С помощью модели можно реализовывать актуальные нелинейные эффекты. Хаотизацию траектории через каскад бифуркаций удвоения периода можно получить в итерациях известных зависимостей для расчета пополнения запасов рыб, как в ${{x}_{{n + 1}}} = a{{x}_{n}}{{e}^{{ - b{{x}_{n}}}}},$ a > e² и в x_{n + 1} = ${{{{a{{x}_{n}}} \mathord{\left/ {\vphantom {{a{{x}_{n}}} {1 + ({{x}_{n}}{\text{/}}B)}}} \right. \kern-0em} {1 + ({{x}_{n}}{\text{/}}B)}}}^{b}}$, b > 2, где a – репродуктивный потенциал, b – отражает давление факторов среды. Мы не считаем данное свойство с фрактальным аттрактором и континуумом неустойчивых траекторий актуальным для наших задач. По сравнению с применявшимися ранее для расчетов нелинейными итерационными моделями из обзора [36] получим оригинальные свойства динамики траекторий модели, интересные для проблемы прогнозирования события коллапса рыбных запасов.

Будем использовать (1.2), (2.1) с дополнением (4.1), (4.2) и так найдем разделение фазового пространства для траектории минимум одной неустойчивой точкой. Такая стационарная точка $x_{r}^{*} = \phi (x_{r}^{*})$, окрестность которой покидают траектории при любых малых возмущениях, называется репеллером в противоположность устойчивому притягивающему множеству – аттрактору Λ. Можно сказать, что репеллер динамической системы – инвариантное множество, превращающееся в аттрактор при обращении времени [37]. В простом случае репеллер исполняет роль границы, когда близкие начальные точки ${{x}_{{01}}} \in (x_{r}^{*} + \varepsilon ),$ ${{x}_{{02}}} \in (x_{r}^{*} - \varepsilon )$ просто монотонно притягиваются к разным аттракторам или $\mathop {\lim }\limits_{n \to \infty } {{\phi }^{n}}({{x}_{{01}}}) = - \infty $, $\mathop {\lim }\limits_{n \to \infty } {{\phi }^{n}}({{x}_{{02}}}) = + \infty $. Неустойчивые стационарные точки итераций будем различать: изолированные репеллеры без точек-прообразов или открытые репеллерные точки, имеющие точки-прообразы (справа от себя или слева) и прообразы этих прообразов. Важное условие для зависимости – положение экстремумов ${{R}_{{\min }}} > {{R}_{{\max }}}$.

Нам важно, что если точка $\exists {{x}_{{r2}}}$ – прямой прообраз, который под действием оператора эволюции ϕ отображается в репеллерную точку $\phi ({{x}_{{r2}}}) = x_{r}^{*}$, то она тоже будет принадлежать инвариантному множеству итераций. Прямых прообразов у репеллера может быть более одного, и с каждым будет связано инвариантное множество не притягивающихся к аттракторам точек-прообразов ${{\phi }^{{ - n}}}(x_{r}^{*})$. Из-за свойств комбинаций прообразов у таких точек-репеллеров усложняется граница области притяжения аттракторов. Возможен сценарий, когда аттрактор пересечется со своей границей.

Бифуркацией называют просто качественное перестроение фазового портрета динамической системы, и они позволяют видеть изменения в поведении траектории. У непрерывных и дискретных систем бифуркации разные, хотя и две из трех выглядят сходными. Будем использовать бифуркации при построении сценарных моделей и для описания ситуаций с управлением. В качестве критерия устойчивости у стационарных точек итераций используем значение производной: $\phi {\kern 1pt} '(x{\text{*}}) \in ( - 1,1)$ [38]. Широко известно понятие “странного аттрактора”, обладающего свойством локальной неустойчивости. Странный аттрактор, строго говоря, не обязан быть хаотическим [39], но в статье мы осознано не будем развивать эту популярную в прошлом веке тематику. О применении “фракталоподобных” объектов в моделях экодинамики писали ранее в [40]. Присутствие хаотических аттракторов в биологических моделях было сильно переоценено, так как подобное поведение приводит к противоречиям при сравнении с реальными наблюдениями за водоемами при изменении их трофического статуса, известными в биологической литературе как “парадокс обогащения” (“paradox of enrichment”) [41]. Мы не считаем возникновение глобального странного аттрактора достоинством для модели конкретной популяции севрюги или трески.

Интересная нам модельная зависимость из (1.2)–(2.1) с триггерной компонентой (4.1), (4.2) будет обладать более чем одним максимумом, а итерации получат две области притяжения альтернативных аттракторов. У неунимодальной функции не выполняются условия теоремы Синжера [42], которые необходимы для реализации сценария перехода к глобальному хаотическому аттрактору через каскад бифуркаций удвоения периода цикла – по теории Фейгенбаума образования цикла бесконечного периода p при конечном увеличении параметра [43]. При нарушении критериев Синжера в некоторый момент при изменении параметров там возникнет два альтернативных цикла периода p = 2.

В работе Блох и Любич [44], обобщившей результаты Гукейнхеймеpа [45], показано, что для функциональных итераций возможно четыре топологических типа аттракторов: простое равновесие x* (цикл конечного периода), аттрактор гомеоморфный канторовскому множеству (это нигде не плотное множество, не имеющее внутренних точек) и интервальный аттрактор как объединение бесконечного множества несвязных отрезков, которые могут создать все точки ${{\phi }^{{ - n}}}(x_{r}^{*})$. Четвертый тип – соленоидальный аттрактор.

Модель может обладать возможностью образования хаотического движения из-за множества точек, которые не входят в область притяжения аттракторов, так как являются прообразами неустойчивых стационарных точек-репеллеров. При изменении положения экстремумов нашей зависимости $\varphi (\lambda S)$ эти граничные $\partial \Omega $ для области притяжения $\Omega $ точки сформируют континуальное множество никуда не притягивающихся точек. Возникает иной тип переходного хаотического движения, чем в теории Фейгенбаума при накоплении каскада бифуркаций удвоения. Для итераций ${{x}_{n}} = f({{x}_{n}}) \pm \iota $ возможно появление трех типов метаморфозов аттракторов. Бифуркации стационарных точек итераций бывают прямые и обратные. Прямая бифуркация – удвоение периода цикла ${{p}_{m}} = {{2}^{{i + 1}}}$, обратная бифуркация – “ополовинивание периода” ${{p}_{m}} = {{2}^{{i - 1}}}$. Для обратной бифуркации необязательно уменьшать управляющий параметр, существуют итерации, где при увеличении параметра сперва происходит каскад увеличения периода цикла ${{p}_{m}} = {{2}^{{i + 1}}}$, а потом каскад изменений периода с его уменьшением ${{p}_{m}} = {{2}^{{i - 1}}}$ по степеням двойки.

Аттракторы, как компактные подмножества фазового пространства, могут моментально терять свойство инвариантности $f(\Lambda ) \in \Lambda $, если получат непустое пересечение $\Lambda \cap \partial \Omega \ne \emptyset $ с границей $\partial \Omega $ замкнутой области $\Omega ,\forall {{x}_{0}} \in \Omega \mathop {\lim }\limits_{n \to \infty } {{\phi }^{n}}({{x}_{0}}) = \Lambda $, что будет зависеть уже от свойств их области притяжения Ω. Граница $\partial \Omega $ не входит в это множество точек области притяжения Ω, может быть точкой, набором локально несвязных между собой точек, как в нашем примере, или образовывать фрактальную структуру, как известное замкнутое множество Жюлиа, которое само нельзя нарисовать.

Так, частные прикладные задачи вновь пересекаются с фундаментальными проблемами динамических систем. Например, если будем рассматривать итерации функции ${{f}^{{(3)}}}(x;a) \equiv f(f(f(x;a))),$ $f(x;a) = ax{{e}^{{ - bx}}},$ $0 < b < 1$ при значении бифуркационного параметра $a = {{a}_{3}},{{a}_{3}} = 22$, 255, таких, что ${{f}^{n}}(x_{1}^{*};{{a}_{3}}) = {{f}^{{n + 3}}}(x_{1}^{*};{{a}_{3}})$, то области притяжения трех устойчивых стационарных точек $x_{1}^{*},\;x_{2}^{*},\;x_{3}^{*}$ у итераций ${{x}_{{n + 1}}} = {{f}^{{(3)}}}({{x}_{n}};a)$ будут перемешанными “Intermingled basins of attraction” по терминологии в [46]. В там случае для каждой точки $\forall {{x}_{{01}}} \in {{\Omega }_{1}}$, $\mathop {\lim }\limits_{n \to \infty } {{f}^{{(3)n}}}({{x}_{{01}}}) = x_{1}^{*}$ существует сколь угодно малая ε > 0 окрестность и выполнено условие для начальных точек: $\exists {{x}_{{02}}},\;{{x}_{{03}}} \in {{x}_{0}} \pm \varepsilon ,$ ${{x}_{{02}}} \in {{\Omega }_{2}}$, ${{x}_{{03}}} \in {{\Omega }_{3}}$.

6. Нелинейная динамика реального коллапса биоресурсов. Мы разрабатываем модель сценария истощения биоресурсов, который происходит не длительно, как было с запасами осетровых рыб Каспия, но случается внезапно для специалистов ихтиологов – в форме коллапса. Резкий коллапс принципиально отличается от постепенного монотонного истощения запасов рыб. Деградация промысловых запасов трески в Северной Атлантике в 1992 г. – самый масштабный коллапс по экономическим последствиям [47]. В Канаде после 1992 г. 25 тыс. сотрудников потеряли рабочие места от прекращения векового промысла.

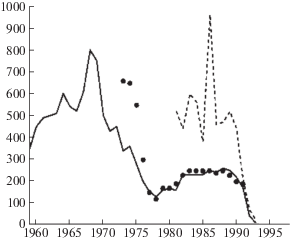
Википедия посвятила коллапсу трески подробную статью, где приведен график динамики уловов перед крахом промысла, но на графике из Википедии представлены не совсем полные данные. Рисунок 2 для анализа гораздо информативнее. На рисунке сплошной линией показана динамика реальных уловов, а точками – размеры квоты, предназначенной для вылова в тыс. тонн. Пунктиром обозначена рассчитанная предполагаемая величина запасов трески, которая, как выяснилось после коллапса, не соответствовала истинному положению. Очевидно, оценка величины запаса S была чрезмерно оптимистичной, а ожидаемая кривая запас-пополнение f(S) для трески выше реальной и не были оценены близкие к пороговым значениям запаса экстремумы кривой.

Резких падений уловов у популяции трески Севера Атлантики (согласно графикам на рис. 2) без восстановления рыбных запасов было два, потому в вычислительном сценарии трансформаций фазового портрета динамической системы должно быть аналогично два.

Рыболовы после первого падения уловов в 1970-х годах не могли пять лет освоить выделенную им квоту. Оценки оптимального изъятия рассчитываются по стандартным когортным моделям и статистическим методам прогнозирования. Потом уловы пришли к равновесию с оценками квот. Долго в 1980-е годы квота трески осваивалась и почти не менялась 10 лет. Вдруг индустрия ловли внезапно обрушилась. Авторы статьи [48], откуда мы привели график, в 1996 г. с пессимизмом прогнозировали восстановление промысла трески у Ньюфаундленда через девять лет, этого не произошло и в 2018 г. Мораторий на вылов рыбы изначально вводили на два года. Никто из авторитетных экспертов-биологов не смог предсказать столь длительную деградацию ценных биоресурсов. Ведь обычно рыбные запасы убывают постепенно и монотонно год за годом. Коллапсы ранее происходили с сельдью и анчоусом – короткоцикловыми рыбами, и они восстанавливали самостоятельно запасы. Восстановиться не смог после коллапса атлантический палтус Hippoglossus hippoglossus, когда-то бывший ценным и обильным промысловым видом.

Треска Gadus morhua – хищник с длинным жизненным циклом, и промысел использовал только несколько поколений. Помимо сокращения численности произошли изменения в генетической структуре популяции. Особи трески стали медленнее набирать вес, но убыстрилось их половое созревание, сократился жизненный цикл. Подобные сдвиги характеристик онтогенеза могут описываться расширенным набором параметров вспомогательных уравнений нашей гибридной вычислительной структуры. О скрытых причинах локальной катастрофы специалисты продолжают дискутировать и 29 лет спустя.

7. Анализ вычислительного сценария коллапса биоресурсов. Для математической реализации подобного сценария коллапса из двух этапов мы предлагаем сценарий с двумя трансформациями в динамике итераций. Зависимость должна обладать четырьмя нетривиальными стационарными $\varphi (R_{i}^{*}) = R_{i}^{*}$ состояниями: $R_{1}^{*} < R_{2}^{*} < R_{3}^{*} < R_{4}^{*}$. Первым изменением выполним обратную касательную бифуркацию (итерационный аналог бифуркации “седло-узла”) с редукцией притягивающего состояния равновесия до неустойчивой точки с ее исчезновением. В данном случае редукцию локального аттрактора $R_{4}^{*}$ запишем таким образом, что $\forall {{R}_{0}} > R_{3}^{*}\mathop {\lim }\limits_{n \to \infty } {{\varphi }^{n}}({{R}_{0}}) = R_{4}^{*}$ и ${\text{|}}\varphi {\kern 1pt} '(R_{4}^{*}){\text{|}} < 1$. Редукцией мы называем изменения, когда две точки $R_{4}^{*}$, $R_{3}^{*}$ сливаются в одну $R_{w}^{*}$ неустойчивую $\varphi (R_{4}^{*}) = \varphi (R_{3}^{*}) = R_{w}^{*}$, и далее эта точка $R_{w}^{*}$ исчезает: $\varphi (R_{w}^{*}) < R_{w}^{*}$. Кривая лежит ниже биссектрисы координатного угла: $\varphi (R > {{R}_{{\min }}}) < R$. Второй целенаправленной трансформацией фазового портрета реализуем граничный кризис интервального аттрактора Λ. Все точки Λ заключаются после редукции $R_{4}^{*}$ в интервале между отображениями ${{R}_{{\min }}}$ и ${{R}_{{\max }}}$ экстремумов зависимости $\varphi $ так, что $\Lambda \subset [\varphi ({{R}_{{\min }}}),\varphi ({{R}_{{\max }}})]$.

Интервальный аттрактор Λ возникает после редукции устойчивой точки $R_{4}^{*}$ вместе с неустойчивой $R_{3}^{*}$ в области, которая включает стационарную точку $R_{2}^{*}$ с прообразами, так как это репеллер открытый и справа и слева. Для такого перестроения фазового портрета необходимо как минимум три неустойчивые стационарные точки при сохранении устойчивости нулевого равновесия. Поведение итераций при изменении параметра будет зависеть от того, имеет ли репеллер $R_{1}^{*}$ прообразы справа. Гибридная система дает возможность масштабировать зависимость по оси R и целенаправленно изменять положения экстремумов $\varphi (\lambda S)$ при изменении параметра триггерной функции σ, как показано на рис. 3. Мы увидим в зависимости от параметров $\sigma ,\;{\kern 1pt} \beta $ репеллеры (на графике точки пересечения с биссектрисой координатного угла), изолированные или имеющие точки-прообразы. На рис. 3, а и б показаны формы зависимости $\varphi (\lambda S)$ в инструментальной среде AnyLogic относительно приведенной на графиках биссектрисы координатного угла. Отметим, что λ – это параметр, который может изменять положение экстремумов φ. Такое различие форм у кривых “запас-пополнение” на рис. 3 мы можем получать, изменяя $\sigma $ и воздействие слагаемого $\Psi [S]\,\beta $ в правой части уравнения (4.1).

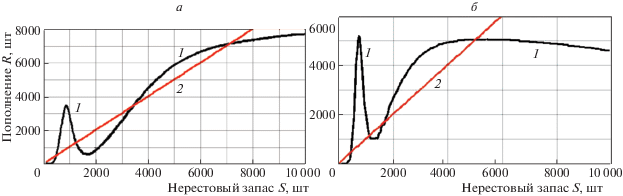
У графиков зависимости на рис. 3 меняется относительное положение репеллеров и экстремумов. На рис. 3, б репеллер $R_{1}^{*}$ изолирован, на рис. 3, а репеллер $R_{1}^{*}$ открытый. Это свойство важно для моделирования экстремальных сценариев, так как точка $R_{1}^{*}$ в модели всегда неустойчива: ${\text{|}}\varphi {\kern 1pt} '(R_{1}^{*}){\text{|}} > 1$. Функция-триггер $\Psi $ не меняет относительное положение четвертого устойчивого равновесия большой численности $R_{4}^{*}$, но действует на положение экстремума $\min \varphi (\lambda S)$ относительно неустойчивого равновесия – репеллера $R_{1}^{*}$. Положение первого репеллера $R_{1}^{*}$ важнее для качественной динамики, чем остальных.

Положим, что изначально в окрестности максимума наша модельная кривая “запас-пополнение” немного превосходит третье равновесие $\varphi (max\varphi (N(0)) \pm \varepsilon ) > R_{3}^{*}$, т.е. $R_{3}^{*}$ получает две прямых точки-прообраза. Если исходное состояние популяции R₀ соответствует диапазону ${{R}_{0}} \in (R_{1}^{*},R_{3}^{*}) \cap \{ {{\varphi }^{{ - n}}}(R_{2}^{*})\} $, то через ряд апериодических флуктуаций траекторией достигается состояние, которому соответствует уровень высокой стабильной численности $R_{4}^{*}$. В сценарии важно множество $\{ {{\varphi }^{{ - n}}}(R_{2}^{*})\} $ – совокупность всегда существующих точек-прообразов у репеллера $R_{2}^{*}$. Все они ни при каких R₀ не притягиваются к аттракторам, но вносят локальные разрывы в его область притяжения.

Зададим в вычислительном эксперименте параметры сценария, где промысловая популяция рыб после нестабильного режима восстановилась до устойчивого равновесия и экологического оптимума. Следовательно, уловы ${{Y}_{n}} = {{R}_{n}}{{q}_{n}}$ нарастают. После оценки позитивного тренда экспертами принимается обоснованное решение увеличить годовую квоту ${{\bar {q}}_{n}}$. Уловы в следующем сезоне демонстрируют исторический максимум, но затем довольно очевидно снижаются. В итерациях запас успешно проходит локальный минимум, не попадая сразу в окрестность критического состояния $R_{1}^{*}$. Промысловые прогнозы гарантированно учли в расчетах высокую эффективность воспроизводства в предыдущие годы. Уловы после спада заметно начинают возвращать былые показатели и нет видимых причин радикально пересматривать долю изъятия ${{\bar {q}}_{n}}$. Такое восстановление обманчиво. В реальности продолжительность роста Y_n связана со случайными факторами.

Величина запаса после интенсификации промысла срывается в апериодический малочисленный режим с непостоянной амплитудой колебаний. В случае запоздалого установления прежней рациональной доли изъятия после колебаний следует то резкое второе падение величины уловов, которое собственно называют “коллапсом”.

На рис. 4 представлен вычислительный сценарий безвозвратного кризиса популяции с промежуточными колебаниями при экспертном управлении интенсивностью промысла. Полагается, что промысел способен полностью освоить выделенную для изъятия квоту вне зависимости от экономических затрат и потери рентабельности рыболовства.

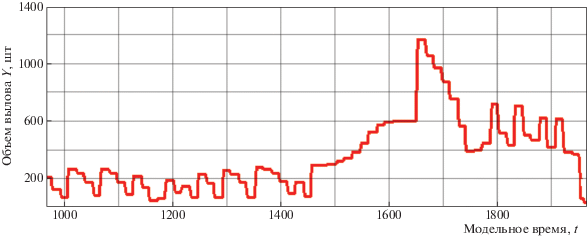
Продолжительность фаз процесса на рис. 4 зависит от изначально повышения ${{\bar {q}}_{n}}$. Для любой популяции ее состояние начнет смещаться влево по кривой $\varphi (\lambda S)$. Сначала сокращение пойдет монотонно, но в случае наличия пороговых эффектов – резко. Пороговые эффекты проявятся не сразу после увеличения квоты. Обратные связи в экосистемах действуют с запаздыванием [49]. Для адекватной оценки реакции популяции на изменение уровня промыслового воздействия необходим больший временной диапазон, чем может позволить себе регулирующая промысел организация для принятия решений. Сценарий показывает, что эксперты при определении промыслового воздействия заведомо не могут обладать релевантной информацией для принятия управленческих решений. Преодолением проблемы может служить использование исторических аналогий, метода составления таблицы описанных характерных ситуаций при различных воздействиях на эксплуатируемые запасы трески Gadus morhua и ответного изменения популяционных характеристик.

Сценарий подтвердил гипотезу, что коллапс запасов крупных долгоживущих рыб –процесс закономерный и растянутый на этапы, которые мы опишем следующим образом.

Этап I. Стабильная популяция после увеличения изъятия попадает в апериодический режим. Наблюдаем режим изменений при меньшей средней за пять лет численности, но с иллюзией активного восстановления. Напомним, что в апериодическом режиме поведение траектории внешне напоминает стохастические колебания из-за сильной зависимости движения траектории ${{\varphi }^{n}}({{R}_{0}})$ от близости к $R_{2}^{*}$ при попадании в окрестность репеллера.

Этап II. Если не введен своевременный мораторий, этап II деградации произойдет решительным образом в среднем через девять модельных сезонов с переходом через порог критического равновесия $R_{1}^{*} > \min \varphi (\lambda S)$. В показанном сценарии доля 0.61 выдерживается, но при q = 0.63 развивается процесс, финал которого именуют коллапсом. Динамике траектории сопутствует особый тип известного свойства чувствительности от выбора начальных точек для хаотических систем. В вычислительных экспериментах время пребывания в режиме флуктуаций будет всегда несколько отличаться.

8. Обсуждение вычислительного сценария коллапса. Гибридная структура позволила в вычислительном эксперименте воспроизвести сценарий коллапса запасов при регулируемом промысле. Коллапс трески у побережья Канады был спровоцирован представлениями о слишком благополучном состоянии биоресурсов [50]. Имело место завышение оценки темпов восполнения запасов трески, которые рассчитывали когортными моделями [51]. Перед критическим порогом эффективность воспроизводства популяции, согласно многим моделям, достаточно высока, что вносит завышенные ожидания в прогнозы. Мораторий на вылов трески ввели с ожиданием вступления в репродуктивный возраст виртуальных “резервных” поколений. Теоретически должны размножаться поколения, не охваченные промыслом, но эти виртуальные резервы не дали эффекта восстановления. Подобным образом с двумя фазами проходят сценарии коллапса разных по жизненному циклу объектов промысла: трески, камчатского краба, палтуса, тунца Thunnus maccoyii и у локальной популяции пеленгаса Азовского моря [52].

Методы оценки запасов и осетровых рыб Каспия, и трески Канады существенно завышали их реальную численность, хотя это были разные методы. Официальный вылов трески остановлен слишком поздно. У осетровых Каспия фаза псевдостабилизации запаса растянулась на 15 лет, с 1977–1992 гг. [53]. Фаза резкого сокращения вылова у двух популяций осетровых рыб Волги аналогична финалу коллапса трески атлантического побережья Канады, из благополучного состояния перешла сразу в этап деградации.

Отличается динамика деградации популяции белуги Huso huso Каспия как длительное и постепенное истощение запасов. В вычислительном эксперименте затянутого коллапса на рис. 5 показана не динамика уловов, как в предыдущем эксперименте, а именно динамика популяционной численности по поколениям. Уровень изъятия в сценарии незначительно превосходит критический. На графике изменения численности поколений рис. 5 гораздо нагляднее проявляется отчетливый апериодический режим флуктуаций со значительной амплитудой величины ежегодного пополнения.

Для осетровых рыб мы можем говорить о моделировании случая продолжительной деградации из трех фаз по сценарию рис. 5. Показатель плодовитости $\lambda $ у осетра и севрюги в 1.4 раза больше, чем задавался для плодовитости трески, что определит такое длительное скользящее сокращение численности вплоть до резкого падения в финале. Сглаживает кривую падения уловов осетровых рыб Каспия искусственный выпуск молоди [54] и предсказуемый эффект убыстрения полового созревания этих рыб [55]. Популяция трески неожиданно медленно для ихтиологов восстанавливает свою численность после коллапса, тогда как осетровым рыбам Каспийского моря угрожает полное исчезновение.

Установленный по экспоненциальному разбеганию ${{R}_{0}},{{R}_{0}} + \varepsilon $ апериодический режим вызван несвязным характером области притяжения аттрактора $R_{4}^{*}$. Область не включает множество не притягивающихся к аттрактору прообразов двух неустойчивых точек: $\Delta = \{ {{\varphi }^{{ - n}}}(R_{2}^{*})\} \cup \{ {{\varphi }^{{ - n}}}(R_{3}^{*})\} $. В случае отрицательного воздействия извне на выживаемость рыб изменится конфигурация стационарных точек $\varphi (R)$, масштабируемая по оси ординат. Для $\varphi (R)$ возможна локальная обратная касательная бифуркация: при слиянии $R_{3}^{*},R_{4}^{*}$ с исчезновением устойчивой стационарной точки $R_{4}^{*}$, при сохранении оставшихся $R_{1}^{*},R_{2}^{*}$. Трансформации вызывают пребывание популяции рыб при меньшей численности запаса S в режиме флуктуаций значительной амплитуды у пополнения. В фазовом пространстве режиму соответствует интервальный аттрактор третьего топологического типа в теореме Дж. Гукэйнхэймeра [45]. Продолжительность колебаний зависит от положения $\varphi $ в минимуме. Если наблюдаем $\varphi ({{R}_{{\min }}}) < R_{1}^{*}$, то реализуются граничный кризис “boundary crisis” интервального аттрактора. Точка $R_{1}^{*}$ – неустойчивое критическое равновесие, если ${{R}_{0}} < R_{1}^{*} - \varepsilon $, то реализуется необратимая деградация ${{R}_{0}} \notin \Delta ,{{\psi }^{n}}({{R}_{0}}) \to 0$. Существует еще внутренний “interior crisis” кризис аттрактора, в нашей модели это явление не возникает.

В сценарии при граничном кризисе аттрактор $\Lambda $ соприкасается с границей своей области притяжения и теряет свойство инвариантности $\varphi (\Lambda ) \in \Lambda $. При $\exists {{R}_{0}} \in \Lambda ,\varphi ({{R}_{0}}) < R_{1}^{*}$ существует непритягивающее множество ${\text{M}} \in {{\Omega }_{1}}$, состоящее из точек ${\rm M},{\rm M} \cap \Delta = \emptyset $, но c хаотическими свойствами. В окрестности множества репеллерных точек $\Delta $ некоторое ограниченное число шагов ${{n}_{\Delta }} < \kappa $ пребывает траектория итераций ${{\varphi }^{n}}({{R}_{0}})$, но хаотизация завершается состоянием ${{\varphi }^{\kappa }}({{R}_{0}}) = 0,$ $\kappa < \infty $. Длительность “деградирующего” переходного режима κ до нулевого значения численности популяции отличается непостоянным значением в вычислительных сценариях из-за чувствительной зависимости от изменения исходного состояния траектории при малых возмущениях: ${{R}_{0}} \pm \varepsilon $.

9. Модификация функции-триггера для модели вспышки вредителя. Концепция методики позволит нам моделировать альтернативную экстремальную ситуацию в жизни популяций. Вспышки численности вредителей – глобальная проблема. Вспышки у насекомых различаются по фазам опасных локальных явлений: от момента запуска, перехода к так называемой эруптивной динамике, выходу на пик и до стадии завершения. Вспышки насекомых – это ярко выраженный переходный режим. Вспышка любых насекомых должна завершаться естественно по внутренним биосистемным причинам.

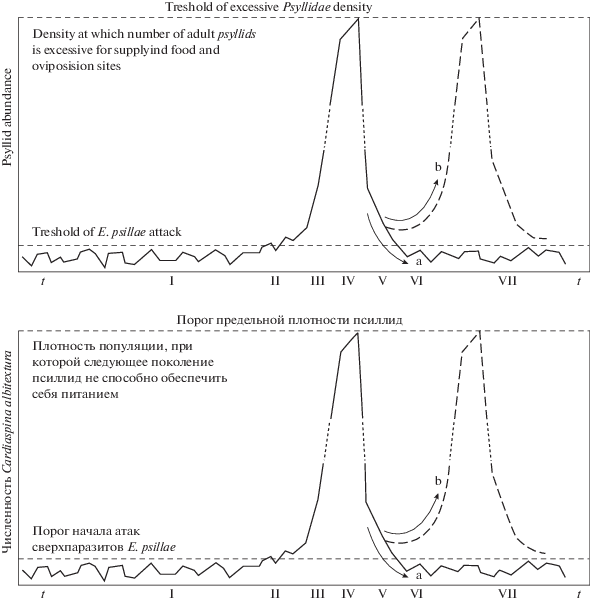
Один из наиболее распространенных сценариев перехода к фазе стремительного роста “вспышке численности” – пороговый. Хрестоматийная ситуация преодоления порога мелкими и малоподвижными насекомыми семейства Psyllidae описана на примере анализа вспышек вредителя эвкалиптовых деревьев в Австралии в работе [56]. На рис. 6 римскими номерами показаны типичные фазы прохождения вспышки: от предпорогового состояния I до полного завершения VII. Данный порог представим математически как неустойчивое равновесие у итераций сложной функциональной зависимости. Проблема в том, что порог должен быть преодолеваем спонтанно. Вспышка на рис. 6 начинается без внешнего воздействия. Вспышка – нечастое экстремальное явление. Непритягивающиеся множества точек-прообразов у неустойчивых стационарных точек делают всю область фрактальным репеллером. Полученный в гибридной модели хаотический репеллер $\Delta $ из-за локально-несвязной границы областей притяжения двух альтернативных аттракторов замечательно преодолевает проблему вычислительного моделирования переходов.

Дополнительно метод с транзитивным хаосом в ограниченном интервале дискретной составляющей времени, числе модельных сезонов u, будет имитировать климатическую волатильность среды размножения насекомых, чувствительных к количеству осадков.

В предложенной ранее нами модели с функцией Ψ есть решение, когда спонтанное преодоление равновесия $R_{3}^{*}$ запускает вспышку вредителя с выходом к устойчивому равновесию большой численности популяции $R_{4}^{*}$. Однако так мы решаем только первую часть проблемы моделирования вспышки – переход к эруптивной фазе под номером III. Такие явления скоро завершаются по двум причинам: экосистема не выдержит подобное состояние долго, лес потеряет листву. Сами личинки “нимфы” псиллид всю листву съесть не в состоянии, но из-за повреждений листьев происходит быстрое распространение фитопатогенных инфекций. Популяция будет быстро уничтожать необходимые ей ресурсы. Скорость распространения псиллид в лесу ограничена, и насекомые сами подвержены инфекциям при большой их скученности на поврежденных растениях.

Нам необходимо описать спонтанное завершение вспышки лесных насекомых. Для описания резкого сокращения выживаемости у питающихся личинок псиллид мы иным образом еще раз модифицируем модель (1.2) нашим универсальным методом:

где параметр ${{с}_{2}} > 1$ характеризует стремительность исчерпания ресурсов, c₁ – масштабирующий коэффициент приближения функции $\Xi (N(\tau ))$ к оси абсцисс. Параметр l варьирует уровень численности, при котором эффект начнет заметно проявлять себя. Мы проведем имплементацию триггерной функции Ξ для стадии развития номер II. Менять значения функция Ξ в расчетах будет тоже при смене кадра. Для насекомых вредителей вторая стадия больше всех требует обилия пищевых ресурсов, потому на максимуме вспышки выживаемость данной стадии из-за (9.1) в расчетах отчетливо сократится:

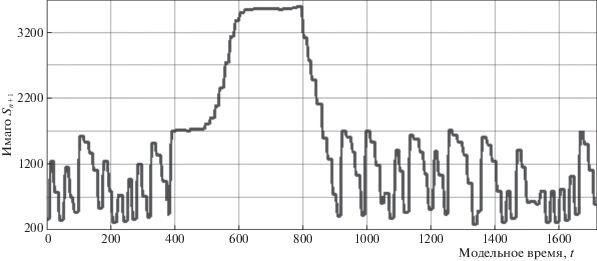
В вычислительном эксперименте модели (1.2), (2.1) с двумя триггерными модификациями (4.1), (4.2) и (9.1), (9.2) мы опишем спонтанный непрогнозируемый переход траектории от хаотической динамики к устойчивому равновесию $R_{4}^{*}$ через порог ${{\varphi }^{u}}(R) > R_{3}^{*},$ $u < \infty $, что составит фазу пика вспышки после промежуточной стабилизации у точки $R_{3}^{*}$. Динамика вспышки с длительным пиком показана в модельном сценарии рис. 7.

Окрестность открытого репеллера $R_{3}^{*}$ служит индикатором начала фазы стремительного увеличения численности. Траектория около $R_{3}^{*}$ в сценарии на рис. 7 находится долго. В эксперименте показано внутренне время вычислительной среды. Число u достаточно для прогнозирования опасных состояний. Порог для запуска вспышки у псиллид создает чрезвычайно интересная система биорегуляторов: хозяин-паразит-сверхпаразит. Осы паразиты второго порядка из многочисленного в Австралии семейства паразитических перепончатокрылых Ichneumonidae не дают быстро размножиться первичным паразитам, которые должны подавлять вредителей эвкалиптового леса. Равновесие при большой численности может только казаться устойчивым. В новом модельном сценарии с Π-образным пиком любое верхнее равновесие будет исчезать из-за действия Ξ, но не сразу, так как репродуктивная активность популяций изменчива, но остается достаточно консервативной характеристикой в масштабе смежных поколений.

В асимптотике нашего сценария траектория вернется к апериодическому движению в интервальном аттракторе – множестве несвязных интервалов, которую составит разность множеств точек $\Phi $ на отрезке между ограничивающими точками-репеллерами:

В полученном сценарии рис. 7 вспышка – это редкое и единичное событие. В реальности старт и завершение вспышек у разных видов весьма разнообразны, нельзя выделить обобщенный единый вариант. В бореальных лесах, где важен фактор зимующего поколения, разрушительные вспышки еловой листовертки или непарного шелкопряда происходят по другому сценарию [57]. Часто вспышки переходят в форму с серией отдельных пиков активности, которые оценивают по площадям пораженного леса. Между соседними пиками вспышек может пройти полтора десятилетия. В фазе VII в работе [56] показан пример вариативности вспышки – скорый повторный пик насекомых.

Заключение. Оригинальная методика вычислительного моделирования была продемонстрирована на примере двух практически важных процессов в водных и лесных живых системах. Мы получили вычислительную структуру, которую правильно называть динамической системой с переопределяемым оператором эволюции $\varphi $. Моделируемые нами ситуации относятся к экстремальной и переходной динамике экосистем. Показано, что нелинейные экологические эффекты и фазы вспышки могут быть математически определены рядом бифуркаций фазового портрета у функциональных итераций. Для многих видов насекомых и рыб мы способны численно рассчитывать именно колебания ювенильной выживаемости, но оценивать их состояние актуально по половозрелому пополнению и исследовать эффективность формирования новых поколений популяций.

В составе нашей методики есть следующие шесть принципов построения структуры и способов анализа поведения популяционных моделей в пространстве параметров.

1. Многокомпонентное время, которое позволяет выделять события в непрерывных интервалах – кадрах времени. С формой (1.1) удобно вводить компоненту событийности при управлении изменением непрерывного процесса, управлять уровнем эксплуатации.

2. Использовать в расчетах вспомогательные показатели при формировании предикатов для переопределения или остановки действия тех основных уравнений, которые описывают именно численность. Параметры этих уравнений не изменяем.

3. Внедрение функций триггерного действия. Такие функции Ξ и Ψ точечно опишут пороговые изменения в непрерывных процессах в узких значениях численности.

4. Внешние факторы изменчивой среды при необходимости учитывать опосредованно во вспомогательных уравнениях.

5. Анализ дискретной составляющей траектории для описания моделируемых экологических явлений проводим с использованием всех обоснованных метаморфозов поведения функциональных итераций. Инструменты предоставят нам фундаментальные теоремы нелинейной динамики [58]. Необходимо учитывать в этом пункте нашей методики, что не все нелинейные эффекты динамических систем получают сущностную биологическую интерпретацию [59]. Некоторые эффекты излишни в моделях биосистем.

6. Исследование нескольких вариантов моделей с управлением мы проводим как сценарное. Включаем в эксперименты логику принятия решений экспертами при внешнем воздействии на биоресурсы, например при выработке новой политики регуляции квот при ведении промысла или установления ограничительных мер во время эпидемий.

В практической части моделирования перспективен сравнительный анализ сценариев и поиск общности у динамики изменений для кардинально различных популяций таких, как треска у берегов Канады, осетровые рыбы Каспия или псиллиды в лесах Австралии. В отличие от коллапса трески, принять необходимые административные решения для предотвращения деградации осетровых Каспия времени было достаточно.

Получена модель вспышки численности, которая завершается самопроизвольно. В данном методе нам не нужно включать изменение параметров из внешних факторов, вызывающее остановку репродуктивной активности. Функции триггерного действия с ограниченными пределами позволят целенаправленно проводить бифуркации, например исчезновение избыточной точки-равновесия. Перестроения правой части происходят предикативно. Предикат гибридного автомата может стать истинным при выполнении одного или нескольких или хотя бы одного из нескольких условий. Предикаты применены к анализу ситуаций коллапса биоресурсов – быстрой и неожиданной деградации запасов рыб, которая не сменяется восстановлением вопреки прогнозам и расчетам специалистов. Регулируемый по принципам оптимальности промысел, как показал наш сценарий, не предотвращает развитие коллапса запасов. Регуляция изъятия с введением квот принципиально не будет безопасной. Превышение на Δq = 4.5% от плановой квоты q кажется экспертам не критичной, однако в прогнозах возврата эти 4.5% запаса ими учтены как размножающиеся особи. От погибших рыб ожидается в прогнозах пополнение, потому ошибка в оценках будет быстро нарастать. Подобная нарастающая ошибка в оценках запаса отмечалась в [60] для краба Paralithodes camtschaticus у берегов Аляски. Более рациональным видится жесткое ограничение технических возможностей промысла. Перспективен лимит размеров орудий лова, запасов горючего на борту или времени работы судов в море. Средства удаленного мониторинга позволяют контролировать суда.

Мы использовали непрерывно-событийное представление времени, где за рассчитанным i-м событием следует перестроение правой части, потому говорим о предикативно-переопределяемых вычислительных гибридных структурах. Подбор регуляторов для базовых уравнений может быть адаптирован к широкому классу моделей с управлением [61], использующих решения дифференциальных уравнений последовательно на наборе временных интервалов или простые функции переходов в [62].

Модель легко модифицировать при расширении числа вспомогательных уравнений уже известными моделями, так уравнение (2.5) изначально предлагалось автором для описания длительных циклов у вредителя леса бабочки-листовертки Choristoneura freemani в [63], которая в резонансных колебаниях вызывает масштабные поражения леса. Потом самостоятельная модель цикличности включена в состав гибридной структуры.

При модификации гибридных моделей можно включать другие поправки из числа внешних факторов во вспомогательные уравнения регуляции воспроизводства биоресурсов. Перспективно в модельных сценариях анализировать несколько достаточно распространенных и опасных экологических ситуаций антропогенного изменения среды [64]. Например, в предикативных структурах удобно учитывать влияние явления эвтофирования водоемов на выживаемость молоди рыб, важного в ситуации ограничения доступа кислорода к кладкам икры [65]. Интересно оценивать скорость восстановления биологической продуктивности рек и озер соответственно темпам специальной биоремедиации водоемов после их загрязнения углеводородами [66]. Наиболее актуальная из возможных биологических областей применения предикативно-переопределяемых систем в настоящее время – моделирование активности разнотипных клеток иммунной системы, вырабатывающих ответ на неизвестную инфекцию. Опасные осложнения COVID-19 при пандемии нового вируса вызваны именно избыточной каскадной реакцией клеток иммунитета – цитокиновым штормом [67]. Гиперцитокинемия провоцирует стремительный респираторный дистресс-синдром ARDS [68], когда легкие быстро теряют функциональность. Эпидемия COVID-19 в разных странах идет по различным сценариям. Обновляемая статистика заражений подтверждает, что базовые SIRS-модели эпидемий [69] с их колебательными режимами не обладают адекватностью для реальных ситуаций.

В одной статье нам удалось объединить методологические проблемы моделирования двух принципиально разных биологических ситуаций. Массовое размножение и резкое падение эффективности воспроизводства выражены как последствия от действия пороговых механизмов регуляции. Анализ двух хрестоматийных сценариев вспышки и коллапса подтвердил гипотезу, что очень разные экстремальные ситуации у видов из далеких друг от друга таксономических групп имеют общность с точки зрения нелинейной динамики и выражаются сходной последовательностью бифуркаций.