Известия РАН. Теория и системы управления, 2021, № 1, стр. 79-90
МЕТОД СТОХАСТИЧЕСКОГО ГРАДИЕНТА С ШАГОМ БАРЗИЛАЙ–БОРВЕЙНА ДЛЯ БЕЗУСЛОВНОЙ НЕЛИНЕЙНОЙ ОПТИМИЗАЦИИ
Л. Ванг a, *, Х. Ву a, И. А. Матвеев b, **
a Нанкинский ун-т аэронавтики и космонавтики
Нанкин, КНР
b Федеральный исследовательский центр “Информатика и управление” РАН
Москва, Россия
* E-mail: wlpmath@nuaa.edu.cn
** E-mail: matveev@ccas.ru
Поступила в редакцию 09.06.2020
После доработки 17.06.2020
Принята к публикации 27.07.2020
Аннотация
Применение алгоритмов стохастического градиента для нелинейной оптимизации вызывает значительный интерес, особенно для случая большой размерности. При этом для скорости сходимости решающее значение имеет выбор величины шага. Предлагаются два новых алгоритма стохастического градиента, использующие улучшенную формулу величины шага Барзилай–Борвейна. Анализ сходимости показывает, что эти алгоритмы дают линейную сходимость по вероятности для сильно выпуклой целевой функции. Вычислительные эксперименты подтверждают, что два предложенных алгоритма имеют лучшие характеристики, чем двухточечные градиентные алгоритмы, и известные методы стохастического градиента.
Введение. Анализ и обработка больших данных применяются сейчас во многих областях: в биостатистике, распознавании образов, финансовом анализе и т.д. Наиболее часто используемые методы нелинейной обработки данных – минимизация ошибок обучения или подбора, т.е. минимизации эмпирического риска [1]. Потребность в создании новых методов обработки диктуется быстрым ростом объема данных. Традиционные алгоритмы оптимизации требуют большого количества вычислений относительно объема данных и это становится неприемлемым. Использование случайных подвыборок данных, а не полной информации в вычислениях – эффективный подход к уменьшению размерности. Здесь возникает задача получения хорошего приближения полных данных.
Метод стохастического градиента в безусловной минимизации восходит к методу стохастической аппроксимации, предложенному Роббинсом и Монро [2]. Более современное название – стохастический градиентный спуск (СГС, stochastic gradient descent, SGD). Формула итераций:
где ${{\vec {x}}_{k}}$ – текущая точка итерации, ${{\vec {g}}_{k}}$ – стохастический градиент, являющийся несмещенной оценкой полного градиента $\nabla f({{\vec {x}}_{k}})$, ηk – величина шага. Метод СГС прост в реализации. При итерациях не требуется точного расчета полного градиента или использования всей информации о выборке. Вместо этого полный градиент оценивается по случайной подвыборке. СГС повышает скорость сходимости относительно объема вычислений по сравнению с традиционными алгоритмами оптимизации, особенно при решении больших задач безусловной минимизации. По этой причине СГС привлекал многих исследователей [3–6]. Однако в исходной постановке метод СГС плохо приспособлен к решению больших задач. Его недостатками являются случайный характер, порождающий дисперсию и увеличение гарантированного времени сходимости, и большее число требуемых шагов (хотя каждый из них простой). В [7] предложен метод стохастического среднего градиента (ССГ, stochastic average gradient, SAG), чтобы уменьшить разброс сходимости. В [8] представлен подход стохастического двойного координатного подъема (СДКП, stochastic dual coordinate ascent, SDCA). На самом деле, оба метода должны хранить градиенты всей выборки. Далее, в [9] предложен метод уменьшения дисперсии стохастического градиента (УДСГ, stochastic variance reduced gradient, SVRG), ускоряющий сходимость стохастического метода первого порядка путем выбора градиента с минимальной оценкой дисперсии. Доказано, что он имеет ту же скорость сходимости, что и СДКП и ССГ, но ему не нужно хранить полный набор градиентов, что очень полезно для больших задач.В методах градиентного спуска необходимо задавать величину шага. Наиболее распространены три способа: постепенно уменьшать шаг, дополнительно к градиенту использовать производные второго порядка, задавать фиксированный шаг вручную (эвристически извне). Все эти способы не являются оптимальными. В 1988 г. Barzilai и Borwein [10] предложили определение величины шага итерации по предыстории из двух точек (ББ). Метод ББ не использует вторые производные (не вычисляет обратный гессиан), но достигает впечатляющих результатов. Метод ББ применен к СГС и УДСГ, доказана линейная сходимость УДСГ-ББ для сильно выпуклой целевой функции [11]. Из-за эффективности метода ББ он весьма популярен и на его основе предложены различные варианты расчетов [12–14]. В [13] метод ББ рассмотрен с точки зрения интерполяции, предложены два модифицированных двухточечных алгоритма. Также экспериментально показано, эти два алгоритма быстрее сходятся в традиционных задачах оптимизации, чем исходный ББ.
Этот подход к решению задач стохастического программирования взят за основу в настоящей статье. Ожидается, что введение модификации [13] в метод УДСГ позволит далее улучшить сходимость за счет небольших дополнительных объема памяти и вычислений.
Остальная часть этой статьи организована следующим образом. В разд. 2 кратко рассмотены два улучшенных метода ББ определения шага, предложенных в [13]. Два новых стохастических алгоритма приведены в разд. 3. В разд. 4 представлен анализ сходимости двух новых алгоритмов. Численные эксперименты описаны в разд. 5, выводы – в разд. 6.
1. Алгоритмы УДСГ и ББ. Машинное обучение можно рассматривать как построение нелинейной системы, минимизирующей ошибку на некоторой обучающей выборке (минимизация эмпирического риска). Формулируя как задачу безусловной оптимизации, можно записать $f(\vec {x}) \to min$, где
Здесь n – число объектов обучающей выборки, ${{\phi }_{i}}:{{\mathbb{R}}^{d}} \to \mathbb{R}$ – функция потерь для i-го объекта. Современные задачи характеризуются большим числом объектов n, равно как большой размерностью признакового пространства d. Модель (1.1) широко используется для решения задач классификации, регрессии и кластеризации в области машинного обучения [15].
Для решения задачи (1.1) в [9] предложен метод стохастического уменьшения дисперсии градиента (УДСГ), показанный в алгоритме 1.
Алгоритм 1. Алгоритм УДСГ.
Вход: частота обновления m, начальная точка ${{x}_{0}}$, величина шага $\eta $.
Шаг 1. Для $k$ = 0, 1, …
Шаг 2: $\vec {x} = {{\vec {x}}_{k}}$.
Шаг 3. Вычислить $\nabla f(\vec {x})$, согласно (1.1).
Шаг 4: ${{\tilde {x}}_{0}} = \vec {x}$.
Шаг 5. Для $t$ = 0, …, $m - 1$.
Шаг 6. Случайно выбрать ${{i}_{t}} \in \{ 1, \ldots ,n\} $.
Шаг 7: ${{\tilde {x}}_{{t + 1}}} = {{\tilde {x}}_{t}} - \eta \left( {\nabla {{\phi }_{{{{i}_{t}}}}}(\mathop {\tilde {x}}\nolimits_t ) - \nabla {{\phi }_{{{{i}_{t}}}}}(\vec {x}) + \nabla f(\vec {x})} \right)$.
Шаг 8. Конец цикла по $t$.
Шаг 9. Вариант I: ${{\vec {x}}_{{k + 1}}} = {{\tilde {x}}_{m}}$.
Шаг 10. Вариант II: ${{\vec {x}}_{{k + 1}}} = {{\tilde {x}}_{t}}$ для случайного $t \in \{ 0, \ldots ,m - 1\} $.
Шаг 11. Конец цикла по k.
Однако в [9] не дан конкретный метод выбора величины шага η. В варианте I скорость сходимости УДСГ очень чувствительна к выбору η, неверный выбор может привести к неэффективности или даже отсутствию сходимости. Могут применяться различные способы вычисления размера шага – наискорейший спуск, Барзилай–Борвейн [10] и т.д. Формула итерации
где ${{H}_{k}} = {{\eta }_{k}}I$. Обозначим ${{\vec {s}}_{{k - 1}}} = {{\vec {x}}_{k}} - {{\vec {x}}_{{k - 1}}}$ и ${{\vec {y}}_{{k - 1}}} = \nabla f({{\vec {x}}_{k}}) - \nabla f({{\vec {x}}_{{k - 1}}})$. В квазиньютоновских методах итерация задается как ${{\vec {x}}_{{k + 1}}} = {{\vec {x}}_{k}} - B_{k}^{{ - 1}}\nabla f({{\vec {x}}_{k}})$, где матрица $B_{k}^{{ - 1}}$ удовлетворяет условиюШаг ББ вычисляется как
(1.3)
${{\eta }_{k}} = \frac{{{\text{||}}{{{\vec {s}}}_{{k - 1}}}{\text{||}}_{2}^{2}}}{{\vec {s}_{{k - 1}}^{{{{{\vec {y}}}_{{k - 1}}}}}.}}$В [11] шаг ББ используется в методах СГС и УДСГ, полученные методы назовем СГС-ББ и УДСГ-ББ.
В [13] шаг ББ рассмотрен с точки зрения интерполяции и предложены два улучшенных метода расчета его величины. Обозначим ${{t}_{k}} = \eta _{k}^{{ - 1}}$. В окрестности точки ${{\vec {x}}_{k}}$ построим две модели целевой функции $f({{\vec {x}}_{k}} + \theta {{\vec {s}}_{{k - 1}}})$. Квадратичная модель
(1.4)
${{q}_{k}}(\theta ) = {{f}_{k}} + \theta {{\nabla }^{{\text{T}}}}f({{\vec {x}}_{k}}){{\vec {s}}_{{k - 1}}} + \frac{1}{2}{{t}_{k}}{{\theta }^{2}}{\text{||}}{{\vec {s}}_{{k - 1}}}{\text{||}}_{2}^{2},$(1.5)
${{\eta }_{k}} = \frac{{{\text{||}}{{{\vec {s}}}_{{k - 1}}}{\text{||}}_{2}^{2}}}{{2({{f}_{{k - 1}}} - {{f}_{k}} + {{\nabla }^{{\text{T}}}}f({{{\vec {x}}}_{k}}){{{\vec {s}}}_{{k - 1}}})}}.$Коническая модель
(1.6)
${{q}_{k}}(\theta ) = {{f}_{k}} + \theta {{\nabla }^{{\text{T}}}}f({{\vec {x}}_{k}}){{\vec {s}}_{{k - 1}}} + \frac{1}{2}{{t}_{k}}{{\theta }^{2}}{\text{||}}{{\vec {s}}_{{k - 1}}}{\text{||}}_{2}^{2} + {{\xi }_{k}}{{\theta }^{3}}$(1.7)
${{\eta }_{k}} = \frac{{{\text{||}}{{{\vec {s}}}_{{k - 1}}}{\text{||}}_{2}^{2}}}{{6({{f}_{{k - 1}}} - {{f}_{k}}) + 4{{\nabla }^{{\text{T}}}}f({{{\vec {x}}}_{k}}){{{\vec {s}}}_{{k - 1}}} + 2{{\nabla }^{{\text{T}}}}f({{{\vec {x}}}_{{k - 1}}}){{{\vec {s}}}_{{k - 1}}}}}.$Величины шагов, рассчитанные по уравнениям (1.5) и (1.7), не только используют градиент текущей и предыдущей точек итерации, но также задействуют значения самой функции. В [13] алгоритмы, индуцируемые вычислением шага, согласно (1.5) и (1.7), даны как алгоритмы 3.1 и 3.2 соответственно. Численные результаты [13] показывают, что эти два алгоритма более эффективны, чем алгоритм градиента с шагом ББ (1.3). Однако алгоритмы [13] используют значения функций и информацию о градиенте всех данных, которые требуют большого объема вычислений.
Возникает вопрос о возможности объединения двух подходов, стохастического градиента и шага ББ, и свойствах полученного метода.
2. Модифицированный алгоритм УДСГ. Внедрим формулы (1.5) и (1.7) расчета величины шага по предыстории в алгоритм УДСГ. Итерация этого метода (алгоритм 1)
(2.1)
${{\tilde {x}}_{{t + 1}}} = {{\tilde {x}}_{t}} - \eta \left( {\nabla {{f}_{{{{i}_{t}}}}}\left( {{{{\tilde {x}}}_{t}}} \right) - \nabla {{f}_{{{{i}_{t}}}}}(\vec {x}) + \nabla f(\vec {x})} \right).$Здесь используется стохастический градиент $\nabla {{f}_{{{{i}_{t}}}}}$ вместо полного градиента $\nabla f$, что уменьшает сложность вычислений. Однако при этом размер шага $\eta $ фиксирован. В [9] подчеркивается, что УДСГ проводит внешний цикл $m$ раз (используя одну несмещенную оценку полного градиента) повторяя шаги (2.1). По аналогии с (1.5) и (1.7) предлагаются две версии шага:
(2.2)
$\eta _{k}^{{(1)}} = \frac{{{\text{||}}{{{\vec {x}}}_{k}} - {{{\vec {x}}}_{{k - 1}}}{\text{||}}_{2}^{2}}}{{m[2({{f}_{{k - 1}}} - {{f}_{k}} + {{\nabla }^{{\text{T}}}}f({{{\vec {x}}}_{k}})({{{\vec {x}}}_{k}} - {{{\vec {x}}}_{{k - 1}}}))]}},$(2.3)
$\eta _{k}^{{(2)}} = \frac{{{\text{||}}{{{\vec {x}}}_{k}} - {{{\vec {x}}}_{{k - 1}}}{\text{||}}_{2}^{2}}}{{m[6({{f}_{{k - 1}}} - {{f}_{k}}) + 4{{\nabla }^{{\text{T}}}}f({{{\vec {x}}}_{k}})({{{\vec {x}}}_{k}} - {{{\vec {x}}}_{{k - 1}}}) + 2{{\nabla }^{{\text{T}}}}f({{{\vec {x}}}_{{k - 1}}})({{{\vec {x}}}_{k}} - {{{\vec {x}}}_{{k - 1}}})]}}.$Таким образом получаются два новых алгоритма стохастического градиента: алгоритмы 2 и 3.
Алгоритм 2. Стохастический градиентный метод с шагом ББ (2.2).
Вход: частота обновления m, начальная точка x0, начальная величина шага η0.
Шаг 1. Для $k$ = 0, 1, …
Шаг 2. Вычислить $f({{\vec {x}}_{k}})$ и $\nabla f({{\vec {x}}_{k}})$, согласно (1.1).
Шаг 3. Если $k > 0$, то исполнять до шага 5.
Шаг 4. Вычислить ${{\eta }_{k}}$, согласно (2.2).
Шаг 5. Конец если.
Шаг 6: ${{\tilde {x}}_{0}} = {{x}_{k}}$.
Шаг 7. Для $t$ = 0, …, m – 1.
Шаг 8. Случайно выбрать ${{i}_{t}} \in \{ 1,...,n\} $.
Шаг 9. Вычислить ${{\tilde {x}}_{{t + 1}}}$, согласно (2.1).
Шаг 10. Конец цикла по $t$.
Шаг 11: ${{x}_{{k + 1}}} = {{\tilde {x}}_{m}}$.
Шаг 12. Конец цикла по $k$.
Алгоритм 3. Стохастический градиентный метод с шагом ББ (2.3).
Вход: частота обновления m, начальная точка x0, начальная величина шага ${{\eta }_{0}}$, константы $\varepsilon \in (0,1)$, $\delta \in \left[ {\frac{\varepsilon }{m},\frac{1}{{m\varepsilon }}} \right]$.
Шаг 1. Для $k$ = 0, 1, …
Шаг 2. Вычислить $f({{\vec {x}}_{k}})$ и $\nabla f({{\vec {x}}_{k}})$, согласно (1.1).
Шаг 3. Если $k > 0$, то исполнять до шага 8.
Шаг 4. Вычислить ${{\eta }_{k}}$, согласно (2.3).
Шаг 5. Если ${{\eta }_{k}} < \tfrac{\varepsilon }{m}$ или ${{\eta }_{k}} > \tfrac{1}{{m\varepsilon }}$, то исполнять до шага 7.
Шаг 6: ${{\eta }_{k}} = \delta $.
Шаг 7. Конец если.
Шаг 8. Конец если.
Шаг 9: ${{\tilde {x}}_{0}} = {{x}_{k}}$.
Шаг 10. Для $t$ = 0, …, $m - 1$.
Шаг 11. Случайно выбрать ${{i}_{t}} \in \{ 1,...,n\} $.
Шаг 12. Вычислить ${{\tilde {x}}_{{t + 1}}}$, согласно (2.1).
Шаг 13. Конец цикла по t.
Шаг 14: ${{x}_{{k + 1}}} = {{\tilde {x}}_{m}}$.
Шаг 15. Конец цикла по k.
Чтобы гарантировать сходимость двух новых алгоритмов, составим необходимое ограничение на величины шагов (2.2) и (2.3). В [11] применяется ограничение
(2.4)
${{\eta }_{k}} \in \left[ {min\left\{ {\varepsilon ,\frac{1}{\delta }} \right\};min\left\{ {\frac{1}{\varepsilon },\frac{1}{\delta }} \right\}} \right],$Эти границы получены и применяются для анализа сходимости в следующем разделе. Алгоритмы 2 и 3 итеративно обновляют размеры шагов при вычислении градиента с уменьшенной случайной дисперсией, что является более гибким, чем УДСГ [9] с фиксированным шагом. Стохастическая итерация и улучшенные величины шагов в алгоритмах 2 и 3 не только экономят много вычислений на каждом шаге, но и сходятся быстрее.
3. Анализ сходимости. В этом разделе докажем, что алгоритмы 2 и 3 линейно сходятся для сильно выпуклых функций. Анализ сходимости основан на следующих предположениях и леммах, которые также используются в [9, 11, 13, 16 ].
Допущение 1. Целевая функция $f(\vec {x})$ сильно выпукла, т.е. существует такая постоянная μ > 0, что для любого $\vec {x},\vec {y} \in {{\mathbb{R}}^{d}}$ выполняется
(3.1)
$f(\vec {y}) \geqslant f(\vec {x}) + {{\nabla }^{{\text{T}}}}f(\vec {x})(\vec {y} - \vec {x}) + \frac{\mu }{2}{\text{||}}\vec {x} - \vec {y}{\text{||}}_{2}^{2}.$Допущение 2. Градиент $\nabla {{\phi }_{i}}(\vec {x})$ каждой компоненты целевой функции непрерывен по Липшицу, т.е. существует такая постоянная L > 0, что для любого $\vec {x},\vec {y} \in {{\mathbb{R}}^{d}}$, верно
Следовательно, $\nabla f(\vec {x})$ также липшиц-непрерывна, т.е.
Лемма 1 [11]. Целевая функция $f(\vec {x})$ удовлетворяет допущениям 1 и 2. Пусть $\vec {x}{\kern 1pt} * = arg\mathop {min}\limits_{\vec {x}} f(\vec {x})$ и
(3.2)
${{\alpha }_{k}} = \mathop {\left( {1 - 2{{\eta }_{k}}\mu (1 - {{\eta }_{k}}L)} \right)}\nolimits^m + \frac{{4{{\eta }_{k}}{{L}^{2}}}}{{\mu (1 - {{\eta }_{k}}L)}},$Лемма 2 [16]. Если f выпукла и ее градиент $\nabla f$ непрерывен по Липшицу, то для любых $\vec {x},\vec {y} \in {{\mathbb{R}}^{d}}$ имеем
Доказательства лемм 1 и 2 можно найти в [11, 16] соответственно. Теперь представим теоремы 1 и 2 о линейной сходимости алгоритмов 2 и 3 по вероятности.
Обозначим $\vec {x}{\kern 1pt} * = arg\mathop {min}\limits_{\vec {x}} f(\vec {x})$ и $\tau = \left( {1 - exp( - \mu {\text{/}}2L)} \right){\text{/}}2$.
Теорема 1. Пусть целевая функция $f(\vec {x})$ удовлетворяет допущениям 1 и 2. Пусть $\{ {{\vec {x}}_{k}}\} _{{k = 1}}^{\infty }$ – последовательность итераций, сгенерированная алгоритмом 2. Если частота обновления $m$ в алгоритме 2 удовлетворяет
(3.3)
$\mathbb{E}{\text{||}}{{\vec {x}}_{k}} - \vec {x}{\kern 1pt} *{\text{||}}_{2}^{2} < {{(1 - \tau )}^{k}}{\text{||}}{{\vec {x}}_{0}} - \vec {x}{\kern 1pt} *{\text{||}}_{2}^{2}.$Доказательство. Поскольку $f(\vec {x})$ удовлетворяет 1 и 2, то
(3.4)
$2({{f}_{{k - 1}}} - {{f}_{k}} + {{\nabla }^{{\text{T}}}}f({{\vec {x}}_{k}})({{\vec {x}}_{k}} - {{\vec {x}}_{{k - 1}}})) \geqslant \mu {\text{||}}{{\vec {x}}_{k}} - {{\vec {x}}_{{k - 1}}}{\text{||}}_{2}^{2}.$(3.5)
$\begin{gathered} 2({{f}_{{k - 1}}} - {{f}_{k}} + {{\nabla }^{{\text{T}}}}f({{{\vec {x}}}_{k}})({{{\vec {x}}}_{k}} - {{{\vec {x}}}_{{k - 1}}})) \leqslant \\ \, \leqslant 2[ - {{\nabla }^{{\text{T}}}}f({{{\vec {x}}}_{{k - 1}}})({{{\vec {x}}}_{k}} - {{{\vec {x}}}_{{k - 1}}}) - \frac{\mu }{2}{\text{||}}{{{\vec {x}}}_{k}} - {{{\vec {x}}}_{{k - 1}}}{\text{||}}_{2}^{2} + {{\nabla }^{{\text{T}}}}f({{{\vec {x}}}_{k}})({{{\vec {x}}}_{k}} - {{{\vec {x}}}_{{k - 1}}})] \leqslant \\ \, \leqslant 2[{{\left( {\nabla f({{{\vec {x}}}_{k}}) - \nabla f({{{\vec {x}}}_{{k - 1}}})} \right)}^{{\text{T}}}}({{{\vec {x}}}_{k}} - {{{\vec {x}}}_{{k - 1}}})] \leqslant 2L{\text{||}}{{{\vec {x}}}_{k}} - {{{\vec {x}}}_{{k - 1}}}{\text{||}}_{2}^{2}. \\ \end{gathered} $Тогда неравенства (3.4) и (3.5) ограничивают размер шага ηk (см. уравнение (2.2)) в алгоритме 2 следующим образом:
На основании определения αk в (3.2), имеем
(3.6)
$\begin{gathered} {{\alpha }_{k}} \leqslant \mathop {\left( {1 - 2\frac{\mu }{{2mL}}\left( {1 - \frac{L}{{m\mu }}} \right)} \right)}\nolimits^m + \frac{{4{{L}^{2}}}}{{m{{\mu }^{2}}\left( {1 - L{\text{/}}(m\mu )} \right)}} \leqslant exp\left\{ { - \frac{\mu }{{mL}}\left( {1 - \frac{L}{{m\mu }}} \right)m} \right\} + \frac{{4{{L}^{2}}}}{{m{{\mu }^{2}} - \mu L}} \leqslant \\ \, \leqslant exp\left\{ { - \frac{\mu }{L} + \frac{1}{m}} \right\} + \frac{{4{{L}^{2}}}}{{m{{\mu }^{2}} - \mu L}} \leqslant exp\left\{ {ln(1 - 2\tau )} \right\} + \frac{{4{{L}^{2}}}}{{4{{L}^{2}}{\text{/}}\tau + \mu L - \mu L}} = 1 - 2\tau + \tau = 1 - \tau . \\ \end{gathered} $Согласно лемме 15 и уравнению (3.6), можно получить формулу (3.3), которая завершает доказательство теоремы 1.
Очевидно, что $\tau \in (0,0.5)$, поэтому сходимость точек итерации, генерируемых алгоритма 2, непосредственно следует из теоремы 1.
Теорема 2. Предположим, что целевая функция $f(\vec {x})$ удовлетворяет допущениям 1 и 2. Обозначим $\vec {x}{\kern 1pt} * = arg\mathop {min}\limits_{\vec {x}} f(\vec {x})$ и $\tau = \left( {1 - exp( - \mu {\text{/}}2L)} \right){\text{/}}2$. Если частота обновления m в алгоритме 3 удовлетворяет
(3.7)
$\mathbb{E}{\text{||}}{{\vec {x}}_{k}} - \vec {x}{\kern 1pt} *{\text{||}}_{2}^{2} < {{(1 - \tau )}^{k}}{\text{||}}{{\vec {x}}_{0}} - \vec {x}{\kern 1pt} *{\text{||}}_{2}^{2}.$Доказательство. Поскольку $f(\vec {x})$ сильно выпуклая, уравнение (3.1) влечет
Согласно лемме 2, получаем
На основании (2.7), откуда ${{\eta }_{k}} \leqslant 1{\text{/}}(m\varepsilon )$, получаем
Согласно определению αk в лемме 1, имеем
Таким образом, уравнение (3.7) легко выводится из леммы 1. Поскольку $\tau \in (0,0.5)$ это гарантирует сходимость $\{ {{\vec {x}}_{k}}\} _{{k = 1}}^{\infty }$ по уравнению (1.2).
4. Численные эксперименты. В этом разделе представлены экспериментальные результаты алгоритмов 2 и 3 для больших данных, подтверждающие вычислительную эффективность двух модифицированных алгоритмов. Для того, чтобы продемонстрировать преимущество адаптивных величин шагов (2.2) и (2.3) над фиксированным шагом, сравнены алгоритмы 2 и 3 с алгоритмами нестохастической оптимизации, такими, как двухточечные алгоритмы 3.1 и 3.2 в [13]. Чтобы продемонстрировать численный эффект модифицированного метода в алгоритмах 2 и 3, они сравниваются также с другими алгоритмами стохастической оптимизации, а именно методами УДСГ [9] и УДСГ-ББ [11]. Модифицированные алгоритмы реализованы для решения стандартной тестовой задачи машинного обучения – логистической регрессии с регуляризацией l2-нормы, т.е.
(4.1)
$f(\vec {x}) = \frac{1}{n}\sum\limits_{i = 1}^n \,ln[1 + exp( - {{b}_{i}}\vec {a}_{i}^{{\text{T}}}\vec {x})] + \frac{\lambda }{2}{\text{||}}\vec {x}{\text{||}} \to min,$Алгоритмы 2 и 3 применяются к трем стандартным наборам тестовых данных. Эти наборы получены с веб-страницы LIBSVM [17]. Таблица 1 содержит информацию об этих наборах данных.
Таблица 1.
Описание наборов данных
| Название набора | Количество объектов | Количество признаков | λ |
|---|---|---|---|
| a8a | 22 696 | 123 | 10–2 |
| w8a | 49 749 | 300 | 10–4 |
| ijcnn1 | 49 990 | 22 | 10–4 |
4.1. Численные результаты на стандартной задаче. Здесь приведено сравнение алгоритмов 10 и 10 с двухточечными (алгоритмы 3.1 и 3.2 в [13]) на наборах данных a8a, w8a. Как предлагается в [9], установлено значение m = 2n. Четыре различных начальных размера шага ${{\eta }_{0}} = 1,0.1,0.01$, 0.001 выбраны для всех четырех участвующих с сравнении алгоритмов. Условие завершения: ${\text{||}}\nabla f({{x}_{k}}){\text{||}} < {{10}^{{ - 6}}}$. В табл. 2 и 3 приведено процессорное время (в секундах). Видно, что алгоритмы 2 и 3 не чувствительны к начальному размеру шага η0. Алгоритмы 2 и 3 потребляют меньше процессорного времени, чем нестохастические аналоги [13] для всех трех наборов данных. Заметно, что для более высокой размерности и количества объектов разница во времени исполнения больше, что отчасти подтверждает тезис о возрастании преимущества стохастрического подхода по мере роста количества обрабатываемых данных.
Таблица 2.
Время исполнения на наборе a8a
| Величина η0 | Алгоритм 3.1 | Алгоритм 3.2 | Алгоритм 2 | Алгоритм 3 |
|---|---|---|---|---|
| 1 | 69.31 | 69.62 | 47.51 | 41.51 |
| 0.1 | 62.92 | 62.53 | 44.13 | 38.59 |
| 0.01 | 60.46 | 59.30 | 43.98 | 39.18 |
| 0.001 | 60.64 | 59.84 | 41.39 | 37.75 |
Таблица 3.
Время исполнения на наборе w8a
| Величина η0 | Алгоритм 3.1 | Алгоритм 3.2 | Алгоритм 2 | Алгоритм 3 |
|---|---|---|---|---|
| 1 | 497.72 | 421.86 | 155.07 | 163.69 |
| 0.1 | 552.30 | 465.34 | 164.44 | 175.29 |
| 0.01 | 548.24 | 484.14 | 163.42 | 165.63 |
| 0.001 | 426.76 | 420.67 | 188.51 | 176.57 |
4.2. Результаты сравнения с УДСГ. Теперь обратимся к экспериментальной оценке поведения алгоримов 10, 10 и УДСГ на наборах данных w8a и ijcnn1. Результаты приведены для трех разных начальных размеров шага η0 ($0.1,0.01,0.001$) для алгоритмов 2 и 3 и таких же фиксированных величин шага для УДСГ. Критерий останова: $f({{\vec {x}}_{k}}) - f(\vec {x}{\kern 1pt} *) < {{10}^{{ - 14}}}$, где $\vec {x}{\kern 1pt} *$ – оптимальное решение, полученное УДСГ с величиной шага, давшей наилучший результат, что является обычной практикой в подобных тестах. В алгоритме 3 установлено $\varepsilon = {{10}^{{ - 6}}}$.
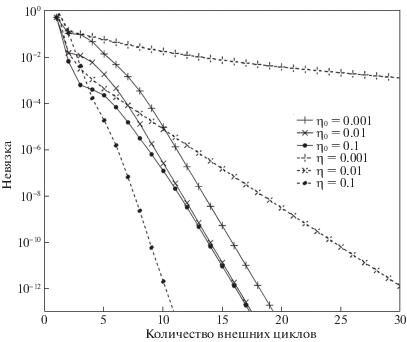
Поведение алгоритмов 2, 3 и УДСГ для наборов данных w8a и ijcnn1 изображено на рис. 1–4. По оси абсцисс отложен номер итерации k, соответствующий внешнему циклу в алгоритмах, а по оси ординат – невязка $f({{\vec {x}}_{k}}) - f(\vec {x}{\kern 1pt} *)$. Кривые, обозначенные η0, – результаты алгоритма 2 (на рис. 1, 3) или алгоритма 3 (на рис. 2, 4), а кривые, обозначенные η, – результаты УДСГ.
Из рис. 1–4 видно, что различные начальные величины шагов мало влияют на поведение алгоритмов 2 и 3, в то время как алгоритм УДСГ очень чувствителен к выбору шага. Ошибочный выбор шага даже делает УДСГ не сходящимся. Хотя алгоритмы 2 и 3 требуют несколько больше итераций, чем УДСГ с лучшими размерами шагов, они намного превосходят УДСГ с двумя другими вариантами размеров шагов. В смысле зависимости сходимости от выбора начального шага алгоритмы 2 и 3 работают устойчивее, чем УДСГ.
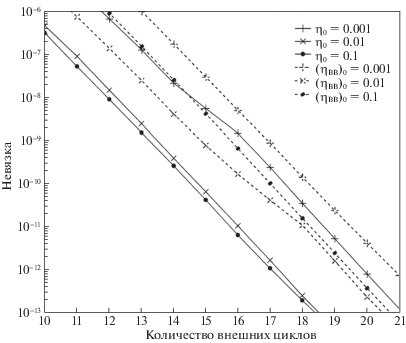
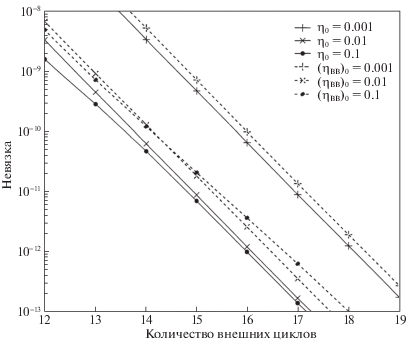
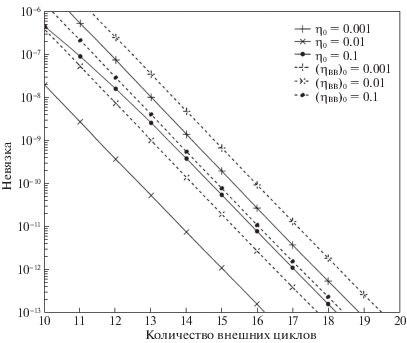
4.3. Результаты сравнения с УДСГ-ББ. Здесь показаны результаты работы алгоритмов 2, 3 и УДСГ-ББ на наборах данных w8a и ijcnn1. Начальные размеры шага η0 заданы те же, что и ранее. Численные экспериментальные результаты приведены на рис. 5–8. Чтобы более четко наблюдать детали поведения, на графиках отброшены первые несколько итераций. Рисунки 5, 6 показывают сравнение между алгоритмами 2, 3 и УДСГ-ББ для набора данных w8a, а рисунки 7, 8 – результаты сравнения на ijcnn1. Пунктирные линии построены методом УДСГ-ББ. Сплошные линии на рис. 5, 7 задаются алгоритмом 2 с разными начальными размерами шагов η0, а на рис. 6, 8 – алгоритмом 3. Все графики 5–8 подтверждают, что алгоритмы 2 и 3 находят оптимум быстрее, чем УДСГ-ББ при одинаковых начальных условиях.
Заключение. Предложены два новых алгоритма стохастического градиента, объединяющих улучшенный расчет шага ББ с методом стохастического градиента. Для сильно выпуклой целевой функции доказана линейная сходимость по вероятности. Экспериментальные результаты для стандартных наборов данных показывают преимущество двух представленных алгоритмов над градиентным спуском с фиксированным размером шага и типичными алгоритмами стохастического градиента УДСГ и УДСГ-ББ.
Список литературы
Chaudhuri K., Monteleoni C., Sarwate D. Differentially Private Empirical Risk Minimization // J. Machine Learning Research. 2011. № 12. P. 1069–1109.
Robbins H., Monro S. A Stochastic Approximation Method // The Annals of Mathematical Statistics. 1951. V. 22. № 3. P. 400–407.
Нестеров Ю.Е. Метод решения задачи выпуклого программирования со скоростью сходимости $O(1{\text{/}}{{k}^{2}})$ // ДАН СССР. 1983. Т. 269. № 3. С. 543–547.
Gaivoronskii A.A. Nonstationary Stochastic Programming Problems // Cybernetics. 1978. V. 14. № 4. P. 575–579.
Polyak B.T. New Method of Stochastic Approximation Type // Automation Remote Control. 1990. V. 51. № 7. P. 937–946.
Xiao L., Zhang T. A Proximal Stochastic Gradient Method with Progressive Variance Reduction // Siam J. Optimization. 2014. V. 24. P. 2057–2075.
Roux R.L., Schmidt M., Bach F. A Stochastic Gradient Method with an Exponential Convergence Rate for Finite Training Sets // Advances in Neural Information Processing Systems. 2012. V. 4. P. 2663–2671.
Shalevshwartz S., Zhang T. Stochastic Dual Coordinate Ascent Methods for Regularized Loss Minimization // J. Machine Learning Research. 2013. V. 14. № 1. P. 567–599.
Johnson R., Zhang T. Accelerating Stochastic Gradient Descent Using Predictive Variance Reduction // Proc. 26th Intern. Conf. Neural Information Processing Systems. Lake Tahoe, NV, USA, 2013. P. 315–323.
Barzilai J., Borwein J.M. Two-point Step Size Gradient Methods // IMA J. Numerical Analysis. 1988. V. 8. № 1. P. 141–148.
Tan C., Ma S., Dai Y.H., Qian Y. Barzilai-Borwein Step Size for Stochastic Gradient Descent // Advances in Neural Information Processing Systems 29 / Eds D.D. Lee, M. Sugiyama, U.V. Luxburg, I. Guyon, R. Garnett. NY, USA: Curran Associates, 2016. P. 685–693.
Raydan M. On the Barzilai and Borwein Choice of Steplength for the Gradient Method // IMA J. Numerical Analysis. 1993. V. 13. № 3. P. 321–326.
Dai Y., Yuan J., Yuan Y.X. Modified Two-point Stepsize Gradient Methods for Unconstrained Optimization // Computational Optimization and Applications. 2002. V. 22. № 1. P. 103–109.
Yuan Y.X. Step-sizes for the Gradient Method // American Mathematical Society. 2008. V. 42. P. 785–796.
Jin X.B., Zhang X.Y., Huang K., Geng G. G. Stochastic Conjugate Gradient Algorithm with Variance Reduction // IEEE Trans. Neural Networks and Learning Systems. 2018. V. 30. № 5. P. 1360–1369.
Nesterov Y. Introductory Lectures on Convex Optimization: A Basic Course. Kluwer Acad. Publ., 2004.
https://www.csie.ntu.edu.tw/ cjlin/libsvmtools/datasets/ Режим доступа: 6 июня 2020 г.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления