Известия РАН. Теория и системы управления, 2021, № 1, стр. 169-176
УПРАВЛЕНИЕ РАБОЧИМИ РЕЖИМАМИ ШАРНИРНОЙ ВЕТРОУСТАНОВКИ
М. З. Досаев a, Л. А. Климина a, *, Е. С. Шалимова a
a НИИ механики МГУ
Москва, Россия
* E-mail: klimina@imec.msu.ru
Поступила в редакцию 30.04.2020
После доработки 14.05.2020
Принята к публикации 27.07.2020
Аннотация
Рассматривается малогабаритное устройство преобразования энергии потока среды, конструкция которого основана на использовании кривошипно-шатунного механизма. На шатуне механизма закреплена лопасть, взаимодействующая с потоком, вал кривошипа соединен с ротором электрогенератора. В системе присутствует управляющее воздействие, позволяющее регулировать, какая часть энергии, отобранной у потока, преобразуется в электроэнергию. Подразумевается, что такое управление осуществляется путем изменения суммарного внешнего сопротивления в локальной цепи электрогенератора установки. Описывается зависимость средней механической мощности на установившихся рабочих режимах от коэффициента усиления управляющего воздействия. Исследуется, как влияют на эту зависимость скорость потока, коэффициент сухого трения в ползуне механизма и другие параметры модели. Для построения соответствующих бифуркационных диаграмм используется численно-аналитический итерационный метод формирования периодических движений с заданными свойствами, развивающий подход Андронова–Понтрягина.
Введение. Моделирование устройств преобразования потока (ветроэнергетических и гидроэнергетических установок) как управляемых динамических систем представляет собой перспективное направление. В качестве средств реализации управления могут выступать различные элементы системы. Широкий спектр работ описывает управление посредством изменения установочного угла лопастей [1–3]. Вероятно, это направление появилось первым в области регулирования работы ветроустановок. Известны исследования по управлению частотой вращения турбины и ротора генератора установки при помощи дифференциальной планетарной передачи [4–6]. Помимо этого возможно управление внешней электрической нагрузкой в цепи генератора в зависимости от изменения скорости ветра. Подобный подход особенно актуален для малогабаритных установок [7]. Последние характеризуются не только небольшими размерами, но и подключением генератора к локальной внешней цепи, нагрузку в которой можно (и весьма целесообразно) регулировать с целью увеличения мощности [8].
Построение замкнутой математической модели малогабаритной горизонтально-осевой ветроустановки на базе относительно простой модели аэродинамического воздействия [9] позволило получить ряд новых результатов по описанию эффекта гистерезиса [7] и построить стратегии регулирования мощности [5, 10].
В работе [11] модель ветроэнергетической системы, предложенная в [9], была модифицирована для описания динамики ветроустановки оригинальной конструкции на базе кривошипно-шатунного механизма. Полученные результаты позволили разработать и спроектировать новый тип устройства преобразования энергии потока [12]. Более того, была построена динамическая модель ветромобиля, использующего для перемещения такую ветроустановку [13]. Макет ветромобиля был собран и протестирован в НИИ механики МГУ.
Для ветроэнергетического устройства указанного нового типа актуально исследование возможностей управления внешней электрической нагрузкой с целью максимизации мощности, отбираемой у потока на рабочем режиме. Подобная задача для других ветроэнергетических систем обсуждалась в [10, 14, 15]. В настоящей работе она рассматривается для кривошипно-шатунной установки. При этом динамическая модель системы усложнена по сравнению с [11] тем, что учитывается сухое трение в ползуне механизма.
При решении задачи максимизации мощности путем изменения значения внешнего сопротивления в цепи генератора установки проводится исследование влияния таких параметров модели, как плотность среды, скорость потока, величина коэффициента сухого трения.
Для формирования рабочих режимов с заданными свойствами (определенным значением мощности, отбираемой у потока) используется итерационный численно-аналитический метод [14], который представляет собой модификацию метода Андронова–Понтрягина [16, 17], примененного для решения подобной задачи в [11]. Модифицированный подход к исследованию установившихся движений позволил (по сравнению с [11]) рассмотреть значительно более широкую область значений параметров модели. Отметим, что указанный метод предназначен для поиска и формирования режимов авторотации с заданными свойствами. Для решения аналогичных задач применительно к режимам автоколебаний разработаны модификации метода, представленные в [18, 19].
1. Постановка задачи. Рассматривается модель устройства преобразования энергии потока, в основу конструкции которого положен кривошипно-шатунный механизм (рис. 1). Другие ветроустановки, в которых используются шарнирные механизмы, рассмотрены, например, в работах [20, 21]. Кривошип OA длины r может вращаться вокруг вертикальной оси O. Шатун AB имеет длину l (l > r). В точке B находится ползун, который может двигаться вдоль горизонтальной направляющей, обозначенной на рис. 1 как ось Oy.
Рис. 1.
Схема кривошипно-шатунной ветроэнергетической установки (вид сверху) и фотография прототипа в малой аэродинамической трубе НИИ механики МГУ
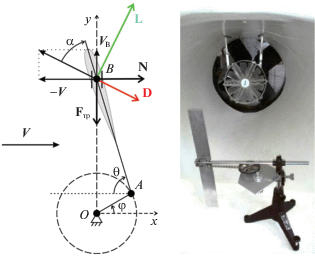
На шатуне установлена прямоугольная лопасть, соединенная с ним жестко. Предполагается, что хорда лопасти направлена по шатуну. Лопасть имеет характерную площадь S и взаимодействует с потоком среды плотности $\rho $, имеющим на бесконечности скорость V, направленную вдоль оси Ох, которая ортогональна оси Оy. Твердое тело “стержень AB + лопасть” характеризуется центральным моментом инерции J2 и массой m. Центр масс этого тела совпадает с точкой А, и предполагается, что компонента нормальной реакции, компенсирующая вес тела, приложена в точке А.
На валу кривошипа установлен ротор генератора установки, J1 – момент инерции твердого тела “кривошип OA + ротор генератора” относительно оси O. Центр масс этого тела расположен на оси О.
Система имеет одну степень свободы. В качестве обобщенной координаты выберем угол φ между осью Ох и кривошипом ОА. Пусть $\theta $ – угол между шатуном AB и осью Ох, тогда cosθ = = $(r{\text{/}}l){\text{cos}}\varphi $ (рис. 1). Отметим, что минимальное значение $\sin \theta $ во время движения системы составляет $\sqrt {1 - {{r}^{2}}{\text{/}}{{l}^{2}}} > 0$.
Кинетическая энергия описанной системы имеет вид
Воздействие потока среды на лопасть будем моделировать как сумму силы D лобового сопротивления и боковой (подъемной) силы L. Будем считать, что точка приложения аэродинамических сил совпадает с точкой В. Значения аэродинамических сил определим на основе квазистатического подхода [8, 9], их проекции на оси Ox и Oy имеют вид
Здесь α – мгновенный угол атаки, т.е. угол между воздушной скоростью точки B и отрезком AB. Воздушная скорость точки B – вектор, имеющий в осях Oxy вид $\{ - V,u\,V\} $. Функции ${{C}_{L}}(\alpha )$, ${{C}_{D}}(\alpha )$ – безразмерные коэффициенты боковой силы и силы сопротивления лопасти. Промежуточные безразмерные переменные u и α определяются по формулам $u = {{V}^{{ - 1}}}r\dot {\varphi }{\text{sin}}(\theta + \varphi ){\text{si}}{{{\text{n}}}^{{ - 1}}}\theta $, $\alpha = - \arctan (u)$ + θ.
При численных расчетах использовались зависимости коэффициентов ${{C}_{D}}(\alpha )$, ${{C}_{L}}(\alpha )$ силы сопротивления и боковой силы от мгновенного угла атаки α, соответствующие стационарным аэродинамическим характеристикам плоской пластины удлинения 8 (т.е. прямоугольной пластины, у которой отношение длин сторон равно 8, более длинная сторона перпендикулярна AB).
На ползун со стороны направляющей действует сухое трение Fтр с коэффициентом f. Будем рассматривать такие движения системы, при которых скорость точки B может быть нулевой только в отдельные моменты времени, но не на каком-либо отрезке времени (далее будет показано, что в рамках построенной модели рабочие режимы системы удовлетворяют этому свойству). Соответственно используем модель трения скольжения, трение покоя не рассматриваем.
Электромеханический момент, описывающий воздействие статора генератора на ротор, будем считать линейным по угловой скорости $\dot {\varphi }$ ротора генератора [8]:
здесь С – коэффициент электромеханического взаимодействия, σ – внутреннее сопротивление генератора (константы, определяемые характеристиками генератора); $R$ – внешнее сопротивление в цепи генератора (будем рассматривать его как управляющее воздействие, подобно работе [15]).В безразмерных переменных и параметрах уравнения движения системы имеют следующий вид:
(1.1)
$\begin{gathered} d\varphi {\text{/}}d\tau = z, \\ dp{\text{/}}d\tau = 0.5k{\text{'}}(\varphi ){{k}^{{ - 2}}}(\varphi ){{p}^{2}} + \varepsilon \left( {Q(\varphi ,z) - cz} \right), \\ \end{gathered} $Здесь z – безразмерная угловая скорость; $p = k(\varphi )z$ – безразмерный импульс; $\tau = Vt{\text{/}}r$ – безразмерное время; $Q(\varphi ,z)$ – безразмерная обобщенная сила; $\mu = {{m}^{{ - 1}}}{{V}^{{ - 2}}}rf$ – безразмерный коэффициент сухого трения, действующего на ползун.
Зависимость $N(\varphi ,z)$ – безразмерная функция, характеризующая проекцию нормальной реакции в ползуне на ось Ox. Параметр c – безразмерный коэффициент полезной нагрузки. Далее будем считать параметр с коэффициентом усиления управляющего воздействия (технически управление осуществляется путем изменения величины $R$ внешнего сопротивления).
Выражение для величины реакции $N(\varphi ,z)$ может быть получено выписыванием второго закона Ньютона для всей системы, для кривошипа, а также закона изменения кинетического момента всей системы относительно точки O:
(1.2)
$\begin{gathered} N(\varphi ,z) = {{{{N}_{1}}(\varphi ,z)} \mathord{\left/ {\vphantom {{{{N}_{1}}(\varphi ,z)} {{{N}_{2}}(\varphi ,z)}}} \right. \kern-0em} {{{N}_{2}}(\varphi ,z)}}, \\ {{N}_{1}}(\varphi ,z) = - {{d}_{1}}k(\varphi )({{{\hat {D}}}_{x}} + {{{\hat {L}}}_{x}}) - {{d}_{1}}({{{\hat {D}}}_{y}} + {{{\hat {L}}}_{y}})\frac{r}{l}\frac{{\cos \varphi }}{{\sin \theta }}\left( {1 + {{d}_{2}} - \frac{{{{J}_{2}}r}}{{{{J}_{1}}l}}\frac{{\sin \varphi }}{{\sin \theta }}} \right) - 2{{d}_{1}}\frac{{{{J}_{2}}{{r}^{2}}}}{{{{J}_{1}}{{l}^{2}}}}cz + \\ + \;\left( {1 + {{d}_{2}}} \right)\left( {1 - \frac{{{{r}^{2}}}}{{{{l}^{2}}}}} \right)\frac{{{{J}_{2}}}}{{m{{l}^{2}}}}\frac{{\cos \varphi }}{{{{{\sin }}^{4}}\theta }}{{z}^{2}}, \\ {{N}_{2}}(\varphi ,z) = k(\varphi ) - \mu \operatorname{sgn} \left( {N(\varphi ,z)\cos \varphi } \right)\frac{r}{l}\frac{{\cos \varphi }}{{\sin \theta }}\left( {1 + {{d}_{2}} - \frac{{{{J}_{2}}r}}{{{{J}_{1}}l}}\frac{{\sin \varphi }}{{\sin \theta }}} \right). \\ \end{gathered} $Выражение $N(\varphi ,z)$ используется для замыкания системы (1.1). Приведенная формула для $N(\varphi ,z)$ является в определенном смысле рекурсивной: требуется информация о знаке величины $(N(\varphi ,z){\text{cos}}\varphi )$, чтобы вычислить ${{N}_{2}}(\varphi ,z)$. При численной реализации определяем два различных значения $N(\varphi ,z)$, соответствующих тому или иному знаку $\left( {N(\varphi ,z)\cos \varphi } \right)$, затем проверяем знаки полученных величин $N(\varphi ,z)$, чтобы установить, какой из двух рассмотренных знаков произведения $\left( {N(\varphi ,z)\cos \varphi } \right)$ корректен. При относительно небольших значениях безразмерного коэффициента трения μ знаменатель ${{N}_{2}}(\varphi ,z)$ функции $N(\varphi ,z)$ не обращается в нуль ни при каких φ и z. При этом знак слагаемого, содержащего множитель $\mu $, не влияет на знак величины $N(\varphi ,z)$ и соответственно указанная выше простая проверка достаточна для однозначного определения знака выражения $\left( {N(\varphi ,z)\cos \varphi } \right)$.
Правая часть (1.1) – функция 2π-периодическая по φ. Орбитально устойчивая 2π-периодическая по φ траектория системы (1.1) соответствует рабочему режиму устройства. Пусть функция $\tilde {z}(\varphi )$ описывает зависимость переменной $z$ от угла $\varphi $ на 2π-периодической траектории.
Для практических приложений представляют интерес значения средней безразмерной угловой скорости и механической мощности на рабочих режимах. Они зависят от коэффициента $c$ полезной нагрузки.
Среднее (по углу за период) значение коэффициента cp механической мощности на рабочем режиме определим следующим образом:
Оценим диапазон значений средней угловой скорости и среднего коэффициента мощности на рабочих режимах в зависимости от параметров модели, а также опишем области притяжения рабочих режимов.
2. Рабочие режимы системы. Будем рассматривать траектории, расположенные в области z > 0, поскольку из [11] следует, что соответствующие режимы намного предпочтительнее с точки зрения отбора мощности у потока, чем режимы, при которых кривошип вращается “по часовой” (z < 0). С целью построения 2π-периодических по φ траекторий системы (1.1) в зависимости от параметров модели воспользуемся методом [14].
В соответствии с этим подходом рассмотрим порождающую гамильтонову систему: при ε = 0 система (1.1) имеет гамильтониан ${{H}_{0}}(\varphi ,p) = 0.5k(\varphi ){{p}^{2}}$. При достаточно малых значениях ε асимптотические оценки характеристик рабочих режимов моделируемой установки получены в [11] в предположении отсутствия трения (f = 0) путем применения метода Андронова–Понтрягина к системе (1.1) как к системе, близкой к гамильтоновой. В настоящей работе используем траектории порождающей консервативной системы с гамильтонианом H0 в качестве нулевой итерации ${{\tilde {z}}_{0}}(\varphi )$ для построения $2\pi $-периодических траекторий, последующие приближения ${{\tilde {z}}_{n}}(\varphi )$ определим по формулам, предложенным в статье [14]. Будем считать, что итерационный процесс сошелся, если максимум (по φ) модуля разности ${{\tilde {z}}_{n}}(\varphi )$ и ${{\tilde {z}}_{{n - 1}}}(\varphi )$ меньше некоторого заданного числа. Если при этом ${{\tilde {z}}_{n}}(\varphi ) > 0$ при всех φ, то используем функцию ${{\tilde {z}}_{n}}(\varphi )$ как итоговое приближение для 2π-периодической траектории $\tilde {z}(\varphi )$.
Рассмотрим случай, соответствующий малогабаритной ветроустановке с конкретными значениями геометрических и инерционных параметров: ${{J}_{1}} = 0.00375$ кг ⋅ м2, ${{J}_{2}} = 0.0375$ кг ⋅ м2, r = 0.1 м, $l = 0.5$ м, $S = 0.003$ м2, $m = 1.225$ кг, ${{S}_{0}} = 0.015$ м2. Пусть величина скорости ветра $V = 7$ м/с; плотность воздуха $\rho = 1.125$ кг/м3. При этих значениях параметров получаем $\varepsilon = 0.5J_{1}^{{ - 1}}\rho S{{r}^{3}}$ = 0.0005.
Помимо этого рассмотрим значения параметров модели, соответствующие работе устройства в потоке воды: $\rho = 1000$ кг/м3, $V = 0.5$ м/с (остальные параметры те же, что и в первом случае). При этом значение безразмерного параметра ε = 0.4. Отметим, что конструкция установки позволяет при использовании системы в воде полностью изолировать ползун от воздействия жидкости, поместив его в защитный кожух, что является характерным (одним из основных) преимуществом установок шарнирного типа, в которых рабочий элемент совершает колебания, а не ротации. Таким образом, при рассмотрении системы как гидроэнергетической по-прежнему можно считать, что в ползуне действует именно сухое трение.
Во всех приведенных случаях знаменатель ${{N}_{2}}(\varphi ,z)$ выражения (1.2) для реакции $N(\varphi ,z)$ не обращается в нуль ни при каких значениях безразмерного коэффициента $\mu $ сухого трения.
На рис. 2, 3 представлены бифуркационные диаграммы средней безразмерной угловой скорости 〈z〉 кривошипа и среднего коэффициента cp механической мощности устройства на режимах авторотации, отвечающих 2π-периодическим решениям системы (1.1), для случая $\varepsilon = 0.0005$ (рис. 2), а также для случая ε = 0.4 (рис. 3). Они построены при различных значениях коэффициента сухого трения f ($f = 0,0.1,0.25,0.5$). На этих диаграммах сплошные линии отвечают притягивающим периодическим решениям, пунктирные – отталкивающим. Достаточное условие орбитальной устойчивости/неустойчивости периодической траектории: отрицательное/положительное значение угла наклона касательной к бифуркационной кривой в точке бифуркационной диаграммы, соответствующей данной траектории. Это условие – следствие того, что параметр c в системе (1.1) отвечает за поворот векторного поля [17].
Рис. 2.
Бифуркационные диаграммы для периодических режимов при $\varepsilon = 0.0005$ (устройство функционирует в потоке воздуха)
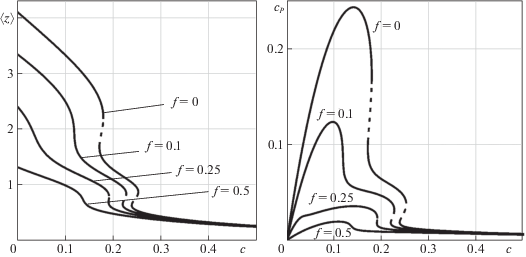
Рис. 3.
Бифуркационные диаграммы для периодических режимов при $\varepsilon = 0.4$ (устройство работает в потоке воды)
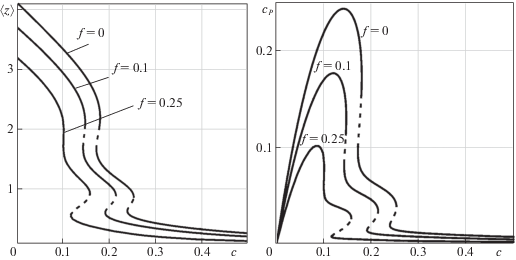
Проиллюстрировано изменение средней (по углу) безразмерной угловой скорости и среднего (по углу) коэффициента cp механической мощности в зависимости от коэффициента c полезной нагрузки. Для всех построенных $2\pi $-периодических траекторий выполнено $\tilde {z}(\varphi ) > 0$ при всех $\varphi $, тем самым скорость точки B (ползуна) не остается нулевой ни на каком интервале времени.
Можно видеть, что при $\varepsilon = {\text{0}}{\text{.0005}}$ в случае f = 0 есть два интервала значений параметра c, для которых существует по два притягивающих 2π-периодических режима. При f = 0.1 и 0.25 такой интервал один. В связи с наличием этих интервалов наблюдается гистерезис характеристик рабочих режимов в зависимости от направления изменения параметра c. При f = 0.5 для всех значений коэффициента $c$ существует только один 2π-периодический режим, который является притягивающим.
При $\varepsilon = 0.4$ в случаях f = 0 и 0.1 есть два диапазона значений параметра c, в которых есть по два притягивающих 2π-периодических режима, а в случае f = 0.25 такой диапазон один.
Сопоставляя диаграммы, отвечающие рабочим режимам установки в воздухе (рис. 2) и в воде (рис. 3), можно отметить, что для этих двух случаев падение угловой скорости и мощности, вызванное влиянием сухого трения, не сильно отличается по количественным показателям. В предельном случае нулевого коэффициента трения f бифуркационные диаграммы коэффициента мощности в воздухе и в воде отличаются друг от друга незначительно.
3. Управление коэффициентом полезной нагрузки. Рассмотрим возможность регулирования механической мощности путем изменения внешнего сопротивления в цепи генератора. Для конкретной установки все размерные параметры модели фиксированы, кроме величины V скорости потока, и значения R внешнего сопротивления, которые описывают текущие условия эксплуатации. При изменении скорости V можно регулировать величину R внешнего сопротивления таким образом, чтобы значение коэффициента c полезной нагрузки соответствовало максимуму коэффициента cp мощности: $c = {{c}_{{opt}}}$. Значение безразмерного коэффициента $\mu $ трения зависит от величины V скорости потока. Соответственно при изменении V меняется значение коэффициента c, доставляющее максимум коэффициента cp мощности (на рис. 2, 3 это отвечает переходу от одной диаграммы к другой). В связи с этим для построения зависимости величины R от скорости V потока требуется информация о функции ${{c}_{{opt}}}(\mu )$, а не об одном значении ${{c}_{{opt}}}$ (в отличие от модели, где не учитывалось трение). В остальном выбор значения ${{R}_{{opt}}}$, которое требуется для поддержания максимальной механической мощности, аналогичен предложенному в работе [15] для другой ветроустановки:
Функция ${{c}_{{opt}}}(\mu )$ строится по абсциссам максимумов диаграмм ${{c}_{p}}(c)$, соответствующих различным значениям $\mu $.
Поскольку значение R всегда положительно, существует предельное значение скорости V потока, при превышении которого нельзя реализовать максимум функции ${{c}_{p}}(c)$ (аналогичное свойство было отмечено для другого типа ветроустановки в работе [15]).
4. Обсуждение результатов. Получены бифуркационные диаграммы для характерных значений средней безразмерной угловой скорости и среднего коэффициента механической мощности на рабочих режимах устройства, которые соответствуют 2π-периодическим траекториям системы (1.1). Продемонстрировано, что в некоторых диапазонах значений параметров существуют два притягивающих периодических режима, области притяжения которых разделяет отталкивающий периодический режим. При таких значениях параметров имеет место гистерезис безразмерной угловой скорости и коэффициента мощности в зависимости от направления изменения коэффициента c, отвечающего за внешние условия функционирования устройства: скорость потока и нагрузку со стороны потребителей в цепи генератора.
Кроме того, из построенных диаграмм следует наличие в модели притягивающих периодических режимов, характеризующихся относительно высокими значениями безразмерной угловой скорости: $\left\langle z \right\rangle > 1$. На таких режимах скорость точки В крыла на определенных фазах движения превышает по величине скорость ветра. Режимы данного типа характерны для ветроустановок с высокими значениями выходной мощности: турбины пропеллерного типа и типа Дарье [22–25].
Продемонстрированы некоторые тенденции зависимости характеристик рабочих режимов от коэффициента сухого трения в ползуне, которое в модели описывается параметром f. В безразмерных параметрах и переменных построены серии бифуркационных диаграмм (рис. 2, 3), соответствующих различным значениям безразмерного коэффициента трения.
Заключение. В работе рассмотрено устройство преобразования энергии потока. В конструкции используется кривошипно-шатунный механизм, на шатуне которого закреплена лопасть. К преимуществам такой системы относятся достаточно высокие значения мощности, отбираемой у потока, а также возможность изоляции всех вращательных элементов от воздействия потока. Последнее свойство позволяет, в частности, использовать устройство не только как ветроэнергетическую установку, но и как гидроэнергетическую.
При моделировании внешних воздействий использованы подходы [7–9]. Математическая модель представлена в форме динамической системы второго порядка. Рабочему режиму установки соответствует периодическая орбитально устойчивая траектория системы. Для отыскания периодических решений и проверки их устойчивости применен метод [14]. Проведен параметрический анализ рабочих режимов. В частности, исследовано влияние трения в ползуне механизма при функционировании в различных средах (воздух, вода). Получены оценки коэффициента мощности на рабочих режимах. Продемонстрировано наличие эффекта гистерезиса мощности в зависимости от направления изменения коэффициента полезной нагрузки.
Предложена стратегия управления внешним сопротивлением, обеспечивающая максимизацию механической мощности на рабочем режиме установки.
Список литературы
Senjyu T., Sakamoto R., Urasaki N., Funabashi T., Fujita H., Sekine H. Output Power Leveling of Wind Turbine Generator for All Operating Regions by Pitch Angle Control // IEEE Trans. Energy Convers. 2006. V. 21. № 2. P. 467–475.
Van T.L., Nguyen T.H., Lee D.C. Advanced Pitch Angle Control Based on Fuzzy Logic for Variable-Speed Wind Turbine Systems // IEEE Trans. Energy Convers. 2015. V. 30. № 2. P. 578–587.
Jiao X., Meng W., Yang Q., Fu L., Chen Q. Adaptive Continuous Neural Pitch Angle Control for Variable Speed Wind Turbines // Asian J. Control. 2019. V. 21. № 4. P. 1966–1979.
Balbayev G., Ceccarelli M. Design and Characterization of a New Planetary Gear Box // New Advances in Mechanisms, Transmissions and Applications. Dordrecht: Springer, 2014. P. 91–98.
Dosaev M., Holub A., Klimina L. Preferable Operation Modes of a Wind Turbine with a Differential Planetary Gearbox // New Trends in Mechanism and Machine Science. 2015. V. 24. P. 545–552.
Su R., Rui X., Wu X., Yin Q. The Design and Analysis of Wind Turbine Based on Differential Speed Regulation // Proc. Inst. Mech. Eng. C: J. Mech. Eng. Sci. 2016. V. 230. № 2. P. 221–229.
Самсонов В.А., Селюцкий Ю.Д. Математическая модель поведения малых ветровых электростанций // Мат. моделирование. 2015. Т. 27. № 2. С. 85–95.
Досаев М.З., Самсонов В.А., Селюцкий Ю.Д., Вен-Лон Лю, Чин-Хуэй Линь. Бифуркации режимов функционирования малых ветроэлектростанций и оптимизация их характеристик // Изв. РАН. МТТ. 2009. № 2. С. 59–66.
Досаев М.З., Самсонов В.А., Селюцкий Ю.Д. О динамике малой ветроэлектростанции // ДАН. 2007. Т. 416. № 1. С. 50–53.
Shalimova E., Klimina L., Lin K.H. On Behavior of a Double Rotor HAWT with a Differential Planet Gear // Tech. Mech. 2017. V. 37. № 2–5. P. 394–399.
Klimina L. Dynamics of a Slider-Crank Wave-Type Wind Turbine // Proc. 14th IFToMM World Congr. Taipei, 2015. P. 582–588. https://doi.org/10.6567/IFToMM.14TH.WC.OS13.007.
Голуб А.П., Досаев М.З., Климина Л.А., Локшин Б.Я., Меснянкин С.Ю., Самсонов В.А., Селюцкий Ю.Д., Симоненко М.М. Устройство для преобразования возобновляемой энергии // Официальный бюллетень федеральной службы по интеллектуальной собственности (Роспатент), сер. Изобретения. Полезные модели. 2018. Т. 2. 2641176.
Klimina L., Dosaev M., Selyutskiy Yu. Asymptotic Analysis of the Mathematical Model of a Wind-Powered Vehicle // Appl. Math. Model. 2017. V. 46. P. 691–697.
Климина Л.А. Метод построения периодических решений в управляемой динамической системе с цилиндрическим фазовым пространством // Изв. РАН. ТИСУ. 2020. № 2. С. 5–16.
Ишханян М.В., Климина Л.А. Ветротурбина класса “Савониус Магнус” с коническими лопастями: динамика и управление // Изв. РАН. ТиСУ. 2020. № 4. С. 160–168.
Понтрягин Л.С. О динамических системах, близких к гамильтоновым // ЖЭТФ. 1934. Т. 4. № 9. С. 234–238.
Андронов А.А., Леонтович Е.А., Гордон И.И., Майер А.Г. Теория бифуркаций динамических систем на плоскости. М.: Наука, 1967.
Климина Л.А. Метод поиска периодических траекторий центрально-симметричных динамических систем на плоскости // Дифференц. уравнения. 2019. Т. 55. № 2. С. 159–168.
Климина Л.А., Селюцкий Ю.Д. Метод построения периодических решений в управляемой динамической системе второго порядка // Изв. РАН. ТиСУ. 2019. № 4. С. 3–15.
Andronov P.R., Dosaev M.Z., Dynnikova G.Y., Selyutskii Y.D., Strekalov S.D. Modeling of Oscillating Wind Turbine // J. Machinery Manufacture and Reliability. 2009. V. 38. № 4. P. 383–387.
Dosaev M., Klimina L., Selyutskiy Y. Wind Turbine Based on Antiparallel Link Mechanism // New Trends in Mechanism and Machine Science. 2017. V. 43. P. 543–550.
Досаев М.З., Климина Л.А., Локшин Б.Я., Селюцкий Ю.Д. Об оптимизации формы лопасти ветротурбины // Изв. РАН. ТиСУ. 2014. № 3. С. 104–112.
Hsiao Y.C., Shyu L.S. Nonlinear Behaviors of a Small Wind Turbine Induced by Aerodynamics and Electromagnetic Field // J. Internet Tech. 2020. V. 21. № 1. P. 33–39.
Климина Л.А. Ротационные режимы движения аэродинамического маятника с вертикальной осью вращения // Вест. МГУ. Сер. 1. Математика, механика. 2009. № 5. С. 71–74.
Chen C., Kuo C. Effects of Pitch Angle and Blade Camber on Flow Characteristics and Performance of Small-Size Darrieus VAWT // J. Vis. 2013. V. 16. P. 65–74.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления


