Известия РАН. Теория и системы управления, 2021, № 1, стр. 160-168

Введение. В область искусственного интеллекта (ИИ), управления и принятия решений при неполной или недостоверной информации входят задачи так называемого объяснения на основе моделей и методов абдуктивных рассуждений (Explanation by abductive reasoning), в том числе в терминах “причина-эффект”. Здесь под “эффектом” или далее также под “наблюдаемым” могут пониматься аномалии, симптомы и вообще некоторые выделенные (особые) состояния системы как объекта анализа и управления.

Понятие абдукции введено логиком и философом Ч.С. Пирсом (C.S. Peirce, 1839–1914 гг.) в форме логических рассуждений, сравнимых, но отличных от дедукции и индукции. Сегодня абдукция чаще всего определяется следующим образом: на основе заданной теории Т предметной области и утверждения G о наблюдаемом эффекте, подлежащем объяснению, найти такую не противоречащую теории Т гипотезу-объяснение Δ, что из Т и Δ выводимо G (модификации см., например, в [1–3]).

В работах по абдуктивному гипотезированию на теорию Т предметной области часто накладываются ограничения, при которых дедукция максимально упрощается, например содержание теории должно иметь форму “if-and-only-if”, т.е. форму семейства эквивалентностей

где в пропозициональном случае c_i – переменные-причины, а E_ij, $j = \overline {1,n} ,$ – элементарные конъюнкции, составленные из переменных-эффектов и их отрицаний, возможно, при дополнительных требованиях к множеству задействованных переменных, частично упорядоченному импликацией [1, 2].

В данной работе не предполагается какой-либо предварительной трансформации теории Т, а в качестве языка представления знаний в разд. 1 вводится S-язык ${{L}_{S}}$ как подмножество пропозиционального языка, но без ослабления его выразительной силы. Допуская использование отрицания переменных, язык ${{L}_{S}}$ шире пропозиционального варианта языка позитивно-образованных формул [4, 5], но обладает тем же свойством подстановочности (см. разд. 1). Свойства языка ${{L}_{S}}$ и вводимых в нем исчислений ${{\mathbb{C}}_{\alpha }}$, ${{\mathbb{C}}_{\beta }}$ обеспечивают гибкое сочетание дедукции с абдуктивным достоверным или правдоподобным выводом.

Вывод в ${{\mathbb{C}}_{\beta }}$ наблюдаемого эффекта $G$ выполняется вместе с синтезом формулы $P$, называемой гипотезой-минорантой и объясняющей эффект $G$ лишь формально. С точностью до эквивалентности гипотеза P логически минимальна (любая гипотеза-причина Δ, объясняющая $G$ в смысле выше приведенного определения, должна быть не слабее $P$: $\Delta \to P$). Гипотеза-миноранта выступает контрольным условием и опорным средством формирования достоверных гипотез Δ, а при наличии сверхтеории $T$ эмпирических знаний миноранта является также и средством вывода правдоподобных гипотез Δ. Эмпирические знания – это знания об априорном множестве потенциально возможных причин-кандидатов и/или о правдоподобных причинно-следственных связях. Из гипотезы P переходом к достаточным условиям, например путем упрощения P или использования эмпирических знаний, получаются либо причины Δ-эффекта G (достоверные или правдоподобные), либо поначалу лишь релевантные обстоятельства (факты, события, “улики”), из которых в рамках теории Т средствами исчислений ${{\mathbb{C}}_{\alpha }}$ и ${{\mathbb{C}}_{\beta }}$ оказываются выводимыми и сами причины.

Заметим, что в проблематике интеллектуализации автономных (беспилотных) агентов с реактивными правилами “условие-действие” понятие “эффект” может иметь также смысл целевого состояния агента [6]. Эта актуальная тема абдуктивной информационной поддержки планирования действий агентов выходит за рамки данной статьи. Актуальной задачей остается также проблематика ранжирования альтернативных объяснений наблюдаемого для сужения множества гипотез до наиболее достоверных с использованием вероятностных, логических и других оценок.

В разд. 1 определяется язык представления знаний, а в разд. 2 – правила преобразования его формул. В разд. 3 вводятся исчисления ${{\mathbb{C}}_{\alpha }}$, ${{\mathbb{C}}_{\beta }}$ и обосновываются их свойства. В разд. 4 применение этих исчислений иллюстрируется примерами из техники и медицины.

1. Представление знаний. В пропозициональном языке L стандартной (классической) семантики выделим подмножество ${{L}_{S}}$. Ввиду свойства подстановочности формул языка ${{L}_{S}}$, которое будет рассмотрено ниже, назовем его S-языком (от английского Substitution). Далее конъюнктами называем элементарные конъюнкции литералов (пропозициональных переменных и/или их отрицаний) и пропозициональные константы false, true. Если в элементарную конъюнкцию (ЭК) входит пара контрарных литералов (переменная и ее отрицание), то по умолчанию такие ЭК заменяются на константу false. Логические связки $ \wedge ,\; \vee ,\;\neg ,\; \to $ в S-языке понимаются стандартно.

Определение 1 (формулы языка ${{L}_{S}}$ и их типы):

1) ЭК $A$ или константа false, – S-формулы; им приписывается тип ∧; это простейшие S-формулы;

2) если ${{F}_{i}}$ – S-формулы типа ∧ ($i = \overline {1,m} $), а G – ЭК или true, то $G \to \left( {\mathop \vee \limits_{i = 1}^m \,{{F}_{i}}} \right)$ – S-формулы типа →;

3) если ${{F}_{i}}$– S-формулы типа → ($i = \overrightarrow {1,m} $), а G – ЭК или true, то $G \wedge \left( {\mathop \wedge \limits_{i = 1}^m \,{{F}_{i}}} \right)$ – S-формулы типа ∧;

4) других формул в языке ${{L}_{S}}$ нет.

Если $m \ne 1$ и некоторое ${{F}_{i}}$ совпадает с false, то возможно упрощение S-формулы очевидным (логически эквивалентным) преобразованием; такие упрощения далее будут подразумеваться.

Каноническим представлением S-формулы $F$ называем ее запись в виде формулы с конъюнктом $true$ в корневой вершине ее структуры:

где $m \geqslant 1,$ ${{n}_{i}} \geqslant 0$ (если n_i = 0, то ${{\Omega }_{i}} = {{A}_{i}}$).

Подформулы некоторой S-формулы F, образуемые в соответствии с индуктивным определением S-формул, называются главными подформулами (ГП). Так, в (1.1) при $n_{i}^{{}} \ne 0$ подформулы 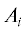и ${{B}_{{ij}}}$ не являются главными, а при $n_{i}^{{}} = 0$ подформула ${{A}_{i}}$ – главная. Выражение ${{F}_{1}} \subseteq F$ означает, что ${{F}_{1}}$ – ГП S-формулы F.

Если $H \subseteq F \in {{L}_{S}},$ $H = D \to \mathop \vee \limits_{i = 1}^n {{H}_{i}}$, то подформула $\left| H \right|$из $H$ вида $\left| H \right| = \mathop \vee \limits_{i = 1}^n {{H}_{i}}$ не является главной. Через ${{\left| H \right|}_{{ - i*}}}$обозначается $\mathop \vee \limits_{i = 1,\,i \ne i*}^n {{H}_{i}}$ (если $H$– типа ∧, то смысл $\left| H \right|$ и ${{\left| H \right|}_{{ - i*}}}$ аналогичен с заменой $ \vee $ на $ \wedge $). Эти обозначения будут использованы в разд. 3 для упрощения записи формул.

Каждой вершине древовидной структуры S-формулы приписываем тип, соответствующий типу ГП, корнем которой эта вершина является. По определению 1 типы ∧ и → вершин вдоль ветви структуры S-формулы F чередуются.

Формулы языка $L$, не принадлежащие подмножеству ${{L}_{S}}$, понимаем стандартно. Например, если ${{F}_{1}},\;{{F}_{2}} \in {{L}_{S}}$, то выражение ${{F}_{1}} \to {{F}_{2}}$, вообще говоря не принадлежащее ${{L}_{S}}$, понимается как в $L$.

В отличие от формул языка $L$ для S-формул F, ${{F}_{1}}$, ${{F}_{2}}$ справедливо свойство подстановочности: если ${{F}_{1}} \subseteq F$ и ${{F}_{2}} \to {{F}_{1}}$ , то $F({{F}_{2}}{\text{/}}{{F}_{1}}) \to F,$ где $F({{F}_{2}}{\text{/}}{{F}_{1}})$ – результат подстановки в $F$ вместо ${{F}_{1}}$ не менее сильной формулы ${{F}_{2}}$.

Язык ${{L}_{S}}$ полон относительно выразительной силы языка $L$. Семантика S-формул очевидна.

2. Преобразования S-формул. Рассмотрим S-формулу F в каноническом представлении (1.1). Конъюнкт ${{A}_{i}}$ называется базой, а конъюнкты ${{B}_{{ij}}}$ (когда ${{n}_{i}} \ne 0$) – вопросами к базе ${{A}_{i}}$. Если ${{B}_{{ij}}} \subseteq {{A}_{i}}$, то вопрос ${{B}_{{ij}}}$ к базе ${{A}_{i}}$ называем уместным. Тождественно ложную S-формулу ($true \to false$) далее для краткости обозначаем ⊥.

Пусть в (1.1) $F \ne \; \bot $, ${{n}_{i}} \ne 0$ и ${{\Phi }_{{ij}}}$ имеют вид

Предположим, что т.е. вопрос ${{B}_{{i*j*}}}$ к базе ${{A}_{{i*}}}$ уместен.

Определение 2 (α-преобразование). Пусть S-формула F имеет вид (1.1), (2.1), (2.2). Тогда, если ${{\Phi }_{{i*j*}}} \ne false$, то α-преобразованием называется такое отображение $\alpha :\;{{L}_{S}} \to {{L}_{S}}$, что

Если же ${{\Phi }_{{i*j*}}} = false$ , то при m > 1

а при m = 1 $\alpha (F) = \, \bot $.

В (2.3) и далее, когда это не вызывает коллизий, конъюнкты рассматриваются как множества входящих в эти конъюнкты элементов. Если ${{\Phi }_{{i*j*}}} \ne false$, то в случае появления в конъюнкте $\{ {{A}_{{i*}}} \cup {{С}_{{i*j*k}}}\} $ из (2.3) контрарных литералов применяем следующие очевидные упрощения формулы $\alpha (F)$: при ${{l}_{{i*j*}}} > 1$ удаляется $\Omega _{{i*j*k}}^{*}$; при ${{l}_{{i*j*}}} = 1$ и m = 1 $\alpha (F)$ заменяется на ⊥; при ${{l}_{{i*j*}}} = 1$ и $m > 1$ удаляется $\Omega _{{i*j*1}}^{*}$. Удаляются и дубли ГП при совпадении $\Omega _{{i*}}^{*}$ с ${{\Omega }_{i}},$ $i \ne i{\kern 1pt} *$.

Пусть $\alpha (F) \ne \, \bot $ и выполняется условие типа (2.2). Применяя α-преобразование к $\alpha (F)$, получим S-формулу ${{\alpha }^{2}}(F)$ и т.д. до тех пор, пока очередной результат еще отличен от ⊥ и выполняется (2.2). Пусть на некотором шаге ${{r}_{1}}$ $({{r}_{1}} \geqslant 0)$ ${{\alpha }^{{{{r}_{1}}}}}(F) \ne \bot $, но α-преобразование уже не применимо ввиду невыполнения (2.2), т.е. $\forall i \in \overline {1,{{m}^{1}}} $, где m¹ – количество баз в ${{\alpha }^{{{{r}_{1}}}}}(F)$, база A_i будет:

1) либо висячей $(n_{i}^{{}} = 0)$ и ввиду упомянутых упрощений отличной от false, либо

2) невисячей $(n_{i}^{{}} \geqslant 1)$ и такой, что $\forall j \in \overline {1,n_{i}^{{}}} $вопросы ${{B}_{{ij}}}$ к базе A_i неуместны (под выражениями ${{A}_{i}}$, ${{B}_{{ij}}}$ понимаются новые конъюнкты в формуле ${{\alpha }^{{{{r}_{1}}}}}(F)$).

Определение 3 (β-преобразование). Пусть ${{I}_{1}}$, ${{I}_{2}}$ – множества индексов $i \in \overline {1,{{m}^{1}}} $, для которых базы A_i  удовлетворяют условиям 1) и 2) соответственно, и

где

Назовем β-преобразованием такое отображение $\beta :\;{{L}_{S}} \to {{L}_{S}}$, что

Формирование условия

называем далее (α, β)-гипотезированием.

3. S-исчисления и их свойства. На основе α- и β-преобразований формул языка ${{L}_{S}}$, рассматриваемых в каноническом представлении, введем два исчисления.

Пусть ${{F}^{1}} = \beta ({{\alpha }^{{{{r}_{1}}}}}(F))$. Применим к ${{F}^{1}}$ α-преобразование максимально возможное число раз ${{r}_{2}}\;({{r}_{2}} \geqslant 1)$. Если ${{\alpha }^{{{{r}_{2}}}}}({{F}^{1}}) \ne \; \bot $, то применим β-преобразование, получив ${{F}^{2}} = \beta ({{\alpha }^{{{{r}_{2}}}}}({{F}^{1}}))$ и т.д. Пусть ${{F}^{{_{n}}}} = \beta ({{\alpha }^{{{{r}_{n}}}}}({{F}^{{n - 1}}}))$ и впервые ${{\alpha }^{{{{r}_{{n + 1}}}}}}({{F}^{{_{n}}}}) = \; \bot $. В результате n-кратного (α, β)-гипотезирования получим условие

именуемое гипотезой-минорантой (ГМ).

Определение 4 (S-исчисления ${{\mathbb{C}}_{\alpha }}$, ${{\mathbb{C}}_{\beta }}$). S-исчисления ${{\mathbb{C}}_{\alpha }} = ( \bot {\kern 1pt} {\kern 1pt} ,\{ \alpha \} )$ и ${{\mathbb{C}}_{\beta }} = ( \bot ,\{ \alpha ,\beta \} )$ – это исчисления в языке ${{L}_{S}}$ c аксиомой ⊥ и указанными преобразованиями в качестве правил вывода. Здесь выводы формулы F – конечные последовательности формул, начинающиеся с формулы F, заканчивающиеся формулой ⊥ и с промежуточными формулами, получаемыми в ${{\mathbb{C}}_{\alpha }}$ с помощью только α-преобразований, а в ${{\mathbb{C}}_{\beta }}$ – с помощью α- и β-преобразований как в построенной ранее для формулы F последовательности: ${{F}^{{_{0}}}},\;{{F}^{{_{1}}}},\;{{F}^{{_{2}}}},...,\;{{F}^{{_{{n + 1}}}}}$, где ${{F}^{{_{0}}}} = F$. Вывод S-формулы F суть ее опровержение.

Теорема 1. Формула $F$ языка ${{L}_{S}}$ противоречива тогда и только тогда, когда F выводима в исчислении ${{\mathbb{C}}_{\alpha }}$.

Доказательство. Пусть формула F – выводима в ${{\mathbb{C}}_{\alpha }}$. Поскольку в процессе вывода формула F конечным числом применений преобразования α приводится к виду ⊥, то для доказательства противоречивости F достаточно доказать, что α – логически эквивалентное преобразование. Пусть F имеет канонический вид (1.1), (2.1), (2.2) или в сокращенном виде

Отсюда в силу условия (2.2) и подстановочности $S$-формул эквивалентными преобразованиями сначала удаляем ${{B}_{{i*j*}}}$. После этого, воспользовавшись дистрибутивностью ∧ относительно ∨, получим

Для доказательства полноты исчисления (т.е. того, что любая противоречивая формула выводима) покажем от противного, что если формула F не выводима, то она выполнима, иначе говоря, для F найдется модель $I$, т.е. интерпретация $I$, в которой F истинна. Пусть F имеет вид (1.1) и не выводима в исчислении ${{\mathbb{C}}_{\alpha }}$.

Рассмотрим каждую базу ${{A}_{i}},\;i \in \overline {1,m} $. Предположим, что A_i – висячая вершина структуры формулы F (т.е. ${{\Omega }_{i}} = {{A}_{i}}$, $\left| {{{\Omega }_{i}}} \right| = \emptyset $). Тогда ${{A}_{i}} \ne false$ ввиду упрощений, упомянутых в конце разд. 1 (в связи с определением 1), и того, что $F \ne \; \bot $. Поэтому интерпретация $I$ вида $I = {{A}_{i}}$ является моделью для Ω_i, а следовательно и для F.

Пусть вершина A_i – невисячая. Если у нее нет уместных вопросов B_ij, $j \in \overline {1,{{n}_{i}}} $, то формируем интерпретацию

где $\neg {{B}_{{ij}}}$ – отрицание конъюнкта ${{B}_{{ij}}}$. Очевидно, что $F$ истинна в ней, так как конъюнкты ${{B}_{{ij}}}$, с которых начинаются все члены конъюнкции – посылки.

Пусть теперь у невисячей базы A_i множество уместных вопросов ${{B}_{{ij}}}$ не пусто. Сформируем из них очередь ${{B}_{i}} = ({{B}_{{i{{j}_{1}}}}},...,{{B}_{{i{{j}_{q}}}}}),$ $\{ {{j}_{1}},...,{{j}_{q}}\} \subseteq \overline {1,{{n}_{i}}} $. Если после просмотра всех баз модель не получена, то очередь каждой базы непустая. Применим α-преобразование к первым вопросам ${{B}_{{i{{j}_{1}}}}}$ всех очередей B_i параллельно. При этом базы A_i приобретут вид $\{ {{A}_{i}} \cup {{С}_{{i{{j}_{1}}k}}}\} $, $k \in \overline {1,{{l}_{{i{{j}_{1}}}}}} $, а ГП типа $({{B}_{{i{{j}_{1}}}}} \to {{\Phi }_{{i{{j}_{1}}}}})$ в них укоротятся до ${{\Psi }_{{i{{j}_{1}}k}}}$; при ${{l}_{{i{{j}_{1}}}}} > 1$ базы размножаются в количестве ${{l}_{{i{{j}_{1}}}}}$.

Повторим выполненный просмотр баз с намерением обнаружить модель $I$ для F. Если, действуя как и раньше, найдем, то доказательство выполнимости F будет завершено, иначе снова для каждой базы из уместных вопросов формируем очередь для применения к ним α-преобразования. В случае неисчерпанности у базы прежней очереди и появления у ней новых уместных вопросов старую очередь с конца наращиваем этими вопросами. Ко всем первым элементам очередей снова применяется α-преобразование и т.д.

В силу невыводимости F и конечности формулы процесс завершится получением такой формулы ${{\alpha }^{n}}(F)$, у которой появится либо висячая база (т.е. без каких-либо вопросов), либо невисячая без уместных вопросов. В обоих случаях конъюнкт базы или его расширение, аналогичное выше использованному, будет искомой моделью I для F. Теорема 1 доказана.

Пусть $\{ T,G,\Delta \} \subset {{L}_{S}}$, $T$ – теория предметной области (контент некоторой базы знаний), $G$ – наблюдаемый эффект. Объяснением наблюдаемого признается гипотеза Δ, удовлетворяющая требованиям:

а) из $T \wedge \Delta $ в исчислении ${{\mathbb{C}}_{\beta }}$ выводимо $G$,

б) $T \wedge \Delta $ – непротиворечиво.

Теорема 2. Пусть ${{F}^{{_{0}}}} = {{(T \wedge \neg G)}^{{{{L}_{S}}}}}$ – образ отрицания формулы $(T \to G)$ в языке ${{L}_{S}}$. Пусть также $P \in {{L}_{S}}$ и P построено (α, β)-гипотезированиями в процессе вывода формулы F⁰в исчислении ${{\mathbb{C}}_{\beta }}$. Тогда $P \leftrightarrow (T \to G)$ и для любой гипотезы Δ, объясняющей $G$, cправедливо $\Delta \to P$.

Доказательство. Докажем от противного, что $P \to (T \to G)$. Пусть истинно P, а $(T \to G)$ ложно, т.е. имеет место $P \wedge {{F}^{{_{0}}}}$. Условие P имеет вид

где $F_{\alpha }^{{k - 1}} = {{\alpha }^{{{{r}_{k}}}}}({{F}^{{k - 1}}}),$ ${{F}^{k}} = \beta (F_{\alpha }^{{k - 1}}).$

Пусть $F_{\alpha }^{{k - 1}}$ имеет вид

При β-преобразовании формулы $F_{\alpha }^{{k - 1}}$ все $P_{i}^{k}$ встраиваются в Ω_i конъюнктивно (см. (2.4), (2.5)), усиливая Ω_i до $\Omega _{i}^{*}$, т.е. ${{F}^{k}} = F_{\alpha }^{{k - 1}}(\Omega _{i}^{*}{\text{/}}\Omega _{i}^{{}},\;\forall i \in \overline {1,{{m}^{k}}} ),$ $\Omega _{i}^{*} = P_{i}^{k} \wedge {{\Omega }_{i}}$.

Так как $F_{\alpha }^{{k - 1}} \leftrightarrow {{F}^{{k - 1}}},$

а $P = \mathop \wedge \limits_{k = 1}^n {{P}^{k}},$ то $P \wedge F_{{}}^{0} \to F_{{}}^{n}.$ Поскольку $F_{{}}^{n} \leftrightarrow F_{\alpha }^{n} = \; \bot $, то полученное противоречие доказывает, что $P \to (T \to G)$: в теории T условие P – объяснение наблюдаемого G.

Рассмотрим теперь необходимость условия P, т.е. что $(T \to G) \to P$. Снова действуя от противного, предположим, что справедливо $(T \to G) \wedge \neg P,$ т.е. $\neg {{F}^{0}} \wedge \neg P$. Проверим, что это приводит к противоречию. Вначале докажем, что

Пусть $F_{\alpha }^{{k - 1}}$ имеет вид (3.1). Так как

то для доказательства (3.2) достаточно вывести противоречие из предположений о том, что справедливо $\forall i \in \overline {1,{{m}^{k}}} \neg {{\Omega }_{i}}$ и $\exists i{\kern 1pt} * \in \overline {1,{{m}^{k}}} \neg P_{{i{\kern 1pt} *}}^{k}$. Возможны только два случая, разбором которых обосновывается (3.2):

1) $\Omega _{{i{\kern 1pt} *}}^{{}} = {{A}_{{i{\kern 1pt} {\kern 1pt} *}}}$, $P_{{i{\kern 1pt} *}}^{k} = ({{A}_{{i{\kern 1pt} *}}} \to false),$ при этом $\neg \Omega _{i}^{\,} \wedge \neg P_{{i{\kern 1pt} *}}^{k}\; \leftrightarrow \;\neg A_{{i{\kern 1pt} *}}^{{}} \wedge A_{{i{\kern 1pt} *}}^{{}} \leftrightarrow false$;

2) Ω_i* = A_i* ∧ $\left( {\mathop \wedge \limits_{j = 1}^{{{n}_{{i*}}}} ({{B}_{{i*j}}} \to {{\Phi }_{{i*j}}})} \right)$, $P_{{i*}}^{k}$ = $\left( {{{A}_{{i*}}} \to \mathop \vee \limits_{j = 1}^{{{n}_{{i*}}}} {{B}_{{i*j}}}} \right)$ , при этом

Так как $F_{{}}^{k} = \beta (F_{\alpha }^{{k - 1}}),$ $F_{\alpha }^{{k - 1}} \leftrightarrow F_{{}}^{{k - 1}}$ и $\beta (F_{\alpha }^{{k - 1}}) \to F_{\alpha }^{{k - 1}}$, то $\forall k \in \overline {1,n} $ $(F_{{}}^{k} \to \;F_{{}}^{{k - 1}})$. Отсюда и из (3.2) следует, что $\neg {{F}^{0}} \to {{P}^{1}} \wedge \neg {{F}^{1}},$ $\neg {{F}^{1}} \to {{P}^{2}} \wedge \neg {{F}^{2}}\;\;, \ldots ,\;\;\neg {{F}^{{n - 1}}} \to {{P}^{n}} \wedge \neg {{F}^{n}}$. Поэтому $\neg {{F}^{0}} \to \mathop \wedge \limits_{k = 1}^n {{P}^{k}}$, т.е. $(T \to G) \to P,$ что и требовалось доказать.

Поскольку всякая гипотеза, объясняющая наблюдаемое $G$, должна удовлетворять по определению условию $T \wedge \Delta \to G$, то отсюда и из доказанного свойства необходимости гипотезы-миноранты $P$ вытекает, что $\Delta \to P$. Теорема 2 доказана.

4. Примеры применения исчислений. Рассмотрим примеры гипотез-минорант P и достаточных условий их выполнимости, полученных путем удаления из минорант элементов, несовместимых с теорией T (примеры 1 и 2), или путем привлечения эмпирических знаний (пример 2). Эмпирические знания могут расширять знания базовой теории об априорном множестве потенциально возможных причин-кандидатов и, кроме того, могут дополнять базовую теорию достоверных причинно-следственных связей также лишь правдоподобными причинно-следственными связями. Преобразованиями миноранты $P$ получаются либо сами причины Δ-эффекта G (достоверные или правдоподобные), либо релевантные обстоятельства (пример 1), из которых в рамках теории Т средствами исчислений ${{\mathbb{C}}_{\alpha }}$ или ${{\mathbb{C}}_{\beta }}$ оказываются выводимыми и сами причины. Не предполагается какой-либо предварительной трансформации теории Т  до формы “if-and-only-if” (см. Введение) с ацикличностью множества “причинных переменных”, частично упорядоченного импликацией [1, 2].

Пример 1. Рассмотрим простой пример из области диагностики автомобиля (знания приведенного ниже типа сформулированы в [7] для иллюстрации концепции экспертных систем в ИИ).

Пусть некоторые пропозициональные переменные языка ${{L}_{S}}$ имеют следующий смысл: Ф – “Фары горят”; Б – “в Баке топливо есть”; К – “топливо поступает в Карбюратор”; Д – “топливо поступает в Двигатель”; В – “двигатель Вращается”; И – “автомобиль Исправен”; А – “проблема – в Аккумуляторе”, З – “проблема – в свечах Зажигания”, С – “проблема – в Стартере”. Допустим, что автомобиль неисправен и выявлены факты Ф, В, К. Предположим, что, помимо этих фактов, базовая теория T включает знания, которые в естественном языке имеют вид: Если топливо поступает в двигатель и двигатель вращается, то проблема – в свечах зажигания. Если в баке топливо есть и топливо поступает в карбюратор, то топливо поступает в двигатель. Если двигатель не вращается, то при горящих фарах проблема – в стартере, при негорящих – в аккумуляторе. Если автомобиль исправен, то проблем в свечах зажигания, стартере и аккумуляторе нет.

Базовая теория $T$ в языке ${{L}_{S}}$ представима формулой:

Наблюдаемое G  состоит в неисправности автомобиля: $G = \neg И$, а вывод объяснения в S-исчислении ${{\mathbb{C}}_{\beta }}$ начинается с формулы ${{F}^{{_{0}}}} = {{(T \wedge \neg G)}^{{{{L}_{S}}}}}$. Ее база $\{ Ф,В,Б,И\} $ при получении F¹ (однократным применением α-преобразования к ${{F}^{{_{0}}}}$) дополнится элементами множества $\{ \neg З,\neg С,\neg А\} $.

Применением β-преобразования получится гипотеза-миноранта

После представления ее в форме элементарной дизъюнкции и удаления из нее членов $\neg Ф,\neg В,\neg Б,\neg И$, контрарных элементам базы из F¹, а также тривиального члена $З \vee С \vee А$ получается объяснение $Д \vee К$ в классе релевантных обстоятельств. Действительно, далее в рамках исчисления ${{\mathbb{C}}_{\alpha }}$ промежуточным элементом вывода формулы ${{(T \wedge \neg G \wedge (Д \vee К))}^{{{{L}_{S}}}}}$, включившей полученное релевантное обстоятельство, оказывается факт $З$ как причина неисправности.

Пример 2. Рассмотрим другой иллюстративный пример, а именно из области медицины [1], не приводя для краткости детальной семантики переменных (cтатья [1] посвящена представлению знаний в диагностике с достоверными и эмпирическими знаниями).

Пусть e, h – симптомы заболевания. Известны болезни $t,d,a$. Допустим, что $\{ t \to e,\;a \to h\} $ – множество достоверных причинно-следственных связей базовой теории T в терминах симптомов e, h и болезней t, a: “болезнь t – причина симптома е “; “болезнь а – причина симптома h “. Пусть $\{ d \to h,a \to e\} $ – правдоподобные (недостоверные) причинно-следственные связи (ППСС) как эмпирические данные “прошлого опыта”; например, ППСС $d \to h$ (соответственно $a \to e$) – это высказывание: “болезнь d (соответственно а) иногда может являться причиной симптома $h$ (соответственно е)”.

Пример интересен, в частности, и тем, что словарь базовой теории $T$ не охватывает словаря ППСС (нет болезни d). Тем не менее, из гипотезы-миноранты, выводимой средствами (α, β)-гипотезирования, получаются все логически возможные в рассматриваемом контексте диагнозы.

Если наблюдается симптом $G = e$, то ${{F}^{{_{0}}}} = {{(T \wedge \neg G)}^{{{{L}_{S}}}}} = (true \to \neg е \wedge [(t \to e) \wedge (a \to h)])$.

В исчислении ${{\mathbb{C}}_{\beta }}$ при выводе F  ⁰ формируется гипотеза-миноранта P = $\mathop \wedge \limits_{k = 1}^2 P({{\alpha }^{{{{r}_{k}}}}}({{F}^{{_{{k - 1}}}}}))$ = = $(\neg e \to (t \vee a)) \wedge (\{ \neg e,a,h\} \to t).$

При этом ${{r}_{1}} = 0,$ ${{r}_{2}} = 3,$ ${{r}_{3}} = 2$ и ${{\alpha }^{{{{r}_{3}}}}}({{F}^{{_{2}}}}) = \; \bot $. Все элементарные дизъюнкции конъюнктивной нормальной формы (КНФ) $(e \vee t \vee a) \wedge (e \vee t \vee \neg a \vee \neg h)$ гипотезы-миноранты P следуют из $t$, т.е. болезнь $t$ – объяснение симптома $e$.

Этот диагноз не использует ППСС. С учетом же их и того, что оба члена КНФ следуют из $a$ и $a \to e$ соответственно, выводится еще одно (лишь правдоподобное) объяснение: “причина – в болезни $a$, если верна ППСС $a \to e$”.

Пусть теперь наблюдаются одновременно не один, а два симптома: $G = e \wedge h$. Выявление причин использует вывод формулы

При этом формируется гипотеза-миноранта

и на ее основе – три следующих объяснения:

1) “комплекс из двух причин {t, a}” (достоверно);

2) “если верна ППСС $a \to e$, то причина – в $a$” (правдоподобно);

3) “комплекс из двух причин d, t и ППСС $d \to h$” (правдоподобно).

Третье объяснение получается из (4.1) после расширения сигнатуры формулы (4.1) дополнительной причинной переменной d путем замены каждой элементарной дизъюнкции на две другие, получающиеся добавлением в одну переменной d, а во вторую – литералы $\neg d$. Каждая из элементарных дизъюнкций расширенной КНФ будет следовать из причин d, t и ППСС $d \to h$, что и оказывается третьим объяснением наблюдаемого комплекса симптомов $G = e \wedge h$. Заметим, что расширение словаря для применимости ППСС $d \to h$ с формированием этого объяснения было необходимо для выполнения лишь второго члена гипотезы-миноранты из (4.1).

Заключение. Работа посвящена проблематике абдуктивного объяснения наблюдаемых эффектов (аномалий, симптомов). Изложен и обоснован метод логического формирования объяснений. Предложены средства представления знаний и вывода объясняющих гипотез. Введен язык, обладающий свойством подстановочности. Свойства языка и вводимых в нем исчислений обеспечивают абдукцию путем сочетания дедукции с гипотезированием. В отличие от известных логических средств абдукции, предложенным методом выводятся гипотезы-миноранты, являющиеся логически необходимыми и достаточными условиями для формального объяснения наблюдаемого. Эту миноранту любая объясняющая гипотеза должна иметь своим логическим следствием.

Гипотеза-миноранта выступает контрольным условием и опорным средством формирования достоверных гипотез, а в случае наличия сверхбазовой теории также эмпирических знаний, то и средством формирования также правдоподобных гипотез. Эмпирические знания могут расширять знания базовой теории об априорном множестве потенциально возможных причин-кандидатов и, кроме того, могут дополнять базовую теорию достоверных причинно-следственных связей также ППСС. Из гипотезы-миноранты переходом к достаточным условиям путем ее упрощения и использования эмпирических знаний получаются либо причины наблюдаемого эффекта (достоверные или правдоподобные), либо поначалу лишь релевантные обстоятельства (факты, события, “улики”), из которых в рамках базовой теории средствами разработанных исчислений оказываются выводимыми и сами причины. Не предполагается какой-либо предварительной трансформации базовой теории, нередко используемой в литературе для упрощения вывода гипотез. Предложенный метод абдуктивного вывода обоснован и проиллюстрирован примерами.

Актуальной задачей остается проблематика ранжирования альтернативных объяснений наблюдаемого для сужения множества гипотез до наиболее достоверных с использованием вероятностных, логических и других оценок. Актуальной задачей на будущее, особенно в проблематике интеллектуализации автономных (беспилотных) агентов, является также задача абдуктивной информационной поддержки планирования действий агентов с развитием полученных здесь результатов.