Известия РАН. Теория и системы управления, 2021, № 1, стр. 124-159

Введение. Когда речь идет о нахождении путей в графах, часто имеют в виду кратчайшие пути, в том числе с учетом их веса. Методы вычисления кратчайших путей принадлежат к числу популярных разделов компьютерной математики. Вместе с тем для управления транспортными сетями актуальны задачи отыскания не только кратчайших, но вообще всех возможных простых путей, и не только между двумя вершинами графа, но также между непересекающимися множествами вершин. Это особенно важно для электрических сетей, поскольку в передаче электроэнергии от одного узла электросети к другому участвуют все электрические цепи, соединяющие эти два узла. Применения разработанного аппарата, рассмотренные в статье, относятся в основном к сфере оперативно-диспетчерского управления электрическими сетями.

Используя накопленный опыт и интуицию, диспетчер в определенных сложных ситуациях может находить решения быстрее и точнее, чем при помощи существующих формальных методов. Но для этого он должен располагать максимально полной информацией о процессах, протекающих в энергосистеме в реальном времени, и эту информацию следует предоставлять ему в форме, наиболее удобной для восприятия [1, 2 ] . В частности, диспетчеру нужно обеспечить возможность видеть на мониторе или видеостене все электрические цепи, соединяющие группы узлов, которые он укажет. Множество таких цепей – простых путей в графе – нужно представлять в компактной форме, удобной также для автоматических приложений. Этой цели служит предложенное в статье понятие графа путей.

1. Постановка задачи. Пусть G – неориентированный граф. Будем решать следующие четыре задачи.

Задача I. Найти совокупность всех простых путей, соединяющих две вершины графа G.

Задача II. Найти совокупность всех простых путей, соединяющих вершину α графа G со всеми вершинами заданного подмножества S множества вершин этого графа, где α ∉ S.

Задача III. Найти совокупность всех простых путей, соединяющих попарно вершины заданного подмножества множества вершин графа G.

Задача I является частным случаем как задачи II, так и задачи III. В свою очередь две последние задачи представляют частные случаи следующей.

Задача IV. Найти совокупность всех простых путей, соединяющих попарно вершины разных множеств, принадлежащих заданному семейству непересекающихся подмножеств множества вершин графа G.

Все четыре задачи актуальны для приложений. Будем называть их задачами соединения вершин графа простыми путями. Соотношение между ними в смысле уровня общности показаны на рис. 1. Стрелки указывают направления обобщения.

Вычисления множеств простых путей, о которых говорится в задачах I–IV, производятся как для отображения этих путей на мониторах оперативно-диспетчерского персонала и на видеостенах в центрах диспетчерского управления, так и для использования в программных приложениях. Предмет настоящей статьи составляют методы построения общих решений этих задач и их приложения к управлению транспортными сетями. Методы общих решений основаны на формулируемых в статье теоремах, доказательства которых даны в Приложении.

Автор не нашел в литературе общепринятых алгоритмов решения задач I–IV. В электронной энциклопедии [3] упоминается задача I, которая названа там “классической”, но никаких ссылок на публикации по ней не дано. На русскоязычных и зарубежных интернет-форумах программистов неоднократно встречается задача I и некоторые случаи задачи IV [4–6]. На форумах и в блогах имеется много советов и рецептов по их решению, среди которых можно встретить и правильные, но без математических обоснований и без ссылок на публикации [7]. Для профессионального математика, владеющего теорией графов, распознавание верных и работоспособных предложений среди этой массы и проверка их корректности может не составить большой проблемы. Однако это, как правило, не под силу обычному программисту, не освоившему теорию графов достаточно глубоко. Обсуждения на форумах свидетельствуют о необходимости систематического изложения теории решений задач I–IV.

В статье рассматриваются только неориентированные графы, не содержащие петель и параллельных ребер. Слово “неориентированный” часто будем опускать. Для однозначности понимания терминов напомним определения некоторых понятий теории графов.

Путем в неориентированном графе называется подграф, образованный объединением ребер, принадлежащих последовательности, в которой каждая пара соседних ребер имеет ровно одну общую вершину. Если α и β – концевые вершины¹¹ этого пути как подграфа, то говорят, что путь соединяет α и β. Путь определяет последовательность вершин, проходимых при движении по нему от α до β. Путь называется простым, если вершины в этой последовательности не повторяются. Это означает, в частности, что концевые вершины простого пути различны. Если α = β, то путь от α до β называется циклом графа. Цикл называется простым, если при его однократном обходе промежуточные вершины не повторяются.

Неориентированный связный граф, имеющий более двух вершин, называется вершинно двусвязным, если после удаления какой-либо его вершины (вместе с инцидентными этой вершине ребрами) оставшийся граф будет связным. Неориентированный связный граф называется реберно двусвязным, если после удаления какого-либо ребра оставшийся граф будет связным. Вершинно двусвязный граф является реберно двусвязным. Реберно двусвязные графы специально в статье не выделяются, поэтому вершинно двусвязные графы далее именуются, как правило, просто двусвязными. Это соответствует распространенной практике.

Максимальный двусвязный подграф неориентированного графа называется его компонентой двусвязности. Если ребро графа не принадлежит никакой компоненте двусвязности графа, оно называется мостом. Блоком графа называется его подграф, являющийся либо компонентой двусвязности, либо мостом (вырожденный блок). Два блока графа могут иметь не более одной общей вершины. Общая вершина двух блоков графа называется шарниром или точкой сочленения (блоков) графа.

В статье показано, что решения задач I–IV сводятся к вычислению блоков графа G – компонент его вершинной двусвязности и мостов. Это вычисление будем называть также анализом двусвязности графа G. Известный алгоритм анализа двусвязности графов разработали Р.Э. Тарьян и Дж.Э. Хопкрофт [8–10]. Этот алгоритм излагается практически во всех руководствах, где рассматривается анализ двусвязности графов [11–18].

2. Операции над графами. Для сокращения и упрощения записи решений задач в статье применяется символика алгебры графов. Используются, прежде всего, обычные операции объединения, пересечения и разности (вычитания) графов. Они обозначаются символами “+”, “&” и “–” соответственно. Применение данных символов вызвано тем, что простейший метод программирования операций над графами в объектно-ориентированных языках (таких, как С++) основан на возможности переопределять смысл этих и некоторых других символов операций [19, 20]. Преобразование алгоритма в компьютерную программу облегчается, когда операции над графами выражены в нем такими символами.

Кроме того, используются четыре специальные операции над неориентированными графами:

A ÷ B – оголение графа A посредством графа B (удаление ребер графа B из графа A);

A * B – приращение графа A в графе B;

A ^ B – простое (односвязное) замыкание графа A в графе B;

A || B – двусвязное замыкание графа A в графе B.

Используемые здесь символы бинарных операций “÷”, “*”, “^” и “ || ” тоже допускают переопределение смысла в языке С++. Для графов эти операции определяются следующим образом.

Операция A÷B оголения²² графа A посредством графа B состоит в удалении из графа A: 1) всех ребер графа A&B и 2) каждой такой вершины графа A&B, которая становится изолированной в остающемся от A графе после удаления из A всех ребер графа A&B. Удаляются в том числе все изолированные вершины графа A, принадлежащие графу B.

При обычном вычитании графов A–B из графа A удаляются все вершины графа B, а также все ребра графа A, инцидентные этим вершинам. При оголении A÷B графа A посредством графа B из A удаляются все ребра графа B, а также каждая такая вершина графа A&B, у которой удалены все инцидентные ей ребра графа A.

Приращение A*B графа A в графе B определяется как объединение графа A со всеми такими ребрами графа B, у которых хотя бы один конец принадлежит A. При этом каждое ребро рассматривается как граф, состоящий из одного этого ребра и двух вершин – концов данного ребра.

Простое (односвязное) замыкание A^B графа A в графе B (или посредством B) есть по определению объединение графа A со всеми компонентами связности графа B, имеющими непустое пересечение с A. Если α – вершина графа G, то α^G есть компонента связности графа G, содержащая вершину α. Операция простого замыкания графов используется во многих алгоритмах анализа топологии электрических схем [21–23]. Из определения операции A^B вытекает ее выражение через операцию приращения:

В правой части этого равенства приращение повторяется до стабилизации результата.

Двусвязное замыкание A || B графа A в графе B (или посредством B) определяется как объединение графа A со всеми компонентами вершиной двусвязности графа A + B, содержащими ребра графа A. Это эквивалентно объединению графа A со всеми простыми циклами графа A + B, имеющими общее ребро с A. Граф A || B равен объединению всех блоков графа A + B, содержащих ребра A, и всех изолированных вершин графа A. Если x – ребро графа G, то x || G есть блок графа G, содержащий ребро x.

Пустой граф обозначаем символом ∅.

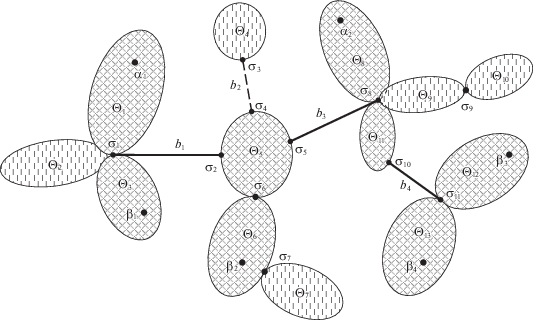
3. Выражение графа простых путей, соединяющих две вершины графа, через структуру двусвязности графа. Пусть {Θ_i} – множество блоков графа G, {σ_j} – множество его шарниров. Построим граф BC(G), множеством вершин которого является {Θ_i} + {σ_j}, т.е. каждая вершина графа BC(G) будет представлять либо блок графа G, либо шарнир. Ребро графа BC(G) по определению есть пара (Θ, σ), когда шарнир σ принадлежит блоку Θ. Граф BC(G) является деревом [24, с. 141]. Это дерево называется деревом блоков и шарниров графа G [13, 25]. Тройку {{Θ_i}, {σ_j}, BC(G)} будем называть структурой двусвязности графа G или его блоковой структурой.

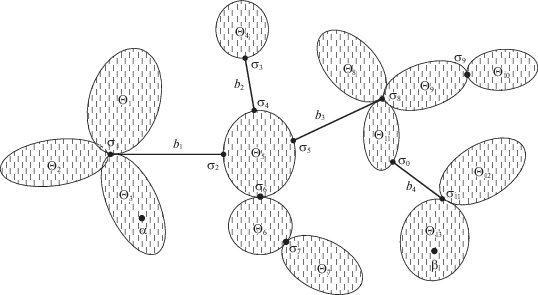
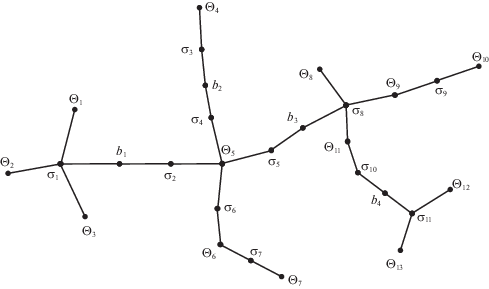
На рис. 2 показан пример декомпозиции связного графа G на блоки: компоненты вершинной двусвязности Θ₁, Θ₂, …, Θ₁₃ и мосты b₁, b₂, b₃, b₄ (сам граф G не показан). Блоки соединены между собой шарнирами σ₁, σ₂, …, σ₁₁. Дерево блоков и шарниров BC(G) графа G показано на рис. 3.

Число простых путей, которые нужно найти в задачах соединения простыми путями вершин графа, растет, вообще говоря, очень быстро относительно роста числа вершин или ребер графа. Например, нетрудно подсчитать, что в полном n-вершинном графе K_n число простых путей только длины n–1 (максимально возможной в этом графе) между двумя вершинами равно (n–2)!. Необходим какой-то более операбельный способ представления множества искомых путей, чем просто их перечисление. Разумный способ такого представления состоит в объединении всех этих путей, как графов. Получаемый граф будем называть графом путей для соответствующей из задач I–IV. Как показано ниже, из него несложно извлечь любой простой путь, участвующий в объединении.

Понятие графа путей дает практически работоспособное решение вопроса об адекватном представлении множеств простых путей, определяемых в задачах I–IV. Во всех приложениях, где требуется получить множество простых путей как решение одной из задач типа I–IV, достаточно построить именно граф этих простых путей.

В случае задачи I графом путей будет объединение всех простых путей в графе G, соединяющих вершины α и β этого графа. Этот граф путей обозначим P(G, α, β). Будем называть его графом простых путей от α до β, а также графом простых путей, соединяющих α и β. Также будем называть этот граф общим решением задачи I для вершин α и β. Всякий простой путь, соединяющий эти две вершины в графе G, будем называть частным решением задачи I. Если вершины α и β принадлежат разным компонентам связности графа G, то считаем граф P(G, α, β) пустым.

Следующая теорема устанавливает, что граф P(G, α, β) строится посредством декомпозиции графа G на блоки.

Теорема 1. Пусть L – простой путь в связном графе G, соединяющий вершины α и β; Θ₀, Θ₁, …, Θ_n – множество всех тех блоков графа G, каждый из которых содержит хотя бы одно из ребер пути L. Тогда:

1) семейство блоков Θ₀, Θ₁, …, Θ_n не зависит от выбора пути L из множества всех простых путей, соединяющих вершины α и β: оно однозначно определено парой α и β;

2) семейство блоков Θ₀, Θ₁, …, Θ_n можно линейно упорядочить в такую цепочку, в которой первый и последний блоки содержат вершины α и β соответственно, а пересечение каждых двух соседних блоков в цепочке состоит из их общего шарнира;

3) граф простых путей, соединяющих α и β, есть объединение блоков Θ₀, Θ₁, …, Θ_n:

Итак, для любой пары вершин α и β неориентированного графа G граф P(G, α, β) простых путей, соединяющих эти две вершины, есть последовательная цепочка блоков графа G, соединенных шарнирами. Эта цепочка блоков определяется только тем, каким блокам графа G принадлежат вершины α и β.

Из теоремы 1 следует также, что если вершина α является шарниром графа G, то графу путей P(G, α, β) принадлежит только один из блоков, которым принадлежит этот шарнир. То же относится к вершине β.

Следствие 1 теоремы 1. Если вершины α и β графа G принадлежат одному блоку Θ этого графа, то граф простых путей P(G, α, β) совпадает с блоком Θ:

Ребро неориентированного графа принадлежит ровно одному блоку. Блок графа G, содержащий ребро x = (α, β), будем обозначать Θ(G, x) или Θ(G, (α, β)). Из следствия 1 теоремы 1 вытекает соотношение, связывающее этот блок с графом простых путей P(G, α, β).

Следствие 2 теоремы 1. Пусть α и β – концы одного ребра графа G. Тогда блок Θ(G, (α, β)) графа G, содержащий ребро (α, β), совпадает с графом простых путей P(G, α, β):

Ребро графа не может принадлежать двум разным блокам. Поэтому блок графа однозначно определяется заданием какого-либо его ребра. Равенство (3.3) выражает блок графа, содержащий заданное ребро, через граф простых путей, соединяющих концы этого ребра. А равенство (3.1), наоборот, выражает граф простых путей, соединяющих две вершины графа, через совокупность блоков графа. Сочетание этих двух формул дает полное выражение соответствия между блоками графа и подграфами простых путей, соединяющих пары вершин в этом графе.

Следствие 3 теоремы 1. Пусть L – простой путь, соединяющий вершины α и β графа G. Тогда

Эта формула непосредственно следует из теоремы 1 и определения операции двусвязного замыкания. Она дает простое выражение общего решения P(G, α, β) задачи I через произвольно взятое частное решение L этой задачи.

Пусть x = (α, β). Тогда ребро x есть простой путь, соединяющий вершины α и β графа G. Из формулы (3.4) получаем

4. Выражение графа простых путей, соединяющих множества вершин графа, через структуру двусвязности графа. Пусть Q – подмножество множества вершин связного графа H; T – дерево, являющееся подграфом графа H. Будем говорить, что дерево T соединяет множество вершин Q, если Q ⊆ T и каждая концевая вершина дерева T принадлежит множеству Q. Дерево T – один из минимальных подграфов графа H в множестве связных подграфов последнего, содержащих все вершины множества Q. Если дерево T, соединяющее множество вершин Q, есть простой путь, то будем говорить, что простой путь T соединяет множество вершин Q.

Пусть S – подмножество множества вершин связного графа G; BC(G) – дерево блоков и шарниров графа G. Как будет показано далее, для решения задач II–IV нужно выделить в этом дереве такое минимальное поддерево, которое будет представлять все блоки графа G, содержащие вершины множества S. Для этого введем понятие вершины дерева BC(G), релевантной множеству S.

Вершину τ дерева BC(G) будем называть релевантной подмножеству S множества вершин графа G, если выполнено одно из двух условий:

– τ представляет шарнир графа G, принадлежащий множеству S;

– τ представляет такой блок графа G, который содержит хотя бы одну вершину множества S, не являющуюся шарниром графа G.

Пусть Q – множество вершин дерева BC(G), релевантных множеству S. Обозначим через Z(G, S) поддерево дерева BC(G), соединяющее множество Q. Дерево Z(G, S) может содержать также вершины графа BC(G), не релевантные множеству S. Эти вершины не будут концевыми в дереве Z(G, S). Это могут быть, во-первых, вершины, представляющие шарниры графа G, не принадлежащие множеству S. Во-вторых, это могут быть вершины, представляющие такие блоки графа G, которые не содержат вершин множества S, отличных от шарниров.

Следующая теорема дает выражение решения задачи IV через структуру двусвязности графа.

Теорема 2. Пусть:

– {S₁, S₂, …, S_K} – семейство попарно непересекающихся подмножеств множества вершин связного графа G; S = S₁ + S₂ + … + S_K;

– W(G, S₁, S₂, …, S_K) – объединение, как графов, всех простых путей, которые соединяют всевозможные пары вершин, принадлежащих различным множествам семейства {S₁, S₂, …, S_K};

– BC(G) – дерево блоков и шарниров графа G;

– Z(G, S) – поддерево дерева BC(G), соединяющее множество вершин дерева BC(G), релевантных множеству S.

Тогда:

1) граф W(G, S₁, S₂, …, S_K) является объединением тех блоков графа G, которые представлены в дереве BC(G) вершинами, принадлежащими поддереву Z(G, S);

2) дерево блоков и шарниров графа W(G, S₁, S₂, …, S_K) получается из дерева Z(G, S) удалением концевых вершин, представляющих шарниры графа G.

Граф W(G, S₁, S₂, …, S_K) будем называть общим решением задачи IV для семейства {S₁, S₂, …, S_K}, а также графом путей, соединяющих попарно вершины семейства {S₁, S₂, …, S_K} непересекающихся подмножеств множества вершин графа G.

Из теоремы 2 следует, что дерево Z(G, S) не зависит от разбиения множества S = S₁ + S₂ + … + S_K на подмножества S₁, S₂, …, S_K. Следовательно, от этого разбиения не зависит и дерево блоков и шарниров графа путей W(G, S₁, S₂, …, S_K). Отсюда вытекает следующее утверждение.

Следствие 1 теоремы 2. Пусть {S₁, S₂, …, S_K} – семейство попарно непересекающихся подмножеств множества вершин связного графа G; W(G, S₁, S₂, …, S_K) – общее решение задачи IV для семейства {S₁, S₂, …, S_K}.

Тогда граф W(G, S₁, S₂, …, S_K) не зависит от разбиения множества S на непересекающиеся подмножества S₁, S₂, …, S_K.

Таким образом, граф путей W(G, S₁, S₂, …, S_K) не зависит от распределения вершин множества S₁ + S₂ + … + S_K между отдельными множествами S₁, S₂, …, S_K. Граф W(G, S₁, S₂, …, S_K) зависит только от объединения S = S₁ + S₂ + … + S_K.

Разбивая множество S на семейство одноэлементных подмножеств, получаем, что задача IV сводится к ее частному случаю – задаче III. Для задачи III теорема 2 получает следующую формулировку.

Следствие 2 теоремы 2. Пусть:

– S – подмножество множества вершин связного графа G;

– W(G, S) – объединение как графов всех простых путей в графе G, соединяющих попарно все вершины множества S;

– BC(G) – дерево блоков и шарниров графа G;

– Z(G, S) – поддерево дерева BC(G), соединяющее множество вершин дерева BC(G), релевантных множеству S.

Тогда:

1) граф W(G, S) является объединением тех блоков графа G, которые представлены в дереве BC(G) вершинами, принадлежащими поддереву Z(G, S);

2) дерево блоков и шарниров графа W(G, S) получается из дерева Z(G, S) удалением концевых вершин, представляющих шарниры графа G.

Граф W(G, S) будем называть графом простых путей, соединяющих вершины множества S в графе G, а также общим решением задачи III для множества S и задачи IV для любого разбиения множества S. Это понятие обобщает понятие общего решения задачи I, каковым является граф путей P(G, α, β).

Поскольку W(G, S) = W(G, S₁, S₂, …, S_K), граф W(G, S₁, S₂, …, S_K) содержит также все простые пути между всеми вершинами каждого из множеств S_k, k = 1, 2, …, K.

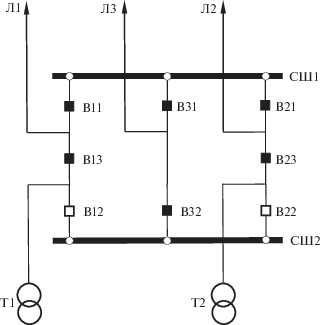
Теорему 2 проиллюстрируем примером графа G, блоковая декомпозиция которого приведена на рис. 2, а дерево блоков и шарниров – на рис. 3. Предположим, что в множестве вершин этого графа выделены два непересекающихся подмножества S₁ = {α₁, α₂} и S₂ = {β₁,β₂, β₃, β₄}. Пусть дано, что эти вершины распределены по компонентам вершинной двусвязности графа G следующим образом (рис. 4):

В соответствии с теоремой 2 строим дерево блоков и шарниров BC(G) графа G и находим в нем поддерево Z(G, S), соединяющее все вершины, релевантные множеству S = S₁ + S₂. На рис. 5 ребра поддерева Z(G, S) показаны сплошными линями, остальные ребра дерева BC(G) – штриховыми линиями.

Согласно теореме 2 и следствию 1 из нее, граф путей W(G, S) есть объединение всех блоков, представленных вершинами поддерева Z(G, S). Находим, что этими блоками будут компоненты вершинной двусвязности Θ₁, Θ₃, Θ₅, Θ₆, Θ₈, Θ₁₁, Θ₁₂, Θ₁₃ и мосты b₁, b₃, b₄. Первые выделены на рис. 4 “сеточной” штриховкой. Прочие компоненты вершинной двусвязности графа G заполнены вертикальной штриховкой. Мосты графа G, принадлежащие графу путей W(G, S), показаны на рис. 4 сплошными линиями, единственный мост b₂, не вошедший в этот граф путей, – штриховой линией.

5. Общие и частные решения задач соединения вершин графа простыми путями. Пусть {S₁, S₂, …, S_K} – семейство попарно непересекающихся подмножеств множества вершин связного графа G; S = S₁ + S₂ + … + S_K. Граф W(G, S₁, S₂, …, S_K), являющийся общим решением задачи IV для семейства {S₁, S₂, …, S_K}, совпадает с общим решением W(G, S) задачи III для множества S.

Обобщая понятие частного решения задачи I, будем называть частным решением задачи III для множества S в связном графе G любое дерево в этом графе, соединяющее все вершины множества S. Частным решением задачи IV для семейства множеств {S₁, S₂, …, S_K} в связном графе G назовем любое дерево в графе G, соединяющее все вершины множества S = S₁ + S₂ + … + S_K.

Найти какое-нибудь частное решение задач III и IV для связного графа G нетрудно, даже не имея общего решения. Построим в графе G какое-нибудь остовное дерево T. Оно будет содержать все вершины графа G. Концевые вершины дерева T могут не принадлежать множеству S. Найдем в дереве T минимальное поддерево T(S), содержащее все вершины множества S. Дерево T(S) соединит множество вершин S графа G. Чтобы получить T(S) из T, нужно концевые вершины, не принадлежащие множеству S, удалить одну за другой из дерева T и получаемых из него деревьев. Дерево T(S) будет частным решением задачи III для множества S в связном графе G, а также задачи IV для любого разбиения множества S.

Имея какое-нибудь частное решение задачи III или IV, нетрудно найти общее решение той и другой задачи. Следующая теорема устанавливает формулу, которая позволяет получить общее решение задачи III или IV, исходя из любого частного решения.

Теорема 3. Пусть S – подмножество множества вершин связного графа G; T(S) – дерево, соединяющее множество вершин S в графе G; W(G, S) – объединение как графов всех простых путей в графе G, соединяющих попарно все вершины множества S. Тогда

Формула (5.1) дает простое выражение общего решения W(G, S) задачи III через произвольно взятое частное решение T(S) этой задачи. То же относится к задаче IV. Данная формула говорит о том, что для построения общего решения W(G, S) нужно найти все блоки графа G, выбрать из них те, которые содержат ребра дерева T(S), и объединить эти блоки как графы. Тем самым отпадает построение дерева блоков и шарниров BC(G) графа G, необходимое при построении общего решения на базе теорем 1 или 2.

Формула (5.1) обобщает формулу (3.4), которая аналогичным образом выражает общее решение задачи I через какое-либо ее частное решение. В обоих случаях общее решение получается благодаря применению операции двусвязного замыкания “ | | ”. Вычисление двусвязного замыкания $T(S)||G$ можно осуществить последовательным присоединением циклов из предварительно найденной фундаментальной системы циклов графа G. Эти циклы нужно объединять через общие ребра сначала с графом T(S), затем с итерационно получаемыми объединениями.

Построение общего решения W(G, S) задач III и IV на основе теоремы 3 допускает также следующую наглядную интерпретацию. Можно считать, что к дереву T(S) добавляются все “обходные” (“шунтирующие”) простые пути, возможные в графе G. “Обходным” путем для связного графа H считаем простой путь, концевые вершины которого принадлежат графу H, а промежуточные вершины этому графу не принадлежат. Такой путь называется также “ручкой” графа H [26, с. 193]. Строим последовательность графов H₀ = T(S), H₁, H₂, …, каждый член которой, кроме начального, получается из предыдущего члена добавлением обходного пути. Продолжаем этот процесс до такого графа H_k, который не будет иметь обходных путей. Граф H_k будет общим решением W(G, S) задачи III, а также IV.

Это построение представляет обобщение известного утверждения о том, что вершинно двусвязный граф можно построить, начав с любого его ребра и добавляя последовательно “ручки” к получаемым графам [26, с. 193]. Последнее можно истолковать как частный случай вышеописанной конструкции – как построение общего решения задачи соединения простыми путями двух смежных вершин α и β на основе частного решения, каковым является ребро (α, β).

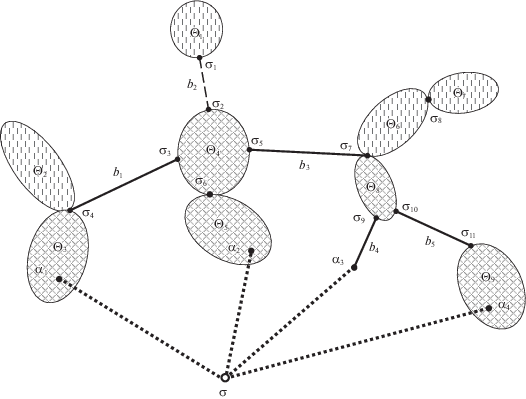
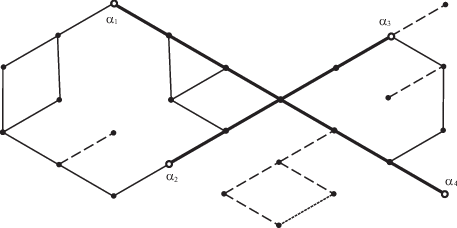
Пример построения общего решения задачи IV на основе частного решения приведен на рис. 6. Все сплошные и штриховые линии изображают ребра исходного графа G. Задано подмножество S = {α₁, α₂, α₃, α₄} множества вершин графа G. Утолщенными сплошными линиями показано дерево T(S), соединяющее вершины множества S. Оно является частным решением задачи IV. Общее решение W(G, S) получается итерационным добавлением к этому дереву всевозможных обходных простых путей. Они изображены сплошными тонкими линиями, штриховые линии – ребра графа G, не вошедшие в граф путей W(G, S).

А как решить обратную задачу – построение частного решения на основе общего решения? Предположим, что имеется граф W(G, S) – общее решение задачи соединения вершин связного графа простыми путями. Извлечь из этого графа какое-нибудь частное решение нетрудно. Достаточно построить какое-нибудь дерево, соединяющее множество вершин S в графе W(G, S). Метод такого построения описан выше для подмножества S множества вершин произвольного связного графа.

Теоремы 1–3 дают решения задач построения множеств простых путей для связных графов. Если граф содержит больше одной компоненты связности, то эти задачи решаются для каждой компоненты независимо от других компонент. Если компонента связности содержит ровно одну вершину α из множества вершин S, то в графе G не существует путей, соединяющих вершину α с другими вершинами множества S. В этом случае считаем по определению, что граф путей W(G, S) не содержит вершину α. Так что в общем случае в графе путей W(G, S) не будет изолированных вершин.

Пусть граф G есть объединение компонент связности C₁, C₂, …, C_M. Пусть для каждого  j = 1, 2, …, M дерево T_j является частным решением задачи III для множества вершин S&C_j в связном графе C_j. Если множество S&C_j содержит не более одной вершины, то T_j есть пустой граф. Частным решением задачи III для множества S назовем граф T₁ + T₂ + … + T_M. Из формулы (5.1) получаем, что общее решение этой задачи выражается формулой

6. Упрощения схемы общего решения. Теоремы 1 и 2 говорят о том, что для решения задач соединения вершин связного графа простыми путями необходим анализ двусвязности этого графа. Если общее решение строить непосредственно на базе этих теорем, то после анализа двусвязности нужно построить дерево блоков и шарниров исходного графа и выделить в нем поддерево, которое представляет общее решение. Если же для построения общего решения воспользоваться теоремой 3, то дерево блоков и шарниров не потребуется, но нужно будет найти сначала какое-нибудь частное решение задачи, и только после этого строить общее решение.

Последний способ допускает следующее развитие: не искать частное решение для соединения множества вершин S в графе G, а добавить в этот граф некоторые ребра и вершины таким образом, чтобы в полученном графе G ' все вершины множества S оказались соединены деревом T ' простого вида – например, звездой или простым путем. Связность исходного графа G при этом не потребуется. Тогда, имея это частное решение T ' задачи соединения вершин множества S в графе G ', строим общее решение W этой задачи на основе теоремы 3. Затем удаляем из W вершины и ребра, которые были добавлены к графу G. Как будет показано ниже, в результате этого удаления из W получится граф, который явится искомым общим решением задачи соединения множества вершин S в графе G.

Этот способ позволяет обойтись без построения и анализа дерева блоков и шарниров. Он сводит решение к анализу только двусвязности связного графа G '.

Дерево T ' можно строить разными способами, руководствуясь соображениями удобства последующих операций. Простейшие варианты – в виде простого пути или в виде графа-звезды. Графом-звездой (или просто звездой) называется неориентированное дерево, все ребра которого инцидентны одной вершине, называемой центром (центральной вершиной) звезды. Ребра звезды называются также ее лучами.

Дерево T ' может содержать ребра как принадлежащие графу G, так и не принадлежащие ему. Если некоторые вершины множества S смежны в графе G, то соединяющие их ребра можно включать в состав дерева T ', но можно и не включать.

Построение общего решения будет сведено к алгоритму вычисления блоков графа G  ' = G + T  ', а также простейшим операциям добавления к графу G некоторого множества ребер и последующего их удаления.

Сначала применим этот метод к задаче I. Пусть требуется найти граф путей P(G, α, β), где α и β – несмежные вершины неориентированного графа G. Связность последнего не предполагается. Дерево T  ' можно образовать из единственного ребра x = (α, β), соединяющего вершины α и β. Вычислим блок Θ(G + x, x) графа G + x. Из полученного блока удалим ребро x. Оставшийся граф будет графом путей P(G, α, β).

Точную формулировку решения дает следующая теорема.

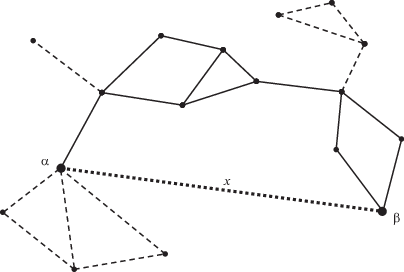
Теорема 4. Пусть α и β – несмежные вершины графа G. Добавим к графу G ребро x = (α, β). Тогда

Эту теорему поясняет пример на рис. 7. Ребра графа G изображены сплошными и штриховыми линиями. Временно добавленное ребро x = (α, β) показано точечной линией. Граф Θ(G + x, x) есть объединение ребер, изображенных сплошными линиями, и временного ребра x. Штриховыми линиями показаны ребра графа G, не принадлежащие путям от α до β в графе G. Граф путей P(G, α, β) = Θ(G + x, x)÷x изображен сплошными линиями³³.

В теореме 4 граф G не предполагается связным, а вершины α и β могут принадлежать разным компонентам связности этого графа. В этом случае в графе G не существует пути, соединяющего вершины α и β, и граф P(G, α, β) должен быть пустым. Убедимся, что формулы (6.1) и (6.2) в этом случае действительно дают пустой граф.

Дополнительное ребро x = (α, β) является мостом в графе G + x. Этот мост есть блок Θ(G + x, x) графа G + x:

По формуле (6.1) получаем

Согласно определению операции оголения, выражение x ÷ x означает, что из ребра x как графа нужно сначала удалить само ребро x без его концов (как ребро второго операнда), а затем посмотреть, не станут ли некоторые вершины первого операнда после этого изолированными. Но концы ребра x действительно станут изолированными вершинами. Операция оголения требует, чтобы вершины первого операнда, ставшие изолированными после удаления ребер, тоже были бы удалены. В итоге операция Θ(G + x, x)÷x даст для P(G, α, β) пустой граф. Значит, формула (6.1) дает пустой граф. То же верно и для формулы (6.2), поскольку Θ(G + x, x) = x || (G + x).

Из теоремы 4 следует, что для нахождения графа простых путей P(G, α, β) достаточно знать всего один блок графа G + x – тот блок, который содержит ребро x = (α, β). Отпадает необходимость построения дерева блоков и шарниров связного графа, а также выявления его минимального поддерева, представляющего те блоки, которые имеют непустое пересечение с множеством S.

Если обе вершины α и β инцидентны некоторому ребру y графа G, то добавлять временное ребро не нужно. Ребро y будет частным решением задачи, а общее решение даст формула

Рассмотрим теперь общую задачу соединения простыми путями подмножества вершин графа, не предполагаемого связным. Следующая теорема является обобщением теоремы 4.

Теорема 5. Пусть подмножество S множества вершин графа G есть множество вершин дерева T; ребра x₁, x₂, …, x_m дерева T не принадлежат графу G и соединяют пары несмежных вершин графа G; остальные ребра дерева T являются ребрами графа G. Тогда граф путей W(G, S) выражается формулой

Возможны различные способы добавления ребер {x₁, x₂, …, x_m} к графу G. Они приводят к разным способам вычисления общего решения задачи соединения вершин.

Способ 1. Пусть S = {α₀, α₁, …, α_N}, N > 0. Предположим, что вершина α₀ не смежна ни с одной из остальных вершин α₁, α₂, …, α_N множества S. Соединим α₀ ребром с каждой из вершин α₁, α₂, …, α_N. Полученный граф-звезду принимаем в качестве дерева T, о котором говорится в теореме 5. Этот способ естествен для решения задачи II.

Следствие 1 теоремы 5. Пусть:

– S = {α₀, α₁, …, α_N} – подмножество множества вершин графа G, N > 0;

– вершина α₀ не смежна ни с одной из вершин α₁, α₂, …, α_N в графе G;

– граф-звезда X = (α₀, α₁) + (α₀, α₂) + … + (α₀, α_N) есть объединение ребер (α₀, α₁), (α₀, α₂), … …, (α₀, α_N), не принадлежащих графу G.

Тогда граф путей W(G, S) выражается формулой

Этот способ иллюстрирует рисунок 8. Исходный граф G состоит из двух компонент связности. Его ребра изображены сплошными и штриховыми линиями. Множество S состоит из пяти вершин: α₀, α₁, α₂, α₃ и α₄. Временно добавленная звезда X = (α₀, α₁) + (α₀, α₂) + (α₀, α₃) + (α₀, α₄) показана точечными линиями. Граф X || (G + X) есть объединение звезды X и ребер, представленных сплошными линиями. Граф путей W(G, S) = (X || (G + X))÷X изображен сплошными линиями, остальные ребра графа G – штриховыми линиями.

Способ 2. Предположим, что каждая вершина в последовательности α₀, α₁, …,α_N не смежна в графе G (он не предполагается связным) с предыдущей и со следующей вершинами. Соединим последовательно эти вершины ребрами так, чтобы получился простой путь от α₀ до α_N. Этот простой путь принимаем в качестве дерева T в теореме 5.

Следствие 2 теоремы 5. Пусть:

– S = {α₀,α₁,…,α_N} – подмножество множества вершин графа G, N > 0;

– в последовательности α₀,α₁,…,α_N соседние вершины не смежны в графе G;

– простой путь Y = (α₀, α₁) + (α₁, α₂) + … + (α_N – 1, α_N) есть объединение ребер (α₀, α₁), (α₁, α₂), …, (α_N – 1, α_N), не принадлежащих графу G.

Тогда граф путей W(G, S) выражается формулой

Расширим далее способы дополнения временными ребрами графа G, не предполагаемого связным. Будем добавлять к графу G ребра, которые будут соединять вершины, принадлежащие множеству S = {α₁,α₂, …, α_N}, где N > 1, с новой временно добавленной вершиной σ. Эту граф-звезду, добавленную к графу G, обозначим X(σ, S):

Используем ее в качестве частного решения задачи соединения простыми путями вершин множества S в расширенном графе G + X(σ, S). В нем общим решением задачи будет граф W(G + X(σ, S), S). Он всегда связен, тогда как граф W(G, S) не будет связным, если каждая из двух или большего числа компонент связности графа G будет содержать больше одной вершины множества S.

Теорема 6. Пусть:

– S = {α₁, α₂, …, α_N} – подмножество множества вершин графа G, N > 1;

– вершина σ не принадлежит графу G;

– X(σ, S) = (σ, α₁) + (σ, α₂) + … + (σ, α_N);

– W(G, S) – граф простых путей, соединяющих вершины множества S в графе G;

– W(G + X(σ, S), S) – граф простых путей, соединяющих вершины множества S в графе G + X(σ, S).

Тогда имеют место соотношения:

Формулы (6.7) и (6.8) выражают общие решения⁴⁴ задач III и IV.

7. Соответствия между вершинной двусвязностью и простой связностью графов при вычислении простых путей. Для полноты теоретического анализа рассматриваемых задач следует остановиться на соотношениях между структурой простой связности анализируемых графов и структурой двусвязности, возникающей в решениях.

Если анализируемый граф состоит из более чем одной компоненты связности, то построение множеств простых путей, соединяющих заданное подмножество вершин графа, производится для каждой компоненты связности по отдельности независимо от остальных компонент. Вместе с тем теоремы 4 – 6 дают способы решения, не зависящие от того, связен ли анализируемый граф или нет.

Построение, рассматриваемое в теореме 6, означает, что для каждой компоненты связности графа G, содержащей хотя бы одну вершину множества S, строится граф-звезда с центром σ, соединяющая все те вершины множества S, которые принадлежат этой компоненте. Все такие звезды, добавляемые к компонентам связности графа G, имеют общий центр – вершину σ. Ниже будет показано, что если C – компонента связности графа G и множество S&C содержит больше одной вершины, то в результате добавления звезды X(σ, S&C) к графу путей W(C, S&C) получается двусвязный граф (рис. 9).

Граф путей W(G + X(σ, S), S) есть объединение некоторых блоков графа G + X(σ, S). Каждый блок графа W(G + X(σ, S), S) определяется некоторой компонентой связности графа G и вершинами из множества S, содержащимися в этой компоненте. Эта связь описывается следующей теоремой.

Теорема 7. Пусть:

– S = {α₁, α₂, …, α_N} – подмножество множества вершин связного графа G, N > 1;

– вершина σ не принадлежит графу G;

– X(σ, S) = (σ, α₁) + (σ, α₂) + … + (σ, α_N);

– W(G + X(σ, S), S) – граф простых путей, соединяющих вершины множества S в графе G + + X(σ, S).

Тогда граф W(G + X(σ, S), S) вершинно двусвязен.

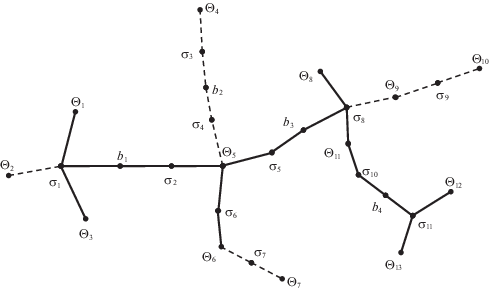
Эту теорему иллюстрирует рисунок 9. На нем показана блоковая декомпозиция некоторого связного графа G. Его блоками являются компоненты вершинной двусвязности Θ₁, Θ₂, …, Θ₉ и мосты b₁, b₂, …, b₅. Они соединяются шарнирами σ₁, σ₂, …, σ₁₁. Множество S состоит из четырех вершин α₁,α₂, α₃, α₄. Компоненты вершинной двусвязности графа G, принадлежащие графу путей W(G, S), заполнены сеточной штриховкой. Мосты графа G, принадлежащие графу путей W(G, S), изображены сплошными линиями. Дополнительные временные ребра (σ, α₁), (σ, α₂), (σ, α₃), (σ, α₄), образующие звезду X(σ, S), показаны точечными линиями. Вершинная двусвязность графа W(G, S) + X(σ, S) = W(G + X(σ, S), S) из рис. 9 очевидна.

Если известно, что все вершины множества S принадлежат одной компоненте связности графа G, то вместо формулы (6.8) можно использовать несколько более простую формулу. Если граф G связен, то, согласно теореме 7, граф путей W(G + X(σ, S), S) состоит из единственного блока. Тогда вместо формулы (6.8) его можно определить по любому из ребер звезды X(σ, S):

где x_j = (σ, α_j), j – любой номер из 1…N.

Следствие теоремы 7. Пусть:

– S = {α₁, α₂, …, α_N} – подмножество множества вершин связного графа G, N > 1;

– вершина σ не принадлежит графу G;

– x_j = (σ, α_j) при j = 1… N;

– граф-звезда X(σ, S) = x₁ + x₂ + … + x_N есть объединение ребер x₁, x₂, …, x_N.

Тогда граф W(G, S) простых путей, соединяющих вершины множества S в графе G, выражается формулой

где  j – любой номер из 1…N.

Эта формула позволяет упростить схему вычисления графа путей W(G, S): достаточно произвести анализ двусвязности графа G + X(σ, S), выбрать его блок, содержащий ребро x_j, и вычесть из этого блока вершину σ.

Пусть вершины множества S принадлежат более чем одной компоненте связности графа G. Тогда построение звезды X(σ, S) будет означать, что для каждой компоненты связности C графа G, содержащей хотя бы одну вершину множества S, строится граф-звезда X(σ, S&C) с центром σ, соединяющая вершины множества S&C. Если в компоненте C имеются две или более вершин множества S, то, в силу теоремы 7, граф W(C + X(σ, S&C), S&C) будет вершинно двусвязным.

Все звезды вида X(σ, S&C), добавляемые к тем компонентам связности графа G, которые содержат хотя бы одну вершину множества S, будут иметь общий центр – вершину σ. Если вершины множества S содержатся более чем в одной компоненте связности графа G, то σ будет шарниром связного графа W(G + X(σ, S), S). В противном случае вершина σ шарниром графа W(G + X(σ, S), S) не будет.

Если компоненте связности C графа G принадлежит ровно одна вершина α множества S, а общее число вершин этого множества больше 1, то в графе путей W(G + X(σ, S), S) вершина α будет связана с вершинами компоненты C единственным ребром (σ, α). Это ребро будет мостом графа W(G + X(σ, S), S).

Из сказанного вытекает следующее обобщение теоремы 7 на случай несвязных графов.

Теорема 8. Пусть:

– S = {α₁,α₂,…,α_N} – подмножество множества вершин графа G;

– вершина σ не принадлежит графу G;

– X(σ, S) = (σ, α₁) + (σ, α₂) + … + (σ, α_N);

– W(G, S) – граф простых путей, соединяющих вершины множества S в графе G;

– W(G + X(σ, S), S) – граф простых путей, соединяющих вершины множества S в графе G + X(σ, S).

Тогда:

1) множество блоков графа путей W(G + X(σ, S), S) взаимно-однозначно соответствует множеству компонент связности графа G, содержащих вершины из множества S;

2) вершина σ является шарниром графа путей W(G + X(σ, S), S) тогда и только тогда, когда вершины множества S принадлежат более чем одной компоненте связности графа G;

3) если C – компонента связности графа G и число вершин множества S&C больше 1, то блок графа W(G + X(σ, S), S), содержащий это множество, вершинно двусвязен;

4) если C – компонента связности графа G и число вершин множества S&C равно 1, то блок графа W(G + X(σ, S), S), которому принадлежит это множество, есть мост.

Теоремы 7 и 8 расширяют содержание нижеследующего утверждения, вытекающего из теоремы 6. Указанное в нем условие, что каждой компоненте связности графа G должны принадлежать не менее двух вершин множества S, является достаточно естественным. Ибо компоненты связности графа G, в которые вершины множества S не входят либо входят по одной, на искомый граф путей не влияют и перед его вычислением могут быть отброшены.

Следствие теоремы 6. Если при выполнении условий теоремы 6 каждая компонента связности графа G содержит не менее двух вершин множества S, то

Эта формула сводит построение общего решения W(G, S) задачи IV к вычислению тех блоков графа W(G + X(σ, S), S), которые содержат вершины из множества S, и последующему удалению из этих блоков временно добавленной вершины σ.

Формула (7.1) похожа на формулу (6.7). Графы, выражаемые правыми частями этих равенств, различаются тогда и только тогда, когда хотя бы одна компонента связности графа G содержит ровно одну вершину из множества S. В граф, выражаемый правой частью формулы (6.7), эта вершина не входит, а в граф правой части формулы (7.1) – входит как изолированная вершина.

Условие отличия от единицы числа вершин множества S в каждой компоненте связности графа G можно снять, если учесть изолированные вершины графа W(G + X(σ, S), S) – σ. Для этого формулу (7.1) можно “исправить” следующим образом:

Обе части этого равенства выражают граф, множество изолированных вершин которого есть S – W(G, S).

Теорему 8 иллюстрирует рис. 10. На нем изображен граф G, состоящий из шести компонент связности C₁, C₂, …, C₆. Они обведены точечными овалами. Задано множество S = {α₁, α₂, …, α₉} из девяти вершин графа G. Они содержатся во всех компонентах связности этого графа, кроме C₃. Компоненте C₁ принадлежит только одна вершина α₁ из множества S. Ее невозможно соединить путями с другими вершинами множества S. То же относится к вершине α₆ в компоненте C₅. Из рис. 10 видно, что граф путей W(G, S) является объединением трех непересекающихся простых путей: α₂β₁β₂α₃, α₄β₃α₅ и α₇α₈α₉.

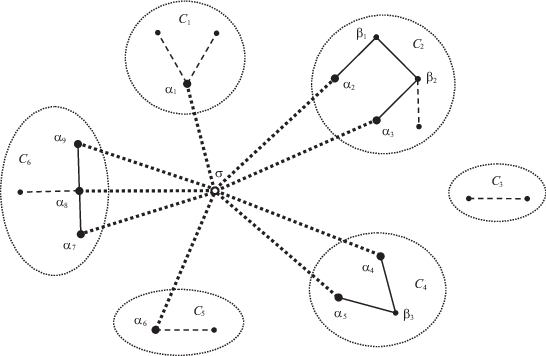
Звезда X(σ, S) = (σ, α₁) + (σ, α₂) + … + (σ, α₉) имеет девять лучей. Они показаны линиями из крупных точек. Центр σ этой звезды является единственным шарниром связного графа путей W(G + X(σ, S), S). Ребра графа G, принадлежащие графу путей W(G + X(σ, S), S), изображены сплошными линиями, остальные ребра графа G – штриховыми линиями.

Граф путей W(G + X(σ, S), S) состоит из пяти блоков. Они соответствуют тем пяти компонентам связности графа G, которым принадлежат вершины множества S. Компоненты C₁ и C₅ содержат по одной вершине множества S. Соответствующие блоки графа путей W(G + X(σ, S), S) являются его мостами (σ, α₁) и (σ, α₆). Каждой из компонент простой связности C₂, C₄ и C₆ графа G принадлежит больше одной вершины множества S. Этим компонентам соответствуют компоненты двусвязности графа W(G + X(σ, S), S): компоненте C₂ – простой цикл σα₂β₁β₂α₃, компоненте C₄ – простой цикл σα₄β₃α₅. Компоненту двусвязности графа W(G + X(σ, S), S), которая соответствует компоненте простой связности C₆ графа G, можно описать как объединение двух простых циклов σα₇α₈ и σα₈α₉, имеющих общее ребро (σ, α₈).

Вычитание из графа W(G + X(σ, S), S) вершины σ (вместе с инцидентными ей ребрами) дает граф, имеющий изолированные вершины α₁ и α₆. Они не должны входить в искомый граф путей W(G, S). Формулу (7.1) нельзя применить к данной конфигурации, так как нарушено условие ее применимости: компоненты связности C₁ и C₅ графа G содержат по одной вершине из множества S. В этой ситуации справедливы формулы (6.7) и (6.8): они удаляют из графа W(G + X(σ, S), S) не только все ребра звезды X(σ, S) и ее центр σ, но также и все вершины множества S, изолированные в графе W(G + X(σ, S), S) – σ.

Для любого графа G дерево блоков и шарниров графа путей W(G + X(σ, S), S) является графом-звездой. Обозначим его Z. Множество блоков графа W(G + X(σ, S), S) находится во взаимно-однозначном соответствии с множеством концевых вершин звезды Z. Тем самым последнее взаимно-однозначно соответствует множеству тех компонент связности графа G, которые содержат хотя бы по одной вершине множества S. Центральная вершина звезды Z представляет шарнир σ графа W(G + X(σ, S), S), если таких компонент имеется не меньше двух.

На рис. 11 показана граф-звезда, являющаяся деревом блоков и шарниров графа путей W(G + X(σ, S), S) из примера на рис. 10. Концевые вершины этой звезды, представляющие блоки графа путей, обозначены символами тех компонент простой связности графа G, которые содержат вершины множества S.

Если для решения задачи соединения вершин графа G простыми путями не использовать описанные приемы добавления вспомогательных ребер и вершин, то оценка сложности алгоритма сводится к оценке сложности анализа двусвязности графа G. Алгоритм Хопкрофта–Тарьяна, выполняющий анализ двусвязности, имеет сложность по числу операций O(n + m), где n – число вершин анализируемого графа, m – число его ребер.

Добавление звезды X(σ, S) к графу G не ухудшает оценку сложности анализа двусвязности по сравнению с анализом просто графа G. При добавлении звезды X(σ, S) к графу G количество вершин графа увеличивается на единицу, а количество ребер может увеличиться не больше, чем на n, где n – число вершин графа G. Отсюда для анализа двусвязности графа W(G + X(σ, S), S) любым из упомянутых методов получается оценка сложности по числу операций

т.е. снова O(n + m), как и для исходного графа G.

8. Применение вычислений множеств простых путей в задачах управления транспортными сетями. Методы вычисления множеств простых путей между узлами сети составляют необходимую часть программно-математического аппарата систем оперативного управления транспортными сетями. В первую очередь это относится к электрическим сетям. Далее предполагается, что транспортная сеть представлена неориентированным графом. Вершины графа называются узлами сети, ребра – ветвями. Некоторые узлы рассматриваются как источники или потребители ресурсов, передаваемых в транспортной сети по ее ветвям. Остальные узлы служат для соединения ветвей.

Для анализа и оценки состояния сети диспетчер и используемое им программное обеспечение должны иметь возможность контролировать множества простых путей, соединяющих те или иные подмножества узлов сети, в том числе соединяющие узлы-источники с узлами-потребителями.

Рассмотрим некоторые задачи управления транспортными сетями, требующие вычисления множеств простых путей между узлами сети. Они затрагивают такие вопросы моделирования и управления, как поддержание штатных режимов функционирования сети, мониторинг оперативного состояния оборудования, контроль планово-ремонтных и противоаварийных операций, восстановление функционирования сети после аварии, безопасность выполняемых операций для персонала, безаварийность операций, тренировки персонала на компьютерных тренажерах.

Пример 1. Контроль надежной связности транспортной сети. К ответственным транспортным сетям обычно предъявляется требование непрерывности функционирования. Оно означает функциональную надежность сети в режиме реального времени. В целом проблематика надежности транспортных сетей, особенно электрических, обширна и сложна. В настоящем примере и некоторых следующих затрагивается только один из ее аспектов – надежность по связности. Для полноценного анализа надежности транспортных сетей необходимо учитывать также потоковый аспект – насколько устойчиво сеть обеспечивает передачу требуемых объемов ресурсов от источников к потребителям. Потоковая надежность определяется топологией сети и пропускной способностью ее ветвей. Кроме того, многое в оперативной надежности сетей, особенно электрических, зависит от автоматики и ручного управления [27].

Одним из основных критериев надежности сложных систем является “критерий N–k”. Система считается надежной по этому критерию, если отказ какого-либо набора из k ее элементов не вызывает нарушения функциональности системы. Применительно к связности транспортной сети “критерий “N–1” означает, что удаление из связного графа сети одной вершины или одного ребра не должно вызывать разделения сети на не связанные между собой части. Первое означает вершинную двусвязность графа сети, второе – его реберную двусвязность.

Вершинно двусвязный граф является также реберно двусвязным, ибо удаление одного ребра из связного графа влечет удаление не более одной вершины. Транспортная сеть, граф которой вершинно двусвязен, называется также неразделимой или закольцованной. Неразделимость сети означает, что эта сеть остается связной после удаления какой-либо одной вершины. Закольцованность означает, что любые две вершины принадлежат некоторому простому циклу. В такой сети: для любого узла α существует обходящий его путь между любой парой узлов, отличных от α; для любой ветви сети существует обходной путь, соединяющий ее концы.

Проверка неразделимости (закольцованности) транспортной сети или выделенной ее части – это проверка вершинной двусвязности соответствующего графа. Если диспетчеру транспортной сети нужно проверить наличие этого свойства у выделенного им фрагмента G сети, то ему достаточно выбрать в этом фрагменте любое ребро x и запустить процедуру вычисления блока графа G, содержащего ребро x. В графе G существует единственный блок, содержащий ребро x. Если этот блок является компонентой вершинной двусвязности графа G, то существует путь между концами ребра x в обход самого этого ребра. В противном случае ребро x является мостом и обходных путей у него нет. Каждая вершина блока и каждое его ребро принадлежат некоторому простому пути, соединяющему две произвольно выбранные вершины этого блока.

Пример 2. Выявление узких мест в топологии транспортной сети. При плановых и аварийных переключениях в электрической сети изменяется граф ее текущей конфигурации. Для оперативного контроля надежности режима электросети диспетчеру необходимо знать ее “узкие места”. Последние определяются не только топологией, но также распределением потоков мощности по сети и состоянием (готовностью и настройкой) автоматических устройств. Поиск “узких мест” в сети начинается с анализа ее топологии. В плане связности “узкими местами” будут прежде всего шарниры и мосты графа текущей конфигурации сети. Для их распознавания диспетчер должен запустить процедуру вычисления блоков этого графа. В результате на схеме сети он сможет увидеть, какие узлы являются шарнирами и какие ветви – мостами при текущем положении коммутационных аппаратов (КА).

Пример 3. Визуализация связей и их резервирования. В число обычных информационных требований диспетчера транспортной (в частности, электрической) сети входят запросы на отображение множества всех связей того или иного типа между двумя задаваемыми узлами сети. Например, показать на схеме сети все замкнутые цепи определенного класса напряжения, соединяющие заданный источник электроэнергии с заданным потребителем. Задача решается вычислением множества всех простых путей между этими узлами. При выводе из работы (состоявшемся или предполагаемом) какой-либо ветви сети диспетчеру необходимо знать, останутся ли связанными между собой узлы, которые были связаны до вывода этой ветви из работы. Остающиеся в работе связи – это резерв по связности относительно отключаемой ветви. Диспетчеру важно знать, существует ли этот резерв.

Пусть G – граф транспортной сети, x – выводимая из работы ветвь сети, α и β – концы этой ветви. Согласно формуле (3.3), граф простых путей, соединявших α и β до вывода из работы ветви x, есть тот блок Θ(G, x) графа G, который содержит ребро (ветвь) x. После вывода из работы ветви x граф простых путей, соединяющих α и β, будет выражаться формулой Θ(G, x)÷x.

Связь между вершинами α и β в графе G будет нарушена после удаления ребра x тогда и только тогда, когда эти вершины окажутся принадлежащими двум разным компонентам простой связности графа G. Компонента связности графа G, содержащая вершину α, выражается формулой α^G; компонента, содержащая вершину β – формулой β^G. Эти компоненты различны тогда и только тогда, когда их пересечение пусто:

Пример 4. Вычисление препятствий при движении из одной вершины транспортной сети в другую. Пусть имеется транспортная сеть “с препятствиями”. Препятствием считаем вершину графа сети, проход через которую невозможен. В электрической сети такими препятствиями могут быть отключенные коммутационные аппараты. Предположим, что в графовой модели электрической сети каждое устройство представлено графом-звездой. Центральная вершина звезды соответствует самому устройству, а периферийные вершины – узлам соединения данного устройства со смежными устройствами. Такая графовая модель называется звездной моделью электросети. В ней, в частности, каждый выключатель и разъединитель изображается двухлучевой звездой. Из звезд отключенных выключателей и разъединителей удалим центральные вершины и смежные с ними ребра. “Препятствиями” для передачи электроэнергии по сети будут центральные вершины двухлучевых звезд, моделирующих отключенные выключатели и разъединители.

Пусть H – множество всех вершин-препятствий в сети G и пусть требуется найти все препятствия на простых путях от вершины α до вершины β. Сначала рассмотрим более простую задачу – узнать, существует ли хотя бы один путь от α до β, свободный от препятствий. При этом анализ двусвязности сети не требуется, достаточно анализа простой связности. Искомый путь существует тогда и только тогда, когда вершина β принадлежит графу α^(G–H). Граф α^(G–H) содержит все те и только те вершины сети, которые достижимы из вершины α в обход препятствий, образующих множество H.

В изначальной задаче о вычислении препятствий естественно предполагать, что вершины α и β не смежны в графе G. Тогда граф простых путей, соединяющих вершины α и β в обход всех препятствий, образующих множество H, можно построить на основе теоремы 4. Для этого соединим вершины α и β временным ребром x = (α, β). Используя формулу (6.1), получаем, что объединение всех простых путей (как графов), соединяющих вершины α и β и не проходящих через вершины множества H, выражается равенством

Для вычисления этого графа нужно выполнить анализ двусвязности графа G – H + x, выбрать блок, содержащий ребро x, и удалить это ребро. Граф, полученный из выбранного блока удалением ребра x, будет искомым графом путей P(G – H, α, β).

Без учета препятствий объединение всех путей, соединяющих вершины α и β, выражается формулой Θ(G + x, x)÷x. Множество всех препятствующих вершин на этих путях дает формула

Вычисление связей между узлами, обходящих заданное множество препятствий, имеет ту же цель, как и предыдущий пример, – визуализацию этих связей для наглядного отображения на мониторе диспетчера. Кроме того, получив по формуле (8.1) множество препятствующих вершин, диспетчер может принять меры по устранению тех или иных из этих препятствий, чтобы восстановить связность между узлами α и β.

Пример 5. Контроль допустимости переключения разъединителя под нагрузкой. В оперативном управлении электросетями к задаче вычисления множества препятствий приводит, в частности, анализ допустимости переключения разъединителей под нагрузкой. Разъединители относятся к числу основных силовых коммутационных аппаратов в сетях высокого напряжения; переключение разъединителя – часто выполняемая операция. Анализ допустимости этой операции производится до ее предполагаемого выполнения. Он может осуществляться либо человеком мысленно, либо автоматическим устройством контроля – по заданному алгоритму. Автоматический контроль производится также при тренировках персонала на компьютерных тренажерах. Методы, описанные в статье, позволяют лаконично выразить алгоритм контроля посредством операций над графами.

Согласно правилам переключений в электрических сетях высокого напряжения, переключение разъединителя под нагрузкой допускается только при наличии замкнутой цепи, шунтирующей данный разъединитель. Это цепь с незначительным сопротивлением, соединяющая полюсы разъединителя в обход его контакта. Шунтирующая цепь не содержит устройств, имеющих большое сопротивление, – линий электропередачи, трансформаторов и др. Она состоит в основном из секций шин и включенных КА – выключателей и других разъединителей. Переключение разъединителя под нагрузкой разрешается при наличии у него хотя бы одной такой шунтирующей цепи. Она предотвращает возникновение электрической дуги в разъединителе во время его переключения. Такая дуга опасна для персонала и оборудования.

Цепь, шунтирующая переключаемый разъединитель, должна быть надежной: она не должна допускать размыкания (человеком или автоматикой), пока меняется положение контакта разъединителя. Для этого должны быть отключены электромагнитные приводы всех входящих в эту цепь КА – на время переключения контролируемого разъединителя. Если в шунтирующей цепи привод коммутационного аппарата включен, то это означает ненадежность включенного положения коммутационного аппарата. Такой коммутационный аппарат будем считать “препятствием” в шунтирующей цепи.

Предположим, что электрическая схема представлена звездной моделью – графом G (см. пример 4). В ней каждый разъединитель описывается двухлучевой звездой. Из звезд отключенных выключателей и разъединителей удалены центральные вершины и смежные с ними ребра. Пусть δ – центральная вершина графа-звезды контролируемого разъединителя, α и β – концевые вершины этой звезды: они соответствуют полюсам разъединителя. Найдем все простые пути в графе G, соединяющие вершины α и β, не проходя через вершину δ. Это будут цепи, шунтирующие контролируемый разъединитель. Найдем в этих цепях все коммутационные аппараты с включенными приводами. Центральные вершины их звезд будут препятствиями в найденных путях. Тогда можно будет установить, существует ли среди найденных шунтирующих цепей надежная цепь. Ею будет простой путь в графе G, соединяющий вершины α и β и не содержащий вершину δ и вершины-препятствия.

Граф-звезда, представляющая контролируемый разъединитель, выражается формулой δ*G. Множество, состоящее из пары вершин α и β (граф без ребер), определяется формулой (δ*G) – δ.

Обозначим через E множество центральных вершин звезд, представляющих все те устройства электрической сети, которые имеют значительное сопротивление. В основном это линии электропередачи и силовые трансформаторы. Через C обозначим множество центральных вершин звезд всех отключенных КА. Тогда граф G–E–C будет объединением всех цепей (в пределах контролируемого участка сети), обладающих достаточно малым сопротивлением. Его вершины представляют в основном секции шин и включенные выключатели и разъединители.

Граф α^(G–E–C) есть объединение всех путей в графе сети, представляющих цепи с достаточно малым сопротивлением, которые содержат узел α. Связь между полюсами α и β разъединителя δ по обходной цепи с достаточно малым сопротивлением имеется тогда и только тогда, когда полюс β принадлежит графу α^(G–E–C–δ).

Обозначим через U множество всех КА, нештатное отключение которых не заблокировано посредством отключения питания их приводов. На привод каждого КА из множества U подан оперативный ток, так что U есть множество “препятствий”. Надежная связь между полюсами α и β разъединителя по обходной цепи с достаточно малым сопротивлением будет существовать тогда и только тогда, когда полюс β принадлежит графу α^(G–E–C–U–δ).

Найдем теперь множество всех “надежных” обходных цепей. Граф δ*G есть двухлучевая звезда с центральной вершиной δ. Этот граф является простым путем в графе G–E–C–U, соединяющим узлы α и β. По теореме 3, объединение всех простых путей, соединяющих узлы α и β в графе G–E–C–U, выражается формулой (δ*G) || (G–E–C–U). Каждый из этих путей представляет “надежную” цепь с достаточно малым сопротивлением между полюсами α и β рассматриваемого разъединителя. Из этих цепей разъединитель шунтируется теми, которые не проходят через его центральную вершину δ. Объединение последних есть

где P(g, σ, τ) обозначает граф простых путей, соединяющих вершины σ и τ графе g.

Пустота данного графа будет означать, что надежных шунтирующих цепей у анализируемого разъединителя нет. Тогда возникает вопрос: имеет ли вообще этот разъединитель шунтирующие цепи, пусть даже с включенным питанием приводов части КА? Если имеет, то следует найти множество таких КА, отключение приводов которых могло бы создать “надежную” шунтирующую цепь. Граф шунтирующих цепей с незначительным сопротивлением, шунтирующих (обходящих) разъединитель δ, есть

А множество шунтирующих КА с включенными приводами есть

Если граф (8.2) не пуст, то отключение приводов этих КА создаст надежные обходные цепи для рассматриваемого разъединителя.

Пример 6. Вычисление всех связей потребителя с источниками. Эта задача возникает, когда нужно оценить надежность снабжения определенного потребителя в транспортной сети. В электрических сетях это означает надежность электропитания. Снабжение тем надежнее, чем больше оно имеет независимых источников. Задача актуальна как в оперативном (онлайновом) управлении электрическими сетями, так и в оффлайновом режиме управления – на стадии проектирования электросети и предварительного исследования ее режимов.

Пусть α – узел в графе G, представляющий потребителя, β₁,β₂, …, β_K – узлы-источники. Их множество обозначим через B. Найдем все простые пути в графе G, соединяющие вершину α с вершинами β₁, β₂, …, β_K. По классификации задач, показанной на рис. 1, это задача типа II. Построим ее решение на основе следствия 1 теоремы 5. Предполагаем, что вершина α не смежна ни с одной из вершин β₁, β₂, …, β_K. Выполнение этого условия легко обеспечить. Допустим, что вершины α и β₁ смежны. Тогда добавим в середину ребра (α, β₁) новую искусственную вершину. Вершины α и β₁ станут несмежными.

Рассматриваемая задача как задача типа II решается добавлением временных ребер (α, β₁), (α, β₂), …, (α, β_K). Их объединение как графов образует звезду. Обозначим ее X. Решение дает формула (6.4). Из нее получаем выражение графа простых путей, соединяющих вершину α с вершинами β₁, β₂, …, β_K:

Пример 7. Вычисление всех связей источника с потребителями. Эта задача аналогична предыдущей. Она возникает при оценке надежности снабжения потребителей из заданного источника. Математическое решение получается по формулам решения предыдущей задачи переменой ролей источников и потребителей.

Пример 8. Распознавание оперативных состояний устройств в электросети. Центры управления электрическими сетями осуществляют в реальном времени мониторинг оперативного состояния оборудования. К числу основных характеристик последнего относится признак наличия/отсутствия тока нагрузки на устройствах. При наличии тока нагрузки устройство считается находящимся “под нагрузкой”. Когда тока нагрузки на устройстве нет, то различают два его состояния – “на холостом ходу” и “без напряжения”. Состояние холостого хода означает, что устройство находится под напряжением, но не “под нагрузкой”.

Прямой метод определения наличия/отсутствия тока нагрузки на устройстве состоит в непосредственном измерении тока соответствующими приборами. Однако в существующих электросетях датчики тока установлены не на всех устройствах, а измерения от имеющихся датчиков не всегда передаются в центр управления. В центре управления для восполнения недостающей информации о токах нагрузки может применяться топологический метод их распознавания. Он основан на правиле: ток нагрузки на устройстве присутствует тогда и только тогда, когда через это устройство проходит замкнутая цепь от какого-нибудь источника до какого-то потребителя. Топологический критерий состояния устройств “под нагрузкой” используется также при имитационном моделировании электросетей.

Предположим, что в графовой звездной модели электрической сети выделена некоторая часть – подграф g. Считаем, что эта часть соединена с окружающей сетью посредством совокупности узлов, состоящей из двух непересекающихся множеств S и C – узлов-источников и узлов-потребителей. Через узлы множества S электроэнергия поступает в схему g, через узлы множества C – уходит к потребителям. Найдем граф всех простых путей W(g, S + C), соединяющих в графе g узлы множества S с узлами множества C. Граф путей W(g, S + C) дает ответ на вопрос, какие устройства, принадлежащие части g электросети, находятся под нагрузкой. Это те и только те устройства, центральные вершины звезд которых принадлежат графу W(g, S + C).

На рис. 12 приведена схема распределительного устройства на подстанции. По линиям электропередачи (ЛЭП) Л1, Л2 и Л3 электроэнергия поступает на данное распредустройство. Через понижающие трансформаторы Т1 и Т2 электроэнергия уходит с распредустройства. Как принято у диспетчеров, на этой схеме вместо изображения всех реальных коммутационных аппаратов показаны “обобщенные выключатели”. Каждый “обобщенный выключатель” представляет неразветвленную цепочку из нескольких выключателей и разъединителей, соединенных последовательно. Он считается “включенным”, когда включены все реальные КА в представляемой им цепочке; в противном случае он считается отключенным. Состояниями “обобщенных выключателей” определяются замкнутые цепи, соединяющие ЛЭП с трансформаторами. На рис. 12 “обобщенные выключатели” изображены квадратиками: включенные – закрашенными, отключенные – незакрашенными.

На рис. 13 приведен граф звездной модели конфигурации данного распредустройства при тех состояниях “обобщенных выключателей”, которые даны на рис. 12. Узлы-источники (ЛЭП) изображены треугольниками, узлы-потребители (трансформаторы) – ромбами. Каждое устройство моделируется звездой: системы шин СШ1 и СШ2 – трехлучевыми звездами, включенные “обобщенные выключатели” – двухлучевыми звездами. Отключенные “обобщенные выключатели” В12 и В22 непосредственно не показаны: из их звезд удалены центральные вершины и все ребра. ЛЭП и трансформаторы отображаются однолучевыми звездами, поскольку в пределах рассматриваемой схемы каждое из этих устройств соединено со смежными устройствами только через один узел.

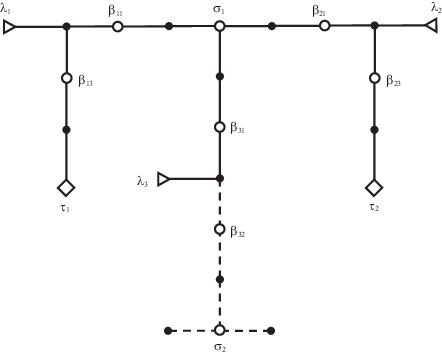
В графе на рис. 13 входам ЛЭП Л1, Л2 и Л3 соответствует множество узлов-источников S = = {λ₁, λ₂, λ₃}; трансформаторам Т1 и Т2 – множество узлов-потребителей C = {τ₁, τ₂}; шинам СШ1 и СШ2 – узлы σ₁ и σ₂. Выключатели В11, В31, В21, В13, В23, В32 представлены соответственно узлами β₁₁, β₃₁, β₂₁, β₁₃, β₂₃, β₃₂. Простые пути, соединяющие узлы-источники с узлами-потребителями, показаны сплошными линиями. Их объединение образует граф путей W(g, S + C). Остальные связи в графе распредустройства изображены прерывистыми линиями.

Из рис. 13 сразу видно, какие устройства внутри схемы находятся под нагрузкой и какие – на холостом ходу. Внутренними (не концевыми) узлами устройств в графе W(g, S + C) будут узлы σ₁, β₁₁, β₃₁, β₂₁, β₁₃, β₂₃. Они отображают систему шин СШ1 и “обобщенные выключатели” В11, В31, В21, В13 и В23. Узлы σ₂ и β₃₂ соединены с узлами-источниками λ₁, λ₂ и λ₃ в связном графе g, но не принадлежат графу путей W(g, S + C). Поэтому представленные ими устройства – система шин СШ2 и “обобщенный выключатель” В32 – находятся под напряжением, но не под нагрузкой, что означает состояние холостого хода.

Пример 9. Восстановление надежной связности сети после аварии. Требования по надежности связей между различными парами узлов транспортной сети могут различаться. К ответственным связям могут предъявляться “критерий N–3” или “критерий N–2”. Для менее ответственных может по соображениям экономии считаться достаточным соответствие “критерию N–1”. Выполнение “критерия N–1” по связности узлов α и β означает наличие между этими узлами двух путей, не имеющих других общих узлов, кроме α и β. Такие пути будем называть внутренне не пересекающимися. Они функционально не зависят друг от друга: повреждение элементов одного из них, выражаемое математически в удалении из него ребер или промежуточных вершин, не влияет на функциональность другого пути. Поскольку речь идет только о связности, пропускная способность ветвей не учитывается. Аналогичным образом в случае выполнения “критерия N–2” по связности узлов α и β эти узлы соединены тремя внутренне не пересекающимися простыми путями.

Пара внутренне не пересекающихся простых путей, соединяющих узлы α и β, образует простой цикл в графе сети. Поскольку простой цикл есть вершинно двусвязный граф, то узлы α и β принадлежат одной компоненте вершинной двусвязности графа сети. И обратно, любые две вершины вершинно двусвязного графа соединены в этом графе двумя внутренне непересекающимися простыми путями. Поэтому поддержание надежной связности на уровне “N–1” для тех пар узлов сети, для которых установлена необходимость в этом (по техническим условиям управления сетью), равносильно обеспечению постоянства распределения вершин графа сети по компонентам его вершинной двусвязности.

Соединение двух узлов сети двумя внутренне непересекающимися путями будем называть двусвязным соединением этих узлов. Два узла сети соединены двусвязно тогда и только тогда, когда они принадлежат одной компоненте вершинной двусвязности графа сети.

Предположим, что при аварии в некоторой неразделимой части транспортной сети связность сети не нарушена, а нарушена только ее неразделимость, так что снизилась надежность этой части сети по связности. Нарушение неразделимости означает появление в сети “узких мест” – шарниров или мостов в ее графе. Для их устранения и восстановления неразделимости сети необходимо на период ремонта вышедшего из строя оборудования оперативно ввести в работу оборудование из ненагруженного (холостого) резерва, если такое оборудование имеется. Что касается электрических сетей, то обычно оборудование, находящееся в ненагруженном резерве, при необходимости может быть включено в работу оперативно – в пределах короткого времени. Оборудование, находящееся в плановом ремонте, также может быть введено в работу в течение определенного времени. В случае нарушения неразделимости участка сети при аварии может рассматриваться вопрос о восстановлении его неразделимости за счет резервного или ремонтируемого оборудования, допускающего оперативное включение.

Обозначим через G граф соединений всего установленного оборудования электрической сети (работающего, ремонтируемого и резервного), через g – граф активной (находящейся в работе) конфигурации электрической сети до аварии. Пусть узлы α и β сети принадлежат некоторой компоненте вершинной двусвязности графа g. Предположим, что из-за аварии (например, на линии электропередачи) оказалась разорвана связь, представленная ребром x на некотором простом пути, соединяющем вершины α и β. Требуется выяснить: 1) сохранилась ли двусвязность соединения узлов α и β; 2) если нет, то можно ли восстановить двусвязное соединение этих узлов за счет резервного и ремонтируемого оборудования, допускающего оперативное включение.

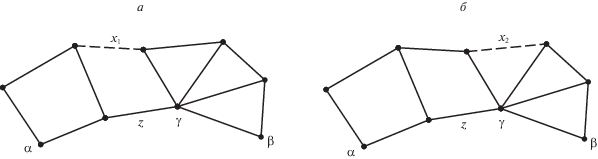
Ответ на первый вопрос утвердителен тогда и только тогда, когда оба узла α и β принадлежат одной компоненте вершинной двусвязности графа g÷x. На второй вопрос ответ утвердителен тогда и только тогда, когда узлы α и β принадлежат одной компоненте вершинной двусвязности графа G÷x.

Если граф g÷x не будет вершинно двусвязным, то в нем должны быть “узкие места” – мосты и шарниры. На рис. 14 изображены два варианта появления “узкого места” после разрыва связи x в транспортной сети, которая была неразделимой до аварии. Разорванная связь x изображена штриховой линией. На рис. 14, а показан случай, когда в результате разрыва связи x₁ появляется мост z. После аварии любой путь от α до β должен проходить через этот мост. На рис. 14, б при разрыве связи x₂ появляется шарнир γ, и каждый путь от α до β будет проходить через этот шарнир.

Рассмотрим теперь, как узнать: 1) сохранилась ли двусвязность соединения для всех тех пар узлов сети, которые имели двусвязное соединение до аварии; 2) для каких пар узлов можно восстановить двусвязное соединение, если оно нарушено.

Ответ на первый вопрос утвердителен тогда и только тогда, когда у графа g÷x распределение вершин между компонентами вершинной двусвязности такое же, как и у графа g. Для проверки нужно вычислить все компоненты вершинной двусвязности графов g и g÷x. Ответ на второй вопрос: восстановление нарушенного двусвязного соединения возможно для тех и только тех пар узлов, которые принадлежат одной компоненте вершинной двусвязности графа G÷x.

Пример 10. Топологический анализ шунтирующих сетей. Электрическая сеть, контролируемая одним центром диспетчерского управления, обычно содержит ЛЭП различных классов напряжения. Основной вклад в передачу электроэнергии по сети вносят ЛЭП самого высокого (для данной сети) класса напряжения. Эти линии имеют наибольшую пропускную способность. На уровне энергообъединений и региональных энергосистем их совокупность называют магистральной сетью. Остальная часть электросети – это регионально-распределительная сеть. Ветви этих сетей представляют ЛЭП, узлы – электростанции, подстанции и обобщенных потребителей. Узлы сопряжения регионально-распределительной сети с магистральной сетью называются центрами питания регионально-распределительной сети. Они принадлежат одновременно и магистральной сети, и регионально-распределительной. Других общих элементов магистральная и регионально-распределительная сети не имеют.

Если два центра питания соединены посредством и магистральных ЛЭП, и регионально-распределительных, то последние называются шунтирующими по отношению к магистральной сети. Всякая шунтирующая ЛЭП представлена в графе регионально-распределительной сети ребром на некотором простом пути между двумя центрами питания. Совокупность шунтирующих ЛЭП вместе с соединяемыми ими подстанциями регионально-распределительной сети будем называть шунтирующей сетью относительно данной пары центров питания. Некоторая часть электроэнергии передается между узлами магистральной сети по шунтирующим сетям. Хотя вклад шунтирующей сети в транспортные функции всей сети относительно невелик, он может составлять существенную часть резерва ее пропускной способности и этим ощутимо влиять на надежность режима сети в целом, на его устойчивость при возмущениях.

Из определения шунтирующей ЛЭП следует, что функцию шунтирования по отношению к магистральной сети выполняют не все ЛЭП и подстанции в регионально-распределительной сети. Возникает следующая задача: для заданной магистральной сети выделить шунтирующую ее сеть в пределах регионально-распределительной сети, контролируемой заданным центром диспетчерского управления.

Обозначим через M граф текущей конфигурации (активной, работающей части) магистральной сети в нормальном режиме. Предполагаем его связным. Через R обозначим граф текущей конфигурации регионально-распределительной сети, контролируемой центром диспетчерского управления. В состав графов M и R входят центры питания регионально-распределительной сети (далее – центры питания). Их множество есть M&R.

Пусть α – один из центров питания. Множество всех центров питания, соединенных с α по шунтирующей сети, дается формулой (α^R)&M. Граф шунтирующей сети равен объединению всех простых путей в графе R, соединяющих ее центры питания. Относительно текущей конфигурации магистральной сети этот граф выражается формулой (M || (M + R))&R. Связная часть графа шунтирующей сети, содержащая центр питания α, выражается формулой (M || (M + + R))&(α^R).

Влияние регионально-распределительных сетей важно учитывать и на нормальные режимы, и особенно на аварийные. Если в аварийной ситуации нарушена связность основной части сети, роль шунтирующей сети может оказаться решающей для устойчивости режима. В этом случае для эффективного оперативного управления сетью диспетчеру необходимо располагать следующей информацией:

а) связывает ли текущая конфигурация шунтирующей сети те узлы магистральной сети, связь между которыми по магистральным линиям нарушена;

б) при наличии ситуации типа а) достаточна ли пропускная способность текущей конфигурации шунтирующей сети для выравнивания небаланса генерируемой и потребляемой мощности между разделившимися областями магистральной сети;

в) если пропускная способность текущей конфигурации шунтирующей сети недостаточна (в частности, нулевая), то существуют ли в шунтирующей сети такие ненагруженные или ремонтируемые ЛЭП, которые можно оперативно ввести в работу и тем обеспечить временную (на период восстановления магистральной сети) связь между разделившимися областями магистральной сети;

г) возможно ли обеспечить приемлемые (на период восстановления магистральной сети) параметры функционирования электросети как целого путем оперативного ввода в работу дополнительных шунтирующих ЛЭП.

Аналогичные задачи возникают при оперативном управлении не только электрическими сетями, но и транспортными сетями других типов. Предположим, например, что в результате природного катаклизма разрушен мост на двухпутной электрифицированной железнодорожной магистрали, но имеются обходные (относительно этого моста) однопутные неэлектрифицированные железнодорожные линии. Оперативно-диспетчерским службам важно знать прежде всего структуру этих “шунтирующих” линий, а затем их пропускную способность и техническое состояние, чтобы оценить возможности временной компенсации нарушенной транспортной связи.

Для ответа на эти вопросы необходимо выделить соответствующие части транспортной сети и вычислить их пропускную способность. Вторая из этих задач лежит за рамками темы статьи. Остановимся на первой.

Обозначим через M ' граф активной конфигурации магистральной электрической сети после аварии. Пусть α и β – два ее узла. Предположим, что в результате аварии узлы α и β оказались не связанными через магистральную сеть. Если при этом они остаются соединенными посредством шунтирующей сети, то часть соединяющего их пути может проходить по магистральным линиям. Тогда находим, что посредством шунтирующей сети узлы α и β будут связаны тогда и только тогда, когда узел β принадлежит графу α^(M ' + R), т.е. при выполнении равенства

Это условие можно записать также равенством, симметричным относительно α и β:

Критерии, выражаемые равенствами (8.3) и (8.4), дают ответ на вопрос а).

Для ответа на вопрос б) нужно вычислить ту часть шунтирующей сети, которая участвует в передаче электроэнергии между узлами α и β магистральной сети, когда связи между ними по магистральным ЛЭП оказались разорваны. Факт разрыва связей по магистральным ЛЭП выражается соотношением (α^M ') & β = ∅. Сохранение связей между α и β посредством шунтирующей сети описывают соотношения (8.3) и (8.4).

Путь, соединяющий узлы α и β после аварии, должен проходить по некоторым ребрам графа R и может частично проходить по графу M '. Найдем граф простых путей, соединяющих узлы α и β, во всей послеаварийной сети. Воспользуемся методом, основанным на теореме 4. Соединим узлы α и β временным ребром x. Объединение всех простых путей, соединяющих вершины α и β в графе M ' + R + x, выражается формулой x || (M ' + R + x). Удаляя ребро x, получаем объединение всех путей, соединяющих α и β после аварии:

Регионально-распределительной сети принадлежит часть этого графа, выражаемая как

Формулы (8.5) и (8.6) представляют те сети, которые нужно исследовать на пропускную способность для ответа на вопрос б).

Для ответа на вопрос в) нужно к графу R добавить ребра, представляющие все ЛЭП регионально-распределительных сетей, которые могут быть оперативно введены в работу из состояния ненагруженного резерва или ремонта. Это же нужно выполнить для решения задачи г). Вычисление пропускной способности сетей не рассматриваем, а построение графа путей между α и β производится изложенными методами. Иногда (например, в распределительных сетях) для решения по восстановлению электроснабжения по временной схеме достаточно анализа топологии, без исследования режима.

Пример 11. Применение графов простых путей в исследованиях уязвимости сетей по связности. В последние годы растет число исследований по алгоритмам, предназначенным для атак на сети с целью ослабления их связности, а также для противодействия таким атакам [28, 29]. Алгоритм эффективной атаки должен находить в графе такие “слабые места” – подграфы определенного вида (вершины, ребра, звезды, клики и т.п.), удаление которых минимизирует некоторую меру связности получаемого графа. Предполагается, что для каждого типа удаляемых подграфов задана стоимость операции удаления подграфа. Задано также ограничение на суммарную стоимость всех операций удаления подграфов в алгоритме. В качестве мер связности графа используются, например, наибольшая величина компоненты связности или число пар соединенных вершин. Величина компоненты связности определяется как число вершин в ней. Две вершины считаются соединенными, если они принадлежат одной компоненте связности.

Данный подход, относящийся к области комбинаторной оптимизации, позволяет исследовать уязвимость таких структур, как сети передачи данных, распространения инфекций, взаимодействия белков и др. Для транспортных сетей он, как правило, недостаточен [30]. Поскольку транспортная сеть служит для передачи ресурса от источников к потребителям, то для нарушения ее функциональности нужно добиваться снижения не общих комбинаторных показателей ее связности, а пропускной способности сети между узлами-источниками и узлами-потребителями. Задача может ставиться, например, как разрыв всех связей между теми и другими. Тогда не следует накладывать ограничение константой на суммарную стоимость операций удаления элементов сети, а нужно требовать только минимизации этой суммы. Для решения такой задачи не нужно анализировать всю сеть – его надо искать в пределах графа простых путей, соединяющих узлы-источники с узлами-потребителями.

Если же суммарные затраты на повреждение сети ограничены константой, то гарантировать полный разрыв связей между источниками и потребителями в общем случае невозможно. Тогда следует добиваться минимизации пропускной способности сети между множествами узлов-источников и узлов-потребителей. Для этого необходимо моделировать потоки в сети, причем достаточно исследовать их не по всей сети, а в пределах графа простых путей, соединяющих источники с потребителями.

Поясним использование графа простых путей между источниками и потребителями в задаче разрыва всех связей между теми и другими на примере схемы, изображенной на рис. 12. Она описана в примере 8; граф ее звездной модели дан на рис. 13. Схема содержит три источника – ЛЭП Л1, Л2 и Л3 и два потребителя – трансформаторы Т1 и Т2. Как и в примере 8, через g будем обозначать граф рассматриваемой электрической схемы, через S и C – множества узлов-источников и узлов-потребителей, через W(g, S + C) – граф простых путей, соединяющих множества S и C в графе g. Ребра графа путей W(g, S + C) показаны на рис. 13 сплошными линиями, остальные ребра графа g – штриховыми линиями. На рис. 13 видно, что для отделения узлов-потребителей τ₁ и τ₂ от узлов-источников λ₁, λ₂, λ₃ нет смысла удалять вершины графа g, не принадлежащие графу путей W(g, S + C).

Если не рассматривать физическое разрушение элементов электросети, а только “цивилизованный” способ вывода их из работы, то он состоит в отключении выключателей. При отключении коммутационного аппарата происходит удаление центральной вершины звезды, представляющей данный КА, из графа звездной модели электросети. Будем считать, что операции отключения выключателей имеют одинаковую стоимость. Тогда для минимизации стоимости отделения потребителей от источников нужно минимизировать число отключений выключателей. Иначе говоря – число удаляемых из графа g вершин, представляющих выключатели.

Из схемы на рис. 12 ясно, что для отделения трансформатора Т1 от источника Л1 необходимо отключить выключатель В13. В результате трансформатор Т1 будет отделен и от остальных источников. В графе путей W(g, S + C) этой операции соответствует удаление вершины β₁₃. При этом граф исходной схемы g преобразуется в граф g–β₁₃, граф путей – в граф W(g–β₁₃, S + C). На рис. 15, а ребра последнего показаны сплошными линиями; остальные ребра графа g–β₁₃ – штриховыми.

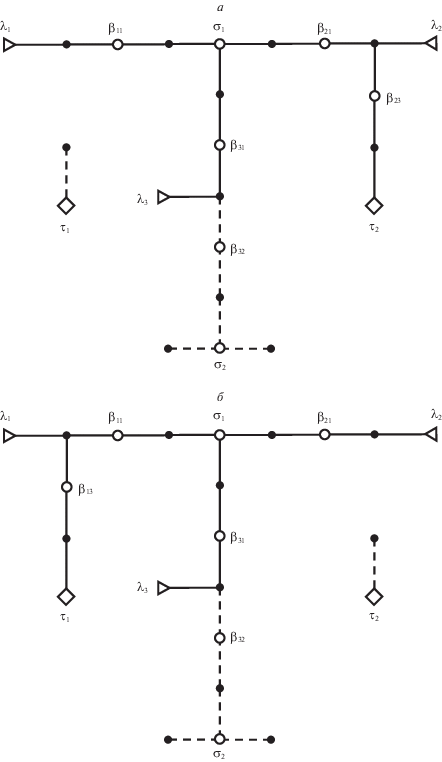
Аналогичным образом для отделения трансформатора Т2 от источника Л2 необходимо отключить выключатель В23. В результате трансформатор Т2 будет отделен также от остальных источников. В графе путей W(g, S + C) этой операции соответствует удаление вершины β₂₃. В результате граф g преобразуется в граф g–β₂₃, граф путей – в граф W(g–β₂₃, S + C). На рис. 15, б ребра последнего показаны сплошными линиями; остальные ребра графа g–β₂₃ – штриховыми.

Из сказанного следует, что для отделения обоих трансформаторов Т1 и Т2 от источников Л1, Л2 и Л3 необходимо и достаточно отключить два выключателя: В13 и В23. В графе g этому будет соответствовать удаление вершин β₁₃ и β₂₃. В результате из этого графа получится граф g–β₁₃–β₂₃, показанный на рис. 16. В нем граф путей, соединяющих источники с потребителями, пуст.

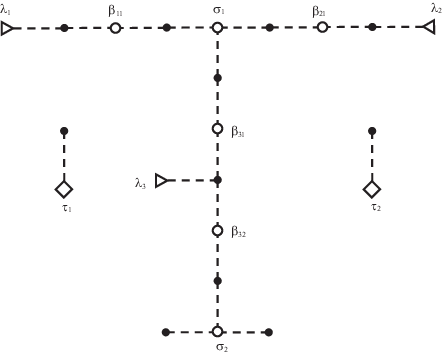
Задачи максимального ослабления связности графов посредством отыскания и удаления их слабых мест (в смысле указанных мер связности, при ограничениях на затраты по удалению) являются в общем случае NP-полными [29]. В то же время алгоритмы вычисления графов путей, описанные в настоящей статье, имеют вычислительную сложность O(n + m), где n – число вершин исходного графа, m – число его ребер. Так что предварительное вычисление графа путей не увеличивает порядок сложности задачи ослабления связности графа, но число вершин и ребер в графе путей может оказаться значительно меньшим, чем в исходном графе. В этом заключается смысл применения аппарата, описанного в настоящей статье, к задачам анализа уязвимости сетей в аспекте связности.

Заключение. В оперативном управлении электрическими сетями одной из типовых задач моделирования и анализа сети является задача отыскания всех простых путей, соединяющих два ее узла. Значимость этой задачи определяется тем, что передачу электроэнергии от одного узла сети к другому обеспечивают все замкнутые электрические цепи, соединяющие эти два узла. Возникают также задачи нахождения всех простых путей, соединяющих группы узлов. Они актуальны и для транспортных сетей других типов.

В статье даны полные решения четырех основных задач для неориентированных графов. Они сформулированы в разд. 1. Задача I является частным случаем задач II и III. Две последние представляют частные случаи задачи IV.

Число простых путей в графе, соединяющих заданные вершины, обычно очень велико. Поэтому нет смысла представлять искомое множество путей именно как множество. В статье предложен другой подход – представлять совокупность всех искомых путей в виде неориентированного графа, являющегося их объединением. Этот граф назван “графом путей”. Он служит практически работоспособным представлением множества простых путей, определяемого в той или иной из задач I–IV. Во всех приложениях, где требуется получить такое множество путей, достаточно построить соответствующий граф путей.

Этот граф можно интерпретировать как “общее решение” задачи соединения множества вершин простыми путями. Под “частным решением” понимается любое минимальное дерево, соединяющее эти вершины. Оно содержит ровно один простой путь между любыми двумя вершинами, подлежащими соединению. Это частное решение легко извлекается из общего решения – из графа путей.

Для всех четырех задач I–IV в статье показано, что граф путей, представляющий общее решение, является объединением некоторого семейства блоков исходного графа. Отсюда вытекает неожиданный результат: граф путей оказывается не зависящим от того, на какие подмножества разбито множество вершин при попарном соединении вершин разных подмножеств этого разбиения. Данный факт означает, в частности, эквивалентность задач II и IV задаче III.

Если исходить из этих результатов, то для построения графа путей необходимо вычислить все блоки и шарниры исходного графа. Затем нужно построить дерево его блоков и шарниров и выделить в нем поддерево, представляющее блоки графа путей. Объединение этих блоков будет искомым графом путей.

Возможно, одна из причин отсутствия в литературе систематического изложения решений задач I–IV заключалась в недостатке понятий и обозначений, позволяющих сделать такое изложение лаконичным и обозримым. В статье введены и применены понятия и обозначения, служащие этой цели: понятие графа простых путей и обозначения ряда операций над графами. Например, с помощью бинарной операции “двусвязного замыкания” графов, обозначенной символом “ || ”, общее решение какой-либо из задач I–IV выражается через любое ее частное решение T краткой формулой T || G, где G – исходный граф. В задаче I частное решение T есть простой путь, в задачах II, III и IV – дерево. Формула T || G представляет объединение тех и только тех блоков графа G, в которых содержатся ребра дерева T. Она подсказывает следующую интерпретацию общего решения: его можно получить добавлением к частному решению T всех “обходных” простых путей в графе G. “Обходным” считается путь, концевые вершины которого принадлежат дереву T, а ребра и промежуточные вершины не принадлежат.

Предложены также упрощения указанной схемы вычисления общего решения. Они избавляют от необходимости строить дерево блоков и шарниров исходного графа и выделять из этого дерева поддерево, представляющее граф путей. Один из таких вариантов упрощения состоит в добавлении к исходному графу G графа-звезды X, соединяющей все те вершины графа G, для которых ищется соединение всевозможными простыми путями. Звезда X будет частным решением подобной задачи, но не в графе G, а в расширенном графе G + X. Общим решением в расширенном графе G + X будет граф X || (G + X). Удаление из последнего графа всех ребер звезды X вместе с ее центральной вершиной σ дает общее решение задачи соединения заданных вершин в исходном графе G. Это общее решение при некоторых естественных ограничениях в постановке задачи выражается простой формулой

При тех же ограничениях имеет место взаимно-однозначное соответствие между множеством компонент связности графа G и множеством компонент двусвязности графа X || (G + X). Оно дополнительно характеризует структуру общего решения.

Все способы построения общих решений задач I–IV требуют анализа двусвязности графов – вычисления их блоков и шарниров. Его можно произвести посредством известного алгоритма Хопкрофта–Тарьяна. По числу операций данный алгоритм имеет порядок сложности O(n + m), где n – число вершин графа, m – число его ребер. Операции, которые при построении графа путей нужно выполнить помимо анализа двусвязности, оценку O(n + m) не ухудшают. Она остается в силе для представленных в статье методов решения задач I–IV.

В статье рассмотрены примеры применения предложенных методов вычисления множеств простых путей в задачах управления конфигурацией транспортных сетей, в особенности электрических. Они связаны с такими прикладными технологиями, как автоматический контроль операций (планово-ремонтных и противоаварийных), поддержание штатных режимов функционирования сети, мониторинг оперативного состояния оборудования, анализ надежности, противодействие атакам на электросети, восстановление электроснабжения после аварии, безопасность выполняемых операций для персонала, безаварийность операций, тренировки персонала на компьютерных тренажерах.