Известия РАН. Теория и системы управления, 2021, № 1, стр. 42-51

Введение. Проблема стабилизации неустойчивого положения равновесия управляемой системы сопряжена с определенными трудностями в особенности, когда число управляющих воздействий меньше числа степеней свободы системы и ресурсы органов управления ограничены. Маятник – хорошо известный пример такой механической системы, который часто используется исследователями в качестве эталона реальных процессов.

Еще более сложным представляется задача стабилизации аналогичных объектов при наложении дополнительных экстремальных условий, например, на время стабилизации – задачи быстродействия. В последнее время задачи быстродействия для маятниковых систем широко обсуждались, например в линейной постановке [1, 2]. В качестве управления здесь выступает или сила, способствующая перемещению основания, или (в других задачах) момент в сочленениях маятниковой системы. Реже речь идет о нелинейной постановке таких задач [3–5].

Определенным источником сложностей, возникающих при нелинейной постановке (помимо проклятия размерности), является линейность управлений, входящих в правые части динамических уравнений. При этом в случае использования стандартных условий оптимальности принципа максимума [6] всегда есть опасность столкнуться с режимами особого управления, которые, как известно, исследуются при численном способе решения краевой задачи с большим трудом. Ниже приводится приближенный подход, связанный с изначальным предположением о том, что управления имеют весьма широкий диапазон изменения и способны практически мгновенно (например, в задаче о неуправляемом стержне, закрепленном на подвижном основании) обеспечить необходимый уровень скорости перемещения основания. Задача быстродействия рассматривается далее в условиях “кинематического” управления. Показано, что при таком подходе порядок системы уравнений уменьшается на единицу, управление входит в уравнения линейно-квадратичным образом, это фактически решает в дальнейшем проблему отсутствия особых и скользящих режимов при самых общих предположениях о правых частях динамических уравнений для маятниковых (и не только маятниковых) систем. Задача быстродействия решается затем численно, прямым перебором экстремалей принципа максимума. Приводятся результаты решения некоторых задач.

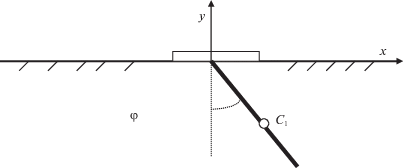
1. Постановка задачи. Рассматривается весомый однозвенный маятник (рис. 1) массы ${{m}_{1}}$, подвешенный на подвижном основании – “тележке” массы ${{m}_{2}}$, могущей с помощью управления перемещаться по горизонтальной оси x. Маятник совершает в вертикальной плоскости плоские колебания, определяемые углом φ. Расстояние центра масс маятника ${{C}_{1}}$ от его точки подвеса равно r. Координаты этого центра масс и его скорость определяются следующими формулами:

Обозначая через J момент инерции маятника относительно его центра масс, нетрудно найти выражения для кинетической и потенциальной энергий такой системы, их первых производных, а затем построить для данной системы уравнения Лагранжа:

Здесь F – сила, вырабатываемая не показанным на рис. 1 приводом, который обеспечивает перемещение тележки по горизонтальной оси $x$, $g$ – ускорение свободного падения.

Обезразмерим переменные задачи

где обозначено

Дифференцирование по безразмерному времени будем обозначать штрихом, опустим значок тильда при описании безразмерных переменных. Кроме того, будем считать, что сила $F$ полностью контролирует поведение (в некоторых пределах) члена, стоящего во втором уравнении (1.1) под знаком дифференциала. Фактически это означает, что импульс u, отвечающий горизонтальному перемещению системы, превращается в нечто аналогичное управлению. В результате деления обеих частей первого уравнения (1.1) на ${{m}_{1}}gr$ и соотношения для $u$ на $({{m}_{1}} + {{m}_{2}}){{g}^{{1/2}}}{{r}^{{1/2}}}$ получаем

где обозначено $a = 1 + J{\text{/}}{{m}_{1}}{{r}^{2}}$, $b = {{m}_{1}}{\text{/}}({{m}_{1}} + {{m}_{2}})$. С учетом сказанного уравнения задачи можем переписать в следующем виде (u – управление):

Поставим вначале задачу перевода маятника из нижнего устойчивого состояния покоя в верхнее неустойчивое. Эта задача может рассматриваться как с условием перевода основания в “начальное” положение, т.е. $x(0) = x(T) = 0$, так и при свободном конечном значении величины x(T). Поскольку правые части в (1.2) не зависят от x, то здесь при свободном значении x(T) возможно (с понижением порядка задачи до второго) рассмотрение случая ${{u}_{{\max }}} = \infty $, когда управлением фактически является сама координата $x$. Прямой выгоды, правда, такое преобразование исходной задачи, по-видимому, не дает, так как если $u(t)$ есть δ-функция, то переменные $P,\varphi $ разрывны. В любом случае надо реализовывать нулевое конечное условие по P; тогда при изменении $u$ скачком до нуля мы автоматически получаем на правом конце и $\varphi _{k}^{'} = 0$. Другое краевое условие, конечно, есть ${{\varphi }_{k}} = \pm \pi $. Итак, краевые условия на правом конце рассматриваемой ниже задачи быстродействия есть ${{P}_{k}} = 0$, ${{\varphi }_{k}} = \pm \pi $.

Выпишем гамильтониан задачи, члены гамильтониана при u и u², а также построим сопряженные уравнения [6]

Значения u, дающие максимум функции $H(u)$, определяются формулами

Согласно (1.5), режимы особого управления в задаче отвечают случаю $A = B \equiv 0$, а протяженные скользящие режимы, характеризующиеся тем, что на них максимум гамильтониана по управлению достигается при нескольких значениях u, отвечают случаю $A \equiv 0,$ B > 0.

2. Особые и скользящие режимы задачи быстродействия. Этот вопрос исследуем в общем виде. Рассматриваемая задача быстродействия относится к типу задач с линейно-квадратичным управляющим воздействием, для которых система дифференциальных уравнений имеет вид

где $y = ({{y}_{1}},{{y}_{2}},...{{y}_{n}})$ – $n$-мерный вектор (и вместе с ним вектор-функции $f,g,h$, неравные тождественно нулю), а $u \in [ - {{u}_{{\max }}},\;{{u}_{{\max }}}],$ ${{u}_{{\max }}} > 0$ – скалярная величина. Основная трудность численного решения оптимальных задач данного типа, а также большинства других нелинейных задач, как хорошо известно, состоит в наличии особых и скользящих участков ее оптимальной траектории, что сильно усложняет ее численный анализ. Покажем, что задачи подобного типа все-таки относятся к разряду удобных для численного исследования. Для решения задачи быстродействия введем в рассмотрение $n$-мерный вектор сопряженных переменных $\psi $: и гамильтониан

1. Исследуем вопрос существования и структуру возможных режимов особого управления в этой задаче. Данным режимам отвечает случай, когда тождественно обращаются в нуль члены при $u$ и u² в гамильтониане (2.3):

Тогда, дифференцируя по времени первое из соотношений (2.4), находим

где

Член при u в формуле (2.5) пропадает. Аналогичное дифференцирование второго условия в (2.4) дает

Здесь уже пропадает член при квадрате управления. Структурно условия (2.5) и (2.6) можно записать как

Исследуем специальный случай, когда $\tilde {B}(\psi ,y) \equiv 0$, и, так сказать, общую ситуацию, когда $\tilde {B}(\psi ,y) \ne 0$ и, согласно условию (2.7),

В общем случае имеем в пространстве $(\psi ,y)$ четыре соотношения: (2.3), (2.4) и второе условие (2.8). Первое из условий (2.8) определяет управление на особом режиме. Можно показать, что дальнейшее дифференцирование гамильтониана H ничего нового не дает. При дифференцировании второго из соотношений (2.8) возникает тривиальное соотношение, вообще говоря, линейно-квадратичное по u с коэффициентами, зависящими от $(\psi ,y)$. Его можно превратить просто в соотношение от $(\psi ,y)$, подставив особое управление из первого условия в (2.8) и т.д. Этот процесс дифференцирования можно продолжать до бесконечности, получая каждый раз следующее соотношение. Важно отметить, что получаемое в очередной раз соотношение независимо от предыдущих уже хотя бы потому, что в его конструкцию входят старшие частные производные $f,g,h$ по вектору y. Тем самым, за исключением случая относительно простых по структуре функций $f,g,h$, у которых старшие производные совпадают с младшими, начиная с некоторого шага, процесс дифференцирования приводит к построению бесконечно большого числа независимых соотношений в то время, как пространство $(\psi ,y)$ конечно. На практике маловероятно, чтобы вся эта бесконечная система соотношений имела общие точки, причем парадоксально, но чем сложнее функции $f,g,h$, тем такая вероятность меньше. В Приложении 1 для рассматриваемой задачи дополнительно, с помощью непосредственного анализа доказывается отсутствие особых режимов управления.

В специальном случае изначально имеется шесть соотношений в пространстве $(\psi ,y)$, поскольку здесь добавляются условия $\tilde {A}(\psi ,y) = \tilde {B}(\psi ,y) = \tilde {C}(\psi ,y) = 0$. Дифференцируя их, можно получать квадратичные уравнения для управления на особом режиме. После этого ситуация повторяется.

2. Для исследования скользящих режимов, отвечающих случаю

в принципе, надо вводить вспомогательную систему уравнений: где ${{\lambda }_{i}}$ – “доли” управления, а ${{u}_{i}}$ – дополнительные базисные управления [7]. Максимум H по ${{u}_{i}}$ “выделяет” в данном случае только два значения: ${{u}_{i}} = {{u}_{{\max }}}$ и ${{u}_{i}} = - {{u}_{{\max }}}$, т.е. достаточно рассматривать два значения ${{\lambda }_{1}},{{\lambda }_{2}}$. Требуется, чтобы все они доставляли максимум новому гамильтониану ${{H}_{*}} = \sum {{{\lambda }_{i}}H{\text{(}}{{u}_{i}}{\text{)}}} $, где под $H({{u}_{i}})$ понимается “старый” гамильтониан $H$. Причем линейная комбинация управлений u_i (которая исчезает в ${{H}_{*}}$ ввиду равенства $\sum\limits_{i = 1}^n {{{\psi }_{i}}} {{g}_{i}}{\text{(}}y{\text{)}} = 0$) присутствует в динамических уравнениях в виде некого ${{u}_{ * }} = {{\lambda }_{1}}{{u}_{{\max }}} - {{\lambda }_{2}}{{u}_{{\max }}} = {{u}_{{\max }}}({{\lambda }_{1}} - {{\lambda }_{2}})$, а квадратичные по u члены образуют в сумме выражение ${{\lambda }_{1}}u_{{\max }}^{2} + {{\lambda }_{2}}u_{{\max }}^{2} \equiv u_{{\max }}^{2}$. В таком же виде, а именно $Bu_{{\max }}^{2}$, эти квадратичные члены входят и в ${{H}_{*}}$. Итак, рассматриваемые соотношения принципа максимума для вспомогательной системы сводятся к уравнениям (2.1)–(2.3), в которых линейные члены образуют некие величины, умноженные на ${{u}_{*}}$, а квадратичные – на $u_{{\max }}^{2}$. Их следует использовать совместно с ограничением $\left| {{{u}_{*}}} \right| \leqslant u_{{\max }}^{{}}$.

Исследование скользящих режимов связано с анализом условий (2.9) с формальной подстановкой во все получаемые выкладки:

Дифференцирование первого из условий (2.9) приводит к

Повторное дифференцирование соотношения (2.10) позволяет определить ${{u}_{*}}$ как функцию переменных $\psi ,y$. С учетом этого для переменных $\psi ,y$ в количестве $2n$ штук возникает, включая сюда и гамильтониан, переопределенная система из 2n + 3 алгебраических и дифференциальных условий. Кроме того, должны выполняться указанные выше неравенства

В ряде случаев, включая сюда и рассматриваемую в работе задачу, этого оказывается достаточно, чтобы прийти к противоречию. В Приложении 1 показан один из способов построения такого противоречия.

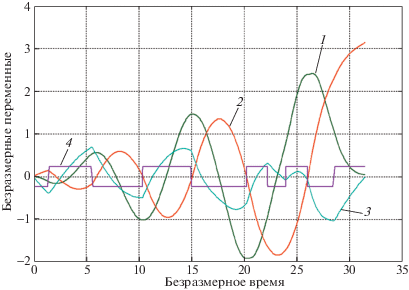
3. Численное исследование задачи. Отсутствие особых и скользящих участков на оптимальной траектории позволяет строить простые, эффективные численные алгоритмы ее решения. На рис. 2, 3 приведены результаты численного исследования (в безразмерных величинах) рассматриваемой задачи быстродействия. При расчетах были выбраны следующие значения коэффициентов системы:

т.е. основание и стержень имеют равные массы, причем стержень однороден. Рисунок 2 отвечает случаю оптимального торможения маятника в верхней точке, причем тележка занимает первоначальное – “нулевое” положение по x; рисунок 3 – случаю такой же конечной конфигурации системы, но обобщенный импульс $P$ системы и конечное положение основания произвольные. Соответствующие времена реализации этих режимов составляют $\tau = 31.50,30.58$. Если в конце не задавать только $P$, то время равно $\tau = 30.59$, график процесса не приводится. Тем самым оптимальные по быстродействию времена во всех постановках отличаются не сильно, равно как и сами режимы управления. На рисунках показаны решения, отвечающие конечному углу $\varphi = \pi $. Им соответствуют, естественно, симметричные решения при конечном $\varphi = - \pi $. Данные оптимальные по быстродействию решения отыскивались при помощи анализа (с неким шагом) всего множества понтрягинских экстремалей задачи. Решения были получены с помощью перебора начальных значений сопряженной системы при варьировании углов $\beta ,\gamma $.

Управления $u$ на рис. 2, 3 имеют девять режимов переключения с $u = {{u}_{{\max }}}$ на $u = - {{u}_{{\max }}}$ и наоборот. Некоторые из них плавные, остальные переключения делаются скачком. Все это, наряду с малой разностью оптимальных значений времен реализации, говорит об определенной близости режимов управления. С физической точки зрения представленные режимы идентичны – они основаны на постепенном “разбалтывании” маятника, требуемое состояние реализуется после третьего периода таких колебаний. Можно ожидать, что при решении задачи быстродействия в строгой постановке ее решения будут сродни данным.

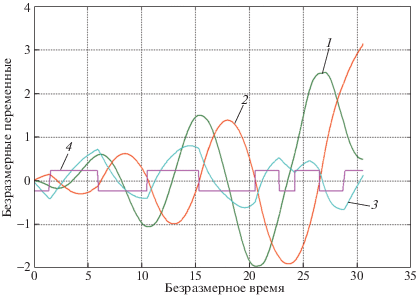
На рис. 4, 5 представлены решения другой задачи для той же механической системы: первоначально маятник находится в покое, в неустойчивом вертикальном положении. Требуется максимально быстро перевести его в такое же вертикальное положение, но так, чтобы основание при этом переместилось вдоль положительного направления оси $x$ на некоторое расстояние s. Иными словами, начальному состоянию отвечают краевые условия вида ${{P}_{0}} = 0$, ${{\varphi }_{0}} = \pm \pi $, а конечному – любой из набора ${{P}_{k}} = 0$, ${{\varphi }_{k}} = \pm \pi ,\;{\kern 1pt} { \pm }3\pi ,\;{\kern 1pt} { \pm }5\pi ,...$ В линеаризированной постановке при ${{\varphi }_{0}} = {{\varphi }_{k}} = \pi $ задача рассматривалась в [1, 2]. Обратимся к случаю b ≈ 0, где $u \approx \dot {x}$, благо в этом случае присутствует отчетливая механическая аналогия. На рис. 4 жирными точками (кривая 1) отмечены безразмерные времена $\tau $, отвечающие безразмерным смещениям s основания. Безразмерная высота (длина) стержня равна двум, т.е. при s = 2 имеем смещение основания на одну длину стержня, при s = 4 – на две длины и т.д. Если не задаваться никакими условиями по $P,\varphi $ на правом конце, то, очевидно, наилучшим по времени является управление $u \equiv {{u}_{{\max }}}$. Тем самым имеем оценку снизу на время быстродействия. Эта нижняя оценка времени процесса представлена на рис. 4 прямой 2. Из рассмотрения рис. 4 вытекает, что истинные наибыстрейшие времена то приближаются к нижней оценке (и даже совпадают с ней в отдельных точках), то удаляются.

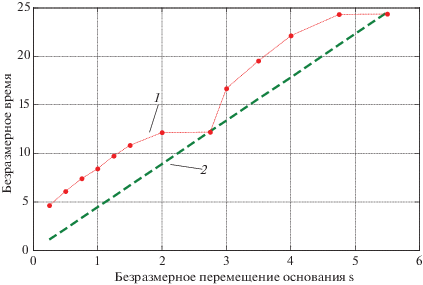
Этому факту можно дать простое физическое объяснение. Изменим скачком скорость основания в начальном положении маятника с нулевой до скорости ${{u}_{{\max }}}\;( = 0.226)$ и будем поддерживать ее некоторое время. Маятник получит некоторую начальную угловую скорость и начнет движение в сторону роста угла φ. Поскольку скорость основания в дальнейшем неизменна, то колебание маятника относительно основания будет носить такой же характер, как если при неподвижном основании просто толкнуть маятник в сторону с некоторой угловой скоростью. При рассматриваемых числовых параметрах системы полное безразмерное время одного свободного колебания маятника с учетом начального толчка равно (примерно) 12.18, причем в конце этого цикла величины $P,\varphi $ равны начальным (плюс $2\pi $ по углу $\varphi $), а основание за то же время перемещается на расстояние $s = 2.75$. Именно в этой точке (и кратных им) нижняя оценка и истинное время быстродействия совпадают, поскольку мгновенное изменение $u = {{u}_{{\max }}}$ на нулевое его значение позволяет остановить маятник, достигший верхнего положения.

Если же значение s меньше 2.75 или несколько больше него, то необходим переход на определенный режим “торможения”, в силу чего тратится как бы избыточное время. Расчеты показывают, что на интервалах $0 \leqslant s \leqslant 2.75,$ $2.75 \leqslant s \leqslant 5.5$ и т.д. картина управления как бы периодически повторяется. Пусть, например, $\;2.75 \leqslant s \leqslant 5.5$. В начале осуществляется переход на управление $u = {{u}_{{\max }}}$ и маятник делает один полный оборот. После этого, в зависимости от того, насколько велика разница $\Delta s = s - 2.75$, делается переход при “малых” Δs на режим $\{ - {{u}_{{\max }}},{{u}_{{\max }}}$, –u_max} (с двумя переключениями и здесь теория [1, 2], примененная к построению управления линеаризованной системой в финальной фазе, дает достаточно хорошее приближение) либо при относительно “больших” Δs – на режим $\{ - {{u}_{{\max }}},{{u}_{{\max }}}\} $ (с одним переключением). При малых Δs процесс набора “недостающих” Δs протекает вблизи значения $\varphi = 3\pi $. Наоборот, при больших Δs ориентиром управления является $\varphi = 5\pi $. При этом в окрестности нижнего положения маятника $\varphi \approx 4\pi $ осуществляется на некоторое время переход на управление $u = - {{u}_{{\max }}}$ (затем снова на u = ${{u}_{{\max }}}$), в результате чего его угловая скорость внизу, а, значит, и общее время второго колебания не сильно изменяются по сравнению со свободным случаем. Из численного анализа можно сделать вывод, что при больших Δs “успокоение” по времени в окрестности $\varphi = 3\pi $ “стоит” дороже.

В качестве иллюстрации случая малых Δs на рис. 5 приведены графики, отвечающие случаю s = 4 (основание смещается на два корпуса маятника). Их маркировка полностью соответствует рис. 2, 3. Заметим, что переход на систему свободного выбора конечного ${{\varphi }_{k}} = \pm (2n + 1)\pi ,$ $n = 0,1$, ..., заметно уменьшает время быстродействия.

Заключение. Показано, что в нелинейных задачах быстродействия для динамической системы с линейно-квадратичной зависимостью от управления особые и скользящие режимы должны, скорее всего, отсутствовать. В рамках “кинематического” способа управления численно решаются две задачи быстродействия для однозвенного маятника, который закреплен на подвижном основании, связанные с переводом маятника в верхнее неустойчивое положение. Такая постановка может быть использована при решении многих других задач быстродействия в системах, описываемых уравнениями Лагранжа (см. Приложение 2, п. 2 ). Все ее отличие от обычной динамической постановки с линейно входящими силой или моментом заключается в том, что ограничение налагается не на эту силу (или момент), а на соответствующую компоненту обобщенного импульса.