Известия РАН. Теория и системы управления, 2021, № 1, стр. 30-41

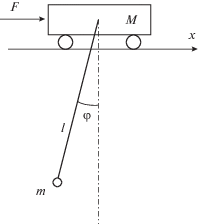
0. Введение. На рис. 1 приводится плоское движение системы из двух тел – маятника на тележке. Первое тело (тележка массы M) движется поступательно вдоль горизонтальной оси Ох без трения. Действующая на него управляющая сила F может менять направление и ограничена по модулю: |F(t)| ≤ F₀. Второе тело – точечная масса m на конце жесткого невесомого стержня длины l, образующего с вертикалью угол φ. В точке его подвеса на тележке трение отсутствует.

В однородном поле тяжести уравнения движения имеют вид [1, с. 265]

Вводя безразмерные константы ε = m/M, a = F₀/(Mg), переменные $x{\kern 1pt} ' = x{\text{/}}l$, u = F/(Mg) и время $t{\kern 1pt} ' = t\sqrt {g{\text{/}}l} $, получим (опуская штрихи)

Полагая массу маятника пренебрежимо малой в сравнении с массой тележки, считаем $\varepsilon \ll 1$ и в пределе при ε = 0 рассмотрим асимптотически близкую систему

Такая модель может служить для приближенного описания процессов управления мостовым краном, который требуется перемещать на заданное расстояние с гашением колебаний груза на тросе. Известную трудность представляет поиск управления, оптимального по быстродействию.

В линейном приближении (в предположении о малости величины φ и с обозначением p для проекции количества движения на Ох) система управления

хорошо изучена в работах [1, 2], где описаны содержательные постановки задач и найдены их оптимальные решения на основе принципа максимума Понтрягина [3]. Для нелинейной системы (0.1) была решена [4] лишь задача оптимального по быстродействию гашения колебаний маятника (при произвольном движении x(t) тележки). Далее будем рассматривать наибыстрейшее перемещение нелинейной системы (0.1) в четырехмерном пространстве. Кроме технических приложений к управлению мостовыми кранами эта задача представляет теоретический интерес как пример оптимального поведения нелинейной системы с двумя степенями свободы.

1. Постановка задачи. Дифференциальные уравнения (0.1) запишем в нормальной форме

Для удобства рассуждений назначим начало отсчета координаты x₁ в середине отрезка (заданной безразмерной длины 2b), соединяющего начальное и требуемое конечное положения тележки. Аналогичная “удвоенная” запись будет удобна и для искомого общего времени 2Т движения системы.

Задача оптимального по быстродействию перемещения тележки с маятником формулируется следующим образом: требуется определить управление u(t), t ∈ [0, 2T], переводящее систему (1.1) из состояния

за наименьшее время 2T в состояние

Будем использовать принцип максимума Понтрягина [3], составляя гамильтониан

Тогда оптимальное управление приобретет вид

где сопряженные переменные должны удовлетворять системе

Замечание 1. Если существует оптимальное управление в задаче (1.1)–(1.5), то записанные в смещенном времени $\tilde {t} = t - T$, $\tilde {t} \in [ - T,T]$ оптимальные решения ${{x}_{1}}\left( {\tilde {t}} \right)$, ${{\varphi }_{1}}\left( {\tilde {t}} \right)$, $u\left( {\tilde {t}} \right)$, ${{\lambda }_{2}}\left( {\tilde {t}} \right)$, ${{\lambda }_{4}}\left( {\tilde {t}} \right)$ будут нечетными функциями, а ${{x}_{2}}\left( {\tilde {t}} \right)$, ${{\varphi }_{2}}\left( {\tilde {t}} \right)$, ${{\lambda }_{1}}\left( {\tilde {t}} \right)$, ${{\lambda }_{3}}\left( {\tilde {t}} \right)$ – четными функциями.

Для доказательства достаточно убедиться, что в новом времени $\tilde {t}$ все соотношения (1.1)–(1.5) инвариантны относительно замены $~\tilde {t} \to - \tilde {t}$, ${{x}_{1}} \to - {{x}_{1}}$, ${{\varphi }_{1}} \to - {{\varphi }_{1}}$, $u \to - u$, ${{\lambda }_{2}} \to - {{\lambda }_{2}}$, ${{\lambda }_{4}} \to - {{\lambda }_{4}}$ при неизменных x₂, ${{\varphi }_{2}}$, ${{\lambda }_{1}}$, ${{\lambda }_{3}}$.

Существование оптимального управления в задаче (1.1)–(1.5) следует из глобальной управляемости системы [5].

Из замечания 1 вытекают соотношения

Замечание 2. Если оптимальное управление (1.4) является кусочно-постоянным с конечным числом переключений, то это число будет нечетным.

Действительно, наряду с моментом переключения T возможны лишь “попарно симметричные” моменты вида t и (2T – t), где t < T.

Заметим, что кроме релейных управлений (с конечным числом точек переключения) в задачах с двумя степенями свободы не исключены особые (вырожденные) управления, иногда интерпретируемые как скользящие режимы с бесконечно быстрыми переключениями управления. Для систем с одной степенью свободы особые управления, как правило, не возникают [6]. Это связано с тем, что если управление входит в уравнения движения линейно, то в записи оптимального управления под знаком sign участвует (в качестве сомножителя) только одна из сопряженных переменных. Если она окажется тождественно равной нулю, то (в силу однородности сопряженной системы) вторая тоже обратится в нуль, что противоречило бы принципу максимума Понтрягина, где сопряженный вектор не может быть нулевым.

Для рассматриваемой системы (1.1) с двумя степенями свободы структура управления (1.4) сложнее, поэтому функции ${{\lambda }_{2}}\left( t \right)$, ${{\lambda }_{4}}\left( t \right)$, не будучи тождественно равными нулю, вместе могут обращать в нуль выражение под знаком sign, т.е. особые управления в таких системах возможны.

В качестве необходимого отступления обсудим наглядные образы для известных оптимальных решений в малой окрестности нуля.

2. Геометрические свойства в линейном приближении. Известно [1, 2] решение задачи оптимального быстродействия для случая, когда обсуждаемая система (1.1) заменяется упрощенной (линейной) моделью в предположении о малости значений всех координат:

Соответствующий гамильтониан

максимален при а сопряженная система имеет линейный вид

В работах [1, 2] показано, что в пространстве $\left( {{{x}_{1}},{{x}_{2}},~{{\varphi }_{1}},{{\varphi }_{2}}} \right)$ такая система переводится из точки (–b, 0, 0, 0) в точку (b, 0, 0, 0) за наименьшее время посредством релейного управления u(t), t ∈ ∈ [0, 2T], имеющего в общем случае три переключения – в моменты времени τ, T и (2T - τ). При совпадении τ = T (“тривиальный” случай) движение будет с одним переключением управления, когда время разгона (торможения) тележки в точности равно периоду колебания маятника относительно отклоненной оси в переносном движении.

При трех переключениях, когда $\tau \ne T$, предложенное в [2] решение сопряженной системы (2.2) представим в виде

так что оптимальное по быстродействию управление будет

Длительность T оптимальной полутраектории можно явно выразить через момент времени τ первого переключения управления:

откуда следует монотонная зависимость величины T (а значит, и величины b) от параметра τ.

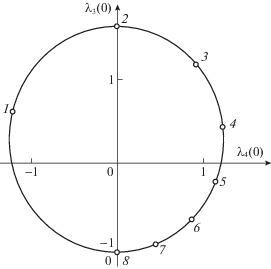
Задавая каждую оптимальную траекторию своим параметром τ, можно изобразить для них начальные значения сопряженных переменных ${{\lambda }_{4}}\left( 0 \right)$, ${{\lambda }_{3}}\left( 0 \right)$ на одноименной плоскости в виде точек, составляющих вместе овальную линию (рис. 2). Номерам i = 0, 1, 2, …, 8 помеченных точек соответствуют значения параметров ${{\tau }_{i}} = i\pi {\text{/}}4$. Точки, соответствующие номерам 0 и 8, на рис. 2 совпадают (далее на рис. 3 – аналогично).

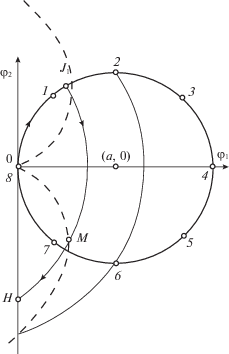
Приведем геометрическую интерпретацию оптимальных движений на фазовой плоскости $\left( {{{\varphi }_{1}},{{\varphi }_{2}}} \right)$, ограничиваясь (ввиду симметрии) изображением полутраекторий (при t ∈ [0, T]) (рис. 3). Каждая из них выходит из точки O с координатами (0, 0) при u = a, продолжаясь по окружности с центром (a, 0) и радиусом a до переключения управления в момент t = τ, например в точке J₁ (рис. 3). Далее при $u = - a$ вычерчивается дуга J₁H окружности с центром (–a, 0). Каждая полутраектория завершается на оси ${{\varphi }_{1}} = 0$ и затем дополняется симметрично относительно этой оси с заменой управлений на противоположные.

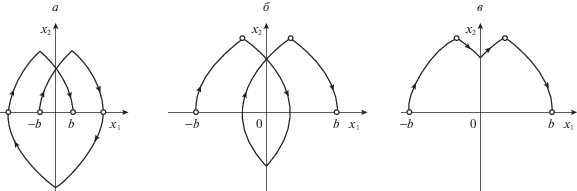
На дуге J₁H показан участок J₁M той же длительности τ, что и для дуги OJ₁. Можно показать (подробности опускаем), что геометрическое место таких точек М есть кардиоида (на рис. 3 она показана пунктиром) с осью симметрии Oφ₁. Ее свойства (т.е. соотношения временных длительностей дуг OJ₁ и J₁H) обуславливают существование трех разных типов оптимальных перемещений тележки (рис. 4, а–в) на фазовой плоскости $\left( {{{x}_{1}},{\text{\;}}{{x}_{2}}} \right)$.

Тип 1. При $0 < \tau < \pi {\text{/}}6$ (рис. 4, а) тележка совершает глубокий реверс, откатываясь в область ${{x}_{1}} < - b$. Если $\tau = \pi {\text{/}}6$, то начальный и конечный пункты будут пройдены дважды.

Тип 2. При $\pi {\text{/}}6 < \tau < \pi {\text{/}}2$ (рис. 4, б) тележка совершает локальный реверс в окрестности нуля. Если $\tau \to \pi {\text{/}}2$, то “петля” фазовой кривой уменьшается, вырождаясь в точку (0, 0).

Тип 3. При $\pi {\text{/}}2 < \tau < 2\pi $ (рис. 4, в) тележка движется без реверсов, т.е. все время имеет скорость ${{x}_{2}} \geqslant 0$. Если $\tau = 2\pi $, то три момента переключения сливаются в один (на оси Ox₂) – этот случай “тривиальный”.

3. Численное решение нелинейной задачи (1.1)–(1.5). Искомые оптимальные траектории должны удовлетворять условиям принципа максимума Понтрягина, т.е. должны быть решениями уравнений (1.1)–(1.5). Из (1.5) следует, что λ₁ = const. Учитывая, что решение системы (1.5) задается с точностью до ненулевого сомножителя, далее везде примем ${{\lambda }_{1}} = 1$. Тогда ввиду (1.6) получим соотношение

где Т – длительность полутраектории. На фазовой плоскости $\left( {{{\varphi }_{1}},{{\varphi }_{2}}} \right)$ она соединяет начало координат и некоторую точку на оси ${{\varphi }_{1}} = 0$. Выражение f(t), стоящее для оптимального управления (1.4) под знаком sign, примет вид

На участках постоянства управления решение системы (1.1), (1.5) сводится к квадратурам [4]. Однако при неизвестном заранее количестве точек переключения управления система трансцендентных уравнений, описывающих куски оптимальных траекторий, становится практически неразрешимой. Учитывая также упомянутую выше возможность особых управлений, следует признать применение численных методов неизбежным.

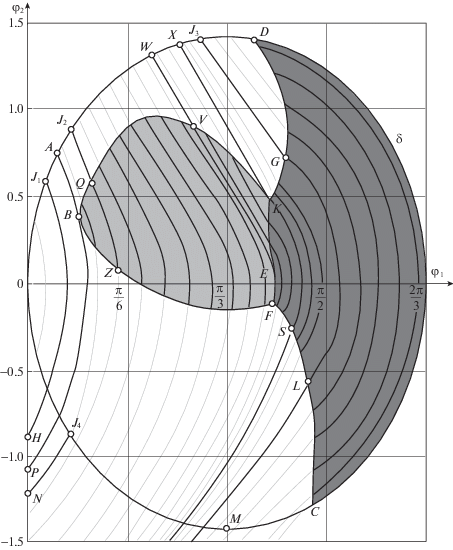
Как правило, численное интегрирование систем на основе принципа максимума затруднено ввиду отсутствия начальных значений сопряженных переменных. В нашем случае эта трудность может быть ослаблена путем учета замечаний 1, 2 и соотношений (1.6), используя которые будем искать оптимальные полутраектории и изображать их проекции на фазовую плоскость $\left( {{{\varphi }_{1}},{{\varphi }_{2}}} \right)$. Для них подразумеваем симметричные (относительно оси ${{\varphi }_{1}} = 0$) продолжения, как это было и в линейном случае (рис. 3).

Простейшая оптимальная полутраектория имеет вид замкнутой линии, далее обозначаемой δ (рис. 5) и имеющей уравнение

В обозначениях $\varphi = {{\varphi }_{1}} - \beta $, где

это уравнение сводится к форме нечувствительной к замене $\varphi \to - \varphi $, ${{\varphi }_{2}} \to - {{\varphi }_{2}}$. Это значит, что точка с координатами (β, 0) является центром симметрии кривой δ.

Движение по кривой δ осуществляется при постоянном управлении $u \equiv + a$ из начальной точки О по часовой стрелке. Сделав полный оборот за время ${{T}_{*}}$, изображающая точка двигается далее из точки О при $u \equiv - a$ по линии, симметричной δ относительно вертикальной оси ${{\varphi }_{1}} = 0$. В итоге при t ∈ [0, ${{T}_{*}}$] тележка осуществляет разгон, а при t ∈ [${{T}_{*}}$, 2${{T}_{*}}$] – торможение. Такое “тривиальное” оптимальное движение с одним переключением управления встречалось и у линейной системы.

Далее везде примем конкретное значение $a = \sqrt 3 $. Тогда ${{T}_{*}}$ ≈ 4.76802, β = π/3.

Как и следовало ожидать, при малых значениях координат нелинейная система качественно близка к линейной и оптимальные по быстродействию перемещения системы (1.1) происходят с тремя переключениями управления. Их можно построить численно, составляя полутраектории из двух частей (на рис. 5 – дуги вида ОJ₁ и J₁Н), по следующему алгоритму. Задавая значение t = τ (момент времени первого переключения управления в точке J₁), можно численным интегрированием найти ${{\varphi }_{1}}\left( \tau \right)$, ${{\varphi }_{2}}\left( \tau \right)$, а также время Т движения из О в Н. Используя соотношение (3.2) и условие переключения управления в виде f(τ) = 0, получим

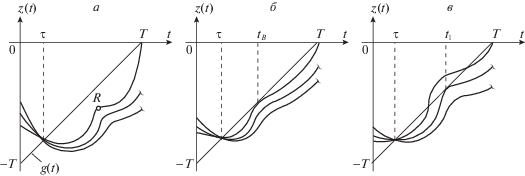
Значение ${{\lambda }_{3}}\left( \tau \right)$ найдется численным перебором с целью достижения условия ${{\lambda }_{4}}\left( T \right) = 0$. Эта процедура иллюстрируется (рис. 6, а) поведением графиков функций

Их разность равна выражению f(t) (3.2), которое определяет знак оптимального управления и должно обращаться в ноль при t = τ и t = Т. Взаимное расположение кривой z(t) и прямой g(t) при $t > \tau $ зависит от выбора ${{\lambda }_{3}}\left( \tau \right)$, так как угол наклона графика z(t) в точке t = τ определяется выражением

где величины ${{\varphi }_{1}}\left( \tau \right)$, ${{\varphi }_{2}}\left( \tau \right)$, ${{\lambda }_{4}}\left( \tau \right)$ уже известны. С уменьшением параметра ${{\lambda }_{3}}\left( \tau \right)$ значение $\dot {z}\left( t \right)$ непрерывно растет, порождая семейство кривых z(t), t ∈ [τ, T], лишь одна из которых (при искомом значении ${{\lambda }_{3}}\left( \tau \right)$) удовлетворит условию z(Т) = g(Т) (рис. 6, а). Найдя численно такое ${{\lambda }_{3}}\left( \tau \right)$, можно затем проинтегрировать систему в обратном времени вдоль дуги J₁О и получить величины ${{\lambda }_{3}}\left( 0 \right)$, ${{\lambda }_{4}}\left( 0 \right)$. Они примерно равны начальным условиям для решения линейной системы (2.3) с тем же моментом времени τ переключения (рис. 2). Из точки Н выходит вторая полутраектория, симметричная относительно оси ${{\varphi }_{1}} = 0$, так что оптимальное управление имеет всего три переключения (в моменты времени τ, Т, 2Т – τ).

Такая схема реализуема только для “малых” значений τ, не превосходящих некоторого критического ${{\tau }_{A}} \approx 0.4572$ (на рис. 5 ему соответствует положение точки А на кривой δ). Особенностью траектории, выходящей из точки А при $u = - a$, является то, что в ее характерной точке В происходит (на мгновение) обращение в нуль выражения f(t) (3.2), т.е. графики z(t) и g(t) не только пересекаются при t = τ и t = Т, но и касаются в момент времени ${{t}_{B}} \in \left( {\tau ,{\text{\;}}T} \right)$ (рис. 6, б). Этому касанию предшествовало с ростом значения $\tau \in \left( {0,{{\tau }_{A}}} \right)$ монотонное приближение к прямой g(t) точки R, которая лежит на кривой z(t) (см. рис. 6, а) и соответствует локальному экстремуму  f(t).

При последующем увеличении значения τ > τ_A описанная выше процедура подбора параметра ${{\lambda }_{3}}\left( \tau \right)$ становится нерезультативной, так как единственному значению ${{\lambda }_{3}}\left( \tau \right)$, обеспечивающему достижение цели z(Т) = g(Т), соответствует лишь график z(t), пересекающий прямую g(t) при t ∈ (τ, T) (рис. 6, в). По этой причине не существует выходящей из точки J₂ (рис. 5) оптимальной фазовой кривой, достигающей оси ${{\varphi }_{1}} = 0$ при постоянном управлении $u = - a$.

Качественное сходство фазовых портретов для нелинейной (рис. 5) и линейной (рис. 3) систем обнаруживается при первом переключении управления не только на дуге OA, но и на завершающем фрагменте кривой δ. Например, оптимальным является движение (при u = a) из О вплоть до точки J₄ с дальнейшим продолжением (при $u = - a$) по кривой J₄N. Необходимый для этого подбор параметра ${{\lambda }_{3}}\left( \tau \right)$ (по описанной выше схеме) возможен для всех точек дуги OC. Точке С соответствует такое критическое значение ${{\tau }_{C}} \approx 3.2387$, при котором график z(t) касается прямой g(t) в некоторый предшествующий момент времени ${{t}_{D}} \in \left( {0,{{\tau }_{C}}} \right)$. Другими словами, на оптимальной траектории с первым переключением в точке С существует точка D (рис. 5), при прохождении через которую управление, как и в точке B, на мгновение обращается в нуль. Найденное значение ${{t}_{D}} \approx 1.293$. Ввиду свободы интерпретации множества меры нуль можно считать, что в точке B – вырожденный участок с особым управлением, а в точке D – сближение двух моментов времени переключения вплоть до совпадения.

Таким образом, оптимальные движения с тремя переключениями управления возможны лишь для ситуаций, когда первому моменту времени переключения (t = τ) на кривой δ (рис. 5) соответствуют точки дуги OA и дуги CO.

В случае первого переключения в точках, близко предшествующих D, численные эксперименты обнаруживают существование оптимальных движений с семью переключениями управления. Такова, например, траектория с переключениями в точках J₃, G, L, затем – на оси ${{\varphi }_{1}} = 0$ и далее – симметрично в левой полуплоскости. Эти точки можно найти варьированием двух параметров T и ${{\lambda }_{3}}\left( \tau \right)$ при известных τ, ${{\varphi }_{1}}\left( \tau \right)$, ${{\varphi }_{2}}\left( \tau \right)$: для каждого значения T находится ${{\lambda }_{4}}\left( \tau \right)$ (3.3), затем подбирается ${{\lambda }_{3}}\left( \tau \right)$ из условия ${{\lambda }_{4}}\left( T \right) = 0$. Искомым окажется то значение T, для которого ${{\varphi }_{1}}\left( T \right) = 0$. Таким способом численно строятся траектории с семью переключениями управления для случаев, когда первое переключение происходит на дуге XD, т.е. когда $\tau \in \left( {{{\tau }_{X}},{{t}_{D}}} \right)$, где ${{\tau }_{X}} \approx 1.015$.

Из найденных точек переключения постепенно составляются линии переключения DK (с “минуса” на “плюс”) и CS (с “плюса” на “минус”). На рис. 5 области движений при $u = - a$ показаны белым цветом, а при u = a – темно-серым.

Численный анализ показывает, что для оптимальных траекторий, выходящих из точек дуги AX на кривой δ (рис. 5), не существует продолжений с конечным числом переключений управления. Зато для каждой из этих траекторий обнаруживается участок с особым управлением ${{u}_{0}}\left( t \right)$, которое принимает свои значения внутри интервала (–a, a). Вместе эти “вырожденные” участки составляют “область особых управлений”, закрашенную на рис. 5 светло-серым. Например, после переключения в точке J₂ (рис. 5) движение продолжается (при $u = - a$) до точки Q, затем – по дуге QZ с особым управлением $u = {{u}_{0}}\left( t \right)$, а потом – из точки Z (при $u = - a$) до оси φ₁ = 0, после чего симметрично продолжается в левой полуплоскости. Здесь следует помнить, что искомое быстродействие означает не скорейшее попадание из точки J₂ на ось φ₁ = 0 (это происходило бы при $u = - a$), а наибольшую дальность перемещения тележки при том времени 2T, которое затрачено на управление системой.

Упомянем, к сведению, следующий факт. Численные эксперименты обнаруживают весьма эффективные по быстродействию полутраектории в виде продолжений из точек дуги AX на кривой δ, когда до попадания на ось φ₁ = 0 вводится еще два переключения управления (при $t = {{t}_{1}}$ и $t = {{t}_{2}}$). Алгоритм вычислений состоял в том, что для каждого фиксированного значения T варьированием параметров τ и t₁ (с доопределением t₂ из условия φ₁(T) = 0) выбиралась наибольшая дальность перемещения тележки. Такие движения с семью переключениями управления не удовлетворяют уравнениям (1.5) принципа максимума, но всего на 1–2% уступают в быстродействии режимам с особым управлением, найденным далее.

Как известно [7], значения особого управления определяются из условия, что на некотором промежутке времени выражение, взятое в формуле для управления под знаком sign, остается тождественно равным нулю. В нашем случае это – выражение  f(t) (3.2), которое приравнивается к нулю вместе с производными по времени, используя также формулы (1.1), (1.5):

Из соотношения (3.7) (с учетом (3.5), (3.6)) получаем формулу для особого управления u₀:

Значения этой функции имеют смысл лишь там, где они не превосходят ограничений на управление $ - a \leqslant {{u}_{0}} \leqslant a$.

В формуле (3.7) коэффициент перед u фактически совпадает с выражением, которое должно быть неотрицательным, согласно необходимому условию Келли для оптимальности особых управлений [7]:

В нашем случае это неравенство выполняется, так как в рассматриваемой области движений (светло-серой на рис. 5) имеем ${{\lambda }_{4}} < 0$ и 0 < φ₁ < π/2.

Построение оптимальных траекторий с особыми управлениями численно выполнялось по следующему алгоритму. Выбиралась конкретная точка (например, J₂) на дуге AX на кривой δ, т.е. принимались значения τ, ${{\varphi }_{1}}\left( \tau \right)$, ${{\varphi }_{2}}\left( \tau \right)$. Задавалось (последовательным приближением) время движения T, вычислялось ${{\lambda }_{4}}\left( \tau \right)$ (3.3) и варьировалось значение параметра ${{\lambda }_{3}}\left( \tau \right)$ с целью достижения условия $\dot {z} = 1$ (3.4). Другими словами, выбиралась такая траектория, для которой график функции z(t) касается прямой g(t), как на рис. 6, в. Найденной точке касания t₁ соответствовал момент времени входа системы в режим особого управления (точка Q на рис. 5). Момент $t = {{t}_{Z}}$ выхода из этого режима (в точке Z на рис. 5) подбирался из условия ${{\varphi }_{1}}\left( T \right) = 0$, а последовательно уточняемым временем T обеспечивалось условие ${{\lambda }_{4}}\left( T \right) = 0$. Таким способом были построены траектории, продолжаемые из точек дуги AW – для них особые управления (3.8) не превосходят a. Пункт W (где ${{\tau }_{W}} \approx 0.9085$) оказался критическим: выходящая из него траектория содержит характерную точку Е, в которой особое управление (3.8) на мгновение достигает верхнего ограничения u = a.

Для движений, продолженных из точек дуги WX, особые управления (3.8) растут от –a до значений, превышающих a, поэтому алгоритм был модифицирован. Момент времени t выхода из режима особого управления и само значение T подбирались так, чтобы дальнейшее движение, удовлетворяющее условиям ${{{\varphi }}_{1}}\left( T \right) = 0$, ${{\lambda }_{4}}\left( T \right) = 0$, проходило сначала при u = a, затем при $u = - a$.

Каждый раз из вновь найденных точек переключения достраивались линии переключения KE (после которой u = a) и SF (после которой $u = - a$). Точка К разделяет сплошную линию переключения DE на две части, так что на участок DK приходят траектории при $u = - a$, а на участок КЕ – при $u = {{u}_{0}}\left( t \right)$ (3.8).

Заметим, что дуга EF является не линией переключения, а частью фазовой кривой, выходящей из W. Если из точки E выпустить непродолжительную траекторию EE₁ при u = a, то она касалась бы дуги EF в точке E, но лежала бы “левее” всех траекторий “u = a”, не совпадая при этом с EF. Иначе говоря, на фазовом портрете (рис. 5) имеется “пустой” сектор, образованный дугами EF и EE₁ и не содержащий участков траекторий. Заметим, что на этом же портрете встречается и наложение участков оптимальных траекторий, например, в виде J₄N. Другими словами, изображение является лишь проекцией семейства оптимальных траекторий (задачи быстродействия с частными краевыми условиями (1.2), (1.3)) на плоскость $\left( {{{\varphi }_{1}},{{\varphi }_{2}}} \right)$.

4. Обсуждение результатов. Большинство показанных на рис. 5 фазовых кривых описывает режимы колебаний маятника. Исключение составляют участки траекторий, лежащих выше сепаратрисы, и продолжениям которых (при $u = - a$) соответствовали бы “режимы вращений”. Эти участки выходят из точек правой половины дуги XD до линии переключения DG, а также из точек дуги MC до оси ${{\varphi }_{1}} = 0$.

Все построенные на рис. 5 полутраектории (вместе с их продолжениями, симметричными относительно оси ${{\varphi }_{1}} = 0$) являются решениями системы (1.1)–(1.5), т.е. удовлетворяют необходимым условиям оптимальности в виде принципа максимума Понтрягина.

Восстановленные для них (интегрированием в обратном времени) начальные значения ${{\lambda }_{4}}\left( 0 \right)$, ${{\lambda }_{3}}\left( 0 \right)$ показаны на рис. 7 в виде непрерывной замкнутой линии, точки которой параметризованы значениями T∈[0, ${{T}_{*}}$]. Для сравнения в этом же масштабе пунктиром показана “овальная” линия, ранее построенная (рис. 2) для линейной системы (2.1)–(2.2). Замкнутость этих линий (рис. 7) обусловлена следующим свойством.

Замечание 3. Двум оптимальным траекториям в задаче (1.1)–(1.5), для которых моменты времени τ первого переключения управления отличаются на величину k${{T}_{*}}$ (k ∈ N), соответствуют одинаковые начальные условия ${{\lambda }_{4}}\left( 0 \right)$, ${{\lambda }_{3}}\left( 0 \right)$.

Это следует, например, из вычисления (3.3), которое не меняется при одновременном изменении τ и T на величину k${{T}_{*}}$.

Говоря о фазовой плоскости $\left( {{{x}_{1}},{\text{\;}}{{x}_{2}}} \right)$, можно увидеть следующие разновидности движения тележки в зависимости от момента времени первого переключения управления τ (его нижний индекс указывает точку переключения на рис. 5). Движения с тремя переключениями управления при $\tau \in \left( {0,{{\tau }_{A}}} \right)$ аналогичны типу 1 (рис. 4, а), а при $\tau \in ({{\tau }_{C}},{{T}_{*}})$ – типу 3 (рис. 4, в).

Новые типы движения (в сравнении с линейной системой) возникают в диапазоне $\tau \in \left( {{{\tau }_{A}},{{\tau }_{X}}} \right)$, где каждая полутраектория содержит участок с особым управлением. При значениях τ, чуть больших τ_A, фазовые кривые $\left( {{{x}_{1}},{\text{\;}}{{x}_{2}}} \right)$ напоминают по форме тип 1, но внутри второй и третьей дуг парабол вставляются непараболические участки (из-за особых управлений). С увеличением τ (например, при первом переключении в точке J₂ на рис. 5) аналогичные искажения появляются внутри второй и третьей дуг парабол фигуры, ранее отвечавшей типу 2 (рис. 4, б).

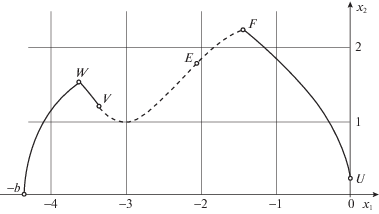
На рис. 8 показана половина фазовой кривой $\left( {{{x}_{1}},{\text{\;}}{{x}_{2}}} \right)$ для случая ${{\tau }_{W}} = 0.9085$, которому на рис. 5 соответствует полутраектория OWVEFU (с неизображенным завершением в точке U на оси ${{\varphi }_{1}} = 0$). Пунктирной линии соответствует дуга VEF с особым управлением u₀, достигшим на мгновение (в точке Е) значения a.

С увеличением значения $\tau \in \left( {{{\tau }_{W}},{{\tau }_{X}}} \right)$ этот рисунок 8 эволюционирует за счет пунктирной линии VEF: точки V и E постепенно сближаются, а дуга EF заменяется удлиняющейся параболой. При $\tau = {{\tau }_{X}}$ точки V и E сливаются, так что от фигуры (рис. 8) остается лишь чередование восходящих и нисходящих парабол. С дополнением зеркальной (относительно оси Ox₂) полутраектории получается фазовая кривая с семью переключениями управления.

При дальнейшем увеличении $\tau \in \left( {{{\tau }_{X}},{{t}_{D}}} \right)$ у таких кривых на плоскости $\left( {{{x}_{1}},{\text{\;}}{{x}_{2}}} \right)$ восходящие дуги парабол (где u = a) удлиняются, а нисходящие (где $u = - a$) укорачиваются.

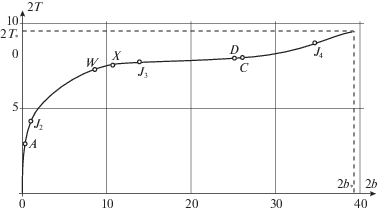
Наконец, на рис. 9 показана зависимость времени быстродействия 2T от задаваемого расстояния 2b, на которое требовалось переместить тележку с гашением колебаний маятника. Таким образом, для каждого заданного расстояния найдено наименьшее время движения. Некоторые точки кривой (рис. 9) снабжены именами тех пунктов первого переключения управления, которые ранее обсуждались на рис. 5. Характерное расстояние $2{{b}_{*}}$ соответствует времени быстродействия $2{{T}_{*}}~$ (для режима с одним переключением управления, названного выше “тривиальным”). При дальнейшем увеличении аргумента 2b, согласно замечанию 3, кривая (рис. 9) может строиться с теми же значениями сопряженного вектора, но уже из точки $(2{{b}_{*}},2{{T}_{*}})$ и т.д.

Заключение. В работе получено численное решение задачи оптимального по быстродействию горизонтального перемещения тележки с маятником на требуемое расстояние из заданного положения равновесия в другое такое же состояние с гашением колебаний. Построены траектории, удовлетворяющие необходимым условиям оптимальности (в виде принципа максимума Понтрягина) для асимптотически близкой нелинейной системы, когда масса маятника пренебрежимо мала в сравнении с массой тележки. Оказалось, что для оптимальных по быстродействию траекторий встречаются как кусочно-постоянные управления (с одним, тремя и семью моментами переключения), так и особые управления.

Заметим, что в линейной системе (2.1) величина a (ограничения на управление) характеризует степень достоверности модели, поскольку max|φ₁| = 2a, но не влияет на геометрические свойства оптимальных решений. Для нелинейной системы (1.1) роль величины a, очевидно, более важна. При малых значениях a даже в нелинейной системе все оптимальные по быстродействию траектории могут иметь одно или три переключения управления. Более содержательными являются случаи достаточно больших значений a, когда на фазовой плоскости $\left( {{{\varphi }_{1}},{{\varphi }_{2}}} \right)$ кривая δ (рис. 5) рассекается вертикальной осью ${{\varphi }_{1}} = \pi {\text{/}}2$. Тогда левее этой оси обязательно появляется линия переключения, поскольку в окрестности оси (где ${\text{cos}}{{\varphi }_{1}} \approx 0$) оптимальное управление в силу соотношений (1.4) и (3.1) может быть только положительным. Этой линии переключения предшествует область с особыми оптимальными управлениями.

Принятое в статье допущение ε = 0 упростило выкладки и изложение, но не исказило существенных свойств системы при малых значениях ε. Численные эксперименты показывают, что, например, при ε = 0.3 вид оптимальных траекторий на плоскости $\left( {{{\varphi }_{1}},{{\varphi }_{2}}} \right)$ качественно не отличается от рис. 5.

Заметим, наконец, что проблема управления платформами, несущими на себе осцилляторы, маятники или упругие звенья, остается актуальной. Ей посвящены, например, недавние работы [8, 9].