Известия РАН. Теория и системы управления, 2021, № 1, стр. 3-10

Введение. Под телематическим устройством далее будет пониматься любое устройство, работающее в сетевой среде, пропускающее через себя потоки сетевых пакетов и осуществляющее ту или иную их обработку (например, коммутацию или фильтрацию). Типичными примерами универсальных устройств такого рода могут служить межсетевые экраны или маршрутизаторы, причем как магистральные, так и периферийные. Между тем во многих прикладных задачах сетевой инженерии возникает необходимость изучения и более специальных образцов устройств телематики. Излагаемые в настоящей статье методы и алгоритмы первоначально предназначались для расчета телематических устройств, задействованных в серии космических экспериментов “Контур”, которые посвящены управлению робототехническими комплексами на борту Международной космической станции (МКС) [1]. Тем не менее, методы эти могут быть полезны и в более широком классе сетевых задач, которые хотя и отличаются по своему физическому содержанию от задач космической робототехники, но имеют сходное математическое описание. Речь идет, например, об обработке информационных потоков, возникающих при управлении движением летательных аппаратов, при автоматическом беспилотном вождении автотранспорта и других аналогичных упомянутым выше задачах.

Применяемые в инженерной практике сетевые технологии чрезвычайно разнообразны [2], причем они заметно опережают в своем развитии и практическом внедрении разработку соответствующих аналитических моделей и их теоретическое обоснование.

Хорошо известно, что основной аналитический метод исследования телематических устройств в настоящее время базируется на их трактовке как специфических систем массового обслуживания (СМО) [3, 4]. Требуемые для адекватного описания реального процесса обработки сетевых пакетов в таких системах модели СМО достаточно сложны и должны удовлетворять ряду общих ограничений.

Важнейшее из них состоит в том, что используемые при описании телематических устройств модели СМО должны быть многопотоковыми [5]. Дело в том, что суммарный поток на входе реально существующих телематических устройств, как правило, формируется несколькими независимыми источниками информации. Составляющие этого потока могут различаться по многим признакам: по скорости передачи через каналы связи, пропускной способности используемых виртуальных соединений, алгоритмам обработки в узлах коммутации, доступному объему буферной памяти, допустимому уровню потерь, способам защиты информации и целому ряду других свойств, подобных перечисленным выше.

Число таких маргинальных потоков в суммарном входящем информационном потоке телематического устройства, вообще говоря, может быть произвольным и зависит как от конкретного физического содержания решаемой сетевой задачи, так и от точности выбранной математической модели. В настоящей статье мы ограничимся простейшей моделью, включающей два потока. Так, например, в упомянутой выше задаче управления роботами на борту МКС [1] роль высокоприоритетного потока играл поток пакетов команд управления роботом и данных телеметрии, а роль низкоприоритетного потока – поток пакетов, фонового видеопотка, обеспечивающего саму возможность визуального наблюдения за происходящим на борту МКС.

Введение приоритетов между маргинальными потоками здесь является принципиально важным моментом при постановке задачи и моделирует реально применяемые алгоритмы диспетчеризации телематических устройств. Приоритет определенного вида запросов означает их предпочтение при обслуживании. Существует множество разновидностей приоритетов, основными из которых являются абсолютный и относительный [6, 7]. При абсолютном приоритете вновь поступившие высокоприоритетные требования прерывают обслуживание низкоприоритетных и вытесняют их с канала обслуживания. Относительный приоритет всего лишь ставит высокоприоритетные требования первыми в очередь на обслуживание, не прерывая при этом обработку низкоприоритетных запросов.

Приоритет в обслуживании часто дополняют введением выталкивающего механизма. Подробнее всего изучен детерминированный выталкивающий механизм [8]. Он означает, что вновь подошедшее высокоприоритетное требование всегда будет выталкивать низкоприоритетное из буфера, когда тот переполнен. Такой механизм порождает дилемму: если его включить, то в буфере начнут преобладать высокоприоритетные требования, а если выключить, то там станут превалировать низкоприоритетные запросы. Между тем для эффективной работы телематического устройства необходим надлежащий баланс тех и других [5].

Для его достижения был предложен вероятностный (или рандомизированный) выталкивающий механизм, при котором выталкивание низкоприоритетных требований из накопителя происходит по случайному закону с некоторой заданной вероятностью $\alpha \in [0,1]$. Последняя играет роль параметра управления и служит для тонкой настройки телематического устройства.

Впервые такой выталкивающий механизм был предложен в [9, 10]. В указанных работах он был реализован применительно к двухпотоковой марковской одноканальной СМО с относительным приоритетом. Авторы настоящей статьи ранее решили аналогичную задачу для случая абсолютного приоритета, характерного именно для задач управления сложными техническими системами, передающими информацию о своем состоянии через сетевую среду [11, 12]. Здесь следует отметить, что теория приоритетных СМО с вероятностным выталкивающим механизмом в последние годы существенно продвинулась вперед в плане усложнения моделей рассматриваемых систем. Были изучены более сложные разновидности приоритета, например чередуюшийся [13] и рандомизированный [14], учтен фактор повторных требований [15–18], а также возможность наличия отрицательных требований [19]. Все это позволяет при необходимости строго и корректно описать именно те алгоритмы диспетчеризации телематических устройств, которые требуются по самому смыслу решаемой сетевой задачи.

В задачах телематики особый интерес представляет расчет вероятностей потерь. В работах [9–12] был открыт интересный и практически значимый эффект. При некоторых значениях коэффициентов загрузки СМО по высокоприоритетному и низкоприоритетному трафику зависимость вероятностей потери от параметра выталкивания $\alpha $ оказалась близка к линейной. Это явление получило наименование “линейного закона потерь” и нашло экспериментальное подтверждение. Знание областей линейности позволяет рационально выбрать благоприятные режимы загрузки, в которых управление пакетными коммутациями существенно упрощается и ускоряется, причем в реальном времени.

Настоящая статья посвящена построению границ применимости линейного закона потерь для двухпотоковой марковской одноканальной СМО с абсолютным приоритетом [11, 12], имеющей, согласно классификации [8], сокращенное обозначение $\overrightarrow {{{M}_{2}}} {\text{/}}M{\text{/}}1{\text{/}}k{\text{/}}f_{2}^{1}$. Именно эта модель послужила в качестве исходной и базовой для всего цикла работ, посвященных управлению роботами на МКС. Она же представляет наибольший интерес в тех задачах, где требуется обеспечить максимальные преимущества высокоприоритетному потоку информации.

1. Описание модели системы массового обслуживания. Рассмотрим двухпотоковую СМО конечной емкости k следующего вида. Пусть μ обозначает интенсивность обслуживания, λ_i – интенсивность i-го маргинального потока, а ${{\rho }_{i}} = {{\lambda }_{i}}{\text{/}}\mu $ – коэффициент загрузки по этому потоку при i = 1, 2. Состояние СМО будем характеризовать фазовым вектором $\overrightarrow N = \{ {{N}_{1}},{{N}_{2}}\} $, причем N₁ – число требований первого типа, а N₂ – число требований второго типа в системе. Финальные вероятности P (${{N}_{1}} = i,{{N}_{2}} = j)$ будем обозначать через P_{i, j} при i = $\overline {0,k} $, $j = \overline {0,k - i} $, так что суммарное число требований в системе ${{N}_{1}} + {{N}_{2}}$ не превосходит ее емкости k. Вероятность потери требования l-го типа запишем как $P_{{{\text{пот}}}}^{{(l)}}$ , где l = $\overline {1,2} $. Приоритетным будем считать первый поток. Задача заключается в том, чтобы на плоскости загрузочных коэффициентов $({{\rho }_{1}},{{\rho }_{2}})$ найти те области, в пределах которых зависимость $P_{{{\text{пот}}}}^{{(1)}}$ и $P_{{{\text{пот}}}}^{{(2)}}$ от параметра α будет близка к линейной. Авторы работ [4, 5] высказали гипотезу, что это возможно только в слабозагруженной сети, когда значения ρ_i невелики. В действительности картина областей линейности оказывается гораздо более сложной.

При построении границ действия линейного закона потерь воспользуемся методом [11, 12]. Результаты применения указанного метода представим в наиболее общем и универсальном виде, изложив их в форме соответствующих теорем.

Теорема 1. Вероятности ${{P}_{{i,j}}}$ удовлетворяют системе линейных уравнений

где ${{\delta }_{{i,j}}}$ – дельта-символ Кронекера, а k – емкость накопителя системы.

Для реальных значений k найти P_i,j непосредственно из системы (1.1) затруднительно. С ростом k быстро растет ее порядок, равный (k + 1)(k + 2)/2, а также погрешность вычислений. Последняя максимальна для вероятностей P_i,j с наибольшим суммарным индексом i + j = k, которые как раз и определяют вероятности потери.

2. Метод производящих функций. Удобнее решать задачу методом производящих функций [5, 9–12]. Используя уравнения (1.1), производящая функция вероятностей P_i,j

может быть преобразована к некоторому специальному дробно-полиномиальному виду, задаваемому следующей теоремой.

Теорема 2. Производящая функция (2.1) представима в виде дроби

числитель и знаменатель которой таковы: причем индексы полиномов указывают на их порядок по аргументу u.

Знаменатель (2.4) имеет относительно u два корня, однако они не могут быть полюсами G. Точно такие же корни должны иметь и числитель дроби (2.3), иначе функция (2.2) не являлась бы полиномом, как того требует ее определение (2.1). Устраняя полюса так, как это описано в [6, 7], получим

причем полином ${{R}_{k}}$ содержит только так называемые “опорные” вероятности ${{p}_{i}} = {{P}_{{k - i,i}}}$, суммарный индекс которых i + j = k. Приравнивая коэффициенты при комбинациях степеней вида ${{u}^{{k - i}}}{{{v}}^{i}}$ в обеих частях равенства (2.5), получим “укороченную” систему уравнений относительно только опорных вероятностей p_i, имеющую порядок всего лишь k + 1. Конкретный вид укороченной системы задается следующим утверждением.

Теорема 3. Вероятности p_iподчиняются системе линейных уравнений вида

При i = k коэффициенты (2.6) постоянны, а именно ${{a}_{{k,j}}} \equiv 1$, ${{b}_{{k,j}}} \equiv 0$, а при всех остальных значениях индексов $0 \leqslant i \leqslant k - 1$ они выражаются в виде

где $\beta = - {{\rho }_{2}}\rho _{1}^{{ - 1/2}}$, $c_{i}^{s} = C_{i}^{s}({{t}_{0}})$, ${{t}_{0}} = (1 + \rho )\rho _{1}^{{ - 1/2}}{\text{/}}2$, $\rho = {{\rho }_{1}} + {{\rho }_{2}}$, причем $C_{i}^{s}(x)$ обозначает полином Гегенбауэра порядка i от аргумента x с индексом s.

Искомые вероятности потери выражаются через опорные вероятности p_i, удовлетворяющие системе (2.8)–(2.9), линейным образом. Эти выражения имеют вид некоторой линейной комбинации опорных вероятностей, коэффициенты которой даются следующей теоремой.

Теорема 4. Вероятности потери требований обоих типов даются выражениями

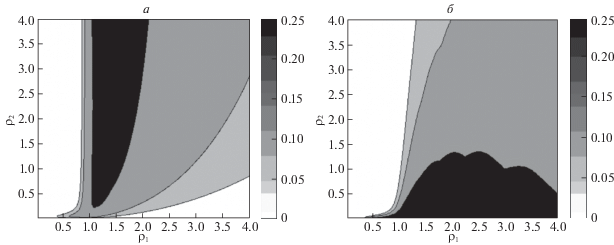
3. Численные результаты. В процессе исследования рассматриваемой модели СМО были выявлены два практически интересных режима загрузки, при которых ее поведение оказалось качественно различным. Указанные режимы представлены на рис. 1. Эти режимы проявляют себя только при достаточно сильной загрузке системы, которая превышает ее номинальную пропускную способность, т.е. когда суммарная загрузка ${{\rho }_{1}} + {{\rho }_{2}} > 1$.

Исходя из выражений (2.8), (2.9) видно, что вероятности потери $Q_{{{\text{пот}}}}^{{(i)}}(\alpha ,{{\rho }_{1}},{{\rho }_{2}})$ при любом k зависят от трех параметров. Построим их линейную аппроксимацию по первому параметру α в следующем виде:

Ее точность будем характеризовать максимумом относительной погрешности по всем допустимым значениям вероятности выталкивания:

Тогда проверка линейности закона потерь сведется к построению линий уровня функций Δ_i и выявлению тех областей, где погрешность ${{\Delta }_{i}} < \varepsilon $ (далее примем $\varepsilon = 0.01$).

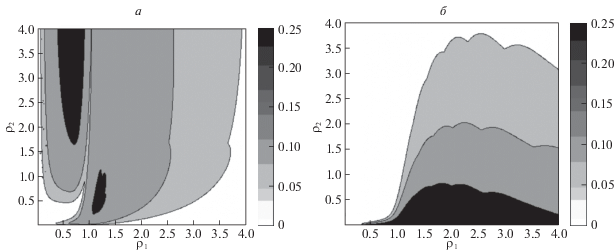
Линии уровня Δ₁ и Δ₂ для системы с абсолютным приоритетом при k = 31 приведены на рис. 2 (области линейности закрашены белым цветом). Для сравнения на рис. 3 построены аналогичные области  в случае относительного приоритета [4, 5]. Области линейности не оказываются локализованными  вблизи  начала  координат, как это предполагалось первоначально в работах [5, 9, 10], а вытянуты вдоль координатных осей ${{\rho }_{1}}$ и ${{\rho }_{2}}$. Усиление приоритета с относительного до абсолютного приводит к некоторому их сужению.

Коэффициенты линейной аппроксимации (3.2) можно вычислить аналитически, поскольку как при нулевой, так и при единичной вероятности выталкивания рассматриваемая СМО превращается в классические системы, обладающие известным точным решением. Поэтому в пределах областей линейности анализ потерь пакетов сведется к тривиальным алгебраическим вычислениям. Это кардинально упрощает управление пакетными коммутациями и резко повышает оперативность управления. Описанный метод был применен при решении задач удаленного управления робототехническими комплексами на борту МКС в рамках космического эксперимента “Контур” [1, 5, 11, 12]. В этом эксперименте приоритетный поток был образован пакетами управления и телеметрии, которые передавались с помощью транспортного протокола TCP (transmission сontrol protocol). Фоновый видеопоток составили пакеты по протоколу UDP (user datagram protocol). Был сконструирован специальный прибор, на панель управления которого был выведен регулятор, позволяющий плавно менять вероятность выталкивания. С его помощью оператор стремился достичь надлежащего компромисса между устойчивостью управления роботом, с одной стороны, и качественным, хорошо читаемым видеоизображением, с другой стороны. На основе последнего оператор и принимал свои управленческие решения.

4. Оптимальная настройка вероятностного выталкивающего механизма. Введение вероятностного выталкивающего механизма в контур управления телематическим устройством приводит к появлению еще одного дополнительного параметра задачи – вероятности выталкивания α, которую здесь удобно использовать в качестве параметра управления системой. Процесс принятия оператором решения, касающегося выбора конкретного числового значения α, можно автоматизировать. Для этого предлагается поставить и решить задачу оптимальной настройки вероятностного выталкивающего механизма. Задача эта заключается в подборе оптимального значения вероятности выталкивания α при заданных коэффициентах загрузки ρ₁ и ρ₂, а также заданной емкости системы k. При этом необходимо ограничить сверху вероятность потерь для низкоприоритетных требований соответствующим критическим значением P_кр. В результате приходим к следующей оптимизационной задаче на условный экстремум:

Выбор конкретного числового значения вероятности P_кр определяется физическим содержанием решаемой задачи, а также теми инженерными и техническими ограничениями, которые накладываются на функционирование системы. Например, в упоминавшейся выше задаче об управлении роботами на борту МКС [1] появление ограничения (4.2) проистекало из необходимости иметь устойчивую визуальную картину всего происходящего на борту космической станции.

По смыслу решаемой задачи параметр P_кр может принимать произвольные значения из интервала (0, 1). Пусть вначале он удовлетворяет неравенству

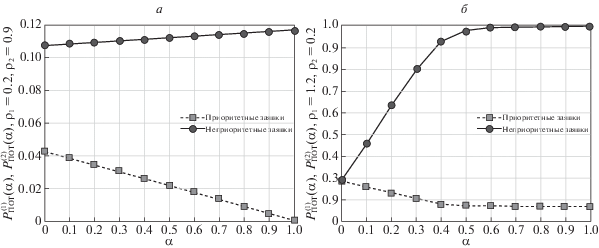
Очевидно, в задаче (4.1), (4.2) целевая функция, а также функция, задающая ограничение (4.2), являются монотонными относительно аргумента α. Это может быть подтверждено как логически по самому физическому смыслу понятия вероятности выталкивания, так и численно приведенными результатами вычислений (см. рис. 1). Поэтому решение поставленной задачи оптимизации α = α_opt, когда P_кр удовлетворяет (4.3), будет определяться из решения нелинейного уравнения вида

Теперь допустим, что заданное по условию критическое значение выходит за пределы интервала (4.3). Если оно превышает его верхнюю границу, т.е.

то тогда вся кривая потерь низкоприоритетных требований будет лежать ниже уровня P_кр и условие (4.2) будет выполняться автоматически при всех α. Следовательно, оптимальное значение α_opt = 1 и оптимальным будет детерминированный выталкивающий механизм, предложенный Г.П. Башариным [8]. В противном случае, когда P_кр лежит ниже левой границы интервала (4.3) и выполняется условие кривая потерь низкоприоритетных требований целиком лежит выше критического уровня и задача (4.1), (4.2), строго говоря, не имеет решения. Здесь нужно либо изменить коэффициенты загрузки, либо, если это допустимо, подкорректировать критический уровень P_кр, увеличив его до левой границы интервала (4.3). При этом α_opt = 0, а оптимальным становится полное отсутствие выталкивания, которое также разбиралось в [8].

В разд. 3 были построены области действия линейного закона потерь. Если выбирать коэффициенты загрузки (ρ₁, ρ₂) только из этих областей, то решение задачи оптимизации существенно упрощается, так как уравнение (4.4) превращается в линейное алгебраическое уравнение и решается тривиально в явном виде. Допустим, что критический уровень потерь низкоприоритетных требований удовлетворяет неравенству (4.3). Тогда, используя линейную аппроксимацию кривой потерь вида (3.1), получаем следующее оптимальное значение вероятности выталкивания:

Входящие в это выражение вероятности потери при граничных значениях параметра выталкивания α = 0 и α = 1, разумеется, могут быть подсчитаны методом, изложенным в настоящей статье, однако гораздо проще взять готовые аналитические выражения, имеющиеся в литературе. Для системы с абсолютным приоритетом и детерминированным выталкивающим механизмом (α = 1) они приведены в [5], а для такой же системы без выталкивания можно воспользоваться классическими результатами из [20, 21].

Следует отметить, что полученные в настоящей статье формулы оптимальной настройки вероятностного выталкивающего механизма полностью сохранят свою силу и для других видов приоритета, если только система работает в условиях действия линейного закона потерь. Границы действия линейного закона потерь были ранее построены авторами для целого ряда разновидностей приоритетов, которые выходят за рамки настоящей статьи: для чередующегося приоритета [13], рандомизированного приоритета [14], а также для абсолютного и относительного приоритетов при наличии повторных [15–18] и отрицательных [19] требований.

Заключение. В статье рассмотрен метод расчета характеристик телематического устройства, моделируемого с помощью двухпотоковой системы массового обслуживания конечной емкости. Первый поток считается высокоприоритетным и обладает абсолютным приоритетом по обслуживанию, а также приоритетом по постановке в очередь в форме так называемого вероятностного выталкивающего механизма. Последний означает, что вновь подошедшее высокоприоритетное требование, заставшее накопитель полностью заполненным, имеет право вытеснить оттуда одно из низкоприоритетных требований с заданной вероятностью α. Эта вероятность может служить весьма эффективным параметром управления информационными потоками на входе телематического устройства. Надлежащий выбор α позволяет рационально управлять высокоприоритетным трафиком, не ущемляя при этом низкоприоритетный трафик. Как показывают расчеты, чувствительность сети к выбору вероятности вытеснения оказывается существенно более высокой, чем к выбору типа приоритета по обслуживанию. Важно заметить, что в предлагаемом способе управления телематическое устройство удается плавно настроить на желаемый режим его функционирования. Для случая марковской модели системы в статье предложен эффективный вычислительный алгоритм, позволяющий сетевым инженерам и проектировщикам без особых усилий оценивать возможные варианты эксплуатации разнообразных устройств телематики. Он основан на построении областей действия линейного закона потерь, в которых вероятность потери обоих типов запросов линейным образом зависит от параметра α. Для рассмотренной системы поставлена и аналитически решена задача управления вероятностью потери высокоприоритетных требований при наличии ограничения на потери низкоприоритетных заявок.