Известия РАН. Теория и системы управления, 2021, № 1, стр. 11-23

Введение. Настоящая публикация является логическим продолжением статьи [1], посвященной разработке методов построения так называемых скользящих наблюдателей, работающих в скользящем режиме и использующих особенности этого режима [2], и предназначенных для решения задачи идентификации дефектов. Указанные наблюдатели описываются дифференциальным уравнением с разрывной правой частью и обеспечивают возникновение в системе скользящего режима при соблюдении определенных условий. Системы, в которых возникает скользящий режим, в русскоязычной литературе называются системами с переменной структурой, поэтому такие наблюдатели также можно назвать наблюдателями с переменной структурой.

Последние 20 лет скользящие наблюдатели активно применяются для решения задачи идентификации дефектов в различных системах – линейных [3, 4], нелинейных [5–7], сингулярных [8], а также ряде практических приложений [9–12]. Во всех этих публикациях на исходную систему накладывается ряд ограничений, обсуждаемых ниже.

В этой статье метод на основе скользящих наблюдателей используется для решения задач идентификации дефектов в нелинейных системах при действии на них возмущений. Как и в [1], в основе предлагаемого подхода лежит идея применения редуцированной (имеющей меньшую размерность) модели исходной системы, что дает возможность уменьшить размерность скользящих наблюдателей по сравнению с известными работами [3–8], где строятся наблюдатели полного порядка. За счет этого удается ослабить ограничения, накладываемые на системы, по сравнению с теми, которые накладываются известными методами [3, 4, 7], и расширить класс систем, для которых можно построить скользящие наблюдатели. Последнее объясняется тем, что исходная система может обладать свойствами, которые не совместимы с требованиями, накладываемыми в работах [3, 4, 7]. В то же время модель минимальной размерности такими свойствами не будет обладать.

1. Скользящие наблюдатели, основные соотношения. Рассмотрим класс технических систем, описываемых нелинейной моделью

Здесь $x(t) \in {{R}^{n}}$, $u(t) \in {{R}^{m}}$, $y(t) \in {{R}^{l}}$ – векторы состояния, управления и выхода; $F \in {{R}^{{n \times n}}}$, $G \in {{R}^{{n \times m}}}$, $D \in {{R}^{{n \times q}}}$, $L \in {{R}^{{n \times p}}}$ и $H \in {{R}^{{l \times n}}}$ – известные постоянные матрицы; $d(t) \in {{R}^{q}}$ – вектор-функция, описывающая дефекты: при их отсутствии $d(t) = 0$, при появлении дефекта d(t) становится неизвестной функцией времени; $\rho (t) \in {{R}^{p}}$ – неизвестная функция времени, описывающая действующие на систему возмущения, $\Psi (x,u)$ – нелинейная составляющая:

${{A}_{1}}, \ldots ,{{A}_{s}}$ – матрицы-строки; ${{\varphi }_{1}}, \ldots ,{{\varphi }_{s}}$ – нелинейные (возможно, недифференцируемые) функции, удовлетворяющие условию Липшица по аргументу $x$, откуда следует, что функция $\Psi (x,u)$ также удовлетворяет условию Липшица, т.е. $N \geqslant 0$ – некоторая константа. Предполагается, что известны и ограничены нормы $\left\| {d(t)} \right\|$ и $\left\| {\rho (t)} \right\|$ векторов d(t) и $\rho (t)$.

Для ряда практических значимых функций условие (1.2) не выполняется, однако выполняется обобщенное условию Липшица:

где $M \geqslant 0$ – некоторая константа. В дальнейшем, говоря об условии (1.3), мы будем рассматривать только упомянутые функции.

Отметим, что появление функции $d(t) \ne 0$ обусловлено изменением параметров системы из-за каких-либо происходящих в ней неблагоприятных процессов. Если, например, изменение входящих в матрицу F параметров вызвало ее вариацию $\Delta F(t)$, то $Dd(t) = \Delta F(t)x(t)$ (см. соотношение (6.3) в примере). Такое представление дефектов нередко используется как в отечественной, так и зарубежной литературе по технической диагностике [13, 14].

Коротко напомним основные результаты из [7], используемые в настоящей работе. Предполагается, что дефект $d(t)$ скалярный, q = 1 и ${\text{rank}}(HL) = {\text{rank}}(L)$, что позволяет представить систему (1.1) в виде

где ${{z}_{1}}{\text{(}}t{\text{)}}$, ${{z}_{2}}{\text{(}}t{\text{)}}$, $w_{1}^{{}}{\text{(}}t{\text{), }}w_{2}^{{}}(t)$ – векторы состояния и выходов соответствующих подсистем, ${{z}_{1}}{\text{(}}t{\text{)}} \in {{R}^{{n - q}}}$, ${{z}_{2}}{\text{(}}t{\text{)}} \in {{R}^{q}}$, $z(t) = {{(z_{1}^{{\text{т}}}{\text{(}}t{\text{) }}z_{2}^{{\text{т}}}(t))}^{{\text{т}}}} = Tx(t)$, ${{(w_{1}^{{\text{т}}}{\text{(}}t{\text{) }}w_{2}^{{\text{т}}}(t))}^{{\text{т}}}} = Sy(t)$ для некоторых невырожденных матриц T и S, ${{(f_{1}^{{\text{т}}}{\text{(}}x{\text{,}}u{\text{) }}f_{2}^{{\text{т}}}{\text{(}}x{\text{,}}u{\text{)}})}^{{\text{т}}}} = TC\Psi (x(t),u(t))$. Дополнительно предполагается, что пары $({{F}_{{11}}},{{H}_{{11}}})$ и $({{F}_{{22}}},{{H}_{{22}}})$ наблюдаемы, а функции ${{f}_{1}}(x,u)$ и ${{f}_{2}}(x,u)$ удовлетворяют условию Липшица по аргументу x: для некоторых ${{\gamma }_{1}},{{\gamma }_{2}} > 0$. Далее для каждой из подсистем строятся скользящие наблюдатели полного порядка: где ${{\hat {z}}_{1}}(t)$, ${{\hat {z}}_{2}}(t)$, ${{\hat {w}}_{1}}(t)$, ${{\hat {w}}_{2}}(t)$ – векторы состояния и выходов подсистем наблюдателя, ${{e}_{{{{w}_{1}}}}}(t) = {{\hat {w}}_{1}}(t) - {{w}_{1}}(t)$, ${{e}_{{{{w}_{2}}}}}(t) = {{\hat {w}}_{2}}(t) - {{w}_{2}}(t)$ – ошибки наблюдения выходов, матрицы усиления ${{W}_{1}}$ и ${{W}_{2}}$ выбираются так, чтобы сделать матрицы ${{F}_{{11}}} - {{W}_{1}}{{H}_{{11}}}$ и ${{F}_{{22}}} - {{W}_{2}}{{H}_{{22}}}$ устойчивыми (это возможно из-за наблюдаемости пар $({{F}_{{11}}},{{H}_{{11}}})$ и $({{F}_{{22}}},{{H}_{{22}}})$), ${{Q}_{1}}$ и ${{Q}_{2}}$ выбираются так, что для некоторых симметрических положительно-определенных матриц P₁ и P₂ выполняются равенства

Константы ${{g}_{1}}$ и ${{g}_{2}}$ выбираются из условий ${{g}_{1}} > {{\gamma }_{2}}$, ${{g}_{2}} > {{\gamma }_{1}} + {{\gamma }_{2}}$.

В [7] доказывается, что при определенных дополнительных предположениях оценка функции d(t) может быть представлена в виде

где δ – малый положительный скаляр.

В настоящей работе по аналогии с [7] задача идентификации дефекта решается при наличии возмущений, однако предположение ${\text{rank}}(HL) = {\text{rank}}(L)$ не делается и функция d(t) может быть векторной. Кроме того, строится только один скользящий наблюдатель, причем пониженной размерности, позволяющий оценить векторную функцию d(t). Рассмотрим вначале эту задачу для случая скалярной функции d(t).

2. Построение редуцированной модели в случае скалярного дефекта d(t). Решение поставленной задачи опирается на редуцированную модель системы (1.1), которая в общем случае описывается уравнением

где ${{x}_{*}} \in {{R}^{k}}$ – вектор состояния меньшей размерности k < n, ${{F}_{*}}$, ${{G}_{*}}$, ${{J}_{*}}$, ${{H}_{*}}$, ${{D}_{*}}$ и ${{L}_{*}}$ – матрицы, подлежащие определению, функция ${{C}_{*}}\Psi ({{x}_{*}},y,u)$ имеет вид ${{A}_{{*1{{i}_{1}}}}},{{A}_{{*2{{i}_{1}}}}}, \ldots ,{{A}_{{*1{{i}_{p}}}}},{{A}_{{*2{{i}_{p}}}}}$ – матрицы, подлежащие определению, ${{i}_{1}}$, …, i_p – номера нелинейностей, входящих в модель (2.1). Как обычно [15], предполагается, что при отсутствии дефектов и возмущений выполняются равенства ${{x}_{*}}(t) = \Phi x(t)$ и ${{y}_{*}}(t) = {{R}_{*}}y(t)$ для некоторых матриц $\Phi $ и ${{R}_{*}}$. Известно [15, 16], что эти матрицы удовлетворяют условиям

Рассмотрим метод построения модели (2.1) минимальной размерности, не чувствительной к возмущениям, на основе которой может быть построен скользящий наблюдатель. Для анализа возможности построения такой модели введем матрицу L₀ максимального ранга, такую, что ${{L}_{0}}L$ = 0. Известно [15], что условие нечувствительности к возмущениям имеет вид $\Phi L = 0$; тогда из максимальности ранга матрицы L₀ следует $\Phi = T{{L}_{0}}$ для некоторой матрицы T. Заменим матрицу $\Phi $ в выражении ${{R}_{*}}H = {{H}_{*}}\Phi $ на $T{{L}_{0}}$: ${{R}_{*}}H = {{H}_{*}}T{{L}_{0}}$ и перепишем его в виде

Это уравнение имеет нетривиальное решение, когда между строками матриц H и ${{L}_{0}}$ существует линейная зависимость, откуда следует, что критерием его нетривиального решения является условие

Аналогично уравнение $\Phi F = {{F}_{*}}\Phi + {{J}_{*}}H$ после указанной подстановки приводится к виду

а условием его нетривиального решения есть неравенство

Условия (2.3) и (2.4) являются необходимыми, т.е. их выполнение не гарантирует возможности построения модели, не чувствительной к возмущениям, поскольку в уравнения, на основе которых они получены, входит неизвестная матрица T. Если хотя бы одно из условий (2.3), (2.4) не выполняется, модели, не чувствительной к возмущениям, не существует. Ниже предполагается, что эти условия верны, т.е. явные препятствия для построения модели с указанным свойством отсутствуют.

Отметим также, что простые достаточные условия возможности построения модели, не чувствительной к возмущениям, имеют вид $HL = 0$ и $FL = 0$, что следует из уравнений (2.6), приведенных ниже, но эти условия достаточно редко выполняются на практике.

Для упрощения процедуры построения модели матрицы ${{F}_{*}}$ и ${{H}_{*}}$ ищутся в канонической форме следующего вида:

предполагается вначале, что выход ${{y}_{*}}$ – скаляр.

Для определения остальных матриц воспользуемся логико-динамическим подходом [16], согласно которому вначале находятся матрицы Φ, ${{R}_{*}}$ и ${{J}_{*}}$, описывающие линейную часть системы, затем проверяется возможность построения нелинейной составляющей $\Psi ({{x}_{*}},y,u)$ и при положительном исходе проверки строятся матрицы ${{C}_{*}}$ и ${{A}_{{*i}}}$, $i = \overline {1,s} $.

Используя (2.5), получим из (2.2) уравнения для строк матриц $\Phi $ и J:

Известно [1, 15], что строка $(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - {{J}_{{*1}}}}&{...}&{ - {{J}_{{*k}}}} \end{array})$ удовлетворяет уравнению

где

Уравнение имеет нетривиальное решение, если

Число k не превышает $n - 1$; это связано с тем, что модель должна быть не чувствительной к возмущениям, а при $k = n$ она будет заведомо чувствительна к ним.

Отметим, что модель, не чувствительная к возмущениям, может не существовать; в этом случае методом, предложенным в [1], может быть построена модель с минимальной чувствительностью к возмущениям.

Из последнего условия определяется минимальная размерность k, при которой уравнение (2.7) имеет решение, находится решение этого уравнения, из (2.6) определяются строки матрицы $\Phi $ и проверяется условие

Если оно выполняется, принимается ${{G}_{*}} = \Phi G$, ${{D}_{*}} = \Phi D$ и ${{C}_{*}} = \Phi C$; матрицы ${{A}_{{*1i}}}$ и ${{A}_{{*2i}}}$, $i = \overline {{{i}_{1}},{{i}_{p}}} $, входящие в функцию $\Psi ({{x}_{*}},y,u)$, определяются из (2.2). При невыполнении условия (2.9) ищется другое решение уравнения (2.7) при прежней или увеличенной размерности k. Предполагается, что ${{D}_{*}} \ne 0$.

В результате модель (2.1) принимает вид

3. Построение скользящего наблюдателя для скалярного случая. По аналогии с [1, 7] скользящий наблюдатель ищется в виде

матрица K выбирается так, чтобы ${{F}_{{**}}} = {{F}_{*}} - K{{H}_{*}}$ стала устойчивой матрицей, где разрывная функция ${v}(t)$ ищется в виде ${{e}_{y}}(t) = {{\hat {y}}_{*}}(t) - {{y}_{*}}(t) = {{\hat {y}}_{*}}(t) - {{R}_{*}}y(t)$ – ошибка по выходу; правила выбора матрицы Q и положительного скаляра g обсуждаются ниже. Отметим, что поскольку матрицы ${{F}_{*}}$ и ${{H}_{*}}$ ищутся в каноническом виде (2.5), матрица K всегда существует. Выбор элементов матрицы K и скаляра g влияет на скорость сходимости наблюдателя.

Отметим, что использование разрывной функции ${v}(t)$ приводит к многократным переключениям в наблюдателе (3.1).

Введем ошибку по состоянию $e(t) = {{\hat {x}}_{*}}(t) - {{x}_{*}}(t)$; нетрудно видеть, что ${{e}_{y}}(t) = {{H}_{*}}e(t)$. Используя (2.10) и (3.1), запишем уравнение динамики ошибки e(t):

где символом $\Delta \Psi (t)$ обозначена разность ${{C}_{*}}(\Psi ({{\hat {x}}_{*}}(t),y(t),u(t)) - \Psi ({{x}_{*}}(t),y(t),u(t)))$.

Нетрудно видеть, что если функция $\Psi (x,u)$ удовлетворяет обобщенному условию Липшица (1.3) по аргументу x, то и функция ${{C}_{*}}\Psi ({{\hat {x}}_{*}},y,u)$ удовлетворяет этому условию по аргументу ${{x}_{*}}$ для некоторых неотрицательных ${{N}_{*}}$ и ${{M}_{*}}$:

Отметим, что ${{M}_{*}}$ может принимать два значения: ненулевое, обусловленное видом функции $\Psi (x,u)$, которое используется для выявления условий существования и реализации скользящего режима, и нулевое при наступлении этого режима, поскольку известно [4], что в скользящем режиме $e(t) = 0$, т.е. ${{\hat {x}}_{*}}(t) = {{x}_{*}}(t)$, и, согласно (3.4), можно принять ${{M}_{*}} = 0$.

Так как матрица ${{F}_{{**}}}$ устойчива, то для произвольной симметрической положительно-определенной матрицы W существует положительно-определенная матрица P, удовлетворяющая уравнению $F_{{**}}^{{\text{т}}}P + P{{F}_{{**}}} = - W$. По аналогии с (1.3) предположим, что для некоторой матрицы $Q$ выполняется равенство

Теорема 1. Если ${{\lambda }_{{\min }}}(W) > 2{{N}_{*}}\left\| P \right\|$ и скаляр g удовлетворяет условию

то скользящее движение системы (3.3) асимптотически устойчиво.

Доказательство. Рассмотрим функцию Ляпунова

и, используя (3.5), найдем ее производную по времени:

Из сказанного выше следует, что первое слагаемое в (3.7) принимает вид $ - {{e}^{{\text{т}}}}(t)We(t)$ для положительно-определенной матрицы W.

Преобразуем выражение $({{D}_{*}}{{({v}(t) - d(t))}^{{\text{т}}}}Pe(t) + {{e}^{{\text{т}}}}(t)P{{D}_{*}}({v}(t) - d(t))$ с учетом (3.2) и (3.5):

Добавим к полученному выражению слагаемые $ - {{e}^{{\text{т}}}}(t)We(t)$ и $2{{(Pe(t))}^{{\text{т}}}}\Delta \Psi (t)$ и преобразуем полученный результат:

В последнем неравенстве учтены (3.4), условия теоремы и тот факт, что положительная определенность матрицы W эквивалентна условию ${{\lambda }_{{\min }}}(W) > 0$. Таким образом, $\dot {V}(t) < 0$, что доказывает теорему.

Поскольку в скользящем режиме $\dot {e}(t) = 0$ и $e(t) = 0$, из уравнения (3.3) следует ${{D}_{*}}({v}(t) - d(t))$ + + ΔΨ(t) = 0, а так как с учетом замечания после (3.4) можно принять $\left\| {\Delta \Psi (t)} \right\| \leqslant {{N}_{*}}\left\| {e(t)} \right\|$, то функция d(t) может быть оценена в виде

где δ – малая положительная константа. Следует отметить, что полученное выражение зависит только от ошибки по выходу ${{e}_{y}}(t) = {{\hat {y}}_{*}}(t) - {{R}_{*}}y(t)$.

Если условие ${{\lambda }_{{\min }}}(W) > 2{{N}_{*}}\left\| P \right\|$ не выполняется, то сходимость наблюдателя может быть обеспечена при более жестких условиях на скаляр g. Для простоты рассмотрим случай, когда ${{M}_{*}} = 0$.

Теорема 2. Если cкаляр g удовлетворяет условию

то скользящее движение системы (3.3) асимптотически устойчиво.

Доказательство. Добавим к выражению (3.8) слагаемое $2{{(Pe(t))}^{{\text{т}}}}\Delta \Psi (t)$ и преобразуем полученный результат:

в последнем неравенстве учтено условие (3.9) теоремы. Так как слагаемые $ - {{e}^{{\text{т}}}}(t)We(t)$ и элемент $ - 2g\left\| {Q{{H}_{*}}e(t)} \right\| - 2{{(Q{{H}_{*}}e(t))}^{{\text{т}}}}d(t) + 2{{(Pe(t))}^{{\text{т}}}}\Delta \Psi (t)$ в (3.10) в сумме составляют функцию $\dot {V}(t)$, а матрица W положительно определена, то $\dot {V}(t) < 0$, что доказывает теорему.

Усилим условие (3.9) теоремы, записав его с учетом (3.4) в виде

для некоторого скаляра ${{N}_{{**}}} > 0$. Так как ошибка e(t) неизвестна, то для вычисления скаляра g предлагается два варианта действий.

1. Задать максимальное значение переменной $\left\| {e(t)} \right\|$ в (3.11) исходя из реального значения ошибки $e(t)$ при t = 0, учитывая, что в скользящем режиме $e(t) = 0$. Недостаток варианта состоит в том, что величина cкаляра g получается завышенной, что может негативно сказаться на реализации скользящего режима.

2. Вычислять величину $\left\| {e(t)} \right\|$ в процессе реализации скользящего режима на основе измеряемой ошибки ${{e}_{y}}(t)$. Это в предположении, что нелинейный член входит только в уравнение для переменных ${{x}_{{*1}}}(t)$ и ${{\hat {x}}_{{*1}}}(t)$ моделей (2.10) и (3.1) соответственно, можно сделать следующим образом. Поскольку матрицы ${{F}_{*}}$ и ${{H}_{*}}$ реализованы в канонической форме (2.5), то ${{e}_{y}}(t) = {{H}_{*}}e(t)$ = = e₁(t). Уравнения для остальных переменных модели (3.1) имеют следующий вид (рассмотрим для простоты $k = 3$):

где ${{\psi }_{2}}(u(t),y(t))$ и ${{\psi }_{3}}(u(t),y(t))$ – произвольные функции, k₂ и k₃ – элементы матрицы K. Тогда уравнения для ошибок ${{e}_{2}}(t)$ и ${{e}_{3}}(t)$ принимают следующий вид: откуда

Полученные компоненты вектора $e(t)$ используются в (3.11), обеспечивая таким образом режим адаптации скользящего наблюдателя к величине ошибки $e(t)$.

Отметим также, что предложенный подход может быть использован также для оценки величины возмущения $\rho (t)$ на основе редуцированной модели (2.1), не чувствительной к дефекту. Для построения такой модели используется подход, описанный в разд. 2, с заменой L в матрице ${{B}^{{(k)}}}$ на D. Оцененное таким образом возмущение $\rho (t)$ предлагается использовать в дополнительном диагностическом наблюдателе, чувствительном как к дефекту, так и возмущениям. Такой наблюдатель может быть построен известными методами [1, 15].

4. Случай векторного дефекта d(t). В случае, когда d(t) – векторная функция, редуцированная модель (2.1) также должна иметь векторный выход ${{y}_{*}}(t)$, что в общем случае предполагает ее максимально возможную размерность. Для построения такой модели описанную выше процедуру предлагается модифицировать следующим образом. Матрица ${{F}_{*}}$ модели также ищется в канонической форме (2.5), но первое уравнение в (2.6) не используется; из-за этого уравнение (2.7) изменяется:

где

Оно имеет нетривиальное решение, если

В отличие от скалярного случая, ищется не минимальное, а максимальное значение k, при котором выполняется условие (4.2); из (4.1) находятся матрицы ${{\Phi }_{1}}$, ${{J}_{{*1}}}$, …, ${{J}_{{*k}}}$, после чего из соотношений (2.6) определяются строки ${{\Phi }_{2}}$, …, ${{\Phi }_{k}}$ матрицы $\Phi $ и проверяется условие (2.9). Если оно выполняется, принимается ${{G}_{*}} = \Phi G$, ${{D}_{*}} = \Phi D$ и ${{C}_{*}} = \Phi C$; матрицы ${{A}_{{*1i}}}$ и ${{A}_{{*2i}}}$, $i = \overline {1,s} $, входящие в функцию $\Psi ({{x}_{*}},y,u)$, определяются из (2.2). При невыполнении условия (2.9) ищется другое решение уравнения (4.1) при прежней или уменьшенной размерности k.

Для определения матриц ${{R}_{*}}$ и ${{H}_{*}}$ уравнение ${{R}_{*}}{{H}_{*}} = H\Phi $ записывается в виде

откуда и находятся искомые матрицы. Критерием его решения является условие

Предполагается, что пара $({{F}_{*}},{{H}_{*}})$ наблюдаема, в этом случае существует такая матрица K, что ${{F}_{{**}}} = {{F}_{*}} - K{{H}_{*}}$ – устойчивая матрица [7]. В остальном процедура построения скользящего наблюдателя и оценки функции d(t) совпадает с рассмотренной в разд. 3.

5. Частный случай. Рассмотрим частный случай, когда нелинейная составляющая ${{C}_{*}}\Psi ({{x}_{*}}(t)$, y(t), u(t)) в (2.10) не зависит от переменной ${{x}_{*}}(t)$. Нетрудно видеть тогда, что поскольку $\Delta \Psi = 0$, уравнение ошибки (3.3) становится линейным, и решение задачи упрощается. Действительно, будем искать скользящий наблюдатель в виде

где матрица K выбирается так, чтобы ${{F}_{{**}}} = {{F}_{*}} - K{{H}_{*}}$ стала устойчивой матрицей, разрывная функция ${v}(t)$ ищется в виде (3.2), функция ${{\Psi }_{*}}(y(t),u(t))$ по предположению зависит только от переменных y и u, матриц Q и скаляр g выбираются, как и выше. Отметим, что если ${{C}_{*}} = 0$, то наблюдатель (5.1) не содержит нелинейной составляющей.

Тогда уравнение динамики ошибки $e(t)$ принимает вид

По аналогии с теоремой можно показать, что при указанном выборе матрицы Q и скаляра g $\mathop {\lim }\limits_{t \to \infty } e(t) = 0$ скользящее движение системы, описывающей динамику ошибки e(t), асимптотически устойчиво. Доказательство этого утверждения аналогично первой части теоремы, где рассматриваются линейные составляющие.

Приведем два достаточных критерия независимости нелинейной составляющей ${{C}_{*}}\Psi ({{x}_{*}}(t)$, y(t), u(t)) от переменной ${{x}_{*}}(t)$, следующие из вида этой составляющей и (2.2):

1) каждая строка A_i  линейно выражается через строки матрицы H, что эквивалентно равенству

2) если некоторая строка A_i не выражается через строки матрицы H, то i-я строка матрицы ${{C}_{*}}$ нулевая.

6. Пример. Для проверки работоспособности предлагаемого в статье метода было проведено моделирование работы синтезированных наблюдателей для идентификации типовых дефектов в электроприводах многозвенных манипуляторов. Полная модель рассмотренного электропривода с учетом люфта и упругости механической передачи, сухого и вязкого трений, а также нелинейных составляющих взаимовлияний между степенями подвижности многозвенника имеет вид

где ${{x}_{1}}(t) = {{\alpha }_{r}}(t)$ и ${{x}_{2}}(t) = {{\dot {\alpha }}_{r}}(t)$ – угол поворота вала редуктора и его скорость соответственно, ${{x}_{3}}(t)$ = = α_d(t) и ${{x}_{4}}(t) = {{\dot {\alpha }}_{d}}(t)$ – угол поворота оси двигателя и его скорость соответственно, ${{x}_{5}}(t) = {{I}_{a}}(t)$ – ток якоря; C – жесткость механической передачи; ${{i}_{r}}$ – передаточное отношение редуктора, ${{M}_{{\text{1}}}}$ и ${{M}_{{\text{2}}}}$ – величины сухого трения движения в редукторе и двигателе соответственно, ${{K}_{r}}$ и ${{K}_{d}}$ – коэффициенты вязкого трения редуктора и двигателя соответственно, ${{J}_{d}}$ – момент инерции ротора двигателя и вращающихся частей редуктора, приведенный к ротору, ${{K}_{M}}$ – моментный коэффициент электродвигателя, ${{K}_{{\omega {\kern 1pt} }}}$ – коэффициент противо-э.д.с., ${{R}_{d}}$ – активное сопротивление цепи якоря, ${{L}_{d}}$ – индуктивность цепи якоря, ${{K}_{U}}$ – коэффициент усиления усилителя мощности, u(t) – напряжение на входе усилителя мощности; ${{H}_{M}}$, ${{h}_{M}}$ и ${{M}_{E}}$ – приведенные к валу редуктора переменные составляющие всех моментных воздействий на электропривод; $f(\beta )$ – функция, описывающая люфт в механической передаче: $\beta = {{x}_{3}} - {{i}_{r}}{{x}_{1}}$, $\sigma $ – величина люфта.

Нетрудно проверить, что функция ${\text{sign }}x$ не удовлетворяет условию Липшица (2.1), однако удовлетворяет его обобщению в виде

для всех $x$, $x{\text{'}}$, т.е. ${{N}_{*}} = 0$, ${{M}_{*}} = 2$.

Дефект моделируется следующим образом:

что соответствует изменению активного сопротивления цепи якоря электродвигателя на величину ${{\tilde {R}}_{d}}(t)$ (например, при его значительном нагреве). Возмущение $\rho (t) = - \tilde {M}(t){\text{/}}{{H}_{M}}$ обусловлено наличием внешнего нагрузочного момента $\tilde {M}(t)$ на валу редуктора. Отметим, что при отсутствии изменения сопротивления ${{\tilde {R}}_{d}}(t) = 0$ и, следовательно, $d(t) = 0$, в случае, когда ${{\tilde {R}}_{d}}(t) \ne 0$, d(t) становится неизвестной функцией времени.

Полагаем, что измеряемыми являются переменные ${{x}_{1}}(t)$, ${{x}_{3}}(t)$ и ${{x}_{5}}(t)$, рассматриваемую систему опишем следующими матрицами, согласно модели (1.1):

Построим линейную модель, инвариантную к возмущению. Можно показать, что k = 2; решение, формально получаемое на основе (2.7), в данном случае необходимо корректировать для выполнения условий скользящего режима, в частности, чтобы матрица W была положительно-определенной; в результате получаем

Поскольку аргумент функции $f(\beta )$ выражается через вектор $y(t)$, условие (2.9) выполняется автоматически, ${{C}_{*}} = \Phi C = {{(\begin{array}{*{20}{c}} 0&1 \end{array})}^{{\text{т}}}}$, что в итоге приводит к модели следующего вида:

где ${{x}_{{*1}}}(t) = {{x}_{5}}(t)$, ${{x}_{{*2}}}(t) = {{x}_{4}}(t)$. Так как ${{D}_{*}} = \Phi D = {{(1\,\,0)}^{{\text{т}}}} \ne 0$, построенная модель чувствительна к дефекту.

Сравнивая (2.10) и (6.4), получаем матрицы, описывающие линейную часть системы:

Полагаем $K = {{(0.3{\kern 1pt} - {\kern 1pt} 0.002)}^{{\text{т}}}}$. Из (3.5) следует, что можно принять $P: = Q: = 1$; в результате скользящий наблюдатель описывается уравнениями

где ${{e}_{y}}(t) = {{\hat {y}}_{*}}(t) - {{y}_{3}}(t)$,

Поскольку P = 1 и $\left\| {{{D}_{*}}} \right\| = 1$, то условие (3.6) теоремы принимает вид

Поскольку ${{N}_{*}} = 0$, а матрица W по построению является положительно-определенной, то условие ${{\lambda }_{{\min }}}(W) > 2{{N}_{*}}\left\| P \right\|$ выполняется автоматически. Оценка функции d(t) дается выражением

Проведем моделирование системы (6.1) с наблюдателем (6.5). При моделировании задавались следующие значения параметров рассматриваемого следящего электропривода: ${{J}_{d}} = 0.0001$ кг ⋅ м², ${{k}_{\omega }} = {\text{0}}{\text{.02}}$ В ⋅ с, ${{K}_{U}} = {\text{100}}$, ${{R}_{d}} = 0.4$ Ом, ${{L}_{d}} = 0.004$ Гн, ${{i}_{r}} = 100$, ${{K}_{M}} = 0.02$ Н ⋅ м/A, ${{C}_{r}} = 2$ Нм/рад, ${{M}_{{\text{1}}}} = 1$ Нм, ${{M}_{{\text{2}}}} = 0.01$ Нм, ${{K}_{d}} = {{10}^{{ - 5}}}$ Нмc/рад, ${{K}_{r}} = {{10}^{{ - 2}}}$ Нмc/рад, $\sigma = 0.01$ рад. Для обеспечения заданных показателей качества управления в прямой цепи электропривода использовался типовой ПИД-регулятор (пропорционально-интегрально-дифференцирующий регулятор). При этом в качестве входного воздействия на электропривод подавалось следующее желаемое значение угла поворота выходного вала редуктора: $\alpha _{r}^{{\text{ж}}}(t) = {\text{sin}}\,(t)$.

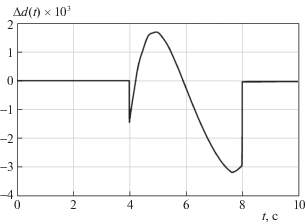
При моделировании возмущение имитировалось функцией $\tilde {M}(t) = 7\sin (0.8{\text{ }}t)$ Нм на интервале 0–10 с; дефект – функцией ${{\tilde {R}}_{d}}(t) = 0.1(1 - {{e}^{{ - (t - 4)}}})$ Ом на интервале 4–8 с.

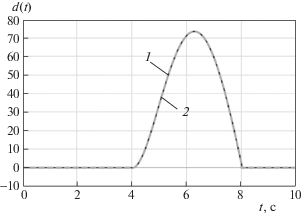
На рис. 1 представлены графики функций d(t) и ее оценки $\hat {d}(t)$ построенным наблюдателем (6.5), на рис. 2 – график ошибки идентификации $\Delta d(t) = d(t) - \hat {d}(t)$ этой функции. Из этих рисунков можно видеть, что построенный нелинейный скользящий наблюдатель позволяет своевременно определить момент времени появления дефекта d(t), а также обеспечить достаточно точную оценку величины этого дефекта. Кроме того, поскольку на интервалах 0–4 и 8–10 с значение $\hat {d}(t)$ равно нулю, ясно, что построенный наблюдатель не чувствителен к возмущению $\rho (t)$.

Таким образом, результаты моделирования на примере идентификации типовых дефектов, возникающих в следящих электроприводах, показали работоспособность предложенного в статье метода робастного поиска и идентификации дефектов на основе скользящих наблюдателей.

Заключение. С использованием метода на основе скользящих наблюдателей в работе решаются задачи обнаружения, поиска и идентификации дефектов в технических системах, описываемых нелинейными моделями с постоянными коэффициентами, в присутствии возмущений. Построение скользящего наблюдателя осуществляется на основе редуцированной (имеющей меньшую размерность) модели исходной системы, обладающей избирательной чувствительностью по отношению к дефектам и возмущению. Это обеспечивает снижение размерности средств диагностирования и позволяет ослабить ограничения, накладываемые на исходную систему, для возможности построения скользящих наблюдателей.

Результаты моделирования подтвердили работоспособность синтезированных с помощью предложенного в статье метода построения скользящих наблюдателей.