Известия РАН. Теория и системы управления, 2021, № 2, стр. 71-93
МАЯТНИКОВЫЙ АКСЕЛЕРОМЕТР С ЦИФРОВЫМ УПРАВЛЕНИЕМ И НОВЫМИ ФУНКЦИОНАЛЬНЫМИ ВОЗМОЖНОСТЯМИ
В. И. Гребенников a, *, Е. А. Депутатова a, **, Д. М. Калихман a, Л. Я. Калихман a, В. В. Скоробогатов a
a ПО “Корпус” (Филиал ФГУП “НПЦАП им. акад. Н.А. Пилюгина”)
Саратов, Россия
* E-mail: lidkalihman@yandex.ru
** E-mail: deputatova@bk.ru
Поступила в редакцию 19.11.2018
После доработки 21.09.2020
Принята к публикации 30.11.2020
Аннотация
Рассматривается кварцевый маятниковый акселерометр компенсационного типа, особенностью которого является применение в контуре управления цифрового усилителя обратной связи (для реализации дискретного регулятора и алгоритмической компенсации погрешностей от разбалансировки маятника и температурных зависимостей смещения нуля и масштабного коэффициента). Проблема связана с построением цифровой системы управления рассматриваемого акселерометра, обеспечивающего высокоточное измерение проекции на ось чувствительности действующего кажущегося ускорения объекта, на котором установлен акселерометр. Дается решение данной проблемы, позволяющее находить алгоритмы цифрового управления при использовании различных методов синтеза дискретных регуляторов контура управления. Проводится анализ полученных решений во временной и частотной областях, подтверждающий высокое качество регулирования. Приводятся результаты экспериментальных исследований.
Введение. Современным направлением развития инерциальных систем управления подвижных объектов является технология БИНС – бесплатформенных инерциальных навигационных систем. Блоки чувствительных элементов БИНС, как правило, содержат измерители угловой скорости (гироскопы) и измерители кажущегося ускорения (акселерометры) [1]. В последнее время кварцевые маятниковые акселерометры (КМА) компенсационного типа нашли широкое применение в системах управления летательными аппаратами и космическими объектами. К зарубежным производителям указанных приборов относятся фирмы “Honeywell” (США), “Safran” (Франция), “InnaLabs” (Ирландия). К акселерометрам отечественных фирм относятся прибор АК-15 разработки ПАО “Московский институт электромеханики и автоматики”, изготавливаемый заводом “Утес” (г. Ульяновск), прибор КХ67-041 разработки и изготовления производственного объединения “Корпус” (г. Саратов), а также прибор ВА-3 разработки ООО “Научно-производственный комплекс “Электрооптика” (г. Москва). Между приборами космической и авиационной направленности есть ряд отличий. Например, к измерителям в авиации предъявляются более жесткие требования по температурному диапазону от –65 до +85°С, так как они, как правило, располагаются в “нежилом” отсеке самолета и подвержены воздействию температур в достаточно широком диапазоне: по широтам – от пустынь до крайнего севера, а по высотам – от земной поверхности до стратосферы, тогда как измерители, используемые в космонавтике, находятся, как правило, в “жилом” отсеке, отсюда и диапазон температур колеблется от 0 до +40°С. Кроме того, к приборам космической и авиационной направленности предъявляются высокие требования по временной стабильности выходных параметров, для космоса вследствие долгосрочного нахождения на орбите (сроки до года), для авиации это связано с тем, что, хотя полет самолета продолжается не более суток, однако длительная стоянка в аэропорту не позволяет производить калибровку измерительных приборов, установленных на его борту. Эти и многие другие особенности предопределяют некоторую разницу в технических требованиях к приборам в авиации и космонавтике, что, в конечном счете, приводит к ряду отличий в подходах к их разработке. Так, например, в приборах космического применения при компенсации температурных погрешностей не нужно учитывать явление гистерезиса масштабного коэффициента и смещения нулевого сигнала, так как в диапазоне температур от 0 до +40°С он особо не проявляется, тогда как в авиационном температурном диапазоне от –65 до +85°С учет этого явления обязателен.
Важнейшей технической характеристикой акселерометра является погрешность масштабного коэффициента (линейность выходной характеристики), определяющая класс измерителя линейных ускорений. В авиации и пилотируемой космонавтике, как правило, диапазон измеряемых кажущихся ускорений не превышает ±10 g вследствие практической невозможности выдерживания пилотом больших перегрузок без существенного вреда для здоровья. В беспилотных системах и ракетах боевого применения, особенно в системах, совершающих маневры при достижении цели, возможны и большие диапазоны измеряемых ускорений. Для акселерометров с широким диапазоном измерения от ±20 до ±50 g выявлена одна специфическая погрешность, приводящая к нелинейности данной характеристики, названная разбалансировкой маятника [2]. Разбалансировка возникает вследствие несовпадения точек приложения к маятнику трех сил: инерционной силы, пропорциональной измеряемому ускорению, силы Ампера, реализуемой магнитоэлектрическим датчиком момента, и газодинамической силы, возникающей при перемещении маятника в герметичном корпусе, заполненном инертным газом. Взаимное смещение точек приложения этих трех сил возникает по конструкторским и технологическим причинам и приводит к возрастанию погрешности масштабного коэффициента на ускорениях свыше ±20 g до уровня 0.8%, т.е. более чем в 80 раз в сравнении с той же погрешностью на ускорениях до ±10 g (до уровня 0.01%). В работе [2] предложен конструктивный способ решения данной задачи, однако появление цифрового усилителя обратной связи в контуре управления акселерометра позволяет рассмотреть алгоритмический способ компенсации указанной погрешности.
Для решения задач аппаратного обеспечения в современных системах управления применяют, как правило, аналого-цифровое преобразование (АЦП) сигналов датчиков перемещений; цифроаналоговое, частотно-импульсное или широтно-импульсное формирование сигнала цепи обратной связи [3], когда управляющий сигнал в определенной форме поступает на исполнительный элемент измерителя. Теоретически можно применять любой из указанных способов для формирования управляющего сигнала в цифровом усилителе обратной связи, однако в [4] было показано, что наиболее перспективным является построение цифрового усилителя с широтно-импульсным модулятором (ШИМ).
1. Постановка задачи. В предлагаемой статье рассматривается несколько задач, связанных с построением компенсационного контура управления чувствительным элементом акселерометра и расчетом параметров его функциональных элементов, с разработкой алгоритма работы дискретного регулятора и алгоритмов компенсации погрешностей, обусловленных температурными возмущениями и разбалансировкой маятника. Задача синтеза алгоритма цифрового управления включает выбор метода синтеза, обеспечивающего наилучшее качество регулирования по результатам оценки запасов устойчивости, частотных характеристик и переходных процессов, формирование дискретного управляющего полинома в конечно-разностной форме, прошиваемого в микроконтроллер в цифровом усилителе обратной связи, а также разработку и реализацию алгоритмов повышения точности прибора.
Модернизация и совершенствование кварцевых маятниковых акселерометров компенсационного типа с цифровым управлением в контуре обратной связи является актуальной научной и технической проблемой, решение которой позволяет создать измерители кажущегося ускорения с новыми функциональными возможностями.
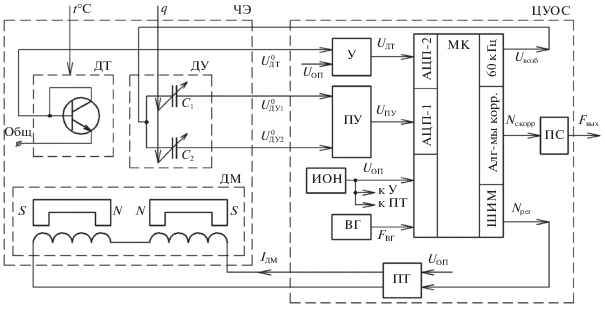
2. Функциональный состав и принцип работы маятникового акселерометра с цифровым управлением. Функционально-кинематическая схема кварцевого маятникового акселерометра (КМА) компенсационного типа с цифровым управлением изображена на рис. 1.
На рис. 1 введены следующие обозначения: ЧЭ – чувствительный элемент; q – проекция на ось чувствительности акселерометра вектора действующего кажущегося ускорения; t°C – значения температуры; ДТ – датчик температуры; ДУ – датчик угла; ДМ – датчик момента; Общ. – общая точка; C1, C2 – переменные емкости ДУ; S, N – обозначения полюсов постоянных магнитов ДМ; ЦУОС – цифровой усилитель обратной связи; У – усилитель сигнала ДТ; ПУ – предварительный усилитель сигналов ДУ; ИОН – источник опорных напряжений; ВГ – внешний генератор; МК – микроконтроллер; ПС – преобразователь сигнала; ПТ – переключатель тока; $U_{{{\text{ДТ}}}}^{0}$, UДТ – напряжения ДТ до усиления и после; UДУ1, UДУ2, UПУ – напряжения ДУ до усиления и после; IДМ – ток датчика момента (ток цепи обратной связи); Uоп – опорное напряжение питания МК, У и ПТ; FВГ – тактовая частота работы МК, формируемая ВГ; Uвозб – напряжение возбуждения ДУ; Nрег – сигнал с выхода регулятора в МК; Nскорр – алгоритмически скорректированный в МК выходной сигнал; Fвых – выходная цифровая информация акселерометра.
В соответствии с рис. 1 КМА состоит из ЧЭ (включающего маятниковую пластину (на рис. 1 не показана), ДУ, ДМ и ДТ) и ЦУОС, построенного на базе МК и содержащего усилители У и ПУ, а также ПТ для формирования направления протекания и величины тока IДМ в зависимости от знака и величины действующего ускорения q и вспомогательные элементы для работы функциональной электроники – это ИОН для выработки стабилизированных напряжений и ВГ для формирования тактовой частоты работы МК.
КМА с ЦУОС работает следующим образом. Под действием ускорения q формируется входной момент, который определяется моментом силы инерции. Он отклоняет маятник от нулевого положения, угол отклонения маятника измеряется емкостным ДУ, построенным по обращенной мостовой схеме. На выходе ДУ формируются напряжения рассогласования мостовой схемы UДУ1 и UДУ2, поступающие на вход ПУ, который входит в состав ЦУОС. Выходное напряжение ПУ UПУ = (UДУ1 – UДУ2)KПУ = UДУKПУ, где KПУ – коэффициент усиления ПУ, в МК ЦУОС преобразуется в широтно-модулированные импульсы напряжения, управляющие переключателем тока цепи обратной связи IДМ, который поступает на исполнительный элемент – магнитоэлектрический датчик момента. Датчик момента в свою очередь формирует уравновешивающий момент и возвращает маятник в исходное нулевое положение. На базе МК в ЦУОС реализован дискретный регулятор, обеспечивающий требуемые динамические характеристики и запасы устойчивости. С выхода МК снимается также скорректированная в соответствии с алгоритмами повышения точности акселерометра выходная цифровая информация Fвых, обусловленная протекающим через нагрузку током IДМ и пропорциональная действующему ускорению q. В качестве Fвых можно сформировать коды в формате RS-232, RS-485, код Манчестер, унитарный код или любой другой в зависимости от требований, предъявляемых к объекту, на котором будет устанавливаться акселерометр. При технологической отладке макетного образца акселерометра с ЦУОС достаточно снимать выходной сигнал в формате RS-232.
Для формирования алгоритма температурной коррекции используются сигналы ДТ, расположенного внутри корпуса ЧЭ и выполненного на биполярном транзисторе, а для формирования алгоритма компенсации разбалансировки маятника – сами показания на выходе регулятора в МК, пропорциональные действующему ускорению q.
Высокоточные показания КМА обеспечиваются применением компенсационных принципов, главным образом принципом обратной связи при магнитоэлектрическом способе уравновешивания маятника, а также использованием наиболее совершенного упругого материала в подвесе маятника – кварцевого стекла [5].
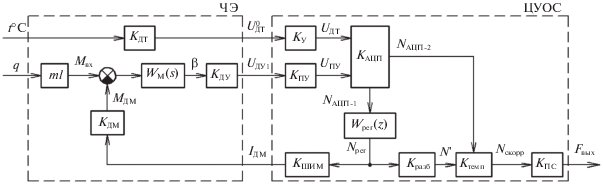
3. Математическая модель акселерометра и аппаратное обеспечение для его реализации. Структурная схема КМА с ЦУОС, составленная в соответствии с функционально-кинематической схемой (рис. 1), но без учета ПТ, коэффициент передачи которого математически закладывается в коэффициент передачи KШИМ, и без вспомогательных элементов, не влияющих на систему управления “КМА–ЦУОС”, а именно без ИОН и ВГ, приведена на рис. 2.
На рис. 2 помимо введенных ранее (на рис. 1) приняты следующие обозначения: ml – маятниковость; Мвх – входной момент; МДМ – момент, формируемый ДМ; Wм(s) – передаточная функция маятника; s – символ преобразования Лапласа, s = α + jω (α – действительная часть s, j – мнимая единица, ω – частота входного сигнала); β – угол отклонения маятника; KДТ, KДУ, KДМ, KУ, KПУ, KАЦП, KШИМ, KПС – коэффициенты передачи соответствующих элементов; Wрег(z) – z-преобразование передаточной функции регулятора; NАЦП-1, NАЦП-2 – сигналы на выходе АЦП, пропорциональные действующему ускорению и температуре соответственно; Kразб, Kтемп – поправочные коэффициенты (функционалы) выходного сигнала при разбалансировке маятника и воздействии температуры.
Передаточная функция объекта управления – ЧЭ акселерометра в соответствии с рис. 2 имеет вид
в которой передаточная функция маятника принимается такой же, как в работе [6]:(3.2)
${{W}_{{\text{м}}}}(s) = 1{\text{/}}({{J}_{\beta }}{{s}^{2}} + {{n}_{\beta }}s + {{C}_{{\text{т}}}}),$Параметры КМА с ЦУОС разработки ПО “Корпус” [6] без коэффициентов цифрового регулятора, подлежащих определению, сведены в табл. 1, где ед.ц.к. – условное обозначение количества единиц цифрового кода nц.к, используемых как размерность числовых значений при расчетах внутри микроконтроллера, т.е. все математические операции от АЦП до ШИМ выполняются в условно названных нами ед.ц.к.
Таблица 1.
Параметры КМА с ЦУОС
| Параметр | Числовое значение, единица измерения | Параметр | Числовое значение, единица измерения |
|---|---|---|---|
| q | (1 – 50) g | KДМ | 150 г ⋅ см/А |
| t °C | (–65 – +85)°С | KДТ | 1.15 × 10–3 В/град |
| ml | 0.15 г ⋅ см/g | KУ | 16.97 |
| Jβ | 1.2 × 10–4 г ⋅ см ⋅ с2 | KПУ | 2.93 |
| nβ | 0.05 г ⋅ см ⋅ с | KАЦП | 1638.4 ед.ц.к./В |
| Cт | 1.6 г ⋅ см/рад | KШИМ | 1 × 10–5 А/ед.ц.к. |
| KДУ | 182 В/рад | KПС | 1 (для RS-232) |
С учетом передаточной функции (3.2) и численных значений параметров (табл. 1) передаточная функция (3.1) примет вид
(3.3)
${{W}_{{{\text{ЧЭ}}}}}(s) = \frac{{182 \times 150}}{{1.2 \times {{{10}}^{{ - 4}}}{{s}^{2}} + 0.05s + 1.6}} = \frac{{1.71 \times {{{10}}^{4}}}}{{({{Т}_{{1{\text{ЧЭ}}}}}s + 1)({{Т}_{{2{\text{ЧЭ}}}}}s + 1)}},$АЦП представляет собой ключ, замыкающийся через промежутки времени То.с (период дискретности работы цепи обратной связи) на очень малое время δ ≪ То.с и превращающий выходное напряжение ПУ из непрерывной функции в решетчатую, последовательность цифровых значений которой поступает на вход вычислителя МК.
В соответствии с рис. 2 алгоритм работы ЦУОС можно записать через дискретную передаточную функцию в следующем виде:
(3.4)
${{W}_{{{\text{ЦУОС}}}}}(z) = {{I}_{{{\text{ДМ}}}}}(z){\text{/}}{{U}_{{{\text{ДУ}}}}}(z) = {{K}_{{{\text{ПУ}}}}}{{K}_{{{\text{АЦП}}}}}{{W}_{{{\text{рег}}}}}(z){{K}_{{{\text{ШИМ}}}}},$(3.5)
$\sum\limits_{i = 0}^k {{{a}_{i}}{{I}_{{{\text{ДМ}}}}}[(n - i){{T}_{{{\text{о}}{\text{.с}}}}}]} = \sum\limits_{j = 0}^m {{{b}_{j}}{{U}_{{{\text{ДУ}}}}}[(n - j){{T}_{{{\text{о}}{\text{.с}}}}}]} ,\quad n = 1,2,...,\infty ,\quad m \geqslant k.$В соответствии с рис. 2 и выражением (3.4) алгоритм работы МК запишется как
(3.6)
${{W}_{{{\text{рег}}}}}(z) = {{N}_{{{\text{рег}}}}}(z){\text{/}}{{N}_{{{\text{АЦП}} - 1}}}(z) = {{W}_{{{\text{ЦУОС}}}}}(z){\text{/}}({{K}_{{{\text{ПУ}}}}}{{K}_{{{\text{АЦП}}}}}{{K}_{{{\text{ШИМ}}}}}) = 20.8311{{W}_{{{\text{ЦУОС}}}}}(z).$Для вычислений в соответствии с (3.5) на каждом из отрезков времени nТо.с МК затрачивает время τ, внося тем самым запаздывание. Современные МК обладают быстродействием, обеспечивающим обработку цифровых алгоритмов с частотой десятки килогерц. Если выбрать период дискретности достаточно малым, то все постоянные времени WЧЭ(s) будут расположены в области низких частот. В этом случае можно не учитывать запаздывание (время τ), затрачиваемое на вычисления в соответствии с (3.5).
Акселерометр с цифровой обратной связью проектируется так, чтобы полоса пропускания составляла не менее 500 Гц, т.е. частота среза разомкнутой системы ωср ≈ 500 ⋅ 2π ≈ 3.14 × 103 с–1. В соответствии с требованиями теоремы Котельникова–Шеннона период дискретности работы цифровой системы должен отвечать требованию Tо.с < 2/ωср ≈ 0.64 × 10–3 с. Если выбрать с запасом То.с = 0.1 × 10–3 с, то частота работы обратной связи определится как fо.с = 1/То.с = 1/(0.1 × × 10–3 с) = 10 кГц.
Покажем, как рассчитываются коэффициенты ЦУОС, сведенные в табл. 1, при выборе его аппаратного обеспечения.
Коэффициент передачи 12-разрядного АЦП, встроенного в МК 1986ВЕ93У фирмы “ПКК “Миландр” (г. Зеленоград), имеет вид
Коэффициент передачи ШИМ
где $I_{{{\text{ДМ}}}}^{{\max }}$ – максимально допустимый ток, протекающий через катушки ДМ; NШИМ – количество минимальных интервалов в периоде ШИМ, соответствующих одной ед.ц.к. nц.к:Коэффициент передачи усилителя У, построенного по инвертирующей схеме на базе операционного усилителя (ОУ) 140УД17АН1ВК с входным резистором Rу1 = 8.25 кОм и резистором в обратной связи ОУ Rу2 = 140 кОм, вычисляется следующим образом:
Коэффициент передачи ДТ можно найти из выражения
4. Синтез дискретного регулятора акселерометра. За последние годы в теории автоматического управления разработан целый комплекс методов синтеза дискретных регуляторов, среди которых можно отметить такие, как традиционный метод (с построением желаемых частотных характеристик), метод прямой дискретизации, метод линейно-квадратической дискретной оптимизации (LQD-оптимизации), метод H∞, метод построения гибридного, нейросетевого регуляторов и др. Рассмотрим несколько методов синтеза дискретного регулятора акселерометра для проведения сравнительного анализа характеристик замкнутой системы управления “КМА–ЦУОС”.
4.1. Традиционный метод (с построением желаемых частотных характеристик). Согласно этому методу, необходимо выполнить переход от непрерывной передаточной функции WЧЭ(s) к дискретной частотной характеристике WЧЭ (jλ), где λ – псевдочастота [7]. В работе [7] предложен способ перехода, основанный на формировании WЧЭ (jλ) отдельно для областей низких и высоких частот. При этом низкими считаются частоты ωн < 2/Tо.с, высокими – ωв ≥ 2/Tо.с, где 2/То.с ≈ 20 × 103 с–1. Поскольку частоты ω1ЧЭ и ω2ЧЭ намного меньше 2/То.с, то постоянные времени передаточной функции (3.3) находятся в области низких частот, в которой частоты ω и λ практически совпадают.
Поскольку период дискретности То.с выбран с большим запасом и было показано, что запаздыванием можно пренебречь, тогда переход от WЧЭ(s) к WЧЭ( jλ) будет заключаться в замене символа s на jλ и умножении числителя на (1 – jλTо.с /2) [7]. При переходе к дискретной частотной характеристике при заданном значении Tо.с получим
(4.1)
${{W}_{{{\text{ЧЭ}}}}}(j\lambda ) = \frac{{1.71 \times {{{10}}^{4}}(1 - 0.5 \times {{{10}}^{{ - 4}}}j\lambda )}}{{(0.2863 \times {{{10}}^{{ - 1}}}j\lambda + 1)(0.262 \times {{{10}}^{{ - 2}}}j\lambda + 1)}}.$По характеристике (4.1) строится ЛАЧХ располагаемого объекта управления, приведенная на рис. 3 (кривая 1).
Рис. 3.
ЛАЧХ: 1 – располагаемого объекта управления; 2 – разомкнутой скорректированной системы “КМА–ЦУОС” (желаемые характеристики)
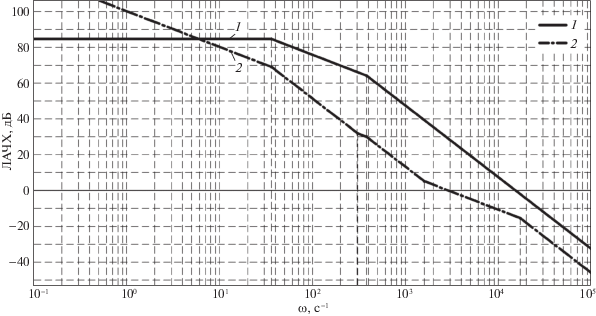
На рис. 3 также строится желаемая ЛАЧХ (кривая 2) разомкнутой скорректированной системы “КМА–ЦУОС”, при которой обеспечиваются астатизм системы, запасы устойчивости по амплитуде и фазе, а также требуемые динамические характеристики.
По разности кривых 1 и 2 (рис. 3) записывается дискретная частотная характеристика ЦУОС:
(4.2)
${{W}_{{{\text{ЦУОС}}}}}(j\lambda ) = \frac{{6.016(0.33 \times {{{10}}^{{ - 2}}}j\lambda + 1)(0.66 \times {{{10}}^{{ - 3}}}j\lambda + 1)}}{{j\lambda \cdot (0.66 \times {{{10}}^{{ - 4}}}j\lambda + 1)}}.$С помощью подстановки в (4.2)
находится дискретная передаточная функция ЦУОС:(4.4)
${{W}_{{{\text{рег}}}}}(z) = \frac{{2.57{{z}^{2}} - 4.701z + 2.142}}{{{{z}^{2}} - 1.138z + 0.1379}}.$4.2. Метод прямой дискретизации. Согласно работе [6], аналоговый усилитель обратной связи (АУОС) КМА имеет передаточную функцию:
(4.5)
${{W}_{{{\text{АУОС}}}}}(s) = {{I}_{{{\text{ДМ}}}}}(s){\text{/}}{{U}_{{{\text{ДУ}}}}}(s) = \frac{{0.2(2.05 \times {{{10}}^{{ - 6}}}s + 1)(0.6 \times {{{10}}^{{ - 4}}}s + 1)(3.3 \times {{{10}}^{{ - 4}}}s + 1)(8.8 \times {{{10}}^{{ - 2}}}s + 1)}}{{s(3.27 \times {{{10}}^{{ - 5}}}s + 1)(3.95 \times {{{10}}^{{ - 5}}}s + 1)(2.34 \times {{{10}}^{{ - 9}}}{{s}^{2}} + 8 \times {{{10}}^{{ - 5}}}s + 1)}}.$В связи с тем, что некоторые постоянные времени регулятора (4.5) более чем на порядок меньше величины, обратной требуемой полосы пропускания (1/ωср ≈ 3.2 × 10–4 с) системы “КМА–АУОС”, упростим передаточную функцию (4.5) и запишем ее в следующем эквивалентном (по результатам математического моделирования) виде:
Метод прямой дискретизации заключается в переходе от оператора Лапласа s к дискретному оператору z аналогично выражению (4.3), что наиболее просто выполнить с помощью программного комплекса Matlab (функция c2d(…) [8]). Таким образом, передаточная функция дискретного регулятора при заданном значении Tо.с, реализуемого на базе МК и с учетом введения АЦП, ШИМ и нового ПУ с соответствующими коэффициентами передачи (табл. 1), примет вид
(4.6)
${{W}_{{{\text{рег}}}}}(z) = \frac{{2.954{{z}^{3}} - 5.717{{z}^{2}} + 2.903z - 0.1388}}{{{{z}^{3}} - 1.144{{z}^{2}} + 0.1764z - 0.03275}}.$4.3. Метод LQD-оптимизации. Методика построения дискретного регулятора указанным методом рассматривается в [9]. Полное название метода звучит как метод линейно-квадратической дискретной оптимизации, цифровой фильтрации и теории наблюдающих устройств минимальной размерности типа Луенбергера.
Метод, основанный на процедурах LQD-оптимизации и цифровой фильтрации дискретных систем [9–11], позволяет учесть запаздывание по управлению и требование астатизма. Необходимость введения астатизма связана с тем, что для обеспечения малого угла отклонения маятника акселерометра, что является одним из основных требований при разработке подобных приборов [12], и, в частности, для устранения статической ошибки по этому углу при постоянном измеряемом ускорении регулятор контура акселерометра должен быть астатическим. Основными этапами этого метода являются: составление математической модели объекта управления контура КМА в форме дифференциальных уравнений для выбранных переменных состояния, переход к дискретной модели с учетом принятой частоты дискретизации и запаздывания по управлению на один такт и ее расширение за счет модели запаздывания и искусственно вводимого дискретного интегратора для реализации требования астатизма. Дальнейшее решение связано с построением регулятора по измеряемому выходу на базе наблюдателя Луенбергера минимальной размерности [13] и применением стандартных процедур дискретной оптимизации, основанных на решении соответствующих уравнений Риккати. При этом исходными данными этих процедур, помимо матриц расширенного объекта, являются также некоторые весовые матрицы Q и Ψ для уравнений Риккати и скалярный коэффициент передачи α вводимого дискретного интегратора для обеспечения астатизма системы, которые выбираются так, чтобы обеспечить необходимое качество регулирования.
Объект управления КМА, согласно структурной схеме, приведенной на рис. 2, описывается передаточной функцией (3.3) и включает датчик момента, подвижный элемент акселерометра (маятник) и датчик угла. Принимая в качестве переменных состояния y = UДУ – измеряемый выход и ωβ – угловую скорость маятника (${{\omega }_{\beta }} = \dot {\beta }$), можно получить модель соответствующего объекта, которая без учета внешнего воздействия q будет представляться следующими уравнениями:
Если ввести вектор состояний x = colon{y, ωβ}, то можно получить следующее векторно-матричное описание:
(4.7)
$\begin{gathered} \dot {x}(t) = {{A}_{0}}x(t) + {{B}_{0}}u(t), \\ y(t) = {{C}_{0}}x(t), \\ \end{gathered} $(4.8)
${{A}_{0}} = \left[ {\begin{array}{*{20}{c}} 0&{{{K}_{{{\text{ДУ}}}}}} \\ { - J_{\beta }^{{ - 1}}{{С}_{{\text{т}}}}K_{{{\text{ДУ}}}}^{{ - 1}}}&{ - J_{\beta }^{{ - 1}}{{n}_{\beta }}} \end{array}} \right],\quad {{B}_{0}} = \left[ {\begin{array}{*{20}{c}} 0 \\ { - J_{\beta }^{{ - 1}}{{K}_{{{\text{ДМ}}}}}} \end{array}} \right],\quad {{C}_{0}} = \left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right].$Пусть $y(i) = y(t){{|}_{{iT{\text{o}}{\text{.c}}}}}$ – оцифрованное с помощью АЦП в момент t = iTо.с значение измеряемого выхода объекта; i = 0, 1, 2, … – дискретное время (номер такта). И пусть u(i) – значение управления, вычисляемое в МК на i-м такте и прикладываемое к объекту (с помощью ШИМ) по истечении этого такта. Требуется определить дискретную передаточную функцию цифрового регулятора Wрег(z) так, чтобы обеспечить устойчивость и необходимое качество регулирования контура КМА как автономной системы.
Составим дискретную модель непрерывного объекта (4.7). С учетом запаздывания по управлению на один такт такая модель будет описываться уравнениями:
где А, В, С – числовые матрицы, определяемые по известным формулам перехода [10, 11]:Для учета запаздывания по управлению введем вспомогательную переменную xτ(i) = u(i – 1), а для учета требования астатизма дополним объект (4.9) дискретным интегратором μ(i + 1) = = μ(i) + αTо.сy(i) с некоторым коэффициентом передачи α. Формально это приводит к тому, что к модели объекта (4.9) добавляются уравнения:
которые затем, после решения задачи синтеза, должны быть отнесены к регулятору. Последнее, в частности, означает, что новые переменные xτ и μ, определенные как управление из предыдущего такта и выход интегратора, доступны для использования в алгоритме управления, в силу чего они могут быть отнесены к дополнительным измеряемым переменным. Таким образом, если ввести векторы для расширенного состояния $\bar {x} = colon\{ \mu ,x,{{x}_{\tau }}\} $ и новых измеряемых выходов $\bar {y} = colon\{ \mu ,y,{{x}_{\tau }}\} $, то эквивалентное описание дискретной модели объекта примет вид(4.11)
$\begin{gathered} \bar {x}(i + 1) = \bar {A}\bar {x}(i) + \bar {B}u(i), \\ \bar {y}(i) = \bar {C}\bar {x}(i), \\ \end{gathered} $(4.12)
$\bar {A} = \left[ {\begin{array}{*{20}{c}} 1&{\alpha {{T}_{{{\text{о}}{\text{.с}}}}}С}&0 \\ {{{0}_{{2 \times 1}}}}&A&B \\ 0&{{{0}_{{1 \times 2}}}}&0 \end{array}} \right],\quad \bar {B} = \left[ {\begin{array}{*{20}{c}} 0 \\ {{{0}_{{2 \times 1}}}} \\ 1 \end{array}} \right],\quad \bar {C} = \left[ {\begin{array}{*{20}{c}} 1&{{{0}_{{1 \times 2}}}}&0 \\ 0&C&0 \\ 0&{{{0}_{{1 \times 2}}}}&1 \end{array}} \right].$Здесь и далее 0α × β обозначает нулевой блок соответствующих размеров.
Для решения задачи будем использовать подход, основанный на объединении регулятора по состоянию и наблюдающего устройства. Причем в качестве последнего целесообразно использовать наблюдатель Луенбергера минимальной размерности, который позволяет получить динамический регулятор по измеряемому выходу наименьшего (в рамках данного подхода) порядка. Тогда полные уравнения регулятора будут иметь вид [9]
(4.13)
$\begin{gathered} \bar {\xi }(i + 1) = \bar {W}\bar {\xi }(i) + \bar {K}{\kern 1pt} \bar {y}(i) + \bar {T}\bar {B}u(i), \\ u(i) = \bar {F}\hat {\bar {x}}(i) = \bar {F}(\bar {V}\bar {\xi }(i) + \bar {U}\bar {y}(i)), \\ \end{gathered} $(4.14)
$\bar {T}\,\bar {A} - \bar {W}\,\bar {T} = \bar {K}\,\bar {C},\quad \bar {U}\,\bar {C} + \bar {V}\,\bar {T} = I,$Решение уравнений (4.14) основано на таком выборе матрицы $\bar {T}$, при котором гарантированно обеспечивается существование обратной от блочной матрицы $colon\{ \bar {C},\bar {T}\} $. Используя структуру $\bar {C}$ из (4.12) и учитывая выражение для С = С0 из (4.8), выберем матрицу $\bar {T}$:
(4.15)
$\bar {T} = \left[ {\begin{array}{*{20}{c}} 0&T&0 \end{array}} \right],\quad T = \left[ {\begin{array}{*{20}{c}} L&I \end{array}} \right],$(4.16)
$\begin{gathered} \bar {U} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ {{{0}_{{2 \times 1}}}}&U&{{{0}_{{2 \times 1}}}} \\ 0&0&1 \end{array}} \right],\quad \bar {V} = \left[ {\begin{array}{*{20}{c}} 0 \\ V \\ 0 \end{array}} \right],\quad U = \left[ {\begin{array}{*{20}{c}} 1 \\ { - L} \end{array}} \right],\quad V = \left[ {\begin{array}{*{20}{c}} 0 \\ I \end{array}} \right], \\ \bar {W} = \bar {T}\,\bar {A}\,\bar {V} = TAV = W,\quad \bar {K} = \bar {T}\,\bar {A}\,\bar {U} = \left[ {\begin{array}{*{20}{c}} 0&K&{TB} \end{array}} \right],\quad K = TAU. \\ \end{gathered} $Анализируя данные выражения, можно увидеть, что регулятор (4.13) будет полностью определяться двумя матрицами $\bar {F}$ и L, которые должны быть найдены таким образом, чтобы контур КМА был устойчивым и имел необходимые показатели качества. Следует отметить, что если выполняются уравнения (4.14), то полюсами замкнутого контура КМА будут являться [10, 11] собственные числа матриц $\bar {A} + \bar {B}\,\bar {F}$ и W = TAV = A22 + LA12, где Aij, i, j = 1, 2, – блоки матрицы А исходного объекта (4.9), соответствующие разбиению вектора состояний этого объекта на две части: $x = {\text{ }}{{[y\;v]}^{{\text{T}}}}$, ${v} = {{\omega }_{\beta }}$. Тогда для определения матриц $\bar {F}$ и L можно использовать любой из известных методов теории многомерных систем, в частности, метод, основанный на применении процедур линейно-квадратической оптимизации и оптимальной фильтрации, которые для дискретных систем представляются выражениями
(4.17)
$\bar {F} = - {{(1 + {{\bar {B}}^{{\text{T}}}}P\bar {B})}^{{ - 1}}}{{\bar {B}}^{{\text{T}}}}P\bar {A},\quad L = - {{A}_{{22}}}SA_{{12}}^{{\text{T}}}{{(I + {{A}_{{12}}}SA_{{12}}^{{\text{T}}})}^{{ - 1}}},$(4.18)
$\begin{gathered} P = {{{\bar {A}}}^{{\text{T}}}}P\bar {A} + Q - {{{\bar {A}}}^{{\text{T}}}}P\bar {B}{{(1 + {{{\bar {B}}}^{{\text{T}}}}P\bar {B})}^{{ - 1}}}{{{\bar {B}}}^{{\text{T}}}}P\bar {A}, \\ S = {{A}_{{22}}}SA_{{22}}^{{\text{T}}} + \Psi - {{A}_{{22}}}SA_{{12}}^{{\text{T}}}{{(I + {{A}_{{12}}}SA_{{12}}^{{\text{T}}})}^{{ - 1}}}{{A}_{{12}}}S{{A}_{{22}}}. \\ \end{gathered} $В этом случае устойчивость контура КМА будет гарантирована, а необходимое качество регулирования может быть достигнуто выбором весовых матриц Q, Ψ и коэффициента α введенного интегратора.
Обратимся к регулятору (4.13), который с использованием (4.15)–(4.18) оказывается полностью определенным, но для расширенного объекта (4.11), (4.12). Чтобы построить модель регулятора для исходного объекта, подставим выражения (4.16) в уравнения (4.17), представляя найденную матрицу $\bar {F}$ в блочной форме: $\bar {F} = [\begin{array}{*{20}{c}} {{{F}_{\mu }}}&{{{F}_{x}}}&{{{F}_{\tau }}} \end{array}]$, где Fμ, Fτ – скалярные коэффициенты. Тогда с учетом структуры вектора $\bar {y}$ получим
Добавим к этому описанию уравнения (4.10) и введем новый вектор состояний ξ = $colon\{ \mu ,\bar {\xi }$, xτ}. В результате, после преобразований, окончательно получим модель искомого регулятора в форме Коши:
(4.19)
$\begin{gathered} \xi (i + 1) = {{A}_{r}}\xi (i) + {{B}_{r}}y(i), \\ u(i) = {{F}_{1}}\xi (i) + {{F}_{2}}y(i), \\ \end{gathered} $(4.20)
$\begin{gathered} {{A}_{r}} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&W&{TB} \\ {{{F}_{\mu }}}&{{{F}_{x}}V}&{{{F}_{\tau }}} \end{array}} \right],\quad {{B}_{r}} = \left[ {\begin{array}{*{20}{c}} {\alpha {{T}_{{{\text{о}}{\text{.с}}{\text{.}}}}}} \\ K \\ {{{F}_{x}}U} \end{array}} \right], \\ {{F}_{1}} = [\begin{array}{*{20}{c}} {{{F}_{\mu }}}&{{{F}_{x}}V}&{{{F}_{\tau }}} \end{array}],\quad {{F}_{2}} = {{F}_{x}}U. \\ \end{gathered} $Отметим, что данный алгоритм синтеза, включая переход к дискретному объекту (4.9) с последующими вычислениями по уравнениям (4.17), (4.18) и формулам (4.15), (4.16), (4.20), легко реализуется с использованием стандартных операторов и процедур комплекса Matlab. В результате определяются матрицы регулятора (4.19) и его дискретная передаточная функция, которая затем применяется для формирования алгоритма вычисления управления u(i) на текущем i-м такте.
В частности, для решения задачи синтеза цифрового регулятора КМА подбираются следующие весовые матрицы из (4.18): Q = diag{105; 104; 103; 1}, Ψ = I и коэффициент передачи интегратора (4.10): α = 6 × 103.
В результате решения задачи и после округления некоторых коэффициентов (в процессе анализа переходных процессов) была получена следующая дискретная передаточная функция цифрового регулятора:
(4.21)
${{W}_{{{\text{рег}}}}}(z) = \frac{{5.574{{z}^{3}} - 10.1{{z}^{2}} + 4.559z}}{{{{z}^{3}} - 0.5351{{z}^{2}} - 0.2124z - 0.2524}},$(4.22)
${{W}_{{{\text{рег}}}}}(z) = \frac{{5.574z(z - 0.9551)(z - 0.8563)}}{{(z - 1)({{z}^{2}} + 0.4649z + 0.2524)}}.$Заметим, что полученная дискретная передаточная функция (4.22) содержит в качестве сомножителей операторы z и 1/(z – 1), которые означают соответственно компенсацию запаздывания по управлению на один такт и наличие интеграторов, обеспечивающих астатизм.
5. Анализ результатов во временной и частотной областях. Анализ замкнутой системы управления “акселерометр–усилитель обратной связи” во временной области проводится в среде Simulink программного комплекса Matlab по структурной схеме, приведенной на рис. 2. При этом в качестве усилителя рассматриваются аналоговый с передаточной функцией (4.5) (для определения робастного регулятора среди рассчитанных цифровых путем сравнения полученных результатов) и цифровые с дискретными передаточными функциями (4.4), (4.6) и (4.21), построенные различными методами синтеза. Задающее воздействие принимается в виде единичной функции q = 1(t), соответствующей изменению действующего ускорения на 1g.
Графики переходных процессов, полученные путем математического моделирования, приведены на рис. 4 и 5. На рис. 4 представлены реакции системы по току датчика момента. Из рассмотренных графиков следует, что качество регулирования вполне удовлетворительное. В частности, время регулирования составляет не более 1.7 × 10–3 с, перерегулирование – не более 32%. Отметим, что эти показатели примерно соответствуют прототипу разработки – КМА с АУОС, для которого время регулирования составляет 3.5 × 10–3 с, а перерегулирование – 39.7%.
Рис. 4.
Переходные процессы по току датчика момента КМА с различными регуляторами: 1 – аналоговый; 2 – дискретный, рассчитанный традиционным методом; 3 – дискретный, рассчитанный методом прямой дискретизации; 4 – дискретный, рассчитанный методом LQD-оптимизации
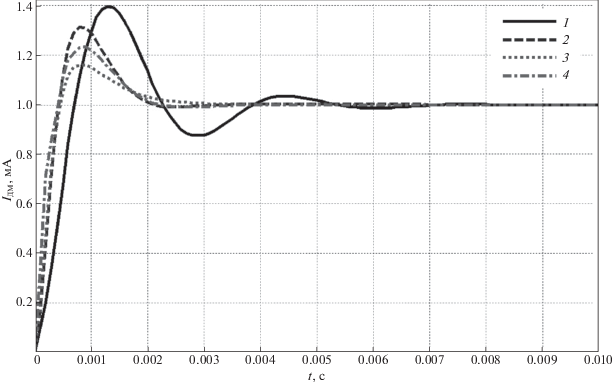
Рис. 5.
Переходные процессы по углу отклонения маятника КМА с различными регуляторами: 1 – аналоговый; 2 – дискретный, рассчитанный традиционным методом; 3 – дискретный, рассчитанный методом прямой дискретизации; 4 – дискретный, рассчитанный методом LQD-оптимизации
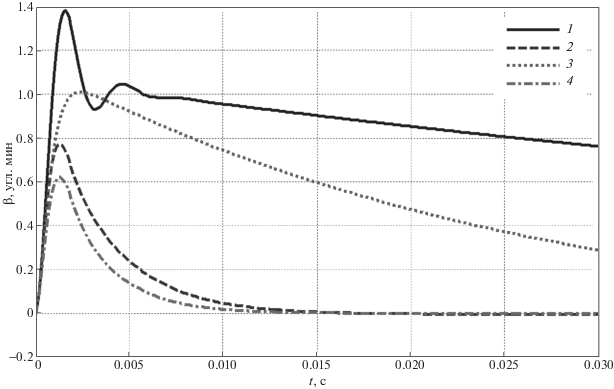
На рис. 5 представлены реакции системы по углу отклонения маятника акселерометра при действии ускорения q = 1 g. Из приведенных графиков следует, что максимальный угол отклонения для систем с ЦУОС не превышает 1 угл. мин, в то время как для акселерометра с АУОС эта величина достигает 1.4 угл. мин.
На рис. 6 и 7 в основной полосе частот представлены частотные характеристики КМА с указанными регуляторами. В частности, на рис. 6 приведены логарифмические характеристики разомкнутого контура управления. Из этих характеристик установлено, что частота среза разомкнутого контура для всех вариантов КМА с ЦУОС составляет примерно 540 Гц, что соответствует заданной при синтезе; запасы устойчивости по амплитуде составляют примерно 14 дБ, а запасы устойчивости по фазе – примерно 53°. Полученные частотные показатели качества характеризуют данную систему как систему с высокими робастными свойствами, причем у прототипа – КМА с АУОС, запасы устойчивости составляют 22.4 дБ и 34.7° соответственно.
Рис. 6.
ЛАЧХ и ФЧХ разомкнутого контура управления КМА с различными регуляторами: 1 – аналоговый; 2 – дискретный, рассчитанный традиционным методом; 3 – дискретный, рассчитанный методом прямой дискретизации; 4 – дискретный, рассчитанный методом LQD-оптимизации
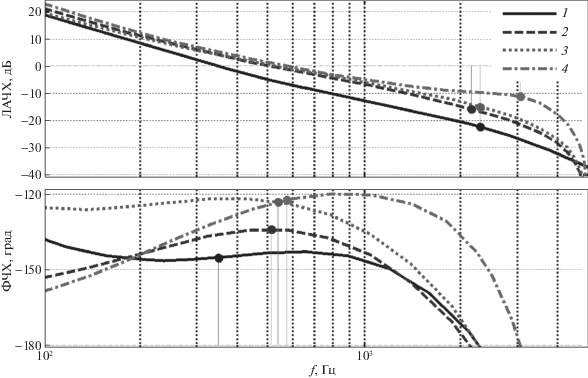
Рис. 7.
АЧХ замкнутых систем управления от задающего воздействия к току датчика момента КМА с различными регуляторами: 1 – аналоговый; 2 – дискретный, рассчитанный традиционным методом; 3 – дискретный, рассчитанный методом прямой дискретизации; 4 – дискретный, рассчитанный методом LQD-оптимизации
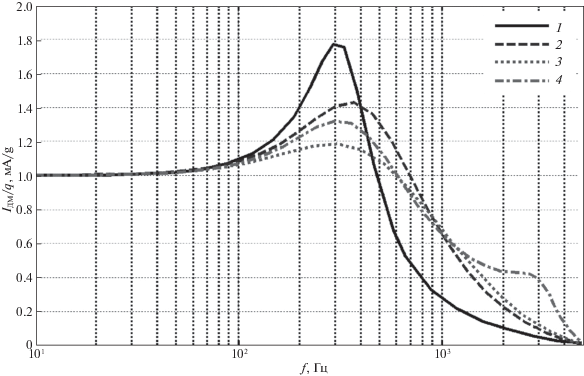
На рис. 7 приведены АЧХ замкнутых систем КМА с указанными регуляторами от задающего воздействия к току датчика момента, из которых установлено, что полоса пропускания для всех вариантов применения ЦУОС составила примерно 960 Гц. Показатель колебательности для акселерометров с ЦУОС уменьшился до величины 1.4 по сравнению с этим показателем для КМА с АУОС, величина которого составляет 1.77.
Результаты математического моделирования сведены в табл. 2, из анализа которой следует, что наилучшими характеристиками обладает КМА с ЦУОС с регулятором (4.4), рассчитанным традиционным методом с построением желаемых частотных характеристик. Кроме того, порядок числителя и знаменателя в (4.4) ниже, чем в дискретных передаточных функциях (4.6) и (4.21), что повлияет в конечном итоге на быстродействие системы. Передаточную функцию дискретного регулятора (4.4) можно представить в следующем виде:
(5.1)
${{W}_{{{\text{рег}}}}}(z) = \frac{{2.57 - 4.701{{z}^{{ - 1}}} + 2.142{{z}^{{ - 2}}}}}{{1 - 1.138{{z}^{{ - 1}}} + 0.1379{{z}^{{ - 2}}}}}$(5.2)
$\begin{gathered} {{N}_{{{\text{рег}}}}}(n{{T}_{{{\text{о}}{\text{.с}}}}}) = 1.138{{N}_{{{\text{рег}}}}}[(n--1){{T}_{{о.с}}}]--0.1379{{N}_{{{\text{рег}}}}}[(n--2){{T}_{{{\text{о}}{\text{.с}}}}}] + \\ + 2.57 \times {{N}_{{{\text{АЦП}} - 1}}}(n{{T}_{{{\text{о}}{\text{.с}}}}})--4.701{{N}_{{{\text{АЦП}} - 1}}}[(n--1){{T}_{{{\text{о}}{\text{.с}}}}}] + 2.142{{N}_{{{\text{АЦП}} - 1}}}[(n--2){{T}_{{{\text{о}}{\text{.с}}}}}],~ \\ \end{gathered} $Таблица 2.
Результаты математического моделирования работы КМА с АУОС и ЦУОС
| Параметр, единица измерения | Числовое значение | |||
|---|---|---|---|---|
| КМА с АУОС (прототип) | КМА с ЦУОС с дискретным регулятором, рассчитанным традиционным методом |
КМА с ЦУОС с дискретным регулятором, рассчитанным методом прямой дискретизации |
КМА с ЦУОС с дискретным регулятором, рассчитанным методом LQD-оптимизации |
|
| Время регулирования, с | 3.5 × 10–3 | 1.7 × 10–3 | 1.7 × 10–3 | 1.7 × 10–3 |
| Перерегулирование, % | 39.7 | 31.2 | 16.1 | 23.5 |
| Резонансный угол отклонения маятника при 1 g, угл. мин (рад) | 1.38 (0.4 × 10–3) |
0.77 (0.23 × 10–3) |
1.01 (0.3 × 10–3) |
0.62 (0.18 × 10–3) |
| Частота среза, Гц | 352 | 520 | 538 | 573 |
| Запас устойчивости по амплитуде, дБ |
22.4 | 15.6 | 14.9 | 11.2 |
| Запас устойчивости по фазе, град | 34.7 | 45.6 | 56.8 | 57.4 |
| Полоса пропускания, Гц | 575 | 963 | 989 | 927 |
| Показатель колебательности | 1.77 | 1.42 | 1.18 | 1.32 |
Таким образом, уравнение (5.2) является алгоритмом работы ЦУОС, обеспечивающим требуемые динамические характеристики и запасы устойчивости акселерометра.
6. Алгоритмы повышения точности. Рассмотрим два алгоритма, связанных с компенсацией погрешностей от разбалансировки маятника и от температурных зависимостей смещения нуля и масштабного коэффициента и позволяющих повысить точностные характеристики акселерометра.
6.1. Алгоритмическая компенсация погрешностей от разбалансировки маятника. В [2] приведено экспериментальное подтверждение нелинейной зависимости масштабного коэффициента выходного сигнала акселерометра от действующего ускорения, вследствие разбалансировки маятника. Нелинейный характер зависимости понятен и из физики явления. Если центр масс смещен относительно геометрического центра системы сил, то при действии линейного ускорения пластина будет испытывать не только изгибной момент вокруг оси торсиона, но и скручивающий момент вокруг оси, лежащей в плоскости маятника и перпендикулярной оси торсиона. К этому возмущающему моменту добавляется момент вследствие неравномерности рабочего зазора ДМ, что и определяет ярко выраженную нелинейную зависимость масштабного коэффициента акселерометра при значительных величинах линейных ускорений. Для обеспечения стабильности масштабного коэффициента в [2] предложен способ корректировки параметров системы действующих сил, заключающийся в следующем. Выполняют смещение точки приложения инерционной силы путем перемещения центра масс, для чего на маятник либо устанавливают балансировочный груз, либо выполняют балансировочное отверстие.
Предлагаемый метод может быть с успехом применен при изготовлении опытных образцов акселерометров, однако в серийном производстве могут возникнуть проблемы, связанные со следующими факторами. Характер и величина взаимного смещения точек приложения упомянутых трех сил для каждого изготавливаемого акселерометра – индивидуальны. На одном акселерометре можно выполнить подбор груза либо балансировочного отверстия и арочных выборок, обеспечивающих компенсацию разбалансировки. При изготовлении акселерометров в производстве такой индивидуальный подбор элементов компенсации мало технологичен. Если же ввести в документацию акселерометра одинаковое для всех изготавливаемых акселерометров размещение балансировочного отверстия и арочных выборок либо балансировочный груз определенной величины, то это может дать обратный эффект.
Разработка акселерометра с ЦУОС позволяет решить данную проблему методами алгоритмической компенсации. Суть предлагаемого метода состоит в следующем.
1. На центрифуге испытуемый прибор устанавливается так, чтобы его ось чувствительности была направлена вдоль действия центробежной силы. Задаются различные величины перегрузки и записываются показания прибора, после чего вычисляется поправочный коэффициент масштаба для каждой величины перегрузки, показывающий, во сколько раз выходная информация прибора отличается от требуемой при действующем ускорении, из соотношения:
В практическом применении не обязательно точно задавать абсолютные значения ускорения на прибор, а достаточно знать, во сколько раз воздействие отличается от начального амплитудой в 1 g. Удобно использовать воздействия, отличающиеся в целое число раз от начального. Количество величин перегрузок следует выбирать, исходя из монотонности кривой погрешности масштаба и требуемой точности компенсации. В результате получается табличная зависимость поправочного коэффициента масштаба от выходной информации прибора.
2. Для алгоритмической компенсации погрешности масштабного коэффициента зависимость поправочного коэффициента целесообразно аппроксимировать. В зависимости от формы кривой погрешности возможно применение различных методов интерполяции и аппроксимации. Для компенсации погрешности масштабного коэффициента кварцевого маятникового акселерометра оказался наиболее удобным метод интерполяции с помощью кубического сплайна [14]. Пример аппроксимации поправочного коэффициента приведен на рис. 8 для экспериментально снятых значений выходного сигнала акселерометра в диапазоне действующих перегрузок от ±1 до ±30 g.
Рис. 8.
Результаты работы алгоритма расчета поправочных коэффициентов при разбалансировке маятника акселерометра в диапазоне измерения от ±1 до ±50 g: 1 – поправочный коэффициент в диапазоне измерения от –1 до –50 g; 2 – поправочный коэффициент в диапазоне измерения от 1 до 50 g; 3 – аппроксимация кубическим сплайном в диапазоне от –1 до –50 g; 4 – аппроксимация кубическим сплайном в диапазоне от 1 до 50 g
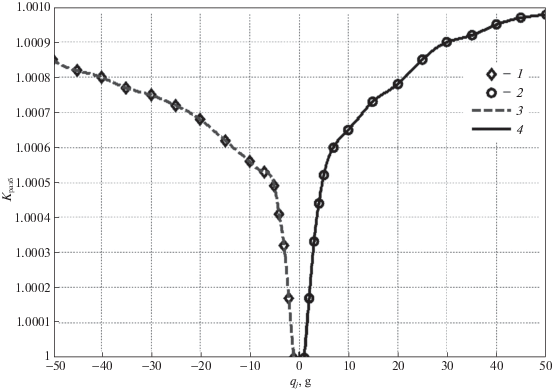
3. Коэффициенты полиномов сплайна записываются в память МК в ЦУОС и используются в расчете поправочного коэффициента масштаба для текущего значения выходной информации в соответствии со структурной схемой, приведенной на рис. 2: N ' = KразбNрег.
На рис. 9 приведены результаты испытаний КМА с ЦУОС и ШИМ-управлением током датчика момента в диапазоне от 1 до 50 g. Из графиков, представленных на рис. 9, видно, что в результате компенсации разбалансировки маятника погрешность масштабного коэффициента не превышает 0.01% во всем диапазоне измерений, тогда как до компенсации она доходила до 0.14%.
Рис. 9.
Результаты экспериментальных исследований погрешности масштабного коэффициента акселерометра в диапазоне измерения от 1 до 50 g: 1 – до алгоритмической компенсации; 2 – после компенсации
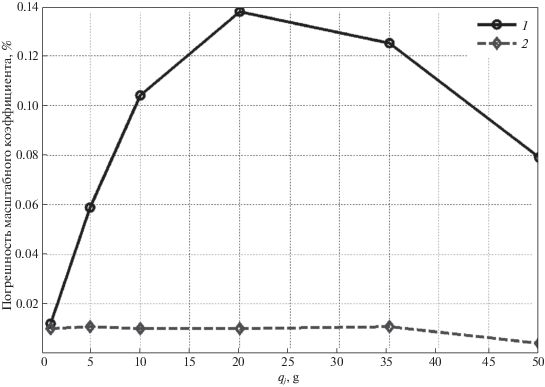
Таким образом, погрешность масштабного коэффициента на ускорениях свыше 10 g после введения алгоритмической компенсации снижается более чем в 14 раз в сравнении с той же погрешностью на ускорениях до 10 g.
6.2. Алгоритмическая компенсация погрешностей от температурных зависимостей смещения нуля и масштабного коэффициента. Особенностью всех КМА как отечественных, так и зарубежных является существенная зависимость их характеристик, таких, как систематическая составляющая смещения нулевого сигнала (или смещения нуля) и масштабный коэффициент, от изменения температуры окружающей среды. Температурная зависимость носит, как правило, нелинейный характер [5] и заключается в следующем.
1. Изменение смещения нуля КМА при изменении температуры происходит вследствие термоупругих деформаций, возникающих в маятнике, а также вследствие разной толщины золотого напыления (с обеих сторон маятника), реализующего емкостный датчик угла. Напыление в свою очередь вносит неоднородность в упругодеформируемое кварцевое стекло – материал маятника. Исследования, проведенные на предприятии ПО “Корпус”, показали, что отличие толщин золотого покрытия, нанесенного на одну и другую стороны маятника, на величину 0.02 мкм (при номинальном значении толщины покрытия 0.2 мкм) приводит к температурному изменению величины смещения нуля на 3 × 10–3 g при изменении температуры на 30°С.
2. Температурная зависимость масштабного коэффициента КМА в основном определяется зависимостью от температуры индукции в рабочем зазоре датчика момента, состоящего из медных катушек и постоянных магнитов.
Кварцевый маятниковый акселерометр (прибор КХ67-041) исследовался во ВНИИМ им. Д.И. Менделеева в процессе выполнения его аттестации для введения в ранг рабочего эталона. При этом исследования проводились на установках ЭУП-3 и ДЦ-3, входящих в состав Государственного эталона первого рода ГЭТ 94-01. При этом выходной сигнал Fвых в функции от измеряемого кажущегося ускорения записывался в следующем виде:
(6.1)
${{F}_{{{\text{вых}}}}} = {{K}_{{\text{м}}}}({{K}_{0}} + q + {{K}_{2}}{{q}^{2}} + {{K}_{3}}{{q}^{3}} + {{K}_{{{\text{о}}{\text{.м}}}}}q{{q}_{{{\text{о}}{\text{.м}}}}} + {{K}_{{{\text{о}}{\text{.п}}}}}q{{q}_{{{\text{о}}{\text{.п}}}}} + {{\delta }_{0}}{{q}_{{{\text{о}}{\text{.п}}}}} + {{\delta }_{1}}{{q}_{{{\text{о}}{\text{.м}}}}}),$По результатам аттестации во ВНИИМ им. Д.И. Менделеева были получены следующие значения коэффициентов математической модели (6.1):
Из результатов аттестации следует, что акселерометр обладает высокой стабильностью масштабного коэффициента, комплексная оценка нелинейности этой характеристики составляет 0.005%. Факторами, влияющими на высокую линейность и стабильность во времени масштабного коэффициента акселерометра, являются методы технологического процесса изготовления акселерометра, обеспечивающие отсутствие остаточных напряжений в кварцевой пластине акселерометра, равномерность рабочего зазора в датчике момента и стабильность величины магнитной индукции в рабочем зазоре.
В ходе температурных испытаний акселерометра было замечено, что зависимости масштабного коэффициента и смещения нуля от температуры имеют параболическую форму, которую можно описать полиномом второй степени. Для расчета коэффициентов полиномов используются по четыре точки на температурной кривой. В ходе экспериментальных отработок алгоритма термокомпенсации замеры производились при четырех температурах, °С: 5, 20, 35 и 50. Температурные точки могут быть выбраны другие, в зависимости от условий эксплуатации прибора.
Измерения и расчет температурной коррекции проходят следующим образом. На каждой температуре проводятся замеры в четырех положениях акселерометра на оптической делительной головке (ОДГ). Для этого акселерометр устанавливается на площадку ОДГ базовой поверхностью. Площадка ОДГ предварительно горизонтируется (горизонтальное положение площадки соответствует значению 0° на шкале ОДГ). С помощью ОДГ задаются четыре угловых положения: 0, 90, 180 и 270°. По показаниям в положениях 90 и 270° определяется смещение нуля по формуле
Положения 0 и 180° соответствуют измерениям –1 g и +1 g. Показания в этих положениях корректируются с учетом смещения нуля по формулам
В результате этих операций становятся известными значения систематической составляющей нулевого сигнала и масштабного коэффициента для положительных и отрицательных ускорений для каждой температуры. Также в ходе измерений на каждой температуре фиксируются показания термодатчика акселерометра. По этим данным рассчитываются коэффициенты аппроксимирующих квадратичных полиномов, зависящих от показаний термодатчика:
Полученные коэффициенты полиномов записываются в программу работы микроконтроллера. В программе на этапе вычисления поправок термокомпенсации вычисляются поправки смещения нуля и масштабного коэффициента для положительных и отрицательных ускорений с использованием соответствующих полиномиальных выражений и текущего показания термодатчика. Перед выдачей выходной информации о действующем ускорении в интерфейс производится коррекция по формуле:
При этом весь циклический алгоритм делится на две части: асинхронную и синхронную, выполняемую в МК. В асинхронной части производится вычисление температурных поправок в зависимости от оцифрованного значения показаний термодатчика и в соответствии с запрограммированными коэффициентами полиномов термокомпенсации. Поскольку процесс изменения температуры является медленно меняющимся, то нет необходимости рассчитывать температурные поправки синхронно с основным алгоритмом. Это вычисление происходит в свободное от расчетов время вычисления основного алгоритма.
Графики, приведенные на рис. 10 и 11, иллюстрируют работу термокомпенсации погрешностей масштабного коэффициента при измерении ускорения амплитудой ±1 g и систематической составляющей нулевого сигнала в диапазоне температур от –60 до +85°С, характерном для эксплуатационных условий в авиации. Замер характеристик осуществлялся как при нагреве, так и при охлаждении прибора. Согласно графикам, происходит расхождение кривых при нагреве и охлаждении прибора, связанное с явлением температурного гистерезиса акселерометра (рис. 10 и 11).
Рис. 10.
Зависимость показаний акселерометра при измерении +1 и –1 g (по модулю) при нагреве (1 и 2) и при охлаждении (3 и 4) от температуры: а – до компенсации, б – после компенсации
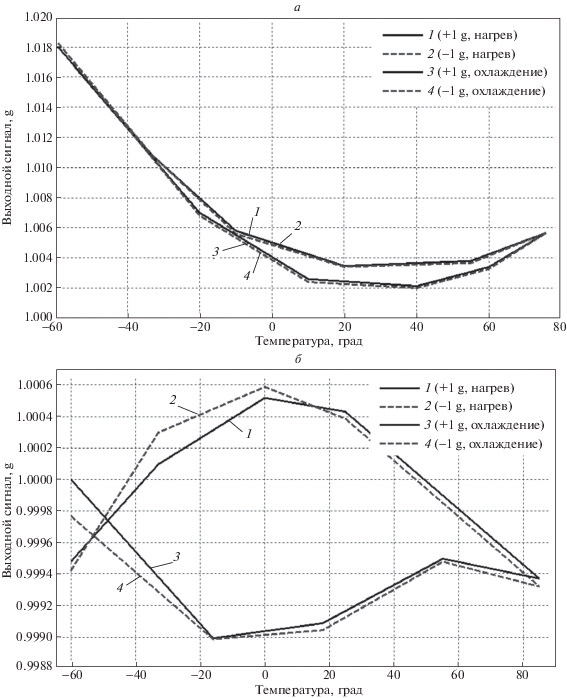
Рис. 11.
Зависимость систематической составляющей нулевого сигнала (н.с.) акселерометра при нагреве (1) и при охлаждении (2) от температуры: а – до компенсации, б – после компенсации
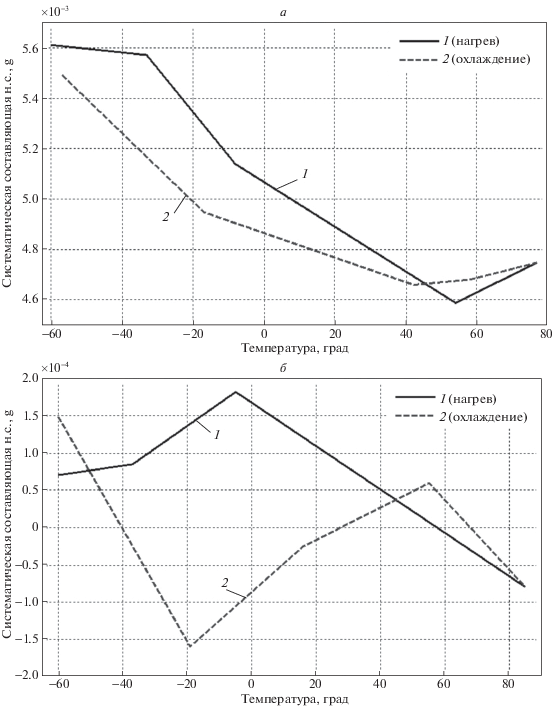
Таким образом, при испытаниях акселерометра в диапазоне температур от –60 до +85°С погрешность масштабного коэффициента после введения алгоритмической компенсации уменьшается с 18 × 10–3 до 6 × 10–4 g и систематической составляющей нулевого сигнала – с 5 × 10–3 до 1 × 10–4 g.
7. Преимущества использования цифрового управления по сравнению с аналоговым в контуре обратной связи акселерометра. Применение цифрового усилителя обратной связи в контуре управления рассматриваемого измерителя кажущегося ускорения придает ему новые функциональные возможности.
1. Сокращение общего количества ЭРИ (электрорадиоизделий) и уменьшение габаритно-массовых характеристик измерительного канала, включающего, кроме собственно акселерометра с УОС (усилителем обратной связи), блок преобразования информации и вторичный источник питания. На рис. 12 приведены 3D-модель КМА с ЦУОС, где показана возможность реализации всех плат электроники в одном конструктиве, и фото ныне реализованного макетного образца. На рис. 12, б обозначено: 1 – ЧЭ, 2 – макет ЦУОС, 3 – оснастка для крепления ЧЭ на испытательном оборудовании.
2. Реализация требуемого количества алгоритмов повышения точности прибора, что ограничено лишь вычислительной мощностью встроенного в ЦУОС микроконтроллера, с разгрузкой бортовой цифровой вычислительной машины (БЦВМ) подвижного объекта от компенсационных алгоритмов первичного измерителя. Это в свою очередь исключает многоконтурную систему обмена данными (между бортовым вычислителем и измерителем) и, кроме того, при замене измерителя не требует перепрошивки бортового вычислителя.
3. Расширение диапазона измеряемых ускорений от ±10 до ±50 g без внесения изменений в конструкцию прибора.
4. Коррекция динамических характеристик измерителя в зависимости от объекта, на который он будет устанавливаться, путем изменения коэффициентов цифрового регулятора в контуре обратной связи.
5. Сохранение широкой полосы пропускания измерителя по сравнению с вариантом применения МК в выходном каскаде, а не в контуре обратной связи.
6. Упрощение организации любого требуемого вида выходной информации (унитарный код, RS-232, RS-485, код Манчестер и т.п.).
7. Возможность перехода к построению адаптивной системы управления, теоретически описанной в книге [15].
Заключение. Рассмотрен кварцевый маятниковый акселерометр, особенностью которого является применение в контуре управления цифрового усилителя обратной связи, придающего прибору новые функциональные возможности. Приведено описание аппаратного обеспечения ЦУОС с расчетом соответствующих коэффициентов, работы алгоритмов цифрового управления, полученных с использованием различных методов синтеза дискретных регуляторов, и алгоритмов повышения точности, связанных с компенсацией погрешностей от разбалансировки маятника и температурных зависимостей смещения нуля и масштабного коэффициента, что подтверждено результатами экспериментальных исследований.
В табл. 3 приведены технические характеристики двух акселерометров – с аналоговым усилителем обратной связи, рассматриваемый как прототип разработки, и с цифровой обратной связью, дискретный регулятор которого рассчитан традиционным методом, в котором реализованы алгоритмы повышения точности. К табл. 3 добавлены следующие примечания.
Таблица 3.
Технические характеристики КМА с АУОС и ЦУОС
| Параметр, размерность | Величина | Примечание | |
|---|---|---|---|
| КМА с АУОС | КМА с ЦУОС | 1 | |
| Диапазон измерения, g | ±10 | ±10 – ±50 | 2 |
| Масштабный коэффициент | 1.0–1.32 В/g | 1000 ед.ц.к./g | 3 |
| Нестабильность масштабного коэффициента (не более), % | 0.02 | 0.02 | 4 |
| Систематическая составляющая нулевого сигнала (в пределах), g | ±10 × 10–3 | ±1 × 10–3 | – |
| Случайная составляющая нулевого сигнала (не более), g: | – | ||
| – в 10-минутном запуске, | 20 × 10–6 | – | |
| – в 30-минутном запуске, | – | 5 × 10–6 | |
| – в 3-часовом запуске | 40 × 10–6 | 20 × 10–6 | |
| Случайная составляющая нулевого сигнала от запуска к запуску (не более), g | 1 × 10–4 | 1 × 10–4 | – |
| Порог чувствительности (не более), g | 0.5 × 10–6 | 0.5 × 10–6 | – |
| Полоса пропускания сигнала (по уровню 0.7), не менее, Гц | 200 | 300 | 5 |
| Время готовности (не более), с: | – | ||
| – функциональной, | – | 1 | |
| – точностной | 1200 | 300 | |
| Ресурс, ч | 11000 | 11000 | – |
| Срок службы, лет | 12 | 12 | – |
| Рабочий диапазон температур, °C | 0…+40 | –65…+85 | 6 |
| Масса, не более, кг | 0.3 | 0.1 | – |
| Потребляемая мощность (не более), Вт | 3 | 1.5 | 7 |
| Входное напряжение, В | $27_{{ - 4}}^{{ + 7}}$ | $27_{{ - 4}}^{{ + 7}}$ | – |
Примечание 1. КМА с АУОС включает в себя собственно акселерометр и АУОС, а также вторичный источник питания и блок преобразования выходного сигнала из аналогового в унитарный код. КМА с ЦУОС содержит акселерометр, ЦУОС и вторичный источник питания; преобразователь сигнала не требуется, так как выходной сигнал прибора уже цифровой; тип выходного интерфейса может быть следующим: RS-232, RS-485, код Манчестер, унитарный код и т.д.
Примечание 2. Диапазон измеряемых ускорений для КМА с ЦУОС может быть выбран любым из диапазона от ±10 до ±50 g. При необходимости верхний предел может быть понижен до ±1 g.
Примечание 3. Масштабный коэффициент для КМА с ЦУОС может быть обеспечен любой.
Примечание 4. Нестабильность масштабного коэффициента дается во всем температурном диапазоне и во всем диапазоне измерений. Для КМА с ЦУОС указанный параметр приводится с учетом компенсации температурных погрешностей и погрешностей от разбалансировки маятника на ускорениях, амплитуда которых свыше 1 g.
Примечание 5. Полоса пропускания сигнала для КМА с ЦУОС выбирается в диапазоне 100–1000 Гц программным способом.
Примечание 6. Рабочий диапазон температур для КМА с ЦУОС может быть “космический” – (0…+40)°C или “авиационный” – (–65…+85)°C с обеспечением алгоритмической компенсации температурных зависимостей масштабного коэффициента и систематической составляющей нулевого сигнала.
Примечание 7. Указана мощность, потребляемая измерительным каналом. В случае диапазона температур (0…+40)°C и уменьшения диапазона измерения мощность для КМА с ЦУОС может быть уменьшена до 1.1 Вт.
Проведенный анализ во временной и частотной областях для разомкнутой и замкнутой системы “КМА–ЦУОС” показал, что предложенные алгоритмы цифрового управления обладают высокими робастными свойствами и обеспечивают хорошее качество переходных процессов. При этом независимо от выбранного метода синтеза в приборе обеспечиваются требуемые динамические характеристики, различными остаются лишь порядки числителя и знаменателя полученных дискретных передаточных функций регуляторов, реализация которых ограничена производительностью применяемого МК.
Таким образом, динамические свойства акселерометра с ЦУОС практически не зависят от выбора способа синтеза регулятора, а определяются аппаратными возможностями системы управления.
Из полученных результатов следует, что в КМА, применяемых в современных БИНС навигационного класса точности, желательно применять ЦУОС с реализованными в нем компенсационными алгоритмами для коррекции температурных и иных погрешностей измерителя, естественно, помимо некомпенсируемых погрешностей, связанных с технологией изготовления прибора, с гистерезисом постоянных магнитов и т.п. Все это позволит существенно расширить функциональные возможности не только современных первичных измерителей, но и всей БИНС в целом.
Сделанные выводы нашли свое подтверждение на летных испытаниях, прошедших в августе–сентябре 2019 г. в составе шестиосного прибора БИЛУ (блок измерителей линейного ускорения), где в качестве измерительного канала был использован КМА с ЦУОС, описанный в настоящей работе. Прибор БИЛУ работал в системе управления космическим кораблем (КК) “Союз МС-14” с роботом “Фёдором” на борту. Прибор функционировал на участках выведения на орбиту, стыковки и расстыковки КК с Международной космической станцией (МКС), при посадке на участках торможения и раскрытия парашютов. После успешной посадки спускаемого аппарата прибор БИЛУ был доставлен на завод-изготовитель для проверки точностных характеристик после летных испытаний. Все основные параметры, внесенные в формуляр прибора при сдаче заказчику, подтвердили практически без изменений свои точностные характеристики, что свидетельствует о верности как теоретических посылок, так и высокой надежности цифровой системы управления, реализованной на отечественной элементной базе.
Список литературы
Ишлинский А.Ю. Ориентация, гироскопы и инерциальная навигация. М.: Наука, 1976. 672 с.
Сео Дже Бом. Оптимизация параметров и моделирование рабочих режимов в компенсационных акселерометрах типа Q-flex и Si-flex: Автореф. дис. … канд. техн. наук. М., 2012. 16 с.
Берендс Д.А., Кукулиев Р.М., Филиппов К.К. Приборы и системы автоматического управления с широтно-импульсной модуляцией. Л.: Машиностроение, 1982. 280 с.
Скоробогатов В.В. Основы разработки безобогревных термоинвариантных измерителей угловых скоростей и кажущихся ускорений для систем управления ракетно-космическими объектами: Автореф. дис. … канд. техн. наук. Саратов, 2018. 24 с.
Мельников В.Е. Электромеханические преобразователи на базе кварцевого стекла. М.: Машиностроение, 1984. 160 с.
Калихман Д.М. Прецизионные управляемые стенды для динамических испытаний гироскопических приборов / Под ред. В.Г. Пешехонова. СПб.: Изд-во ЦНИИ “Электроприбор”, 2008. 273 с.
Федоров С.М., Литвинов А.П. Автоматические системы с цифровыми управляющими машинами. М.–Л.: Энергия, 1965. 320 с.
Дьяконов В.П. Matlab 6.5 SP1/7 + Simulink 5/6®. Основы применения. Серия “Библиотека профессионала”. М.: СОЛОН-Пресс, 2005. 800 с.
Садомцев Ю.В. Конструирование систем управления с обратной связью по критериям точности и грубости. Саратов: СГТУ, 2003. 297 с.
Изерман Р. Цифровые системы управления. М.: Мир, 1984. 541 с.
Куо Б. Теория и проектирование цифровых систем управления / Пер. с англ. М.: Машиностроение, 1986. 446 с.
Распопов В.Я. Микромеханические приборы: учебное пособие. М.: Машиностроение, 2007. 400 с.
Luenberger D.G. On introduction to observers // IEEE Trans. Autom. Contr. 1971. V. AC-16.
Бахвалов Н.С. Численные методы. Т. 1. М.: Наука, 1973. 632 с.
Александров А.Г. Оптимальные и адаптивные системы: Учеб. пособие для вузов по спец. “Автоматика и управление в технических системах”. М.: Высш. шк., 1989. 263 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления