Известия РАН. Теория и системы управления, 2021, № 2, стр. 94-105
ОПТИМИЗАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО СОПРОВОЖДЕНИЯ ВОЗДУШНЫХ ОБЪЕКТОВ НА ОСНОВЕ ЛОКАЛЬНЫХ КВАДРАТИЧНО-БИКВАДРАТНЫХ ФУНКЦИОНАЛОВ. II. ИССЛЕДОВАНИЕ ЭФФЕКТИВНОСТИ МЕТОДА
В. С. Верба a, И. Р. Загребельный a, b, *, В. И. Меркулов a, Е. А. Руденко c, **
a АО “Концерн “Вега”
Москва, Россия
b МГТУ им. Н.Э. Баумана
Москва, Россия
c МАИ (национальный исследовательский ун-т)
Москва, Россия
* E-mail: ilya-zagrebelnyi@mail.ru
** E-mail: rudenkoevg@yandex.ru
Поступила в редакцию 08.06.2020
После доработки 18.08.2020
Принята к публикации 30.11.2020
Аннотация
Приведены результаты исследований эффективности оптимального радиолокационного угломера при сопровождении целей, движущихся по траекториям различной сложности. Следящая система угломера получена в первой части данной статьи локальной минимизацией квадратично-биквадратного функционала качества.
0. Введение. В работе [1] решена задача локальной квадратично-биквадратной оптимизации линейных систем автоматического сопровождения воздушных объектов. Там же рассмотрено и ее применение к синтезу управления типовым приводом антенны следящего радиолокационного угломера [2]:
(0.1)
$\begin{gathered} {{{\dot {\varphi }}}_{{\text{у}}}} = {{\omega }_{{\text{у}}}},\quad {{\varphi }_{{\text{у}}}}(0) = {{\varphi }_{{{\text{у0}}}}}, \\ {{{\dot {\omega }}}_{{\text{у}}}} = - \frac{1}{T}{{\omega }_{{\text{у}}}} + \frac{b}{T}{{u}_{{\text{у}}}},\quad {{\omega }_{{\text{у}}}}(0) = {{\omega }_{{{\text{у0}}}}}, \\ \end{gathered} $(0.2)
$\begin{gathered} {{{\dot {\varphi }}}_{{\text{т}}}} = {{\omega }_{{\text{т}}}} + \frac{{{{j}_{{\text{т}}}}}}{{\dot {D}}},\quad {{\varphi }_{{\text{т}}}}(0) = {{\varphi }_{{{\text{т0}}}}}, \\ {{{\dot {\omega }}}_{{\text{т}}}} = - \frac{{2\dot {D}}}{D}{{\omega }_{{\text{т}}}} - \frac{{{{j}_{{\text{т}}}}}}{D},\quad {{\omega }_{{\text{т}}}}(0) = {{\omega }_{{{\text{т0}}}}}. \\ \end{gathered} $Здесь ${{\varphi }_{{\text{т}}}}$, ${{\omega }_{{\text{т}}}}$ – бортовой пеленг цели и угловая скорость линии визирования цели; ${{\varphi }_{{\text{у}}}}$, ${{\omega }_{{\text{у}}}}$ – угол поворота равносигнального направления антенны и скорость его изменения; ${{\varphi }_{{{\text{у0}}}}}$, ${{\omega }_{{{\text{у0}}}}}$, ${{\varphi }_{{{\text{т0}}}}}$, ${{\omega }_{{{\text{т0}}}}}$ – значения этих координат на момент захвата цели; b, $T$ – коэффициент передачи сигнала управления ${{u}_{{\text{у}}}}$ и постоянная времени угломера; $D$, $\dot {D}$ – дальность до цели и скорость ее изменения; ${{j}_{{\text{т}}}}$ – поперечное ускорение цели, манипулируя которым можно реализовать траектории различной сложности.
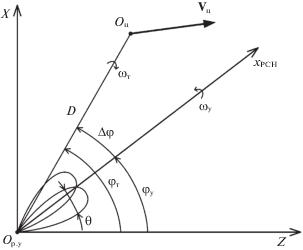
Геометрия текущего взаимного расположения цели и угломера показана на рис. 1, на котором ${{O}_{{{\text{р}}{\text{.у}}}}}$ и ${{O}_{{\text{ц}}}}$ – точки расположения радиолокационного угломера и цели, ${{{\mathbf{V}}}_{{\text{ц}}}}$ – вектор скорости цели, ${{x}_{{{\text{РСН}}}}}$ – положение равносигнального направления (РСН) в горизонтальной плоскости, определяющее величину ${{\varphi }_{{\text{у}}}}$.
С целью уменьшения ошибок слежения за углом $\Delta \varphi = {{\varphi }_{{\text{т}}}} - {{\varphi }_{{\text{у}}}}$ и угловой скоростью Δω = = ${{\omega }_{{\text{т}}}} - {{\omega }_{{\text{у}}}}$ в [1] был получен локально оптимальный по минимуму изменяющегося во времени функционала
(0.3)
${{I}_{t}} = \int\limits_0^t {{{k}_{\omega }}u_{{\text{у}}}^{2}(\tau )d\tau } + {{\left[ {\begin{array}{*{20}{c}} {\Delta \varphi } \\ {\Delta \omega } \end{array}} \right]}^{{\rm T}}}\left[ {\begin{array}{*{20}{c}} {{{q}_{{11}}}}&{{{q}_{{12}}}} \\ {{{q}_{{12}}}}&{{{q}_{{22}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta \varphi } \\ {\Delta \omega } \end{array}} \right] + {{\left\{ {{{{\left[ {\begin{array}{*{20}{c}} {\Delta \varphi } \\ {\Delta \omega } \end{array}} \right]}}^{{\rm T}}}\left[ {\begin{array}{*{20}{c}} {{{p}_{{11}}}}&{{{p}_{{12}}}} \\ {{{p}_{{12}}}}&{{{p}_{{22}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta \varphi } \\ {\Delta \omega } \end{array}} \right]} \right\}}^{2}}$(0.4)
${{u}_{{\text{у}}}} = {{K}_{1}}\Delta \varphi + {{K}_{2}}\Delta \omega + {{K}_{3}}\Delta {{\varphi }^{3}} + {{K}_{4}}\Delta {{\varphi }^{2}}\Delta \omega + {{K}_{5}}\Delta \varphi \Delta {{\omega }^{2}} + {{K}_{6}}\Delta {{\omega }^{3}}$(0.5)
$\begin{gathered} {{K}_{1}} = \frac{b}{{{{k}_{\omega }}T}}{{q}_{{12}}},\quad {{K}_{2}} = \frac{b}{{{{k}_{\omega }}T}}{{q}_{{22}}},\quad {{K}_{3}} = \frac{{2b}}{{{{k}_{\omega }}T}}{{p}_{{11}}}{{p}_{{12}}}, \\ {{K}_{4}} = \frac{{2b}}{{{{k}_{\omega }}T}}(2p_{{12}}^{2} + {{p}_{{11}}}{{p}_{{22}}}),\quad {{K}_{5}} = \frac{{6b}}{{{{k}_{\omega }}T}}{{p}_{{12}}}{{p}_{{22}}},\quad {{K}_{6}} = \frac{{2b}}{{{{k}_{\omega }}T}}p_{{22}}^{2}. \\ \end{gathered} $Здесь ${{q}_{{11}}}$, ${{q}_{{12}}}$, ${{q}_{{22}}}$ – коэффициенты квадратичного штрафа за ошибки слежения $\Delta \varphi $, $\Delta \omega $; ${{p}_{{11}}}$, ${{p}_{{12}}},$ ${{p}_{{22}}}$ – коэффициенты соответствующего биквадратного штрафа, определяющие в законе (0.4) веса нелинейных слагаемых.
Целью дальнейшего изложения является исследование эффективности закона управления (0.4), (0.5) и его разновидностей при сопровождении целей, маневрирующих по сложным законам, в том числе и со сменой знаков производных.
1. Условия исследования. Исследование эффективности предложенного метода оптимизации по минимуму квадратично-биквадратных функционалов качества выполнялось на примере сопровождения радиолокационным угломером высокоскоростных целей, двигающихся по траекториям различной сложности, в том числе и со сменой знака производных. Необходимо отметить, что существующие следящие угломеры неспособны сопровождать такие цели [3].
При этом полагалось, что угломер входит в состав моноимпульсной радиолокационной системы (РЛС) с двухлепестковой диаграммой направленности с шириной $\theta = 4^\circ $ (рис. 1) с полосой рабочей зоны $0.5\theta = \pm 2^\circ $ [4], а цели перемещаются в пространстве со сверхзвуковой скоростью.
Исследования проводились путем моделирования траекторий полета цели (0.2) по трем различным траекториям. В качестве показателей эффективности использовались текущие ошибки сопровождения по углу и угловой скорости. Если при этом выполнялось условие $\left| {\Delta \varphi } \right| \geqslant 2^\circ $, то регистрировался срыв сопровождения.
Для выяснения влияния отдельных слагаемых оптимального закона управления (0.4) на качество сопровождения исследования проводились при использовании следующих вариантов:
– полный закон (0.4) с коэффициентами (0.5):
(1.1)
${{u}_{{{\text{у1}}}}} = {{K}_{1}}\Delta \varphi + {{K}_{2}}\Delta \omega + {{K}_{3}}\Delta {{\varphi }^{3}} + {{K}_{4}}\Delta {{\varphi }^{2}}\Delta \omega + {{K}_{5}}\Delta \varphi \Delta {{\omega }^{2}} + {{K}_{6}}\Delta {{\omega }^{3}};$– без куба ошибки по углу $\Delta {{\varphi }^{3}}$:
(1.2)
${{u}_{{{\text{у2}}}}} = {{K}_{1}}\Delta \varphi + {{K}_{2}}\Delta \omega + {{K}_{4}}\Delta {{\varphi }^{2}}\Delta \omega + {{K}_{5}}\Delta \varphi \Delta {{\omega }^{2}} + {{K}_{6}}\Delta {{\omega }^{3}};$– без куба ошибки по угловой скорости $\Delta {{\omega }^{3}}$:
(1.3)
${{u}_{{{\text{у3}}}}} = {{K}_{1}}\Delta \varphi + {{K}_{2}}\Delta \omega + {{K}_{3}}\Delta {{\varphi }^{3}} + {{K}_{4}}\Delta {{\varphi }^{2}}\Delta \omega + {{K}_{5}}\Delta \varphi \Delta {{\omega }^{2}};$– без куба ошибки по углу $\Delta {{\varphi }^{3}}$ и смеси $\Delta \varphi \Delta {{\omega }^{2}}$, что соответствует использованию в критерии (0.3) диагональной матрицы биквадратных штрафов $\left( {{{p}_{{12}}} = 0} \right)$:
(1.4)
${{u}_{{{\text{у4}}}}} = {{K}_{1}}\Delta \varphi + {{K}_{2}}\Delta \omega + {{K}_{4}}\Delta {{\varphi }^{2}}\Delta \omega + {{K}_{6}}\Delta {{\omega }^{3}};$– без кубов ошибок и по углу $\Delta {{\varphi }^{3}}$ и по угловой скорости $\Delta {{\omega }^{3}}$:
(1.5)
${{u}_{{{\text{у5}}}}} = {{K}_{1}}\Delta \varphi + {{K}_{2}}\Delta \omega + {{K}_{4}}\Delta {{\varphi }^{2}}\Delta \omega + {{K}_{5}}\Delta \varphi \Delta {{\omega }^{2}};$– без куба ошибки по углу $\Delta {{\varphi }^{3}}$ и смеси $\Delta {{\varphi }^{2}}\Delta \omega $:
(1.6)
${{u}_{{{\text{у6}}}}} = {{K}_{1}}\Delta \varphi + {{K}_{2}}\Delta \omega + {{K}_{5}}\Delta \varphi \Delta {{\omega }^{2}} + {{K}_{6}}\Delta {{\omega }^{3}};$– без кубов ошибок по углу $\Delta {{\varphi }^{3}}$, по угловой скорости $\Delta {{\omega }^{3}}$ и смеси $\Delta \varphi \Delta {{\omega }^{2}}$:
(1.7)
${{u}_{{{\text{у7}}}}} = {{K}_{1}}\Delta \varphi + {{K}_{2}}\Delta \omega + {{K}_{4}}\Delta {{\varphi }^{2}}\Delta \omega \,;$– типовой линейный алгоритм сопровождения, который соответствует одному из лучших вариантов существующих угломеров [2]:
Исследования проводились в несколько этапов:
– проверялась способность всех управлений устранять первоначальные ошибки захвата $\Delta \varphi (0) = \pm 1.5^\circ $ и $\Delta \omega (0) = \pm 10$ град/с в различных сочетаниях по знаку;
– изучались показатели сопровождения цели, движущейся равноускорено прямолинейно;
– исследовалась работоспособность всех вариантов управления при сопровождении цели, движущейся по окружности на некотором удалении от РЛС с периодической сменой знаков производных бортовых пеленгов и дальности;
– оценивались возможности всех законов управления при сопровождении цели, движущейся по квазисинусоидальной траектории (маневр “змейка”).
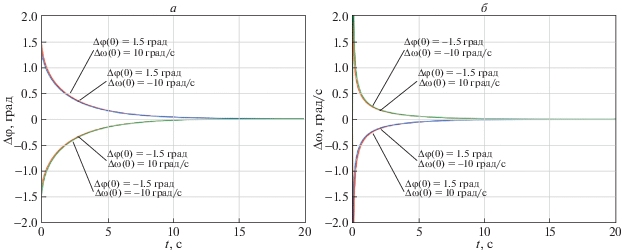
2. Результаты исследований. Проведенные исследования показали, что все варианты управления устойчиво устраняют первоначальные ошибки захвата при их различном сочетании по знаку. В качестве примера на рис. 2 показаны эпюры устранения ошибок захвата по углу и угловой скорости при использовании управления (1.1). Все остальные варианты управления (1.2)–(1.8) также устойчиво устраняют ошибки захвата, но с несколько худшими показателями точности и времени отработки.
Рис. 2.
Текущие ошибки по углу (а) и угловой скорости (б) при отработке алгоритмом (1.1) первоначальных ошибок захвата различных знаков
При сопровождении цели, движущейся равноускорено прямолинейно, ошибки сопровождения устраняются всеми вариантами сигналов управления, обеспечивая высокоточное сопровождение в установившемся режиме с некоторым увеличением ошибок сопровождения по углу и угловой скорости на начальном этапе. Исследование этого этапа позволяет прийти к заключению, что при сопровождении целей, маневрирующих без смены знака производных угловых координат, все варианты управления (1.1)–(1.7) по сравнению с традиционным пропорционально-дифференциальным методом (1.8) несколько улучшают точность сопровождения.
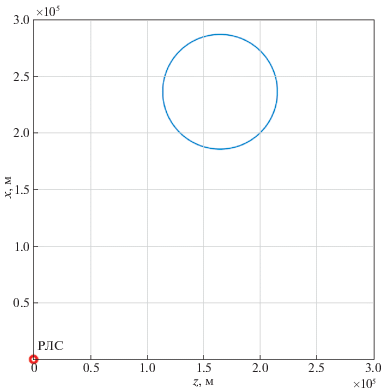
2.1. Сопровождение цели, движущейся по окружности. Положение цели, движущейся по окружности на определенном расстоянии от РЛС, показано на рис. 3, а результаты исследований иллюстрируются рис. 4–12.
Рис. 4.
Бортовой пеленг цели (пунктирная линия) и угол поворота антенны (сплошная линия) для алгоритма (1.1) при движении цели по окружности
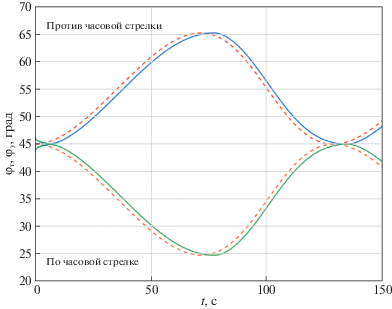
Рис. 5.
Ошибки сопровождения по углу (а) и угловой скорости (б) для алгоритма (1.1) при движении цели по окружности
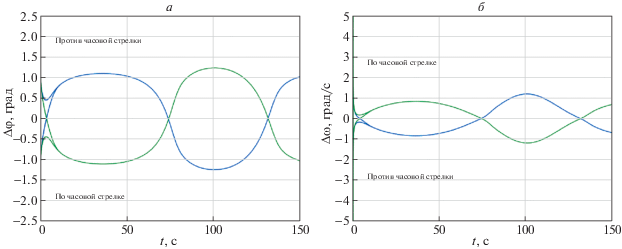
Рис. 6.
Ошибки сопровождения по углу для алгоритмов (1.2) (а) и (1.3) (б) при движении цели по окружности
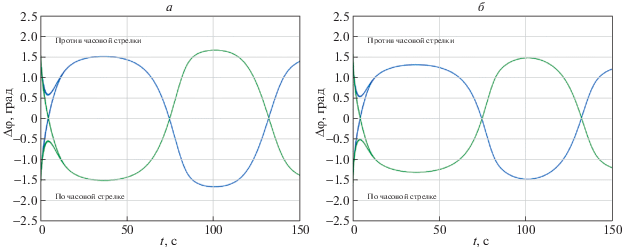
Рис. 7.
Бортовой пеленг цели (пунктирная линия) и угол поворота антенны (сплошная линия) для алгоритма (1.4) при движении цели по окружности

Рис. 9.
Бортовой пеленг цели (пунктирная линия) и угол поворота антенны (сплошная линия) для алгоритмов (1.6) и (1.7) при движении цели по окружности
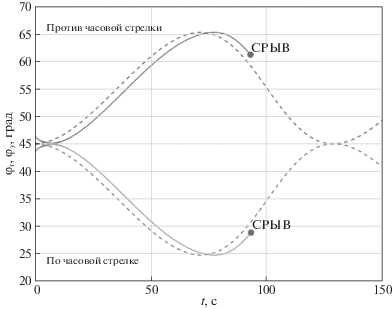
Рис. 11.
Бортовой пеленг цели (пунктирная линия) и угол поворота антенны (сплошная линия) для алгоритма (1.8) при движении цели по окружности

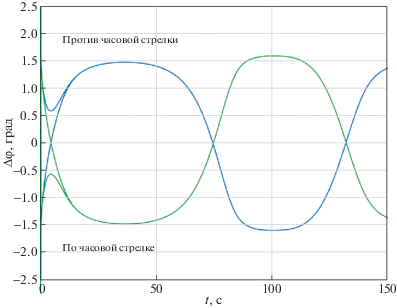
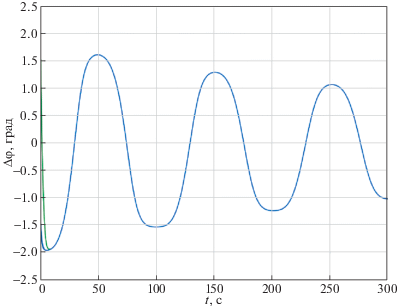
На рис. 4 представлено изменение углового положения цели и угла поворота антенны в процессе сопровождения при использовании полного закона управления (1.1), а на рис. 5 – реализуемые при этом ошибки сопровождения по углу и угловой скорости. Из них видно, что закон управления (1.1), обеспечивая отработку ошибок захвата, реализует высокую точность сопровождения цели $\left| {\Delta \varphi } \right| \leqslant 1.3^\circ $, $\left| {\Delta \omega } \right| \leqslant 1.2\,{{{\text{град}}} \mathord{\left/ {\vphantom {{{\text{град}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$, движущейся со сменой знаков производных дальности и углов, с большим запасом устойчивости $\left| {0.5\theta - \Delta \varphi } \right| > 0.5^\circ $.
Способы управления без учета $\Delta {{\varphi }^{3}}$ (1.2) и без учета $\Delta {{\omega }^{3}}$ (1.3) также обеспечивают бессрывное сопровождение, но с несколько худшими показателями точности. Графики ошибок сопровождения для этих законов приведены на рис. 6.
Рисунок 7 иллюстрирует показатели точности закона управления (1.4), полученного при условии использования в критерии (0.3) диагональной матрицы биквадратного штрафа $({{p}_{{12}}} = 0)$. Результаты исследований подтвердили его способность сопровождать цели, движущиеся по окружности, но с несколько худшей по сравнению с (1.1) точностью и меньшим запасом устойчивости.
Рисунок 8, характеризующий точность закона управления (1.5), который не учитывает кубических составляющих $\Delta {{\varphi }^{3}}$, $\Delta {{\omega }^{3}}$, свидетельствует о его возможности сопровождать цели, движущиеся по окружности, но с несколько худшей точностью.
Исследование вариантов без учета $\Delta {{\varphi }^{3}}$ и $\Delta {{\varphi }^{2}}\Delta \omega $ (1.6) и без учета $\Delta {{\varphi }^{3}}$, $\Delta \varphi \Delta {{\omega }^{2}}$ и $\Delta {{\omega }^{3}}$ (1.7) показало, что, практически обладая одинаковыми свойствами, данные законы не обеспечивают бессрывное сопровождение. Графики, поясняющие их работу, приведены на рис. 9, 10.
Графики текущих пеленгов, углов поворота антенны и ошибок сопровождения для традиционного угломера (1.8) представлены на рис. 11, 12.
Из рис. 5–8 видно, что полный вариант закона управления (1.1) и его разновидности (1.2)–(1.5) обеспечивают высокоточное бессрывное сопровождение цели при ее движении как по часовой, так и против часовой стрелки при любом наборе ошибок захвата. При этом хорошо просматривается сглаживающее влияние кубических слагаемых ${{K}_{3}}\Delta {{\varphi }^{3}}$ и ${{K}_{6}}\Delta {{\omega }^{3}}$ в области больших ошибок сопровождения. Так что достаточно высокими показателями точности и устойчивости обладают законы управления, содержащие хотя бы одно кубическое слагаемое.
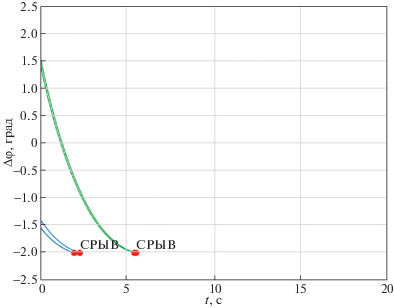
В то же время дополнительное исключение любого смешанного слагаемого $\Delta \varphi \Delta {{\omega }^{2}}$ или $\Delta {{\varphi }^{2}}\Delta \omega $ приводит к нарастанию текущих ошибок и срыву сопровождения (рис. 9, 10). Особенно показательны эпюры ошибок сопровождения (рис. 11, 12) для традиционного пропорционально-дифференциального метода (1.8), который приводит к срыву существенно быстрее, чем другие варианты управления.
Анализируя результаты исследований этого этапа, можно прийти к заключению, что разработанный метод оптимизации, в отличие от других, позволяет синтезировать управление, которое обеспечивает бессрывное сопровождение целей, движущихся по сложным траекториям со сменой знака производной дальности и угловой координаты.
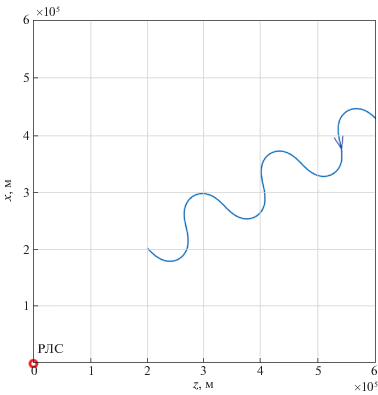
2.2. Сопровождение цели, движущейся по квазисинусоидальной траектории. Для практики наибольшую ценность имеют результаты сопровождения цели, которую существующие угломеры неспособны беспрерывно сопровождать и которая обычно используется для уклонения от средств поражения [3]. Траектория такого движения цели показана на рис. 13, а графики показателей сопровождения – на рис. 14–18.
Рис. 14.
Бортовой пеленг цели (пунктирная линия) и угол поворота антенны (сплошная линия) для алгоритма (1.1) при маневре цели “змейка”
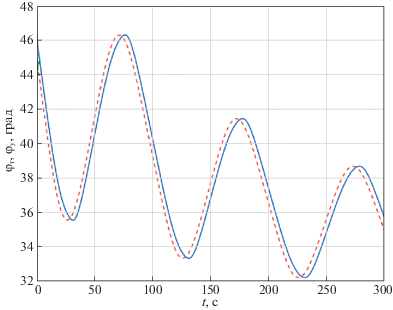
Рис. 15.
Ошибки сопровождения по углу (а) и угловой скорости (б) для алгоритма (1.1) при маневре цели “змейка”
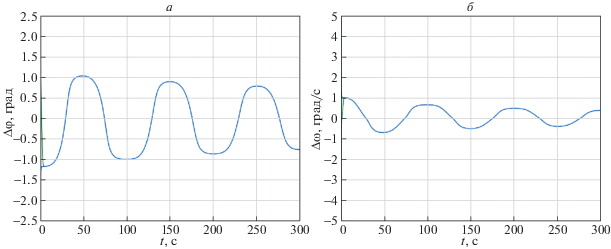
Рис. 17.
Бортовой пеленг цели (пунктирная линия) и угол поворота антенны (сплошная линия) для алгоритма (1.8) при маневре цели “змейка”

При этом на рис. 14 показаны зависимости бортового пеленга и угла поворота антенны для закона управления (1.1), а на рис. 15 – соответствующие графики ошибок слежения по углу и угловой скорости. Из этих двух рисунков видно, что цель устойчиво сопровождается с тенденцией снижения ошибок сопровождения и по углу, и по угловой скорости.
На рис. 16 приведены графики ошибок сопровождения по углу, общие для законов управления (1.2)–(1.5). Они качественно повторяют рис. 15, а, но с несколько худшей точностью.
Остальные варианты управления (1.6), (1.7) и особенно традиционный метод (1.8) не обеспечивают бессрывного сопровождения целей, двигающихся по квазисинусоидальной траектории. В качестве примера на рис. 17, 18 приведены графики траекторий отслеживаемых углов и соответствующих ошибок сопровождения для традиционного алгоритма (1.8).
Заключение. Предложенный способ синтеза систем на основе минимизации квадратично-биквадратных функционалов качества позволяет сформировать более эффективные законы управления. Они решают задачи бессрывного сопровождения новых типов целей, недоступные для типовых систем автосопровождения, оптимизированных по минимуму квадратичных функционалов качества.
При этом для формирования оптимального закона (1.1) не требуется знания старших производных угловых координат, а достаточно знания бортовых пеленгов, углового положения антенны и скоростей их изменения. Последние довольно просто формируются по результатам измерений углового положения антенны и пеленгаторов в плоскостях управления летательного аппарата-носителя.
Необходимо подчеркнуть, что, манипулируя видом биквадратного слагаемого функционала качества и его коэффициентами, можно получить широкий набор алгоритмов бессрывного высокоточного сопровождения для различных областей техники.
Список литературы
Верба В.С., Меркулов В.И., Руденко Е.А. Оптимизация систем автоматического сопровождения воздушных объектов на основе локальных квадратично-биквадратных функционалов. Ч. I. Синтез оптимального управления // Изв. РАН. ТиСУ. 2021. № 1. С. 24–29.
Автоматическое сопровождение целей в РЛС интегрированных авиационных комплексов. Т. 2. Сопровождение одиночных целей / Под ред. В.С. Вербы. М.: Радиотехника, 2018. 486 с.
Авиационные системы радиоуправления. Т. 3. Системы командного радиоуправления. Автономные и комбинированные системы наведения / Под ред. А.И. Канащенкова и В.И. Меркулова. М.: Радиотехника, 2004. 320 с.
Многофункциональные радиолокационные комплексы истребителей / Под ред. В.Н. Лепина. М.: Радиотехника, 2014. 296 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления