Известия РАН. Теория и системы управления, 2021, № 2, стр. 3-13

Введение. Для практических приложений важное значение имеет задача качения колеса по неровной поверхности. Возрождение интереса к этой классической задаче [1] связано с внедрением в практику роботизированных систем нового типа (шарообразных роботов) и поиском новых движителей для таких систем [2, 3]. Для решения задач управления шарообразным роботом необходимы, в частности, методы численного интегрирования уравнений качения по неровной поверхности. Частным случаем рассматриваемой задачи является задача качения тяжелого колеса по криволинейному профилю.

Основная трудность решения задачи качения связана с тем, что сила реакции и момент, действующие на колесо в точке касания, заранее не известны и должны быть определены из некоторых алгебраических соотношений (связей), следующих из дополнительных предположений о характере качения [1]. Для случая плоской поверхности, решение данной задачи в квадратурах было получено Пэнлеве [1] в конце XIX в., однако его обобщение на случай произвольного криволинейного профиля затруднительно. С другой стороны, хорошо известно, что попытки прямого численного решения уравнений движения механических систем, стесненных неголономными связями, часто приводят к отсутствию устойчивости и сходимости процесса счета, а также нарушению условий связи. Одной из наиболее ранних работ, известной авторам, где ставится и решается проблема стабилизации связей, является статья [4], в которой предложен метод построения устойчивого алгоритма для случая одного дополнительного уравнения связи. Метод приобрел популярность и вызвал большое число публикаций (см., например, [5–7] и приведенные там ссылки), посвященных его дальнейшему развитию, обобщению на более широкий класс систем и обсуждению вопросов численной реализации.

Изложенный в настоящей работе подход позволяет расширить класс систем, к которым применима техника стабилизации связей, и включить в рассмотрение такие системы, в которых уравнения связей и/или правые части дифференциальных уравнений зависят не только от обобщенных координат и скоростей, но и от некоторых дополнительных переменных, входящих в уравнения нелинейно. Пример такой системы – тяжелое колесо, катящееся без отрыва и проскальзывания по криволинейному профилю: уравнения связей, наложенных на систему, нелинейно зависят от угла наклона касательной к кривой в точке касания колеса, который не входит в число обобщенных координат. Применение классического варианта метода стабилизации связей потребовало бы решения нелинейного алгебраического уравнения для нахождения этого угла на каждом шаге интегрирования. В рамках же предлагаемого подхода указанная трудность преодолевается включением данного угла в число переменных и добавлением одного дифференциального уравнения первого порядка, что позволяет получить устойчивый алгоритм численного решения задачи, при работе которого алгебраические соотношения и дифференциальные уравнения выполняются с заданными точностями на больших интервалах времени.

1. Постановка задачи. Рассмотрим механическую систему со связями. Будем полагать, что уравнения движения записаны в виде системы дифференциальных уравнений первого порядка с линейно зависящей от неизвестного вектора реакций связей $N \in {{R}^{m}}$ правой частью:

Здесь, $X \in {{R}^{n}}$ – вектор состояния системы, а $n \times m$-матрица $B(X)$ и вектор $\widetilde F(X)$ – непрерывно-дифференцируемые функции. В частном случае механической системы с p степенями свободы, описываемой уравнениями Ньютона или Лагранжа, $X = {{[{{x}_{1}},{{\dot {x}}_{1}}, \ldots ,{{x}_{p}},{{\dot {x}}_{p}}]}^{{\text{T}}}}$, где x_i, $i = \overline {1,p} $, – обобщенная координата и n = 2p. Однако, как это будет видно из примера в разд. 3, указанный случай не исчерпывает всех возможностей, так что в общем случае размерность n системы (1.1) не связана напрямую с числом степеней свободы и, в частности, может быть и нечетной.

Будем полагать, что связи заданы в виде m алгебраических уравнений (ограничений)

и что начальные условия в (1.1) удовлетворяют указанным ограничениям. Предположим, что функции  f_i  имеют непрерывные частные производные до порядка n включительно и что уравнения (1.2) определяют гладкое многообразие $\mathcal{M}$ в ${{R}^{n}}$, которому принадлежит искомая траектория движения. Для системы (1.1), (1.2) рассматривается задача о поиске приближенного решения. Под приближенным решением с точностью $\delta $ здесь, следуя А.Ф. Филиппову [8], понимаются вектор-функции $X(t)$ и $N(t)$, такие, что ${\text{||}}\dot {X} - F(X,N){\text{||}} < \delta $ и ${\text{|}}{{f}_{i}}{\text{|}} < \delta ,$ $\forall t \in [0,{{t}_{1}}],$ $\forall i = \overline {1,m} $.

В силу того, что правые части системы (1.1) включают неизвестные функции (реакции связей N), решение задачи не может быть получено применением стандартных процедур численного интегрирования. Таким образом, возникает необходимость в разработке метода численного решения системы дифференциально-алгебраических уравнений вида (1.1), (1.2).

Причина, по которой уравнения движения заданы в виде системы дифференциальных уравнений первого порядка, заключается в том, что правые части уравнений или условия связей могут зависеть не только от обобщенных координат и скоростей, но и от некоторых дополнительных переменных, динамика которых не обязательно описывается уравнениями второго порядка (пример такой системы рассматривается в разд. 3). Запись уравнений движения в виде (1.1) позволяет нам рассматривать такие системы и системы, описываемые дифференциальными уравнениями второго порядка (уравнениями Ньютона или Лагранжа), в рамках единого подхода и, таким образом, расширить класс систем, к которым применим предлагаемый метод.

2. Идея предлагаемого подхода. Уравнения (1.2) вместе с (1.1) образуют замкнутую систему n + m уравнений относительно n + m неизвестных функций $(X,N)$ и при этом алгебраические уравнения (1.2) не зависят явно от переменных N. Такого рода задачи возникают в теории управления и, в частности, в задачах стабилизации движения. Рассмотрим, например, классическую задачу о стабилизации траектории движения x*(t) управляемого объекта с одним входом, описываемого нелинейной аффинной системой:

где $\Phi (x)$ и $\beta (x)$ – гладкие функции. Требуется найти такое скалярное управление в виде обратной связи $u = u(x)$, при котором в пределе выполняется (не зависящее явно от управления u) алгебраическое уравнение $x - x{\kern 1pt} *(t) = 0$. В теории управления предложено несколько подходов к решению этой задачи, таких, как линеаризация обратной связью и бэкстеппинг [9, 10]. В качестве основной идеи в этих методах предлагается дифференцировать невязку $y = x(t) - x{\kern 1pt} *(t)$ до тех пор, пока не появится u, после чего подставить производные в соответствующее эталонное линейное уравнение относительно y и выразить из него $u$. Аналогичный прием применяется при линеаризации с помощью обратной связи системы с m входами и m выходами [10]. Указанная идея используется и в рассматриваемой задаче о поиске приближенного решения системы (1.1) с ограничениями (1.2).

Обозначим через ${{r}_{i}}$ порядок наименьшей производной по времени функции ${{f}_{i}}(X)$ в силу системы (1.1), (1.2), которая явно зависит по крайней мере от одной компоненты вектора N. Так как правая часть (1.1) линейно зависит от $N$, r_i-я производная  f_i в силу (1.1) также зависит от N линейно, т.е. для любых $X \in \mathcal{M}$

где ${{A}_{i}}(X)$ – вектор-строка длины m и ${{\varphi }_{i}}(X)$ – сумма всех не зависящих от $N$ членов, в то время как для любых $j < {{r}_{i}}$, ${{d}^{j}}{{f}_{i}}{\text{/}}d{{t}^{j}}$ явно от N не зависит.

Составим теперь из строк ${{A}_{i}}(X)$ $m \times m$-матрицу $A(X)$. Следуя А. Исидори [10], будем говорить, что система (1.1), (1.2) имеет векторную относительную степень $\{ {{r}_{1}}, \ldots ,{{r}_{m}}\} $ в точке $X{\kern 1pt} * \in \mathcal{M}$, если матрица $A(X{\kern 1pt} *)$ не вырождена. В дальнейшем предполагается, что рассматриваемая система имеет векторную относительную степень $({{r}_{1}},...,{{r}_{m}})$ во всех точках $X \in \mathcal{M}$.

Для механической системы в подавляющем числе случаев либо ${{r}_{i}} = 1$ (например, для неголономных ограничений), либо ${{r}_{i}} = 2$. Хотя рассмотрение общего случая произвольного r_i не представляет принципиальных трудностей (см., например, [11, 12] и приведенные там ссылки) для простоты изложения, будем считать далее, что для всех условий связи ${{r}_{i}} \leqslant 2$, и введем обозначение ${{\dot {f}}_{i}}$ и ${{\ddot {f}}_{i}}$ для первой и второй производных функций ${{f}_{i}}$ по времени в силу системы (1.1), (1.2).

Так как уравнения (1.2) на искомой траектории выполняются тождественно, левые части в формулах (2.1) также тождественно равны нулю:

откуда следует, что искомый вектор $N$ удовлетворяет уравнению где $X \in \mathcal{M}$ и $\varphi (X) = {{[{{\varphi }_{1}}, \ldots ,{{\varphi }_{m}}]}^{{\text{T}}}}$.

Однако, как замечено в [4–6], использование уравнений (2.2) для численного нахождения вектора N недопустимо из-за неконтролируемого роста невязок алгебраических уравнений (1.2), возникающего при наличии сколь угодно малых ошибок задания начальных данных или неточности метода построения приближенного решения, так как общее решение уравнений (2.2) имеет вид ${{f}_{i}}(t) = {{c}_{{i2}}}t + {{c}_{{i1}}}$ для ${{r}_{i}} = 2$ и ${{f}_{i}}(t) = {{c}_{{i1}}}$, если ${{r}_{i}} = 1$, где константы интегрирования определены начальными условиями: ${{c}_{{i1}}} = {{f}_{i}}(0)$ и ${{c}_{{i2}}} = {{\dot {f}}_{i}}(0)$.

Следуя подходу, предложенному в [13], заменим систему (2.2) новой системой дифференциальных уравнений относительно  f_i, удовлетворяющей следующим условиям:

1) порядок i-го дифференциального уравнения новой системы совпадает с порядком i-го уравнения в (2.2);

2) решения новой системы уравнений и системы (2.2) при нулевых начальных условиях совпадают;

3) любое решение новой системы, соответствующее ненулевым начальным условиям, экспоненциально стремится к нулю.

Указанным условиям удовлетворяют, например, уравнения вида

для невязок, соответствующих связям с ${{r}_{i}} = 2$, и для невязок, соответствующих связям с ${{r}_{i}} = 1$. Выбор коэффициентов из однопараметрического семейства в уравнении (2.4) ($\lambda _{i}^{2}$ и $2{{\lambda }_{i}}$) сделан для удобства обозначений и последующих выкладок; в общем случае оба (положительных) коэффициента могут выбираться независимо друг от друга. Напомним, что порядок каждого дифференциального уравнения выбирается так, чтобы старшая производная соответствующей ${{f}_{i}}$ явно зависела от сил N, а коэффициенты уравнений ${{\lambda }_{i}}$ определяют показатели экспоненциального убывания невязок.

Подставляя правые части выражений в (2.1) вместо производных ${{\ddot {f}}_{i}}$ и ${{\dot {f}}_{i}}$ в (2.4) и (2.5) соответственно, получим отличную от (2.3) линейную алгебраическую систему уравнений относительно реакций связей N:

где $\lambda = [{{\lambda }_{1}}, \ldots ,{{\lambda }_{m}}]$, $\varphi (X,\lambda ) = {{[{{\varphi }_{1}}(X,{{\lambda }_{1}}), \ldots ,{{\varphi }_{m}}(X,{{\lambda }_{m}})]}^{{\text{T}}}}$ и ${{\varphi }_{i}}(X,{{\lambda }_{i}})$ определено при ${{r}_{i}} = 2$ формулой и при ${{r}_{i}} = 1$ формулой

Так как допускаются ненулевые невязки, уравнения (2.6) определены не только на многообразии, но и некоторой его окрестности. По предположению о наличии векторной относительной степени во всех точках многообразия матрица A(X) не вырождена при любых $X \in \mathcal{M}$. Следовательно, найдется окрестность многообразия, в которой эта матрица также не вырождена и систему (2.6) можно разрешить относительно N:

Подставляя (2.9) в (1.1) и интегрируя полученную замкнутую разрешенную относительно старших производных систему обыкновенных дифференциальных уравнений при помощи стандартного метода численного интегрирования, такого, как методы Рунге–Кутта или Адамса, находим искомую траекторию движения системы. Полученное решение будет δ-решением системы (1.1), (1.2), (2.9) по Филиппову, если вторые производные правой части системы ограничены на компактном замыкании окрестности области интегрирования.

Если начальные условия в (1.1) удовлетворяют ограничениям (1.2), то ${{f}_{i}}(0) = 0$, $i = \overline {1,m} $, и если ${{r}_{i}} = 2$, то ${{\dot {f}}_{i}}(0) = 0$. Так что решением уравнений (2.4) и (2.5) будут функции ${{f}_{i}}(t) \equiv 0$, $i = \overline {1,m} $, т.е. для точного решения выполнены условия (1.2). Если начальные условия не удовлетворяют ограничениям (1.2), метод дает приближенное решение задачи, при этом невязки ограничений стремятся экспоненциально к нулю. Выбирая достаточно большие коэффициенты ${{\lambda }_{i}}$ (и уменьшая при этом шаг интегрировании, см. [5]), можно добиться сколь угодно высокой точности $\delta $-решения задачи. Ошибки, связанные с неточным заданием начальных условий, не только не накапливаются, но и убывают экспоненциально с показателями $ - {{\lambda }_{i}}$, что позволяет получить решение задачи на больших интервалах времени с высокой точностью. Выбор шага интегрирования и коэффициентов ${{\lambda }_{i}}$, а также метода численного интегрирования системы обыкновенных дифференциальных уравнений выходит за рамки настоящей статьи и далее не рассматривается (интересующийся читатель может найти обсуждение задачи согласованного выбора численных значений для шага интегрирования и коэффициентов ${{\lambda }_{i}}$, например, в [5, 6]).

Замечание. Обратимость матрицы $A(X)$ при любых X, принадлежащих многообразию, не является необходимым условием применимости метода. Разрешимость уравнений (2.6) в таком случае исследуется дополнительно с использованием специфики решаемой задачи. Например, в задаче о качении колеса, рассматриваемой в следующем разделе, доказывается аналитически, что решение системы алгебраических уравнений (2.6) существует и при обращении детерминанта матрицы в нуль.

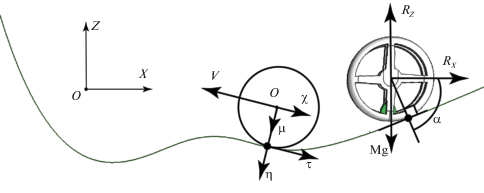
3. Качение тяжелого обруча по криволинейному профилю. В качестве иллюстрации применим описанный в предыдущем разделе метод для численного интегрирования уравнений качения тяжелого колеса (обруча) по криволинейному профилю (рис. 1).

Обозначим через $M$ и $r$ массу и радиус колеса. Пусть x и z – координаты центра колеса относительно горизонтальной и вертикальной осей неподвижной системы координат соответственно, а $\theta $ – угол поворота обруча вокруг центра, принимающий положительные значения при повороте против часовой стрелки. После освобождения от связей уравнения движения обруча [1] могут быть записаны в виде

где $g$ – ускорение свободного падения, $J = M{{r}^{2}}$ – момент инерции обруча, ${{R}_{x}}$ и ${{R}_{z}}$ – проекции силы реакции опоры на оси координат и Q – вращающий момент относительно центра масс. Уравнения (3.1) не могут быть проинтегрированы непосредственно, так как сила реакции и момент не известны. Для их нахождения мы далее выпишем алгебраические соотношения, следующие из дополнительных, сформулированных ниже предположений о характере качения.

Пусть форма желоба, по которому катится обруч, задана неявно уравнением $h(x,z) = 0$. Будем предполагать, что частная производная $h_{z}^{'}$ функции $h(x,z)$ по z нигде не равна нулю (профиль не содержит вертикальных участков) и что кривая является допустимой для данного обруча, т.е. кривизна кривой в любой точке меньше 1/r. Обозначим через ${{x}_{a}}$ и ${{z}_{a}}$ текущие координаты точки обруча, в которой он касается кривой: ${{x}_{a}} = x + rcos\alpha $, ${{z}_{a}} = z + rsin\alpha $, где $ - \pi < \alpha < 0$ – угол между осью x и вектором, направленным из центра обруча в точку касания (рис. 1).

Предположим, что колесо катится по желобу, не теряя с ним контакта, что система консервативна и что нет проскальзывания. Первые два условия имеют вид

и где E₀ – полная энергия системы в начальный момент времени. Условие качения без проскальзывания можно записать как равенство нулю проекции скорости точки колеса, касающейся кривой, на касательное к кривой направление: (обычно используемое условие качения без проскальзывания ${{\dot {x}}^{2}} + {{\dot {z}}^{2}} - {{(r\dot {\theta })}^{2}} = 0$ в данном случае не годится, так как, наряду с истинным движением, оно допускает и физически нереализуемое движение, при котором колесо вращается в противоположную сторону). Описывающие систему уравнения (3.1)–(3.4) имеют вид, отличный от (1.1), (1.2), так как алгебраические уравнения (3.2) и (3.4) зависят не только от переменных состояния, но и от дополнительной переменной $\alpha $.

Введем обозначения $\eta = {{[h_{x}^{'}({{x}_{a}},{{z}_{a}}),h_{z}^{'}({{x}_{a}},{{z}_{a}})]}^{{\text{T}}}}$ и $\tau = {{[ - h_{z}^{'}({{x}_{a}},{{z}_{a}}),h_{x}^{'}({{x}_{a}},{{z}_{a}})]}^{{\text{T}}}}$ для нормали к кривой и касательного вектора в точке касания с колесом (в дальнейшем, для краткости будем опускать аргументы функции $h({{x}_{a}},{{z}_{a}})$ и ее производных), $v = {{[\dot {x},\dot {z}]}^{{\text{T}}}}$ для вектора скорости центра колеса, $\mu = {{[cos\alpha ,sin\alpha ]}^{{\text{T}}}}$ для единичного вектора, лежащего на прямой, соединяющей центр колеса и точку касания с кривой, и $\chi = {{[ - sin\alpha ,cos\alpha ]}^{{\text{T}}}}$ для ортогонального ему вектора (рис. 1). Очевидно, что при качении колеса без отрыва от кривой векторы $\mu $ и $\tau $ ортогональны, $(\mu ,\tau ) \equiv 0$, т.е. должно выполняться условие

В классическом варианте метода стабилизации связей на каждом шаге интегрирования пришлось бы численно решать нелинейное алгебраическое уравнение (3.5) для того, чтобы выразить α через обобщенные координаты и скорости. В рамках же предлагаемого подхода для приведения системы уравнений к виду (1.1), (1.2) предлагается расширить пространство состояний, включив α в число переменных состояния, и добавить к системе (3.1) дифференциальное уравнение относительно новой переменной (из дальнейшего будет ясно, почему в данном случае можно ограничиться уравнением первого порядка):

Так как неизвестная функции $U \in R$ входит линейно в правую часть уравнения (3.6), мы можем рассматривать ее как еще одну “реакцию связей”, а уравнение (3.5) – в качестве четвертого алгебраического уравнения связи.

Таким образом, мы получаем систему (3.1), (3.6) дифференциальных уравнений порядка семь относительно семи переменных состояния, $X = {{[x,z,\theta ,\dot {x},\dot {z},\dot {\theta },\alpha ]}^{{\text{T}}}}$, и четыре алгебраических уравнения (3.2)–(3.5) для определения четырех неизвестных “реакций связей”, компонент вектора $N = {{[{{R}_{x}},{{R}_{z}},Q,U]}^{{\text{T}}}}$, в правой части системы. В соответствии с изложенным в предыдущем разделе методом обозначим левые части уравнений (3.2)–(3.5) через ${{f}_{1}}$, ${{f}_{2}}$, ${{f}_{3}}$ и ${{f}_{4}}$ соответственно. Дифференцируя первое алгебраическое уравнение, получаем

Так как скалярное произведение $(\tau ,\mu )$ тождественно равно нулю на многообразии, производная ${{f}_{1}}$ по времени в силу системы (3.1)–(3.6) не зависит явно от N. Второе дифференцирование дает

Непосредственным дифференцированием нетрудно показать, что $\dot {\eta } = {{H}_{2}}v + r\dot {\alpha }{{H}_{2}}\chi $, где

Подставляя полученное выражение в формулу для ${{\ddot {f}}_{1}}$, получаем

и вторая производная ${{f}_{1}}$ в силу системы (3.1)–(3.6) принимает вид

Дифференцируя f₂ и f₃ по времени в силу уравнений (3.1)–(3.6), находим

и

Коэффициент при $\dot {\alpha }$ на многообразии равен нулю в силу ортогональности векторов ${v}$ и $\mu $, и мы окончательно получаем

Производная ${{f}_{4}} \equiv (\mu ,\tau )$ равна

где $\dot {\mu } = {{[ - sin\alpha ,cos\alpha ]}^{{\text{T}}}}\dot {\alpha } = \dot {\alpha }\chi $ и

Дифференцируя касательный вектор $\tau $:

после несложных выкладок находим

Подставляя полученные выражения в формулу для ${{\dot {f}}_{4}}$, получаем производную  f₄ в силу системы (3.1)–(3.6):

Так как после первого дифференцирования появляется компонента вектора N, ${{r}_{4}} = 1$. В отличие от классического варианта метода стабилизации связей, в котором голономные ограничения надо дифференцировать дважды, второе дифференцирование не требуется, что в свою очередь и объясняет, почему мы ограничились дифференциальным уравнением первого порядка для α.

Из (3.7)–(3.10) находим матрицу $A(X)$:

где $d = {\text{||}}\nabla h{\text{||}} - (\chi ,{{H}_{2}}\chi )r$, и правые части системы φ₁(X, λ) = $ - Mgh_{z}^{'} + M(v,{{H}_{2}}v) + \lambda _{1}^{2}M{{f}_{1}} + 2{{\lambda }_{1}}M{{\dot {f}}_{1}}$, ${{\varphi }_{2}}(X,\lambda ) = {{\lambda }_{2}}{{f}_{2}}$, ${{\varphi }_{3}}(X,\lambda ) = - Mgcos\alpha + {{\lambda }_{3}}M{{f}_{3}}$, и φ₄(X, λ) = $ - (v,{{H}_{2}}\chi ) + {{\lambda }_{4}}{{f}_{4}}$.

В соответствие с обсуждаемым в разд. 2 методом решение задачи о качении сводится по существу к решению системы четырех алгебраических уравнений $A(X)N = - \varphi (X,\lambda )$, где $\varphi (X,\lambda )$ – вектор с компонентами ${{\varphi }_{i}}(X,\lambda )$, $i = \overline {1,4} $, подстановке найденного вектора $N(X,\lambda )$ в систему дифференциальных уравнений (3.1), (3.6) и численному интегрированию полученной системы.

Для проверки обратимости матрицы $A(X)$ найдем ее детерминант при $X \in \mathcal{M}$:

Принимая во внимание, что при $X \in \mathcal{M}$ пары векторов η, μ и $v$, $\chi $ коллинеарны и, следовательно, выполняются соотношения $(\eta ,\mu ) = {\text{||}}\nabla h{\text{||}}$, $\tau = {\text{||}}\nabla h{\text{||}}\chi $, ${v} = - r\dot {\theta }\chi $, откуда $(v,\tau ) = - r{\text{||}}\nabla h{\text{||}}\dot {\theta }$, получаем окончательно следующую формулу для детерминанта на многообразии:

Покажем, что величина d не может быть равна нулю. Используя формулу

для радиуса кривизны кривой, заданной неявно уравнением $h(x,z) = 0$, находим

В силу предположения о допустимости кривой, $r < \rho $ и, следовательно, d > 0.

Таким образом, на многообразии детерминант равен нулю тогда и только тогда, когда $\dot {\theta } = 0$, т.е. когда колесо останавливается в верхней точке своей траектории перед тем, как катиться в противоположную сторону, при этом ${{\varphi }_{1}} = - Mgh_{z}^{'}$, ${{\varphi }_{2}} = {{\varphi }_{4}} = 0$ и ${{\varphi }_{3}} = - Mgcos\alpha $. Обозначим через X* точку многообразия, в которой детерминант матрицы A равен нулю. Пусть ${{X}^{k}} \in \mathcal{M}$ – произвольная стремящаяся к особой точке последовательность принадлежащих многообразию точек, ${{X}^{k}} \to X{\kern 1pt} *$. Введем обозначение ${{A}_{k}} = A({{X}^{k}})$ и ${{\varphi }^{k}} = \varphi ({{X}^{k}},\lambda )$. Нетрудно проверить, что уравнение ${{A}_{k}}{{N}^{k}} = {{\varphi }_{k}}$ разрешимо при любых k и его решение N^k стремится к вектору $N{\kern 1pt} * = {{[R_{x}^{*},R_{z}^{*},Q{\kern 1pt} *,U{\kern 1pt} *]}^{{\text{T}}}}$, где

Таким образом, уравнение (2.3) имеет решение $N = - {{A}^{{ - 1}}}(X)\varphi (X)$ при любых $X \in \mathcal{M}$, которое в точках необратимости матрицы A(X) достраивается до непрерывного. Тем самым описанный в предыдущем разделе метод применим к рассматриваемой задаче.

4. Численное моделирование. Численное моделирование проводилось с помощью разработанной И.В. Матросовым системы компьютерной алгебры DExpert. Эта система позволяет автоматически находить аналитические выражения для неизвестных реакций и в формульном виде подставлять их в правую часть уравнений движения системы, после чего производить численное интегрирование.

В численных расчетах рассматривалось движение колеса массы M = 1 и радиуса $r = 0.01$ по кривой, заданной уравнением $z = {{x}^{4}} + a{{x}^{3}} - b{{x}^{2}} - ax - (1 - b)$, $a = 0.13,$ $b = 0.5$ (все параметры системы – безразмерные).

Профиль кривой показан на рис. 1. Начальные условия выбирались так, чтобы координата x_a точки касания колеса и кривой при любых $t$ принадлежала отрезку [–1, 1]. При этом колесо совершало периодическое движение между двумя крайними точками. Интегрирование проводилось как на коротких, так и длительных интервалах времени (до нескольких сотен прохождений профиля туда и обратно).

Для интегрирования замкнутой системы использовался явный метод Рунге–Кутта второго порядка с постоянным шагом $h = {{10}^{{ - 5}}}$. Результаты численных экспериментов показали, что показатели ${{\lambda }_{i}}$ при таком шаге должны выбираться из диапазона [1, 10⁵], что согласуется с результатами в [5, 14]. При любых ${{\lambda }_{i}}$ из указанного диапазона максимальная невязка в установившемся режиме меньше 10^–7 и достигает минимума ($\mathop {max}\limits_{i = \overline {1,4} } {\text{|}}{{\delta }_{i}}{\text{|}} < 7 \times {{10}^{{ - 9}}}$) при ${{\lambda }_{i}} = {{10}^{3}}$. Заметим, что при том же значении ${{\lambda }_{i}}$ уменьшение шага до $h = {{10}^{{ - 6}}}$ позволяет уменьшить максимальную невязку на три порядка: $\mathop {max}\limits_{i = \overline {1,4} } {\text{|}}{{\delta }_{i}}{\text{|}} < 5 \times {{10}^{{ - 12}}}$.

Чтобы определить константу $\delta $ в определении Филиппова из разд. 1, необходимо также оценить абсолютную ошибку численного метода, используемого при интегрировании системы дифференциальных уравнений, разрешенных относительно старших производных. В нашем случае при применении методов Рунге–Кутта и Адамса второго порядка можно использовать известную оценку $\delta < \hat {C}{{h}^{2}}$ [15, 16]. Константа $\hat {C}$ определяется максимальным значением нормы гессиана правой части системы разрешенных относительно старших производных дифференциальных уравнений [15, 16] и в данном численном примере не превосходит величины 10². Получение более точной оценки довольно трудоемко (см., например, вычисление $\hat {C}$ и $\delta $ в скалярном случае в работе [17]) и далеко выходит за рамки настоящей статьи.

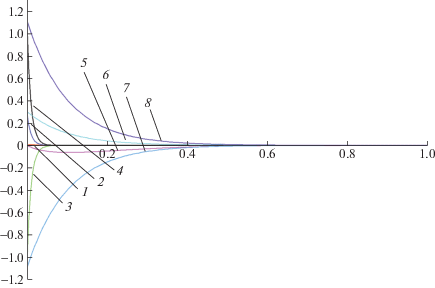
Выбор значений ${{\lambda }_{i}}$ из допустимого диапазона определяет скорость, с которой убывают начальные невязки. Чем больше ${{\lambda }_{i}}$, тем быстрее убывают невязки. На рис. 2 показаны графики невязок, вызванных ошибками в начальных данных, на начальном отрезке времени интегрирования при двух различных показателях, ${{\lambda }_{i}} = 10$ (кривые 5–8) и ${{\lambda }_{i}} = 100$ (кривые 1–4), $i = \overline {1,4} $. Как и следовало ожидать, увеличение на порядок значения ${{\lambda }_{i}}$ ускоряет убываниe начальных невязок.

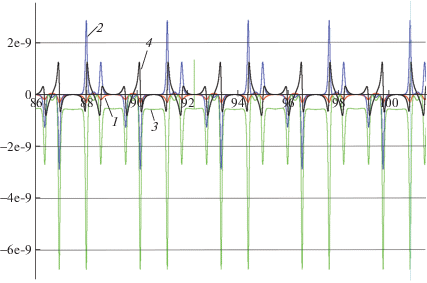
При интегрировании на больших интервалах времени ошибки в начальных данных оказывают пренебрежимо малый эффект на результат, и невязки вызываются ошибками, связанными с конечностью  шага  интегрирования.  Типичная картина таких невязок показана на рис. 3, где цифрами 1–4 отмечены графики невязок ${{f}_{i}}(t)$, $i = \overline {1,4} $, соответственно, на интервале времени с 86 по 101 единицу времени. Интегрирование проводилось на длительном интервале времени при шаге $h = {{10}^{{ - 5}}}$ и ${{\lambda }_{i}}$ = 10³. Как видно из рисунка, величина максимальной из невязок (${{f}_{3}}$) не превышает $7 \times {{10}^{{ - 9}}}$.

Следующий рисунок иллюстрирует утверждение разд. 2 о недопустимости использования уравнений (2.3) (соответствуют нулевым ${{\lambda }_{i}}$) для численного нахождения сил реакций. На рис. 4 показаны профиль, по которому должно катиться колесо (верхняя кривая), и траектория, описываемая точкой $({{x}_{a}},{{z}_{a}})$, полученная при ${{\lambda }_{i}} = 0$, $i = \overline {1,4} $, на интервале времени, соответствующем двукратному прохождению профиля туда и обратно. Из рис. 4 видно, насколько сильно отличается действительная траектория точки контакта колеса с кривой от кривой, по которой она должна двигаться, при том что начальные условия были выбраны достаточно точными ($\mathop {max}\limits_{i = \overline {1,4} } {\text{|}}{{\delta }_{i}}(0){\text{|}} < 1.0{{e}^{{ - 6}}}$). Таким образом, очевидно, что попытка численного интегрирования уравнений качения без стабилизации связей заведомо обречена на неудачу.

Заключение. Предложен подход к решению задачи численного интегрирования уравнений движения механических систем с ограничениями, основанный на стабилизации связей. На базе предлагаемого подхода, разработан метод численного решения задачи качения колеса по криволинейному профилю, обеспечивающий регуляризацию в процессе счета и позволяющий получить решение задачи на больших интервалах времени с высокой точностью.

Отметим, что приведенный метод может быть адаптирован для решения задач управления/стабилизации механических систем. Действительно, легко видеть, что если $X = (x,\dot {x})$, то рассматриваемая в статье задача может быть интерпретирована как задача стабилизации аффинной системы управления с векторным входом N и векторным выходом $Y = ({{y}_{1}}, \ldots ,{{y}_{m}})$, где ${{y}_{i}} = {{f}_{i}}(X)$. Более того, в рамках предлагаемого подхода можно исследовать управляемые механические системы с априори неизвестными реакциями связей, полагая, что вектор $N$ включает в себя как управления, так и реакции связей, и записывая систему в виде (1.1), (1.2). При этом часть компонентов векторного выхода будет представлять собой ограничения, наложенные на систему, а другие – цели управления.