Известия РАН. Теория и системы управления, 2021, № 2, стр. 14-24
ДВУМЕРНАЯ МОДЕЛЬ ДЛЯ ОЦЕНКИ ЭФФЕКТИВНОСТИ УГЛОВЫХ ИЗМЕРЕНИЙ ПО ЭЛЛИПТИЧЕСКИМ ОРБИТАМ
А. М. Ануфриев a, *, Ю. А. Горицкий a, Д. Г. Тигетов b, **
a МЭИ
Москва, Россия
b АО “ВНИИРТ”
Москва, Россия
* E-mail: goritskiy@yandex.ru
** E-mail: david.tigetov@gmail.com
Поступила в редакцию 21.11.2019
После доработки 23.04.2020
Принята к публикации 27.07.2020
Аннотация
Рассматриваются неблагоприятные для наблюдателя орбиты, плоскость которых проходит вблизи плоскости орбиты. Замена движения наблюдателя приближенно эквивалентным движением на плоскости орбиты приводит к простой двумерной модели измерения-движения. Определяются границы Рао–Крамера для оценок параметров орбит. Углы места наблюдения связаны с истинными аномалиями и параметрами орбиты нелинейными уравнениями. Дифференцирование уравнений по параметрам орбиты дает матрицу Якоби одиночных угловых измерений, а затем и информационную матрицу Фишера, которая является основой для анализа точности. Наиболее сложная часть определения матрицы Фишера состоит в вычислении производных истинных аномалий по параметрам орбиты; эта часть основана на численном решении дифференциального уравнения, выражающего второй закон Кеплера. Приведены примеры вычисления границ точности оценок в широком диапазоне практических скоростей и углов падения. Результаты показывают, что по угловым измерениям возможно получить практически интересные точности по некоторым параметрам.
Введение. Предполагается, что наземный наблюдатель в дискретные моменты времени может измерять только угловые координаты объекта. Объект находится в свободном движении со скоростью, меньшей первой космической, на высотах не более 1000 км. Решается вопрос о том, можно ли по угловым измерениям оценить параметры движения с практически интересной точностью. Для ответа учитываем лишь основное, пренебрегая многочисленными влияющими на точность факторами: считаем, что движение кеплеровское, а измерения производятся с дискретностью Δt и со случайной погрешностью, дисперсия которой – σ2. Цель работы – описать для инженера-разработчика приближенное, но достаточно простое средство анализа.
Задача оценивания параметров орбит космических тел (КТ) по угловым измерениям не является новой [1–9], однако с изменением технических средств измерения, требований к точности и вычислительных возможностей задача приобретает различные особенности. В частности, актуальна ситуация пассивной радиолокации, высокой частоты измерений, мощных вычислительных средств и высоких требований к точности определения расстояния от измерителя до точки падения.
Простые алгоритмы оценивания [1, 5, 6, 10] основаны на построении точечной оценки состояния КТ в фиксированный момент времени. Начальную оценку угловых величин получают регрессией угловых измерений, используя полиномы; оценки радиальных величин находят как корни трансцендентных уравнений орбитального движения, связывающих радиальные и угловые величины. Полученную оценку применяют в качестве начального приближения в различных методах уточнения, [1, 3–6], связанных с минимизацией квадратичной формы отклонения. В [7] излагается альтернативный подход, связанный с аппроксимацией апостериорной плотности вероятности состояния КТ, получаемой при аппроксимации априорной плотности вероятности состояния КТ и функции преобразования состояния [11–13].
Анализ эффективности методов оценивания обычно связывают с границами дисперсий многомерного неравенства Рао–Крамера, [1, 14–19]. В [1] теоретическая граница Рао–Крамера используется как эталонная мера ошибки оценивания, а в фундаментальной отечественной работе [5] авторы приводят универсальные соотношения для приближенного вычисления ошибок оценивания параметров орбит, которые в частном случае независимых гауссовых ошибок измерений совпадают с границей Рао–Крамера. Вычисление границ в ряде случаев представляет отдельную нетривиальную задачу, [14–16], например, в [15, 16] для вычисления границ Рао–Крамера в задаче фильтрации двумерного движения используется специализированная система координат угловых измерений. В данной работе при вычислении матрицы Фишера численно решается дифференциальное уравнение, представляющее второй закон Кеплера.
Разработчикам алгоритмов необходимо знать, с какой частотой и точностью нужно измерять и какую точность на каких орбитах можно получить. Эти вопросы могут прояснить информационные оценки точности, которая зависит от параметров орбиты. На практике особо выделяют класс траекторий, направленных в сторону наблюдателя, для которых весьма характерными являются малые изменения азимута. Малые изменения азимута имеют место в тех случаях, когда движение наблюдателя, связанное с вращением Земли, происходит вблизи плоскости орбиты. В этих случаях задачу можно приближенно считать двумерной, проецируя движение наблюдателя на плоскость орбиты, а единственным источником информации – измерения угла места. Ситуации с малыми изменениями азимута интересны также тем, что они наименее благоприятны для оценки параметров движения, и потому анализ их точности может служить ориентиром для использования угловых измерительных систем.
Цель данной работы состоит в том, чтобы предложить инженерам-разработчикам алгоритмов достаточно простые инструменты для приближенной оценки возможной точности при угловых измерениях. Задача оценки точности решается, опираясь на два момента, отличающих ее от других. 1. Выделено семейство неблагоприятных для наблюдателя орбит; это орбиты, плоскость которых касается орбиты движущегося наблюдателя, и точка касания является точкой пересечения соответствующих траекторий. 2. Обоснована простая приближенная плоская модель движения–измерения, в которой истинное движение наблюдателя (вне плоскости орбиты КТ) без изменения его скорости заменяется движением в плоскости орбиты КТ по окружности земной сферы.
Далее необходимо сделать следующие пояснения. Во-первых, нас интересуют орбиты, которые могут закончиться в окрестности наблюдателя. Во-вторых, семейство орбит, которые заканчиваются в точке наблюдателя (и в этой точке окружность наблюдателя касается плоскости орбиты), являются наиболее неблагоприятными в том смысле, что иначе информации будет больше, и тогда и качество оценок должно быть выше. Действительно, если в момент падения в эту точку вектор скорости наблюдателя не лежит в плоскости орбиты, то измерительной информации по орбите будет больше (чем в случае касания) за счет азимутальных измерений. Если же отодвинем точку падения от точки наблюдателя, то диапазон изменения угла места увеличится и мы опять имеем увеличение информации.
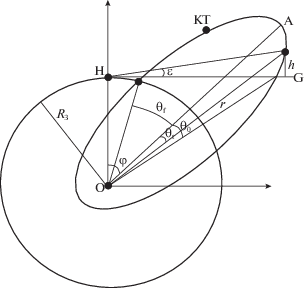
1. Двумерная модель измерения. 1.1. Предварительная схема: неподвижный наблюдатель. Рассматривается ситуация, в которой точка наблюдения Н (рис. 1) находится в плоскости орбиты и она неподвижна. В дальнейшем учтено влияние движения вне этой плоскости. Объект движется по эллипсу, главная ось которого составляет угол φ относительно направления на точку Н наблюдения. Орбита характеризуется трехмерным параметром а:
φ – угол между наблюдателем Н и главной осью эллипса, р – фокальный параметр, е – эксцентриситет орбиты. Уравнение орбиты в полярных координатах(1.1)
$r(\theta ) = {p \mathord{\left/ {\vphantom {p {(1 - e\cos \theta }}} \right. \kern-0em} {(1 - e\cos \theta }}),$(1.2)
${\text{tg}}(\varepsilon ) = \frac{{r({\theta })\cos (\varphi - {\theta }) - {{R}_{{\text{З}}}}}}{{r({\theta })sin(\varphi - {\theta })}} = {\text{ctg}}(\varphi - \theta ) - \frac{{{{R}_{{\text{З}}}}(1 - e\cos \theta )}}{{psin(\varphi - {\theta })}},$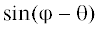 имеем
имеем
(1.3)
$sin(\varphi - \theta ){\text{tg}}\left( {\varepsilon } \right) = {\text{cos}}(\varphi - \theta ) - \left( {{{{{R}_{{\text{З}}}}} \mathord{\left/ {\vphantom {{{{R}_{{\text{З}}}}} p}} \right. \kern-0em} p}} \right)(1 - e\cos \theta ).$Это соотношение определяет ε = ${\varepsilon }({\theta };{\varphi },p,e)$, как функцию θ и параметров орбиты, но $\theta = \theta (t)$ – функция времени, и потому для любого фиксированного момента t
– функция трех переменных (заметим, что$\theta (t) = \theta (t;{\varphi ,}p,e)$ – тоже функция (φ, р, е)). По значению ε и фиксированным параметрам (φ, р, е) орбиты можно определить аномалию $\theta $, решая уравнение (1.3), сводимое к квадратному: ${\theta } = h(\varepsilon ;{\varphi ,}p{\text{,}}e)$ (см. Приложение). Для произвольного момента t значение $\theta (t)$ при известных параметрах орбиты р и е определяется по дифференциальному уравнению (второй закон Кеплера о постоянстве секториальной скорости) с начальным условием: при t = t0 ${\theta = }{{{\theta }}_{0}}$; ${\omega }(\theta ;p,e) = {{\sqrt {p{\mu }} } \mathord{\left/ {\vphantom {{\sqrt {p{\mu }} } {{{r}^{2}}}}} \right. \kern-0em} {{{r}^{2}}}} = (\sqrt {\mu } {\text{/}}{{p}^{{3/2}}}){{(1 - e\cos {\theta })}^{2}}$ – угловая скорость; $\mu = 3.9860044 \times {{10}^{{14}}}$ м3/с2 – геоцентрическая гравитационная постоянная.В дискретные моменты времени t0, t1, …, tn, ti = ti – 1 + Δt, i = 1, …, n, имеем измерения
(1.5)
${{x}_{i}} = \varepsilon ({{t}_{i}};a) + {{\delta }_{i}},\quad {{\varepsilon }_{i}}(a) = {{\delta }_{i}},\quad a = (\varphi ,p,e),$В некоторый известный момент времени t0 имеется начальное измерение
По значению $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varepsilon } {}_{0}$ по (1.3) определим приближенно ${{{\tilde {\theta }}}_{0}}(a)$ – аномалию ${{{\theta }}_{0}}$ в момент t0 как функцию параметра а (начальное условие при t = t0):
(1.6)
$\theta = {{\tilde {\theta }}_{0}}(a) = h({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varepsilon } }_{0}};\varphi ,p,e) = {{\theta }_{0}}(a) + {{\delta }_{\theta }},$1.2. Учет движения наблюдателя вследствие вращения Земли. Наблюдатель вследствие вращения Земли движется по окружности вдоль своей параллели. Будем считать траекторию КТ неблагоприятной для измерителя, если плоскость орбиты КТ касается орбиты движущегося измерителя, и точка касания является общей точкой (точкой пересечения) для соответствующих траекторий. Эти траектории характеризуются, во-первых, настолько малым диапазоном измеряемых азимутальных углов, что измерениями азимута можно пренебречь, и, во-вторых, диапазон изменения угла места минимален при последних (наиболее информативных) наблюдениях (так как траектория входит в точку О наблюдения). Следовательно, траектории неблагоприятны, если в момент падения вектор скорости наблюдателя лежит в плоскости орбиты.
Если реверсировать время, то можно сформулировать так: неблагоприятны для измерителя те траектории, которые исходят из точки наблюдения, и орбитальная плоскость проходит через вектор скорости наблюдателя. В этом случае взаимное движение выглядит следующим образом: из точки касания О начинаются одновременно два движения: наблюдатель движется по окружности – параллели с широтой φН, а КТ движется в орбитальной плоскости.
Простые соображения показывают, что существует фиктивное движение измерителя (по окружности сферы SЗ Земли в орбитальной плоскости), эквивалентное (в смысле получения углов места) истинному движению (вне орбитальной плоскости). Для этого достаточно, чтобы в любой момент времени два расстояния (от КТ до фиктивного движения и до истинного движения) были одинаковы. С помощью такого эквивалентного фиктивного движения Δφ(t) задача сводится к плоской. Однако фиктивное эквивалентное движение зависит от точки расположения КТ.
Построим приближенно эквивалентное движение, независимое от КТ. Заменим равномерное движение наблюдателя вдоль своей параллели движением по окружности S3 сферы в орбитальной плоскости, сохранив его линейную скорость ${{{\omega }}_{{\text{З}}}}{{R}_{{\text{З}}}}\cos {{{\varphi }}_{{\text{Н}}}}$. Заметим, что для экватора ${{{\varphi }}_{{\text{Н}}}} = 0$ и на северном полюсе ${{{\varphi }}_{{\text{Н}}}} = {\pi /}2$, это фиктивное движение является эквивалентным.
Оценим это приближение. Оба движения, истинное и фиктивное, исходят (вернее, приходят)
одновременно в общую точку О. Определим разность длин двух отрезков, исходящих из точки КТ на истинную траекторию
и на фиктивную. Если длины в любой момент одинаковы, $\Delta d = 0$, то углы места равны. Если они не одинаковы, $\Delta d \ne 0$, то оценим величину погрешности Δε(t; d, 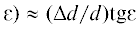 измеряемого угла места или величину сдвига $\Delta l(t;d,{\varepsilon }) \approx {{\Delta d} \mathord{\left/ {\vphantom {{\Delta d} {\cos {\varepsilon }}}} \right. \kern-0em} {\cos {\varepsilon }}}$ фиктивного наблюдателя, при котором угол места равен истинному. Необходимые формулы
даны в Приложении. В табл. 1 в каждой клетке приведены расчетные значения $\Delta l$ и $\Delta {\varepsilon }$, зависящие от расположения КТ (угла ε и дальности d) и времени t движения до точки О; значение широты принято φН = 60°.
измеряемого угла места или величину сдвига $\Delta l(t;d,{\varepsilon }) \approx {{\Delta d} \mathord{\left/ {\vphantom {{\Delta d} {\cos {\varepsilon }}}} \right. \kern-0em} {\cos {\varepsilon }}}$ фиктивного наблюдателя, при котором угол места равен истинному. Необходимые формулы
даны в Приложении. В табл. 1 в каждой клетке приведены расчетные значения $\Delta l$ и $\Delta {\varepsilon }$, зависящие от расположения КТ (угла ε и дальности d) и времени t движения до точки О; значение широты принято φН = 60°.
Таблица 1.
Значения $\Delta l$ (слева) в метрах и $\Delta \varepsilon $ (справа) в угловых минутах
| t, с | ε, град | d, км | |||
|---|---|---|---|---|---|
| 100 | 300 | 600 | 1000 | ||
| 100 | 12 | 0.13, 0.001 | 0.15, 0.0004 | 0.15, 0.0002 | 0.15, 0.0002 |
| 48 | 0.14, 0.0036 | 0.15. 0.001 | 0.15. 0.0006 | 0.15, 0.0004 | |
| 72 | 0.17, 0.006 | 0.16, 0.002 | 0.16, 0.001 | 0.15, 0.0006 | |
| 300 | 12 | 2.9, 0.021 | 3.7, 0.009 | 3.8, 0.005 | 3.9, 0.005 |
| 48 | 3.35, 0.086 | 3.84, 0.033 | 3.98, 0.017 | 4.04, 0.01 | |
| 72 | 4.65, 0.152 | 4.46, 0.049 | 4.31, 0.023 | 4.23, 0.014 | |
| 600 | 12 | 19, 0.136 | 25, 0.06 | 28, 0.033 | 30, 0.021 |
| 48 | 23, 0.59 | 29.5, 0.25 | 30.6, 0.13 | 31.5, 0.08 | |
| 72 | 35.9, 1.17 | 36.8, 0.40 | 35.5, 0.19 | 34.5, 0.11 | |
Видно, что смещение $\Delta l(t,\varepsilon ,d)$ относительно эквивалентных точек меньше 5 м в диапазоне до 300 с и до 72° при дальностях от 100 до 1000 км. Если $\Delta l$ переводить в погрешность $\Delta {\varepsilon }$ по углу места, то, например, за 300 с до точки О при дальности 300 км и ε = 48° имеем $\Delta l$ = 3.84 м, что означает $\Delta {\varepsilon } \approx 0.033$ угл. мин., что меньше с.к.о. измерения в сотни раз.
Фиктивное движение при вычислениях учитывается добавлением к неизвестному параметру φ в (1.2) линейно изменяющееся во времени (со скоростью ${{{\omega }}_{{\text{З}}}}\cos {{{\varphi }}_{{\text{Н}}}}$) слагаемое Δφ(t) = = $ \pm {\kern 1pt} {{{\omega }}_{{\text{З}}}}{\text{cos}}{{{\varphi }}_{{\text{Н}}}}$(T – t), T – момент падения, причем $\Delta {\varphi (}T) = 0$. Заметим, что формулы производных по параметрам, необходимые для матрицы Фишера, остаются без изменения; изменяются лишь их значения при вычислениях.
2. Вычисление матрицы Фишера. Информационная матрица Фишера, как известно, есть
(2.1)
$F(a) = {{{\sigma }}^{{ - {\text{2}}}}}\sum\limits_{i = 1}^n {{{{\left( {{{\partial {{\varepsilon }_{i}}} \mathord{\left/ {\vphantom {{\partial {{\varepsilon }_{i}}} {\partial a}}} \right. \kern-0em} {\partial a}}} \right)}}^{{\text{T}}}}\left( {{{\partial {{\varepsilon }_{i}}} \mathord{\left/ {\vphantom {{\partial {{\varepsilon }_{i}}} {\partial a}}} \right. \kern-0em} {\partial a}}} \right)} ,$Производные (∂εi/∂a) функций определяются из уравнения (1.2), и при фиксированном $t = {{t}_{i}}$ их можно выписать в явном виде (см. Приложение). Эти функции зависят от аномалии ${\theta = \theta (}t{\text{)}}$ и от ее производных по параметрам:
(2.2)
${{\partial {\varepsilon }} \mathord{\left/ {\vphantom {{\partial {\varepsilon }} {\partial {\varphi }}}} \right. \kern-0em} {\partial {\varphi }}} = {{\Phi }_{1}}(\theta ,{{\theta }_{{\varphi }}}),\quad {{\partial {\varepsilon }} \mathord{\left/ {\vphantom {{\partial {\varepsilon }} {\partial p}}} \right. \kern-0em} {\partial p}} = {{\Phi }_{2}}(\theta ,{{\theta }_{p}}),\quad {{\partial {\varepsilon }} \mathord{\left/ {\vphantom {{\partial {\varepsilon }} {\partial e}}} \right. \kern-0em} {\partial e}} = {{\Phi }_{3}}(\theta ,{{\theta }_{e}}),$(2.3)
${{d{{{\theta }}_{p}}} \mathord{\left/ {\vphantom {{d{{{\theta }}_{p}}} {dt}}} \right. \kern-0em} {dt}} = {{{\omega }}_{p}}{\theta ,}\quad {{d{{{\theta }}_{e}}} \mathord{\left/ {\vphantom {{d{{{\theta }}_{e}}} {dt}}} \right. \kern-0em} {dt}} = {{{\omega }}_{e}},\quad {{d{{{\theta }}_{{\varphi }}}} \mathord{\left/ {\vphantom {{d{{{\theta }}_{{\varphi }}}} {dt}}} \right. \kern-0em} {dt}} = {{{\omega }}_{{\varphi }}},$3. Некоторые расчетные результаты. 3.1. Неподвижный наблюдатель. Исходные параметры орбит: α и V – угол падения и скорость КТ (формулы связи $(V,{\alpha })$ с $(p,e)$ даны в Приложении); Lа = ${\varphi }{{R}_{З}}$ – расстояние до точки апогея; Ha – высота в апогее; φ – угол главной оси выбирался так, чтобы орбита была “неблагоприятной”, Δt = 5с – дискретность измерений, σ = 6' – стандартная ошибка измерений; N – количество наблюдений (доля времени наблюдения составляет 0.9).
Результаты нижних границ для с.к.о. приведены в табл. 2 для следующих параметров: σVa – скорости Va в апогее, σVy – вертикальной Vy скорости, σΔ – расстояния Δ до точки падения. По результатам делаем следующие выводы:
Таблица 2.
Расчетные значения границ с.к.о. для Va, Vy и Δ
| Характеристики по орбитам | Угол α, град | ||||||
|---|---|---|---|---|---|---|---|
| 12 | 24 | 36 | 48 | 60 | 72 | ||
| V = 1 км/с | Ha, км | 2.2 | 8.6 | 17.8 | 28.4 | 38.6 | 46.5 |
| La, км | 21 | 39 | 49 | 51 | 44 | 30 | |
| N | 7 | 14 | 21 | 27 | 31 | 34 | |
| σΔ, м | 1108 | 571 | 287 | 180 | 161 | 118 | |
| ${{{\sigma }}_{{{{V}_{a}}}}}$, м/c | 43 | 12 | 4.6 | 2.3 | 1.5 | 0.9 | |
| ${{{\sigma }}_{{{{V}_{y}}}}}$, км/c | 2.98 | 2.87 | 1.8 | 1.34 | 1.62 | 1.41 | |
| V = 2 км/с | Ha, км | 9.4 | 35.8 | 74.3 | 118 | 159 | 191 |
| La, км | 88 | 160 | 202 | 208 | 179 | 120 | |
| N | 15 | 29 | 43 | 55 | 64 | 69 | |
| σΔ, м | 1440 | 1170 | 645 | 543 | 406 | 306 | |
| ${{{\sigma }}_{{{{V}_{a}}}}}$, м/c | 36.3 | 13.6 | 5.6 | 3.4 | 2.0 | 1.2 | |
| ${{{\sigma }}_{{{{V}_{y}}}}}$, км/c | 5.7 | 10 | 7.3 | 8.5 | 7.7 | 7 | |
| V = 3 км/с | Ha, км | 23 | 87 | 179 | 282 | 377 | 450 |
| La, км | 216 | 387 | 480 | 486 | 411 | 273 | |
| N | 22 | 44 | 65 | 85 | 101 | 104 | |
| σΔ, м | 3562 | 1936 | 1359 | 1027 | 719 | 547 | |
| ${{{\sigma }}_{{{{V}_{a}}}}}$, м/c | 53.2 | 15.6 | 7.5 | 4.3 | 2.4 | 1.4 | |
| ${{{\sigma }}_{{{{V}_{y}}}}}$, км/c | 2.49 | 2.45 | 2.48 | 2.45 | 2.0 | 1.83 | |
– горизонтальную составляющую Va можно оценить с точностью до единиц и десятков м/с,
– точность по месту падения для высоких и с малой скоростью орбит можно получить порядка сотен метров (выделено 571, 645, 719, …),
– вертикальную составляющую вектора скорости оценить невозможно (погрешности порядка единиц километров в секунду).
3.2. Подвижный наблюдатель. Широта наблюдателя принята равной ${{{\varphi }}_{{\text{н}}}}$ = 60°. При встречном движении наблюдателя и КТ результаты показаны в табл. 3. Видим увеличение всех значений (понятна причина: увеличение скорости взаимного приближения). При движении в одну сторону наблюдателя и КТ результаты показаны в табл. 4. Наблюдаем уменьшение всех значений (из-за уменьшения скорости взаимного приближения).
Таблица 3.
Границы с.к.о. для Va, Vy и Δ
| Характеристики по орбитам | Угол α, град | ||||||
|---|---|---|---|---|---|---|---|
| 12 | 24 | 36 | 48 | 60 | 72 | ||
| V = 1 км/с | σΔ, м | 1680 | 872 | 440 | 277 | 252 | 187 |
| ${{{\sigma }}_{{{{V}_{a}}}}}$, м/c | 65.4 | 18.4 | 7.2 | 3.7 | 2.6 | 1.6 | |
| ${{{\sigma }}_{{{{V}_{y}}}}}$, км/c | 4.5 | 4.4 | 2.7 | 2.0 | 2.4 | 2.1 | |
| V = 2 км/с | σΔ, м | 1790 | 1450 | 806 | 680 | 508 | 385 |
| ${{{\sigma }}_{{Va}}}$, м/c | 45.3 | 17.1 | 7.1 | 4.4 | 2.6 | 1.6 | |
| ${{{\sigma }}_{{Vy}}}$, км/c | 7.1 | 13 | 9.1 | 10 | 9.4 | 8.4 | |
| V = 3 км/с | σΔ, м | 4130 | 2250 | 1600 | 1200 | 835 | 636 |
| ${{{\sigma }}_{{{{V}_{a}}}}}$, м/c | 61.2 | 18.2 | 8.8 | 5 | 2.9 | 1.8 | |
| ${{{\sigma }}_{{{{V}_{y}}}}}$, км/c | 29 | 28 | 29 | 28 | 23 | 21 | |
Таблица 4.
Границы с.к.о. для Va, Vy и Δ
| Характеристики по орбитам | Угол α, град | ||||||
|---|---|---|---|---|---|---|---|
| 12 | 24 | 36 | 48 | 60 | 72 | ||
| V = 1 км/с | σΔ, м | 649 | 334 | 170 | 109 | 98 | 71 |
| ${{{\sigma }}_{{{{V}_{a}}}}}$, м/c | 25.2 | 6.9 | 2.6 | 1.3 | 0.8 | 0.4 | |
| ${{{\sigma }}_{{{{V}_{y}}}}}$, км/c | 1.7 | 1.7 | 1.1 | 0.85 | 1.1 | 0.95 | |
Заключение. Выделено семейство неблагоприятных для наблюдателя орбит, плоскость которых касается орбиты движущегося наблюдателя, и точка касания является точкой пересечения соответствующих траекторий. Обоснована простая приближенная плоская модель движения–измерения, в которой истинное движение наблюдателя (вне плоскости орбиты КТ) без изменения его скорости заменяется движением в плоскости орбиты КТ по окружности земной сферы. Обоснование проведено вычислением погрешностей.
На этой модели проанализирована потенциальная точность с помощью информационной матрицы Фишера. Вычисление матрицы Фишера основано на численном решении дифференциального уравнения, выражающего второй закон Кеплера.
Рассчитаны границы для точностей параметров для семейства неблагоприятных орбит. Примеры показывают, что по угловым измерениям возможно получение практически интересных точностей для некоторых параметров (например, горизонтальной составляющей скорости).
В Приложении приведены все формулы, необходимые для проведения аналогичных расчетов.
Список литературы
Chang C.B. Optimal State Estimation of Ballistic Trajectories with Angle-only Measurements // M.I.T., Lincoln Laboratory, Technical Note 1979–1. 1979.
Chang C.B., Tabaczynski J. Application of State Estimation to Target Tracking // IEEE Trans. Automatic Control. 1984. V. 29. № 2. P. 98–109.
Саврасов Ю.С. Методы определения орбит космических объектов. М.: Машиностроение, 1981.
Cаврасов Ю.С. Алгоритмы и программы в радиолокации. М.: Радио и связь, 1985.
Аким Э.Л., Энеев Т.М. Определение параметров движения космического летательного аппарата по данным траекторных измерений // Космич. исслед. 1963. Т. 1. № 1. С. 5–50.
Молотов Е.П., Тучин А.Г. Навигация космических аппаратов при исследовании дальнего космоса. М.: Радиотехника, 2016.
Колесса А.Е., Пругло А.В., Равдин С.С. Восстановление орбит по угловым измерениям // Радиотехника. 2005. № 10. С. 5–9.
Булычев В.Ю., Булычев Ю.Г., Ивакина С.С. Пассивная локация на основе угловых и мощностных измерений системы пеленгаторов // Изв. РАН. ТиСУ. 2014. № 1. С. 65–73.
Булычев В. Ю., Булычев Ю.Г., Ивакина С.С. Угломерно-энергетический метод нестационарной пассивной локации на базе однопозиционной системы // Изв. РАН. ТиСУ. 2015. № 5. С. 122–136.
Chang C.B., Athans M., Whiting R. Onthe Stateand Parameter Estimation for Maneuvering Reentry Vehicles // IEEETrans. Automatic Control. 1977. V. 22. № 1. P. 99–105.
Колесса А.Е. Рекуррентные алгоритмы фильтрации для некоторых систем с нелинейностями кусочно-линейного типа // АиТ. 1986. № 4. С. 48–55.
Колесса А.Е. Некоторые прикладные вопросы кусочно-линейной фильтрации // АиТ. 1986. № 5. С. 61–69.
Колесса А.Е. Точные формулы оптимальной фильтрации для нестационарной кусочно-линейной задачи оценивания параметра // АиТ. 1989. № 12. С. 69–80.
Miller R.W. A Lower Boundon Angle – only Tracking Accuracy // M.I.T. Lincoln Laboratory. Project Report No. RMP–149. 1978.
Brehard T., le Cadre J.P. Closed-Form Posterior Cramer – Rao Bounds for Bearings – Only Tracking // IEEE Trans. Aerospace and Electronic Systems. 2006. V. 42. № 4.
Brehard T., le Cadre J.P. Closed – form Posterior Cramer – Rao Bound for a Maneuvering Target in the Bearings – Only Tracking Context Using Best – Fitting Gaussian Distribution // 9thIntern. Conf. on Information Fusion. Florence, Italy. 2006.
Farina A., Benvenuti D., Ristic B.Tracking a Ballistic Target: Comparison of Several Nonlinear Filters // IEEE Trans. Aerospace and Electronic Systems. 2002. V. 38. № 3. P. 854–867.
Farina A., Ristic B., Timmoneri L.Cramer – Rao Bound for Nonlinear Filtering with Pd < 1 and its Application to Target Tracking // IEEE Trans. Signal Processing. 2002. V. 50. № 8. P. 1916–1924.
Ristic B., Farina A., Benvenuti D., Arulampalam M.S. Performance Bounds and Comparison of Nonlinear Filters for Tracking a Ballistic Object on Re-entry // IEEE Proceedings – Radar, Sonar and Navigation. 2003. V. 150. № 2. P. 65–70.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления