Известия РАН. Теория и системы управления, 2021, № 3, стр. 57-70
РАСЧЕТ ОПТИМАЛЬНОЙ ЗАГРУЗКИ ВОЗДУШНЫХ ТРАНСПОРТНЫХ СРЕДСТВ С УЧЕТОМ ПРИОРИТИЗАЦИИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
И. П. Богданов a, В. А. Нестеров b, *, В. А. Судаков a, **, К. И. Сыпало c, ***, Н. Б. Топоров d, ****
a ИПМ им. М.В. Келдыша РАН
Москва, Россия
b МАИ (национальный исследовательский ун-т)
Москва, Россия
c Центральный аэрогидродинамический ин-т им. проф. Н.Е. Жуковского
Жуковский, Россия
d Национальный исследовательский центр “Институт им. Н.Е. Жуковского”
Москва, Россия
* E-mail: nesterov_46@inbox.ru
** E-mail: sudakov@ws-dss.com
*** E-mail: ksypalo@tsagi.ru
**** E-mail: toporov@nrczh.ru
Поступила в редакцию 01.02.2019
После доработки 07.10.2020
Принята к публикации 30.11.2020
Аннотация
Исследуется задача оптимального размещения неоднородного набора грузов на бортах заданного множества авиатранспортных средств. Рассматриваемая задача формализована как задача смешанного целочисленного линейного программирования, в которой оптимизируется количество предметов на бортах наиболее приоритетных авиатранспортных средств, а также суммарная масса загруженных объектов. При этом приоритеты летательных аппаратов рассчитываются с помощью комбинированных методов многокритериального анализа альтернатив. Предложена технология поиска ее точного решения, реализованная в форме открытого веб-сервиса.
Введение. Планирование доставки значительных объемов грузов с учетом совокупности ограничений представляет собой актуальную задачу, стоящую перед многими коммерческими и государственными корпорациями, предприятиями и организациями. Данная деятельность подразумевает регулярную необходимость выбора наилучшего способа размещения значительного количества различных предметов внутри трехмерных контейнеров (грузовых отсеков летательных аппаратов, контейнеров, трюмов кораблей, складов и др.). Рациональный способ размещения должен соответствовать варианту укладки, при котором [1]:
– используется минимальное число контейнеров;
– выбираются средства транспортировки, обладающие наилучшими значениями заданных критериев оценки (например, стоимостных и инерционных характеристик, доли привлекаемой отечественной техники и др.);
– загружается множество предметов с максимальной суммарной массой.
В случае нерационального расположения объектов увеличиваются финансовые затраты (на аренду помещений, фрахт судов, горюче-смазочные материалы и др.), продолжительность и сложность погрузочно-разгрузочных работ, а также вероятность повреждения предметов при транспортировке. В случае нарушения ограничений на центровку существенно возрастает риск катастроф.
Рассматриваемая задача относится к классу задач условной оптимизации, называемых в литературе задачами оптимальной упаковки, загрузки либо укладки контейнеров. В данном исследовании рассмотрена задача оптимального размещения грузов на бортах заданного упорядоченного множества летательных аппаратов (ЛА). ЛА упорядочены в соответствии с возрастанием приоритета их использования в логистике. Требуется максимизировать число предметов на бортах наиболее приоритетных ЛА, а также суммарную массу всех загруженных предметов. При этом грузы не должны выходить за пределы ЛА, а также пересекаться друг с другом. Не должны нарушаться требования по центровке ЛА.
В статье разработано аналитическое описание пространства решений рассмотренной задачи оптимизации загрузки воздушного транспорта (ОЗВТ). Данное аналитическое описание позволило формализовать введенные условия в виде линейных уравнений и неравенств, а саму задачу – в виде задачи смешанного целочисленного линейного программирования (СЦЛП). Реализовано программное обеспечение открытого веб-сервиса поиска точного решения задачи ОЗВТ, доступного в сети Интернет ученым, исследователям, разработчикам прикладных систем логистики.
Разработанная технология позволяет вычислять точное решение задачи ОЗВТ для случая небольшого числа контейнеров и грузов и, таким образом, может быть применена для проверки качества решения, получаемого с помощью эвристических методов. Для случая большей размерности точное решение оценивается методами, использующими построенное аналитическое описание задачи.
Внедрение указанных систем позволит повысить эффективность применения авиационной техники и инфраструктуры за счет рационального выбора ЛА (с помощью средств многокритериального анализа) и оптимизации размещения грузов на борту выбранных ЛА. Кроме того, уменьшение числа полетов окажет положительное влияние на окружающую среду вследствие сокращения эмиссии вредных веществ и снижения уровня шума. В перспективе полученные результаты могут стать основой для разработки отдельных функциональных модулей систем поддержки принятия решений в сфере организации авиационных грузовых перевозок.
1. Обзор основных направлений исследований. В литературе рассматривается существенное количество типов задач упаковки (загрузки, укладки) контейнеров, различающихся [2]:
– оптимизируемыми целевыми функциями;
– количеством контейнеров: укладка может осуществляться в единственный контейнер либо в совокупность нескольких контейнеров;
– характеристиками совокупности контейнеров: множество контейнеров может либо состоять из контейнеров одинаковых формы и размеров, либо быть слабо неоднородным (т.е. состоять из контейнеров, относящихся к одному из немногочисленных типов, при том что количество контейнеров каждого типа достаточно велико), либо быть сильно неоднородным (в случае, если среди контейнеров мало или нет одинаковых);
– характеристиками совокупности грузов: множество грузов может либо состоять из предметов одинаковых форм и размеров, либо быть слабо неоднородным, либо быть сильно неоднородным;
– формой контейнеров и/или грузов: как правило, считается, что контейнеры и грузы имеют форму прямоугольных параллелепипедов (кубоидов), примеры исключений можно найти в работе [3], посвященной упаковке предметов мебели, и в статье [4], где предполагается, что контейнеры могут иметь форму усеченных кубоидов;
– набором учитываемых практических ограничений [1] и т.д.
Классификация различных постановок задач упаковки контейнеров, а также обширный обзор методов их решения (163 научно-технических источника) приведены в [2].
Задачи оптимальной загрузки относятся к классу NP-трудных задач [5], и для нахождения их точного решения в общем случае требуется полный перебор возможных вариантов распределения предметов по контейнерам. В связи с этим в настоящее время активно развиваются эвристические подходы, позволяющие относительно быстро строить приближенные решения. Пример эвристического метода упаковки единственного контейнера, основанного на алгоритмах комбинирования предметов в блоки-кубоиды и сведения задачи трехмерной укладки к задаче двумерной укладки, приведен в [6]. В случае загрузки нескольких контейнеров широко применяют следующие стратегии размещения грузов [7]:
– упаковка контейнеров осуществляется последовательно (упаковка очередного контейнера начинается после заполнения предыдущего), например, см. [8], где данная стратегия используется совместно с механизмами динамической приоритизации грузов;
– происходит предварительное распределение наборов грузов по контейнерам (например, в [9] для этой цели применяется поиск с запретами), после чего применяются алгоритмы укладки предметов в каждый отдельный контейнер и алгоритмы перераспределения грузов между контейнерами;
– одновременно упаковываются несколькo контейнеров.
В [7, 10] задача упаковки нескольких контейнеров сформулирована как задача целочисленного линейного программирования, при этом для каждого рассматриваемого типа контейнера полагаются известными так называемые “паттерны” – способы размещения в них грузов имеющихся типов. Так как при значительном количестве типов контейнеров и грузов число всех возможных способов размещения будет очень велико, применяются эвристические алгоритмы построения некоторого достаточно представительного набора “паттернов” (таким образом, данный подход не гарантирует нахождения точного решения).
Наряду с эвристическими подходами разрабатываются методы, позволяющие строить точное решение для случая небольшого количества контейнеров и грузов. Как правило, предлагается аналитическая модель размещения предметов, позволяющая записать задачу загрузки в форме задачи СЦЛП, точное решение которой может быть найдено, например, методом ветвей и границ.
В [11–13] рассматривается модель размещения, в которой переменные, определяющие расположение объекта (данные переменные соответствуют координатам одного из углов либо центра масс объекта), являются непрерывными. Для формализации условий отсутствия пересечения грузов для каждой пары предметов вводятся переменные-индикаторы того, что один из грузов находится левее/правее, выше/ниже, сзади/спереди другого груза. В [4] используются аналогичные переменные-индикаторы отсутствия пересечений, но переменные, определяющие расположение объекта, полагаются целочисленными.
В [14] представлен подход, основанный на дискретизации пространства (т.е. введении конечной сетки) внутри контейнера. Размещение предметов, определяемое размещением их левых нижних передних углов, возможно только в узлах введенной сетки. В целях формализации условий отсутствия пересечения объектов для каждого типа груза и каждой упорядоченной пары точек конечной сетки априори вычисляется отображение-индикатор того, что область пространства, занимаемая размещенным в первой точке грузом указанного типа (за исключением его правой, верхней и задней граней), содержит вторую точку.
2. Постановка задачи. Рассмотрим следующий вариант задачи упаковки сильно неоднородной совокупности предметов в сильно неоднородное множество контейнеров. Имеется набор грузов, предназначенных для отправки с помощью самолетов либо вертолетов, а также совокупность контейнеров (соответствующих грузовым отсекам ЛА), в которых предполагается осуществлять доставку указанных грузов (в настоящем исследовании будем считать, что в каждом ЛА есть единственный грузовой отсек). Предполагается, что контейнеры и грузы имеют форму прямоугольных параллелепипедов (произвольных размеров), при этом загрузка отдельных предметов в ЛА происходит таким образом, чтобы боковые грани кубоидов-грузов были параллельны/перпендикулярны стенкам контейнеров. Для простоты будем считать, что грузы нельзя поворачивать. Предметы, помещенные в контейнеры, не должны выходить за границы контейнеров, а также не должны пересекаться друг с другом.
Для каждого груза задана его масса и габариты (длина, ширина и высота). Для каждого контейнера заданы его грузоподъемность, габариты, а также диапазон, в котором должен находиться центр масс совокупности всех грузов, размещенных в данном контейнере (для простоты в дальнейшем будем предполагать, что центры масс отдельных предметов совпадают с их геометрическими центрами). Кроме того, предполагается, что контейнерам присвоены приоритеты, рассчитанные с помощью комбинированного метода [15, 16].
Содержательно задача ОЗВТ состоит в том, чтобы, с одной стороны, разместить как можно больше предметов в более приоритетных контейнерах, а с другой – в том, чтобы упаковать в контейнеры грузы, характеризующиеся наибольшей суммарной массой.
Построим аналитическую модель размещения грузов в контейнерах, которая позволит формализовать рассматриваемую задачу как задачу СЦЛП. Так как для случая сильно неоднородных контейнеров и грузов дискретизация пространства (аналогично [14]) может привести к задаче неприемлемо большой размерности, то целесообразно строить формализацию, схожую с предложенными в [11–13].
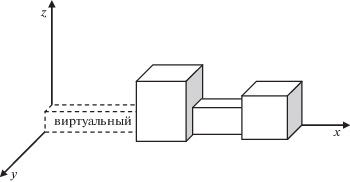
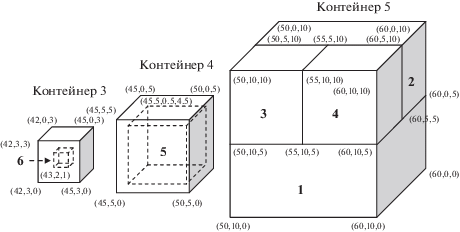
Введем прямоугольную систему координат в трехмерном пространстве. По оси x будем откладывать длину контейнеров и грузов, по оси y – ширину контейнеров и грузов, а по оси z – высоту контейнеров и грузов. Добавим в имеющееся множество контейнеров дополнительный воображаемый контейнер с наименьшим приоритетом. Длина указанного контейнера (в дальнейшем будем его называть виртуальным, а остальные контейнеры – реальными) равна сумме длин всех грузов, ширина – ширине самого широкого груза, а высота – высоте самого высокого груза. Грузоподъемность виртуального контейнера равна сумме масс всех грузов. Центр масс совокупности предметов, загруженных в данный контейнер, может находиться в любой его точке. В виртуальном контейнере окажутся все грузы, которые не получится разместить в реальных контейнерах. Расположим все контейнеры один за другим слева направо вдоль оси x в порядке увеличения приоритета таким образом, чтобы грани контейнеров были параллельны координатным плоскостям, а левый нижний задний угол каждого контейнера располагался бы на оси x. При данном размещении самое правое положение будет занимать самый приоритетный реальный контейнер, а самое левое – виртуальный контейнер, левый нижний задний угол которого будет находиться в начале координат. Графическая схема расположения контейнеров приведена на рис. 1.
Пронумеруем все контейнеры в соответствии с возрастанием приоритета (номер 1 получит виртуальный контейнер). Введем следующие обозначения: $g$ – количество контейнеров, n – количество грузов, ${{m}_{i}}$, $i = \overline {1,n} $, – масса i-го груза, Mj, $j = \overline {1,g} $, – грузоподъемность j-го контейнера, li, ${{w}_{i}},{{h}_{i}}$, $i = \overline {1,n} $, – длина, ширина и высота i-го груза, ${{L}_{j}},{{W}_{j}},{{H}_{j}}$, $j = \overline {1,g} $, – длина, ширина и высота j-го контейнера, тогда для виртуального контейнера:
Формализуем ограничения задачи в форме линейных уравнений и неравенств. Каждый из грузов размещен в одном и только одном контейнере:
Грузы не должны пересекаться, т.е. занимать один и тот же объем. Сначала запишем условие пересечения для любых двух различных номеров грузов ${{i}_{1}} = \overline {1,n - 1} $ и ${{i}_{2}}\left( {{{i}_{1}}} \right) = \overline {{{i}_{1}} + 1,n} $ (для простоты в дальнейшем вместо ${{i}_{2}}({{i}_{1}})$ будем писать i2). Грузы пересекаются, если у них пересекаются проекции по всем осям (см. рис. 2):
(2.2)
$\begin{gathered} ({{x}_{{{{i}_{2}}}}} < {{x}_{{{{i}_{1}}}}} + {{l}_{{{{i}_{1}}}}})\& ({{x}_{{{{i}_{1}}}}} < {{x}_{{{{i}_{2}}}}} + {{l}_{{{{i}_{2}}}}})\& ({{y}_{{{{i}_{2}}}}} < {{y}_{{{{i}_{1}}}}} + {{w}_{{{{i}_{1}}}}})\& ({{y}_{{{{i}_{1}}}}} < {{y}_{{{{i}_{2}}}}} + {{w}_{{{{i}_{2}}}}})\& \\ \,\& ({{z}_{{{{i}_{2}}}}} < {{z}_{{{{i}_{1}}}}} + {{h}_{{{{i}_{1}}}}})\& ({{z}_{{{{i}_{1}}}}} < {{z}_{{{{i}_{2}}}}} + {{h}_{{{{i}_{2}}}}}). \\ \end{gathered} $Отрицание предиката (2.2) дает условие отсутствия пересечений:
(2.3)
$\begin{gathered} ({{x}_{{{{i}_{2}}}}} \geqslant {{x}_{{{{i}_{1}}}}} + {{l}_{{{{i}_{1}}}}}) \vee ({{x}_{{{{i}_{1}}}}} \geqslant {{x}_{{{{i}_{2}}}}} + {{l}_{{{{i}_{2}}}}}) \vee ({{y}_{{{{i}_{2}}}}} \geqslant {{y}_{{{{i}_{1}}}}} + {{w}_{{{{i}_{1}}}}}) \vee ({{y}_{{{{i}_{1}}}}} \geqslant {{y}_{{{{i}_{2}}}}} + {{w}_{{{{i}_{2}}}}}) \vee \\ \, \vee ({{z}_{{{{i}_{2}}}}} \geqslant {{z}_{{{{i}_{1}}}}} + {{h}_{{{{i}_{1}}}}}) \vee ({{z}_{{{{i}_{1}}}}} \geqslant {{z}_{{{{i}_{2}}}}} + {{h}_{{{{i}_{2}}}}}). \\ \end{gathered} $Условия “ИЛИ” можно заменить условиями “И” путем ввода дополнительных булевых переменных ${{a}_{{{{i}_{1}},{{i}_{2}}}}},{{b}_{{{{i}_{1}},{{i}_{2}}}}},{{c}_{{{{i}_{1}},{{i}_{2}}}}}$:
(2.4)
${{x}_{{{{i}_{1}}}}} - {{x}_{{{{i}_{2}}}}} - M{{a}_{{{{i}_{1}},{{i}_{2}}}}} - M{{b}_{{{{i}_{1}},{{i}_{2}}}}} - M{{c}_{{{{i}_{1}},{{i}_{2}}}}} \leqslant - {{l}_{{{{i}_{1}}}}},$Если ${{a}_{{{{i}_{1}},{{i}_{2}}}}} = 0$, ${{b}_{{{{i}_{1}},{{i}_{2}}}}} = 0$, ${{c}_{{{{i}_{1}},{{i}_{2}}}}} = 0$, то ограничение (2.4) является существенным, иначе – ограничение (2.4) всегда выполняется.
Остальные ограничения формируются аналогично. Каждое из указанных ограничений становится существенным при соответствующей комбинации ${{a}_{{{{i}_{1}},{{i}_{2}}}}},{{b}_{{{{i}_{1}},{{i}_{2}}}}},{{c}_{{{{i}_{1}},{{i}_{2}}}}}$, указанной в скобках:
(2.5)
$\left\{ \begin{gathered} {{x}_{{{{i}_{2}}}}} - {{x}_{{{{i}_{1}}}}} - M\left( {1 - {{a}_{{{{i}_{1}},{{i}_{2}}}}}} \right) - M{{b}_{{{{i}_{1}},{{i}_{2}}}}} - M{{c}_{{{{i}_{1}},{{i}_{2}}}}} \leqslant - {{l}_{{{{i}_{2}}}}},\quad \left( {{{a}_{{{{i}_{1}},{{i}_{2}}}}} = 1,{{b}_{{{{i}_{1}},{{i}_{2}}}}} = 0,{{c}_{{{{i}_{1}},{{i}_{2}}}}} = 0} \right), \hfill \\ {{y}_{{{{i}_{1}}}}} - {{y}_{{{{i}_{2}}}}} - M{{a}_{{{{i}_{1}},{{i}_{2}}}}} - M\left( {1 - {{b}_{{{{i}_{1}},{{i}_{2}}}}}} \right) - M{{c}_{{{{i}_{1}},{{i}_{2}}}}} \leqslant - {{w}_{{{{i}_{1}}}}},\quad \left( {{{a}_{{{{i}_{1}},{{i}_{2}}}}} = 0,{{b}_{{{{i}_{1}},{{i}_{2}}}}} = 1,{{c}_{{{{i}_{1}},{{i}_{2}}}}} = 0} \right), \hfill \\ {{y}_{{{{i}_{2}}}}} - {{y}_{{{{i}_{1}}}}} - M\left( {1 - {{a}_{{{{i}_{1}},{{i}_{2}}}}}} \right) - M\left( {1 - {{b}_{{{{i}_{1}},{{i}_{2}}}}}} \right) - M{{c}_{{{{i}_{1}},{{i}_{2}}}}} \leqslant - {{w}_{{{{i}_{2}}}}},\quad \left( {{{a}_{{{{i}_{1}},{{i}_{2}}}}} = 1,{{b}_{{{{i}_{1}},{{i}_{2}}}}} = 1,{{c}_{{{{i}_{1}},{{i}_{2}}}}} = 0} \right), \hfill \\ {{z}_{{{{i}_{1}}}}} - {{z}_{{{{i}_{2}}}}} - M{{a}_{{{{i}_{1}},{{i}_{2}}}}} - M{{b}_{{{{i}_{1}},{{i}_{2}}}}} - M\left( {1 - {{c}_{{{{i}_{1}},{{i}_{2}}}}}} \right) \leqslant - {{h}_{{{{i}_{1}}}}},\quad \left( {{{a}_{{{{i}_{1}},{{i}_{2}}}}} = 0,{{b}_{{{{i}_{1}},{{i}_{2}}}}} = 0,{{c}_{{{{i}_{1}},{{i}_{2}}}}} = 1} \right), \hfill \\ {{z}_{{{{i}_{2}}}}} - {{z}_{{{{i}_{1}}}}} - M\left( {1 - {{a}_{{{{i}_{1}},{{i}_{2}}}}}} \right) - M{{b}_{{{{i}_{1}},{{i}_{2}}}}} - M\left( {1 - {{c}_{{{{i}_{1}},{{i}_{2}}}}}} \right) \leqslant - {{h}_{{{{i}_{2}}}}},\quad \left( {{{a}_{{{{i}_{1}},{{i}_{2}}}}} = 1,{{b}_{{{{i}_{1}},{{i}_{2}}}}} = 0,{{c}_{{{{i}_{1}},{{i}_{2}}}}} = 1} \right). \hfill \\ \end{gathered} \right.$Для того, чтобы исключить недопустимые комбинации ${{a}_{{{{i}_{1}},{{i}_{2}}}}},{{b}_{{{{i}_{1}},{{i}_{2}}}}},{{c}_{{{{i}_{1}},{{i}_{2}}}}}$, введем ограничение:
(2.6)
${{a}_{{{{i}_{1}},{{i}_{2}}}}} + 2{{b}_{{{{i}_{1}},{{i}_{2}}}}} + 4{{c}_{{{{i}_{1}},{{i}_{2}}}}} \leqslant 5.$Следующий блок ограничений соответствует условиям строгого попадания груза в назначенный контейнер. В нелинейном виде данные ограничения имеют следующую форму. Для любых $i = \overline {1,n} $, $j = \overline {1,g} $: если ${{r}_{{ij}}} = 1$, то
(2.7)
$\begin{gathered} \left\{ \begin{gathered} {{x}_{i}} \geqslant L_{j}^{*},\quad {{x}_{i}} + {{l}_{i}} \leqslant L_{j}^{*} + {{L}_{j}}, \hfill \\ {{y}_{i}} \geqslant 0,\quad {{y}_{i}} + {{w}_{i}} \leqslant {{W}_{j}}, \hfill \\ {{z}_{i}} \geqslant 0,\quad {{z}_{i}} + {{h}_{i}} \leqslant {{H}_{j}}, \hfill \\ \end{gathered} \right. \\ L_{1}^{*} = 0,\quad L_{j}^{*} = \sum\limits_{u = 1}^{j - 1} {{{L}_{u}},} \quad j = \overline {2,g} . \\ \end{gathered} $Условие “если ${{r}_{{ij}}} = 1$” вносится в ограничения (2.7) следующим образом:
(2.8)
$\left\{ \begin{gathered} {{x}_{i}} + M\left( {1 - {{r}_{{ij}}}} \right) \geqslant L_{j}^{*},\quad {{x}_{i}} + {{l}_{i}} - M\left( {1 - {{r}_{{ij}}}} \right) \leqslant L_{j}^{*} + {{L}_{j}}, \hfill \\ {{y}_{i}} \geqslant 0,\quad {{y}_{i}} + {{w}_{i}} - M\left( {1 - {{r}_{{ij}}}} \right) \leqslant {{W}_{j}}, \hfill \\ {{z}_{i}} \geqslant 0,\quad {{z}_{i}} + {{h}_{i}} - M\left( {1 - {{r}_{{ij}}}} \right) \leqslant {{H}_{j}}. \hfill \\ \end{gathered} \right.$Неравенство (2.9) задает ограничения на грузоподъемность каждого контейнера:
(2.9)
$\forall j = \overline {1,g} {\kern 1pt} :\quad \sum\limits_{i = 1}^n {{{m}_{i}}{{r}_{{ij}}}} \leqslant {{M}_{j}}.$Ограничения на допустимое положение центра масс для любого контейнера $j = \overline {1,g} $ имеют вид, задаваемый неравенствами:
(2.10)
$\left\{ \begin{gathered} X_{j}^{{\min }} + L_{j}^{*} \leqslant \frac{{\sum\limits_{i = 1}^n {{{m}_{i}}{{r}_{{ij}}}\left( {{{x}_{i}} + {{{{l}_{i}}} \mathord{\left/ {\vphantom {{{{l}_{i}}} 2}} \right. \kern-0em} 2}} \right)} }}{{\sum\limits_{v = 1}^n {{{m}_{v}}{{r}_{{vj}}}} }} \leqslant X_{j}^{{\max }} + L_{j}^{*}, \hfill \\ Y_{j}^{{\min }} \leqslant \frac{{\sum\limits_{i = 1}^n {{{m}_{i}}{{r}_{{ij}}}\left( {{{y}_{i}} + {{{{w}_{i}}} \mathord{\left/ {\vphantom {{{{w}_{i}}} 2}} \right. \kern-0em} 2}} \right)} }}{{\sum\limits_{v = 1}^n {{{m}_{v}}{{r}_{{vj}}}} }} \leqslant Y_{j}^{{\max }}, \hfill \\ Z_{j}^{{\min }} \leqslant \frac{{\sum\limits_{i = 1}^n {{{m}_{i}}{{r}_{{ij}}}\left( {{{z}_{i}} + {{{{h}_{i}}} \mathord{\left/ {\vphantom {{{{h}_{i}}} 2}} \right. \kern-0em} 2}} \right)} }}{{\sum\limits_{v = 1}^n {{{m}_{v}}{{r}_{{vj}}}} }} \leqslant Z_{j}^{{\max }}. \hfill \\ \end{gathered} \right.$В ограничения (2.10) входят произведения булевых и непрерывных переменных, которые требуется привести к линейному виду. Для этого введем дополнительные переменные: ${{r}_{{ij}}}{{x}_{i}}$ заменяются на $p_{{ij}}^{1} = {{r}_{{ij}}}{{x}_{i}}$ путем ввода ограничений:
(2.11)
$p_{{ij}}^{1} \leqslant M{{r}_{{ij}}},\quad p_{{ij}}^{1} \leqslant {{x}_{i}},\quad p_{{ij}}^{1} \geqslant {{x}_{i}} - M\left( {1 - {{r}_{{ij}}}} \right),\quad p_{{ij}}^{1} \geqslant 0.$Аналогично осуществляются замены $p_{{ij}}^{2} = {{r}_{{ij}}}{{y}_{i}}$ и $p_{{ij}}^{3} = {{r}_{{ij}}}{{z}_{i}}$:
(2.12)
$\left\{ \begin{gathered} p_{{ij}}^{2} \leqslant M{{r}_{{ij}}},\quad p_{{ij}}^{2} \leqslant {{y}_{i}},\quad p_{{ij}}^{2} \geqslant {{y}_{i}} - M\left( {1 - {{r}_{{ij}}}} \right),\quad p_{{ij}}^{2} \geqslant 0, \hfill \\ p_{{ij}}^{3} \leqslant M{{r}_{{ij}}},\quad p_{{ij}}^{3} \leqslant {{z}_{i}},\quad p_{{ij}}^{3} \geqslant {{z}_{i}} - M\left( {1 - {{r}_{{ij}}}} \right),\quad p_{{ij}}^{3} \geqslant 0. \hfill \\ \end{gathered} \right.$Воспользовавшись (2.11) и (2.12), можно переписать (2.10) в следующей форме:
(2.13)
$\left\{ \begin{gathered} (X_{j}^{{\min }} + L_{j}^{*})\sum\limits_{v = 1}^n {{{m}_{v}}{{r}_{{vj}}}} \leqslant \sum\limits_{i = 1}^n {{{m}_{i}}(p_{{ij}}^{1} + {{{{r}_{{ij}}}{{l}_{i}}} \mathord{\left/ {\vphantom {{{{r}_{{ij}}}{{l}_{i}}} 2}} \right. \kern-0em} 2})} \leqslant (X_{j}^{{\max }} + L_{j}^{*})\sum\limits_{v = 1}^n {{{m}_{v}}{{r}_{{vj}}}} , \hfill \\ Y_{j}^{{\min }}\sum\limits_{v = 1}^n {{{m}_{v}}{{r}_{{vj}}}} \leqslant \sum\limits_{i = 1}^n {{{m}_{i}}(p_{{ij}}^{2} + {{{{r}_{{ij}}}{{w}_{i}}} \mathord{\left/ {\vphantom {{{{r}_{{ij}}}{{w}_{i}}} 2}} \right. \kern-0em} 2})} \leqslant Y_{j}^{{\max }}\sum\limits_{v = 1}^n {{{m}_{v}}{{r}_{{vj}}}} , \hfill \\ Z_{j}^{{\min }}\sum\limits_{v = 1}^n {{{m}_{v}}{{r}_{{vj}}}} \leqslant \sum\limits_{i = 1}^n {{{m}_{i}}(p_{{ij}}^{3} + {{{{r}_{{ij}}}{{h}_{i}}} \mathord{\left/ {\vphantom {{{{r}_{{ij}}}{{h}_{i}}} 2}} \right. \kern-0em} 2})} \leqslant Z_{j}^{{\max }}\sum\limits_{v = 1}^n {{{m}_{v}}{{r}_{{vj}}}} . \hfill \\ \end{gathered} \right.$Ограничения на суммарный объем грузов для каждого контейнера имеют вид
(2.14)
$\forall j = \overline {1,g} {\kern 1pt} :\quad \sum\limits_{i = 1}^n {{{l}_{i}}{{w}_{i}}{{h}_{i}}{{r}_{{ij}}}} \leqslant {{L}_{j}}{{W}_{j}}{{H}_{j}}.$Качество варианта загрузки определяется координатами расположения грузов по оси x (чем правее расположен груз, тем лучше), а также суммарной массой грузов, размещенных в реальных контейнерах. Тогда целевую функцию задачи ОЗВТ можно записать в виде суммы величин xi и ${{m}_{i}}{{r}_{{ij}}}$, взятых с весовыми коэффициентами α и β:
(2.15)
$\alpha \sum\limits_{i = 1}^n {{{x}_{i}}} + \beta \sum\limits_{i = 1}^n {\sum\limits_{j = 2}^g {{{m}_{i}}{{r}_{{ij}}}} } $.Таким образом, задача ОЗВТ представляет собой задачу поиска максимума функции (2.15) по непрерывным переменным ${{x}_{i}},{{y}_{i}},{{z}_{i}},p_{{ij}}^{d}$, $i = \overline {1,n} $, $j = \overline {1,g} $, $d = \overline {1,3} $, и бинарным переменным rij, ${{a}_{{{{i}_{1}},{{i}_{2}}}}},{{b}_{{{{i}_{1}},{{i}_{2}}}}},{{c}_{{{{i}_{1}},{{i}_{2}}}}}$, $i = \overline {1,n} $, $j = \overline {1,g} $, ${{i}_{1}} = \overline {1,n - 1} $, ${{i}_{2}} = \overline {{{i}_{1}} + 1,n} $, при ограничениях (2.1), (2.4)–(2.6), (2.8), (2.9), (2.11)–(2.14). Заметим, что допустимое множество указанной задачи не является пустым, так как допустимому решению соответствует, в частности, размещение всех грузов друг за другом в виртуальном контейнере.
В настоящем исследовании для простоты предполагается, что грузы нельзя поворачивать. Тем не менее возможность поворотов может быть учтена, и при этом множество ограничений задачи останется линейным.
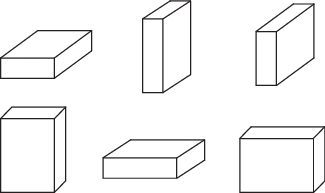
Один из возможных способов заключается в следующем. Существует шесть различных вариантов пространственной ориентации размещаемого груза, имеющего форму прямоугольного параллелепипеда (при котором его грани параллельны стенкам контейнера) (рис. 3). Можно рассматривать все эти шесть вариантов ориентации одного груза как альтернативные грузы. Таким образом исходный вариант для каждого груза i нужно дополнить еще пятью. Если какие-то варианты поворотов грузов запрещены, то вариантов будет не шесть, а меньше. Для корректного решения оптимизационной задачи следует заменить ограничение (2.1) по таким грузам на новое ограничение, которое говорит, что из всех вариантов размещения следует выбрать только один. Если I – это множество номеров допустимых вариантов, то новое ограничение примет вид
3. Технологии точного решения задач СЦЛП. Предлагаемый подход. Построенная формализация задачи ОЗВТ относится к классу задач СЦЛП, для которых существуют точные алгоритмы, гарантирующие нахождение глобального решения (хотя поиск оптимума может требовать значительного времени и ресурсов). На практике наиболее широко используются алгоритмы метод ветвлений и отсечений, основанные на комбинированном применении метода ветвей и границ [17] и метода отсекающих плоскостей [18].
Используемый метод реализован в представленных в настоящий момент на рынке коммерческих системах (например, IBM ILOG CPLEX [19], Gurobi [20], FICO Xpress [21] и др.), а также в ряде некоммерческих комплексов (например, SCIP [22], MINTO [23], GLPK [24], COIN-OR branch and cut [25] и другие публикации, например [26]). Однако использование данных пакетов возможно только, когда целевая функция и ограничения записаны в стандартизированной форме, без этого решение поставленной задачи невозможно.
В рамках настоящего исследования была сформирована технология решения задачи ОЗВТ, основанная на использовании системы WS-DSS, созданной одним из авторов данной статьи [27], и комплекса SCIP, разработка ученых из Германии [22].
Портал веб-сервисов поддержки принятия решений WS-DSS, находящийся в открытом доступе, позволяет публиковать в сети Интернет произвольные консольные программные реализации математических моделей на Ruby, а также обеспечивает возможность подключения других веб-сервисов и организации “цепочки” вызовов математических моделей с передачей входных/выходных параметров между ними. Обработка моделей, реализованная диспетчером очередей Sidekiq, масштабируется потоками обработчиками (workers) на произвольном количестве узлов вычислительного кластера.
В качестве оптимизатора использовался SCIP, являющийся в настоящее время одним из наиболее быстрых некоммерческих решателей для СЦЛП и смешанного целочисленного нелинейного программирования. Для нахождения оптимума данный комплекс применяет алгоритм ветвей и отсечений, метод генерации столбцов, а также ряд эвристических способов поиска допустимых решений, позволяющих сократить пространство перебора [28].
На рис. 4 и 5 приведены примеры представления исходных данных задачи (параметров типов контейнеров и типов грузов соответственно) в системе WS-DSS.
На рис. 6 рассмотрен фрагмент представления выходных данных, сформированных в результате работы программы.
В целях верификации разработанного программного обеспечения были проведены тестовые испытания расчетной системы на примерах, содержащих до 10 грузов и до 5 контейнеров (включая виртуальный). Сопоставление результатов численного моделирования с осуществленным вручную перебором продемонстрировало общую адекватность результатов работы предложенной технологии. Ниже представлены результаты численного моделирования для задачи размещения шести грузов в четырех реальных контейнерах. Предполагается, что контейнеры упорядочены и пронумерованы в соответствии с возрастанием приоритета (виртуальный контейнер получает номер 1, а наиболее приоритетный реальный контейнер – номер 5). Значения параметров реальных контейнеров – грузоподъемности (в килограммах) и габаритов (в метрах) – приведены в табл. 1. Параметры виртуального контейнера автоматически рассчитываются в соответствии с правилами, описанными в разд. 2. Значения параметров грузов – массы (в килограммах) и габаритов (в метрах) – представлены в табл. 2. Весовые коэффициенты целевой функции полагаются равными 0.5: $\alpha = \beta = 0.5$.
Таблица 1.
Параметры контейнеров
| Номер контейнера | Грузоподъемность, кг | Длина | Ширина | Высота |
|---|---|---|---|---|
| м | ||||
| 2 | 1200 | 7 | 7 | 7 |
| 3 | 1200 | 3 | 3 | 3 |
| 4 | 64.1 | 5 | 5 | 5 |
| 5 | 1200 | 10 | 10 | 10 |
Таблица 2.
Параметры грузов
| Номер груза | Масса, кг | Длина | Ширина | Высота |
|---|---|---|---|---|
| м | ||||
| 1 | 500 | 10 | 10 | 5 |
| 2 | 250 | 10 | 5 | 5 |
| 3 | 125 | 5 | 5 | 5 |
| 4 | 125 | 5 | 5 | 5 |
| 5 | 64 | 4 | 4 | 4 |
| 6 | 1 | 1 | 1 | 1 |
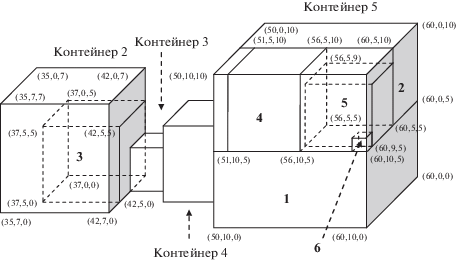
В начале предположим, что границы диапазонов допустимого положения центров масс загруженных предметов совпадают с границами контейнеров. По итогам расчета, проведенного с помощью разработанной технологии, грузы 1–6 были размещены в контейнерах 2 и 5. Распределение предметов по указанным контейнерам схематично показано на рис. 7 (крупные цифры соответствуют номерам грузов).
В соответствии с правилами построения целевой функции оптимизатор стремится разместить как можно больше грузов как можно ближе к правой стенке контейнера 5, а также упаковать все имеющиеся грузы в реальные контейнеры. Грузы 1 и 2 могут поместиться только в контейнер 5. Кроме данных грузов, в контейнер 5 можно упаковать либо грузы 3 и 4, либо грузы 5, 6, а также один из грузов 3 или 4. В результате расчета был выбран вариант с упаковкой трех грузов, обеспечивающий большее значение первого слагаемого целевой функции. Груз 3, не попавший в контейнер 5, не может разместиться в контейнере 4 из-за ограничений на грузоподъемность, не может разместиться в контейнере 3 из-за размеров и располагается в контейнере 2 вплотную к его правой стенке.
В целях верификации функционала, связанного с обеспечением центровки, пересчитаем рассмотренный пример при дополнительном требовании размещения центров масс совокупностей упакованных грузов в геометрических центрах реальных контейнеров. Добавление данного ограничения привело к тому, что контейнер 5 оказался полностью заполненным (в нем разместились грузы 1–4), в центрах контейнеров 4 и 3 разместилось по одному грузу (грузы 5 и 6 соответственно), а контейнер 2 остался незадействованным. Распределение предметов по реальным контейнерам схематично показано на рис. 8. В точности выдерживания ограничений на положения центров масс грузов можно убедиться непосредственной проверкой. В частности, координаты центра масс совокупности предметов, размещенных в контейнере 5, совпадают с координатами геометрического центра данного контейнера:
Численное моделирование проводилось на сервере AWS t2.small (1 vCPU, 2 Gb RAM, 20 Gb SSD). Результаты экспериментов продемонстрировали, что время поиска решения существенно зависит не только от количества контейнеров и грузов, но и от соотношения их габаритов. В качестве иллюстрации в табл. 3 приведено время расчета оптимального распределения 10 одинаковых грузов размером 1 × 1 × 1 (здесь и далее размеры указаны в метрах) по четырем реальным контейнерам при различных значениях длины наиболее вместительного реального контейнера. Разработанный метод позволяет рассчитать решение за приемлемое с точки зрения практики время не более чем для 10–15 грузов (например, время решения задачи размещения 15 одинаковых грузов размером 1 × 1 × 1 в одном реальном контейнере размером 14.2 × 1.2 × 1.2 составило около 11 ч). Вычислить оптимальное распределение большего количества грузов за разумное время удалось только в специальных случаях – в частности, для решения задачи размещения 30 грузов размером 1 × 1 × 1 в 29 реальных контейнерах размером 1.2 × 1.2 × 1.2 потребовалось около 20 мин, а для решения задачи размещения 100 грузов размером 1 × 1 × 1 в 1 реальном контейнере размера 10 × 10 × 10 – около 5 мин. Возможные подходы к построению оценок точного решения исследуемой задачи в случае высокой размерности рассматриваются в разд. 4.
Таблица 3.
Время расчета для тестовых примеров
| Габариты грузов | Габариты реальных контейнеров | Время расчета |
|---|---|---|
| 1 × 1 × 1 (10 шт.) | $10.2 \times 1.2 \times 1.2$, $2.2 \times 1.2 \times 1.2$, $2.2 \times 1.2 \times 1.2$, $1.2 \times 1.2 \times 1.2$ | <0.5 с |
| 1 × 1 × 1 (10 шт.) | $9.2 \times 1.2 \times 1.2$, $2.2 \times 1.2 \times 1.2$, $2.2 \times 1.2 \times 1.2$, $1.2 \times 1.2 \times 1.2$ | ≈1 ч |
| 1 × 1 × 1 (10 шт.) | $4.2 \times 1.2 \times 1.2$, $2.2 \times 1.2 \times 1.2$, $2.2 \times 1.2 \times 1.2$, $1.2 \times 1.2 \times 1.2$ | ≈2.5 ч |
4. Обсуждение предложенного подхода. Практическая значимость. К явным достоинствам разработанной математической модели решаемой задачи ОЗВТ стоит отнести возможность применения стандартных методов решения задач СЦЛП для поиска ее экстремума. Построенная модель схожа с предложенными в [11–13], но вследствие использования единого координатного пространства для всех контейнеров требует вдвое меньше бинарных переменных для формализации линейных условий отсутствия пересечения грузов. Если в указанных работах число переменных-индикаторов того, что один из грузов находится левее/правее, выше/ниже, сзади/спереди другого груза, равно 6n(n – 1)/2 = $3n\left( {n - 1} \right)$, то в предложенной модели общее количество переменных ${{a}_{{{{i}_{1}},{{i}_{2}}}}},{\text{ }}{{b}_{{{{i}_{1}},{{i}_{2}}}}},{\text{ }}{{c}_{{{{i}_{1}},{{i}_{2}}}}}$, ${{i}_{1}} = \overline {1,n - 1} $, ${{i}_{2}} = \overline {{{i}_{1}} + 1,n} $, равно ${{3n\left( {n - 1} \right)} \mathord{\left/ {\vphantom {{3n\left( {n - 1} \right)} 2}} \right. \kern-0em} 2}$. Также единое координатное пространство позволяет избежать необходимости формировать блоки ограничений, записываемых для каждой пары грузов и каждого контейнера (например, см. состоящий из ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O} }}({{n}^{2}}g)$ неравенств блок (7) в [11]). Кроме того, замена произведений пар непрерывной/бинарной и бинарной переменных на одну непрерывную переменную (по аналогии с [4]) позволяет записать в линейной форме условия на положения центров масс для всех контейнеров.
К явным недостаткам разработанной технологии, учитывая NP-трудность задачи ОЗВТ, необходимо отнести значительное время и мощные вычислительные ресурсы, которые могут потребоваться для решения (при достаточно большом количестве контейнеров и грузов время, необходимое для поиска оптимума, будет неприемлемым с практической точки зрения). Тем не менее стоит заметить, что предложенную технологию целесообразно применять для верификации и калибровки разрабатываемых приближенных эвристических подходов к решению задачи ОЗВТ на тестовых примерах. Кроме того, на основе предложенной аналитической модели могут быть разработаны методы аппроксимации точного решения задачи ОЗВТ. Например, нижние оценки рассчитываются с помощью эвристических алгоритмов поиска допустимых точек построенной задачи СЦЛП [28], а верхние, в частности, – путем решения линейных релаксационных задач, полученных удалением ряда ограничений из задачи ОЗВТ. Альтернативным способом аппроксимации решения для случая задач высокой размерности представляется применение подходов, основанных на последовательном многократном применении разработанного метода для заполнения контейнеров по частям. В этом случае последовательно многократно решаются оптимизационные задачи СЦЛП, каждая из которых задана формулами (2.1), (2.4)–(2.6), (2.8), (2.9), (2.11)–(2.15) для отдельных подмножеств грузов. К ограничениям на оптимизируемые грузы добавляются ограничения на грузы, которые уже размещены на предыдущем шаге декомпозиции.
В построенной формализации нет ограничений, связанных с тем, что незакрепленные дополнительными техническими средствами грузы должны надежно опираться на другой груз либо на пол контейнера. В результате расчета может оказаться, что предметы частично или полностью висят в воздухе. В частных случаях данная проблема может быть решена с помощью постобработки результатов моделирования (по итогам которой координаты грузов будут скорректированы в ручном режиме, если это позволят ограничения на положение центров масс). Перспективным альтернативным подходом представляется добавление в целевую функцию слагаемого, представляющего собой взвешенную сумму координат грузов по оси z, взятую со знаком “минус”.
С точки зрения демонстрации и популяризации результатов проведенных работ предложенную технологию выгодно отличает реализация в форме открытого сервиса, доступного в сети Интернет. Кроме того, научной новизной настоящего исследования является возможность использования оригинальных комбинированных методов многокритериального анализа альтернатив для выбора предпочтительных ЛА.
Направления дальнейших исследований включают в себя модификацию формализации задачи с целью учета пределов допустимого давления на грузы, необходимость обеспечения устойчивости предметов, требований группировки заданных наборов грузов, более сложных форм контейнеров, а также других ограничений, возникающих на практике. Кроме того, возрастающая сложность рассматриваемых задач (вследствие добавления новых ограничений и увеличения количества контейнеров и грузов) потребует разработки дополнительных эвристических подходов, которые бы позволили строить на основе сформированной модели достаточно эффективные варианты загрузки (не обязательно являющиеся глобально оптимальными).
В перспективе разработанная технология может стать основой для составной части комплекса, функционал которого будет нацелен на решение более сложных задач, например, подразумевающих формирование расписаний авиаперевозок при ограничениях на количество, характеристики и доступность ЛА, ограничений на летные условия и на сроки доставки и т.д. [29, 30].
Заключение. Формализована задача оптимизации загрузки ЛА с учетом центровки при ряде допущений относительно параметров грузов и принципов их размещения в отсеках. Данная задача относится к классу задач СЦЛП. Для ее решения адаптирован точный алгоритм решения по методу ветвей и отсечений.
Предложенная технология апробирована на множестве примеров. Разработано программное обеспечение открытого веб-сервиса, реализующего возможности рационального размещения грузов на борту ЛА с учетом центровки. Направления дальнейшего развития разработанного программного комплекса, нацелены на расширение множества задач, которые можно будет решать с его помощью.
Созданная технология допускает интеграцию с комбинированными методами многокритериального анализа альтернатив с целью определения приоритетов загружаемых ЛА. Практическое применение представленной технологии в перспективе позволит снизить общие финансовые затраты на воздушную транспортировку грузов, сократит время погрузочно-разгрузочных работ, а также поспособствует повышению безопасности грузоперевозок.
Список литературы
Bischoff E.E., Ratcliff M.S.W. Issues in the Development of Approaches to Container Loading // Omega, The Intern. J. Management Science. 1995. V. 23. № 4. P. 377–390.
Bortfeldt A., Wäscher G. Constraints in Container Loading – A State-of-the-art Review // Europ. J. Operational Research. 2013. V. 229. Iss. 1. P. 1–20.
Egeblad J., Garavelli C., Lisi S., Pisinger D. Heuristics for Container Loading of Furniture // Europ. J. Operational Research. 2010. V. 200. Iss. 3. P. 881–892.
Paquay C., Schyns M., Limbourg S. A Mixed Integer Programming Formulation for the Three-Dimensional Bin Packing Problem Deriving from an air Cargo Application // Intern. Transactions in Operational Research. 2016. V. 23. Iss. 1–2. P. 187–213.
Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982. 416 с.
Псиола В.В. О приближенном решении 3-мерной задачи об упаковке на основе эвристик // Интеллектуальные системы. 2007. Т. 11. Вып. 1–4. С. 83–100. URL: http://intsys.msu.ru/magazine/archive/v11(1-4)/psiola-083-100.pdf (дата обращения: 14.01.2019).
Eley M. A Bottleneck Assignment Approach to the Multiple Container Loading Problem // OR Spectrum. 2003. V. 25. Iss. 1. P. 45–60.
Lim A., Ma H., Xu J., Zhang X. An Iterated Construction Approach with Dynamic Prioritization for Solving the Container Loading Problems // Expert Systems with Applications. 2012. V. 39. Iss. 4. P. 4292–4305.
Jin Z., Ito T., Ohno K. The Three-Dimensional Bin Packing Problem and Its Practical Algorithm // JSME Intern. J.J. Series C. 2003. V. 46. Iss. 1. P. 60–66.
Che C.H., Huang W., Lim A., Zhu W. The Multiple Container Loading Cost Minimization Problem // Europ. J. Operational Research. 2011. V. 214. Iss. 3. P. 501–511.
Chen C.S., Lee S.M., Shen Q.S. An Analytical Model for the Container Loading Problem // Europ. J. Operational Research. 1995. V. 80. Iss. 1. P. 68–76.
Padberg M. Packing Small Boxes Into a Big Box // Mathematical Methods of Operations Research. 2000. V. 52. Iss. 1. P. 1–21.
Hong Ha H.T., Nananukul N. Air Cargo Loading Management System for Logistics Forwarders // Proceedings of 2016 Intern. Conf. on Urban Planning, Transport and Construction Engineering (ICUPTCE’16). Pattaya, 2016. P. 51–58.
Junqueira L., Morabito R., Yamashita D.S. Three-Dimensional Container Loading Models with Cargo Stability and Load Bearing Constraints // Computers & Operations Research. 2012. V. 39. Iss. 1. P. 74–85.
Осипов В.П., Судаков В.А. Комбинированный метод поддержки принятия многокритериальных решений // Препринты ИПМ им. М.В. Келдыша. 2015. № 30. 21 с. URL: http://www.keldysh.ru/papers/2015/preprint.asp?id=2015-30 (дата обращения: 14.01.2019).
Dutov A.V., Nesterov V.A., Sudakov V.A., Sypalo K.I. Fuzzy Preference Domains and Their Use for Selecting an Electronic Flight Bag for Flight Crews // J. of Computer and Systems Sciences International. 2018. V. 57. № 2. P. 230–238.
Korte B., Vygen J. Combinatorial Optimization: Theory and Algorithms. Berlin Heidelberg: Springer-Verlag, 2006. 597 p.
Ху Т. Целочисленное программирование и потоки в сетях. М.: Мир, 1974. 519 с.
IBM ILOG CPLEX. URL: https://www.ibm.com/analytics/cplex-optimizer (дата обращения: 14.01.2019).
Gurobi. URL: http://www.gurobi.com/ (дата обращения: 14.01.2019).
FICO Xpress. URL: https://www.fico.com/en/products/fico-xpress-optimization (дата обращения: 14.01.2019).
SCIP. URL: https://scip.zib.de/ (дата обращения: 14.01.2019).
MINTO. URL: http://coral.ie.lehigh.edu/~minto/ (дата обращения: 14.01.2019).
GLPK. URL: https://www.gnu.org/software/glpk/ (дата обращения: 14.01.2019).
COIN-OR branch and cut. URL: https://projects.coin-or.org/Cbc (дата обращения: 14.01.2019).
Linderoth J.T., Ralphs T.K. Noncommercial Software for Mixed-Integer Linear Programming // Integer Programming: Theory and Practice. CRC Press Operations Research Series, 2005. P. 253–303.
Портал веб-сервисов поддержки принятия решений WS-DSS. URL: http://ws-dss.com (дата обращения: 14.01.2019).
Achterberg T. SCIP: Solving Constraint Integer Programs // Mathematical Programming Computation. 2009. V. 1. № 1. P. 1–41.
Pollaris H., Braekers K., Caris A., Janssens G.K., Limbourg S. Vehicle Routing Problems with Loading Constraints: State-Of-The-Art and Future Directions // OR Spectrum. 2015. V. 37. Iss. 2. P. 297–330.
Бахтин В.А., Богданов И.П., Осипов В.П., Рыков Ю.Г., Смирнов А.А., Судаков В.А. Оптимизация перевозок однородной продукции между оптовыми складами // Препринты ИПМ им. М.В. Келдыша. 2018. № 65. 26 с. https://doi.org/10.20948/prepr-2018-65. URL: http://library.keldysh.ru/preprint.asp?id=2018-65 (дата обращения: 14.01.2019).
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления