Известия РАН. Теория и системы управления, 2021, № 3, стр. 71-84

0. Введение. В классических задачах анализа или оптимального синтеза коммуникационных сетей пропускные способности отдельных дуг (коммуникаций) являются либо фиксированной величиной, либо функцией от способа распределения ресурсов, либо величиной или функцией, зависящей от значения некоторого неопределенного фактора, либо случайной величиной [1–8]. Ограничения классических задач такого рода, как правило, есть балансы интенсивностей в узлах коммуникационной сети. Отличительными особенностями задач данного типа в классических постановках выступают:

1) отсутствие временных параметров перемещения каких-либо заданных объемов;

2) отсутствие абсолютных значений объемов перемещения в сети (рассматриваются лишь значения пропускных способностей дуг, т.е. перемещаемые по ним объемы в единицу времени), например, задача о максимальном потоке в двухполюсной сети;

3) отсутствие рассмотрения скоростей потоков по дугам сети;

4) пропускные способности дуг не зависят от величины плотности потоков.

В данной работе интенсивности потоков на дугах коммуникационной сети, в отличие от классических постановок задач транспортного типа, например, задачи о максимальном потоке, зависят от плотности потоков и определяются выражениями вида

где y_j – интенсивность потока на дуге j, p_j – плотность потока на дуге  j, V_j(p_j) – скорость потока по дуге  j при заданной плотности потока, Г – множество дуг коммуникационной сети.

Под скоростью потока понимается скорость, например, транспортных единиц потока, км/ч, которая предполагается равной у всех транспортных единиц потока на конкретной дуге коммуникационной сети, но может различаться для различных коммуникаций. Под плотностью потока подразумевается количество транспортных единиц на единицу длины транспортной коммуникации, един/км, которая также предполагается неизменной на всех участках конкретной дуги коммуникационной сети, но может различаться для различных коммуникаций. Под интенсивностью потока понимается количество транспортных единиц, проходящих через фиксированное сечение транспортной коммуникации в единицу времени, един/ч. Каждая коммуникация имеет единственную числовую характеристику интенсивности вследствие сделанных выше предположений о неизменности плотности потока и скорости потока на отдельных транспортных коммуникациях, что исключает ситуации какой-либо неоднородности, как то накопления или разрыва транспортного потока на всем протяжении коммуникации.

Далее формализуем задачи рассматриваемого типа на примере конкретной предметной области, а именно планирования эвакуации населения крупных городов.

1. Задача формирования эвакуационных планов населения. В качестве предметной области, приводящей к постановкам задач, которые не обладают в отличие от классических особенностями 1)–4), описанными ранее, являются задачи формирования эвакуационных планов крупных городов. Коротко содержательный сюжет таких задач может быть описан следующим образом.

Имеется сеть городских улиц, а также дорог и магистралей, выводящих в загородную зону. В общем случае рассматриваются как автомобильные, так и железнодорожные магистрали, ветки метрополитена, участки речного транспорта. Однако в целях упрощения представляемой модели рассмотрим сеть только автотранспортных коммуникаций. В данной модели сеть представляется ориентированным графом, т.е. набором вершин и направленных дуг. Улицам с двусторонним движением в сети соответствует пара дуг противоположного направления. Вершины сети предполагаются трех типов. Тип 1 – пункты вывоза или площадки посадки (ПП), т.е. места формирования, загрузки и отправления транспортных колонн. В пунктах данного типа прибывающие транспортные единицы, после некоторой временной задержки, вызванной вышеописанными процедурами, продолжают движение по предписанным им маршрутам в коммуникационной сети. Тип 2 – промежуточные вершины транспортной сети, т.е. места ответвления или пересечения улиц и магистралей. В вершинах данного типа происходит слияние и расщепление транспортных потоков. Тип 3 – пункты ввоза, места высадки эвакуируемых в безопасной зоне или приемные эвакуационные пункты (ПЭП). В пунктах данного типа прибывающие транспортные единицы, после некоторой временной задержки, вызванной процедурами высадки и, возможно, какими-либо техническими регламентными процедурами, продолжают движение по предписанным им маршрутам в коммуникационной сети.

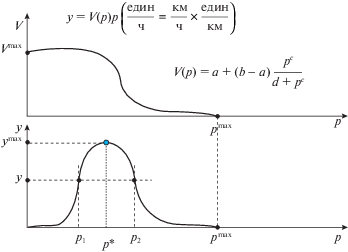
Каждая дуга характеризуется длиной и набором некоторых свойств (количество полос, качество покрытия и т.д.). Для удобства реализации рассматриваемые свойства (кроме количества полос) агрегируют в понятие “категория дороги”. Данные свойства определяют среднюю скорость транспортных средств на данной дуге в зависимости от плотности загрузки дуги (количество автотранспортных средств на единицу длины). Данная зависимость предполагается известной. Построение данной зависимости является отдельной подзадачей, которая рассматривалась, например, в [9]. Типичным видом зависимостей V(p) являются функции S-образной формы (рис. 1). В этом случае тип зависимости интенсивности потока от плотности потока также представлен на рис. 1.

Для каждой вершины типа 1 известно количество эвакуируемых из данной вершины. Вершины типа 2 являются транзитными, т. е. разность входящего и исходящего потоков эвакуируемых в них равна 0. Для каждой вершины типа 3 известно предельно допустимое количество эвакуируемых, которые могут быть доставлены на данную площадку (емкость площадки). В задаче необходимо указать некоторую систему маршрутов (синтез маршрутов) и распределение транспортных средств по данным маршрутам (распределение ресурсов) таким образом, чтобы время эвакуации было минимальным. Более точный состав характеристик эвакуационного плана, являющийся результатом решения оптимизационной модели, будет приведен далее. Под временем эвакуации понимается время, необходимое для вывоза всех эвакуируемых с площадок посадки на приемные эвакуационные пункты.

На основе описанной выше модели процесса эвакуации рассматриваются задачи двух типов.

1. Задачи синтеза оптимального эвакуационного плана, включающие в себя полностью или частично: формирование системы ПП (местоположение и количество эвакуируемых), формирование системы ПЭП (местоположение и количество эвакуируемых), формирование системы маршрутов колонн, распределение транспортных средств по маршрутам, распределение численностей эвакуируемых по маршрутам. Данный тип задач может рассматриваться как в детерминированном случае, так и в условиях риска или при наличии внешних неопределенных факторов.

2. Задачи анализа имеющегося эвакуационного плана с точки зрения оценки времени его реализации. Данный тип задач аналогично может рассматриваться как в детерминированном случае, так и в условиях риска или при наличии внешних неопределенных факторов.

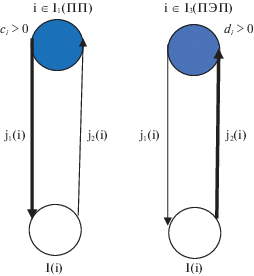
В статье представлена формализация задачи определения оптимальных интенсивностей потоков и интегральных объемов перевозок на дугах многополюсной коммуникационной сети с критерием на минимум времени проведения эвакуации в детерминированном случае. Предположим, что маршруты эвакуации, проходящие через пункты вывоза (ПП), осуществляют вывозы из данных пунктов и не являются транзитными для этих пунктов вывоза. Аналогичное предположение действует для маршрутов, проходящих через пункты ввоза (ПЭП). Возможность данных предположений обоснована тем, что ПП и ПЭП не являются транзитными площадками и не располагаются непосредственно на магистралях коммуникационной сети, а связаны с ними дополнительными коммуникациями. Схематично коммуникации ПП и ПЭП представлены на рис. 2. Для каждого из этих пунктов вводятся по две дополнительные дуги, соединяющие их с основной транспортной коммуникационной сетью. При этом предполагается, что для пунктов ПП (I ∈ I₁) по дуге  j₂(i) прибывает только пустой транспорт, а по дуге  j₁(i) выезжает только нагруженный. Аналогичное предположение для пунктов ПЭП (i ∈ I₃) – по дуге  j₁(i) выезжает только пустой транспорт, а по дуге j₂(i) прибывает только нагруженный. Однако допускается, что как пункты ПП, так и пункты ПЭП могут обслуживаться несколькими различными маршрутами. Множество дуг типа  j₁(i) и  j₂(i), где i ∈ ${{I}_{{1~}}} \cup ~{{I}_{3}}$, обозначим как J.

Задача анализа и синтеза эвакуационных планов крупных городов рассматривалась автором в [10]. Однако в отличие от данной работы в ней не был представлен аналитический подход для решения оптимизационной задачи, а предлагалась имитационная модель для оценки временных параметров эвакуационных планов. Вопросы формализации и алгоритмизации задач транспортного типа с переменными интенсивностями потоков рассматривались автором также в [11], однако в отличии от нее в данной статье не накладывается ограничений на структуру циклических маршрутов, рассмотрены две группы алгоритмов, а именно для предопределенной системы маршрутов и формируемой системы маршрутов, а также рассмотрены задачи минимизации объемов транспортных средств.

Для формирования математической постановки данной задачи предварительно необходимо решить серию задач безусловной оптимизации, а именно вида max V_j(p_j)p_j,  j ∈ Γ, для нахождения значений $y_{j}^{{{\text{max}}}}$ – максимально возможных интенсивностей дуг коммуникаций сети. Существование конечных максимумов у приведенных функций очевидно из рис. 1. Предполагаем также, что $y_{j}^{{{\text{max}}}}$ > 0, так как иначе перемещение потока по дуге  j невозможно и ее следует исключить из рассмотрения. Для дуг, введенных дополнительно для вершин ПП и ПЭП и обозначенных ранее, как множество J, также определяются величины максимально возможных интенсивностей этих дуг $y_{j}^{{{\text{max}}}}$. Однако они определяются не как максимальные значения функций V_j(p_j)p_j, а экспертно, исходя из пропускных возможностей конкретных ПП и ПЭП. Эти величины соответствуют максимально возможным интенсивностям потоков, которые данная площадка сможет обслуживать без образования накапливающихся очередей. Далее приведем математическую постановку задачи минимизации времени перевозок в многополюсной коммуникационной сети с переменными интенсивностями потоков. В качестве потока рассматривается поток однотипных транспортных средств, осуществляющих перемещение людей в процессе эвакуации.

Введем некоторые дополнительные обозначения. Пусть $p_{j}^{{{\text{max}}}}$ – максимально возможная плотность потока на дуге  j, т. е. такая плотность, при которой скорость потока становится равной нулю (рис. 1), $p_{j}^{*}$ – плотность потока, при которой достигается максимальное значение интенсивности потока на дуге  j (рис. 1), C(k), D(k) – множества индексов дуг, входящих в вершину k и исходящих из нее соответственно, n – количество вершин в ориентированном графе, представляющем рассматриваемую коммуникационную сеть, т.е. $\left| {{{I}_{1}} \cup {{I}_{2}} \cup {{I}_{3}}} \right| = n$, m – количество дуг данного ориентированного графа, т.е. $\left| {{{\Gamma }} \cup J} \right| = m$, I₁ – множество вершин, соответствующих пунктам ПП, I₂ – множество транзитных вершин, I₃ – множество вершин, соответствующих пунктам ПЭП, y_j  – интенсивность потока по дуге  j, как было определено ранее, z_j – общее количество эвакуируемых, перевезенных по дуге  j, V – вместимость одного транспортного средства (предполагаются однотипными), t – время перевозки, c_k – необходимый объем вывоза (количество людей) в k-м пункте вывоза, d_k – ограничение на объем ввоза (количество людей) в k-м пункте ввоза.

Фактически в данной задаче рассматриваются два потока в сети. Первый поток – это поток автотранспортных средств, который характеризуется интенсивностями, определяемыми для каждой дуги, которые в свою очередь ограничены своими максимально допустимыми значениями $y_{j}^{{{\text{max}}}}$. Поток соответствует задаче о перевозке с нулевыми значениями запасов и потребностей для всех вершин, т.е. является циклическим. В потоке могут присутствовать как загруженные транспортные средства, так и незагруженные. Второй поток – это поток эвакуируемых, перевозимых из пунктов ПП в пункты ПЭП. Он соответствует задаче о перевозке с заданными объемами вывоза c_k в пунктах ПП и заданными объемами ввоза d_k в пунктах ПЭП. Задача состоит в скоординированном определении обеих потоков с целью минимизации общего времени перевозки.

Формализованная постановка задачи имеет следующий вид:

Ограничение (1.2) определяет цикличность потока интенсивностей, т.е. для всех вершин сети сумма интенсивностей входящих потоков равна сумме интенсивностей исходящих. Ограничения (1.3)–(1.5) определяют балансы потока эвакуируемых соответственно в вершинах ПП, транзитных вершинах и вершинах ПЭП. Ограничения (1.6) соответствуют тому, что общее время на реализацию перевозок не может быть меньше, чем время перевозки на каждой из дуг сети. Ограничения (1.7) определяют допустимые интенсивности на дугах сети.

Следует отметить, что в данной постановке оптимальное время, найденное в задаче (1.1), отличается от реального минимального времени эвакуации, поскольку в задаче рассматривается только стационарный поток с постоянными плотностями потоков на дугах сети. Фактически мы не учитываем периоды нестационарности в начале процесса эвакуации и при его завершении. Однако будем предполагать эти периоды малыми относительно общего времени проведения эвакуации.

Задача (1.1) является задачей условной нелинейной (ограничения (1.6)) оптимизации. В постановке задачи (1.1) в отличие от классической задачи о перевозках присутствуют интенсивности потоков, а также рассматриваются временные параметры перемещения. Отметим также, что задача (1.1) не всегда имеет решение. Предполагаем, что выполнено условие сбалансированности задачи, а именно

В силу замкнутости и ограниченности множества допустимых решений задачи (1.1), отсутствие решения может быть вызвано только недостаточностью коммуникационных дуг в структуре ориентированного графа транспортной сети. Необходимое и достаточное решение задачи (1.1) определяется теоремой Гейла [12]. Далее предполагаем разрешимость задачи (1.1).

Выше при описании содержательной постановки задачи были сформулированы следующие предположения: для пунктов ПП (i ∈ I₁) по дуге  j₂(i) прибывает только пустой транспорт, а по дуге  j₁(i) выезжает только нагруженный и аналогичное предположение для пунктов ПЭП (i ∈ I₂) – по дуге  j₁(i) выезжает только пустой транспорт, а по дуге j₂(i) прибывает только нагруженный. Однако в математической постановке (1.1) данной задачи эти предположения не отражены. Далее покажем, что задача (1.1) в случае ее разрешимости имеет решение, удовлетворяющее этим предположениям.

Пусть вектор (t*, z*, y*) есть решение задачи (1.1). Построим некоторый новый вектор решений (t*, $\tilde {z}$, y*), следуя соотношениям:

${{\tilde {z}}_{{{{j}_{1}}\left( i \right)}}}$ = 0, ${{\tilde {z}}_{{{{j}_{2}}(i)}}} = z_{{{{j}_{2}}(i)}}^{*}{\text{\;}} - z_{{{{j}_{1}}(i)}}^{*}$ = ${{d}_{i}}$, $i \in {{I}_{3}}$, ${{\tilde {z}}_{j}}$ = ${{z}_{j}}$, для остальных дуг.

Покажем, что построенный вектор (t*, $\tilde {z}$, y*) есть допустимый вектор задачи (1.1). Для этого необходимо убедиться, что для него выполнены ограничения (1.3) – (1.6).

Проверим ограничения (1.3):

Проверим ограничения (1.4). Очевидно, что необходимо проверить их только для тех вершин, которые соединены с вершинами из множеств I₁ и I₃, они имеют обозначения I(i) (рис. 2).

Проверим ограничения (1.4) для вершин из множества I₂, которые соединены с вершинами из множества I₁:

⇒ $0 = z_{{{{j}_{1}}\left( i \right)}}^{*}{\text{\;}} - z_{{{{j}_{2}}\left( i \right)}}^{*}$ + S ⇒ ${{\tilde {z}}_{{{{j}_{1}}\left( k \right)}}}$ – ${{\tilde {z}}_{{{{j}_{2}}\left( k \right)}}}$ + S = ($z_{{{{j}_{1}}\left( i \right)}}^{*}{\text{\;}} - z_{{{{j}_{2}}\left( i \right)}}^{*}$) + S = 0, где S – сумма перевозок по всем остальным входящим и исходящим дугам в вершину I(i), для которых ${{\tilde {z}}_{j}}$ = ${{z}_{j}}$.

Проверим ограничения (1.4) для вершин из множества I₂, которые соединены с вершинами из множества I₃:

⇒ $0 = z_{{{{j}_{1}}\left( i \right)}}^{*}{\text{\;}} - z_{{{{j}_{2}}\left( i \right)}}^{*}$ + S ⇒ ${{\tilde {z}}_{{{{j}_{1}}\left( i \right)}}}{\text{\;}} - {{\tilde {z}}_{{{{j}_{2}}\left( i \right)}}}$ + S = 0 – ($z_{{{{j}_{2}}\left( i \right)}}^{*}{\text{\;}} - z_{{{{j}_{1}}\left( i \right)}}^{*}$) – 0 + S = 0, где S – сумма перевозок по всем остальным входящим и исходящим дугам в вершину I(i), для которых ${{\tilde {z}}_{j}}$ = ${{z}_{j}}$.

Проверим ограничения (1.5):

⇒ ${{z}_{{{{j}_{1}}\left( k \right)}}}$ – ${{z}_{{{{j}_{2}}\left( k \right)}}} = {{d}_{k}} \Rightarrow {{\tilde {z}}_{{{{j}_{1}}\left( k \right)}}}{\text{\;}} - {{\tilde {z}}_{{{{j}_{2}}\left( k \right)}}}$ = 0 – ($z_{{{{j}_{2}}\left( i \right)}}^{*} - z_{{{{j}_{1}}\left( i \right)}}^{*}){\text{\;}} = {{d}_{k}}$.

Проверим ограничения (1.6). Его необходимо проверить для дуг типа ${{j}_{1}}\left( i \right)$ и ${{j}_{2}}\left( i \right)$, где $i \in {{I}_{1}} \cup {{I}_{3}}$.

Проверим ограничение (1.6) для дуг типа ${{j}_{1}}\left( i \right)$, $i \in {{I}_{1}}:$

Проверим ограничение (1.6) для дуг типа ${{j}_{2}}\left( i \right)$, $i \in {{I}_{1}}{\text{:}}$

Проверим ограничение (1.6) для дуг типа ${{j}_{1}}\left( i \right)$, $i \in {{I}_{3}}{\text{:}}$

Проверим ограничение (1.6) для дуг типа ${{j}_{2}}\left( i \right)$, $i \in {{I}_{3}}{\text{:}}$

Таким образом, показано, что построенный вектор (t*, $\tilde {z}$, y*), есть допустимый вектор задачи (1.1). Поскольку ему соответствует оптимальное значение функционала t*, то он является и оптимальным решением.

Как было отмечено выше, задача (1.1) – задача нелинейной условной оптимизации, однако использование замены переменных ${{w}_{j}} = t{{y}_{j}},~j = \overline {1,m} ,$ и обоснованное выше преобразование приводят задачу (1.1) к следующей задаче (1.9) линейного программирования:

Оптимальные значения переменных z* и t* из решения задачи (1.9) сохраняют свои значения и для решения задачи (1.1), а оптимальные значения переменных y* задачи (1.1) восстанавливаются исходя из следующих соотношений:

Содержательно возникает задача, напоминающая задачу о перевозках с некоторым мультипликативным параметром t. В терминах этой классической сетевой задачи задача (1.9) сводится к вопросу: на сколько минимально можно умножить величины максимально возможных интенсивностей потоков на дугах так, чтобы задача о перевозках осталась разрешимой в рамках заданных объемов спроса и предложения в сети?

Строго говоря, утверждать, что задача (1.1) определяет именно минимальное время проведения эвакуации без дополнительных исследований, было бы преждевременно. Действительно, в задаче (1.1) определяются оптимальные значения интенсивностей на дугах коммуникационной сети, при которых достигается минимальное время эвакуации. Однако вопрос о том, насколько достижимы эти интенсивности в рамках принятой модели осуществления эвакуации c использованием циклических транспортных маршрутов, остается открытым. Если автотранспортный парк ограничен, то возникает также вопрос, достаточен ли он для достижения оптимальных значений интенсивностей и соответственно полученного минимального времени осуществления перевозки. В силу этого на данном этапе результат задачи (1.1) более корректно трактовать как оценку снизу для минимального времени проведения эвакуации.

Как было отмечено выше, рассматриваемая модель эвакуации предполагает движение потока транспортных средств по некоторым циклическим маршрутам с забором эвакуируемого населения в ПП и выгрузкой в ПЭП. Далее приведем алгоритмы решения задач 1 и 2 соответственно, которые были определены выше.

Задача 1. Система маршрутов не известна. Положения и емкости ПП (c_k) и ПЭП (d_k) известны. Результатом задачи минимизации времени проведения эвакуации является определение оптимальной системы маршрутов, а также оптимального количества эвакуируемых, перевозимых по каждому из маршрутов, и оптимальное распределение имеющегося количества однотипных транспортных средств по сформированной системе маршрутов. Какие-либо неопределенные внешние факторы отсутствуют.

Задача 2. Система маршрутов известна. Положения и емкости ПП (c_k) и ПЭП (d_k) также известны. Результатом задачи минимизации времени проведения эвакуации является оптимальное распределение имеющегося количества однотипных транспортных средств по заданной системе маршрутов, а также оптимального количества эвакуируемых, перевозимых по каждому из маршрутов. Какие-либо неопределенные внешние факторы отсутствуют.

2. Алгоритм решения задачи 1. Приведем далее алгоритм решения задачи минимизации времени эвакуации для задачи типа 1.

Шаг 1. Определение значений $y_{j}^{{{\text{max}}}}$. Для каждой из дуг коммуникационной сети из множества Г решается задача безусловной оптимизации максимизации функции одной переменной V_j(p_j)p_j, j ∈ Γ, для нахождения максимально возможного значения плотности соответствующего потока $y_{j}^{{{\text{max}}}}$. Для множества дополнительно введенных дуг J значения $y_{j}^{{{\text{max}}}}$, как было отмечено ранее, определяются экспертно.

Шаг 2. Нахождение минимального времени выполнения перевозок. Решаем задачу (1.1) путем сведения ее к задаче (1.9). Рассматриваем полный набор коммуникаций сети. Заметим, что задача (1.1) разрешима тогда и только тогда, когда разрешима задача (1.9). Оптимальный набор интенсивностей по дугам получаем, используя соотношения (1.10).

Шаг 3. Определение минимально необходимого объема транспортных средств. При решении (1.1) критерием задачи была минимизация времени реализации перевозки. При этом получаемые значения объемов перевозок, интенсивностей потоков, плотностей потоков и объемов транспортных средств позволяют реализовать время перевозки t*, но иным критериям, вообще говоря, не удовлетворяют. Поэтому для определения минимального количества транспортных средств, необходимых для реализации перевозки за время t*, решается новая задача:

где x_j – количество транспортных средств на дуге  j, а l_j – протяженность коммуникации j. Величины x_j полагаем неизменными в силу нашего предположения о стационарности рассматриваемого потока. Соответственно определенные ранее плотности потоков, находятся из соотношений ${{p}_{j}} = {{x}_{j}}{\text{/}}{{l}_{j}}$.

Оптимальное решение задачи (2.1) по функционалу обозначим как $R_{{{\text{min}}}}^{*}$. Следует отметить, что задача (2.1) является нелинейной задачей условной оптимизации в силу ограничений (2.2). Предложим далее способ получения некоторой оценки сверху $R_{{{\text{min}}}}^{ + }$ для величины $R_{{{\text{min}}}}^{*}$, т.е. $R_{{{\text{min}}}}^{*} \leqslant R_{{{\text{min}}}}^{ + }$. Оценку $R_{{{\text{min}}}}^{ + }$ можно найти через решение следующей линейной оптимизационной задачи:

Пусть y* есть решение задачи (2.3), а $R_{{{\text{min}}}}^{ + }$ – ее оптимальное значение по функционалу. Найдем оптимальные значения плотностей потока на дугах путем последовательного решения нелинейных уравнений вида $y_{j}^{*} = {{V}_{j}}({{p}_{j}}){{p}_{j}},j \in {{\Gamma }}$, при найденных в ходе решения задачи (2.3) значениях вектора y*. Поскольку возможны несколько решений для p_j, то будем рассматривать минимальное из них, т.е. ${{p}_{j}} \in \left[ {0;~p{\text{*}}} \right]$ (рис. 1). Отметим также, что для задачи (2.1) соответствующие значения p_j получаются непосредственно из решения ${{p}_{j}} = {{x}_{j}}{\text{/}}{{l}_{j}}$. Далее на основе найденных значений p_j проведем расчет объема транспортных средств, задействованных на каждой из дуг сети, как x_j = p_jl_j, $j \in \Gamma .$ Тогда вектор (t*, x, y*) есть допустимое решение задачи (2.3), а следовательно, получена некоторая оценка сверху $R_{{{\text{min}}}}^{ + }$ для величины $R_{{{\text{min}}}}^{*}$, т.е. $R_{{{\text{min}}}}^{*} \leqslant R_{{{\text{min}}}}^{ + }$. Основанием полагать, что данная оценка будет иметь определенную близость к значению $R_{{{\text{min}}}}^{*}$, является факт монотонной зависимости величины ${{y}_{j}}$ от ${{p}_{j}}$ на отрезке [$0;~p{\text{*}}$] (рис. 1). Поскольку, как отмечено ранее, рассматривается только минимальное из решений p_j, следовательно, имеет место монотонная зависимость и от x_j, согласно соотношениям (2.2).

Шаг 4. Проверка достаточности количества транспортных средств. Проверяется выполнение условия $R_{{{\text{min}}}}^{ + } \leqslant R$, где R – общее количество имеющихся транспортных средств. Если оно верно, то переходим к шагу 5 для распределения транспортных ресурсов по системе маршрутов, используя полученный в ходе решения задачи (2.3) вектор интенсивностей y. В противном случае решается задача (2.1) и проверяется условие $R_{{{\text{min}}}}^{*} \leqslant R$. Если оно выполнено, то также переходим к шагу 5, используя найденный в ходе решения задачи (2.1) вектор интенсивностей y. Иначе переходим к шагу 7. Заметим, что невязка в неравенстве $R_{{{\text{min}}}}^{*} \leqslant R$ в случае его невыполнения соответствует дополнительному количеству транспортного ресурса, которое обеспечило бы достижимость минимально возможного времени эвакуации при заданных объемах перевозок и параметрах транспортных коммуникаций.

Шаг 5. Формирование системы циклических маршрутов. Как отмечалось выше, в задачах (1.1), (2.1) и (2.3) присутствуют два потока – эвакуируемых и транспортных средств. Поскольку оба потока являются потоками задачи о перевозках, они, следуя Форду и Фалкерсону [12], могут быть заданы в виде “дуги-цепи”, т.е. в виде отображение h множества направленных “квазипутей” (из множества вершин пунктов вывоза I₁ в множество вершин пунктов ввоза I₃) в множество неотрицательных чисел таким образом, чтобы выполнялись следующие соотношения:

где P – множество направленных “квазипутей”, N_i – множество дуг, входящих в i-й “квазипуть”, h(N_i) – интенсивность потока по i-у “квазипути”. В работе [13] вводится определение “квазипути” и дается конструктивное доказательство существования представления в виде совокупности направленных “квазипутей” любого допустимого потока. Заметим, что такое представление, вообще говоря, не единственно.

Решение задачи (1.9) по переменным w, а следовательно, и по переменным y исходной задачи (1.1) есть допустимый план перевозок для задачи о перевозках, в которой все вершины являются транзитными. Аналогичное утверждение справедливо и для потоков интенсивностей y задач (2.1) и (2.3). Поэтому для потоков интенсивностей y этих задач можно обосновать более сильный результат, чем разложение “дуги-цепи”, а именно возможность разложения “дуги-циклы”. Другими словами, задать отображение h множества P направленных “квазициклов” [13, 14], соединяющих представителей из множества вершин пунктов вывоза I₁ с представителями множества вершин пунктов ввоза I₃, в множество неотрицательных чисел таким образом, чтобы выполнялись соотношения (2.4).

Поскольку, как и в случае разложения “дуги-цепи”, разложение “дуги-циклы”, вообще говоря, не единственно, то выберем одно из возможных разложений в виде “дуги-циклы” оптимального потока y, полученного через решение задачи (2.1) или (2.3). Именно это разложение и примем за искомую систему циклических маршрутов.

Шаг 6. Распределения транспортных ресурсов по системе маршрутов. Распределения транспортных ресурсов по системе маршрутов произведем на основе следующих соотношений:

где $j \in {\text{Г}},\;i \in P,~$ $p_{j}^{i}$ – есть частичная плотность потока на дуге  j, создаваемая потоком по i-му циклическому маршруту, $x_{j}^{i}$ – количество транспортных средств i-го маршрута, дислоцирующихся на дуге j, p_j – плотности потоков на дугах, полученные на шаге 3 либо из решения задачи (2.1), либо (2.3). Плотность потока на дуге есть сумма частичных плотностей, создаваемых потоками по маршрутам, которые проходят, через данную дугу. Аналогично интенсивность потока на дуге есть сумма интенсивностей по маршрутам, проходящим через данную дугу.

Проверим, что использование соотношений (2.5) не нарушает оптимальных количеств транспортных ресурсов на дугах, вычисленных на шаге 3 при решении задачи (2.1). Действительно, при $j \in \Gamma ,~\;i \in P$

что в точности соответствует соотношениям (2.2).

Вычисление количества задействованных транспортных средств на отдельном маршруте происходит по формулам

где X_i – транспортный ресурс, выделенный на маршрут i. Алгоритм формирования оптимальной системы циклических маршрутов и оптимального распределения транспортного ресурса по маршрутам завершен.

Шаг 7. Случай недостаточности количества транспортных средств (нахождение минимального времени перевозок). В случае, если проверка достаточности транспортных средств на шаге 4 не дает положительного результата, решение задачи (1.1) в ее первоначальном варианте, как уже отмечалось, не дает оптимального времени проведения эвакуации, а лишь его оценку снизу. Тогда произведем решение следующей задачи:

Задача (2.6) является нелинейной задачей условной оптимизации, которую, по-видимому, не удается свести к линейной. В задаче (2.6) в отличие от задачи (1.1) появляются переменные x количества транспортных единиц и выраженные через них плотности транспортных потоков на дугах сети. Пусть значение t* есть минимальное время выполнения перевозки, полученное как решение задачи (2.6).

Шаг 8. Случай недостаточности количества транспортных средств (формирование системы маршрутов и распределение транспортных средств). Далее реализуем действия, предусмотренные шагами 5 и 6 данного раздела. Это и завершает алгоритм формирования оптимальной системы циклических маршрутов и оптимального распределения транспортного ресурса по маршрутам.

3. Алгоритм решения задачи 2. Приведем далее алгоритм решения задачи минимизации времени эвакуации для задачи 2. Основная сложность данной задачи по сравнению с рассмотренной в разд. 2 заключается в том, что даже в том случае, если в качестве множества дуг Г рассмотреть его подмножество Γ*, ${{\Gamma *}} \subset {{\Gamma }}$, состоящее только из дуг, входящих в заданную систему маршрутов, и далее следовать вышеописанному алгоритму, может возникнуть проблема на шаге 5. Среди допустимых представлений циклического потока в виде “дуги-циклы” может не оказаться заданной системы маршрутов. Поэтому привязка к заданной системе маршрутов должна изначально присутствовать в формализованной постановке задачи. Обозначим множество индексов заданных маршрутов, как и ранее, как P, а множество индексов дуг маршрута i – как ${{N}_{i}}$.

Шаг 1. Определение значений $y_{j}^{{{\text{max}}}}$. Для каждой из дуг коммуникационной сети из множества Γ* решается задача безусловной оптимизации максимизации функции одной переменной ${{V}_{j}}({{p}_{j}}){{p}_{j}}$, $j \in {{\Gamma *}}$, для нахождения максимально возможного значения плотности соответствующего потока $y_{j}^{{{\text{max}}}}$. Для множества дополнительно введенных дуг J значения $y_{j}^{{{\text{max}}}}$ определяются экспертно.

Шаг 2. Нахождение минимального времени выполнения перевозок. Решаем следующую задачу:

Задача (3.1) содержательно аналогична задаче (1.1) рассмотренной выше. Отличие состоит в сужении множества рассматриваемых дуг, присутствии в задаче новых переменных h, обозначающих интенсивности потоков заданной системы маршрутов, и новых ограничениях (3.2), которые определяют разложение интенсивностей потоков на дугах по интенсивностям заданной системы маршрутов.

Как и (1.1), задача (3.1) является задачей нелинейной условной оптимизации, однако, так же как и в случае задачи (1.1), использование замены переменных ${{w}_{j}} = t{{y}_{j}},~$ $j \in \left\{ {{{\Gamma *}} \cup J} \right\},~$и обоснованное выше для задачи (1.1) допустимое преобразование вектора z приводят задачу (3.1) к следующей задаче линейного программирования:

Оптимальные значения переменных z* и t* из решения задачи (3.3) сохраняют свои значения и для решения задачи (3.1), а оптимальные значения переменных y* задачи (3.1) восстанавливаются:

Шаг 3. Определение минимально необходимого объема транспортных средств. При решении задачи (3.1) критерием задачи было время реализации перевозки. При этом получаемые значения объемов перевозок, интенсивностей потоков, плотностей потоков и объемов транспортных средств позволяют реализовать полученное время перевозки t*, но иным критериям, вообще говоря, не удовлетворяют. Поэтому для определения минимального количества транспортных средств, необходимых для реализации перевозки за время t*, решается новая задача:

Оптимальное решение задачи (3.5) по функционалу обозначим как $R_{{{\text{min}}}}^{*}$. Следует отметить, что задача (3.5) является нелинейной задачей условной оптимизации. Как и в алгоритме предыдущего раздела, предложим способ получения некоторой оценки сверху $R_{{{\text{min}}}}^{ + }$ для величины $R_{{{\text{min}}}}^{*}$, т.е. $R_{{{\text{min}}}}^{*} \leqslant R_{{{\text{min}}}}^{ + }$. Оценку $R_{{{\text{min}}}}^{ + }$ можно найти через решение линейной оптимизационной задачи:

Пусть y* – решение задачи (3.6), а ее оптимальное значение по функционалу есть $R_{{{\text{min}}}}^{ + }$. Найдем оптимальные значения плотностей потока на дугах путем последовательного решения нелинейных уравнений вида $y_{j}^{*} = {{V}_{j}}({{p}_{j}}){{p}_{j}},j \in {{\Gamma *}}$, при найденных в ходе решения задачи (3.6) значениях вектора y*. Поскольку возможны несколько решений для p_j, то будем рассматривать минимальное из них, т.е. ${{p}_{j}} \in \left[ {0;~p{\text{*}}} \right]$ (рис. 1). На основе найденных значений p_j проведем расчет объема транспортных средств, задействованных на каждой из дуг сети, как x_j = p_jl_j, $j \in {{\Gamma *}}$.

Тогда вектор (t*, x, y*) есть допустимое решение задачи (3.6), а следовательно, получена некоторая оценка сверху $R_{{{\text{min}}}}^{ + }$ для величины $R_{{{\text{min}}}}^{*}$, т.е. $R_{{{\text{min}}}}^{*} \leqslant R_{{{\text{min}}}}^{ + }$. Основанием полагать, что данная оценка будет иметь определенную близость к значению $R_{{{\text{min}}}}^{*}$, является факт монотонной зависимости величины y_j от p_j на отрезке [$0;~p{\text{*}}$] (рис. 1), поскольку, как отмечено ранее, рассматривается только минимальное из решений p_j, следовательно, имеет место монотонная зависимость и от ${{x}_{j}}$.

Шаг 4. Проверка достаточности количества транспортных средств. Проверяется выполнение условия $R_{{{\text{min}}}}^{ + } \leqslant R$, где R – общее количество имеющихся транспортных ресурсов. Если оно верно, то переходим к шагу 5 для распределения транспортных ресурсов по системе маршрутов, используя полученный в ходе решения задачи (3.6) вектор интенсивностей y. В противном случае решается задача (3.5) и проверяется условие $R_{{{\text{min}}}}^{*} \leqslant R$. Если оно выполнено, то также переходим к шагу 5, используя полученный в ходе решения задачи (3.5) вектор интенсивностей y. Иначе переходим к шагу 6. Заметим, что невязка в неравенстве $R_{{{\text{min}}}}^{*} \leqslant R$, в случае его невыполнения, соответствует дополнительному количеству транспортного ресурса, которое обеспечило бы достижимость минимально возможного времени эвакуации при заданных объемах перевозок и параметрах транспортных коммуникаций.

Шаг 5. Распределения транспортных ресурсов по системе маршрутов. Распределения транспортных ресурсов по системе маршрутов произведем на основе следующих соотношений:

где $j \in {{\Gamma *}},\;i \in P,$ $p_{j}^{i}$ – частичная плотность на дуге  j, создаваемая потоком по i-му циклическому маршруту, $x_{j}^{i}$ – количество транспортных средств i-го маршрута, дислоцирующихся на дуге  j, p_j – плотности потоков на дугах, полученные на шаге 3 либо из решения задачи (3.5), либо (3.6). Плотность потока на дуге есть сумма частичных плотностей, создаваемых потоками по маршрутам, которые проходят через данную дугу. Аналогично интенсивность потока на дуге есть сумма интенсивностей по маршрутам, проходящим через данную дугу.

Вычисление количества задействованных транспортных средств на отдельном маршруте происходит по формулам

где X_i – транспортный ресурс, выделенный на маршрут i. Алгоритм формирования оптимальной системы циклических маршрутов и оптимального распределения транспортного ресурса по маршрутам завершен.

Шаг 6. Случай недостаточности количества транспортных средств (нахождение минимального времени перевозок). В случае, если проверка достаточности транспортных средств на шаге 4 не дает положительного результата, решение задачи (3.3), как уже отмечалось, не дает оптимального времени проведения эвакуации, а лишь его оценку снизу. Тогда произведем решение следующей задачи:

Задача (3.8) является нелинейной задачей условной оптимизации, которую, по-видимому, не удается свести к линейной. Пусть значение t* есть минимальное время выполнения перевозки, полученное как решение задачи (3.8).

Шаг 7. Случай недостаточности количества транспортных средств (распределение транспортных средств). Далее реализуем действия, предусмотренные шагом 5 данного раздела. Это и завершает алгоритм формирования оптимальной системы циклических маршрутов и оптимального распределения транспортного ресурса по маршрутам.

4. Минимизация объема транспортных ресурсов при заданном директивном времени перевозки. В задачах разд. 2 и 3 ставился вопрос о минимизации количества задействованных в перевозке транспортных средств. Однако этот критерий рассматривался как критерий второй приоритетности после критерия минимизации времени перевозки. Фактически был применен метод лексикографического целевого программирования [15]. В настоящем разделе приведем задачу минимизации количества необходимых транспортных средств при условии заданного директивного времени перевозки, в которое необходимо уложиться. Как и в случае минимизации времени перевозки, задача рассматривается в двух постановках: с набором маршрутов, формируемых в ходе решения задачи и с изначально заданным набором маршрутов.

Математическая постановка данной задачи в случае системы маршрутов, формируемых в ходе решения задачи, имеет вид задачи (2.1), в которой в качестве входного параметра t* рассматривается заданное директивное время выполнения перевозки.

Математическая постановка данной задачи в случае изначально заданной системы маршрутов, имеет вид задачи (3.5), в которой в качестве входного параметра t* рассматривается заданное директивное время выполнения перевозки.

Заключение. В статье представлены постановки задач минимизации времени перевозок в многополюсной сети, в которой скорости и, как следствие, интенсивности потоков на коммуникациях сети зависят от плотности потоков на этих коммуникациях. Рассмотрены также постановки задач минимизации необходимого объема транспортных ресурсов. Задачи приводятся, как в случае множества маршрутов, формируемого в ходе решения задачи и с изначально заданным набором маршрутов. Полезность представленных в статье алгоритмов решения задач о перевозках в многополюсной сети с переменными интенсивностями потоков состоит в том, что в ряде случаев при достаточном количестве транспортных средств они позволяют избежать решения сложных нелинейных задач математического программирования большой размерности. Алгоритмы дают также возможность определить минимальное количество транспортных средств, обеспечивающее достижимость минимально возможного времени эвакуации при заданных объемах перевозок и параметрах транспортных коммуникаций.

В рассматриваемых задачах предполагается, что трафик коммуникационной сети формируется полностью из транспортных средств, осуществляющих заданную перевозку. Однако на практике вероятен случай, когда в коммуникационной сети присутствует фоновый внешний трафик, который также должен учитываться при оценке допустимых интенсивностей потоков на коммуникациях сети. Приведенные в статье математические постановки и алгоритмические результаты в этом случае остаются верными с точностью до замены зависимостей интенсивностей потоков на дугах от плотности транспортного потока перевозки, а именно их необходимо рассматривать в виде ${{y}_{j}} = {{V}_{j}}({{a}_{j}} + {{p}_{j}}){{p}_{j}},$ где a_j – фоновые интенсивности потоков на коммуникации j, оцененные, например, как среднеожидаемые. Существенного усложнения алгоритмов численного решения рассматриваемых задач эта замена, по-видимому, не повлечет.