Известия РАН. Теория и системы управления, 2021, № 3, стр. 11-22
СИНТЕЗ ПРОСТЫХ РОБАСТНЫХ РЕГУЛЯТОРОВ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ ДИНАМИЧЕСКИХ СИСТЕМ
В. А. Мозжечков *
ЗАО “Инженерно-технический центр “Привод”, Тульский государственный ун-т
Тула, Россия
* E-mail: itc@tulaprivod.ru
Поступила в редакцию 14.04.2020
После доработки 24.09.2020
Принята к публикации 30.11.2020
Аннотация
Рассматривается задача синтеза динамических регуляторов с простой структурой в составе линейной стационарной динамической системы со скалярным управлением и векторной обратной связью при наличии возмущающего воздействия. Простым регулятором назван регулятор, структуру которого невозможно упростить, поскольку упрощение, состоящее в исключении из нее любого элемента, приводит к невозможности выполнить все требования, предъявляемые к синтезируемой системе. Учитывается условие обеспечения робастности синтезируемой системы с использованием оригинального показателя грубости регулятора. Предложенный показатель позволяет выделить среди множества простых регуляторов такой, который придает системе максимальную робастность. Предложен метод решения рассматриваемой задачи, приведен пример его реализации.
Введение. В теории управления значительное внимание уделяется получению не только эффективных, но и простых решений. Одной из первых работ, посвященных проблеме минимизации сложности системы управления при ее математическом синтезе, стала публикация [1]. В ней сложность регулятора оценивалась порядками числителя и знаменателя передаточной функции регулятора. Затем в [2–5] идея учета сложности при синтезе систем управления была представлена в форме принципа, названного авторами принципом сложности. В [6] была поставлена и решена задача упрощения структуры линейной системы, синтезированной методом аналитического конструирования оптимальных регуляторов, путем замены точного решения приближенным, предполагающим исключение несущественных обратных связей. При этом сложность системы оценивалась взвешенной суммой ненулевых элементов матрицы обратных связей. В [7, 8] был предложен метод синтеза регуляторов минимального порядка, основанный на использовании методов нелинейного программирования для приближенного решения задачи размещения полюсов синтезируемой системы. Решению задачи определения оптимального набора обратных связей с целью минимизации сложности системы, оцениваемой порядком регулятора, посвящена работа [9]. В [10–15] описана проблема существования и построения стабилизаторов низкого порядка для линейных систем. Методы синтеза стабилизирующих регуляторов с использованием линейных матричных неравенств, учитывающие требование ограничения сложности регулятора, были рассмотрены в [16–18]. Ограничение сложности системы с помощью простейших регуляторов с заданной структурой реализовано в методах, представленных в [12, 19–23]. Задачи упрощения регуляторов, синтезированных классическими методами теории управления, решены в [6, 10, 15, 17, 20, 22, 24–30].
В работах [31, 32] простым регулятором предложено называть регулятор, структуру которого невозможно упростить, поскольку упрощение, состоящее в исключении из нее любого элемента, приводит к невозможности выполнить все требования, предъявляемые к синтезируемой системе.
В структуре простого регулятора отсутствуют избыточные элементы: каждый элемент необходим, а их совокупность достаточна для обеспечения желаемых характеристик системы. Выявление множества простых регуляторов, соответствующих указанному определению, предполагает использование следующего правила сравнения сложности структур регуляторов: рассматриваемая структура сложнее, чем некоторая другая, если в ней содержатся все элементы другой структуры и некоторые дополнительные элементы. Указанное правило сравнения сложности выгодно отличается от сравнения сложности по порядку регуляторов, поскольку более полно учитывает информацию, заключенную в описании регулятора.
В результате применения предложенного правила сравнения сложности выявляется в общем случае не единственный вариант, а множество вариантов простых регуляторов, обеспечивающих придание системе желаемых характеристик. Найденные простые регуляторы обеспечивают разную степень чувствительности характеристик системы к изменениям параметров объекта управления, т.е. обеспечивают различную робастность системы. Рациональным основанием выбора единственного варианта из найденного множества простых регуляторов является максимизация робастности системы.
Проблема проектирования робастных систем в значительной мере ассоциирована с проблемой синтеза регуляторов низкой сложности. Это обусловлено тем, что именно при синтезе робастных систем с особой остротой проявилась проблема хрупкости [33] (низкой робастности) регуляторов высокого порядка. Обнаружилось, что робастность системы не удается обеспечить только назначением соответствующих характеристик замкнутой системы (например, больших запасов устойчивости, узкой полосы пропускания, H∞-оптимизации и т.д.). Структура регулятора оказалась существенным фактором, от которого зависит робастность системы. Причем снижение порядка регулятора, как правило, позволяло ее повысить. В этой связи были предложены методы синтеза робастных систем, основанные на назначении соответствующих требований к характеристикам замкнутой системы в сочетании с использованием регулятора низкого порядка с заданной структурой [19–23]. Однако при этом оставалась недостаточно исследованной зависимость робастности системы от структуры регулятора.
В данной работе предложен показатель грубости регулятора, математически описывающий связь структуры регулятора и робастности системы, позволяющий выделить из множества простых структур регуляторов структуру, оптимальную по критерию робастности. Разработан формализованный метод синтеза динамических регуляторов с простой структурой в составе линейной системы со скалярным управлением и векторной обратной связью при наличии возмущающего воздействия, позволяющий находить простую структуру регулятора, оптимальную по критерию робастности.
1. Предварительное обсуждение задачи. Далее будет показано, что искомые коэффициенты α1, α2, …, αn полиномов операторного уравнения, описывающего регулятор, определяются линейным векторным уравнением
где G1, G2, …, Gn, h – векторы-столбцы, их элементы – числа. Значения векторов G1, G2, …, Gn определяются параметрами объекта управления. Вектор h составлен из коэффициентов полиномов передаточных функций синтезируемой системы по управляющему и возмущающему воздействиям.Регулятор с набором коэффициентов α1, α2, …, αn можно упростить, если некоторые коэффициенты обнулить и рассматривать их как константы, равные нулю, а требование (1.1) обеспечить настройкой остальных (настраиваемых) коэффициентов, значения которых можно свободно выбирать. Например, регулятор, описываемый передаточной функцией (α1p2 + α2p + α3)/(α4p2 + + α5p + α6), где p – комплексная переменная преобразования Лапласа, можно упростить и получить PID-регулятор, если принять α4 = α6 ≡ 0, или PI-регулятор, если принять α1 = α4 = α6 ≡ 0. Регулятор первого порядка с передаточной функцией (α2p + α3)/(α5p + α6) получается, если принять α1 = α4 ≡ 0. В данном примере рассмотрен динамический регулятор со скалярной обратной связью по выходу системы. Очевидно, аналогичные упрощения могут производиться и по отношению к операторным уравнениям, описывающим регуляторы с векторной обратной связью, в которой кроме выхода системы (управляемой переменной) используется произвольный набор переменных состояния и возмущающего воздействия.
Сокращение набора настраиваемых коэффициентов и, таким образом, упрощение регулятора ограничивается необходимостью выполнения условия (1.1). Набор настраиваемых коэффициентов {αi}, i ∈ S ⊆ {$\overline {1,n} $} должен быть таким, чтобы обеспечивалась возможность выполнить условие (1.1) выбором значений этих коэффициентов при условии равенства нулю остальных коэффициентов, т.е. при условии αi ≡ 0, ∀i ∉ S.
Набор S взаимно однозначно определяет структуру регулятора, поэтому далее будем отождествлять набор S и структуру регулятора. В некотором наборе S могут присутствовать избыточные элементы, т.е. такие, которые можно исключить из S, сохранив возможность выполнения условия (1.1). Исключение компонент из S эквивалентно обнулению соответствующих коэффициентов αi в (1.1). Если исключить из некоторого набора S все избыточные компоненты, получим набор, в котором исключение любой компоненты приводит к невозможности выполнить все требования, предъявляемые к синтезируемой системе.
Определение 1. Набор S, обеспечивающий выполнение всех требований к синтезируемой системе, в котором исключение любой компоненты приводит к невозможности выполнить все требования к синтезируемой системе, будем называть простым набором, определяющим простую структуру регулятора. Соответствующий регулятор с простым набором настраиваемых коэффициентов {αi}, i ∈ S ⊆ {$\overline {1,n} $}, является простым регулятором (регулятором несокращаемой сложности).
Регулятор с набором настраиваемых коэффициентов {αi}, i ∈ S ⊆ {$\overline {1,n} $}, позволяет реализовать равенство (1.1), т.е. придать системе желаемые характеристики, если пространство векторов Gi, i ∈ S (векторов GS) содержит вектор h или, что эквивалентно, если вектор h принадлежит линейной оболочке [34] векторов GS.
Набор векторов GS является простым, если составляющие его векторы линейно независимы, а их оболочка содержит вектор h. В таком случае исключение любого вектора из набора GS приводит к выходу вектора h из их оболочки. Иными словами, простой набор GS является базисом в пространстве векторов {GS, h}.
Простой регулятор может быть не единственным, т.е. может быть несколько простых регуляторов, обеспечивающих решение задачи синтеза, особенно в случае, когда допускается приближенное выполнение условия (1.1). Простые регуляторы в силу использования различных наборов S различаются перечнем обратных связей, передаточными функциями, а также робастностью системы, использующей данный регулятор. Выбор предпочтительного варианта регулятора основывается на учете указанных различий. Для каждого простого набора векторов GS уравнение (1.1) однозначно определяет значения настраиваемых коэффициентов регулятора {αi}, i ∈ S.
Таким образом, свобода выбора при синтезе простых регуляторов имеется лишь в части выбора структуры регулятора S.
В данной работе в качестве оценочного показателя при выборе структуры простого регулятора будем рассматривать степень робастности системы, обеспечиваемой регулятором. Считаем, что значения компонент вектора h назначены при определении желаемых передаточных функций замкнутой системы по управляющему и возмущающему воздействиям с учетом требований робастности. В таком случае малые изменения вектора h не приводят к потере устойчивости и значительному ухудшению характеристик системы.
Робастность системы можно обеспечить, если исключить возможность больших изменений вектора h в результате малых изменений параметров объекта управления. Для этого необходимо, чтобы структура S регулятора обеспечивала малую чувствительность вектора h к вариациям параметров объекта управления.
Вариации параметров объекта вызывают отклонения векторов Gk, k ∈ S, от их номинальных значений на величины ΔGk, что, согласно (1.1), приводит к изменению вектора h. Отклонение Δhk вектора h от номинала, обусловленное отклонением ΔGk, определяется, согласно (1.1), равенством Δhk = αkΔGk. Следовательно, $\left\| {\Delta {{h}_{k}}} \right\|$ = αk$\left\| {\Delta {{G}_{k}}} \right\|$, где – $\left\| {\, \cdot \,} \right\|$ норма вектора, откуда получаем
Коэффициент чувствительности γk вектора параметров h системы к вариациям параметров объекта, проявляющимся через вектор Gk, определим как отношение относительного приращения $\left\| {\Delta {{h}_{k}}} \right\|$/$\left\| h \right\|$ нормы вектора h к относительному приращению $\left\| {\Delta {{G}_{k}}} \right\|$/$\left\| {{{G}_{k}}} \right\|$ нормы вектора Gk. Тогда с учетом (1.2) получаем
Для простого набора S, согласно правилу Крамера [34], αk = det(h,GS\k)/detGS, где detGS – детерминант (определитель) матрицы GS, а det(h, GS\k) – определитель матрицы, получаемой из матрицы GS заменой столбца Gk, k ∈ S на столбец h. Следовательно, равенство (1.3) можно записать в виде
(1.4)
${{\gamma }_{k}} = \frac{{\left\| {{{G}_{k}}} \right\|\det (h,{{G}_{{S\backslash k}}})}}{{\left\| h \right\|\det {{G}_{S}}}}.$В общем случае, включающем приближенное выполнение равенства (1.1), значения {αi}, i ∈ S, будем определять методом наименьших квадратов. Тогда αk = det($G_{S}^{{\text{T}}}$h, ΓS\k)/detΓS, где detΓS – определитель матрицы Грама системы векторов GS, т.е. определитель матрицы ΓS = GSTGS; при этом det($G_{S}^{{\text{T}}}$h, ΓS\k) – определитель матрицы, получаемой из матрицы ΓS заменой в ней столбца, соответствующего Gk, k ∈ S, на столбец $G_{S}^{{\text{T}}}$h. Следовательно,
(1.5)
${{\gamma }_{k}} = \frac{{\left\| {{{G}_{k}}} \right\|\det ({{G}_{S}}^{{\text{T}}}h,{{\Gamma }_{{S\backslash k}}})}}{{\left\| h \right\|\det {{\Gamma }_{S}}}}.$Из полученных выражений (1.3)–(1.5) следует, что чувствительность γk возрастает: 1) с ростом длины вектора Gk, отнесенной к длине вектора h; 2) при приближении к нулю определителя detΓS, т.е. при слабой степени линейной независимости векторов GS, 3) при возрастании определителя det($G_{S}^{{\text{T}}}$h, ΓS\k), т.е. при приближении вектора h к вектору нормали гиперплоскости, в которой лежат векторы Gi, i ∈ S\k (векторы GS\k).
Перечисленные факторы, вызывающие возрастание коэффициентов γk, являются фундаментальными причинами высокой чувствительности системы к параметрическим возмущениям.
Гиперчувствительность системы к вариациям параметров объекта имеет место, как следует из сказанного выше, если: 1) в наборе векторов GS есть вектор Gk с длиной существенно больше длины вектора h; 2) векторы GS почти линейно зависимы, т.е. лежат почти целиком в некоторой гиперплоскости ℑ их полного пространства; 3) вектор h почти ортогонален линейной оболочке векторов GS\k. В таком случае вектор Gk расположен под малым углом к гиперплоскости ℑ и малое его отклонение может привести его в ℑ, т.е. в оболочку векторов GS\k. В результате вектор h, согласно (1.1), совершит поворот, переместившись из исходного положения в гиперплоскость ℑ. Поскольку вектор h в исходном положении почти ортогонален ℑ, то угол его поворота окажется большой, его новое положение окажется квазиортогонально номинальному положению. Дальнейший поворот вектора Gk с пересечением гиперплоскости ℑ может развернуть вектор h на угол, близкий 180°. В таком случае малое отклонение вектора Gk вызовет большое отклонение вектора h и соответствующее изменение пропорций коэффициентов полиномов передаточных функций замкнутой системы вплоть до смены их знаков, что влечет за собой изменение характеристик системы вплоть до потери устойчивости.
В качестве показателя, оценивающего чувствительность системы к вариациям параметров объекта, при использовании регулятора со структурой, определяемой набором S, будем применять норму вектора γ = (γk), k ∈ S, т.е. величину
В частности, могут использоваться нормы, описываемые формулой
Чувствительность γ(S) при использовании нормы ${{\left\| {{\gamma }} \right\|}_{\infty }}$ возрастает или, как минимум, остается неизменной при усложнении регулятора, т.е. при смене значения S на значение S ' ⊃ S имеем γ(S ') ≥ γ(S). Этим объясняется феномен снижения грубости регуляторов с ростом их порядка, отмечаемый многими авторами [19–23, 33].
Определение 2. Робастность системы, в которой используется регулятор со структрой S, будем оценивать показателем
Высокой робастности и низкой чувствительность системы к вариациям параметров объекта соответствуют большие значения ρ(S) и наоборот.
Показатель робастности ρ(S) является функцией набора S ⊆ {$\overline {1,n} $}. Следовательно, рациональный выбор конкретного набора S и, таким образом, выбор структуры регулятора позволяет оптимизировать робастность системы.
В данной статье предложен метод поиска простого набора S* и соответствующего ему регулятора, доставляющего максимум показателю робастности (1.7). Далее сформулируем рассматриваемую задачу более детально.
2. Математическая постановка задачи. Будем считать, что объект управления описывается системой уравнений:
где x – вектор состояния, $\dot {x}$ = dx/dt, t – время, u, f – скалярное управляющее и возмущающее воздействия, y – вектор выходов, доступных для использования в качестве сигналов обратной связи в регуляторе, его первая компонента y1 является выходом синтезируемой системы, A, C и Bu, Вf – заданные постоянные матрицы и векторы соответствующих размерностей, их элементы – действительные числа.Из уравнений (2.1), (2.2) следует уравнение, отражающее зависимость вектора выходов y от воздействий u, f:
где a(p) – характеристический полином объекта управления, bu(p), bf (p) – векторы, компоненты которых – полиномы числителей передаточных функций объекта управления соответственно по управляющему и возмущающему воздействиям, p – комплексная переменная преобразования Лапласа.Регулятор опишем уравнением
где g – скалярное задающее воздействие (вход синтезируемой системы), r(p), qg(p), qf(p) – полиномы, $\ell (p)$ – полиномиальный вектор-строка, r(p) – характеристический полином регулятора, qg(p), $\ell (p)$, qf(p) – числители передаточных функций регулятора соответственно по задающему воздействию, по каналам обратных связей и по возмущающему воздействию.Из уравнений (2.3), (2.4) следует уравнение, отражающее зависимость выхода синтезируемой системы y1 от воздействий g, f:
в нем где hs(p) – характеристический полином синтезируемой системы, hg(p), hf(p) – полиномы числителей передаточных функций синтезируемой системы соответственно по задающему и возмущающему воздействиям, c(p) – вектор, i-я компонента которого определяется выражением ci(p) = = [bui(p)bf1(p) – bfi(p)bu1(p)]/a(p), причем ci(p) – полином. Oбъект управления является управляемым по выходу y1 относительно управляющего воздействия u, поэтому bu1(p) ≠ 0.Считаем заданными желаемые значения коэффициентов полиномов hs(p), hg(p), hf(p), обеспечивающие соответствие характеристик системы назначенным требованиям.
Уравнения (2.6)–(2.8) линейны относительно искомых полиномов регулятора и сводятся в результате приравнивания коэффициентов при одинаковых степенях оператора p к системе уравнений (1.1), которая в матричной форме записи имеет вид
где вектор неизвестных α составлен из коэффициентов искомых полиномов регулятора qg(p), qf(p), $\ell (p)$, r(p), а вектор h – из коэффициентов полиномов синтезируемой системы hs(p), hg(p), hf(p). Матрица G = (Gk), k ∈ {$\overline {1,n} $}, составлена из столбцов Gk, элементы которых определяются параметрами объекта управления, согласно уравнениям (2.6)–(2.8).Набор S номеров координат вектора α, свободно выбираемых при решении уравнения (2.9), определяет структуру регулятора с учетом уравнения (2.4) и тождеств αi ≡ 0, ∀i∉S.
Необходимым условием допустимости структуры регулятора S является возможность выборa значений настраиваемых параметров, указанных в S, выполнить требование (2.9) с приемлемой точностью. Это условие описывается формулой
(2.10)
$\exists \alpha :{\text{|}}G\alpha --h{\text{|}} \leqslant \Delta ,\quad {{\alpha }_{i}} \equiv 0,\quad \forall i \in S,~~~~~~$Кроме условия (2.10) при проверке допустимости структуры S будем учитывать список ψ заведомо недопустимых (запрещенных) структур S. В список ψ можно включить наборы S, требующие либо исключающие тождество нулю в (2.10) тех или иных компонент вектора α. В обязательном порядке в запрещающий список ψ включим наборы S, которые предполагают тождество нулю одновременно всех αi, обозначающих коэффициенты полинома r(p), тем самым запретим тождество r(p) ≡ 0. При необходимости в ψ можно включить наборы, запрещающие присутствие в них некоторых сочетаний свободных и тождественных нулю компонент вектора α. Например, можно учесть требование согласования порядков полиномов регулятора: degr(p) ≥ max(degli(p), degqg(p), degqf(p)), i ∈ I, где I – множество номеров компонент вектора y. Для этого в запрещающий список ψ добавляют все наборы S, для которых условие согласования порядков заведомо не выполняется.
Множество допустимых структур регуляторов и соответствующих им допустимых наборов S обозначим как ζ. Допустимость набора S определяется формулой
(2.11)
$S \in \zeta \Leftrightarrow (S \notin \psi )\& (\exists \alpha :{\text{|}}G\alpha --h{\text{|}} \leqslant \Delta ,{{\alpha }_{i}} \equiv 0,\forall i \notin S).~$Определение 3. Структура регулятора, определяемая допустимым набором S, является простой, если не существует допустимый набор S', являющийся подмножеством набора S, т.е.
(2.12)
$S \in \Omega \Leftrightarrow (S \in \zeta )\& (\bar {\exists }S' \in \zeta :S{\kern 1pt} ' \subset S),~$Настраиваемые параметры αS = {αi}, i ∈ S, регулятора с простой структурой, определяемой набором S ∈ Ω, вычисляются методом наименьших квадратов из условия минимизации невязки решения уравнения (2.9), дополненного тождествами αi ≡ 0, ∀i ∉ S. Таким образом
где A+ – матрица, псевдообратная для GS, т.е. A + = (ATA)–1AT, где A = GS .Решаемая задача состоит в поискe простого набора S*, доставляющего максимум показателю робастности (1.7), т.е. требуется найти:
(2.14)
$S{\text{*}} \in \Omega :\rho \left( {S{\text{*}}} \right) = \mathop {{\text{max}}}\limits_{S \in \Omega } \rho (S).$Набор S* определяет искомую структуру регулятора, оптимального по показателю робастности (1.7).
3. Метод решения. Сформулированная выше задача является задачей конечномерной оптимизации. В ней заданы матрица G, вектор h, множество ψ, величина Δ. Требуется с учетом ограничений (2.11), (2.12) определить структуру S* и соответствующие ей, согласно (2.13), значения настраиваемых параметров регулятора, обеспечив, согласно (2.14), максимум целевой функции ρ(S), вычисляемой по формулам (1.5)–(1.7). В рассматриваемой задаче целевая функция ρ(S) является нелинейной действительной функцией дискретного аргумента S ⊂ {$\overline {1,n} $}. Ограничения, стесняющие выбор значений S, описываются нелинейными функциями и логическими условиями. Такое сочетание целевой функции, области определения ее аргумента и ограничений выходит за рамки канонических задач, решаемых известными методами оптимизации. Поэтому разработан представленный ниже метод, существенно учитывающий специфику рассматриваемой задачи.
3.1. Описание метода. Предлагаемый метод сводится к следующим действиям.
Шаг 1. Проверяем условие (2.10) для S = {$\overline {1,n} $}. Если оно не выполняется, то задача неразрешима, допустимых наборов S не существует; иначе переходим к шагу 2.
Шаг 2. Анализируем наборы S с числом элементов (кардинальным числом) равным рангу матрицы G, т.е. наборы, для которых card(S) = rank(G), где card(⋅), rank(⋅) – функции определения кардинального числа множества и ранга матрицы. Если очередной анализируемый набор S не запрещен (не указан в списке ψ) и столбцы GS линейно независимы, тогда вычисляем αS по формуле (2.13). Если в αS отсутствуют нулевые компоненты, набор S является простым, иначе простым будет набор S\S ', где S ' – множество номеров нулевых компонент вектора αS. Проверяем соответствие характеристик системы заданным требованиям при использовании регулятора с найденной простой структурой. В случае успешного прохождения проверки для найденного простого набора и соответствующих ему параметров регулятора все его надмножества включаем в ψ, вычисляем значение показателя робастности (1.7) и, если оно лучше рекордного, это значение запоминаем как новый рекорд, а соответствующий ему набор S # – как наилучший. Запоминаем значение αS# вектора настраиваемых параметров регулятора со структурой S #. Если анализируемый набор S не запрещен, но столбцы GS линейно зависимы, тогда рекурсивно выполняем шаги 1 и 2, присвоив матрице G значение GS. Если проанализированы все наборы S, для которых card(S) = rank(G), поиск завершен.
Шаг 3. Присваиваем искомому набору S*, определяющему оптимальную структуру регулятора, значение S #, искомым значениям параметров αS* – значение αS#.
3.2. Обоснование метода. На шаге 1 проверяется требование (2.10) для полного набора S = {$\overline {1,n} $}, поэтому невозможность его выполнения исключает наличие допустимых наборов S ⊂ {$\overline {1,n} $}. На шаге 2 исключены наборы, для которых card(S) > rank(G), поскольку такие наборы избыточны: любой линейно независимый набор S с card(S) = rank(G) определяет всю линейную оболочку столбцов матрицы G, поэтому расширение набора S не расширяет возможностей выполнения условия (2.10). Набор S на шаге 2 признается простым при выполнении условий, эквивалентных условиям (2.12). Действительно: проверяется условие S ∈ ζ, а проверка условия $\bar {\exists }$S ' ∈ ζ: S ' ⊂ S сведена к эквивалентной проверке линейной независимости столбцов GS в сочетании с контролем отсутствия нулей в αS. Если набор S допустимый, но GS линейно зависимы, можно сократить этот набор и искать простые наборы среди его подмножеств предлагаемым методом, поэтому в указанном случае выполняется рекурсивное выполнение шагов 1 и 2 после присвоения матрице G значения GS.
3.3. Вычислительные аспекты метода. Проверку требования (2.10) для S = {$\overline {1,n} $} целесообразно осуществить путем вычисления нормального псевдорешения [34, 35] системы (2.9) $\tilde {x}$ с использованием псевдообратной матрицы Мура–Пенроуза [35]. Вектор псевдорешения $\tilde {x}$ является ортогональной проекцией вектора h на линейную оболочку столбцов матрицы G и значение |Gα – h| минимально, когда α = $\tilde {\alpha }$. В результате условие (2.10) для S = {$\overline {1,n} $} сводится к условию |G$\tilde {\alpha }$ – h| ≤ Δ. Перед поиском псевдорешения $\tilde {x}$ целесообразно нормализовать уравнения (2.9), поделив каждое уравнение на значение его правой части, если это значение отлично от нуля. В результате погрешности выполнения уравнений (2.9) не будут существенно различаться. Ранг матрицы при реализации рассматриваемого метода можно вычислять как количество отличных от нуля сингулярных чисел. При проверке отличия чисел от нуля целесообразно использовать известные рекомендации [35] по учету ограниченной точности представления чисел в машинной арифметике.
4. Пример. Рассмотрим задачу синтеза регулятора системы управления электроприводом с учетом конечной жесткости механической передачи движения от двигателя к нагрузке. Объект управления, включающий в себя двигатель постоянного тока, редуктор и нагрузку, описывается [36] системой уравнений (2.1), (2.2), в которой в рассматриваемом примере матрица C – единичная матрица,
Полиномы $h_{g}^{*}$(p), $h_{s}^{*}$(p) желаемой передаточной функции замкнутой системы по задающему воздействию φн(p)/g(p) = $W_{g}^{*}$(p) = $h_{g}^{*}$(p)/$h_{s}^{*}$(p) имеют следующие значения:
С целью обнуления статической ошибки слежения, вносимой возмущающим воздействием, потребуем равенство нулю младшего коэффициента полинома $h_{f}^{*}(p)$ желаемой передаточной функции системы по возмущающему воздействию ${{\varphi }_{{\text{н}}}}(p){\text{/}}f(p) = W_{f}^{*}(p)$ = $h_{f}^{*}(p){\text{/}}h_{s}^{*}(p)$. Значения остальных коэффициентов полинома $h_{f}^{*}(p)$ не назначаем.
Зададим максимально допустимый порядок регулятора равным двум. Считаем, что в передаточных функциях регулятора порядок знаменателя должен быть не меньше, чем порядок числителя, т.е. порядок полиномов qg(p), qf(p), $\ell (p)$ не должен превышать порядка полинома r(p). Кроме того, в наборе обратных связей, реализуемых регулятором, обязательно присутствие обратной связи по выходной переменной. Учитывая недоступность для использования в регуляторе значений возмущающего воздействия f, считаем qf(p) ≡ 0. Из коэффициентов полиномов регулятора qg(p), l1(p), l2(p), l3(p), l4(p), l5(p), r(p), остающихся неизвестными, составляем вектор-столбец искомых параметров регулятора:
В список ψ запрещенных наборов включим наборы S, предполагающие тождество нулю одновременно всех коэффициентов полинома r(p), тем самым запретим тождество r(p) ≡ 0. Кроме того, в ψ включаем наборы S, для которых заведомо не выполняется вышеуказанное условие согласования порядков полиномов регулятора, а также наборы S, не содержащие компоненту вектора α, которая соответствует обратной связи по выходной переменной.
Из (2.6)–(2.8), следуя известным правилам перехода от полиномиальных уравнений к алгебраическим [34], получаем систему уравнений вида (2.9), определяющих связь назначенных значений коэффициентов полиномов hg(p), hs(p), hf (p) с параметрами объекта управления и вектором искомых коэффициентов регулятора α. Задаем допустимую невязку приближенного решения уравнения (2.9): Δ = $\left\| h \right\|{\text{/}}100$.
В соответствии с предложенным методом, убедившись в выполнении условия (2.10) для S = {$\overline {1,n} $}, переходим к анализу наборов S, составленных из компонент вектора α с числом элементов card(S) = rank(G) = 10. Следуя предложенному методу, находим простые структуры и среди них – структуру S*, доставляющую максимум целевой функции ρ(S), вычисляемой по формулам (1.5)–(1.7). Параметры $\alpha _{S}^{*}$ определяются формулой (2.13).
В результате поиска найдено 306 простых структур регуляторов, соответствующих условиям (2.11), (2.12) и, следовательно, обеспечивающих выполнение всех требований, предъявляемых к синтезируемой системе. Все они при номинальных значениях параметров объекта управления в равной мере обеспечивают реализацию назначенной желаемой передаточной функции замкнутой системы. Однако они существенно различаются по робастности: соответствующие им значения показателя чувствительности синтезируемой системы ${{\left\| {{\gamma }} \right\|}_{\infty }}$, вычисленные, согласно (1.5), (1.6), лежат в диапазоне от 0.68 до 2.85 × 105, что, согласно (1.7), соответствует значениям показателя робастности ρ(S) в диапазоне от 3.5 × 10–6 до 1.47. Проверка показывает, что параметрическое возмущение приводит к потере устойчивости системы, использующей регулятор с низким значением ρ(S). Например, возмущение, состоящее в отклонении на 15% от номиналов параметров c, χ в меньшую сторону и параметра Jl в большую сторону, приводит систему к потере устойчивости, если в ней применен регулятор со значением ρ(S) менее 0.15 × 10–3. Таким образом, оказалось, что из 306 найденных простых структур только 110 способны сохранить устойчивость системы при указанном возмущении. Причем подавляющее большинство (107 из 110) структур, сохраняющих устойчивость, имеют значение ρ(S) более 6.5 × 10–3. Среди них положительно выделяются структуры с ρ(S) > 0.1. Все они демонстрируют малые отклонения переходной функции (реакции на единичное ступенчатое управляющее воздействие) системы от номинальной при вышеуказанном параметрическом возмущении.
Структуре S*, оптимальной по показателю робастности ρ(S), соответствует значение ρ(S*) = 1.47. Регулятор с этой структурой описывается операторным уравнением
Он реализует обратную связь по переменным y1 ≡ φн, y2 ≡ ωн и y4 ≡ ω с коэффициентами передачи l1(p) = l10; l2(p) = l21p; l4(p) = l40 + l42p2. Его характеристический полином r(p) = r1p + r2p2, а коэффициент передачи в цепи задающего воздействия qg(p) = qg0 + qg1p + qg2p2.
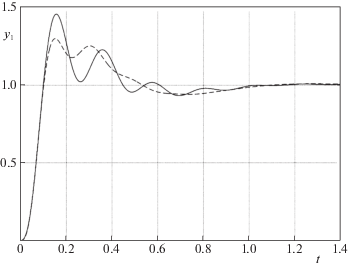
На рис. 1 представлен график переходной функции системы с регулятором, имеющим оптимальную структуру S*, при наличии параметрического возмущения (сплошная линия) в сравнении с графиком (пунктирная линия) номинальной переходной функции синтезируемой системы. Сопоставление графиков демонстрирует малое отклонение возмущенной переходной функции (сплошная линия) системы с регулятором S* от номинальной переходной функции (пунктирная линия).
Рис. 1.
График возмущенной (сплошная линия) и номинальной (пунктирная линия) переходной функции системы с оптимальным робастным регулятором (ρ(S) = 1.47)
Структуры, характеризующиеся низким значением показателя робастности ρ(S), демонстрируют большое отклонение возмущенной переходной функции системы от номинальной и ее высокую колебательность, что свидетельствуeт о существенном снижении запасов устойчивости системы.
На рис. 2 и 3 представлены графики переходных функций системы с регулятором, характеризующимся низким значением показателя робастности ρ(S).
Рис. 2.
График возмущенной (сплошная линия) и номинальной (пунктирная линия) переходной функции системы с регулятором низкой робастности (ρ(S) = 0.0084)
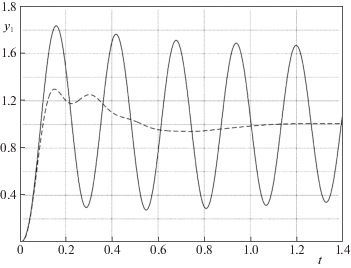
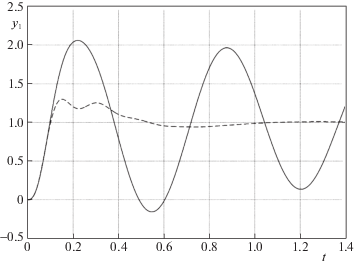
Рис. 3.
График возмущенной (сплошная линия) и номинальной (пунктирная линия) переходной функции системы с регулятором низкой робастности (ρ(S) = 0.0066)
Простой регулятор c минимальным показателем робастности (ρ(S*) = 3.5 × 10–6) описывается уравнением
Он реализует обратную связь по переменным y1 ≡ φн, y2 ≡ ωн, y3 ≡ φ и y4 ≡ ω с коэффициентами передачи l1(p) = l10; l2(p) = l20; l3(p) = l30; l4(p) = l40 + l41p. При вышеуказанном параметрическом возмущении система с таким регулятором оказывается неустойчивой.
Таким образом, рассмотренный пример демонстрирует эффективность применения предложенного метода синтеза простых робастных регуляторов с использованием показателя робастности ρ(S), вычисляемого, согласно (1.5)–(1.7).
Заключение. Предложен формализованный метод решения задачи синтеза регулятора с простой структурой в составе линейной системы со скалярным управлением и векторной обратной связью при наличии возмущающего воздействия. Синтезируемый регулятор придает замкнутой системе заданные характеристики и максимальную робастность, оцениваемую с использованием оригинального показателя грубости.
Список литературы
Солодовников В.В. Синтез корректирующих устройств следящих систем при типовых воздействиях // АиТ. 1951. Т. 12. Вып. 5. С. 352–388.
Солодовников В.В., Ленский В.Л. Синтез систем управления минимальной сложности // Изв. АН СССР. Техн. кибернетика. 1966. № 2. С. 56–68.
Солодовников В.В., Бирюков В.Ф., Тумаркин В.И. Принцип сложности в теории управления. М.: Наука, 1977. 344 с.
Solodovnikov V. Poorly Defined Problems of Stochastic Optimization and Their Solution with the Aid of the Principle of Complexity // IFAC Proceedings Volumes. 1977. V. 10. № 6. P. 649–651.
Солодовников В.В., Тумаркин В.И. Теория сложности и проектирование систем управления. М.: Наука, 1990. 168 с.
Параев Ю.И., Смагина В.И. Задачи упрощения структуры оптимальных регуляторов // АиТ. 1975. № 6. С. 180–183.
Balestrino A., Celentano G. CAD of Minimal Order Controllers // IFAC Proceedings Volumes. 1979. V. 12. № 7. P. 1–8.
Balestrino A., Celentano G. Dynamic Controllers in Linear Multivariable Systems // Automatica. 1981. V. 17. № 4. P. 631–636.
Гайдук А.Р. Выбор обратных связей в системе управления минимальной сложности // АиТ. 1990. № 5. С. 29–37.
Kell L.H., Bhattacharyya S.P. State-space Design of Low-order Stabilizers // IEEE Trans. Automat. Contr. 1990. V. 35. № 2. P. 182–186.
Gu D.W., Choi B.W., Postlethwaite I. Low-order Stabilizing Controllers // IEEE Transactions on Automatic Control. 1993. V. 38. № 11. P. 1713–1717.
Wang Q.G., Lee T.H., He J.B. Low-order Stabilizers for Linear Systems // Automatica. 1997. V. 33. № 4. P. 651–654.
Fan J.C., Kobayashi T. A Simple Adaptive PI Controller for Linear Systems with Constant Disturbances // IEEE Transactions on Automatic Control. 1998. V. 43. № 5. P. 733–736.
Grieder P., Kvasnica M., Baotić M., Morari M. Stabilizing Low Complexity Feedback Control of Constrained Piecewise Affine Systems // Automatica. 2005. V. 41. № 10. P. 1683–1694.
Sano H. Low Order Stabilizing Controllers for a Class of Distributed Parameter Systems. Automatica. 2018. V. 92. P. 49–55.
Bu J., Sznaier M. A Linear Matrix Inequality Approach to Synthesizing Low-Order Suboptimal Mixed 𝓁1/Hp Controllers // Automatica. 2000. V. 36. № 7. P. 957–963.
Grigoriadis K.M., Skelton R.E. Low-order Control Design for LMI Problems Using Alternating Projection Methods // Automatica. 1996. V. 32. № 8. P. 1117–1125.
Wang S., Chow J.H. Low-order Controller Design for SISO Systems Using Coprime Factors and LMI // IEEE Transactions on Automatic Control. 2000. V. 45. № 6. P. 1166–1169.
Bhattacharyya S.P., Shapellat H., Keel L. Robust Control: the Parametric Approach. Upper Saddle River. N.J.: Prentice Hall, 1995. 672 p.
Киселев О.Н., Поляк Б.Т. Синтез регуляторов низкого порядка по критерию H∞ и по критерию максимальной робастности // АиТ. 1999. № 3. С. 119–130.
Гончаров В.И., Лиепиньш А.В., Рудницкий В.А. Синтез робастных регуляторов низкого порядка // Изв. РАН. ТиСУ. 2001. № 4. С. 36–43.
Грязина Е.Н., Поляк Б.Т., Тремба А.А. Синтез регуляторов низкого порядка по критерию H∞: параметрический подход // АиТ. 2007. № 3. С. 94–105.
Козлов О.С., Скворцов Л.М. Синтез простых робастных регуляторов // АиТ. 2015. № 9. С. 102–114.
Anderson B.D.O., Liu Y. Controller Reduction: Concepts and Approaches // IEEE Trans. Automat. Control. 1989. V. 34. P. 802–812.
Mustafa D., Glover K. Controller Reduction by H∞-balanced Truncation // IEEE Transactions on Automatic Control. 1991. V. 36. № 6. P. 668–683.
Домбровский В.В. Понижение порядка линейных многомерных систем при H∞ ограничениях // АиТ. 1994. № 4. С. 123–132.
Домбровский В.В. Синтез динамических регуляторов пониженного порядка при H∞ ограничениях // АиТ. 1996. № 11. С. 10–17.
Аполонский В.В., Тарарыкин С.В. Методы синтеза редуцированных регуляторов состояния линейных динамических систем // Изв. РАН. ТиСУ. 2014. № 6. С. 25–33.
Аполонский В.В., Копылова Л.Г., Тарарыкин С.В. Редуцирование регуляторов линейных динамических систем на основе анализа физических особенностей объекта // Изв. РАН. ТиСУ. 2016. № 5. С. 5–21.
Зотов М.Г. Алгоритм конструирования оптимальных регуляторов заданной сложности // Изв. РАН. ТиСУ. 2017. № 3. С. 3–11.
Мозжечков В.А. Синтез линейных регуляторов с простой структурой // АиТ. 2003. № 1. С. 27–41.
Мозжечков В.А. Простые структуры в теории управления. Тула: ТулГУ, 2000. 216 с.
Bhattacharyya S.P. Robust Control Under Parametric Uncertainty: An Overview and Recent Results // Annual Reviews in Control. 2017. V. 44. P. 45–77.
Воеводин В.В. Линейная алгебра. М.: Наука, 1980. 400 с.
Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений. М.: Мир, 1980. 280 с.
Крутько П.Д. Управление исполнительными системами роботов. М.: Наука, 1991. 336 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления


