Известия РАН. Теория и системы управления, 2021, № 3, стр. 23-38

Введение. Начиная с основополагающих работ А.М. Летова [1, 2] классическая задача синтеза оптимальных регуляторов в линейных системах с квадратичными критериями оптимальности до настоящего времени остается одной из центральных в теории и технике автоматического управления [3–8]. Большинство работ в этом направлении относится к системам с сосредоточенными параметрами (ССП), для которых известные результаты получены методами вариационного исчисления, принципа максимума Понтрягина, динамического программирования для детерминированных моделей объекта [1–5] и с привлечением аппарата функций Ляпунова и линейных матричных неравенств в условиях ограниченной неопределенности модельных представлений [6–8].

Проблема аналитического конструирования оптимальных регуляторов (АКОР) в линейно-квадратичных задачах оптимизации обладает принципиальной спецификой в системах управления динамическими объектами с распределенными параметрами (СРП), в рамках моделей которых описывается широкий круг управляемых процессов самой различной физической природы [9]. Возникающие здесь особенности связаны прежде всего с необходимостью решения задачи АКОР в условиях бесконечной размерности пространственно распределенной управляемой величины [10–13].

Задачи синтеза СРП в указанной постановке рассматривались путем распространения на системы с распределенными параметрами метода динамического программирования в идеализированных и реализуемых условиях соответственно полного и неполного измерения управляемых функций состояния объекта [10–13]. Основные результаты решения проблемы АКОР в ССП и СРП получены применительно к задачам со свободным или подвижным правым концом траектории движения объекта с использованием классических условий трансверсальности на гладкой границе области допустимых конечных состояний управляемой системы.

Однако в целом ряде типичных для приложений и представляющих самостоятельный интерес ситуаций требования к конечному состоянию СРП предъявляются в чебышевской метрике в форме допустимой величины ошибки равномерного приближения управляемой величины к заданному распределению в пространственной области ее определения [13–15]. Известные условия трансверсальности неприменимы на негладкой границе соответствующего целевого множества в бесконечномерном фазовом пространстве СРП, что существенно усложняет решение краевой задачи оптимального управления. В целях опознания конечной точки оптимального процесса здесь могут быть использованы ее специальные альтернансные свойства, определяемые по схеме конструктивного альтернансного метода, который является распространением на задачи оптимизации теории нелинейных чебышевских приближений [13–15].

В настоящей работе предлагается метод решения задачи АКОР для линейных моделей СРП параболического типа в условиях равномерных оценок целевых множеств применительно к детерминированному варианту и в условиях воздействия множественных возмущений. Развиваемый подход существенно опирается на результаты решения задачи оптимального программного управления с помощью альтернансных свойств искомых экстремалей [13–15].

1. Постановка задачи. Пусть управляемая величина $Q(x,t)$ объекта с распределенными параметрами описывается в зависимости от пространственной координаты $x \in [{{x}_{0}},{{x}_{1}}]$ и времени $t \in \left[ {0,t{\kern 1pt} *} \right]$ одномерным линейным уравнением второго порядка в частных производных параболического типа с самосопряженным дифференциальным оператором в его правой части:

с начальными и граничными условиями при сосредоточенном внутреннем ${{u}_{v}}(t)$ или граничном ${{u}_{s}}(t)$ кусочно-непрерывных управляющих воздействиях; заданных достаточно гладких функциях ${{f}_{v}}(x)$, ${{f}_{\eta }}(x),$ $b(x)$, $c(x)$, ${{c}_{1}}(x)$; постоянных коэффициентах ${{\alpha }_{0}},{{\alpha }_{1}} \geqslant 0,$ ${{\beta }_{0}},{{\beta }_{1}} > 0$ и кусочно-непрерывных внешних возмущениях ${{\eta }_{1}}(t),$ ${{\eta }_{2}}(t)$, учитываемых далее только по каналу управляющего воздействия. Управляющие и возмущающие воздействия не стесняются никакими дополнительными ограничениями.

Всюду далее исключается для простоты случай одновременного использования ${{u}_{v}}(t)$ и ${{u}_{s}}(t)$, полагая

Пусть необходимо обеспечить за фиксируемое априори конечное время t* заданную точность ε равномерного приближения конечного пространственного распределения управляемой величины $Q(x,t{\kern 1pt} *)$ к требуемому $Q{\kern 1pt} *{\kern 1pt} *(x) = Q{\kern 1pt} *{\kern 1pt} * = 0$, согласно соотношению

определяющему оцениваемое в равномерной метрике целевое множество конечных состояний СРП [13–15].

Пусть далее эффективность процесса управления объектом (1.1)–(1.6) оценивается квадратичным функционалом качества, определяемым для простоты и наглядности без потери общности основных результатов в следующей типичной для приложений частной форме:

с постоянными положительными весовыми коэффициентами ρ_Q и ρ_η.

Применение к уравнениям объекта (1.1)–(1.3) конечного интегрального преобразования по пространственному аргументу с ядром, равным его собственным функциям ${{\varphi }_{n}}({{\mu }_{n}},x),$ $n = 1,2,...$, где $\mu _{n}^{2}$ – собственные числа, приводит к представлению СРП бесконечной системой обыкновенных дифференциальных уравнений первого порядка для временных мод ${{\bar {Q}}_{n}}({{\mu }_{n}},t)$ разложения $Q(x,t)$ в сходящийся в среднем ряд по ${{\varphi }_{n}}({{\mu }_{n}},x)$ [16]:

Здесь ${{k}_{{vn}}},{{k}_{{1n}}},$ $\bar {Q}_{{}}^{{(0)}}({{\mu }_{n}})$ – моды конечных интегральных преобразований функций ${{f}_{v}}(x),\;{{f}_{\eta }}(x)$ и ${{Q}_{0}}(x)$ соответственно, ${{k}_{{sn}}},{{k}_{{2n}}}$ – известные постоянные коэффициенты [16].

Можно показать [17, 18], что в малостеснительных условиях выполнения усиленных [17, 18] условий Коши–Липшица система уравнений (1.8) имеет единственное решение при заданных воздействиях $u(t)$, $\eta (t),$ которое с любой требуемой точностью при необходимости аппроксимируется решением “укороченной” системы, образуемой достаточно большим конечным числом $N$ первых уравнений (1.8) при ${{\bar {Q}}_{n}}({{\mu }_{n}},t) = 0$ $\forall n > N$, т.е. оказывается допустимой конечномерная аппроксимация модели (1.8) при $n = \overline {1,N} ,$ $N < \infty $. Всюду далее на этом основании учитываются ${{N}_{1}}$ мод ${{\bar {Q}}_{n}},\,n = \overline {1,{{N}_{1}}} $ в (1.8), где ${{N}_{1}} = \infty $ или ${{N}_{1}} = N < \infty $ в зависимости от используемой схемы анализа и возможностей практической реализации исследуемых алгоритмов управления. Конкретный выбор числа N₁ должен производиться при проектировании системы управления, исходя из практически требуемой точности описания модели объекта N₁уравнениями (1.8).

Переход к описанию СРП в (1.8), (1.9) в терминах модальных переменных приводит в силу ортонормированности семейства собственных функций [16] к представлению критерия (1.7) в следующем виде:

а требования (1.6) к конечному состоянию объекта представляются условием

Рассматриваемая задача АКОР сводится к определению алгоритма обратной связи $u(Q,\,t,\,\eta )$, обеспечивающего перевод не полностью определенного в условиях воздействия внешних возмущений бесконечномерного объекта (1.8), (1.9) в требуемое конечное состояние (1.11) при минимально возможном значении критерия оптимальности (1.10).

В типичных частных случаях внешнее возмущение η(t) в (1.5) определяется заданной кусочно-непрерывной функцией времени [3, 4].

2. Программное оптимальное управление при детерминированном возмущении. Структура оптимального управления. На сформулированную бесконечномерную задачу оптимизации распространяется принцип максимума Понтрягина [13, 19]. Базовое условие

достижения на соответствующих оптимальному процессу величинах $\bar {Q}{\kern 1pt} {\text{*}}(t),\;u{\kern 1pt} {\text{*}}(t),\;\psi {\kern 1pt} {\text{*}}(t)$ максимума функции Понтрягина Н по переменной и для рассматриваемой задачи оптимизации (1.8)–(1.11) где $\bar {Q}(t) = (\bar {Q}_{n}^{{}}({{\mu }_{n}},t)),$ $n = \overline {1,{{N}_{1}}} ,$ и вектор сопряженных переменных $\psi (t) = \left( {{{\psi }_{n}}(t)} \right),$ $n = \overline {1,{{N}_{1}},} $ описывается системой уравнений определяет в открытой области изменения управляющих воздействий программное оптимальное управление $u{\kern 1pt} {\text{*}}(t)$ в форме явной функции от $\psi {\kern 1pt} {\text{*}}(t)$:

Здесь

Краевая задача принципа максимума. Уравнения (1.8) с подстановкой управляющего воздействия в виде (2.4) образуют совместно с (2.3) линейную программно-управляемую систему, замыкаемую относительно неизвестных $\bar {Q}(t)$ и $\psi (t)$ требованиями (1.11) к конечному состоянию объекта:

где по-прежнему k_n определяется, согласно (2.5), и ${{\tilde {k}}_{n}} = {{k}_{{1n}}},$ $\eta (t) = {{\eta }_{1}}(t),$ если $u(t) = {{u}_{v}}(t),$ ${{\tilde {k}}_{n}} = {{k}_{{2n}}},$ $\eta (t) = {{\eta }_{2}}(t),$ если $u(t) = {{u}_{s}}(t)$.

Решение этой системы может быть представлено в векторно-матричной форме [3, 4]:

Здесь

вектор-столбец коэффициентов ${{\tilde {k}}_{n}}$; А – матрица коэффициентов системы (2.6); ${{e}^{{At}}}$ – определяемая известными способами [3, 4, 20, 21] нормированная фундаментальная матрица размерностью $2{{N}_{1}} \times 2{{N}_{1}}$ (матричная экспонента), столбцами которой являются линейно-независимые решения однородной системы (2.6) при ${{\eta }_{1}} = {{\eta }_{2}} = 0$.

Матричная экспонента представляется в блочном виде

где блоки $A_{{ij}}^{{}}(t);$ $i,j = 1,2$, – известные матрицы размерности ${{N}_{1}} \times {{N}_{1}}$ в соответствии со структурой системы уравнений (2.6) [3, 4, 20].

Параметризация управляющих воздействий. Согласно (2.7), $\psi (t)$, а, следовательно, и программное управление (2.4) определяются для каждой известной величины $\bar {Q}(0)$ с точностью до вектора $\psi (0)$ начальных значений сопряженных функций, выступающих, таким образом, в роли параметрического представления $u{\kern 1pt} {\text{*}}(t)$ [22, 23]. Однако для СРП такой подход оказывается неконструктивным, прежде всего, в силу бесконечной размерности этого вектора в (2.6) при ${{N}_{1}} = \infty $. В работе [15] применительно к требованиям (1.11), предъявляемым к $\bar {Q}{\kern 1pt} {\text{*}}(t{\kern 1pt} {\text{*}})$, предложен конструктивный способ последовательной конечномерной параметризации управляющих воздействий (“$\psi $-параметризация”) на множестве М-мерных векторов ${{\psi }^{{(M)}}} = ({{\tilde {\psi }}_{i}}),$ $i = \overline {1,M} ;$ ${{\tilde {\psi }}_{i}} = {{\psi }_{i}}(t{\kern 1pt} *),$ $M < {{N}_{1}}$, конечных значений ${{\tilde {\psi }}_{i}}$ первых М сопряженных функций в (2.6) при равных нулю всех остальных значениях ${{\psi }_{i}}(t{\kern 1pt} *)$:

С возрастанием М обеспечивается попадание под действием параметризуемых на множестве параметров (2.9) управляющих воздействий вида (2.4) в сужающееся к началу координат в пространстве $({{\bar {Q}}_{n}})$ целевое множество, гарантируя выполнение условий (1.11) для достижимых значений $\varepsilon $ при некотором конечном значении $M \geqslant 1$ [15].

С целью определения в явной форме $\psi $-параметризованного управления найдем вектор ${{[{{\psi }^{{\text{T}}}}(0)\,\,{{\bar {Q}}^{{\text{T}}}}(0)]}^{{\text{T}}}}$ из (2.7) при $t = t{\kern 1pt} *$ и, подставляя результат опять в (2.7), получим решение системы (2.6) в форме его зависимости от конечного состояния ${{[{{\psi }^{{\text{T}}}}(t{\kern 1pt} *)\;{{\bar {Q}}^{{\text{T}}}}(t{\kern 1pt} *)]}^{{\text{T}}}}$:

С учетом блочного представления (2.8) матричной экспоненты равенство (2.10) определяет векторы $\psi (t)$ и $\bar {Q}(t)$ в следующей форме:

где и ${{\hat {A}}_{{ij}}};$ $i,j = 1,2$, – подобные (2.8) блоки обратной матрицы ${{e}^{{ - At}}}$.

После подстановки (2.8) в (2.7) будем иметь, согласно (2.7), при $t = t{\kern 1pt} *$:

где

Определяя $\psi (0)$ из (2.14) и подставляя результат в (2.15), получим следующее выражение для $\bar {Q}(t{\kern 1pt} *)$ в форме линейной функции начального состояния объекта $\bar {Q}(0)$ и априори неизвестных конечных значений $\psi (t{\kern 1pt} *)$ сопряженных переменных:

где

При описании $\bar {Q}(t{\kern 1pt} *)$ в (2.11), (2.12) соотношением (2.17) получим, согласно (2.11), следующее выражение для вектора ψ*(t) в оптимальном процессе в зависимости от его параметризуемой конечной величины ψ*(t*) в (2.9) и начального состояния объекта $\bar {Q}(0){\text{:}}$

Искомое программное управление (2.4)

где K – матрица – строка, ψ*(t) – матрица-столбец, определяется в ψ-параметризованной форме в виде линейной зависимости от ${{\psi }^{{(M)}}}$ в (2.9) после подстановки (2.19) в (2.20).

Редукция к задаче полубесконечной оптимизации. Интегрирование уравнений системы (2.6) с ψ-параметризованным управляющим воздействием вида (2.9), (2.19), (2.20) позволяет получить при заданном детерминированном воздействии $\eta (t)$ зависимости $Q(x,{{\psi }^{{(M)}}})$ управляемой величины в конце процесса управления и критерия оптимальности ${{I}_{1}}({{\psi }^{{(M)}}})$ в (1.9), (1.10) для каждого значения $\bar {Q}(0)$ в форме явных функций только своих аргументов [15].

В результате осуществляется точная редукция исходной задачи оптимального управления к задаче полубесконечной оптимизации (ЗПО) [13–15]:

на экстремум функции ${{I}_{1}}({{\psi }^{{(M)}}})$ конечного числа М переменных ${{\tilde {\psi }}_{i}},\;i = \overline {1,M} $, с бесконечным числом ограничений, порождаемых требованием выполнения условия (1.11) для всех $x \in [{{x}_{0}},{{x}_{1}}]$.

Как показано в [15], для заданной величины ε в (1.11) размерность М вектора ${{\psi }^{{(M)}}}$ однозначно определяется соотношением

где

Значения $\varepsilon _{{\min }}^{{(\upsilon )}}$ образуют, как правило, убывающую цепочку неравенств с возрастанием $\upsilon $, и задача (2.21) оказывается разрешимой, если $\varepsilon \geqslant {{\varepsilon }_{{\inf }}}$. Здесь точная нижняя грань ${{\varepsilon }_{{\inf }}}$ достижимых значений $\varepsilon $ оказывается равной минимаксу $\varepsilon _{{\min }}^{{(\rho )}}$, где $\rho = \infty $ при ${{\varepsilon }_{{\inf }}} = 0$ и $\rho < \infty $ при ${{\varepsilon }_{{\inf }}} > 0$ соответственно для управляемых и неуправляемых относительно $Q{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(x) \equiv 0$ объектов [13].

Решение задачи полубесконечной оптимизации. Решение ЗПО (2.21)–(2.23) относительно вектора параметров ${{\psi }^{{(M)}}}$, а также априори неизвестной величины минимакса $\varepsilon _{{\min }}^{{(M)}}$ в (2.22) в случае, когда $\varepsilon = \varepsilon _{{\min }}^{{(M)}}$, может быть получено в условиях малостеснительных ограничений альтернансным методом [13, 14]. Метод базируется на специальных альтернансных свойствах искомого значения $\psi _{*}^{{(M)}} = (\tilde {\psi }_{i}^{*}),$ $i = \overline {1,M} ,$ являющихся аналогом условий экстремума в теории нелинейных чебышевских приближений, и дополнительной информации о форме кривой пространственного распределения результирующего состояния $Q(x,\psi _{*}^{{(M)}})$ управляемой величины, диктуемой закономерностями предметной области. Согласно альтернансным свойствам, равные допустимой величине ε одинаковые значения максимальных отклонений $\mathop {\max }\limits_{x \in [{{x}_{0}},{{x}_{1}}]} {\text{|}}Q(x,\psi _{*}^{{(M)}}){\text{|}}$ достигаются в некоторых точках $x_{j}^{0},\;j = \overline {1,R} ,$ на отрезке $[{{x}_{0}},{{x}_{1}}]$. Общее число R этих точек, где R = M при заданном ε: $\varepsilon _{{\min }}^{{(M)}} < \varepsilon < \varepsilon _{{\min }}^{{(M - 1)}}$ и $R = M + 1,$ если $\varepsilon = \,\varepsilon _{{\min }}^{{(M)}}$, равно числу искомых неизвестных в ЗПО (2.21)–(2.23), порождая тем самым замкнутую относительно этих неизвестных систему соотношений

При наличии дополнительной информации из предметной области о форме кривой $Q(x,\psi _{*}^{{(M)}})$ на отрезке $[{{x}_{0}},{{x}_{1}}] \mathrel\backepsilon x$, позволяющей при известной функции $\eta (t)$ идентифицировать координаты $x_{j}^{0}$ и знаки $Q(x_{j}^{0},\psi _{*}^{{(M)}})$, равенства (2.24), дополненные условиями существования экстремума функции $Q(x,\psi _{*}^{{(M)}})$ в точках $x_{{{{j}_{g}}}}^{0} \in \operatorname{int} [{{x}_{0}},{{x}_{1}}]$, $g = \overline {1,{{R}_{1}}} ,$ где ${{R}_{1}} \leqslant R$ и $x_{{{{j}_{g}}}}^{0} \in \{ x_{j}^{0}\} $, переводятся в систему уравнений

с однозначно определяемым знаком ε в каждой точке $x_{j}^{0}$, которая разрешается относительно $\tilde {\psi }_{i}^{*},\;i = \overline {1,M} ;$ значений $x_{{{{j}_{g}}}}^{0}$, $g = \overline {1,{{R}_{1}}} $, а также $\varepsilon _{{\min }}^{{(\upsilon )}}$, если в (2.22) $\varepsilon = \varepsilon _{{\min }}^{{(\upsilon )}}$.

Пространственное распределение управляемой величины $Q(x,\psi _{*}^{{(M)}})$ в конце оптимального процесса описывается рядом (1.9) с вектором модальных переменных $\bar {Q}{\kern 1pt} {\text{*}}(t{\kern 1pt} {\text{*}})$, и, следовательно, система равенств (2.25) приводится к следующему виду:

где $n = \overline {1,{{N}_{1}}} ;$ $\,j = \overline {1,R} ;\,$ $\bar {\varepsilon } = ({{\varepsilon }_{i}}),\,$ $i = \overline {1,R} ;$ ${{\varepsilon }_{i}} = \pm \varepsilon ,$ $\,g = \overline {1,{{R}_{1}}} $.

Подстановка (2.17) в (2.26) при $\psi (t{\kern 1pt} {\text{*}})$ = ψ*(t*) приводит к линейной системе R уравнений

относительно вектора ψ*(t*), представляемого в форме (2.9) с М неизвестными компонентами $\tilde {\psi }_{i}^{*},\;i = \overline {1,M} $, и $\varepsilon _{{\min }}^{{(M)}}$ в случае $\varepsilon = \varepsilon _{{\min }}^{{(M)}}$ в (2.25). При $\varepsilon :\,\varepsilon _{{\min }}^{{(M)}} < \varepsilon < \,\varepsilon _{{\min }}^{{(M - 1)}}$ решение системы R = M уравнений (2.28) относительно ψ*(t*) при априори фиксируемом значении $\bar {\varepsilon }$ принимает следующий вид для каждой заданной величины $\bar {Q}(0)$:

Здесь значения $x_{j}^{0}$ в элементах матрицы Ф должны быть определены дополнением (2.29) системой уравнений (2.27) с подстановкой $\bar {Q}{\kern 1pt} {\text{*}}(t{\kern 1pt} {\text{*}})$ в форме (2.17). В итоге выражения (2.19), (2.20) и (2.29) полностью определяют искомый алгоритм оптимального программного управления.

Об учете ограничений на управляющие воздействия. Предлагаемый способ расчета программного оптимального управления соответствует традиционному методу исследования задачи АКОР в открытой области изменения u(t), позволяющему, во-первых, определить минимально достижимые значения квадратичного функционала качества и, во-вторых, установить по полученным результатам предельные значения u(t), необходимые для реализации максимального эффекта по величине ${{I}_{1}}$ в (1.10). Тем не менее существенный интерес представляют задачи АКОР с учетом априори заданных ограничений

с известными граничными значениями ${{u}_{{\min }}},\,{{u}_{{\max }}} = {\text{const}}$, если эти ограничения нарушаются на протяжении оптимального процесса с линейным управлением вида (2.4). Равенства могут достигаться в различные моменты времени на протяжении оптимального процесса, образуя в общем случае многочисленные возможные варианты компоновки управляющих воздействий $\tilde {u}{\kern 1pt} *(t)$ из различных участков в соответствии с (2.4), (2.31).

В типичном частном случае ограничения на $\tilde {u}{\kern 1pt} {\text{*}}(t)$ достигаются только на начальной стадии процесса управления, на протяжении которой $\tilde {u}{\kern 1pt} {\text{*}}(t) = {{u}_{{\max }}},$ $t \in [0,{{t}_{1}}],$ ${{t}_{1}} < t{\kern 1pt} *$, где момент t₁ определяется по найденному линейному алгоритму u*(t) как корень уравнения $u{\kern 1pt} {\text{*}}({{t}_{1}}) = {{u}_{{\max }}}$. В такой ситуации состояние объекта $\bar {Q}({{t}_{1}})$, найденное интегрированием уравнений модели (1.8) с управлением $u(t) = {{u}_{{\max }}},\,t \in [0,\,{{t}_{1}}]$, можно рассматривать в роли начального $\bar {Q}(0)$ на последующем временном интервале $[{{t}_{1}},t{\text{*}}]$, где программное управление вида (2.4) определяется по описанной выше схеме.

Аналогичным образом может быть найдено программное управление и при других вариантах его построения с учетом ограничений в (2.30).

3. Синтез оптимальной системы управления. Рассмотрим далее задачу синтеза в условиях линейного алгоритма (2.4) оптимального программного управления. Решение этой задачи построения оптимального регулятора $u{\kern 1pt} {\text{*}}(Q,t)$ существенно зависит от характера информации о внешнем возмущении $\eta (t)$ в уравнениях моделей объекта (1.1)–(1.3).

3.1. Синтез оптимального регулятора при заданном внешнем возмущении. Пусть $\eta (t)$ в (1.5), (1.8) – известная функция времени. Определим конечное состояние модели (2.6) из уравнения (2.10):

откуда получим, используя представление матричной экспоненты в блочной форме (2.8): где подобно (2.16)

В оптимальном процессе $(\bar {Q}{\kern 1pt} {\text{*}}(t),\psi {\kern 1pt} {\text{*}}(t))$ соотношения (3.2), (3.3) принимают следующий вид:

где значения $\bar {Q}{\kern 1pt} {\text{*}}(t{\kern 1pt} {\text{*}})$ и ψ*(t*) фиксируются расчетом программного управления, согласно (2.17), (2.29).

После умножения слева равенств (3.5) и (3.6) соответственно на известные в соответствии с (2.17), (2.29) ${{N}_{1}} \times {{N}_{1}}$-матрицы ${\text{diag}}\,[\bar {Q}_{j}^{*}(t{\kern 1pt} *)]$, $\bar {Q}{\kern 1pt} {\text{*}}(t{\kern 1pt} {\text{*}}) = (\bar {Q}_{j}^{*}(t{\kern 1pt} {\text{*}}))$, $j = \overline {1,{{N}_{1}}} $ и ${\text{diag}}\,[\psi _{j}^{*}(t{\kern 1pt} *)]$, ψ*(t*) = = $(\psi _{j}^{*}(t{\kern 1pt} *))$, $j = \overline {1,{{N}_{1}}} $, левые части соотношений (3.5) и (3.6) становятся одинаковыми. Последующее вычитание этих уравнений приводит к следующему результату:

однозначным образом определяющему зависимость $\psi {\kern 1pt} {\text{*}}(t,\psi {\kern 1pt} {\text{*}}(t{\kern 1pt} {\text{*}}),\bar {Q}(0),\bar {Q}(t))$ от своих аргументов при заданном кусочно-непрерывном воздействии $\eta (t)$ по предварительно вычисляемым решениям системы уравнений (2.26), (2.27) в условиях (2.17).

Подстановка (3.7) в выражение (2.20) для программного управления приводит к линейному закону синтеза оптимального регулятора с нестационарными коэффициентами обратных связей в детерминированной системе управления с полным измерением состояния $\bar {Q}(t)$:

Здесь матрицы ${{T}_{1}}$ и ${{T}_{2}}$ представляются, согласно (3.8)–(3.11), известными функциями времени с фиксируемыми на протяжении процесса управления значениями $\bar {Q}(0)$, которые определяются по результатам наблюдения $\bar {Q}(t)$ в момент $t = 0$.

Переход в (3.12) от $\bar {Q}(t)$ к измеряемому выходу объекта ${{Q}_{u}}({{x}_{u}},t) = (Q({{x}_{{uj}}},t))$ в $r$ точках x_uj ∈ $[{{x}_{0}},{{x}_{1}}],$ $j = \overline {1,r} $, определяется, согласно (1.9), векторно-матричным уравнением наблюдения

В условиях $r < {{N}_{1}}$ неполного измерения состояния для восстановления вектора $\bar {Q}(t)$ по значениям $Q(x_{u}^{{}},\,t)$ требуется построение наблюдателя полного или пониженного порядка [21]. Если по условиям требуемой точности моделирования объекта (1.8) можно ограничиться учетом только М первых составляющих $\bar {Q}(t)$ с минимальным их числом М, требуемым для решения системы уравнений (2.28) относительно представляемого в форме (2.9) вектора $\psi {\kern 1pt} {\text{*}}(t{\kern 1pt} {\text{*}})$, то $\bar {Q}(t)$ непосредственно определяется решением системы уравнений (3.13) при r = M, ${{N}_{1}} = N = M$:

Подстановка (3.14) в (3.12) приводит к линейному алгоритму детерминированного синтеза с обратными связями по измеряемому выходу объекта:

Аналитическое решение задачи синтеза с учетом ограничений на управляющие воздействия становится невозможным в силу нелинейности в таком случае П-системы принципа максимума. Широко распространенный способ определения $\tilde {u}{\kern 1pt} {\text{*}}(Q_{u}^{{}},t)$ в первом приближении заключается в дополнении алгоритма $u{\kern 1pt} {\text{*}}(Q_{u}^{{}},t)$ в (3.15) характеристикой усилительного звена с насыщением [1, 2, 4]:

Однако такой результат может не обеспечить требуемую точность ε приближения к заданному конечному состоянию объекта. Более точный результат может быть получен для известного варианта структуры программного управления $\tilde {u}{\kern 1pt} {\text{*}}(t)$ при законе регулирования $\tilde {u}{\kern 1pt} {\text{*}}(Q_{u}^{{}},t)$, компонуемом из участков (2.31) выхода $\tilde {u}{\kern 1pt} {\text{*}}(t)$ на ограничения и линейных алгоритмов обратной связи в форме (3.15) на остальных интервалах изменения $\tilde {u}{\kern 1pt} {\text{*}}(t)$ вида (2.4).

3.2. Синтез оптимального регулятора в условиях неопределенности множественных внешних возмущений. Антагонистические алгоритмы программного управления. Сложная задача синтеза в условиях воздействия множественных возмущений может быть рассмотрена в игровой постановке с антагонистическими программными управлениями $u(t)$ и $\eta (t)$ в форме линейной дифференциальной игры с объектом управления (1.8) и критерием оптимальности I₁ в (1.10) [7, 24–26]. При этом оптимальное управление $u{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t)$ и наиболее “неблагоприятное” возмущение $\eta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t)$ находятся, согласно стратегии получения наилучшего гарантированного результата:

в задаче со свободным конечным состоянием $Q(x,t{\kern 1pt} *)$ с целью определения “наихудшей” величины $\eta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t)$.

При аддитивном характере зависимости подынтегральной функции критерия (1.10) от антагонистических управлений $u(t)$ и $\eta (t)$ их оптимальные значения $u{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t)$ и $\eta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t)$ в (3.16) могут быть найдены из условия существования седловой точки игры [24–26]:

путем распространения на рассматриваемую задачу принципа максимума Понтрягина, согласно которому в каждой точке непрерывности функций $u{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t)$ и $\eta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t)$ выполняется базовое соотношение [24–26]

Здесь функция $H\left( {\bar {Q}(t),u(t),\psi (t),\eta (t)} \right)$ и вектор $\psi (t)$ сопряженных переменных опять определяются, согласно (2.2), (2.3).

В таком случае $u{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t)$ по-прежнему находится в виде (2.4), а $\eta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t)$ представляется аналогично (2.4) в форме линейной зависимости от $\psi {\kern 1pt} *(t)$:

Подстановка $u(t)$ и $\eta (t)$ в виде (2.4) и (3.19) в уравнения (1.8), (2.3) приводит аналогично (2.6) к программно-управляемой системе, замыкаемой относительно неизвестных $\bar {Q}(t)$ и $\psi (t)$ условиями трансверсальности:

в задаче со свободным правым концом траектории $\bar {Q}(t{\kern 1pt} {\text{*}})$ [4, 13]:

Решение однородной системы уравнений (3.21) представляется подобно (2.8), (2.10) в векторно-матричной форме

где $\tilde {A}$ – матрица коэффициентов в (3.21) и ${{\tilde {A}}_{{ij}}}$ в (3.22) – блоки обратной матрицы ${{e}^{{ - \tilde {A}(t)}}}$.

Отсюда аналогично (2.19) в условиях $\psi {\kern 1pt} {\text{*}}(t{\kern 1pt} {\text{*}}) = 0$ получаем следующее выражение для $\psi {\kern 1pt} {\text{*}}(t)$:

где ${{\tilde {B}}_{1}}(t{\kern 1pt} *)$ определяется аналогично (2.18) при замене матрицы A на $\tilde {A}$.

Подстановка (3.23) в (3.19) позволяет найти $\eta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t)$ в виде явной зависимости от t:

Редукция к задаче синтеза с заданным детерминированным возмущением. Задача синтеза при множественных возмущениях может быть сведена к рассмотренной в разд. 3.1 задаче конструирования оптимального регулятора при заданном детерминированном внешнем воздействии $\eta (t) = \eta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t)$ в (3.24). Действительно, при любом реализуемом возмущении $\eta _{{}}^{0}(t)$ будем иметь в соответствии с (3.16)–(3.18) в условиях существования седловой точки рассматриваемой дифференциальной игры

Здесь

согласно требованиям (1.6), где $\left| {Q(x,\psi _{*}^{{(M)}}(\eta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}),\eta )} \right|$ – конечное состояние объекта при оптимальном $\psi _{{}}^{{(M)}}$-параметризованном управлении $u{\kern 1pt} {\text{*}}(t)$, найденном при $\eta (t) = \eta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t)$ путем решения задачи (1.8)–(1.11) с заданной величиной ε, а ${{\varepsilon }_{0}}$ непосредственно находится вычислением максимума по $\eta $ в (3.26).

Как следует из (3.25), синтез оптимального управления $u{\kern 1pt} {\text{*}}(\bar {Q},t)$ при заданном детерминированном возмущении $\eta _{{}}^{0}(t) = \eta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t)$ в условиях (3.26) отвечает верхней оценке достижимых значений минимизируемого критерия I₁ на множестве допустимых возмущений в соответствии с требованиями стратегии управления по принципу наилучшего гарантированного результата.

4. Синтез оптимального регулятора для управления нестационарным процессом теплопроводности. В качестве примера, представляющего самостоятельный интерес, рассмотрим задачу аналитического конструирования оптимального регулятора для управления процессом нагрева неограниченной пластины.

Пусть температурное поле Q(x, t) пластины описывается линейным однородным уравнением теплопроводности вида (1.1)–(1.3) в относительных единицах [16, 27]:

с заданными начальными и граничными условиями при граничном управляющем воздействии ${{u}_{s}}(t)$ в характерных условиях воздействия на него заданного детерминированного возмущения

Модальное описание объекта (4.1)–(4.3) сводится к бесконечной системе дифференциальных уравнений вида (1.8)–(1.9):

где [16]

Задача сводится к определению алгоритма обратной связи ${{u}_{s}}(Q,t)$, обеспечивающего перевод объекта (4.5), (4.6) за заданное время t* в требуемое конечное состояние $Q{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(x) = Q{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}} = 0$ с заданной точностью равномерного приближения $\varepsilon > 0$, согласно (1.11), при минимальном значении квадратичного критерия качества (1.10), где выберем ${{\rho }_{Q}} = 1$.

Оптимальное программное управление $(1 + {{k}_{0}})u_{s}^{*}(t)$ находится в форме (2.4) при ${{k}_{n}} = {{k}_{{sn}}}$, а П-система принципа максимума представляется в виде однородной системы уравнений (2.6), где в рассматриваемом примере следует принять

Вычисление матричной экспоненты. Примем далее для большей простоты и наглядности получаемых результатов ${{N}_{1}} = N = 2$, ограничиваясь учетом только двух модальных переменных в сумме (4.6). В таком случае матричная экспонента в (2.7) является нормированной фундаментальной 4 × 4-матрицей системы (2.6) следующего вида [3, 20, 21]:

Здесь $Z(t)$ – матрица линейно-независимых решений однородной системы уравнений (2.6) [3, 20, 21]:

где $p_{i}^{{}},\,i = \overline {1,\,4} $, – различающиеся корни характеристического уравнения $\gamma _{{}}^{{(i)}} = (\gamma _{j}^{{(i)}}),$ $j = \overline {1,\,4} $, – корни уравнения и E – единичная матрица.

Матричная экспонента e^At представляется в блочной форме (2.8), где

Здесь

и $G_{{is}}^{{}}$ – алгебраическое дополнение s-го элемента i-го столбца G.

Характеристическое уравнение (4.9) приводится к равенству

из которого после простых преобразований получим с учетом (4.7) при ${{\mu }_{1}} = 0$ следующие действительные значения для четырех корней ${{p}_{i}}$ в (4.8), (4.12):

Решение уравнения (4.10) приводит к значениям коэффициентов $\gamma _{j}^{{(i)}}$ в (4.12):

Выражения (4.8)–(4.16) полностью определяют матричную экспоненту в (2.7), (2.8) применительно к рассматриваемому примеру.

Расчетная система уравнений альтернансного метода. Предлагаемый способ $\psi _{{}}^{{(N)}}$-параметризации управляющего воздействия приводит к представлению $\psi {\kern 1pt} {\text{*}}(t{\kern 1pt} *)$ в форме (2.9).

Для типичного в приложениях случая $\varepsilon = \varepsilon _{{\min }}^{{(2)}}$ в (2.21) здесь следует принять M = 2, согласно (2.22), и тогда в соответствии с (2.9) $\psi {\kern 1pt} {\text{*}}(t{\kern 1pt} {\text{*}}) = (\tilde {\psi }_{i}^{*}),$ $i = 1,2;$ $\psi _{i}^{*}(t{\kern 1pt} {\text{*}}) = 0,$ $i > 2$, в системе уравнений (2.28). При подстановке $B(t{\kern 1pt} *)$ и ${{B}_{1}}(t{\kern 1pt} *)$ в форме (2.18), (4.13) система (2.28) после элементарных вычислений приводится к следующему виду:

где и все элементы 2 × 2-матриц ${{F}^{{(1)}}}$ и ${{F}^{{(2)}}}$ становятся известными функциями ${{\psi }_{{ks}}}(t{\kern 1pt} *)$, ${{\bar {Q}}_{{ks}}}(t{\kern 1pt} *)$; $k = \overline {1,2} ;$ $s = \overline {1,4} $ в (4.11).

При $\varepsilon = \varepsilon _{{\min }}^{{(2)}}$ в (2.21) следует принять $R = M + 1 = 3$ в (2.24). Тогда будем иметь матрицу Ф размерностью 3 × 2 в (2.26), подстановка которой в (4.17) позволяет получить, согласно (2.24), на основании (4.6) систему трех равенств:

которая замыкается относительно всех неизвестных $\tilde {\psi }_{1}^{*},\;\tilde {\psi }_{2}^{*},\;\varepsilon _{{\min }}^{{(2)}},\;x_{{{{j}_{g}}}}^{0},$ $g = \overline {1,{{R}_{1}}} $, ${{R}_{1}} \leqslant R$, условиями (2.25) существования экстремума $Q(x,\psi _{*}^{{(2)}})$ в точках $x_{j}^{0} \in \operatorname{int} [0,1]$, записываемыми в аналогичной (4.19) форме.

Физические закономерности поведения нестационарных температурных полей в оптимальном процессе нагрева пластины и альтернансные свойства $Q(x,\psi _{*}^{{(2)}})$ определяют в рассматриваемом примере, подобно [13, 14], при $M = 2$, $\varepsilon = \varepsilon _{{\min }}^{{(2)}}$, ${{Q}_{0}} = \operatorname{const} $ в (4.2) форму кривой $Q(x,\psi _{*}^{{(2)}})$ результирующего распределения температуры по пространственной координате (рис. 1), что позволяет заведомо идентифицировать в (4.19) координаты точек $x_{1}^{0} = 0$, $x_{2}^{0} = x_{{{{j}_{g}}}}^{0} = x_{{{{j}_{1}}}}^{0} \in (0,1)$, $x_{3}^{0} = 1$ и знаки $Q(x_{j}^{0},\psi _{*}^{{(2)}})$. В результате равенства (4.19), дополняемые условиями существования экстремума (2.27) в одной точке $x_{2}^{0}$, редуцируются аналогично [13, 14] к замкнутой системе линейных по $\tilde {\psi }_{1}^{*},\;\tilde {\psi }_{2}^{*}$ уравнений вида (2.25):

разрешаемой относительно всех искомых величин стандартными численными методами.

Аналитическое конструирование оптимального регулятора. Согласно (3.12), получаем линейный с нестационарными коэффициентами алгоритм оптимального управления с обратными связями по состоянию $\bar {Q}(t) = \left( {\bar {Q}_{i}^{{}}(t)} \right)$, $i = 1,2$:

где матрицы ${{T}_{1}},\,\,{{T}_{2}}$ вычисляются, согласно, (3.8), (3.9), (3.11), при $\psi {\text{*}}(t{\kern 1pt} {\text{*}}) = (\tilde {\psi }_{i}^{*},i = 1,2;\;\psi _{i}^{*}(t{\kern 1pt} *) = 0$, i > 2), найденном в результате решения системы уравнений (4.20). Произведение ${{T}_{1}}{{T}_{2}}$ оказывается в результате 2 × 2-матрицей, все элементы которой становятся известными функциями ψ_ks(t), ${{\bar {Q}}_{{ks}}}(t)$ в (4.12), однозначно определяющими закон (4.21) синтеза оптимального регулятора. При наличии двух измерителей выхода объекта в точках ${{x}_{{u1}}},{{x}_{{u2}}} \in [0,1]$ получаем систему двух линейных уравнений в (3.13): разрешаемую относительно $\bar {Q}_{1}^{{}}(t)$, $\bar {Q}_{2}^{{}}(t)$.

Подстановка этого решения в (4.21) определяет алгоритм синтеза оптимальной обратной связи по выходу объекта в форме (3.15):

где ${{\Phi }_{u}} = [{{\varphi }_{n}}(\mu _{n}^{{}},{{x}_{{uj}}}]$; $n,j = 1,2$.

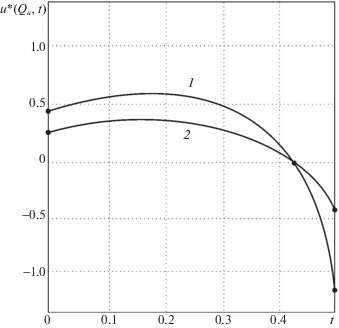
На рис. 1, 2 представлены некоторые расчетные результаты, полученные при $Q{\kern 1pt} *{\kern 1pt} * = 0,$ $t{\kern 1pt} * = 0.5,$ ${{k}_{0}}$ = 0.1 для двух различных значений ${{Q}_{0}}$ (кривые 1 – ${{Q}_{0}} = - 0.25;$ $\tilde {\psi }_{1}^{*} = 0.648;$ $\tilde {\psi }_{2}^{*} = - 1.161;$ $\varepsilon _{{\min }}^{{(2)}}$ = = 0.0043; кривые 2 – ${{Q}_{0}} = - 0.1;$ $\tilde {\psi }_{1}^{*} = 0.260;$ $\tilde {\psi }_{2}^{*} = - 0.464;$ $\varepsilon _{{\min }}^{{(2)}} = 0.0023$) при выборе двух измерителей выхода объекта в точках ${{x}_{{u1}}} = 0;$ ${{x}_{{u2}}} = 1$. На рис. 1 показаны распределения температуры по толщине пластины в конце оптимального процесса нагрева. Рисунок 2 иллюстрирует поведение в процессе нагрева оптимальных управляющих воздействий, изменяющихся во времени по алгоритму (4.23) в зависимости от текущих значений измеряемых сигналов обратной связи с нестационарными коэффициентами передачи. Как следует из приведенных данных, алгоритм (4.23) оптимального управления обеспечивает при различных начальных условиях заданную точность приближения к требуемому конечному состоянию объекта.

Заключение. Предлагаемый метод аналитического конструирования оптимальных регуляторов в линейно-квадратичной задаче управления системами с распределенными параметрами параболического типа разработан применительно к характерным для приложений оценкам целевых множеств конечных состояний объекта в равномерной метрике. Полученные уравнения регуляторов сводятся к линейным алгоритмам обратной связи с фиксируемыми предварительным расчетом нестационарными коэффициентами. Погрешности реализации предлагаемых алгоритмов обратной связи непосредственно по неполному измерению состояния системы определяются требованиями к точности описания модели объекта укороченной системой уравнений для модальных составляющих управляемой величины.