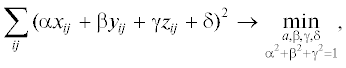Известия РАН. Теория и системы управления, 2021, № 4, стр. 111-118

Введение. Сканирующий туннельный микроскоп представляет собой устройство, которое позволяет измерять рельеф поверхности с точностью до долей нанометра. Он состоит из трехстепенного манипулятора, на конце которого закреплен зонд в виде иглы с радиусом закругления острия порядка 1 нм. Основная область его применения – получение изображения нанообразований и их структур на поверхности исследуемого образца с максимально возможным разрешением.

Система управления обеспечивает перемещение иглы, расположенной на конце пьезоманипулятора, на расстоянии туннельного зазора от исследуемой поверхности. Туннельный зазор – это зазор, который преодолевают туннелирующие электроны, при приложении разности потенциалов между измеряемой поверхностью образца и иглой.

Измерения проводятся в узлах сетки, шаг которой может быть задан до десятых долей нанометра. В результате измерений получается двумерный массив расстояний от иглы до высот поверхности.

Второй функцией системы управления микроскопом является визуализация нанорельефа. Наличие этой функции обусловлено необходимостью учета при интерпретации измерений технологических особенностей реализации движения иглы и условий протекания туннельного тока. Кроме этого, важна возможность оперативной оценки качества проведенных измерений. Функция визуализации должна обеспечить наглядное и достоверное представление результатов измерений в виде графического образа отсканированной поверхности.

До последнего времени функция графической визуализации результатов измерений была достаточно простой. Она обеспечивала представление измерений в виде проекции на двумерную плоскость, в которой высота точки кодируется с использованием метода градиентной закраски [6]. Более точное представление результатов измерений было нецелесообразно в виду того, что не существовало способа измерения размеров острия иглы.

Задача определения формы и размеров острия иглы была успешно решена в работах [1–3]. В [4, 5] сформулированы необходимые и достаточные условия, которым должна удовлетворять поверхность нанорельефа для того, чтобы она совпала с поверхностью, полученной с помощью алгоритма обработки измерений, предложенного в [1–3]. В основе их лежит условие достижимости каждой точки рельефа для касания туннельной оболочкой острия иглы. В работе [2] продемонстрированы возможности по устранению погрешностей измерений, вызванных гистерезисом пьезодвигателей. Эти результаты служат основанием для дальнейшего развития метода представления измерений путем проекции на плоскость.

1. Метод градиентной закраски. Основным способом выделения структуры рельефа поверхности на изображении является раскрашивание участков двумерного изображения массива высот поверхности (скана) в цвет, который определяется относительной высотой расположения участка.

Наибольшее распространение получила палитра из четырех цветов, схожая с той, которая применяется в географических картах (синий, зеленый, желтый и красный, причем синий цвет соответствует наиболее низко расположенным точкам) [6–10]. Достаточно часто пользователю предоставлена возможность самостоятельно выбирать палитру и число основных цветов в ней [7, 9].

Расширенный набор основных цветов позволяет точнее передавать структуру рельефа поверхности. При ограниченном наборе цветов трудно выделить мелкие объекты в силу того, что при небольшом перепаде высот изменения яркости трудно различимы для глаза.

2. Построение подстилающей плоскости. Обозначим через OXYZ систему координат, в которой проводились измерения. Точка О – точка начала измерений. Ось OZ направлена вдоль оси зонда вверх, ось OX – вдоль линии сканирования, ось OY образует с ними правую тройку.

Улучшить различимость мелких объектов можно, если использовать для проекции такую плоскость, относительно которой перепад высот точек массива измерений минимален. Отношение размеров мелких объектов к общему перепаду высот окажется существенно большим, вследствие чего станет возможным наблюдать такие объекты, которые ранее не были различимы. В дальнейшем плоскость, используемая для проекции, называется подстилающей.

В программном обеспечении туннельных микроскопов подстилающая плоскость ищется путем решения задачи, в которой вместо кратчайшего расстояния до плоскости минимизируется среднеквадратичное отклонение [6]. Коэффициенты a, b и d выбираются такими, которые минимизируют вертикальное среднеквадратичное отклонение точки от плоскости:

Здесь z_ij – измеренное значение поверхности рельефа в узле сетки, x_ij, y_ij – координаты узлов. Суммирование идет по всем узлам.

Распространенность такого подхода объясняется простотой решения задачи (2.1), которая сводится к нахождению корней системы линейных уравнений третьего порядка [6]. Достоинством критерия (2.1) является то, что для всех видов нанорельефа получаемое изображение соответствует реальности.

Этим свойством обладают далеко не все критерии. Например, известный критерий минимизации среднеквадратичного расстояния [11]

в котором абсолютная величина выражения αx_ij + βy_ij+ γz_ij + δ равна расстоянию от точки с координатами (x_ij, by_ij, z_ij) до плоскости, задаваемой уравнением αx + βy + γz + δ = 0. При значительном перепаде высот задача (2.2) может привести к вертикальной плоскости. Например, нетрудно убедиться в том, что она является решением для цилиндрической поверхности с образующей, параллельной плоскости измерения, и основанием в виде верхней половины эллипса, вертикальная h и горизонтальная w полуоси которого удовлетворяют неравенству h ≫ w.

Распознать случай, в котором получена вертикальная подстилающая плоскость, по изображению достаточно сложно в силу того, что пользователю неизвестно, какая картинка должна получиться.

В выражении (2.1) |z_ij – (ax_ij + by_ij + d)| является длиной вертикального отрезка, заключенного между точкой измерения M_ij(x_ij, y_ij, z_ij) и подстилающей плоскостью. Его длина зависит от выбора системы координат, в которой решается задача (2.1). Длину отрезка в системе координат OXYZ обозначим через μ_0ij:

Левая часть выражения (2.1) представляет собой функцию I₀(a, b, d), вычисляемую в той же системе координат:

Обозначим через $I_{0}^{*}$ = I₀(a₀, b₀, d₀) значение функции I₀(a, b, d), полученное в результате решения задачи (2.1) в системе координат OXYZ. Здесь a₀, b₀, d₀ – значения переменных a, b, d, при которых достигается минимальное значение функции. В системе координат OXYZ они являются коэффициентами уравнения подстилающей плоскости P₀, заданной уравнением z₀₌ a₀x + b₀y + d₀.

Покажем, что в подходящей системе координат решение задачи (2.1) приводит к меньшей величине, чем $I_{0}^{*}$.

3. Итерационный метод нахождения подстилающей плоскости. Обозначим через ${{\nu }_{{0ij}}}$ и ${{\nu }_{{1ij}}}$ расстояния от точки измерений M_ij(x_0ij, y_0ij, z_0ij) до плоскости OXYZ и подстилающей плоскости P₀ соответственно. Имеет место неравенство ${{\nu }_{{1ij}}} < {{\mu }_{{0ij}}}$. Из него следует, что

В системе координат OXYZ

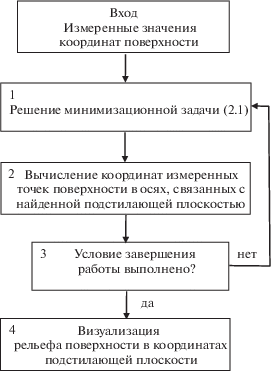
в силу того, что ν_0ij = |z_ij|. Значение $I_{0}^{*}$ = I₀(a₀, b₀, d₀) получено в результате решения минимизационной задачи (2.1), поэтому I₀(0, 0, 0) < $I_{0}^{*}$. В результате

Повторим описанную процедуру далее в соответствии с алгоритмом, который изображен на рис 1. На шаге n вводится система координат O_nX_nY_nZ_n, связанная подстилающей плоскостью P_{n – 1}, которая была найдена на предыдущем шаге работы алгоритма: O_nX_n ∈ P_{n – 1}, O_nY_n ∈ P_{n – 1}, O_nZ_n ⊥ ⊥ P_{n – 1}. В блоке 1 решается минимизационная задача (2.1) и находятся коэффициенты a_n, b_n, d_n уравнения подстилающей плоскости P_n.

Затем строится система координат O_{n + 1}X_{n + 1}Y_{n + 1}Z_{n + 1}, связанная с плоскостью P_n. В качестве начала координат O_{n + 1} берется произвольная точка подстилающей плоскости. Взаимно перпендикулярные оси O_{n + 1}X_{n + 1} и O_{n + 1}Y_{n + 1} лежат в подстилающей плоскости, ось O_{n + 1}Z_{n + 1} перпендикулярна к ней. Для того, чтобы сохранить ориентацию изображения на подстилающей плоскости, целесообразно направить ось O_{n + 1}X_{n + 1} вдоль оси OX.

В блоке 2 вычисляются координаты точек измерений M_ij(x_nij, y_nij, z_nij) в осях O_n X_nY_n Z_n.

Пусть μ_nij – длина вертикального отрезка, заключенного между точкой M_ij и плоскостью P_n. В осях O_nX_nY_nZ_n μ_nij = |z_nij – (a_nx_nij + b_ny_nij + d_n)| и

Здесь $I_{n}^{*}$ = I_n (a_n, b_n, d_n) – решение задачи (2.1), найденной на шаге n.

Обозначим через ν_nij и ν_{(n+ 1)ij} расстояния от точки измерений M_ij(x_nij, y_nij, z_nij) до плоскости O_nX_nY_nZ_n и подстилающей плоскости P_n соответственно. Принимая во внимание, что ν_{(n+ 1)ij} < μ_nij, имеем

При решении задачи (2.1) на шаге n + 1 для плоскости O_nX_nY_nZ_n значение функции

поэтому

В результате имеем неравенство

При работе алгоритма получается монотонно убывающая положительная последовательность сумм:

Предел последовательности обозначим через S. Покажем, что каждая из последовательностей коэффициентов a_n, b_n, d_n ограниченна.

В общем случае нанорельеф представляет собой поверхность, полная кривизна которой почти во всех точках положительна. В окрестности любой такой точки, внутренней для поверхности, можно выбрать сферу B малого радиуса r, для которой ее проекция Пр(B) на произвольную плоскость будет целиком принадлежать проекции измеряемого нанорельефа A: Пр(B) ⊂ Пр(A).

Пусть теперь какая-либо из последовательностей a_n, b_n, d_n неограниченна. Тогда последовательность норм линейных операторов ||z_n – (a_nx_n + b_ny_n + d_n)||, (x_n, y_n, z_n) ∈ O_nX_nY_nZ_n также будет неограниченной. Отсюда неограниченны последовательности значений функций z_n – (a_nx_n + b_ny_n + d_n), которые они принимают на проекции сферы Пр_n(B) на плоскость O_nX_nY_n: (x_n, y_n) ∈ Пр_n(B).

В результате последовательность s_n будет представлять собой сумму квадратов членов, часть которых неограниченно возрастает, что противоречит установленному выше свойству о монотонном убывании s_n. Каждая из ограниченных последовательностей a_n, b_n, d_n имеет предельные точки. Обозначим любой их набор через A, B, D соответственно. Покажем, что A = B = 0.

Введем прямоугольную систему координат O_S X_S Y_S Z_S , в которой точка O_S лежит на предельной подстилающей плоскости, заданной уравнением z – (Ax + By + D) = 0, и ось O_SZ_S направлена перпендикулярно к ней.

Предположим, что сформулированное выше утверждение неверно. Решим минимизационную задачу (2.1) в системе координат O_SX_SY_SZ_S. Если хотя бы один из двух коэффициентов A или B отличен от 0, то найденная подстилающая плоскость наклонена к плоскости O_SX_SY_S под некоторым углом. К ней можно применить итерационный алгоритм и найти лучшее, чем S, решение задачи (2.1).

Из доказанного утверждения следует, что последовательности a_n и b_n имеют предел.

Сформулированное свойство позволяет заключить, что по мере работы алгоритма наклон подстилающей плоскости будет изменяться все меньше и, следовательно, она будет стремиться к своему предельному положению в пространстве. Это можно использовать для определения момента окончания работы рассматриваемого алгоритма. Его работу следует прекратить, если в блоке 3 оба коэффициента a_n и b_n становятся меньше некоторой заданной величины. В качестве условия остановки алгоритма можно также использовать известные критерии близости членов последовательности s_n к своему пределу S.

4. Геометрические свойства найденного решения. Обозначим через π предельную подстилающую плоскость. В системе координат O_SX_SY_SZ_S она задается уравнением z – D = 0. Коэффициенты этого уравнения являются предельными значениями коэффициентов уравнений плоскостей, получаемых в процессе работы рассмотренного выше итерационного алгоритма в собственных координатах O_nX_nY_nZ_n.

В силу того, что решение задачи (2.1) в системе координат O_SX_SY_SZ_S  совпадает с плоскостью π, имеет место равенство

Выражение (4.1) с точностью до множителя (который определяется только числом узлов сетки измерений) пропорционально среднеквадратичному отклонению измеренных точек нанорельефа от плоскости z – D = 0. Из этого следует, что полученная подстилающая плоскость может быть найдена путем решения задачи минимизации (2.2). Единственность ее решения позволяет заключить, что последовательность d_n имеет только одну предельную точку.

Задача (2.2) обычно решается методом градиентного спуска. В настоящей работе предлагается использовать итерационный алгоритм, каждый шаг которого состоит в применении штатной функции нахождения подстилающей плоскости к результату работы алгоритма на предыдущем шаге. В настоящее время в системе управления туннельным микроскопом эта функция применяется однократно. Таким образом, предложенный способ решения позволяет избежать разработки новых программных модулей и связанных с этим вопросов верификации, обеспечения надежности их работы и интегрирования в существующий программный код.

После того, как подстилающая поверхность найдена, в блоке 4 она используется для визуализации измерений.

5. Сравнение методов. Штатная подсистема визуализации измерений выполняет только один шаг рассмотренного выше алгоритма. Таким образом, для того, чтобы улучшить точность визуального представления измерений, достаточно реализовать возможность применения подсистемы к преобразованным ею координатам точек столько раз, сколько необходимо.

Штатные средства визуализации позволяют пользователю следить за изменениями картинки в пошаговом режиме. Итерационный метод решения задачи так же, как и задача (4.2), при большом перепаде высот нанорельефа может приводить к решению в виде вертикальной плоскости. Визуальное наблюдение за изменением получаемого изображения позволяет остановить работу алгоритма, как только разрешение деталей сцены перестает улучшаться.

В преимуществе выбора подстилающей плоскости с помощью итерационного метода нетрудно непосредственно убедиться, сравнивая изображения, приведенные на рис. 2 и 3. Размеры областей нанорельефа указаны в нанометрах. Ось OX, вдоль которой движется игла при сканировании, в плоскости рисунка направлена по горизонтальной оси, OY – по вертикальной. Числа, нанесенные по осям координат, обозначают размеры участка сканирования. Во всех примерах сетка сканирования имеет размер 128 × 128 точек.

В нижней части рисунков показана палитра, с помощью которой кодируется высота точек рельефа относительно подстилающей плоскости и перепад высот в нанометрах. Приведены уравнения подстилающих плоскостей, на которые проектировались результаты измерений. В приведенных примерах итерационный алгоритм останавливался, если изменение всех коэффициентов подстилающей плоскости оказывалось менее 0.01.

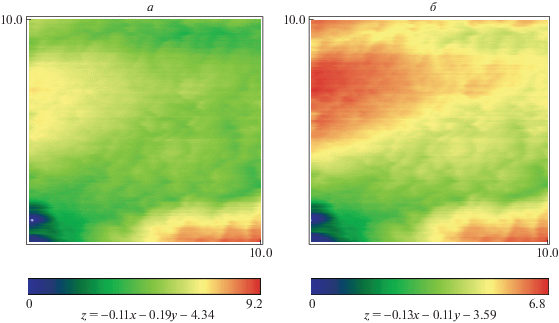
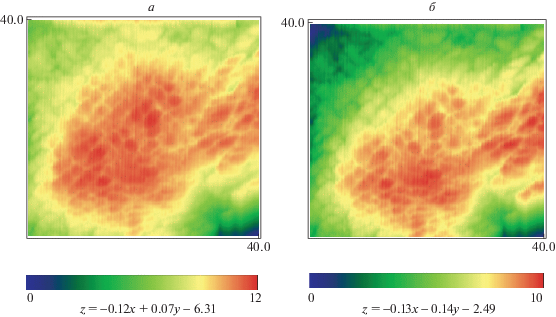
На рис. 2, а и 3, а подстилающая плоскость вычисляется с помощью метода наименьших квадратов, на рис. 2, б и 3, б – итерационным методом.

Рисунок 2 получен путем сканирования поверхности меди, нанесенной методом вакуумного напыления на стеклянную подложку. Сравнивая указанные на рис. 2, а и б параметры закраски, нетрудно заметить, что применение метода итераций позволило уменьшить перепад высот на треть. Коэффициенты подстилающей плоскости вычислены на третьем шаге работы итерационного алгоритма. Время работы алгоритма составило 1 с.

Непосредственное сравнение рисунков показывает также, что предлагаемый метод приводит к более информативной закраске. На рис. 2, б лучше видна структура рельефа поверхности: “ложбина”, закрашенная зеленым цветом, между двумя выпуклыми участками красного цвета. Лучше различимы границы выпуклостей, можно точнее измерить их размеры.

На рис. 3 показан участок поверхности платины, полученный вакуумным напылением на стеклянной пластине. Использование итерационного метода позволило уменьшить перепад высот с 12 до 10 нм, т.е. улучшить разрешение на 15%. В результате на рис. 3, б четче прослеживается структура поверхности, чем на рис. 3, а. Действительно, из рис. 3, а можно сделать вывод о том, что нанообразования, закрашенные красным цветом, лежат на одной высоте, т.е. в центре рельеф близок к некоторой плоскости. Рисунок 3, б показывает, что на самом деле она является выпуклой.

Коэффициенты подстилающей плоскости вычислены на пятом шаге работы итерационного алгоритма. Время работы алгоритма составило 1.5 с.

Результаты применения метода итераций и метода наименьших квадратов сравнивались на достаточно большом количестве измерений различных поверхностей. Во всех случаях изображение, получаемое методом итераций, было более информативным. Существенное увеличение визуального разрешения связано с известным эффектом восприятия, при котором большее значение имеет не линейный размер мелких объектов, а их площадь, которая увеличивается двукратно. В случае рис. 3 увеличение площади составляет 30%.

Следует заметить, что использование метода итераций не приводит к существенному увеличению времени расчетов, так как даже для сканов с изображением, имеющим разрешение 256 × × 256 точек, оно не превышает нескольких секунд. Полученные результаты позволяют рекомендовать метод итераций для включения в штатные средства обработки изображений зондовых микроскопов.

Заключение. Предложенный способ увеличения точности представления результатов измерений нанорелефа поверхности основан на известном методе построения подстилающей плоскости, который традиционно используется в туннельной микроскопии. Это упрощает задачу совершенствования функции визуализации измерений, применяемой в современных системах управления туннельным микроскопом.

В большинстве исследованных примеров представления измерений поверхности удается найти такую подстилающую плоскость, в которой перепад высот меньше на 15% по сравнению с плоскостями, построенными стандартными средствами. При этом в отдельных случаях перепад уменьшается в 1.5 раза. Во всех проведенных экспериментах с помощью метода итераций обеспечивается более точное отображение мелких структурных элементов поверхности.