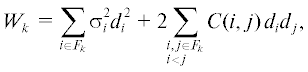Известия РАН. Теория и системы управления, 2021, № 4, стр. 94-110
ОПТИМИЗАЦИЯ УПРАВЛЕНИЯ РАБОТАМИ ЛОГИСТИЧЕСКОГО ПРОЕКТА В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
П. С. Кошелев a, *, А. В. Мищенко b, **
a МГТУ им. Н.Э. Баумана (национальный исследовательский ун-т)
Москва, Россия
b Национальный исследовательский ун-т “Высшая школа экономики”
Москва, Россия
* E-mail: kosh-mail@yandex.ru
** E-mail: alnex4957@rambler.ru
Поступила в редакцию 30.11.2019
После доработки 13.01.2021
Принята к публикации 29.03.2021
Аннотация
Разрабатываются методы решения задачи оптимизации выполнения работ проекта в сфере логистики с учетом неопределенности. С помощью методов исследования операций построены математические модели изучаемых процессов и сформулированы методы решения рассматриваемых задач. Приводится ряд примеров, демонстрирующих возможности использования описанных методов и моделей в практической деятельности.
Введение. Многие задачи управления так или иначе связаны с распределением ограниченных ресурсов. Моделирование оптимального их применения часто сводится к решению задач теории расписаний, сетевого планирования, формирования производственных программ предприятия, планирования обработки заявок в конвейерных системах, распределения транспортных средств по маршрутам. Перечисленные задачи часто используются при оценке эффективности проектов, реализуемых в различных сферах народного хозяйства, таких, как промышленное производство, системы складирования, транспорт, центры по обработке больших информационных данных. Общая постановка этих задач заключается в том, чтобы упорядочить во времени выполнение определенных действий при соблюдении ряда условий. Каждое действие состоит из элементарных операций, называемых работами (заявками или заданиями), которые могут быть либо подготовлены заранее, либо поступать динамически. Организация выполнения работ осуществляется таким образом, чтобы минимизировать один из следующих показателей: время выполнения всех работ, среднее взвешенное время завершения работ, объем незавершенной обработки заявок за определенный период, потери времени на ожидание обработки заявок. Моделирование распределения ограниченных ресурсов часто сводится к решению линейных и нелинейных задач дискретной оптимизации, большинство которых относится к NP-трудным, которые характеризуются экспоненциальным ростом объема вычислений при увеличении размерности задачи [1]. Это обстоятельство, а также то, что находить оптимальное решение часто приходится в условиях неточной исходной информации, определяет актуальность разработки эффективных методов управления ограниченными ресурсами.
В предлагаемой статье основное внимание будет уделено оптимизации управления проектом при изменяющихся длительностях работ. Несмотря на то, что на текущий момент времени созданы многочисленные методы и модели оптимизации управления ресурсами проектов, тем не менее, при решении проблемы минимизации инвестиционной фазы проекта в условиях неопределенности и риска существует определенный дефицит соответствующего количественного инструментария. При этом именно инвестиционная фаза как наиболее трудоемкая и капиталоемкая играет существенную роль в успехе всего проекта. Ошибки планирования на этом периоде, вызванные неучтенным риском, могут привести к значительным потерям.
Рассмотрена детерминированная модель теории расписаний, предполагающая использование нескладируемых ресурсов с учетом матричного задания времени выполнения операций исполнителями и предложен метод ветвей и границ получения оптимального решения. Получены методы оценки устойчивости расписаний при выполнении непрерываемых работ проекта при различных способах задания изменения их длительности. В ситуации, когда длительности работ заданы как случайные величины, предложена двухкритериальная модель оценки эффективности расписания.
Модели оптимального управления ограниченными ресурсами рассматривались в ряде публикаций отечественных и зарубежных авторов. Например, оптимизационные задачи оценки эффективности производственных программ в условиях неопределенности исследуются в [2, 3]. Методы оценки устойчивости расписаний при изменении параметров задачи анализируются в [4, 5]. Динамические и статические модели и методы управления ограниченными ресурсами на транспорте рассмотрены в [6–8]. Точные и приближенные алгоритмы построения оптимальных расписаний для планирования работы многопроцессорной вычислительной техники представлены в [9–11]. Модели и методы управления ограниченными ресурсами, которые сводятся к решению минимаксных задач, приведены в [12–18].
1. Описание моделей. Традиционно общая постановка задачи календарного планирования заключается в следующем. Необходимо выполнить n работ проекта, технологическая последовательность которых задана ориентированным ациклическим графом. Для завершения каждой работы необходимы ресурсы нескладируемого вида.
Нескладируемые ресурсы – ресурсы, высвобождаемые после окончания работы и используемые для последующих задач (машины, компьютеры, станки) [19].
В детерминированной постановке заданы также длительности работ ti. Объемы нескладируемых ресурсов, как правило, ограничены. В этой ситуации необходимо определить такую последовательность выполнения работ, которая, не нарушая ресурсных ограничений и ограничений, накладываемых на последовательность их осуществления, обеспечивает минимизацию времени завершения всех работ проекта.
В рамках этой постановки задачи рассматриваются отдельно ситуации, когда для выполнения работ проекта необходим фиксированный объем нескладируемых ресурсов, или объем ресурсов может меняться, увеличивая или уменьшая при этом длительность работ.
В случае, если в качестве нескладируемых ресурсов используются исполнители (машины, станки, приборы), наиболее часто встречаются следующие постановки задач.
1. Для осуществления каждой работы применяется один исполнитель из $m$ имеющихся, и увеличение числа исполнителей, выделяющихся для выполнения работы, не приводит к уменьшению ее длительности. Время реализации работы одинаково у всех исполнителей.
2. Для выполнения каждой работы $i$, $i = \overline {{\text{1,}}n} $, может использоваться от одного до ${{k}_{i}}$ исполнителей $({{k}_{i}} = \overline {1,m} )$. Длительность работы равна ${{{{t}_{i}}} \mathord{\left/ {\vphantom {{{{t}_{i}}} e}} \right. \kern-0em} e}$, $e = \overline {1,{{k}_{i}}} $, здесь e – число исполнителей работы i, ${{t}_{i}}$ – продолжительность работы $i$, если ее делает один исполнитель.
3. Работа i может осуществляться любым числом исполнителей от 1 до $m$. Длительность работы i, как и ранее, равна ${{{{t}_{i}}} \mathord{\left/ {\vphantom {{{{t}_{i}}} e}} \right. \kern-0em} e}$ в ситуации, когда время выполнения работы одинаково у всех исполнителей $(e = \overline {1{\text{,}}m} )$. Тогда оптимальный по быстродействию план заключается в следующем. Вначале все исполнители делают работу один, затем работу два и т.д., т.е. каждую работу выполняют все исполнители. Длина расписания в этом случае равна:
где $m$ – число исполнителей работ проекта.4. Работа $i$ может выполняться ${{k}_{i}}$ исполнителями $({{k}_{i}} = \overline {1,m} )$, и время осуществления работы исполнителями разное. В этом случае время выполнения работы i исполнителем j задается числом ${{t}_{{ij}}}$, $i = \overline {1{\text{,}}n} {\text{;}}j = \overline {1{\text{,}}m} $. Если случаи 1–3 подробно изучены в специальной литературе [20–23], то ситуация реализации работ несколькими исполнителями с разным временем выполнения работ практически не изучена. Далее данная постановка задачи будет обсуждаться подробнее.
2. Постановка задачи и метод решения. Рассмотрим ситуацию, когда необходимо сделать $n$ работ проекта, технологическая последовательность которых задана ориентированным графом. Время выполнения работы $i$ исполнителем $j$ определяется величиной ${{t}_{{ij}}}$, $i = \overline {1{\text{,}}n} $; $j = \overline {1{\text{,}}m} $. Если работа $i$ не может быть осуществлена исполнителем $j$, то ${{t}_{{ij}}} = \infty $. Если работа $i$ может выполняться исполнителями $e$ и k, то время реализации работы $i$ исполнителями $e$ и $k$ равно:
(2.1)
${{t}_{i}}{\text{(}}e,k{\text{)}} = \frac{{\text{1}}}{{\frac{{\text{1}}}{{{{t}_{{ie}}}}} + \frac{{\text{1}}}{{{{t}_{{ik}}}}}}} = \frac{{{{t}_{{ie}}}{{t}_{{ik}}}}}{{{{t}_{{ie}}} + {{t}_{{ik}}}}}.$Формула (2.1) может быть получена исходя из следующих соображений: если работа $i$ происходит за время ${{t}_{{ie}}}$ и ${{t}_{{ik}}}$ соответственно исполнителями $e$ и $k$, то за одну единицу времени при условии, что исполнители осуществляют работу $i$ совместно, они выполнят ${1 \mathord{\left/ {\vphantom {1 {{{t}_{{ie}}}}}} \right. \kern-0em} {{{t}_{{ie}}}}} + {1 \mathord{\left/ {\vphantom {1 {{{t}_{{ik}}}}}} \right. \kern-0em} {{{t}_{{ik}}}}}$ часть работы $i$ или ${{({{t}_{{ie}}} + {{t}_{{ik}}})} \mathord{\left/ {\vphantom {{({{t}_{{ie}}} + {{t}_{{ik}}})} {({{t}_{{ie}}}{{t}_{{ik}}})}}} \right. \kern-0em} {({{t}_{{ie}}}{{t}_{{ik}}})}}$. Следовательно, вся работа $i$ будет сделана исполнителями $k$ и $e$ за время ${{({{t}_{{ie}}}{{t}_{{ik}}})} \mathord{\left/ {\vphantom {{({{t}_{{ie}}}{{t}_{{ik}}})} {({{t}_{{ie}}} + {{t}_{{ik}}})}}} \right. \kern-0em} {({{t}_{{ie}}} + {{t}_{{ik}}})}}$. Естественным образом формула (2.1) может быть обобщена на случай, если работа $i$ исполняется множеством исполнителей ${{M}_{i}}$:
(2.2)
${{t}_{i}}{\text{(}}{{M}_{i}}{\text{)}} = \frac{{\text{1}}}{{\sum\limits_{j \in {{M}_{i}}} {\frac{{\text{1}}}{{{{t}_{{ij}}}}}} }},$При решении задачи минимизации времени реализации работ в условиях выполнения их исполнителями с различным временем осуществления работы необходимо не только задать последовательность проведения работ, но и определить, какие именно исполнители должны сделать каждую работу. Для этого в случае непрерываемых работ может быть использован метод ветвей и границ, вычислительная схема которого заключается в следующем.
Шаг 1. Вычисление нижней оценки оптимальной продолжительности расписания. Пусть технологическая последовательность выполнения работ задается ориентированным графом.
Оценим продолжительность каждой работы с помощью формулы (2.2) следующим образом:
(2.3)
$t_{i}^{{{\text{min}}}} = \frac{{\text{1}}}{{\sum\limits_{j \in {{M}_{i}}} {\frac{{\text{1}}}{{{{t}_{{ij}}}}}} }};\quad i = \overline {1,n} ,$Данная задача является NP-трудной, поскольку к NP-трудным относится задача оптимизации выполнения работ несколькими идентичными исполнителями при условии, что каждую работу может осуществлять один исполнитель [1].
Далее найдем длину критического пути на графе для ситуации, когда в качестве длительностей работ приняты величины $t_{i}^{{\min }}$, $i = \overline {1{\text{,}}n} $. Обозначим эту величину через $S_{{{\text{кр}}}}^{{{\text{min}}}}$ и определим ${{T}_{{\text{н}}}} = S_{{{\text{кр}}}}^{{{\text{min}}}}$ (индекс “н” в ${{T}_{{\text{н}}}}$ соответствует словосочетанию “нижняя оценка”).
Очевидно, что за время, меньшее, $S_{{{\text{кр}}}}^{{{\text{min}}}}$, все работы проекта выполнены быть не могут.
Шаг 2. Вычисление верхней оценки оптимальной продолжительности расписания. Традиционно в качестве верхней оценки используется продолжительность какого-либо допустимого расписания. Будем формировать расписание, исходя из следующих соображений: если исполнитель e в момент времени $\tau $, $\tau \geqslant {\text{0}}$, может быть назначен для выполнения нескольких работ, то исполнитель выделяется той работе, которая входит в путь максимальной длины $S_{j}^{{{\text{max}}}}{\text{(}}\tau {\text{)}}$, рассчитанный с учетом частичного или полного завершения работ этого пути к моменту времени $\tau $.
Используя этот приоритет при формировании расписания, мы получим один из возможных допустимых планов, продолжительность которого обозначим через ${{T}_{{\text{в}}}}$ (индекс “в” в ${{T}_{{\text{в}}}}$ соответствует словосочетанию “верхняя оценка”). Если ${{T}_{{\text{в}}}} = {{T}_{{\text{н}}}}$, то оптимальное решение получено. В противном случае (если ${{T}_{{\text{в}}}} > {{T}_{{\text{н}}}}$) переходим к шагу 3 описываемого алгоритма.
Шаг 3. На этом шаге в предположении, что вычислены ${{T}_{{\text{н}}}}$ и ${{Т}_{{\text{в}}}}$, анализируется эффективность очередного формируемого допустимого расписания путем вычисления текущих нижних оценок $T_{{\text{н}}}^{{{\text{тек}}}}{\text{(}}\tau {\text{)}}$ в момент времени $\tau $, связанный с окончанием одной из выполняемых работ и выделением освободившегося исполнителя для очередной работы. Расчет текущей нижней оценки происходит следующим образом:
где $\tau $ – момент времени, в который вычисляется $T_{{\text{н}}}^{{{\text{тек}}}}(\tau )$, считая τ = 0 моментом начала работ проекта; $T_{{\text{н}}}^{{}}(\tau )$ – нижняя оценка оптимальной продолжительности работ с учетом полного или частичного завершения работ проекта к моменту $\tau $.Далее сравниваем значения $T_{{\text{н}}}^{{{\text{тек}}}}(\tau )$ и ${{T}_{{\text{в}}}}$. Если $T_{{\text{н}}}^{{{\text{тек}}}}(\tau ) \geqslant {{T}_{{\text{в}}}}$, то данное расписание не будет оптимальным, оно отбраковывается, переходим к анализу очередного расписания. Если $T_{{\text{н}}}^{{{\text{тек}}}}(\tau )$ < < Tв, то формирование текущего расписания продолжается, т.е. в момент времени $\tau $ выбирается очередная работа и для ее выполнения выделяется один или несколько исполнителей. Продолжительность работы вычисляется с использованием формулы (2.2). В результате подобного анализа каждого допустимого расписания оно будет или отбраковано, или полностью сформировано. В последнем случае сравниваем его продолжительность T* с величиной ${{T}_{{\text{в}}}}$. Если $T{\kern 1pt} * < {{T}_{{\text{в}}}}$, то в дальнейшем полагаем ${{T}_{{\text{в}}}} = T{\kern 1pt} *$.
Предлагаемый алгоритм заканчивает свою работу при следующих вариантах.
1. При очередной корректировке ${{T}_{{\text{в}}}}$ получим ${{T}_{{\text{в}}}} = {{T}_{{\text{н}}}}$. В этом случае оптимальным будет то расписание, длина которого равна ${{T}_{{\text{н}}}}$.
2. Рассмотрены все допустимые расписания, тем не менее, последнее значение ${{T}_{{\text{в}}}} > {{T}_{{\text{н}}}}$. Тогда выбираем в качестве оптимального плана тот, которому соответствует последнее (минимальное) значение ${{T}_{{\text{в}}}}$.
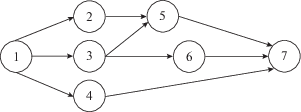
Рассмотрим пример вычисления оптимального расписания с использованием предложенного метода ветвей и границ для следующей ситуации. Пусть задан ориентированный граф, представляющий технологическую последовательность выполнения работ (рис. 1).
Будем считать, что в проекте будут участвовать два исполнителя, для которых время выполнения работы задается матрицей $T = ({{t}_{{ij}}})$ ($i = \overline {1{\text{,}}n} $; $j = \overline {1{\text{,}}m} $, здесь $i = \overline {1{\text{,}}7} $; $j = 1;2$) следующего вида:
Используя формулу (2.3), найдем минимально возможную продолжительность работ: $t_{{\text{1}}}^{{{\text{min}}}} = 1{\text{/}}((1{\text{/}}1) + (1{\text{/}}1.2))$ = 0.55, аналогично: $t_{{\text{2}}}^{{{\text{min}}}} = {\text{1}}{\text{.2}}$; $t_{{\text{3}}}^{{{\text{min}}}} = {\text{1}}{\text{.6}}$; $t_{{\text{4}}}^{{{\text{min}}}} = {\text{2}}{\text{.4}}$; $t_{{\text{5}}}^{{{\text{min}}}} = {\text{2}}{\text{.8}}$; $t_{{\text{6}}}^{{{\text{min}}}} \approx {\text{3}}{\text{.4}}$; $t_{{\text{7}}}^{{{\text{min}}}}$ = 3.8.
Согласно рис. 1, определим работы, входящие в каждый из четырех путей ориентированного графа: $\left| {{{S}_{{\text{1}}}}} \right| = \left\{ {{\text{1,2,5,7}}} \right\}$; $\left| {{{S}_{{\text{2}}}}} \right| = \left\{ {{\text{1,3,5,7}}} \right\}$; $\left| {{{S}_{{\text{3}}}}} \right| = \left\{ {{\text{1,3,6,7}}} \right\}$; $\left| {{{S}_{{\text{4}}}}} \right| = \left\{ {{\text{1,4,7}}} \right\}$. Здесь $\left| {{{S}_{j}}} \right|$ – множество работ, входящих в путь $j$, $j = \overline {{\text{1,4}}} $. С учетом определения $t_{i}^{{{\text{min}}}}$, $i = \overline {1,7} $, и $\left| {{{S}_{j}}} \right|$ вычислим минимально возможную длину каждого пути ориентированного графа: $S_{{\text{1}}}^{{{\text{min}}}} = {\text{0}}{\text{.55 + 1}}{\text{.2 + 2}}{\text{.8 + 3}}{\text{.8}} = {\text{8}}{\text{.35}}$, по тому же принципу: $S_{{\text{2}}}^{{{\text{min}}}} = {\text{8}}{\text{.75}}$; $S_{{\text{3}}}^{{{\text{min}}}} = {\text{9}}{\text{.35}}$; $S_{{\text{4}}}^{{{\text{min}}}} = {\text{6}}{\text{.75}}$.
Таким образом, если каждую работу будут выполнять два исполнителя, то критическим путем будет путь ${{S}_{{\text{3}}}}$ и его длина с учетом формулы (2.3) будет равна:
Поэтому $T_{{\text{н}}}^{{}} = {\text{9}}{\text{.35}}$.
Для того, чтобы получить верхнюю оценку продолжительности оптимального плана, сформируем допустимое расписание с использованием эвристики, предложенной в описании метода ветвей и границ.
В момент времени τ = 0 можно начать выполнять только первую работу, и для этого выделяется первый исполнитель, который заканчивает первую работу в момент времени ${{\tau }_{{\text{1}}}} = {\text{1}}$. Далее, с учетом структуры ориентированного графа, изображенного на рис. 1, начиная с момента ${{\tau }_{{\text{1}}}}$ можно выполнять работы два, три и четыре. При условии, что работа три лежит на критическом пути, ей выделяется первый исполнитель, а работе два – второй исполнитель, так как работа два входит в первый путь, который продолжительнее четвертого пути. В момент времени ${{\tau }_{{\text{2}}}} = {\text{3}}{\text{.4}}$ заканчивается вторая работа и второй исполнитель передается четвертой работе. В момент времени ${{\tau }_{{\text{3}}}} = {\text{4}}$ заканчивается третья работа и первый исполнитель передается для выполнения пятой работы. В момент времени ${{\tau }_{{\text{4}}}} = {\text{8}}$ заканчивается четвертая работа и второй исполнитель начинает выполнять шестую работу. В момент τ = 9 заканчивается пятая работа, а в момент времени $\tau = {\text{14}}{\text{.8}}$ завершается выполнение шестой работы.
Работу семь оба исполнителя выполняют совместно в течение 3.8 единицы времени. Таким образом, продолжительность расписания ${{T}_{{{\text{к}}{\text{.п}}}}}$ равна:
Индекс “к.п” в ${{T}_{{{\text{к}}{\text{.п}}}}}$ соответствует словосочетанию “критический путь”.
С учетом описанного выше метода ветвей и границ ${{T}_{{\text{в}}}} = {\text{18}}{\text{.6}}$.
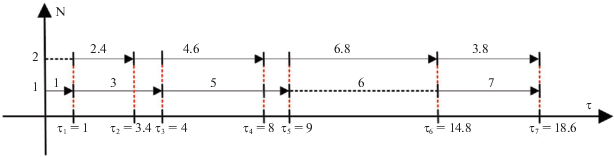
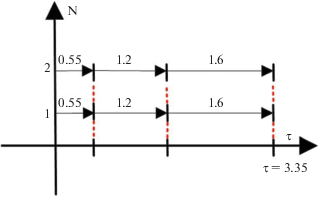
Сформированное расписание с использованием диаграммы Ганта будет выглядеть следующим образом (рис. 2).
Замечание. Здесь и далее на оси N полужирным отмечены номера работ, числа, выделенные курсивом, обозначают их длительность. Горизонтальная пунктирная линия в области шестой работы показывает, что в рассматриваемом допустимом расписании в период с момента τ = 9 и до $\tau = 14.8$, пока второй исполнитель выполняет шестую работу, первый исполнитель простаивает. Вертикальные пунктирные линии в данном случае не несут какой-либо смысловой нагрузки и присутствуют просто для наглядности.
В ситуации, если возможно в момент времени τ = 9 подключить к выполнению работы шесть первого исполнителя, она будет иметь следующую продолжительность:
Следовательно, момент времени ${{\tau }_{6}}$, в который будет завершена работа шесть, равен
а все работы будут выполнены в моментПоэтому в качестве улучшенной верхней оценки можно принять
Расписание с длительностью $T = {\text{16}}{\text{.7}}$ также может быть улучшено за счет того, что работе один для ее выполнения выделяются оба исполнителя. В этом случае, как было показано выше, время ее осуществления равно 0.55.
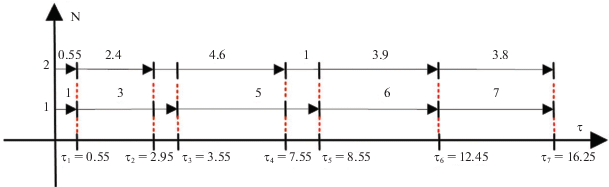
Тогда диаграмма Ганта улучшенного расписания будет выглядеть следующим образом (рис. 3).
Таким образом, при совместном выполнении двумя исполнителями работ один, семь и частично совместном выполнении работы шесть удалось снизить значение верхней оценки с ${{T}_{{\text{в}}}} = {\text{18}}{\text{.6}}$ до ${{T}_{{\text{в}}}} = {\text{16}}{\text{.25}}$.
Как было отмечено выше, если ${{T}_{{\text{в}}}} > {{T}_{{\text{н}}}}$, то необходим дальнейший анализ допустимых расписаний с вычислением текущих нижних оценок $T_{{\text{н}}}^{{{\text{тек}}}}({{\tau }_{i}})$, где ${{\tau }_{i}}$ – момент завершения работы с номером i, $i = \overline {1{\text{,}}n} $.
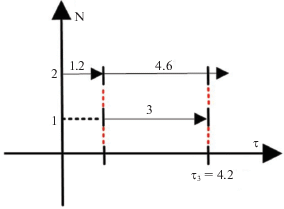
Рассмотрим диаграмму Ганта при формировании второго допустимого расписания (рис. 4) и вычислим одну из текущих оценок в момент завершения работы три, выполняемой первым исполнителем при формировании второго допустимого расписания.
С учетом формулы (2.4)
Для того, чтобы определить ${{T}_{{\text{н}}}}({{\tau }_{{\text{3}}}})$, необходимо рассчитать минимальные длительности путей ${{S}_{{\text{1}}}}$, ${{S}_{{\text{2}}}}$, ${{S}_{{\text{3}}}}$, ${{S}_{{\text{4}}}}$ с учетом полного или частичного их выполнения к моменту времени ${{\tau }_{{\text{3}}}}$. Путь ${{S}_{{\text{1}}}}$ уменьшился на величину длительности первой работы в случае, если она выполнялась двумя исполнителями, поэтому $S_{{\text{1}}}^{{{\text{min}}}}({{\tau }_{{\text{3}}}}) = S_{{\text{1}}}^{{{\text{min}}}} - t_{{\text{1}}}^{{{\text{min}}}} = {\text{8}}{\text{.35}} - {\text{0}}{\text{.55}}$ = 7.8.
Учитывая, что во втором и третьем пути работы один и три выполнены, получим $S_{{\text{2}}}^{{{\text{min}}}}({{\tau }_{{\text{3}}}}) = {\text{8}}.75 - 0.55$ – 1.6 = 6.6; $S_{{\text{3}}}^{{{\text{min}}}}({{\tau }_{{\text{3}}}}) = 9.35 - 0.55 - 1.6 = {\text{7}}{\text{.2}}$.
Работа четыре на диаграмме Ганта (рис. 4) выполнена на три единицы. Поэтому ее остаток в долях от всей длительности составит величину Δ, которая вычисляется по следующей формуле:
Если эту часть работы будут осуществлять исполнители один и два, то время выполнения остатка этой работы $t_{{\text{4}}}^{{{\text{min}}}}({{\tau }_{{\text{3}}}})$ составит:
Таким образом, $S_{{\text{4}}}^{{{\text{min}}}}({{\tau }_{{\text{3}}}})$ можно вычислить как
С учетом предлагаемого метода ветвей и границ (шаг 3) $T_{{\text{н}}}^{{{\text{min}}}}({{\tau }_{{\text{3}}}})$ для формируемого расписания вычисляется по формуле
Следовательно, величина первой текущей нижней оценки равна
Так как $T_{{\text{н}}}^{{{\text{тек}}}}({{\tau }_{{\text{3}}}}) < {{T}_{{\text{в}}}} = {\text{16}}{\text{.25}}$, то формирование данного расписания должно быть продолжено.
Учитывая комбинаторный характер данного алгоритма, может быть использована усеченная схема метода ветвей и границ. Отличие этой схемы от ранее изложенной состоит в том, что на шаге 2 алгоритма и при каждой последующей корректировке $T_{{\text{в}}}^{{}}$ вычисляется величина $T_{{\text{в}}}^{{}} - {{T}_{{\text{н}}}}$. Если эта величина удовлетворяет требованию
то полученный допустимый план выбирается в качестве оптимального. Здесь $\delta > {\text{0}}$ – величина, характеризующая требуемую точность решения.3. Управление работами проекта в условиях неопределенности и риска. В разд. 2 статьи рассмотрена задача оптимизации работ проекта по критерию быстродействия в ситуации, когда работы могут выполняться различными исполнителями за различное время. Время проведения работы исполнителем в условиях детерминированных исходных данных модели задается следующей матрицей:
Здесь $n$ – число работ, $m$ – число исполнителей. Напомним, что каждая работа i может выполняться как одним исполнителем, так и группой исполнителей ${{M}_{i}}$, такой, что $\forall {{t}_{{ij}}} \in {{M}_{i}}$, ${{t}_{{ij}}} < \infty $.
Предложенный выше метод решения может определить оптимальную последовательность работ в условиях, когда элементы матрицы $T = ({{t}_{{ij}}})$ детерминированы. В то же время на практике часто встречаются ситуации, когда определить однозначно элементы матрицы T невозможно, тогда возможны такие варианты их количественной оценки.
1. Элементы матрицы tij могут меняться в заданных диапазонах, т.е. ${{t}_{{ij}}} \in [t_{{ij}}^{{\text{1}}},t_{{ij}}^{{\text{2}}}]$, $i = \overline {1{\text{,}}n} $; $j = \overline {1{\text{,}}m} $. Здесь $t_{{ij}}^{{\text{1}}}$ – минимальное значение элемента матрицы ${{t}_{{ij}}}$, а $t_{{ij}}^{{\text{2}}}$ – максимальное значение элемента матрицы tij и, кроме того, tij может принимать любое значение из диапазона $[t_{{ij}}^{{\text{1}}},t_{{ij}}^{{\text{2}}}]$.
2. Среди элементов матрицы T существует некоторое ее подмножество элементов $T{\kern 1pt} ' \subseteq T$, обладающих тем свойством, что их величина может получать приращение $\varepsilon > {\text{0}}$.
3. Элементы матрицы tij есть случайные величины с известным законом распределения, полученным или на основе накопленной статистики, или путем экспертных оценок. При этом эксперты могут использовать свои знания о проектах-аналогах [24].
Ниже будут изучены некоторые подходы к оптимизации управления работами проектов в рассмотренных ситуациях.
3.1. Интервальное задание времени осуществления работы исполнителями. В ситуации, когда ${{t}_{{ij}}} \in [t_{{ij}}^{{\text{1}}},t_{{ij}}^{{\text{2}}}]$ и задано множество исполнителей ${{M}_{i}}$, которые могут выполнить работу i, вообще говоря, за различное время, продолжительность работы $i$ будет меняться в интервале
(3.1)
${{\tau }_{i}} \in \left[ {\frac{{\text{1}}}{{\sum\limits_{j \in {{M}_{i}}} {\frac{{\text{1}}}{{t_{{ij}}^{{\text{1}}}}}} }};\frac{{\text{1}}}{{\sum\limits_{j \in {{M}_{i}}} {\frac{{\text{1}}}{{t_{{ij}}^{{\text{2}}}}}} }}} \right].$Соответственно с учетом формулы (3.1) продолжительность любого расписания ${{R}_{e}}$, $e = \overline {1{\text{,}}L} $, будет также изменяться в интервале $[T_{e}^{1},T_{e}^{2}]$. Здесь $T_{e}^{1}$ и $T_{e}^{2}$ – минимальная и максимальная продолжительность расписания ${{R}_{e}}$. Если работы не прерываемы, то, как было доказано в [4], длительность любого допустимого расписания может быть представлена в виде следующей формулы:
Здесь ${{F}_{k}}$ – подмножество работ исходного множества работ проекта $F$, т.е. ${{F}_{k}} \subseteq F$.
Таким образом, определяя для каждой работы $i$ множество исполнителей ${{M}_{i}}$, мы находим диапазон длительности работы $i$ в ситуации, если элементы матрицы времени выполнения работы $T$ заданы интервально. Соответственно длительность каждого расписания также задана интервально.
Возникает вопрос: как выбрать из множества допустимых расписаний кратчайшее?
Существует одна ситуация, когда этот выбор очевиден: например, если существует расписание K, такое, что $T_{k}^{{\text{2}}} \leqslant T_{j}^{{\text{1}}}$; $j = \overline {1,L} $; $j \ne k$. Здесь L – число всех возможных допустимых расписаний. Очевидно, что расписание ${{R}_{k}}$ будет оптимальным при любых значениях ${{t}_{{ij}}} \in [t_{{ij}}^{{\text{1}}},t_{{ij}}^{{\text{2}}}]$.
В остальных случаях для нахождения одного (или нескольких) оптимальных расписаний необходимы дополнительные исследования. Сформируем множество расписаний, которые при некоторых значениях ${{t}_{{ij}}} \in [t_{{ij}}^{{\text{1}}},t_{{ij}}^{{\text{2}}}]$, $i = \overline {1{\text{,}}n} $; $j = \overline {1{\text{,}}m} $, могут быть оптимальными. Для этого зададим $T_{p}^{1} = \mathop {\min T_{j}^{1}}\limits_{j = \overline {1{\text{,}}L} } $ и включим расписание ${{R}_{p}}$ в множество потенциально оптимальных расписаний ${{O}_{{{\text{опт}}}}}$. Расписание называется потенциально оптимальным, если существуют длительности работ из области допустимых значений, при которых данное расписание оптимально.
Определим $T_{q}^{2} = \mathop {{\text{min}}T_{j}^{2}}\limits_{j = \overline {1{\text{,}}L} } $ и включим расписание ${{R}_{q}}$ в множество ${{O}_{{{\text{опт}}}}}$. И, наконец, включим в множество ${{O}_{{{\text{опт}}}}}$ все те расписания, у которых $T_{j}^{1} < T_{q}^{2}$, $j = \overline {1{\text{,}}L} $.
Далее, так как в ${{O}_{{{\text{опт}}}}}$ входят все расписания, которые потенциально могут быть оптимальными, выделим среди допустимых планов ${{O}_{{{\text{опт}}}}}$ план ${{R}_{m}} \in {{O}_{{{\text{опт}}}}}$ и зададим множество, на котором может изменяться время выполнения работы исполнителями, при котором ${{R}_{m}}$ будет оптимальным, следующей системой неравенств:
(3.2)
$\left\{ \begin{gathered} t_{{ij}}^{{\text{1}}} \leqslant {{t}_{{ij}}} \leqslant t_{{ij}}^{{\text{2}}};\quad i = \overline {1{\text{,}}n} ;\quad j = \overline {1{\text{,}}m} {\text{;}} \hfill \\ \sum\limits_{i \in {{F}_{m}}} {\frac{{\text{1}}}{{\sum\limits_{j \in M_{i}^{m}} {\frac{{\text{1}}}{{{{t}_{{ij}}}}}} }} \leqslant } \,\sum\limits_{i \in {{F}_{k}}} {\frac{{\text{1}}}{{\sum\limits_{j \in M_{i}^{k}} {\frac{{\text{1}}}{{{{t}_{{ij}}}}}} }}} ,\quad k = \overline {1{\text{,}}{{L}_{1}}} \hfill \\ \end{gathered} \right.,$Аналогично формуле (3.2) может быть определена область изменения tij для любого другого плана ${{R}_{i}} \in {{O}_{{{\text{опт}}}}}$.
Таким образом, предложен механизм формирования всех возможных оптимальных расписаний при изменении длительностей выполнения работ исполнителями в диапазоне $t_{{ij}}^{{\text{1}}} \leqslant {{t}_{{ij}}} \leqslant t_{{ij}}^{{\text{2}}}$ и для каждого такого оптимального расписания выделена область изменения времени выполнения каждой работы исполнителем, в которой данное расписание остается оптимальным. Такие области изменения времени осуществления работ исполнителями для расписания называют еще областями устойчивости этих расписаний [4].
3.2. Планирование выполнения работ проекта в условиях увеличения длительностей работ. Рассмотрим ситуацию, когда среди элементов матрицы $T = ({{t}_{{ij}}})$, $i = \overline {1{\text{,}}n} $; $j = \overline {1{\text{,}}m} $, существует некоторое подмножество элементов $T{\kern 1pt} ' \subseteq T$, обладающих тем свойством, что если ${{t}_{{ij}}} \in T{\kern 1pt} '$, то величина этого элемента может увеличиться на некоторое $\varepsilon > {\text{0}}$. Рассмотрим, как будет реагировать оптимальное расписание на увеличение значений элементов ${{t}_{{ij}}} \in T{\kern 1pt} '$.
Отметим, что в этом случае длительность работы $i$ при выполнении ее исполнителями множества ${{M}_{i}}$ с учетом формулы (2.2) вычисляется следующим образом:
(3.3)
${{t}_{i}}({{M}_{i}}) = \frac{{\text{1}}}{{\sum\limits_{j \in {{M}_{i}}} {\frac{{\text{1}}}{{{{t}_{{ij}}} + {{\Delta }_{{ij}}}}}} }};\quad i = \overline {1,n} ,$В определении величины ${{\Delta }_{{ij}}}$ через $T{\kern 1pt} '$ обозначено множество возмущенных элементов матрицы $T$ $(T{\kern 1pt} ' \subseteq T)$, т.е. таких элементов, величина которых может возрасти на число $\varepsilon > 0$. Источником подобных возмущений может выступать как окружающая, так и внутренняя среда проекта [25].
Рассмотрим ситуацию, когда работу i могут выполнять два исполнителя и длительность выполнения работы i первым и вторым исполнителем по отдельности составляет ${{t}_{{i1}}}$ и ${{t}_{{i{\text{2}}}}}$. Если ${{t}_{{i1}}} \in T{\kern 1pt} '$ и ${{t}_{{i2}}} \in T{\kern 1pt} '$, то с учетом формул (2.2) и (3.3) получим
(3.4)
${{t}_{i}}({{M}_{i}}) = \frac{{\text{1}}}{{\frac{{\text{1}}}{{{{t}_{{i{\text{1}}}}} + \varepsilon }} + \frac{{\text{1}}}{{{{t}_{{i{\text{2}}}}} + \varepsilon }}}}.$Здесь в множество ${{M}_{i}}$ входят первый и второй исполнители.
Преобразуя правую часть формулы (3.4), найдем
(3.5)
${{t}_{i}}({{M}_{i}}) = \frac{{({{t}_{{i1}}} + \varepsilon )({{t}_{{i2}}} + \varepsilon )}}{{{{t}_{{i1}}} + {{t}_{{i2}}} + {\text{2}}\varepsilon }}.$Из формулы 3.5 следует, что предел длительности работы ${{t}_{i}}({{M}_{i}})$ в этом случае равен
Из рассмотренного примера, в частности, следует, что при выполнении работ несколькими исполнителями интенсивность роста длительности работы $i$ при увеличении $\varepsilon $ определяется тем, сколько элементов ${{\Delta }_{{ij}}}$ в формуле (3.3) положительны. Учитывая, что длительность расписания ${{R}_{i}}$ для непрерываемых работ задается суммарной длительностью некоторого подмножества работ ${{F}_{i}}$, получим, что длительность работы $e$ расписания ${{R}_{q}}$ $\tau _{e}^{q}$ вычисляется с помощью следующего выражения:
(3.6)
$\tau _{e}^{q} = \frac{{\text{1}}}{{\sum\limits_{j \in M_{e}^{q}} {\frac{{\text{1}}}{{{{t}_{{ej}}} + {{\Delta }_{{ej}}}}}} }},$Введем показатель, характеризующий число элементов ${{t}_{{ej}}}$ из $T{\kern 1pt} '$ в правой части выражения (3.6):
(3.7)
$W_{{ej}}^{q} = \left\{ \begin{gathered} {\text{1}}, \quad {\text{если в календарном плане}} {{R}_{{q }}}{\text{работу }}e{\text{ выполняет исполнитель}} \;j\; {\text{и}}\; {{t}_{{ej}}} \in T{\kern 1pt} '; \hfill \\ {\text{0}}\quad {\text{в противном случае}}. \hfill \\ \end{gathered} \right.$С учетом формулы (3.7) число ненулевых элементов ${{\Delta }_{{ej}}}$ в правой части выражения (3.6) $\Omega _{e}^{q}$ может быть вычислено следующим образом:
С использованием формулы (3.8) определим для каждого расписания ${{R}_{q}}$ величину ${{V}_{q}}$ по следующей формуле:
Здесь ${{F}_{q}}$ – подмножество работ проекта, суммарная длительность которых задает продолжительность плана ${{R}_{q}}$. Очевидно, что Vq определяет максимальную степень полинома от ε, выражающего длительность расписания, как величину, зависящую от параметра ε.
Расписание с наименьшим значением Vq вычисляется с помощью формулы
где $L$ – число допустимых расписаний.Расписание ${{R}_{e}}$ обладает тем свойством, что, начиная с некоторого положительного числа $\varepsilon {\kern 1pt} '$, для всех значений возмущений $\varepsilon {\kern 1pt} ' < \varepsilon < \infty $ оптимальным расписанием будет расписание ${{R}_{e}}$. Это объясняется тем, что степень полинома от $\varepsilon $, задающего его длительность, будет наименьшей по сравнению с другими расписаниями.
С учетом формул (3.1.1) и (3.5) продолжительность каждого расписания ${{R}_{q}}$, $q = \overline {1{\text{,}}L} $, ${{T}_{q}}$ в ситуации, когда существует множество возмущенных элементов $T{\kern 1pt} ' \subseteq T$, может быть представлена как функция параметров ${{t}_{{ij}}}$, $i = \overline {1{\text{,}}n} $; $j = \overline {1{\text{,}}m} $, и $\varepsilon $, т.е.
Согласно (3.5), ${{f}_{q}}({{t}_{{ij}}},\varepsilon )$ есть сумма дробных функций, в знаменателе и числителе которых стоят многочлены от ${{t}_{{ij}}}$ и $\varepsilon $. При этом степень многочлена по $\varepsilon $ в числителе всегда больше, чем степень многочлена по $\varepsilon $ в знаменателе (следствие формулы (3.5)), при росте $\varepsilon $:
для всех $\varepsilon $ начиная с некоторого $\varepsilon > \varepsilon {\kern 1pt} *$.Учитывая нелинейный рост длительности Tq от $\varepsilon $ и непрерывность функций ${{f}_{k}}{\kern 1pt} ({{t}_{{ij}}},\varepsilon {\text{)}}$ по $\varepsilon $, проанализируем, как меняется оптимальное расписание при росте $\varepsilon $. Рассмотрим значение функций ${{f}_{q}}({{t}_{{ij}}},\varepsilon )$ в условиях отсутствия возмущения $\varepsilon $, т.е. при $\varepsilon = {\text{0}}$. Пусть оптимальным в этих условиях будет план ${{R}_{e}}$. Рассмотрим уравнения от $\varepsilon $:
(3.9)
${{f}_{e}}(\varepsilon ) = {{f}_{j}}(\varepsilon ),\quad j = \overline {1{\text{,}}L} ,\quad j \ne e.$Пусть εj – минимальное положительное решение уравнения (3.9). Выберем ${{\varepsilon }_{k}} = \mathop {{\text{min}}}\limits_{j = \overline {1{\text{,}}L} } {{\varepsilon }_{j}}$. Следовательно, на интервале увеличения $\varepsilon \in {\text{(0,}}{{\varepsilon }_{k}}{\text{)}}$ оптимальным будет расписание ${{R}_{e}}$. Начиная со значения $\varepsilon > {{\varepsilon }_{k}}$, оптимальным будет расписание ${{R}_{k}}$. Решая уравнения (3.9) на области увеличения $\varepsilon > {{\varepsilon }_{k}}$ и выбирая минимальное положительное решение ${{\varepsilon }_{p}}{\text{(}}{{\varepsilon }_{p}} > {{\varepsilon }_{k}}{\text{)}}$, определим зону увеличения $\varepsilon $ для оптимального расписания ${{R}_{k}}$ и далее для оптимального расписания ${{R}_{p}}$.
Таким образом, если известен диапазон увеличения возмущения ${\text{0}} \leqslant \varepsilon \leqslant D$, то интервал ${\text{(0,}}D{\text{)}}$ может быть разбит на отрезки, характеризующиеся тем, что при увеличении возмущения $\varepsilon $ в рамках фиксированного отрезка оптимальное расписание не меняется. Область увеличения возмущения ε, на которой фиксированное расписание остается неизменным, называют областью устойчивости расписания.
Рассмотрим пример использования предлагаемой методики определения области устойчивости расписания. Пусть для реализации проекта необходимо сделать три работы. Работы могут выполняться в любой последовательности двумя исполнителями. Матрица времени выполнения работы исполнителем $T$ задана следующим образом:
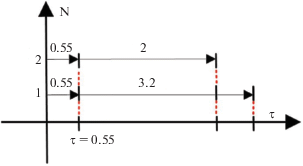
В множество возмущенных элементов $T{\kern 1pt} ' \subseteq T$ включен один элемент $T{\kern 1pt} ' = {\text{\{ }}{{t}_{{{\text{22}}}}}{\text{\} }}$. Рассмотрим два расписания в ситуации, когда $\varepsilon = {\text{0}}$, и изобразим соответствующие диаграммы Ганта (рис. 5, 6):
Согласно плану ${{R}_{{\text{1}}}}$, каждая работа выполняется двумя исполнителями, поэтому их длительности соответственно равны: $t_{{\text{1}}}^{{}} = 1{\text{/}}((1{\text{/}}1) + (1{\text{/}}1.2)) = {\text{0}}{\text{.55}}$; $t_{{\text{2}}}^{{}} = {\text{1}}{\text{.2}}$; $t_{{\text{3}}}^{{}} = {\text{1}}{\text{.6}}$. Длина первого расписания
Согласно плану ${{R}_{{\text{2}}}}$, вначале выполняется двумя исполнителями работа один, затем первый исполнитель осуществляет работу два, а второй исполнитель – работу три. Соответственно длина второго расписания
Таким образом, при $\varepsilon = {\text{0}}$ оптимальным является план ${{R}_{{\text{1}}}}$.
Согласно формуле (3.3), длина расписания ${{R}_{{\text{1}}}}$ при наличии возмущения $\varepsilon $ составит:
Приравняем значения ${{T}_{{\text{1}}}}{\text{(}}\varepsilon {\text{)}}$ и ${{T}_{{\text{2}}}}{\text{(}}\varepsilon {\text{)}}$: $3.75 = 2.15 + (4.8 + 2\varepsilon ){\text{/}}(4.4 + \varepsilon )$. Отсюда $\varepsilon = {\text{5}}{\text{.5}}$. Следовательно, расписание ${{R}_{{\text{1}}}}$ оптимально, если величина возмущения $\varepsilon $ не превышает числа 5.5, т.е. ${\text{0}} \leqslant \varepsilon \leqslant {\text{5}}{\text{.5}}$, расписание ${{R}_{{\text{2}}}}$ оптимально, если $\varepsilon > {\text{5}}{\text{.5}}$.
3.3. Стохастическое задание продолжительности работ проекта. Рассмотрим ситуацию, когда длительности выполнения работ проекта ${{t}_{{ij}}}$, $i = \overline {1,n} $; $j = \overline {1,m} $, являются случайными величинами с заданным законом распределения, т.е.
Здесь ${{p}_{k}}$, $k = \overline {1{\text{,}}Q} $, – вероятность того, что длительность выполнения работы $i$ исполнителем j равна ${{t}_{{ijk}}}$, $\sum\limits_{k = {\text{1}}}^Q {{{P}_{k}} = {\text{1}}} $, ${{p}_{k}} \geqslant 0$.
В этом случае можно в качестве времени выполнения работы исполнителем принять его математическое ожидание, т.е.
Далее для определения оптимального плана выполнения работ можно использовать метод ветвей и границ, предложенный в статье. Также будем считать, что работы не прерываемы и каждая выполняется одним исполнителем.
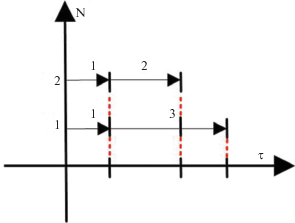
Учитывая, что продолжительность выполнения работ каждым исполнителем задана как случайная величина, длительность каждого расписания также будет случайной величиной. Для непрерываемых работ продолжительность каждого расписания ${{R}_{k}}$ может быть представлена суммой продолжительностей работ некоторого подмножества работ ${{F}_{k}} \subseteq F$ [4] (здесь $F$ – множество всех работ проекта). Определим риск расписания, согласно [22], как дисперсию длительности всех работ, входящих в ${{F}_{k}}$:
где $\sigma _{i}^{2}$ – дисперсия продолжительности работы с номером $i$; $C(i,j)$ – ковариация продолжительностей работ с номерами i и j $(i \in {{F}_{k}};\;j \in {{F}_{k}};\;i < j)$; ${{W}_{k}}$ – количественная оценка риска расписания, оцениваемого как дисперсия длительностей работ множества ${{F}_{k}}$ с учетом их выполнения одним исполнителем.Показатель ${{d}_{i}}$, задающий долю длительности работы в длине расписания, определяется следующим образом:
(3.11)
${{d}_{i}} = \frac{{\overline {{{\tau }_{i}}} }}{{\sum\limits_{j \in {{F}_{k}}} {\overline {{{\tau }_{j}}} } }},$Таким образом, в условиях задания элементов матрицы $T = ({{t}_{{ij}}})$, $i = \overline {1{\text{,}}n} $; $j = \overline {1{\text{,}}m} $, как случайных величин с заданным распределением вероятностей, эффективность каждого расписания выполнения работ проекта может быть определена по двум критериям:
1) математическое ожидание длительности выполнения работ расписания;
2) риск расписания, оцениваемый как дисперсия продолжительности расписания.
Рассмотрим пример оценки эффективности расписания в условиях стохастического задания времени выполнения работы исполнителями. Пусть для реализации проекта необходимо выполнить три работы. Работы можно выполнять в любой последовательности. Выполнять работы будут два исполнителя, у которых время выполнения работы ${{t}_{{ij}}}$ $(i = 1,2,3;\;j = 1,2)$ является случайной величиной, распределение которой дается следующей таблицей 1.
Приведем следующее расписание выполнения работ проекта: вначале оба исполнителя выполняют работу один, затем второй исполнитель делает работу два, а первый исполнитель работу три. Диаграмма Ганта для такого расписания представлена на рис. 7.
Как отмечалось выше, эффективность расписания в ситуации стохастической матрицы времени выполнения работы исполнителем $T$ определяется двумя показателями: математическим ожиданием длительностей работ и риском расписания, оцениваемым как волатильность его длительности.
Рассчитаем математическое ожидание длительности расписания. Для этого вычислим математическое ожидание длительности при выполнении работ один, два и три.
Обозначим соответствующие возможные значения длительности первой работы через ${{\tau }_{{{\text{11}}}}}$, ${{\tau }_{{{\text{12}}}}}$, ${{\tau }_{{{\text{13}}}}}$, заданные с вероятностью ${{p}_{{\text{1}}}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, ${{p}_{{\text{2}}}} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$, ${{p}_{{\text{3}}}} = {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}$: ${{\tau }_{{{\text{11}}}}} = 1{\text{/}}((1{\text{/}}1) + (1{\text{/}}1.2)) = {\text{0}}{\text{.55}}$. Аналогично ${{\tau }_{{{\text{12}}}}} = {\text{0}}{\text{.51}}$; ${{\tau }_{{{\text{13}}}}} = {\text{0}}{\text{.68}}$. Следовательно, математическое ожидание длительности выполнения работы один при условии ее реализации исполнителями один и два равно:
Соответственно, математическое ожидание длительностей работ два и три при условии, что работу два выполняет второй исполнитель, а работу три – первый исполнитель, равно:
Из диаграммы Ганта на рис. 7 следует, что математическое ожидание расписания $\overline T $ равно:
Величина $T$ складывается из ожидаемого времени выполнения работы один двумя исполнителями и ожидаемого времени выполнения работы три первым исполнителем.
Таким образом, ${{F}_{{\text{1}}}} = \left\{ {{\text{1}},{\text{2}}} \right\}$, ${{F}_{{\text{3}}}} = \left\{ {\text{1}} \right\}$, где ${{F}_{1}}$ и ${{F}_{3}}$ соответственно задают множества исполнителей, выполняющих первую и третью работы.
Воспользуемся формулой (3.10) для оценки риска предложенного расписания:
Рассчитаем ${{d}_{{\text{1}}}}$ и ${{d}_{{\text{3}}}}$ с учетом формулы (3.11):
Вычислим ковариацию длительностей работ один и три:
Подставив полученные значения в формулу (3.10), получим количественную оценку риска предложенного расписания:
Таким образом, для сформированного расписания математическое ожидание его продолжительности $\overline T = {\text{3}}{\text{.66}}$ единицы времени, а риск расписания (его волатильность) $w = {\text{0}}{\text{.0007}}$.
Что же касается допустимой величины риска, то, по всей видимости, уровень риска является субъективной величиной, т.е. каждый инвестор самостоятельно определяет допустимый уровень риска, хотя и существуют наиболее распространенные характеристики уровня риска проекта, являющиеся по сути универсальными [26].
Полученную двухкритериальную оценку плана можно сравнить с подобными оценками для других допустимых расписаний и, используя методы сведения многокритериальных оценок к одному критерию, выбрать наилучший вариант.
Заключение. Основное внимание было уделено рассмотрению подходов к оптимизации управления проектами в сфере логистики в условиях неточного задания длительностей работ. Объективное существование неопределенности и риска – неотъемлемый компонент любой экономической деятельности [27], при этом одной из причин низкой степени осознания менеджером необходимости эффективно управлять рисками в рамках всей организации является сложность идентификации и измерения риска при принятии решений [28].
На сегодняшний день проблема риска стала предметом как общетеоретических, так и ориентированных на практику исследований, в том числе и в России. Анализируя современное развитие общества, можно говорить о том, что сложность социально-экономического взаимодействия неуклонно возрастает, что ведет к пропорциональному росту неопределенности в организационно-экономических и социально-экономических системах, способной повлиять на механизм реализации взаимодействия между субъектами систем. В свою очередь рост неопределенности, достигая некоторого критического уровня, может повлиять не только на механизм взаимодействия в системе, но и поставить вопрос о дальнейшем ее существовании как целостной структуры [29]. Данное рассуждение в значительной степени применимо и к системам логистики.
Показателем того, что факторы неопределенности и риска продолжают играть существенную роль при оценке эффективности сложных систем, является то, что за последние несколько десятилетий целый ряд работ именно в этой области был отмечен нобелевскими премиями (в том числе К. Эрроу, Г. Марковиц, У. Шарп, Дж. Акерлоф, Ф. Найт) [30].
Ввиду того, что степень неопределенности той среды, в которой современные предприятия осуществляют свою деятельность, имеет скорее тенденцию к росту, чем к снижению, интерес к подобным исследованиям выглядит вполне закономерным. Следовательно, потребность в создании и совершенствовании методик, позволяющих учесть и минимизировать риск и неопределенность в процессе управления проектами, также будет скорее всего возрастать.
Таблица 1.
Время выполнения работ исполнителями проекта
| Вероятность | Элементы матрицы T | |||||
|---|---|---|---|---|---|---|
| ${{t}_{{{\text{11}}}}}$ | ${{t}_{{{\text{12}}}}}$ | ${{t}_{{{\text{21}}}}}$ | ${{t}_{{{\text{22}}}}}$ | ${{t}_{{{\text{31}}}}}$ | ${{t}_{{{\text{32}}}}}$ | |
| 1/2 | 1.0 | 1.2 | 2.0 | 2.4 | 3 | 3.3 |
| 1/3 | 0.9 | 1.1 | 2.1 | 2.3 | 3.2 | 3.4 |
| 1/6 | 1.3 | 1.4 | 1.9 | 2.2 | 2.9 | 3.2 |
Список литературы
Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982.
Мищенко А.В., Халиков М.А. Распределение ограниченных ресурсов в задаче оптимизации производственной деятельности предприятия // Изв. АН СССР. Техн. кибернетика. 1991. № 6.
Мищенко А.В., Пилюгина А.В. Динамические модели управления научно-производственными системами // Вестн. МГТУ им. Баумана. Сер. Приборостроение. 2019. № 2.
Мищенко А.В., Сушков Б.Г. Задача оптимального распределения ресурсов на сетевой модели при линейных ограничениях на время выполнения работ // ЖВМ и МФ. 1980. Т. 10. № 5.
Мищенко А.В., Когаловский В.М. Проблемы устойчивости задач производственного планирования в машиностроении // Экономика и мат. методы. 1992. № 3.
Мищенко А.В. Устойчивость решений в задаче перераспределения транспортных средств в случае экстренного закрытия движения на участке метрополитена // Изв. АН СССР. Техн. кибернетика. 1990. № 3.
Мищенко А.В. Задача распределения транспортных средств по автобусным маршрутам при неточно заданной матрице корреспонденций пассажиропотока // Изв. АН СССР. Техн. кибернетика. 1992. № 2.
Катюхина О.А., Мищенко А.В. Динамические модели управления транспортными ресурсами на примере организации работы автобусного парка // Аудит и финансовый анализ. 2016. № 2. С. 156–167.
Косоруков Е.О., Фуругян М.Г. Некоторые алгоритмы распределения ресурсов в многопроцессорных системах // Вестн. МГУ. Сер. 15. Вычисл. математика и кибернетика. 2009. № 4. С. 34–37.
Фуругян М.Г. Планирование вычислений в многопроцессорных АСУ реального времени с дополнительным ресурсом // АиТ. 2015. № 3.
Косоруков Е.О., Фуругян М.Г. Алгоритмы распределения ресурсов в многопроцессорных системах с нефиксированными параметрами // Некоторые алгоритмы планирования вычислений и организации контроля в системах реального времени. М.: ВЦ РАН, 2011. С. 40–51.
Mironov A.A., Tsurkov V.I. Transport-type Problems with a Criterion // AиT. 1995. № 12. C. 109–118.
Миронов А.А., Цурков В.И. Наследственно-минимаксные матрицы в моделях транспортного типа // Изв. РАН. ТиСУ. 1998. № 6. С. 104–121.
Mironov A.A., Levkina T.A., Tsurkov V.I. Minimax Estimations of Expectates of Arc Weights in Integer Networks with Fixed Node Degrees // Applied and Computational Mathematics. 2009. T. 8. № 2. C. 216–226.
Mironov A.A., Tsurkov V.I. Class of Distribution Problems with Minimax Criterion // Doklady Akademii Nauk. 1994. V. 336. № 1. P. 35–38.
Tizik A.P., Tsurkov V.I. Iterative Functional Modification Method for Solving a Transportation Problem // Automation and Remote Control. 2012. V. 73. № 1. P. 134–143.
Mironov A.A., Tsurkov V.I. Hereditarily Minimax Matrices in Models of Transportation Type // J. Computer and Systems Sciences International. 1998. V. 37. № 6. P. 927–944.
Mironov A.A., Tsurkov V.I. Minimax in Transportation Models with Integral Constraints. 1 // J. Computer and Systems Sciences International. 2003. V. 42. № 4. P. 562–574.
Светлов Н.М., Светлова Г.Н. Информационные технологии управления проектами. М.: ФГОУ ВПО РГАУ–МСХА им. К.А. Тимирязева, 2007. С. 6.
Баркалов С.А., Воропаев В.И., Секлетова Г.И. и др. Математические основы управления проектами / Под ред. В.М. Буркова. М.: Высш. шк., 2005.
Мищенко А.В. Методы управления инвестициями в логических системах. М.: ИНФРА-М, 2009.
Секерина А.Б. Риск-менеджмент инвестиционного проекта / Под ред. Грачевой М.В. М.: Юнити-Дана, 2009.
Танаев В.С., Шкурба В.В. Введение в теорию расписаний. М.: Наука, 1975. 256 с.
Ильин Н.И., Лукманова И.Г., Немчин А.М., Никешин С.Н., Петрова С.Н., Романова К.Г., Шапиро В.Д. Управление проектами. СПб.: ДваТри, 1996. С. 187.
Разу М.Л., Якутин Ю.В., Разу Б.М., Бронникова Т.М., Титов С.А. Управление проектом: основы проектного управления / Под ред. М.Л. Разу. М.: Компания КноРус, 2006.
Иванов В.В., Ковалев В.В., Лялин В.А. Инвестиции. М.: ТК Велби, 2003.
Кузовлева И.А., Марченко Д.С. Управление рисками и неопределенностью при оценке эффективности девелоперского проекта // ФӘН-Наука. 2012. № 8. С. 26–28.
Россошанская О.В., Рач Д.В. Риск как категория компетентностного похода в управлении проектами // Управление проектами и развитие производства. 2009. № 2. С. 1–9.
Кузьмин Е.А. Неопределенность в экономике: понятия и положения // Вопросы управления. 2012. № 2. С. 80–92.
Евстратов Р.М. Неопределенность, вероятность, действие как главные составляющие предпринимательского риска // Основы экономики, управления и права. 2013. № 1. С. 58–61.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления